Extensive gene tree discordance and hemiplasy shaped the genomes of North American columnar cacti

Significance

Convergent and parallel evolution (homoplasy) is widespread in the tree of life and can obscure evidence about phylogenetic relationships. Homoplasy can be elevated in genomes because individual loci may have independent evolutionary histories different from the species history. We sequenced the genomes of five cacti, including the iconic saguaro of the Sonoran Desert and three other columnar cacti, to investigate whether previously uncharacterized features of genome evolution might explain long-standing challenges to understanding cactus phylogeny. We found that 60% of the amino acid sites in proteins exhibiting homoplasy do so because of conflicts between gene genealogies and species histories. This phenomenon, termed hemiplasy, is likely a consequence of the unusually long generation time of these cacti.

Abstract

Few clades of plants have proven as difficult to classify as cacti. One explanation may be an unusually high level of convergent and parallel evolution (homoplasy). To evaluate support for this phylogenetic hypothesis at the molecular level, we sequenced the genomes of four cacti in the especially problematic tribe Pachycereeae, which contains most of the large columnar cacti of Mexico and adjacent areas, including the iconic saguaro cactus (Carnegiea gigantea) of the Sonoran Desert. We assembled a high-coverage draft genome for saguaro and lower coverage genomes for three other genera of tribe Pachycereeae (Pachycereus, Lophocereus, and Stenocereus) and a more distant outgroup cactus, Pereskia. We used these to construct 4,436 orthologous gene alignments. Species tree inference consistently returned the same phylogeny, but gene tree discordance was high: 37% of gene trees having at least 90% bootstrap support conflicted with the species tree. Evidently, discordance is a product of long generation times and moderately large effective population sizes, leading to extensive incomplete lineage sorting (ILS). In the best supported gene trees, 58% of apparent homoplasy at amino sites in the species tree is due to gene tree-species tree discordance rather than parallel substitutions in the gene trees themselves, a phenomenon termed “hemiplasy.” The high rate of genomic hemiplasy may contribute to apparent parallelisms in phenotypic traits, which could confound understanding of species relationships and character evolution in cacti.

Cactaceae have undergone adaptive radiation on a continental scale in the Americas. Occurring from arid deserts to alpine steppes and tropical forests, they exhibit a remarkable diversity of growth forms, ranging from tiny, nearly subterranean “buttons” to giant columnar or candelabra forms, epiphytes, and leafy shrubs (1). Classification of the family’s 1,438 species (2) has been unusually fraught, with taxonomic treatments recognizing anywhere from 20 to 233 genera (1–4), and classification above the genus level being equally problematic (1, 5). In part this has been attributed to homoplasy (ref. 1, p. 18 and ref. 6, p. 45), the independent evolutionary origin of the same trait (7). For example, early taxonomists combined the giant columnar cacti of North and South America into one large genus Cereus Mill (3). Later split into numerous smaller genera, this association was sometimes maintained at a suprageneric rank (8), but molecular phylogenies clearly show North and South American Cereus are separate clades (6, 9).

Frequent convergence in growth habit may reflect design limitation (10) of the relatively simple cactus body plan of stem succulence, simplified branching, and loss or reduction of leaves (9) (ref. 11, p. 536). In cacti, convergent simplification via paedomorphosis (12), along with parallelisms among close relatives, has also obscured phylogeny (13, 14). This may help explain the finding that <50% of (nonmonotypic) cactus genera are monophyletic (15). Taxonomic impediments take on special significance in cacti because of the unusually high fraction of species of conservation concern (31% estimated in ref. 16). Despite its potential significance, homoplasy has been quantified in cacti for only a small number of phenotypic traits (14, 17). Here, we focus on the genomes of cacti and assess the degree to which apparent homoplasy among these species is elevated due to discordance between gene trees and the species tree.

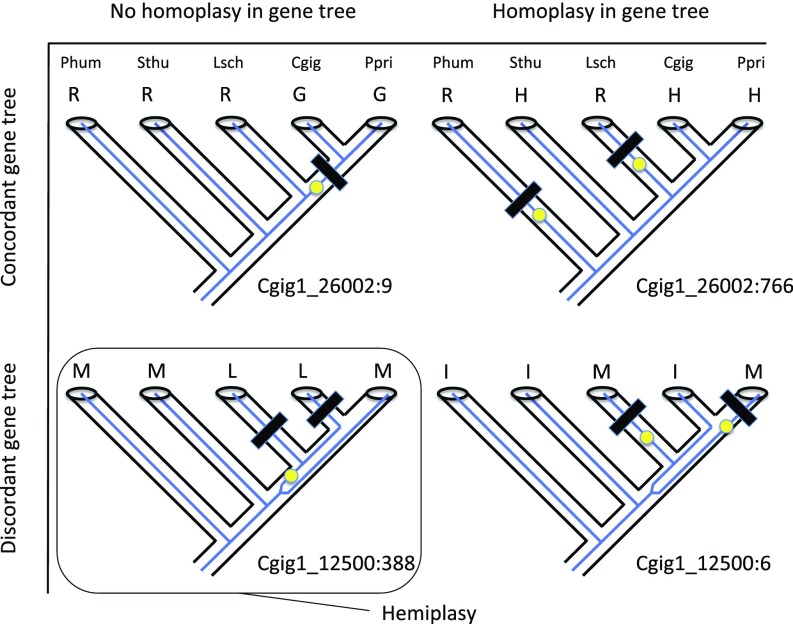
An important but recently recognized contributor to molecular homoplasy is “hemiplasy” (18, 19), originally defined as the apparent multiple origin of a character state on the inferred species tree arising when an inferred gene tree (with no homoplasy) is discordant with that species tree (18–21) (Fig. 1). A slight generalization of this definition is needed to account for characters with homoplasy on both trees (Fig. 1, Lower Right): A character (site) exhibits hemiplasy if the inferred number of character state changes on the species tree is strictly greater than on the gene tree, which occurs only if the two trees are discordant (Materials and Methods).

Fig. 1.

Hemiplasy in amino acid alignments of cacti (genes annotated as Cgig1_gene##:site ##). Hemiplasy occurs when the inferred number of state changes of a trait is greater on the species tree than on the gene tree, which happens only if the two trees are discordant. Gene trees in blue are imbedded in black species trees. Yellow dot is the position of a state change inferred for an amino acid site for this gene tree. Black rectangles are locations where state changes would be inferred on the species tree (alternative equally optimal reconstructions are possible but the number of state changes is the same). Amino acids are indicated at leaf nodes. Three trees have the same number of state changes on species and gene trees, but at Lower Left a homology (one change) on the gene tree is seen as homoplasy (two changes) on the species tree because of discordance (i.e., hemiplasy). Cgig, C. gigantea; Lsch, L. schottii; Phum, P humboldtii; Ppri, P. pringlei; Sthu, S. thurberi.

Genome scale datasets revealed high levels of gene tree discordance (20, 22–24), which suggests a potentially important role for hemiplasy as a contributor to overall molecular homoplasy. Discordance can arise because of incomplete lineage sorting (ILS) and gene flow, which depend, in turn, on demographic factors at the population level, phylogenetic history, divergence times, mutation rate, generation time, and the timing and taxa involved in introgression or hybridization (25). It can also arise from gene duplication and loss (26).

The cactus tribe Pachycereeae is a model for taxonomic and phylogenetic complexities in cacti (27, 28). Its ∼70 species, including most of the columnar cacti of Mexico and adjacent regions, have been dispersed among 6–23 genera in various taxonomic treatments (1, 5, 27). Despite early molecular support for its monophyly (11), broadly sampled recent molecular studies have led to abandonment of the tribe (9, 13, 15), or to recasting it with the informal name, “core Pachycereeae” (6). Notably, homoplasy in vegetative and floral traits has been cited as a factor contributing to its difficult taxonomic history (ref. 28, p. 1086 and ref. 29, p. 556).

To sample widely in Pachycereeae, we sequenced the genomes of four representatives of the two subtribes of Pachycereeae recognized in Gibson and Horak (30) (Table S1) and some earlier treatments. This included the iconic saguaro cactus of the Sonoran Desert (Carnegiea gigantea) to serve as a high-coverage reference assembly, and Pachycereus pringlei (cardón, sahueso), Lophocereus schottii (senita), and Stenocereus thurberi (organ pipe, pitaya), also of the Sonoran Desert, to lower coverage. Pereskia humboldtii, a leafy, Andean cactus, was included as an outgroup (31).

Table S1.

Sample, voucher, and sequence library information for taxa in this paper

Species (Classification*)	Accession and voucher number	Genome size (1C, Gb)†	Sample	Avg. insert size, bp	Seq. format, bp	Read pairs, M	Total size, Gb	Genome coverage, x	NCBI accession no.
C. gigantea (Engelm.) Britton & Rose (Cactoideae/Pachycereeae/Pachycereinae)	Sanderson et al. SGP3 (ARIZ 422853); SGP5 (ARIZ 422854)	1.403	Cgig-PE1	180	2 × 100	150.5	30.1	21.5	SRR5036292
			Cgig-PE2	280	2 × 100	359.1	71.7	51.1	SRR5036295 and SRR5036296
			Cgig-PE3	660	2 × 300	16.6	9.3	6.2	SRR5036293
			Cgig-MP	2,450	2 × 100	133.3	26.6	18.9	SRR5036294
			Total C. gigantea			659.5	137.7	97.7
P. pringlei (S. Watson) Britton & Rose (Cactoideae/Pachycereeae/Pachycereinae)	1978–0232-01 (DES00082012)	nd	Ppri-PE1	377	2 × 150	97.3	28.7	20.4	SRR5137214
L. schottii (Engelm.) Britton & Rose (Cactoideae/Pachycereeae/Pachycereinae)	1979–0344-0101 (DES00082011)	nd	Lsch-PE1	378	2 × 150	120.8	35.7	24.2	SRR5137211
S. thurberi (Engelm.) Buxb. (Cactoideae/Pachycereeae/Stenocereinae)	1939–0076-21–2 (DES00082014)	1.682	Sthu-PE1	355	2 × 150	120.1	35.4	24.9	SRR5137213
P. humboldtii Britton & Rose (Pereskioideae)	1997–0428-01–4 (DES00082013)	nd	Phum-PE1	351	2 × 150	60.7	16.9	17.2	SRR5137212

^*Ref. 5.

^†Kew C-value database (32); nd = not available.

Results and Discussion

The assembly of saguaro’s 1.4-Gb genome (32) from short read libraries (Table S1) spanned 980 Mb, with a scaffold N50 of 61.5 kb (Table S2). Transcriptomes were also assembled (Table S3) and used with other evidence to annotate the saguaro genome. The saguaro genome contains 28,292 protein coding genes; 58% of the assembly consists of transposable elements and retroviral and repeated sequences (Tables S2 and S4). Assemblies from single libraries of the other four cacti were more fragmented (Table S5).

Table S2.

C. gigantea (SGP5) assembly metrics (percent of assembled genome included where appropriate)

Feature	Value
Estimated genome size (k = 17), Mb	1,302
Assembly size, Mb	980.3
Number of contigs	107,828
Longest contig, kb	351.9
Mean contig length, kb	8.9
Contig N50, kb	20.4
Contig L50	12,608
Number of scaffolds	57,409
Longest scaffold, kb	648.6
Mean scaffold length, kb	17.1
Scaffold N50, kb	61.5
Scaffold L50	4,575
Bases called as “N”, %	1.93
CEGMA: Complete, %	75.81
Partial, %	93.15
BUSCO: Complete, %	91.00
Complete duplicate, %	26.00
Fragmented, %	3.60
Missing, %	5.40
Number of genes	28,292
Gene space, Mb (%)	137.2 (14.27)
Average gene size, kb	4.8
Exon space, Mb (%)	37 (3.85)
Average number of exons	5.35
Average exon size, bp	245
Intron space, Mb (%)	100.1 (10.42)
Average intron size, bp	814
Repeats and TE space, Mb (%)	554.4 (57.67)
Noncoding RNAs, kb (%)	541.5 (0.06)
Uncharacterized genome, Mb (%)	269.3 (28.01)

Table S3.

Saguaro transcriptome sequence and assembly results

Tissue	Areoles	Chlorenchyma	Young Roots	Seedlings 5 d	Seedlings 2 mo
Origin/genotype	SGP3	SGP3	SGP3	SGP5 seeds	SGP5 seeds
Sequencing platform	HiSeq	HiSeq	HiSeq	NextSeq	NextSeq
NCBI accession no.	SRR5134694	SRR5134692	SRR5134696	SRR5134695	SRR5134693
Read length, bp	2 × 100	2 × 100	2 × 100	2 × 150	2 × 150
No. of clean pairs, million	62.05	38.6	73.8	119.2	100.3
Average read length, bp	86	90	87	148	149
No. of contigs	46,726	109,410	119,712	331,375	367,762
Total size of contigs, bp	15,820,142	51,020,459	47,269,566	159,844,813	217,297,329
Longest contig, bp	4,257	11,204	7,025	21,524	31,586
Mean contig size, bp	339	466	395	482	591
Median contig size, bp	282	357	311	376	421
N50 contig length, bp	339	540	424	556	762
L50 contig count	15,501	29,310	35,016	90,261	85,805
BUSCO gene models
Complete single-copy no., %	22 (2.8)	183 (19)	80 (8.3)	157 (16)	200 (21)
Complete duplicated no., %	5 (0.5)	168 (17)	60 (6.2)	240 (25)	360 (37)
Fragmented no., %	149 (15)	375 (39)	313 (32)	395 (41)	305 (31)
Missing no., %	780 (81)	230 (24)	503 (52)	164 (17)	91 (9.5)

Table S4.

Repeat annotation of the saguaro genome

Repeat type	Occupied space, kb	No. of repeats	Percentage of repeats	Percentage of genome
Class I (Retrotransposons)
LTR
Copia	60,406.8	47,473	10.90	6.28
Gypsy	216,478.9	154,332	39.05	22.52
Retrovirus	45,424.7	49,813	8.19	4.72
Other LTR	1,466.7	17,130	0.26	0.15
LINE
L1	26,205.8	28,239	4.73	2.73
RTE	14,199.5	18,489	2.56	1.48
Other LINE	10.7	297	0.00	0.01
SINE	4.8	38	0.01	0.01
Other Class I	1,417.2	6,755	0.26	0.15
Class II (DNAt) subclass 1
TIR
Tc1–Mariner	379.7	775	0.07	0.04
hAT	5,959.0	12,698	1.07	0.62
Mutator	5,891.7	10,024	1.06	0.61
PIF–Harbinger	5,912.3	12,556	1.07	0.61
CACTA	13,678.6	14,117	2.47	1.42
Other DNAt	93.4	1,241	0.02	0.01
Class II (DNAt) subclass 2
Helitron	4,765.2	5,768	0.86	0.50
Other Class II	11.9	199	0.01	0.01
Total TEs	402,306.9	379,944	72.57	41.85
Ribosomal DNA	47.3	78	0.01	0.01
Structural repeats	11,566.1	219,361	2.09	1.20
Unclassified	140,488.6	301,355	25.34	14.61
Total repeats	554,408.9	900,738		57.67

Table S5.

Comparison of assembly results for five cacti in this study

Species	C. gigantea	P. pringlei	L. schottii	S. thurberi	P. humboldtii
Flow cytometry est. genome size (Mb, Kew Database)	1,403	—	—	1,682	—
In silico estimated genome size, Mb	1,303	1,410	1,474	1,420	980
Meraculous k-mer value	69	37	55	57	41
No. of scaffolds	57,409	171,584	158,705	159,478	126,352
Total size of scaffolds, bp	980,358,000	629,656,250	797,927,173	853,349,426	414,047,441
Longest scaffold, bp	648,566	68,912	148,470	151,404	58,930
Shortest scaffold, bp	1,000	200	200	200	201
No of contigs > 1 kb	57,378	165,982	155,005	156,573	124,110
Percentage of contigs > 1 kb	100	96.7	97.7	98.2	98.2
No. of contigs > 10 kb	17,976	10,469	19,671	21,527	4,154
Percentage of contigs > 10 kb	31.3	6.1	12.4	13.5	3.3
No. of contigs > 100 kb	1,893	0	11	20	0
Percentage of contigs > 100 kb	3.3	0.0	0.0	0.0	0.0
Mean scaffold size, bp	17,077	3,670	5,028	5,351	3,277
Median scaffold size, bp	3,368	2,347	2,559	2,575	2,338
N50 scaffold length, bp	61,546	5,411	9,302	10,456	4,395
L50 scaffold count	4,575	32,562	21,671	20,352	28,266
scaffold %A	31.06	30.71	31.26	31.34	31.43
scaffold %C	18.08	17.32	17.99	18	17.69
scaffold %G	18.05	17.15	17.86	17.86	17.48
scaffold %T	30.87	29.73	30.49	30.59	30.38
scaffold %N	1.93	5.09	2.39	2.21	3.01
Percentage of assembly in scaffolded contigs	76.0	65.3	66.3	76.3	67.5
Percentage of assembly in unscaffolded contigs	24.0	34.7	33.7	23.7	32.5
Average number of contigs per scaffold	1.9	1.9	1.9	2.2	2.1
Average length of break (>25 Ns) between contigs in scaffold	374.1	194.6	128.9	83.4	81.7
No. of contigs	107,828	333,727	300,317	358,224	261,756
No. of contigs in scaffolds	67,765	247,789	210,664	277,545	198,246
No. of contigs not in scaffolds	40,063	85,938	89,653	80,679	63,510
Total size of contigs, bp	961,496,166	598,104,997	779,678,560	836,766,707	402,983,040
Longest contig, bp	351,939	46,681	81,565	62,746	19,699
No. of contigs > 1 kb	98,083	192,939	201,546	230,699	156,032
Percentage of contigs > 1 kb	91	57.8	67.1	64.4	59.6
No. of contigs > 10 kb	28,004	4,039	12,663	10,821	383
Percentage of contigs > 10 kb	26	1.2	4.2	3	0.1
No. of contigs > 100 kb	216	0	0	0	0
Percentage of contigs > 100 kb	0.2	0.0	0.0	0.0	0.0
Mean contig size, bp	8,917	1,792	2,596	2,336	1,540
Median contig size, bp	3,904	1,172	1,423	1,361	1,191
N50 contig length, bp	20,427	3,174	5,046	4,402	2,335
L50 contig count	12,608	52,530	40,107	52,163	53,282
BUSCO gene models
Complete Single-copy no., %	870 (91)	592 (61)	714 (74)	688 (71)	503 (52)
Complete Duplicated no., %	253 (26)	172 (17)	217 (22)	197 (20)	128 (13)
Fragmented no., %	35 (3.6)	198 (20)	128 (13)	148 (15)	262 (27)
Missing no., %	51 (5.3)	166 (17)	114 (11)	120 (12)	191 (19)
NCBI accession no.	NCQR00000000	NCQS00000000	NCQV00000000	NCQT00000000	NCQU00000000

The high completeness of the gene space in the saguaro assembly (Table S2) let us construct 4,436 alignments of orthologous genes across the five cacti, each of which contained two or more exons for all five taxa, and contiguous introns. Based on gene tree confidence levels estimated from alignments containing all nucleotide positions, sets of alignments differing in phylogenetic robustness (“gene confidence sets”) were compiled for downstream analyses. For example, the 90% gene confidence set comprised 458 genes, with gene trees having maximum likelihood bootstrap support value above 90% for all clades (Table 1). These gene sets provide a control for the effect of weakly supported gene trees on gene tree discordance estimates (33).

Table 1.

Gene tree discordance relative to the Pachycereeae species tree (Fig. 2B)

Gene confidence set	90% set	80% set	70% set	60% set	50% set
N genes	458	786	1,065	1,668	2,291
Gene tree concordance, %*
Edge A†	76	75	74	68	65
Edge B	77	75	75	73	70
Whole tree	63	61	58	52	47
MP-EST edge length‡
Edge A	1.01	0.96	0.94	0.78	0.69
Edge B	1.22	1.21	1.15	1.04	0.93
BPP edge length§
All partition
Edge A	1.23	1.14	1.09	0.95	0.88
Edge B	1.22	1.22	1.18	1.14	1.10
Neutral partition
Edge A	1.24	1.16	1.09	0.97	0.89
Edge B	1.28	1.29	1.24	1.21	1.18
Third partition
Edge A	1.22	1.11	1.08	0.95	0.87
Edge B	1.32	1.34	1.24	1.18	1.12

^*Agreement of gene tree edge bipartitions or entire gene tree with species tree.

^†See Fig. 2B for location of edges.

^‡In coalescent time units. 1 CTU = 2N_e generations.

^§In CTUs estimated from 2D/θ, where D and θ are sequence divergence-scaled edge length and scaled effective population size, respectively, taken from BPP output.

The most robust 90% gene confidence set implies levels of gene tree discordance between Pachycereeae genera (Fig. 2A) comparable to those seen in closely related short-lived angiosperm genera such as Solanum sect. Lycopersicon [time scale of 2 million years (MYR); ref. 24] and the Oryza AA genome clade (2.5 MYR: ref. 22). Species trees constructed using both gene tree-based (MP-EST; ref. 34) and alignment-based methods (BPP; ref. 35) were the same for all gene tree confidence sets and for three different partitioning schemes for the alignments by codon position and intron (Materials and Methods and Fig. 2B). An exhaustive search of tree space indicated a single optimal species tree under the MP-EST pseudolikelihood criterion, and three replicate runs of each MCMC chain in BPP from random starting trees generated this same species tree for all five gene confidence sets, indicating convergence. This optimal tree agreed with previous molecular phylogenetic analyses of mostly plastid genes (6, 28, 29). In the 80% and 90% gene confidence sets, 61% and 63% of gene trees, respectively, agreed with the species tree (Table 1). Estimates of species tree edge lengths for these gene confidence sets in BPP ranged from 1.11 to 1.24 for edge A and from 1.22 to 1.34 for edge B, in “coalescent time units” (= T/2N_e, where T is measured in generations), depending on data partition, with slightly lower values estimated by MP-EST (Table 1).

Fig. 2.

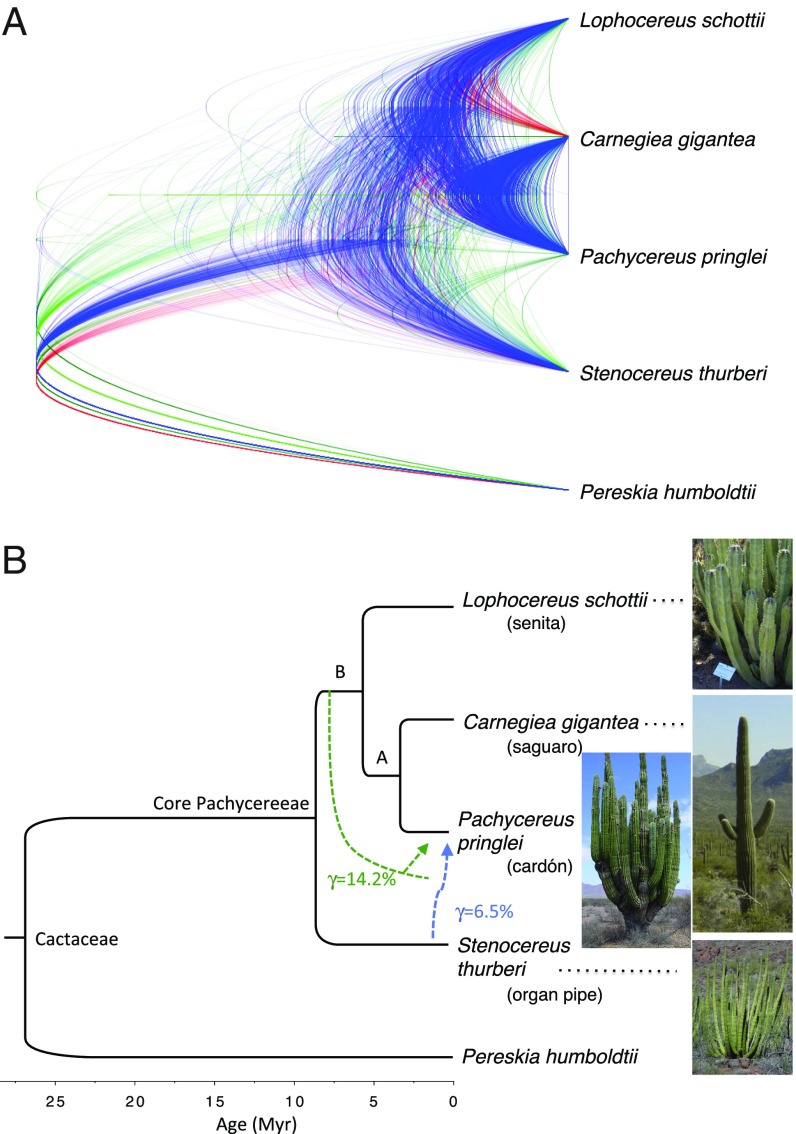
(A) Topological discordance in the 90% gene confidence set of 458 gene trees visualized in DensiTree (78). Blue trees are the most frequent, followed by red and shades of green. (B) Species tree inferred with BPP and MP-EST, which was the same for all gene sets, with divergence times estimated using the Neutral partition. Blue dashed line indicates reticulation, having inferred inheritance probability, γ, on the optimal PhyloNet analysis of the same set of gene trees. Green dashed line indicates position of reticulation on the next best inferred network (Fig. S1). The origin of this reticulation edge earlier than its endpoint implies the existence of an extinct or unsampled taxon.

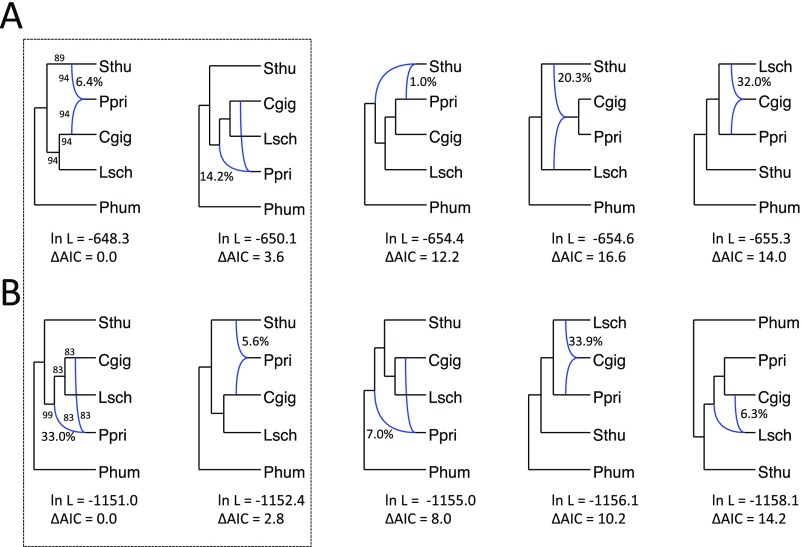
Introgression may also contribute to gene tree discordance. Network reconstruction allowing both ILS and gene flow in PhyloNet (36) indicated substantial support for a network model with one reticulation vs. a tree model (ΔAIC = 17.0 and 28.6 for the 90% and 80% gene sets, respectively; ref. 37), implicating introgression into P. pringlei from either S. thurberi or some more closely related but unsampled or extinct taxon (Fig. 2B and Fig. S1). The best two networks were the same in both gene confidence sets (although the ranking reversed; Fig. S1). Moreover, the “major tree” within these networks (Materials and Methods) was the same as that inferred by species tree methods, and the inheritance probability estimate from the 90% gene confidence set, which indicates the level of introgression, was low (6.5% and 14.2% for the optimal and next best networks in the 90% gene confidence set; although higher in one of the two networks from the 80% gene set). The two optimal networks were consistently recovered in multiple searches from different starting networks, and in each gene set, the two results were substantially better than other suboptimal networks (Fig. S1).

Fig. S1.

PhyloNet (36) network reconstructions for the 90% (A) and 80% (B) gene confidence sets. Likelihood scores decrease from left to right. AIC scores are relative to the optimal networks at Left. Branch lengths are not scaled to sequence divergence, but the lesser of the two inheritance probabilities for reticulation edges is given next to edge in the format ##.#%. Parametric bootstrap probabilities are given next to edges for top scoring networks in A and B, as percentages in the format ##. The dotted box encloses the two best networks in each gene confidence set, and these are the same in A and B, but in reverse ranking. The remaining networks have substantially worse AIC scores relative to the optimal networks in each row.

Intergeneric hybrids are well known in cacti (1, 5), including rare hybrids between P. pringlei and Bergerocactus emoryi in Baja California in a narrow zone where the two species are sympatric (1, 38). Bergerocactus (not sampled here) is more closely related to Carnegiea, Lophocereus, and Pachycereus than to Stenocereus in the most complete cactus phylogeny to date (6). P. pringlei is possibly a recent autotetraploid (39), so postzygotic inviability and sterility barriers (40) would have had to have been overcome if the introgression took place following tetraploidy.

Owing to the limited level of introgression, we inferred demographic history using BPP assuming that ILS is the primary cause of discordance. The neutral mutation rate was estimated from the substitution rate in the “neutral” partition of the alignments (Table S6) assuming a root age of the tree at 26.88 MYR (Materials and Methods). Estimates ranged from μ_G = 5.98 to 6.07 × 10⁻⁸ per site for each generation across the five gene confidence sets. An alternative estimate based on pairwise synonymous K_s distances in CDS regions between Carnegiea and Pereskia from all 4,426 alignments was somewhat higher at μ_G = 8.75 × 10⁻⁸ per site per generation (Table S7). Per year rates are comparable to several angiosperm tree species (41–43), but generation times in the cacti, ranging from 20 to 75 y (44–47), are 2–12 times longer. The BPP estimates of scaled mutation rate (θ = 4 N_eμ_G), imply an N_e of 24,000–39,000 and 31,000–36,000 for edges A and B, respectively, over the 15 gene sets and partitions (Table S6). Combining the BPP estimates of θ with the pairwise K_s estimate of mutation rate produces ancestral N_e of ∼2/3 the BPP estimates. These ancestral N_e values are higher than estimates of recent N_e for some perennial angiosperms [Populus trichocarpa: ∼4,000−6,000 (48); Eucalyptus grandis: ∼11,000 (41); Amborella trichopoda: 5,000 (49)] but comparable to Populus balsamifera (44,000−59,000; ref. 50); and much less than Pinus taeda (560,000; ref. 51).

Table S6.

Demographic inference based on BPP analysis

			Edge A				Edge B				Divergence times*,†
Gene confidence set	Partition	Mutation rate/gen (×10−8)*,‡	Time, Myr	Time, Gen‡	θ	Ne	Time, Myr	Time, Gen‡	θ	Ne	τ1, Myr	τ2, Myr	τ3, Myr
90%	All	4.55	2.43	69,300	0.00512	28,200	2.98	85,100	0.00632	34,700	3.57 ± 0.19 (3.46)	6.00 ± 0.18 (5.40)	8.98 ± 0.22 (8.39)
	Neutral	6.01	2.35	67,100	0.00652	27,200	2.95	84,200	0.00788	32,800	3.36 ± 0.19	5.71 ± 0.18	8.66 ± 0.23
	Third	5.63	2.06	58,800	0.00544	24,200	2.84	81,100	0.00689	30,600	3.45 ± 0.33	5.51 ± 0.29	8.35 ± 0.33
80%	All	4.42	2.33	66,500	0.00518	29,300	2.96	84,700	0.00617	34,800	3.74 ± 0.16	6.07 ± 0.14	9.03 ± 0.18
	Neutral	5.98	2.22	63,500	0.00658	27,500	2.94	84,000	0.00781	32,600	3.54 ± 0.16	5.76 ± 0.15	8.70 ± 0.18
	Third	5.61	1.95	55,700	0.00560	25,000	3.02	86,300	0.00720	32,100	3.55 ± 0.28	5.50 ± 0.24	8.52 ± 0.28
70%	All	4.40	2.35	67,200	0.00545	30,900	2.94	84,000	0.00625	35,500	3.77 ± 0.15	6.13 ± 0.13	9.07 ± 0.16
	Neutral	6.04	2.25	64,300	0.00712	29,400	2.92	83,600	0.00817	33,800	3.60 ± 0.15	5.87 ± 0.12	8.65 ± 0.15
	Third	5.73	1.94	55,400	0.00586	25,500	2.84	81,000	0.00749	32,600	3.57 ± 0.26	5.51 ± 0.21	8.35 ± 0.24
60%	All	4.23	2.34	66,800	0.00593	35,000	2.82	80,700	0.00596	35,300	3.86 ± 0.14	6.20 ± 0.11	9.03 ± 0.13
	Neutral	6.07	2.27	65,000	0.00814	33,500	2.78	79,400	0.00796	32,800	3.61 ± 0.14	5.91 ± 0.10	8.53 ± 0.13
	Third	5.84	1.89	54,000	0.00661	28,300	2.75	78,600	0.00777	33,300	3.67 ± 0.23	5.56 ± 0.18	8.31 ± 0.20
50%	All	4.13	2.38	67,900	0.00641	38,700	2.65	75,600	0.00567	34,300	3.92 ± 0.13	6.29 ± 0.10	8.94 ± 0.12
	Neutral	6.07	2.30	65,800	0.00903	37,200	2.62	74,900	0.00772	31,800	3.61 ± 0.14	5.91 ± 0.10	8.53 ± 0.13
	Third	5.89	1.91	54,500	0.00736	31,300	2.62	74,900	0.00786	33,400	3.62 ± 0.21	5.53 ± 0.16	8.15 ± 0.17

^*Based on 26.88 Myr crown clade age. Node times refer to nodes as follows: τ₁ = (Cgig,Ppri); τ₂ = ((Cgig,Ppri),Lsch); τ₃ = ((Cgig,Ppri),Lsch),Sthu.

^†Plus or minus two SDs of the posterior distribution. Values in brackets for the 90% All partition are means of nine 50-gene independent runs in BEAST 2 using the uncorrelated relaxed clock model (SI Materials and Methods).

^‡Based on 35-y generation time.

Table S7.

Neutral mutation (substitution) rate analyses across cacti

Comparison	Carnegiea–Pereskia
N orthologs	4436
Sequence length, nt (mean ± SD)	786 ± 592 nt
Ka (mean ± SD)	0.0331 ± 0.0220 per site
Ks (mean ± SD)	0.1342 ± 0.0693 per site
Divergence time, t, and range*	26.88 × 106 y (16.67–37.1)
Estimated synonymous rate (=Ks/2t)	2.50 × 10−9 per site/y (1.81–4.02)†
Estimated mutation rate (generation time @ 35 y)	8.75 × 10−8 per site/generation (6.33–14.0)†

^*From time-calibrated tree of Hernández-Hernández et al. (81). Ranges are 95% Bayesian credibility intervals from that paper.

^†Ranges based on divergence time credibility intervals.

The probability that a rooted gene tree with three taxa disagrees with the species tree that contains it is 2/3 e^−T/2Ne, where T is the time in generations along the internal edge of the tree (52). This can be high if T is small, either because divergence time in years is small or generation time is large. Thus, the level of gene tree discordance we inferred in columnar cacti having N_e of 25–40,000, along edges with a duration of 2–3 million years would be far too high were it not for the long generation times of these plants, similar to findings in long-lived conifers (53).

Gene tree discordance has a strong impact on the distribution of protein sequence variation among these genera of cacti in generating hemiplasy. Taking the 80% and 90% gene confidence sets as samples of potentially phenotypically relevant amino acid sequence variation across these genomes, we partitioned the homoplastic amino acid sites in genes on the species tree into three parts: the fraction arising from homoplasy on concordant gene trees (Fig. 1, Upper Right), the fraction arising solely from gene trees with less homoplasy than the species tree but that are discordant with the species tree (hemiplasy: Fig. 1, Lower Left), and the small fraction that arises from homoplasy on discordant gene trees that is equally homoplastic on the species tree (which as yet has no term defined: Fig. 1, Lower Right). Hemiplasy accounts for 58–63% of all apparent homoplasy (Table 2).

Table 2.

Homoplasy and hemiplasy in amino acid alignments of genes

Gene confidence set	90% set	80% set
Concordant gene trees
Variable sites	11,641	17,349
Informative sites	1,091	1,549
Homoplastic sites*	154 (27.8%)†	234 (31.0%)†
Discordant gene trees
Variable sites	6,810	11,572
Informative sites	703	1,102
Homoplastic sites–not hemiplastic‡	79 (14.2%)†	46 (6.1%)†
Homoplastic sites–hemiplastic§	320 (57.9%)†	474 (62.9%)†
Total homoplastic sites on species tree	553	754

^*See Fig. 1, Upper Right.

^†% = percent of all homoplastic sites.

^‡Fig. 1, Lower Right.

^§Fig. 1, Lower Left.

As examples, consider two genes from the 90% gene confidence set having strongly discordant gene trees. Both play potential roles in the physiological adaptation of cacti to arid environments. The saguaro nuclear gene annotated as a chloroplastic NADP-dependent malate dehydrogenase (MDH: Cgig1_18427) is the only 1 of 11 MDH isoforms in the saguaro annotation that is NADP-dependent. It catalyzes the reduction of oxaloacetate to malate in the chloroplast (54) and appears to participate in the fixation of carbon dioxide under both light and dark conditions (55). Together with the cytosolic NAD-dependent MDH, these two isoforms may be primarily responsible for malate formation during dark CO₂ fixation in crassulacean acid metabolism (CAM) plants (56). The MDH gene tree has a single replacement of an ancestral serine with an alanine, but the gene tree is discordant with the species tree, making the alanines appear to have evolved twice on the species tree, when they are in fact hemiplastic.

The gene annotated as a DNAJ JJJ1 homolog (Cgig1_00352) contains a DNAJ domain involved in heat shock protein interactions. Columnar cacti must be able to tolerate internal tissue temperatures that can exceed 50 °C in the summer (5). The gene tree is discordant with the species tree, and 19 of its 20 potentially informative amino acid replacements exhibit homoplasy on the species tree, but only one does on the gene tree, meaning 18 sites are hemiplastic. A search of the National Center for Biotechnology Information (NCBI) CDD database (57) shows that two of these hemiplastic sites are in the conserved DNAJ domain proper, although neither involves known HSP70 interaction sites.

Hemiplasy is not restricted to the coding sequence in this gene. The phylogeny of the 1,000 bp upstream of the start codon, which often contains proximal conserved regulatory elements in plants (58), is the same discordant tree as is found for the coding region. Of 22 potentially informative nucleotide sites there, 21 are homoplastic on the species tree, whereas only two are on the gene tree. Most homoplasy in this noncoding region on the species tree is thus also due to hemiplasy. All of these cases suggest caution in viewing multiple origins of the same amino acid or nucleotide in a species tree as possible evidence of convergent evolution (18).

These conclusions depend on the robustness of various model assumptions. The extent of gene tree discordance and hemiplasy was estimated from gene tree topologies inferred with an HKY substitution model in PAUP*. Estimates of tree topology are generally more robust than estimates of rates, especially at low sequence divergences (59–61), where simple models sometimes even outperform more general ones (62). Mean pairwise nonsynonymous and synonymous distances between the most divergent Pachycereeae were only 1.3% and 4.1% respectively, and about one-half of the 4,436 sequence alignments had bootstrap values below 50%, a consequence of low sequence divergence and short length. Substitution model therefore likely had little impact on estimates of the prevalence of discordance and hemiplasy.

However, our explanation for these levels of hemiplasy in terms of generation time rests on estimates of divergence times and N_e obtained from BPP, which adds the assumptions of panmixia within and no gene flow between species, constant population sizes within tree edges, and no linkage (61). To examine the impact of BPP’s Jukes–Cantor clock model on its estimates of divergence times and effective population sizes, we evaluated more general models with subsets of the data using BEAST (63), finding that the parameter effect sizes were small (SI Materials and Methods and Table S8). Other assumptions were more difficult to test. Panmixia will not be strictly true even for outcrossing columnar cacti, but gene flow is likely high within three of the four Pachycereeae that are bat pollinated (e.g., S. thurberi; ref. 64). We did find limited gene flow between species in PhyloNet analyses, and this can lead to overestimates of population sizes and underestimates of divergence times when using the multispecies coalescent approach (65), but because the rates of ILS correlate with the product of population size and time, these biases potentially counteract each other. However, it is unlikely that population sizes have remained constant within species tree edges. Paleoclimatic and packrat midden evidence document the ebb and flow of Sonoran Desert plant communities during Pleistocene glacial and interglacial periods (66). BPP’s divergence time estimates are biased toward the recent in “more extreme bottleneck scenarios” of population history (67), but shorter edge durations in Pachycereeae would tend to make the observed level of ILS even higher than estimated. Finally, linkage is unlikely to be problematic. Our 80% gene confidence set has an average of 1.8 Mb between genes. Linkage disequilibrium in long-lived, outcrossing angiosperms typically decays in distances from a few kb to 50 kb (41, 48).

Table S8.

Effect of model choice on parameter estimates in nine samples of 50 genes from 90% gene confidence set, assayed in BEAST 2 (63)

Node	(Cgig,Ppri)	((Cgig,Ppri),Lsch)	((Cgig,Ppri),Lsch),Sthu)
JC/HKY
Population size	0.0506 (2.8%)	0.7464 (0.4%)	0.1042 (1.2%)
Divergence time	0.0927 (0.1%)	0.9758 (0.0%)	0.5113 (0.1%)
Clock/UCLN
Population size	0.0458* (10.6%)	0.0406* (5.5%)	0.1516 (4.5%)
Divergence time	0.4262 (0.3%)	0.1473 (3.4%)	0.0547 (0.7%)

Each cell reports P value (effect size in parentheses) in paired t tests. P < 0.05 indicated by asterisk.

The phylogenomic history of saguaro and its relatives exhibits extensive gene tree discordance due to ILS and low rates of introgression. Comparable findings have been seen in rapid and/or very recent radiations (20, 22, 24), but in Pachycereeae, ILS acts at long time scales, between taxonomically divergent genera with very long generation times. A consequence of this discordance is elevated levels of apparent homoplasy in the species tree. The connection between apparent genomic homoplasy arising from ILS and apparent phenotypic homoplasy is probably strongest for traits with a simple genetic architecture (18), such as those involving the function or regulation of a single enzyme (21, 68). In plants, enzymes in biosynthetic pathways for floral pigments or defensive compounds are good candidates (69, 70). Notably, the taxonomic distribution of alkaloids, triterpenes, and sterols have played a role in the systematics of Pachycereeae (30). When hemiplasy arises because of introgression, genetic architecture may be less of an issue because multiple loci may undergo gene flow almost simultaneously (18). In plants, even complex traits with multiple components and fitness effects have been adaptively introgressed (71). Collectively, this body of evidence lends plausibility to the hypothesis that the phenotypic effects of genomic hemiplasy may have exacerbated the long-standing problem of inferring relationships in these charismatic cacti.

SI Materials and Methods

Sampling and Genome Sequencing.

Fresh material was obtained from an individual C. gigantea (Engelm.) Britton & Rose (“SGP5”) growing at the Tumamoc Hill Reserve in Tucson, AZ, and from a second plant purchased at a Tucson nursery (“SGP3”). Fresh material of L. schottii (Engelm.) Britton & Rose [=Pachycereus schottii (Engelm.) D. R. Hunt], P. pringlei (S. Watson) Britton & Rose, P. humboldtii Britton & Rose (=P. horrida DC), and S. thurberi (Engelm.) Buxb. were obtained from cultivated individual plants at the Desert Botanical Garden (Table S1). Genomic DNAs were extracted using a modified cetyltrimethylammonium bromide (CTAB) method (64).

For C. gigantea, paired end (PE) and mate pair (MP) libraries were constructed as described previously (82) (Table S1). The C. gigantea genome was sequenced in four different libraries (insert size ranging from 180 bp to 2.5 kb) on Illumina HiSeq (2 × 100-nt reads) and MiSeq (2 × 300-nt reads) sequencers. Single PE libraries were constructed for Lophocereus, Pachycereus, Pereskia, and Stenocereus and sequenced on Illumina NextSeq 500 (2 × 150 nt reads; Table S1). All reads were deposited in GenBank (Table S1).

Genome Assemblies.

Raw reads were trimmed using Sickle (83) for bases below QV20 and shorter than 20 bp. Genome size was estimated from k-mer frequency using the script KmerFreq_AR from the SOAPdenovo v2.01 suite (84). The C. gigantea data were error-corrected with BLESS v. 0.14 (85), and residual adapter bases were removed with PRINSEQ (86).

For all species, preprocessed reads were assembled de novo in scaffolds with Meraculous v. 2.0.4 (87) with the diploid option enabled. Out of the multiple iterations tested at different k-mer values, the most contiguous saguaro assembly was obtained with a k-mer value of 69; the genomes of P. pringlei, L. schottii, and S. thurberi were assembled with k-mer values of 55, 37, and 57, respectively. Gaps were closed with Platanus (88). Scaffolding was performed with BESST v. 1.2.3 (89) using the paired end and (when available) mate pair libraries; each scaffolding step was followed by a step of gap closing. Low confidence contigs or gaps were broken with REAPR v. 1.0.17 (90), producing the final assembly. Finally, we removed scaffolds and contigs shorter than 1 kb (saguaro) or 200 bp (all other species) that matched the ϕX174 genome, or that aligned to the saguaro chloroplast (82) for 90% of their length and had at least 90% similarity.

Blastx alignments against GenBank databases revealed significant hits only to other plant sequences. Completeness of the gene-space component of the genome assembly was assessed by running CEGMA (91) and BUSCO (92), using for the latter the Plantae database and tomato as the species for the Augustus gene prediction.

Annotation.

A saguaro repeat library was developed using RepeatExplorer (93) parsing the output as described previously (94). The annotation of the repeats in the saguaro assembly was obtained merging the output of RepeatMasker (www.repeatmasker.org/, v. 3.3.0) and Blaster (a component of the REPET package; ref. 95). Reconciliation of the two masked repeat sets was carried out using custom Perl scripts and formatted as gff3 files.

To identify noncoding RNAs, Infernal (96) was run using the Rfam library Rfam.cm.12.2. Hits with an e value higher than the threshold of 1e-5 were removed, as well as results with score below the family-specific gathering threshold. When overlapping loci were predicted, only the hit with the highest score was kept. Transfer RNAs were predicted using tRNAscan-SE (97) with default parameters.

We also obtained transcriptome data for saguaro using an RNA-seq approach. Samples were collected from SGP3 and from seedlings of the SGP5 specimen (Table S3). Libraries were constructed with the Ovation RNA-Seq System V2 (NuGEN) kit and sequenced on an Illumina instrument (Table S3). All reads were deposited in GenBank (Table S3).

The saguaro genome assembly was annotated using the MAKER pipeline (98). Several transcript and protein sequence datasets were identified to aid in gene prediction. Transcript unigenes were generated for the peyote cactus Lophophora williamsii from publicly available RNA-seq datasets (SRR1575212, SRR1575317, and SRR1575216). Saguaro RNA-seq reads were assembled de novo with Trinity r2013-02-25 (99), with the normalization option (Table S3). Assembled transcripts were merged in a unique EST file and clustered at 95% with Usearch v4.2.66 (100).

Protein sequences used for evidence during gene predictions included predicted proteins from Arabidopsis thaliana (TAIR10, ref. 101), Uniprot/Swissprot proteins (102), and GenBank protein sequences for the Caryophyllalean species Beta vulgaris and Spinacia oleracea. After repeat masking and transcript and protein alignment, high-quality saguaro transcript alignments were used to create an initial set of gene models that were used to train the Hidden Markov Model (HMM) for the SNAP gene prediction program (103). MAKER was run a second time, and genes were predicted using SNAP. High-quality SNAP gene predictions (annotation edit distances ≤ 0.2; ref. 104) were used to train the HMM for SNAP a second time, and MAKER was run again allowing the second SNAP HMM to predict genes. High-quality genes from the second SNAP run were then used to train the HMM for AUGUSTUS (105). MAKER was run a final time allowing genes to be predicted by both SNAP and AUGUSTUS. Alignments of single exon transcripts spanning less than 500 bp were excluded from the final MAKER run, and the “always_complete” and “keep_preds” options were set to 1. Predicted genes with 50 amino acids or less were discarded. Overall, 87% of the genes (25,862 models) had annotation edit distance between 0 and 0.5, with more than half (15,635) between 0 and 0.2.

Predicted proteins were analyzed with HMMER hmmscan to identify matching Pfam domains (106, 107). Gene models with support from transcript evidence, protein evidence, and/or matching Pfam domains were retained as an initial high-quality gene set that was further probed to identify and remove transposable element-related genes. Transcripts with homology to known transposable elements (TEs) and containing domains matching TE-related Pfam domains were excluded. The final set of 28,292 predicted genes were functionally annotated using the Trinotate pipeline (trinotate.github.io). Genes were deemed as transcribed if they had a Salmon v.0.6.1 (108) transcripts per million score equal or greater to 5, or if the Lophophora williamsii or Opuntia ficus-indica (SRR 1616998) unigenes aligned for more than 50 bp with at least 80% blastn similarity. Under these criteria, 50% (14,164) of gene models had evidence of transcription from saguaro RNA-Seq data, and two-thirds (18,597) if including evidence from assembled unigenes.

Robustness of BPP Model Assumptions.

BPP’s substitution model for computing gene tree likelihoods is the Jukes–Cantor (JC) model with a molecular clock. We evaluated model choice in BPP relative to more complex models using likelihood ratio tests (109) with likelihoods computed in PAUP*. Of the 2,291 gene alignments in the most inclusive 50% gene confidence set, the JC model was rejected in favor of HKY85 in 97.8% of the alignments (P = 0.05; df = difference in model parameters = 4; base frequencies estimated). The molecular clock was rejected in far fewer: 18.6–21.6% of alignments (P = 0.05; df = #taxa-2 = 3), depending on the confidence set. Results were similar for other partitions. Although few in number, these genes might conceivably have an outsize effect. To estimate the magnitude of overall lineage effects in Pachycereeae, we concatenated all alignments in the 90% gene set in which the gene tree was concordant with the species tree and estimated branch lengths in PAUP* with an HKY85 + Gamma model (estimating ti/tv ratio). There was evidence of a slight slowdown in rate in the Carnegiea/Pachycereus clade, but overall the effect size for lineage effects was small, with a coefficient of variation in root to tip rates of 13.2%.

To examine model robustness in more detail, we compared population size and divergence time parameter estimates (posterior means) from our data using another program, BEAST 2 v. 2.4.6 (63), which implements more substitution models, including a relaxed clock. We estimated parameters in nine independent sets of 50 genes from the 90% gene All partition set comparing either JC/HKY85 models (assuming a clock), or clock/UCLN (uncorrelated lognormal) models (assuming JC). Input files for BEAST, in XML format, were generated in BEAUti using the StarBeast2 package. Models were unlinked across genes, sites, trees, and clock rates. We estimated a single population size for each branch by setting the population model to “constant” population size. We assigned the same priors in BEAST as we had used in BPP, noting that population sizes in BEAST are in units of 2N_eµ, whereas BPP uses units of 4N_eµ. “Clock rates” and SDs for each gene tree were unlinked, and we assumed the default prior exponential distribution for the SD. Number of generations was set to 10–50 million as needed to obtain ESS values above 200; information from the first 10% of the MCMC chains was discarded.

Paired t tests indicated no significant differences between JC and HKY85 models for population size, although estimates at one internal node were nearly significant. Effect sizes of the models (the difference between the mean estimate across replicates in the two treatments) were less than 2.8% (Table S8). Divergence time estimates, which were scaled to the root age, were not significantly different between JC/HKY85 models. Population size estimates were more sensitive to clock/UCLN model differences, but the effect sizes were still small. For two of the three internal edges, population size estimates varied by as much as 10.6% between the clock and UCLN models. Divergence time estimates were less sensitive to the clock/UCLN model assumptions, with no significant t tests and effect sizes of less than 3.4% of the root to tip distance in the tree. Overall, these experiments suggest that these datasets are large enough to uncover significant but subtle differences in parameter estimates between some models. However, these effects are unlikely to be large enough to affect our conclusions.

Materials and Methods

Sampling, Genome Sequencing, and Annotation.

For details of taxa sampled, library construction, genome sequencing, assembly, and annotation, see SI Materials and Methods.

Phylogenomic Analyses.

Gene alignments and gene trees.

Sets of gene trees were inferred from gene alignments constructed from the genome assemblies with custom PERL scripts. CDS and intron regions were extracted from the saguaro genome based on its annotation. Each region was used as a query in blastn searches (72) against the other four cactus assemblies, with an e value cutoff of 10⁻¹⁰ for the intron searches. To enrich for orthologs, (i) a CDS region was kept for further processing if it returned exactly one hit for all four taxa and (ii) the gene was kept if and only if at least two CDS regions from the same gene passed test (i).

We then used predicted saguaro amino acid sequences within the retained CDS regions in pairwise tblastn runs against the nucleotide hits found in each of the four cacti. Thereby, we obtained subject sequences in the same frame as the saguaro query. We used Muscle (73) to align these protein regions and then tranalign (74) to align the underlying nucleotide sequences. Each gene thus consists of CDS regions that have sequence data present for all taxa. Given at least one such region, introns were then evaluated. An intron region was kept if it returned exactly four hits, one per taxon, and each hit covered at least 50% of the query saguaro sequence. Any alignment in which at least one taxon had more than 50% gaps or missing data was excluded from further consideration.

Three partitions of each gene nucleotide alignment were prepared: one having just third positions in codons (“Third”), one having third positions plus introns (“Neutral”); and one having all nucleotide positions (“All”). Bootstrap maximum likelihood majority rule trees for the All positions alignment were constructed with PAUP* v. 4.0a with an HKY85 model (75). “Gene confidence sets” were compiled based on the quality of their trees (e.g., the “90%” set is all genes for which the minimum bootstrap value is 90% for all clades). Sets were assembled at 50, 60, 70, 80, and 90% levels and rooted with Pereskia.

Species tree inference.

Species trees were constructed first by an alignment-based Bayesian method, BPP v.3.3a (35, 61), in which the input was the alignments from a gene confidence set and partition. Convergence of Markov chains was checked by running three chains from random starting trees for each of the five gene confidence sets (burnin = 4,000; number of generations = 40,000). This is aimed at avoiding multiple optima in the posterior (76) and may be more informative than examining acceptance rates or effective sample sizes (35).

The prior for the scaled root divergence time, τ_root, was set to a gamma distribution, based on the mean and variance of pairwise K_s distances between saguaro and Pereskia (Table S7). The prior for scaled population size, θ_root, was set to a gamma distribution with a mean estimated from the modern nucleotide diversity of saguaro, which was estimated, using the program PSMC (77) applied to the saguaro genome scaffolds ≥100 kb in length, to be π = 0.00146 (variance set to half the mean). The rate variation prior was set to a Dirichlet prior with parameter α = 2.

A second, tree-based pseudolikelihood method, MP-EST v. 1.5 (34), was used with an input of all rooted gene trees constructed from the All partition from each gene confidence set. In each, five replicate searches from random starting species trees were done. To check for multiple optima, an exhaustive enumeration of pseudolikelihood scores for all possible ingroup rooted species trees was done by supplying MP-EST with those 15 trees.

Gene tree discordance.

Discordance between gene trees and the inferred species tree was assayed on a clade basis and for the entire gene tree jointly using PAUP*. Discordant gene trees were binned into groups of identical topology by comparing them to all 14 possible rooted discordant binary trees for five taxa using a custom PERL script. Topological discordance in the All partition was visualized using DensiTree (78) by making the gene trees in the 90% gene confidence set ultrametric using a clock model in PAUP* and scaling root ages to 1.0 (Fig. 2A).

Introgression and network reconstruction.

We used InferNetwork_ML in PhyloNet (36) to reconstruct optimal phylogenetic networks using maximum likelihood, using as input gene trees from the All partition [invoked with “InferNetwork_ML (all) h -n 10 -di -o -po -x 20 -s starting_tree”, where h is the maximum allowed number of reticulation events]. Values of h of 0 (a tree) and 1 were each run from three different starting topologies. Each inferred reticulation node has two incident edges with inheritance probabilities γ and 1 − γ. The tree imbedded in the network, obtained by following the path along the larger of the two inheritance probabilities, is called the major tree.

To compare solutions, we used the AIC information criteria (37): AIC = 2k − 2 log L, where k is the number of parameters in the model and L is the maximum likelihood value of the model. To assess the statistical support for the optimal network, we used PhyloNet’s parametric bootstrap procedure with the same search parameters as used previously.

Demographic inference.

We used BPP to infer divergence times and effective population sizes conditional on the species tree found above. To ensure convergence of the Markov chains, we increased the number of generations to 400,000 (burnin = 40,000), leading to all parameter estimates having an acceptable effective sample size (ESS) >500 (79) and acceptance rates lying in the range 0.25–0.40. We also examined parameter traces in Tracer (63). The raw parameter output of BPP is in units of sequence divergence, D = Tμ, where T is the time in generations and μ is the per generation mutation rate per site, and scaled effective population size, θ = 4N_eμ. Note that 2D/θ = T/2N_e is the edge length in “coalescent time units.”

Quantifying Hemiplasy.

For any site in an alignment, let m_S and m_G be the inferred number of state changes on the species and gene trees respectively. If the two trees are concordant, m_S = m_G, but if the trees are discordant, then the number of changes may differ. The simplest case of hemiplasy is m_G = 1 but m_S > 1: A homology on the gene tree is a homoplasy on the species tree (Fig. 1, Lower Left). A site may also exhibit homoplasy on the gene tree: m_G > 1 (Fig. 1, Lower Right). We define a hemiplastic site as one in which m_S > m_G. The exceptional case of m_G > 1 but m_S = m_G is “homoplasy but not hemiplasy.”

Ancestral states for each residue in each protein sequence alignment in the most robust 80% and 90% gene confidence sets were reconstructed using parsimony with PAUP*, and m_S and m_G were computed for all potentially parsimony informative sites. Sites homoplastic on the species tree for concordant gene trees, and sites homoplastic or hemiplastic for nonconcordant gene trees, were tallied by a custom PERL script.

Neutral Mutation Rate Estimates.

We estimated neutral mutation rate from BPP output as sequence divergence from root to tip divided by the crown group age of cacti, since the assumed model is ultrametric. We also used codeml (80) to infer pairwise synonymous divergences in the coding regions across the entire set of gene trees, using the crown age of Cactaceae estimated at 26.88 MYR (81).