Controlling orientational order in block copolymers using low-intensity magnetic fields

Significance

Magnetic field interactions with condensed matter can produce orientationally ordered states that are important for fundamental research and technological applications. Block copolymer (BCP) mesophases typically exhibit weak field coupling, requiring high-intensity fields generated by superconducting magnets to produce such states. This work advances a strategy for circumventing such field intensity limitations and creates highly aligned mesophases using fields an order of magnitude smaller than typically required and that can be produced by simple permanent magnets. We elucidate the roles of molecular mobility, grain size, and ordering kinetics on the mesophase field response. Low-intensity field-directed BCP ordering has potentially profound implications for processing functional materials and developing complex textures by field shaping.

Abstract

The interaction of fields with condensed matter during phase transitions produces a rich variety of physical phenomena. Self-assembly of liquid crystalline block copolymers (LC BCPs) in the presence of a magnetic field, for example, can result in highly oriented microstructures due to the LC BCP’s anisotropic magnetic susceptibility. We show that such oriented mesophases can be produced using low-intensity fields (<0.5 T) that are accessible using permanent magnets, in contrast to the high fields (>4 T) and superconducting magnets required to date. Low-intensity field alignment is enabled by the addition of labile mesogens that coassemble with the system’s nematic and smectic A mesophases. The alignment saturation field strength and alignment kinetics have pronounced dependences on the free mesogen concentration. Highly aligned states with orientation distribution coefficients close to unity were obtained at fields as small as 0.2 T. This remarkable field response originates in an enhancement of alignment kinetics due to a reduction in viscosity, and increased magnetostatic energy due to increases in grain size, in the presence of labile mesogens. These developments provide routes for controlling structural order in BCPs, including the possibility of producing nontrivial textures and patterns of alignment by locally screening fields using magnetic nanoparticles.

Microstructure plays a central role in controlling the use characteristics of materials. As such, there is a persistent and well-founded interest in developing and understanding processing modalities that provide high-fidelity microstructure control in various industrially relevant materials. The high-temperature creep resistance of single-crystal metals relative to their polycrystalline counterparts is a canonical example that is well known in the context of turbine blades. Likewise, increasing yield strength with decreasing grain size in metals as described by the Hall–Petch relation, and the reduction of charge carrier mobility in polycrystalline semiconductors due to grain boundary scattering, further illustrate the point. These examples establish the primacy of grain size as a descriptor that strongly couples microstructure to properties. Understanding ordering kinetics, as broadly captured by classical nucleation theory (CNT), is a requisite starting point for manipulating microstructure in the aforementioned hard condensed matter systems.

Similar considerations apply for soft condensed matter. Block copolymers (BCPs) are an important case in point. BCPs self-assemble by microphase separation to form periodic nanostructures, microdomains, with characteristic length scales ranging from ∼10 to 100 nm. The ability to impart functionality by designing the block chemistry and the molecular weight-based tunability of the nanostructures are highly compelling aspects in the context of creating useful materials. (1) A staggering range of applications are being pursued, including BCPs for lithography, for optical materials, and for high-performance separation and ion-conducting membranes. In many cases, the desired function is reliant on controlling the BCP microstructure. For example, in ion-conducting BCP membranes the orientation of the ion-conducting microdomains must be controlled so that the intrinsic property, the ion mobility in the polymer constituting the conducting microdomain, is optimally reflected in the conductivity of the membrane overall. (2) Here, grain orientation is the descriptor coupling microstructure to properties.

Processing operations applied to control BCP microstructure are commonly referred to as directed self-assembly (DSA) and several such approaches have been developed. (3, 4) Magnetic-field DSA is a particularly versatile method as the fields are space-pervasive and can therefore be used in complex geometries. Further, magnetic field application is free of the concerns regarding dielectric breakdown and electrode contact that are associated with the use of electric fields in BCPs. Magnetic-field DSA is also free of concerns regarding physical contact with a shear-producing surface, as relevant for shear alignment, and the field can be used in the presence of other stimuli such as temperature gradients and structure-directing surface patterns. Additionally, magnetic field DSA is scalable and therefore of great interest as a practical processing method (5). The scalability aspect is underscored by the routine use of magnetic fields in solidification processing of metals and semiconductors, both for controlling melt flow and imparting texture to the microstructure of solidified parts (6).

Despite its considerable potential for processing BCPs, the use of magnetic-field DSA is constrained by the need for high-intensity fields to effect microstructure control (typically >4 T, necessitating superconducting magnets). This constraint has restricted fundamental studies and engineering applications of magnetic field DSA to a small cross-section of researchers. The ability to process BCPs using low-intensity fields, <0.5 T, would be a significant development as it would permit the use of simple low-cost permanent magnets instead of superconducting systems for processing a variety of functional nanostructured polymers. Moreover, such a development would greatly simplify the simultaneous application of secondary stimuli such as shear and temperature gradients during processing. Further, one can readily envision shaping such low-intensity fields with magnetic nanostructures, or using magnetic nanoparticles to impose local fields, to create complex patterns of microdomain orientation. This represents a compelling future possibility.

Here, we demonstrate an approach in which strong alignment of a liquid crystalline (LC) BCP at low fields is enabled by the addition of small quantities of mesogens. The added species coassemble with the LC mesophase of the BCP, resulting in appreciable viscosity reduction and increase of the BCP grain size, although these quantities remain substantially larger and smaller, respectively, than those of the pure mesogen. Highly textured microstructures are produced in the blended samples at fields that are an order of magnitude smaller than the fields required to impart texture to the neat system. We explore the field strengths required for alignment saturation, and the alignment kinetics, for different mesogen concentrations. We find that highly ordered states with orientation distribution coefficients $⟨P_2⟩\approx 1$ can be obtained at 0.5 T for systems containing only about 10 wt % added mesogens, and at 0.2 T for 36 wt %. Our results indicate that the enhanced alignment kinetics and retention of structural order are reliant on LC coassembly rather than simple plasticization as effected by the use of nonmesogenic additives.

Magnetic-Field DSA of BCPs

$${ϵ}_m=\frac{-B^2}{2{\mu }_0}\left(\chi {}_{\parallel }\cos ^2\phi +\chi {}_{\perp }\sin ^2\phi \right)$$ [1]

$${ϵ}_m=\frac{-\mathrm{\Delta }\chi B^2}{3{\mu }_0}⟨P_2(\cos \phi )⟩$$ [2]

Magnetic-field DSA can be performed by cooling a BCP from its high-temperature disordered melt through its order–disorder transition (ODT) at ${\mathrm{T}}_{\text{odt}}$, in the presence of a suitable field. Alignment occurs due to the anisotropy of the magnetic susceptibility, $\chi$, of the self-assembled state, which gives rise to an anisotropic magnetostatic energy density, ${ϵ}_m$, Eq. 1. Here $\mathrm{\Delta }\chi =\left|{\chi }_{\parallel }-{\chi }_{\perp }\right|$, where the parallel direction is along the axis of highest rotational symmetry of the field-interacting structure, and B is the magnetic field strength. The magnetostatic energy can be expressed as a function of the orientation distribution coefficient $⟨P_2⟩=⟨\frac{1}{2}(3{\cos }^2\phi -1)⟩$ (Eq. 2), where $\phi$ is the angle between the field and ${\chi }_{\parallel }$. Alignment of an individual BCP grain occurs when the magnetostatic energy difference between orthogonal orientations is large compared with the thermal energy scale, $|\mathrm{\Delta }{E}_m|=|\mathrm{\Delta }{ϵ}_m|V_g\gg k_{B}T$, where $V_g={\xi }^3$ is the volume of a grain with characteristic dimension $\xi$, and $\mathrm{\Delta }{ϵ}_m=-\mathrm{\Delta }\chi B^2/2{\mu }_0$ is the difference in magnetostatic energy density between orthogonal grain orientations. Alignment therefore requires a minimum product of the grain volume, the magnetic susceptibility anisotropy, and the square of the field strength. As the BCP is cooled through the ODT, alignment begins to occur when nucleated grains have grown beyond the threshold size indicated by the above consideration. The grains rotate under the action of the field, thereby producing oriented microdomains. The alignment proceeds with a characteristic timescale $\tau \sim \eta /(\mathrm{\Delta }\chi B^2)$, where $\eta$ is a generalized system viscosity. The overall alignment dynamics are complex as grain growth occurs together with grain rotation, and due to the fact that the nucleation and growth rates, BCP viscosity, and the BCP $\mathrm{\Delta }\chi$ are all strong functions of temperature in the vicinity of the ODT. From a practical perspective, alignment only occurs within a small window around ${\mathrm{T}}_{\text{odt}}$ (typically 3–5 K) as $\mathrm{\Delta }\chi \equiv 0$ for $\mathrm{T}>{\mathrm{T}}_{\text{odt}}$ and $\tau$ increases rapidly with decreasing temperature in the ordered state as $\eta \sim \exp (1/T)$ (7).

Magnetic-field DSA has been advanced with LC BCPs where $\mathrm{\Delta }\chi$ is $\mathcal{O}({10}^{-6})$ and $\xi$ is $\mathcal{O}({10}^2)$ nm, necessitating fields above 5 T for strong alignment. (7–15) The LC mesophase within the BCP superstructure provides a ≈100- to 1,000-fold increase in $\mathrm{\Delta }\chi$ relative to non-LC BCPs. Conversely, recent work has demonstrated that the intrinsic susceptibility anisotropy ($\mathrm{\Delta }\chi \approx {10}^{-8}$) of non-LC BCPs can be sufficient to provide strong alignment at field strengths of 5–6 T, due to the large grain sizes produced in certain low-molecular-weight BCPs, with $\xi >1\mathrm{\mu }\mathrm{m}$ (16, 17). The aforementioned cases contrast sharply with small-molecule LCs where alignment can be driven readily at fields below 1 T (18–20). The difference is due to the presence of large grains (typically >10 $\mathrm{\mu }$m) and low system viscosities by comparison with macromolecular LCs. The present work shows that such features may be conveniently coopted in LC BCPs to enable magnetic field alignment at remarkably low field strengths.

Results

Self-Assembled Structure and Phase Behavior.

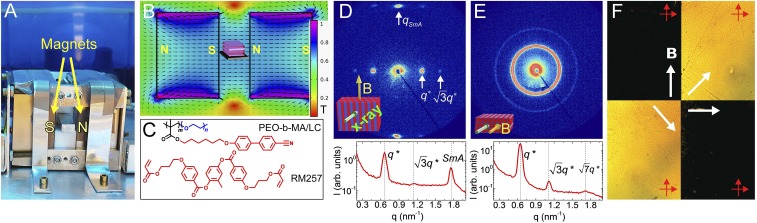
The system studied is a diblock copolymer, poly(ethylene oxide-b-methacrylate/LC), or PEO-b-PMA/LC. The LC block features end-on attachment of cyanobiphenyl mesogens as side chains of a polymethacrylate backbone while the other block is a non-LC polymer, polyethylene oxide. At room temperature the system forms hexagonally packed PEO cylindrical microdomains in a Smectic-A (SmA) mesophase of the PMA-attached cyanobiphenyl mesogens. The structure is shown in Fig. 1. The molecular weight is 13.8 kg/mol with PEO weight fraction $f_{PEO}$ = 0.18. Nearest-neighbor microdomains are separated center-to-center by 11.6 nm and the SmA layer spacing is 3.6 nm. The mesogens have positive magnetic susceptibility anisotropy, $\mathrm{\Delta }\chi >0$, and adopt planar anchoring at the PEO interface such that the LC director and the PEO cylinders align parallel to an applied magnetic field (SI Appendix, Fig. S1).

Fig. 1.

(A) Alignment apparatus using permanent magnets. The magnets are arranged with complementary polarity [i.e., with the north pole (N) surface of one facing the south pole (S) surface of the other]. (B) Finite element modeling of the field intensity distribution. The field strength is ≈0.75 T at the sample position in the gap between the magnets. (C) Chemical structures of the materials used. (D) Small-angle X-ray scattering (SAXS) data for an R = 0.18 sample with X-rays incident normal to field (B). (E) SAXS data for a second R = 0.18 sample with X-rays incident parallel to field. (F) Polarized optical micrographs from thin films under crossed polarizers with field directions as indicated. The large changes in optical transmission and uniformity of the micrographs indicate strong and uniform alignment over the 0.3-mm-wide field of view. The direction of the magnetic field (B) is indicated by the arrow.

SAXS and differential scanning calorimetry (DSC) show that the nematic–isotropic LC clearing transition (at ${\mathrm{T}}_{\mathrm{N}-\mathrm{I}}=78{}^{\circ }\mathrm{C}$) and the BCP ODT (at ${\mathrm{T}}_{\text{odt}}\approx 79{}^{\circ }\mathrm{C}$) are effectively coincident, indicative of a weakly segregated system in which BCP self-assembly is driven by nematic ordering (21). The nematic–smectic A transition is at ${\mathrm{T}}_{\mathrm{N}-\text{SmA}}={73}^{\circ }\mathrm{C}$. The added mesogen is RM257, a commercial phenylene ester diacrylate species commonly used in formulating LCs for displays. Mesogen-blended samples are described by a stoichiometric number R, which is the molar ratio of labile added mesogens to polymer-bound mesogens. Mesogen addition results in gradual changes of the LC BCP phase behavior, with a decrease of ${\mathrm{T}}_{\mathrm{N}-\text{SmA}}$ and a broadening of the nematic window. For example, at R = 0.18, ${\mathrm{T}}_{\mathrm{N}-\mathrm{I}}\approx 79{}^{\circ }\mathrm{C}$ and ${\mathrm{T}}_{\mathrm{N}-\text{SmA}}\approx 61{}^{\circ }\mathrm{C}$. For R = 0.40, ${\mathrm{T}}_{\mathrm{N}-\mathrm{I}}\approx 84{}^{\circ }\mathrm{C}$ and ${\mathrm{T}}_{\mathrm{N}-\text{SmA}}\approx 43{}^{\circ }\mathrm{C}$. The center–center cylinder spacings are relatively unchanged, at 11.6 and 11.3 nm, respectively. R values of 0.18 and 0.40 correspond to free mesogen weight fractions, $f_{RM257}$, of 0.20 and 0.36, respectively, and overall LC weight fractions, $f_{LC}$, of 0.86 and 0.89. RM257 displays a nematic but no smectic phase, with ${\mathrm{T}}_{\mathrm{N}-\mathrm{I}}\approx 130{}^{\circ }\mathrm{C}$. The observed changes on mesogen addition (SI Appendix, Fig. S2) reflect a stabilization of the nematic at the expense of the smectic A phase on increasing RM257 content.

Magnetic Alignment of Neat System.

The magnetic response of the neat material was investigated by slowly cooling samples through the ODT at 0.1 °C/min at different field strengths (SI Appendix, Fig. S1). The occurrence of field alignment is indicated by the equatorial concentration of scattered intensity, corresponding to alignment of the PEO cylindrical microdomains parallel to the applied field. The alignment observed at room temperature is first initiated by cooling into the nematic state where the microstructure is poorly ordered and the alignment is weak (22). Intense reflections at q = 0.63 nm⁻¹ along the equator arise from the BCP superstructure while orthogonal reflections at q = 1.74 nm⁻¹ are due to SmA mesophase. The field dependence shows progressive development of $⟨{\mathrm{P}}_2⟩$ for both BCP superstructure and the SmA layers with a saturation ∼5 T. No alignment is discernible for field strengths lower than ∼1.5 T.

Magnetic Alignment of Mesogen-Blended System.

R = 0.18 blends were subjected to the field generated by a pair of permanent magnets in a custom apparatus (Fig. 1A). The field strength at the sample position is 0.75 T as estimated from finite element simulations (Fig. 1B). The field was applied in the plane of a sample film as it was cooled from its isotropic to ordered states at 0.1 °C/min. SAXS was conducted with X-rays incident perpendicular and parallel to the applied field.

The SAXS data indicate a pronounced alignment of the self-assembled PEO cylindrical microdomains parallel to the applied field, with spot-like reflections along the equatorial line in the 2D scattering pattern when viewed perpendicular to the field direction (Fig. 1D). The smectic layers are aligned perpendicular to the field, as indicated by the spot-like reflections at larger q along the meridional line in the pattern. The orthogonal view, Fig. 1E, reveals a uniform azimuthal intensity distribution, reflecting the orientational degeneracy of the hexagonal lattice in the plane perpendicular to the field and the fact that the lateral grain size is small relative to the size of the X-ray beam (approximately 1 mm) (i.e., we are sampling many grains, each with a random orientation of its hexagonal lattice in the plane perpendicular to the field). Concurrently, the smectic scattering is absent as the smectic layers are no longer in the Bragg condition: The LC layer normal is now parallel to the X-ray beam. The azimuthal intensity distribution for the primary Bragg reflection for the PEO microdomains is concentrated into an exceptionally narrow peak, yielding an FWHM ≈5° from Gaussian fits, and a corresponding orientation distribution coefficient $⟨{\mathrm{P}}_2⟩$ that is close to unity. Polarized optical microscopy observations confirm that the alignment is uniform over large areas (millimeter-scale fields of view), as is evident from the uniformly strong optical anisotropy displayed (Fig. 1F).

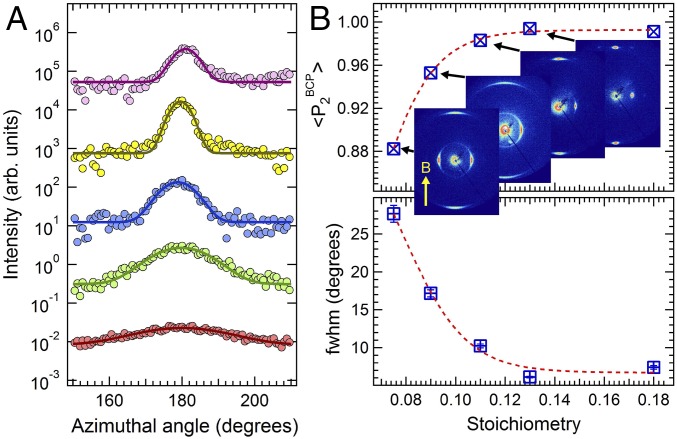
The effect of mesogen concentration on the field response was investigated for compositions ranging from R = 0.075 to 0.40, using a 1 T uniform field generated by a superconducting magnet with a cooling rate of 0.1 °C/min (Fig. 2). A clear response is observable directly from the 2D SAXS data even at a low stoichiometry of R = 0.075, for which the added LC represents only 9 wt % of the system. Above R = 0.11, a remarkable degree of alignment is produced: Sharp BCP reflections with narrow azimuthal intensity distributions yield corresponding orientation distribution coefficients $⟨{\mathrm{P}}_2^{\text{BCP}}⟩>0.98$.

Fig. 2.

Concentration dependence of the alignment of the LC BCP at 1 T at a cooling rate of 0.1 °C/min. (A) Azimuthal intensity profiles fitted with Gaussian function. Top to bottom: R = 0.18, 0.13, 0.11, 0.09, and 0.075. (B) Stoichiometric dependence of FWHM (Bottom) and corresponding order parameter $⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ of the BCP superstructure (Top), with associated 2D SAXS data. Lines are shown as visual guides. The material shows a saturation of the alignment at a stoichiometry of 0.13. The direction of the magnetic field (B) is indicated by the arrow.

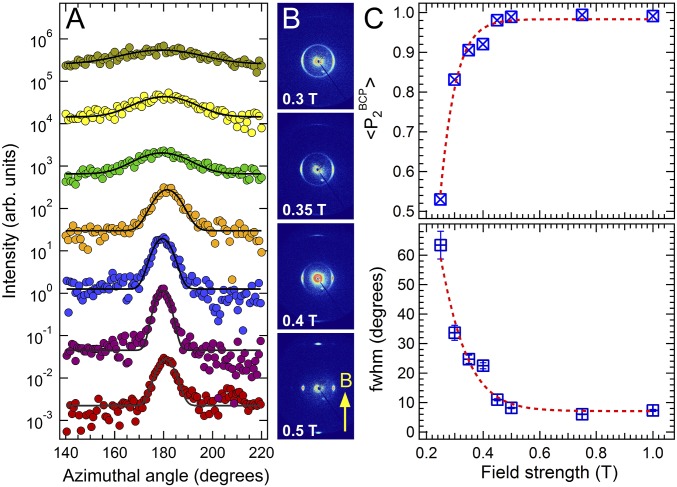
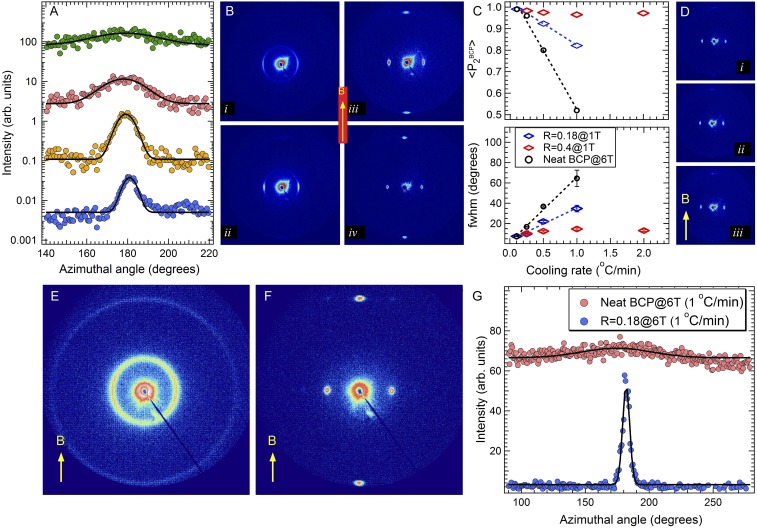
Field-dependent measurements were conducted for R = 0.18 to identify the field strength at which the alignment saturated, for a cooling rate of 0.1 °C/min. The data show that the alignment quality saturates at a very modest field strength of ≈0.5 T (Fig. 3). This saturation field strength for R = 0.18 is over an order of magnitude lower than that required for comparable alignment in the neat sample. The saturation field strength was lower (0.2 T) for R = 0.40 (SI Appendix, Fig. S3), indicating that the presence of larger quantities of free mesogen leads to a more favorable alignment response in this range of mesogen concentrations. Experiments conducted over a range of cooling rates at a fixed field strength further illustrate the sensitivity of the process to the blend composition (Fig. 4). Notably, the alignment quality of mesogen-blended samples (R = 0.18 and 0.40) processed with a 1 T field is superior to that of the neat samples processed at 6 T, for cooling rates larger than 0.1 °C/min (Fig. 4C). The neat system shows a rapid decrease of $⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ with increasing cooling rate at a high field strength of 6 T. The falloff for R = 0.18 is less steep, and is slowest for R = 0.40, highlighting the fact that the presence of free mesogens significantly lessens the kinetic sensitivity of system. This point is further underscored by the large disparity between the strong alignment of a blend sample (R = 0.18) and the nonalignment of a neat LC BCP sample when processed at a fast cooling rate of 1.0 °C/min under a large field of 6 T (Fig. 4 E–G).

Fig. 3.

Field strength dependence of alignment quality at R = 0.18 and a cooling rate of 0.1 °C/min. (A) Azimuthal intensity profiles fitted with Gaussian function. From top to bottom: 0.3, 0.35, 0.4, 0.45, 0.5, 0.75, and 1 T. (B) Representative 2D SAXS data. (C) FWHM of the BCP superstructure and the corresponding order parameter $⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ extracted from the fits. Lines are shown as visual guides. The sample shows a saturation of the alignment at field strength of ∼0.5 T with $⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ = 0.99. The direction of the magnetic field (B) is indicated by the arrow.

Fig. 4.

(A–D) Cooling rate dependence of alignment at 1 T for R = 0.18 and R = 0.40. (A) Gaussian-fitted azimuthal intensity profiles for R = 0.18. From top to bottom the cooling rates are 1, 0.5, 0.25, and 0.1 °C/min. Corresponding 2D SAXS data are shown from i to iv in B. (C) Cooling rate dependence of FWHM (Bottom) and corresponding $⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ values for R = 0.18 and R = 0.40 aligned at 1 T and neat diblock at 6 T. (D) SAXS of R = 0.40 sample aligned at 1 T at selected cooling rates of 2, 0.5, and 0.25 °C/min for i to iii). (E and F) Comparison of alignment of neat diblock (E) and R = 0.18 blend (F) aligned at 6 T with 1 °C/min cooling rate. (G) Corresponding azimuthal intensity dependence. The direction of the magnetic field (B) is indicated by the arrow.

Viscosity and Grain Size Measurements.

The cooling rate dependence of the alignment quality strongly suggests that mesogen addition results in viscosity reduction with the concomitant increase in chain mobility enabling more rapid alignment at a given cooling rate. Another possibility is that mesogen addition changes the size of grains produced during ordering, and that such changes are reflected in the alignment efficacy as might be anticipated based on the process energetics described in Eq. 2. Dynamic rheological measurements were used to evaluate differences in the mobility of neat and mesogen-blended samples. Fig. 5A shows the elastic and viscous moduli ($G\prime$ and $G″$) and the corresponding complex viscosity $\eta \ast$ as a function of temperature spanning the isotropic, nematic, and smectic regimes of the LC BCPs, and the isotropic and nematic windows of the mesogen itself.

Fig. 5.

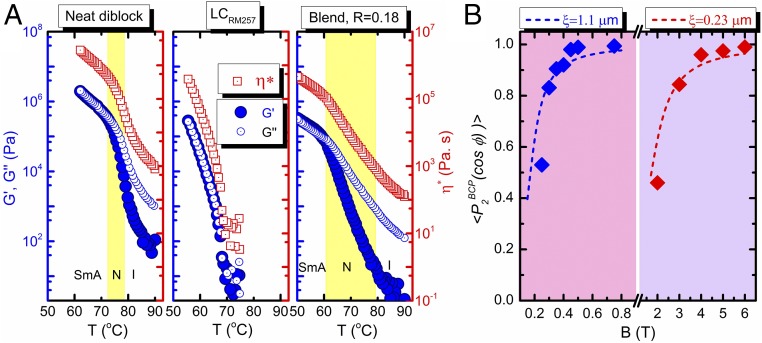
(A) Rheological data (elastic modulus $G\prime$, viscous modulus $G″$, and complex viscosity ${\eta }^{\ast }$) of the neat LC BCP, RM257, and R = 0.18 blend as functions of temperature. The phase transition temperatures are extracted from DSC and SAXS. RM257 is in the nematic phase for the temperatures shown here. The complex viscosity of the blend is approximately one order of magnitude lower than that of the neat sample near their respective effective alignment temperatures of (≈77 °C for neat material and ≈70 °C for the blend). (B) Grain size estimation of the neat diblock and the blend from fits to the experimental field-dependent orientation distribution coefficients using Eq. 3. Fits to the experimental data for a cooling rate of 0.1 °C/min in the SmA at 25 °C yield grain sizes of 0.23 $\mathrm{\mu }\mathrm{m}$ for the neat system and 1.1 $\mathrm{\mu }\mathrm{m}$ for the blend.

Prior work established that field alignment of these LC BCPs is most effective in the nematic window a few kelvin degrees below ${\mathrm{T}}_{\text{odt}}$ where the convolution of mobility and anisotropy provides an optimal response. (22) The alignment in the nematic state is amplified on passage through the nematic–Smectic A transition (SI Appendix, Fig. S4). This effect is underpinned by the increase in effective block segregation strength due to the nematic–Smectic A transition, as reflected by the sharp change in scattered intensity (SI Appendix, Fig. S5). We therefore consider the relative value of $\eta \ast$ at the midpoint of the nematic window as representative of differences in the molecular mobility of the R = 0.18 sample relative to the neat LC BCP. The rheological data indicate that the viscosity and dynamic moduli of the system are significantly reduced by free mesogen addition. The complex viscosity in the nematic state for the R = 0.18 blend (at 70 °C) is an order of magnitude lower relative to the neat diblock nematic state (at 77 °C), supporting the notion that enhanced mobility on mesogen addition plays an important role for the low field alignment. An even larger decrease is apparent for the R = 0.40 blend (SI Appendix, Fig. S6). The blend viscosity, however, is still several orders of magnitude larger than that of the mesogen itself at the same temperatures.

The characteristic grain size $\xi$ of the neat diblock and R = 0.18 blend were determined by considering the field dependence of orientation distribution coefficients extracted from Gaussian fits of azimuthal scattering intensity profiles $I(\varphi ,B)$. $I(\varphi ,B)$ reflects the frequency of occurrence of grains with their easy magnetic axes (i.e., those along ${\chi }_{\parallel }$) at an angle $\varphi$ to the applied field. The probability of such occurrences $p(\varphi ,B)$ is governed by a Boltzmann factor using the magnetostatic energy $E_m$, $p(\varphi ,B)\sim \exp (-E_m/k_{B}T)$, where $E_m$ is a function of the grain size $\xi$, $E_m=-(B^2/2{\mu }_0)\mathrm{\Delta }\chi \xi {}^3\cos ^2\varphi$. The orientation distribution coefficient associated with $E_m$ may be obtained by integration as shown in Eq. 3:

$$⟨{\mathrm{P}}_2^{\text{BCP}}(\cos \varphi )⟩=\frac{{\int }_0^{\pi }\frac{1}{2}(3{\cos }^2\varphi -1)e^{-E_m/k_{B}T}\sin \varphi d\varphi }{{\int }_0^{\pi }{e}^{-E_m/k_{B}T}\sin \varphi d\varphi }.$$ [3]

$⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ determined by Gaussian fits of $I(\varphi )$ for different field strengths (0.2–1 T for R = 0.18; 2–6 T for R = 0) can be modeled using Eq. 3 to estimate the grain size. Data are shown in Fig. 5B. Using an estimate of $\mathrm{\Delta }\chi ={10}^{-6}$, we obtain $\xi \approx$0.23 $\mathrm{\mu }\mathrm{m}$ for the neat diblock and ≈1.1 $\mathrm{\mu }\mathrm{m}$ for the blend. These values represent the characteristic dimensions for grains which at steady state would reproduce the field-dependent orientation distributions observed experimentally. This steady-state assumption and the fact that the degree of alignment observed experimentally is dependent on the cooling rate suggests that the inferred grain sizes underestimate the actual grain sizes to some degree, as observed in prior work (16).

Transmission electron microscopy (TEM) images corroborate the increase in grain size of the blend sample relative to the neat system. This is apparent in both the nonaligned (Fig. 6 A and B) and field-aligned samples (Fig. 6 C and D). Larger fields of view for nonaligned samples are provided in SI Appendix, Fig. S7. For field-aligned samples, the micrographs show that the cylindrical microdomains are oriented with their long axes parallel to the field direction, for the blend aligned at 1 T (Fig. 6D) and for the neat system aligned at 6 T (Fig. 6C), consistent with SAXS observations. Similar grain sizes are observed for nonaligned (Fig. 6A) and aligned (Fig. 6C) neat samples, and the grain size is not appreciably different when viewed parallel (SI Appendix, Fig. S8A) and perpendicular (Fig. 6C) to the field direction for the aligned case. By contrast, the blend sample has a characteristic grain size that is visibly greater, and there is anisotropy as grains are larger along the field direction than across it (SI Appendix, Fig. S8 C and B, respectively). The differences in microstructure of the blend system relative to the neat system are apparent even at lower stoichiometries as shown by TEM data for R = 0.075 (SI Appendix, Fig. S9).

Fig. 6.

(A and C) TEM images of nonaligned and field-aligned (6 T) neat system. PEO domains appear dark due to RuO₄ staining. The view is normal to the field direction for the aligned case. (B and D) TEM images of nonaligned and field-aligned (1 T) R = 0.18 sample. The view is normal to the field direction for the aligned case. The average grain size of the blended samples is considerably larger than in the neat samples. Both nonaligned and aligned blended material show larger persistence of cylindrical domains along the long axis of cylinders relative to the neat material. The images span 1-$\mathrm{\mu }{\mathrm{m}}^2$ areas and are overlaid with a false color mapping as a visual guide (29). The direction of the magnetic field (B) is indicated by the arrow.

Discussion

The approximately fivefold difference in grain size between the neat and blend samples corresponds to over two orders of magnitude difference in magnetostatic energy. At 0.5 T, for $\xi$ = 1.1 $\mathrm{\mu }{\mathrm{m}}^2$, $E_m\approx$ 30 $k_{B}T$ at 70 °C. By comparison, for the neat system with $\xi$ = 0.23 $\mathrm{\mu }\mathrm{m}$, $E_m\approx$ 0.3 $k_{B}T$. This means the driving force for alignment of the neat system does not exceed thermal energy at 0.5 T, which is consistent with the absence of discernible alignment for the neat sample at fields below 1 T. This argument rests on the reasonable assumption that the grain size is independent of the applied field strength.

The development of larger grains in the blend samples is noteworthy. However, grain size does not contribute to alignment kinetics directly as both the magnetostatic energy driving alignment and the hydrodynamic torque resisting grain rotation scale with ${\xi }^3$ (23). CNT for isothermal homogeneous nucleation expresses the average grain size as a function of the grain growth velocity $v$ and the nucleation rate $I$ as $\xi \sim {(v/I)}^{1/4}$ (24, 25). For heterogeneous nucleation, the average grain size is fixed simply by the number density of nucleation sites. Although alignment here is conducted under continuous cooling rather than isothermal annealing, CNT nonetheless provides a useful conceptual framework. From the CNT perspective, the larger grains in the blends relative to the neat system suggests an increase in the effective growth velocity, a decrease in the effective nucleation rate, or some combination thereof, during ordering of the system under continuous cooling. An increase in $v$ solely would permit grains to reach the thermal threshold size earlier during the cooling ramp, and therefore to have an effectively wider processing window (i.e., the period during which mobility is still high enough to permit alignment). By contrast, a decrease in $I$ solely would not be expected to change the alignment response as the grain size during its residence in the high-mobility window would not change.

The above discussion highlights how ordering kinetics can affect alignment. The decreasing sensitivity to cooling rate on mesogen addition suggests that enhanced mobility in the blends plays a role in the enhanced alignment. However, it is difficult to deconvolute the mobility aspect from the influence of the cooling rate on ordering kinetics which may also affect alignment as smaller grains are produced at higher cooling rates. The cooling rate effect is particularly apparent in the alignment disparity observed at high field (6 T) for a cooling rate of 1.0 °C/min (Fig. 4 E–G). At 6 T, if we assume $\xi$ = 0.23 $\mathrm{\mu }\mathrm{m}$, $\mathrm{\Delta }{E}_m^{R=0}\approx 45k_{B}T$, suggesting that $⟨{\mathrm{P}}_2^{\text{BCP}}⟩$ should be $\approx 1$ at steady state. The fact that $⟨{\mathrm{P}}_2^{\text{BCP}}⟩\approx 0$ for a cooling rate of 1.0 °C/min, but $⟨{\mathrm{P}}_2^{\text{BCP}}⟩\approx 1$ for a cooling rate of 0.1 °C/min (Fig. 5B), suggests that the grain sizes produced at the higher cooling rate are substantially smaller than 0.23 $\mathrm{\mu }\mathrm{m}$. That is, the difference in alignment quality is too large to be explained by kinetic factors alone (i.e., due to timescale needed for grain rotation), and there is likely a meaningful difference in the grain sizes produced at the two rates.

The alignment of the blend samples cannot be accounted for by any reasonable increase of their overall susceptibility anisotropies due to mesogen addition. The magnetostatic energy density ${ϵ}_m$ scales only linearly with $\mathrm{\Delta }\chi$, Eq. 2, and the susceptibility anisotropies of the covalently bound cyanobiphenyl mesogens and the added RM257 are similar, both $\approx 2\times {10}^{-6}$ (26–28). As a result, the mesophase magnetic anisotropy overall can change only modestly due to mesogen addition, by ≈3% on adding ≈13 wt % of free mesogen (corresponding to R = 0.11). In our discussions we have used the intrinsic susceptibility anisotropies of the molecular species as proxies for the anisotropies of the mesophases, but the intrinsic molecular anisotropies represent limiting values for the mesophases at temperatures far from the nematic–isotropic transition, strictly speaking, in the zero temperature limit.

We consider the possibility that blending-induced modification of the temperature dependence of $\mathrm{\Delta }\chi$ may play a role, in addition to the mobility and grain size effects highlighted earlier. Mesogen addition could be expected to increase the LC order parameter at any given temperature, which would be reflected in the susceptibility anisotropy. The temperature dependence in the vicinity of the first-order phase transition at $T_{N-I}$ is modeled empirically as $\mathrm{\Delta }\chi (T)=\mathrm{\Delta }{\chi }_0{(1-cT/T_{N-I})}^b$ (30), where $b$ and $c$ are constants, with $b$ = 0.22 and $c$ = 0.98 capturing the behavior of the mean field Maier–Saupe theory (31–33). For small-molecule LCs such as alkyl-cyanobiphenyls and RM257, $b$ is observed to vary between 0.15 and 0.30 while $0.98<c<1$ (26). Analogous temperature dependences are observed in side-chain LC BCPs (34–37). For $b=0.22$ and $c=0.98$, the normalized anisotropy $\mathrm{\Delta }{\chi }^{\ast }=\mathrm{\Delta }\chi /\mathrm{\Delta }{\chi }_0$ at the transition $T^{\ast }=T/T_{N-I}=1$ is 0.42, and at $T^{\ast }=0.98$ (e.g., 63 °C for $T_{N-I}$ = 70 °C), $\mathrm{\Delta }{\chi }^{\ast }=0.49$. In general a sharpening of the temperature dependence by decreasing $b$ from 0.3 to 0.15 will account for no more than $\approx 50\%$ increase in $\mathrm{\Delta }{\chi }^{\ast }$ at $T^{\ast }=0.98$. Given the narrow temperature window in which alignment occurs (i.e., on experimentally relevant timescales), the limited range of variation of the exponent $b$ in $\mathrm{\Delta }\chi (T)$, and the large disparity in the alignment response of the blend vs. neat samples, it is clear that any $\mathrm{\Delta }\chi (T)$ enhancement represents a secondary contribution while mobility and grain size effects are leading-order terms.

The approach advanced here relies on added mesogens to enhance the mobility and grain growth characteristics of the system. As such, consideration needs to be given to the compatibility of labile mesogens with the mesophase of interest. Additional experiments were conducted using two additional mesogens, 6OCB (4′-hexyloxy-4-cyanobiphenyl) and a terthiophene species (5,5′-dihexyl-2,2:5,2-terthienyl). In both cases, the added mesogens facilitated alignment of the PEO-b-PMA/LC system at low-intensity fields at stoichiometries ranging from R = 0.2 to 0.35 (SI Appendix, Figs. S10–S12). We also examined the response of an architecturally distinct system, a brush-type LC BCP based on polylactide and cyanobiphenyl side chains. (38) While alignment of the neat system did not occur at field strengths up to 6 T, the addition of RM257 was effective in promoting alignment at a field strength of 0.75 T (SI Appendix, Fig. S13). Similar efficacy has also been obtained for addition of 6OCB and RM257 to a brush-type LC BCP based on azobenzene side chains. Many commonly used mesogens exhibit wide regimes of miscibility due to their similarity of chemical composition (aromatic containing hydrocarbon compounds) and shape (calamitic, or “needle-like”). This bodes well for efforts to engineer low-intensity field responsiveness in LC BCPs beyond those considered here. It is important to note that experiments conducted using nonmesogenic plasticizing additives, specifically bis(2-ethylhexyl phthalate (dioctyl phthalate) and ethylene glycol, did not produce the same results as found for mesogenic additives. This suggests that while non-LC additives may enhance mobility in the LC BCP they have a sufficiently deleterious effects on either the grain growth kinetics, the LC order (i.e., $\mathrm{\Delta }\chi (T)$), or both.

The concentration of field lines in high-susceptibility materials can be used to screen regions of space from the field, up to a field strength dictated by the material’s saturation magnetization. The field curvature thereby induced and the resulting field intensity modulation can potentially be used to control texture in BCPs. The need for low-intensity field alignment to effect such an outcome is underscored by the fact that the largest saturation magnetization of available materials (for FeCo alloys, ∼2.5 T) is insufficient to fully screen the large fields typically required to control microstructure in BCPs. We anticipate that the approach developed here will enable the fabrication of BCP films with bespoke textures and patterns of alignment through the use of field-screening structures, and motion of films relative to such structures.

Conclusion

We have considered the role of added mesogens on magnetic field alignment of LC BCPs. Our results show that the mesogens enable alignment at field strengths below 1 T. Field- and cooling-rate-dependent experiments as well as rheological characterization conclusively show that the enhanced alignment response is directly linked to improved mobility in the blended systems, and the growth of larger grains. Specifically, sub-1 T alignment is enabled by the large grain size of mesogen-blended samples. The inability to align the neat system at such low field strengths is not due to kinetic limitations associated with grain rotation, but to the fact that the grains of the neat material are below the thermal threshold size for all cooling rates considered (i.e., $E_m<k_{B}T$). By contrast, the rate-dependent differences in alignment at higher fields highlight the role of improved mobility in the blend samples. However, the reduction in grain size that occurs at high cooling rates implies a convolution of mobility and grain size effects in general. Our results suggest routes for controlling texture in LC BCP mesophases using low-cost permanent magnets. Such processing routes are expected to become important for a wide variety of functional molecular materials.

Materials and Methods

Sample Preparation.

PEO2.4k-b-MA/LC11.2k and PEO5k-b-MA/LC25k were obtained from Polymer Source. RM257 was a gift from Teledyne Scientific & Imaging. 6OCB was obtained from Sigma-Aldrich. RM257 (0.1 wt % in ${\text{CHCl}}_3$) was added to the BCP (5 wt % in ${\text{CHCl}}_3$) in appropriate quantities to yield desired compositions and filtered (0.2 $\mathrm{\mu }$m polytetrafluoroethylene). Samples were prepared by evaporative solvent removal at 75 °C followed by isothermal annealing close to ${\mathrm{T}}_{\text{odt}}$ under vacuum to remove any voids. Samples for the permanent and superconducting magnets were 0.5 and 1 mm thick, respectively.

Magnetic Alignment.

Nd bar magnets with surface a field of ≈1.2 T (Applied Magnets) provided a sample field of ≈0.75 T. A superconducting magnet (American Magnetics Inc.) was used to provide fields from 0 to 6 T for field and cooling rate-dependent experiments. Samples were sandwiched between thin Kapton windows on a temperature-controlled stage. The samples were heated above the T_odt, typically to 100 °C, and then cooled at the prescribed rates in the presence of the field.

X-Ray Scattering.

SAXS was conducted on a Rigaku S-MAX3000 instrument using Cu K$\alpha$ radiation ($\lambda$ = 1.542 Å) with a pinhole-collimated 1.3-mm-diameter beam at the sample plane. The instrument houses a superconducting magnet for in situ field experiments. For temperature-resolved measurements, samples were subjected to a heating/cooling rate of 1 ° C/min and equilibrated for 3 min at each temperature before data acquisition.