Integrated field, laboratory, and theoretical study of PKD spread in a Swiss prealpine river

Significance

Predicting how temperature, climate change, and emerging infectious diseases interact to drive local extinction risk for natural populations requires complex integrated approaches involving field data [fish and environmental DNA (eDNA) sampling and hydrological and geomorphological surveys], laboratory studies (eDNA analyses and disease prevalence assessment), and metacommunity modeling. Together, these tools reproduce all of the relevant biological and ecohydrological features of proliferative kidney disease, a major emerging disease impacting native salmonid stocks. We thus provide a predictive framework, applicable to other aquatic pathogens, that may function as a baseline for environmental management decisions aimed at preserving declining and iconic salmonid species.

Abstract

Proliferative kidney disease (PKD) is a major threat to wild and farmed salmonid populations because of its lethal effect at high water temperatures. Its causative agent, the myxozoan Tetracapsuloides bryosalmonae, has a complex lifecycle exploiting freshwater bryozoans as primary hosts and salmonids as secondary hosts. We carried out an integrated study of PKD in a prealpine Swiss river (the Wigger). During a 3-year period, data on fish abundance, disease prevalence, concentration of primary hosts’ DNA in environmental samples [environmental DNA (eDNA)], hydrological variables, and water temperatures gathered at various locations within the catchment were integrated into a newly developed metacommunity model, which includes ecological and epidemiological dynamics of fish and bryozoans, connectivity effects, and hydrothermal drivers. Infection dynamics were captured well by the epidemiological model, especially with regard to the spatial prevalence patterns. PKD prevalence in the sampled sites for both young-of-the-year (YOY) and adult brown trout attained 100% at the end of summer, while seasonal population decay was higher in YOY than in adults. We introduce a method based on decay distance of eDNA signal predicting local species’ density, accounting for variation in environmental drivers (such as morphology and geology). The model provides a whole-network overview of the disease prevalence. In this study, we show how spatial and environmental characteristics of river networks can be used to study epidemiology and disease dynamics of waterborne diseases.

A major goal of disease ecology is to understand how the environment, hosts, and pathogens interact to cause disease outbreaks (1). Consolidating the ecological and evolutionary interactions underlying disease and predicting how and where disease outbreaks are likely to occur remain important and often difficult endeavors. Such predictions are nevertheless crucial in guiding management decisions to prevent the spread and further emergence of major human and wildlife epidemics (2). Predictive frameworks for human diseases, such as cholera (3), have shown the necessity of integrating research from diverse fields to identify key stages in infection cycles that may allow for disruption of the progress of epidemics. In this study, we integrate field and laboratory data with epidemiological and spatial network modeling to create a predictive framework at a river catchment scale for an emerging aquatic disease afflicting native and threatened salmonid species.

Proliferative kidney disease (PKD) affects several salmonid species in temperate rivers and causes major economic losses in salmonid aquaculture. The disease has been recognized as one of the main causes of decline in fish populations over the last decades and as driving the local extinctions of endemic and/or commercially important fish species (4, 5). The disease is caused by the myxozoan endoparasite Tetracapsuloides bryosalmonae, which exploits freshwater bryozoans (mainly Fredericella sultana) as primary host (6, 7). Infection in bryozoans cycles between a cryptic, covert stage and a virulent, overt stage (8). Parasite spores released into water by overtly infected bryozoans may infect salmonids as they contact the gills or the skin. In the kidney, T. bryosalmonae undergoes multiplication, entailing a massive granulomatous nephritis with vascular necrosis (9, 10). Spores excreted via urine into the water may infect bryozoan colonies (11). Mortality within nonnative farmed fish can range from 20 to 95% (12, 13), while the impact on native trout populations is poorly understood. Because disease symptoms and mortality are strongly enhanced by increasing water temperatures, PKD represents a serious threat to salmonid populations in many regions impacted by climate warming (14). A notable increase in PKD incidence in northern Europe has been documented (15–18). A recent outbreak in the Yellowstone River (Montana, the United States) (19, 20) fostered an abnormal kill of mountain whitefish (Prosopium williamsoni) to the point that local wildlife officials temporarily shut down a 300-km-long river stretch to all recreational activities in a bid to impede the parasite spread.

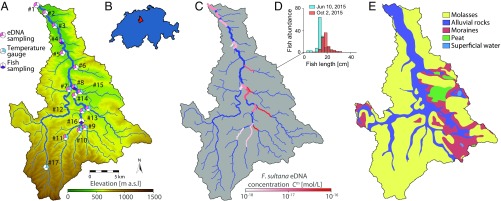
Given the complex lifecycle of the causative agent and the significance of the ecological and environmental factors involved in its transmission (14), mathematical modeling is of paramount importance to understand the epidemiology of PKD in river networks and to possibly assess the effectiveness of mitigation strategies. The first epidemiological model for PKD has recently been developed and expanded into a metacommunity framework (21, 22). At a local scale, the model accounts for epidemiological and demographic dynamics of both hosts (bryozoans and fish), coupling intra- and interannual dynamics and considering the effect of water temperature. In a metacommunity perspective, local community dynamics are embodied through hydrological transport of parasite spores and fish movement, specifically accounting for heterogeneity in habitat characteristics and hydrothermal conditions along the river network. Here, the original model is further developed to incorporate age structure and spawning migration of the fish population. The model is applied to a case study in the Swiss river Wigger (Fig. 1 A and B), where we comprehensively surveyed the brown trout population, the presence of F. sultana (Fig. 1C), and relevant environmental parameters, such as water temperature, for 3 y (2014–2016).

Fig. 1.

Overview of the study area and data. (A) Digital terrain model of the Wigger and extracted river network with location of the sampling sites. Site numbers are introduced by the number sign (#). (B) Position of the Wigger catchment in Switzerland. (C) Mean measured F. sultana eDNA concentration. Ungauged stretches are depicted in blue. (D) Results of fish sampling campaign on site 8 in 2015. The reader is referred to SI Appendix, Fig. S1 for the complete dataset. (E) Geological characterization of the catchment.

Reliable predictions of the spread of infectious diseases and possible management strategies must be based on accurate assessments of the spatial distribution of the invertebrate host (23). In this work, we also developed a model to estimate local F. sultana densities based on temporally repeated and spatially distributed quantitative environmental DNA (eDNA) point measurements. The methodology proposed here opens avenues for a generalized use of eDNA testing for predicting species occurrence and density in natural habitats and especially, in aquatic ecosystems. Because the river acts as an integrator of spatially heterogeneous sources of genetic material (24), the eDNA concentration at a given river cross-section results from a combination of dilution effects and decay processes (25). To account for dilution effects, the contribution of local species’ densities in all stretches upstream is weighted by their relative size (a proxy for the discharge contribution). The decay of the eDNA concentration flowing downstream, because of the progressive damage to the genetic material produced by shear and advection, is modeled through a first-order degradation process (26) with characteristic decay length ${\lambda }_B$. Local species’ densities are correlated to site-specific covariates, and the calibration aims to reveal links between bryozoan presence and specific environmental conditions. The so-obtained bryozoan density map is then used in the metacommunity PKD model.

Results

Bryozoan Habitat Suitability.

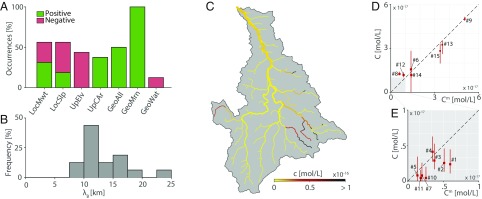
The performances of several models with different sets of explanatory covariates were tested to build a reliable map of bryozoan density across the entire catchment. We deemed as behavioral (or acceptable sensu ref. 27) models with calibration score that exceeded a given threshold (Materials and Methods and SI Appendix). Local bryozoan density was positively correlated with the presence of moraines upstream (present with positive sign in 100% of the behavioral models) (Fig. 2A). Environmental covariates, such as mean water temperature, have a less clear effect on bryozoan density, as their correlation might be positive or negative depending on the particular model. Upstream mean elevation and local slope are, in most cases, negatively associated with bryozoan density. In 43.8% of the behavioral models, the calibrated values of the decay length ${\lambda }_B$ are between 10 and 12.5 km (Fig. 2B). Overall, the capability of the behavioral models to reproduce the mean F. sultana eDNA concentrations measured in the 15 sampling sites ($C^m$) seems satisfactory (Fig. 2 D and E). The predicted spatial distribution of F. sultana eDNA local concentrations (averaged over all behavioral models) is displayed in Fig. 2C.

Fig. 2.

Results from the bryozoan habitat suitability study. (A) Occurrence of covariates in behavioral models. “Positive” and “negative” refer to the signs of the calibrated $\beta$ coefficients. Covariates’ abbreviations are as in SI Appendix, Table S4. GeoAll, percentage of alluvial rocks; GeoMrn, percentage of moraines; GeoWat, percentage of superficial water; LocMwt, local mean water temperature; LocSlp, local slope; UpCAr, contributing area; UpElv, upstream mean elevation. (B) Distribution of calibrated values of ${\lambda }_B$ in behavioral models. (C) Map of local eDNA concentration obtained by averaging results from all behavioral models. (D) Modeled ($C$) vs. observed ($C^m$) F. sultana eDNA concentration. Red lines identify 10th–90th percentile ranges of the distribution of all accepted models; squares represent values averaged over all accepted models. Site numbers are introduced by the number sign (#). (E) Zoomed in view of D.

Epidemiological Model.

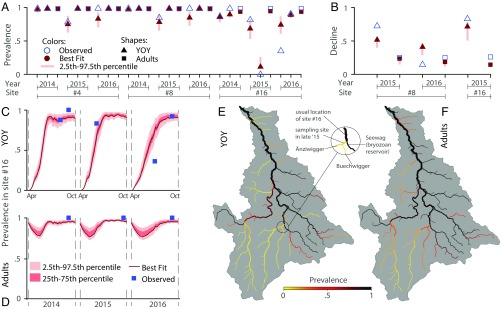
Field surveys assessed PKD prevalence in fish at three sites (4, 8, and 16) (Fig. 1A) both in early summer [for young-of-the-year (YOY)] and in late summer (for both YOY and adults). In the downstream and intermediate sites (4 and 8, respectively), the general pattern is that all fish of all age classes in all sampling dates are infected (Fig. 3A), while in the upstream site, 16 YOY prevalence rates in early summer were always lower than 100%. Notably, in the late 2015 summer sampling, no YOY were found at the usual location of the sampling site 16 (i.e., downstream of the junction of the three tributaries Änziwigger, Buechwigger, and Seewag); hence, the sampling was shifted upstream of the confluence with Seewag (circle in Fig. 3E). None of the YOY sampled on that occasion tested positive for PKD.

Fig. 3.

Results from the epidemiological metacommunity model. Results of calibration against (A) prevalence data and (B) seasonal fish decline measured as the fractional decline of the estimated population size in late summer compared with early summer. In A, the left point of each year group corresponds to YOY early summer sampling. The observed zero-prevalence value was actually measured in a stretch upstream of site 16 (E and in the text). Site numbers are introduced by the number sign (#). Time evolution of modeled prevalence in site 16 for (C) YOY and (D) adult fish. The intraseasonal model is run for 200 d starting on April 1. Note that the YOY prevalence sample in October of 2015 is missing. Maps of best fit-modeled PKD prevalence evaluated at the end of the summer of 2016 for (E) YOY and (F) adults. E features a zoomed in view of site 16.

The epidemiological metacommunity model is capable of reproducing the observed patterns of PKD prevalence (Fig. 3A) and in particular, the late summer 100% prevalence rates observed for both age classes at sites 4 and 8. The model forecasts prevalence rates close to 100% in large parts of the network in late summer for both adults (Fig. 3F) and to a lesser extent, YOY (Fig. 3E). Prevalence in adults tends to be high during the whole season (Fig. 3D), while the initially null prevalence level in YOY (Fig. 3C) is caused by the absence of vertical transmission of PKD in fish. As expected, modeled PKD prevalence is lower in those parts of the network where there are no upstream stretches where predicted bryozoan abundance is high (Fig. 2C). This result agrees with the observed null prevalence upstream of the confluence with the Seewag: indeed, this tributary, unlike the Änziwigger and the Buechwigger, is characterized by high F. sultana density, according to the model of bryozoan suitability (Fig. 2C).

The decrease of brown trout population size was estimated only for sites where two sampling campaigns in the same year were conducted. The decline in fish abundance is captured by the model (Fig. 3B), despite a tendency toward underestimation. This could be attributed to undocumented fishing activity or other possible stress factors not included in the model at this stage.

Discussion

Disease emergence may occur variously through either range expansion of existing pathogens or appearance of new, more virulent agents in existing endemic ranges (28, 29). Environmental change can also trigger the emergence of previously relatively avirulent, endemic parasites by altering the expression of virulence via, for example, temperature-linked effects on host immune function (30). Local abiotic and biotic conditions favoring parasite proliferation might vary in time owing to environmental change. In the case of parasites with complex lifecycles, such conditions must remain conducive to the persistence of multiple susceptible host classes. For example, the correct species of snail and vertebrate hosts are required to coexist at appropriate points during the lifecycle of Schistosoma mansoni parasites to sustain the transmission of schistosomiasis (31). Although T. bryosalmonae exhibits a similarly complex lifecycle with no fish to fish transmission, a notable difference is that long-term parasite persistence in the bryozoan populations is possible, even in the absence of the fish host (22, 32). Parasite propagation along the budding growth of the bryozoan and incorporation into asexually produced resting stages create an effective parasite reservoir, with frequent spillover effects to, for example, stocked and highly susceptible fish. For this type of pathogen, any environmental change favoring establishment of the key reservoir host increases disease risk in all of the other hosts, including those that may be economically relevant. It also greatly complicates eradication of the disease through management measures.

Our model suggests that increased bryozoan density is highly indicative of PKD severity and occurrence, and thus, the key predictive factor for PKD was the habitat suitability for the bryozoan F. sultana. We recovered a strong correlation between the presence of upstream moraines and local abundance of F. sultana. This pattern, which was instrumental in generating the bryozoan density map for the Wigger, might imply that moraines create advantageous conditions for the proliferation of F. sultana by constituting the suitable substrate and/or by affecting geogenic solute concentrations (i.e., the chemical properties of the stream environment). However, moraines are present in a limited area of the watershed, with few sampling sites with notably high F. sultana eDNA concentration; therefore, a spurious correlation cannot be excluded. Understanding the causality and mechanisms that explain why moraines are priming bryozoan presence requires additional survey studies in other catchments and laboratory experiments. Knowledge on habitat requirements of bryozoans might be crucial for disease control purposes, as the strong link between PKD severity and bryozoan density suggests that PKD management might rely on control of bryozoan populations. Other possible strategies might count on the production of resistant fish strains also by eliminating fish stocking and thus, allowing for selection of resistant fish strains in a natural way.

With regard to the epidemiological model, it is noteworthy that, even without specifying different epidemiological parameters for YOY and adults, the model predicts a population size decline of YOY that is almost three times larger than that of adults. Therefore, the higher susceptibility of YOY to PKD revealed by the data can be explained by the not yet acquired immunity rather than by an intrinsic severity of PKD for young fish. The observation that decline in adults predicted by the model is lower than observed values can be explained by an additional fishing mortality term not accounted for by the model (say, widespread anglers’ impacts or other stress factors). Confidence intervals of fish decline are rather narrow, because the main factor influencing adults’ reduction is the natural mortality rate, which was kept constant in the calibration procedure. Other possible stress factors related to temperature increase were already taken into account by the calibration protocol (Materials and Methods and SI Appendix), because the PKD-related mortality is expressed as a function of temperature. The seasonal decrease in the abundance of YOY observed at site 8 in 2016 was considerably low (Fig. 3B). It is remarkable that the model is actually capable of partially reproducing this trend by predicting a lower YOY decrease compared with that of 2015. This is likely because of the shorter time lapse between the two seasonal sampling campaigns and the cooler summer temperatures (SI Appendix has details). Indeed, water temperature proves to be a key driver of PKD impacts on fish population abundance, although its influence on prevalence patterns is minor (21, 22).

In conclusion, our work highlights the profound influence of an emerging aquatic disease on the abundance and seasonal demography of threatened and economically important fish stocks. Our integrated approaches resulted in a comprehensive spatial predictive framework of disease and identified key factors in driving disease patterns in the wild.

Materials and Methods

All information is further developed in SI Appendix.

Study Area and Hydrogeomorphology.

The river Wigger, located in the Swiss plateau, is a tributary of the river Aare and has a length of 48.11 km. It drains a watershed of 382.4 km², which has an elevation range between 396 and 1,409 m above sea level (a.s.l.) at the Mount Napf (Fig. 1 A and B). The Wigger has been subject to endemic PKD for several years (33, 34) [a dataset of PKD occurrence across Switzerland is freely available at the website of the Swiss Federal Geoportal (35)]. The river network was extracted from a 25-m-resolution digital terrain model using the Taudem routine in a geographic information system software (36). The geological characterization of the catchment (Fig. 1E) was obtained by a vectorized geological map of Switzerland provided by the Swiss Federal Office of Topography (Swisstopo) (37). Daily mean discharges measured by the Swiss Federal Office for the Environment in Zofingen (corresponding to site 3 of Fig. 1A) were used to compute time series of discharge for all stretches based on the assumption of proportionality between discharge and contributing area (38).

Field Data Collection.

In the period from May of 2014 to May of 2015, stream water samples were collected at 15 different locations along the river network (Fig. 1A). For each site, 21 samples were taken at irregular intervals. Water samples were analyzed via qPCR to detect and quantify F. sultana 18S rDNA concentration in water. For subsequent data analysis, the target DNA quantity estimated in each water sample was averaged over the 21 temporally distributed samples; the resulting mean concentration $C^m$ (Fig. 1C) was then used as input for the determination of bryozoan habitat suitability. Water temperature has been measured since July of 2014 at 11 sites via HOBO TidbiT v2 data loggers. An additional temperature gauge (site 17) was added in September of 2015. Two loggers, recording data at 15-min intervals, have been deployed per each site. Water temperature is known to affect bryozoan growth rate (39) and may also impact spore shedding.

All YOY trout sampled in this study originated from natural reproduction, as there was no fish stocking in the Wigger in the period 2014–2016. Trout abundance estimation, collection of fish, and kidney sampling were performed according to the Swiss regulations, and the field setup was accepted by the relevant authorities (Veterinärdienst Kanton Luzern, Tierversuchskommission des Kantons Bern, Kantonaler Veterinärdienst des Kantons Aargau) under the number LU05/14+. Fish were caught by electrofishing in early and late summer on sites 4, 8, and 16 (Fig. 1A) over a distance of 100 m. An example of fish density assessment is shown in Fig. 1D. During each sampling trip, 25 YOY brown trout were collected outside the stretch used for density assessment. When available, five adult brown trout (>1 y old) were sampled during the late summer field campaign.

Bryozoan Habitat Suitability.

Let $c_i$ be the bryozoan eDNA concentration that would be measured at site $i$ in the absence of advection (i.e., if site $i$ were an unconnected river stretch). We assume that $c_i$ is proportional to the density of bryozoan biomass at site $i$ and that $c_i$ does not change throughout the season. The deterioration of the eDNA signal from site $i$ measured at a given downstream distance is modeled by first-order kinetics with characteristic decay length ${\lambda }_B$; conversely, we assume no longitudinal dispersion of the eDNA signal. The eDNA concentration measured at a given location $j$ reads, therefore,

$$C_j=\frac{1}{A_j}\sum _{i=1}^{N_s}{p}_{ij}{A}_i^L\exp \left(-\frac{L_{ij}}{{\lambda }_B}\right)c_i\text{,}$$ [1]

where $N_s$ is the number of stretches into which the river network is subdivided; $p_{ij}$ is the generic entry of the connectivity matrix $𝐏$ (i.e., $p_{ij}=1$ if there exists a downstream path connecting $i$ to $j$; 0 otherwise); $A_i^L$ is the direct drainage area of subcatchment $i$; $A_j$ is the upstream contributing area to site $j$; and $L_{ij}$ is the downstream distance between $i$ and $j$. Note that $p_{jj}=\mathrm{\hspace{0.17em}1}$ and $L_{jj}=0$. The sum over all reaches upstream of $j$ (weighted by their relative contribution to the total contributing area, a proxy of river discharge) accounts for the effect of dilution in the eDNA signal.

The local concentration $c_i$ is modeled as $c_i=c_0\exp (𝜷\prime {𝐗}_i)$, where ${𝐗}_i$ is a vector of covariates, while the scalar $c_0$ and the vector $𝜷$, together with ${\lambda }_B$, are parameters that need calibration contrasting field data. The choice of an exponential link function is justified by the fact that $c_i$ must be nonnegative. The chosen explanatory variables, listed in SI Appendix, Table S4, refer to geomorphological, hydrothermal, and geological features of the catchment. Covariates were normalized in the range [−1; 1], where boundaries correspond to the lowest/highest values of the covariates among all subcatchments. Multicollinearity was tested via variance inflation factors to discard correlated predictors.

Epidemiological Model.

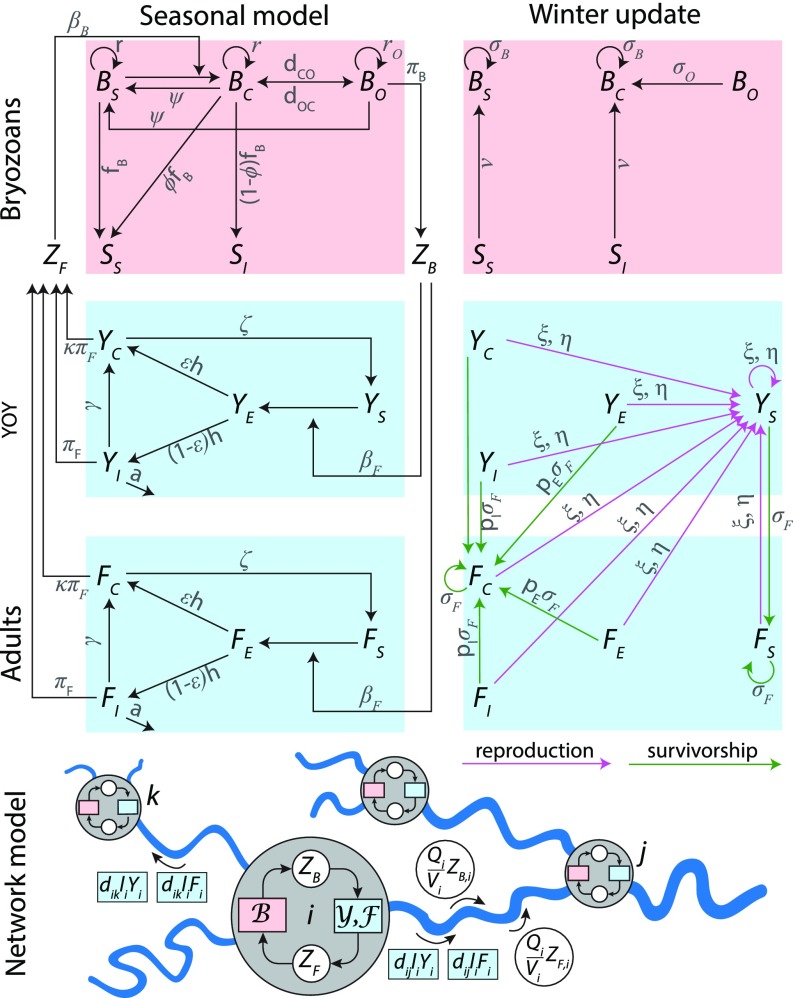
The metacommunity model (Fig. 4), originally presented in ref. 22, was modified to account for fish population age structure. A brief description follows ($B$ indicates bryozoan state variables, $Y$ represents YOY, and $F$ stands for adult fish). During the warm season (Fig. 4, Upper Left), susceptible bryozoans ($B_S$) become covertly infected ($B_C$) after exposure to spores ($Z_F$) released by infected fish. Infection in bryozoans cycles between covert and overt ($B_O$) states. $B_S$ produces uninfected statoblasts $S_S$ (i.e., asexually produced propagules), while $B_C$ releases both uninfected and infected ($S_I$) statoblasts. Infected bryozoans may clear the infection. Susceptible fish ($Y_S$, $F_S$) are exposed to infectious spores ($Z_B$) released by $B_O$. After an incubation phase ($Y_E$, $F_E$), fish can either develop acute PKD ($Y_I$, $F_I$) or directly enter an asymptomatic carrier state ($Y_C$, $F_C$). $Y_I$ and $F_I$ may die owing to PKD or else become long-term parasite carriers. $Y_C$ and $F_C$ may then become susceptible again. $Y_I$, $F_I$, $Y_C$, and $F_C$ shed spores infective to bryozoans. At the beginning of a new warm season (Fig. 4, Upper Right), $B_S$ comprises susceptible colonies that survived during winter and hatched $S_S$; similarly, $B_C$ consists of survived colonies that were infected at the beginning of winter and hatched $S_I$. $Y_S$ includes newborn fish from all classes. $F_S$ is composed of surviving susceptible individuals. The abundance of $F_C$ is determined by the number of individuals belonging to nonsusceptible classes that survived through winter. The abundance of the other classes is null.

Fig. 4.

Schematic representation of the epidemiological model. Intraseasonal local model. Interseasonal local model. Parameters are indicated in gray. Spatial model. All state variables and parameters are listed in SI Appendix, Tables S5 and S6. $\mathcal{B}$, bryozoan submodel; $\mathcal{Y}\text{,}\mathcal{F}$, fish submodel. Adapted from ref. 22.

The local epidemiological model is applied to each river stretch (Fig. 4, Lower) considered as a node of an oriented graph spanning the whole river network. Connectivity between nodes entails passive hydrological transport of parasite spores ($Z_B$, $Z_F$) in the downstream direction and fish movement (modeled as a diffusive process) both upstream and downstream. Spatial heterogeneity in bryozoan and fish suitabilities are included: bryozoan biomass is expressed in dimensionless units, with local carrying capacities assumed to be proportional to $c_i$ and equal to unity for the stretch characterized by the highest $c_i$ value (where $c_i$ values are taken as in Fig. 2C). As for both YOY and adults, fish density at equilibrium is proportional to the mean stretch depth (40), which corresponds to an appropriate parametrization of the effect of density dependence $\xi$. Mobility rates and the diffusion matrix are as in ref. 22, such that, given any spatial distribution of fish at the beginning of the season, the system tends to reach a target equilibrium distribution (which assumes that fish density is proportional to the mean stretch depth) toward the end of the season, provided that the average fish mobility rate $l_{avg}$ is large enough. During winter, the number of newborn fish generated by the female adults living in each stretch are estimated according to a Ricker model (41). As brown trout are subject to spawning migration to seek suitable habitats and subsequent natal homing (42), newborn individuals generated by adults living in a specific stretch are assumed to hatch in suitable upstream stretches according to a gravity model (43). For the sake of simplicity, the same set of epidemiological and mobility parameters was used for both YOY and adult fish.

Details on Model Simulations and Calibration.

The model is calibrated against both prevalence and seasonal population decline data. Fish population decline was estimated only when two population samplings per year were conducted at the same site. In total, 33 data points are available (27 prevalence measurements and 6 fish decline measurements); in the objective function, all data points have equal weight. Calibration was performed via a Metropolis–Hastings algorithm (44).