Three-dimensional mesostructures as high-temperature growth templates, electronic cellular scaffolds, and self-propelled microrobots

Significance

Exploiting advanced 3D designs in micro/nanomanufacturing inspires potential applications in various fields including biomedical engineering, metamaterials, electronics, electromechanical components, and many others. The results presented here provide enabling concepts in an area of broad, current interest to the materials community––strategies for forming sophisticated 3D micro/nanostructures and means for using them in guiding the growth of synthetic materials and biological systems. These ideas offer qualitatively differentiated capabilities compared with those available from more traditional methodologies in 3D printing, multiphoton lithography, and stress-induced bending––the result enables access to both active and passive 3D mesostructures in state-of-the-art materials, as freestanding systems or integrated with nearly any type of supporting substrate.

Abstract

Recent work demonstrates that processes of stress release in prestrained elastomeric substrates can guide the assembly of sophisticated 3D micro/nanostructures in advanced materials. Reported application examples include soft electronic components, tunable electromagnetic and optical devices, vibrational metrology platforms, and other unusual technologies, each enabled by uniquely engineered 3D architectures. A significant disadvantage of these systems is that the elastomeric substrates, while essential to the assembly process, can impose significant engineering constraints in terms of operating temperatures and levels of dimensional stability; they also prevent the realization of 3D structures in freestanding forms. Here, we introduce concepts in interfacial photopolymerization, nonlinear mechanics, and physical transfer that bypass these limitations. The results enable 3D mesostructures in fully or partially freestanding forms, with additional capabilities in integration onto nearly any class of substrate, from planar, hard inorganic materials to textured, soft biological tissues, all via mechanisms quantitatively described by theoretical modeling. Illustrations of these ideas include their use in 3D structures as frameworks for templated growth of organized lamellae from AgCl–KCl eutectics and of atomic layers of WSe₂ from vapor-phase precursors, as open-architecture electronic scaffolds for formation of dorsal root ganglion (DRG) neural networks, and as catalyst supports for propulsive systems in 3D microswimmers with geometrically controlled dynamics. Taken together, these methodologies establish a set of enabling options in 3D micro/nanomanufacturing that lie outside of the scope of existing alternatives.

Growing interest in approaches for 3D micro/nanomanufacturing derives, in part, from the potential to exploit advanced, 3D designs in emergent technologies, from biomedical devices (1–4), microrobotics (5–7), metamaterials (8, 9) and platforms for energy storage and conversion (10, 11) to integrated electronics (12, 13), electromechanical components (14), optics, and optoelectronics (15). Existing fabrication methods include nozzle- and light-based methods in 3D printing (16–19), stress-controlled bending (20–22), colloidal self-assembly (23, 24), templated growth, and others (25–27). Although each offers powerful capabilities, none is without significant, intrinsic limitations––some in realizable geometries, feature sizes, and/or throughputs, others in access to high-performance materials, and yet others in compatibility with state-of-the-art 2D processing techniques such as photolithography, laser cutting, thin-film deposition, epitaxial growth, etching, and doping.

In this context, routes to 3D mesostructures that exploit nonlinear buckling of 2D precursors initiated through stress relaxation in prestrained elastomeric substrates offer some important capabilities. In particular, these methods provide access to complex 3D architectures with critical dimensions that can range from fractions of a micrometer to many centimeters (28–35) in nearly any class of material, including high-performance semiconductors, metals, polymers, hydrogels, and various heterogeneous combinations of these, all in a manner that maintains full compatibility with well-established 2D fabrication, processing, and growth techniques. The result is a broad set of unique design opportunities in 3D electronic, optic, optoelectronic, biomedical, and robotic systems. In all previously reported cases, the 3D mesostructures formed in this manner remain naturally tethered to the elastomeric substrates used for assembly, as hard–soft hybrid micro/nano systems with low effective moduli and high levels of stretchability, the latter of which can be exploited for biointegration and for mechanical tuning of key properties. In many cases of interest, however, the elastomer itself imposes engineering constraints that prevent application in scenarios that require function at elevated temperatures (e.g., templates for materials growth), with high levels of dimensional stability and/or optical functionality (e.g., precision optical microsystems), or in freestanding forms (e.g., microrobotics). The advances outlined in the following directly address these limitations via approaches that include interfacial photopolymerization, nonlinear mechanical deformation, and physical transfer. Demonstrations of these ideas range from 3D mesostructures as frameworks for guided eutectic phase separation and chemical vapor deposition, to scaffolds for growth, recording, and stimulation of neural networks, to propeller fins and directional electrochemical motors for microrobotics.

Results and Discussion

Freestanding 3D Mesostructures.

In mechanical buckling schemes for the assembly of 3D mesostructures, the elastomer substrates remain critical parts of the system as platforms that hold the 3D structures in their designed shapes. Realization of freestanding structures demands additional ideas, two of which appear in Fig. 1. The first starts with drop casting a liquid, photodefinable polymer (epoxy; SU8, Microchem Corp.) onto a 3D mesostructure with a pipette while on its elastomer assembly substrate (silicone; Dragon Skin, Smooth-On, Easton) precoated with a thin layer of Al₂O₃ (50 nm in thickness). Passing UV light through a photomask mounted on the back side of the substrate photopolymerizes a thin layer of the epoxy at the interface, with size and geometry matched to those of the 3D mesostructure (36, 37). Washing away the unexposed areas and then immersing the entire sample in hydrochloric acid (37% by weight) to remove the Al₂O₃ yields freestanding 3D mesostructures supported by thin epoxy bases. Additional details appear in Methods and in SI Appendix, note 1. The UV exposure dose determines the thickness of the base (SI Appendix, Fig. S1). Examples of this simple process include a bilayer flower-like structure of epoxy (thickness: 7 μm, ribbon width: 50 μm) confined with hollow bases (thickness: $\sim$30 μm, inner radius: 300 μm, outer radius: 1 mm, Fig. 1B), a peacock-like structure of Si–epoxy (thickness: 200 nm/7 μm, ribbon width: 50 μm, Fig. 1C) and a collection of double-floor helices of epoxy (thickness: 7 μm, ribbon width: 50 μm, SI Appendix, Fig. S2A), both on a rectangular base (thickness: $\sim$30 μm, length: 1.3 mm, width: 1 mm), and a jellyfish-like structure of Au–epoxy (thickness: 50 nm/7 μm) on a circular base (thickness: $\sim$30 μm, radius: 1 mm, Fig. 1D). In all cases, the 3D structures are mechanically robust and can be mechanically manipulated onto other objects such as human hairs and needle tips as shown in Fig. 1 F and G and SI Appendix, Fig. S2 B–D, without fracture. Bases with other geometries, such as thin rings (thickness: $\sim$50 μm, inner radius: 700 μm, outer radius: 1.1 mm), are also possible (Fig. 1H). Finite-element analysis (FEA) simulations can capture all of the fine details observed in experiment (SI Appendix, Fig. S3A). The success rate of forming 3D freestanding with photodefined bases is ∼90% (i.e., of ∼50 samples, 5 failed). Fracture of the bases, typically near the bonding sites of the 3D mesostructures (SI Appendix, Fig. S4), represents the dominant failure mode. Increasing the thicknesses of the bases can reduce their probability for fracture, thereby improving the yield of this process.

Fig. 1.

Forming freestanding 3D mesostructures. (A) Schematic illustration of a method for forming freestanding 3D mesostructures on thin, photodefined bases, for the case of a jellyfish-type geometry (i) forming a 3D mesostructure (yellow) on an elastomeric substrate (blue) with thin, sacrificial layers of Al₂O₃ (bright red) between the bonding sites and the elastomer, (ii) casting, curing, and patterned back-side exposure of a layer of photodefinable epoxy (SU8) to define the base, (iii) developing the exposed epoxy to form the base (green) integrated with the bottom of the 3D mesostructure, and (iv) releasing the 3D mesostructures into freestanding objects by immersion in HCl to eliminate the Al₂O₃. (B–D) SEM images of freestanding 3D mesostructures made of epoxy (B), silicon–epoxy bilayers (C), and gold–epoxy bilayers (D). (E) Analytical modeling and FEA results of the flatness ratio (defined in SI Appendix, Fig. S9) versus the ratio of bending stiffness for the jellyfish-like mesostructure on a circular base. (F and G) SEM images of freestanding 3D mesostructures suspended by human hairs (F) and needle tips (G). (H) SEM image of a pillar-like 3D structure confined with a narrow, ring-like hollow base. (I) Analytical and FEA results of flatness ratio versus the ratio of bending stiffness for a ribbon mesostructure on a hollow base. (J) Schematic illustration of a route to freestanding 3D mesostructures that exploits controlled, plastic deformation at locations of highest bending induced by the assembly process. (K) SEM images of freestanding 3D mesostructures made of copper (Left), copper–polymer bilayers (Middle), and copper–silicon bilayers (Right). (L) Analytical and FEA results of springback ratio (defined in SI Appendix, Fig. S12) as a function of copper thickness for the box mesostructure in K (Right). (Scale bars, 500 µm.)

In bases that adopt thin and/or narrow designs, mechanical restoring forces associated with the buckled 3D structures can cause additional changes in shape upon release, as shown in Fig. 1G. The average out-of-plane deformation of the base, in the form of a flatness factor (F), defines the extent (SI Appendix, Fig. S3B). Taking into account the square-root dependence of the curvature on the compressive strain (28), the dimensionless form of this flatness factor (F/R, with R being the radius of the polymer base) exhibits a simple scaling as $F/R=a{\left[E_{3\text{D}}{t}_{3\text{D}}^3/\left(E_{\text{base}}{t}_{\text{base}}^3\right)\right]}^b\sqrt{{\epsilon }_{\text{pre}}/\left(1+{\epsilon }_{\text{pre}}\right)}$ (SI Appendix, note 2), where Et³ is the bending stiffness, with E and t being the elastic modulus and film thickness, respectively; the subscripts “3D” and “base” denote the 3D mesostructure and the base, respectively; a and b are dimensionless parameters that depend on the shape of the 3D mesostructure, as determined by FEA. For the jellyfish-like and ring-like cases in Fig. 1 D and H, this scaling law captures the effect of bending stiffness for different parameter combinations, including cases of circular (Fig. 1E) and hollow (Fig. 1I) bases. This finding applies to a broad variety of examples examined here, obtained with a diverse set of topologies transferred onto flat bases (SI Appendix, Fig. S5).

The second route to freestanding 3D mesostructures relies on controlled plasticity induced during assembly. As illustrated in Fig. 1J, the 2D precursor designs in this scheme incorporate thin metal [copper (Cu) in this case] films, most importantly at locations that undergo strong bending as a consequence of the compressive buckling process. Plastic deformations in the Cu can hold the buckled 3D structures in their original shapes even after release from the assembly substrate. Representative examples in Fig. 1K include 3D structures made of Cu (Left, thickness: 5 μm, crease width: 230 μm, ribbon width: 410 μm), Cu–PI (Middle, thickness: 5 μm/7 μm, crease width: 130 μm, ribbon width: 320 μm), and Cu–Si (Right, thickness: 5 μm/1.5 μm, crease width: 250 μm, membrane width: 820 μm). SI Appendix, Fig. S6 A and B provides millimeter-scale examples.

Springback effects associated with the elastic-plastic response, which depend on both the geometry and the prestrain level (SI Appendix, Fig. S6C), are important to consider. For optimized parameters, the extent of springback can be predictably controlled (SI Appendix, Fig. S7A). Quantitative mechanics analyses (SI Appendix, note 3) yield a simple scaling law for the springback ratio (ρ_s, defined in SI Appendix, Fig. S7B) that characterizes the metal/silicon composite design. For prestrains sufficiently large to induce plastic deformations, ρ_s decreases rapidly with increasing Cu thickness (Fig. 1L), and increases in an almost linear manner with increasing prestrain (SI Appendix, Fig. S7 C and D). This scaling law agrees well with both the results of FEA and experiments, thereby establishing it as a reliable design tool for this process. Fracture at the creases is the major form of failure (SI Appendix, Fig. S8), arising from material defects introduced during the fabrication process that can induce nonuniform, localized plastic deformations, with success rates at around 70% (i.e., of ∼20 samples, 6 failed). The location of crack initiation in the SEM image (SI Appendix, Fig. S8) shows good correspondence with predictions from mechanics modeling on the locations of maximum principal strain. Decreasing the thickness of the copper layer (t_Cu) will reduce the strain concentrations at the crease regions, with the potential to reduce the failure rate. Reducing the strain results in a decreased level of plastic deformations at the creases, which also leads to more pronounced springback. Therefore, a balance between the two different considerations (failure rate and springback effect) should be considered.

Transfer Printing of 3D Mesostructures and Hierarchical Geometries.

Fig. 2A presents a different strategy, in the form of a physical transfer scheme that enables direct, physical micromanipulation of 3D mesostructures, here in the context of a trilayer nested cage. The process begins with geometric transformation of a corresponding multilayer stack of 2D precursors via compressive buckling on a silicone elastomer support. Here, a thin film of aluminum oxide (Al₂O₃, 50 nm in thickness) serves as a sacrificial layer that bonds the precursor to the elastomer at precise, lithographically defined locations. Embedding the resulting structure in wax encapsulates the system to allow removal of the Al₂O₃ (immersion in hydrochloric acid, 37% by weight) and release from the silicone without altering the 3D geometry. Methods inspired by 2D transfer-printing techniques allow controlled retrieval and aligned delivery onto a target substrate coated with a thin adhesive layer [e.g., polydimethylsiloxane (PDMS)], conductive silver pastes, biocompatible tissue adhesives, or others). Removal of the wax completes the process. Detailed procedures for various specific examples appear in Methods and SI Appendix, note 1.

Fig. 2.

Transfer printing of 3D mesostructures and hierarchical geometries. (A) Schematic illustration of the method for a representative case of a multilayer, nested cage structure (i) forming of a 3D mesostructure (yellow) on an elastomeric substrate (blue) with thin, sacrificial layers of Al₂O₃ (bright red) between the bonding sites and the elastomer, (ii) applying wax to encapsulate and confine the mesostructure to hold its shape after release from the elastomer by immersion in HCl to eliminate the Al₂O₃, (iii) transfer printing of wax-encapsulated 3D mesostructure onto a target substrate (gray) coated with an adhesive layer (brown), and (iv) dissolving the wax to complete the process. (B–D) Optical micrographs, SEM images, and FEA results (insets on the right top) of a trilayer nested cage of silicon on quartz (B), triangular kirigami array of epoxy on copper foil (C), and 3 × 4 double-floor helices of gold–polyimide bilayers on a silicon wafer (D). (E and F) Optical images of 3D mesostructures on biological substrates, including a jellyfish-like structure on the leaf of a butterfly orchid (E), and a table-tent mixed array on piece of chicken breast (F). (G) Experimental images and FEA results of a hierarchical mesostructure enabled by transfer printing of first-generation 3D mesostructures (spiral cages and tables) onto a 2D precursor to another cycle of 3D assembly (to yield a box). (Scale bars, 500 μm.)

Fig. 2 B–D and SI Appendix, Fig. S9A illustrate the versatility of this approach via micrographs of 3D multilayer, kirigami, origami, and filamentary–network structures on different planar substrates where PDMS (10 µm in thickness) serves as the adhesive. These examples include trilayer nested cages of device-grade monocrystalline silicon (Si; thickness: 1.5 μm, ribbon width from the inner to outer cages: 30, 50, and 80 μm) on a quartz plate (dielectric substrate, Fig. 2B), triangular kirigami arrays in photodefinable epoxy (SU8; thickness: 4 μm, plate radius: 140 μm) on a Cu foil (conductive substrate, Fig. 2C), 3 × 4 double-floor filamentary networks in gold–polyimide (Au–PI; thickness: 50 nm/8 μm, ribbon width: 50 μm) on a Si wafer (semiconducting substrate, Fig. 2D), and windmill-like origami structures in Au–PI (thickness: 50 nm/8 μm, membrane width: 1.2 mm) also on a Si wafer (SI Appendix, Fig. S9A). SI Appendix, Fig. S9B shows SEM images of raised roof arrays in Au–PI (thickness: 50 nm/8 μm, ribbon width: 50 μm) on Cu foil with conductive silver paste as the adhesive.

Quantitative mechanics modeling by FEA (see details in SI Appendix, note 4) shown in Fig. 2 B–D and SI Appendix, Fig. S10 confirms that the process retains the overall 3D shapes at all regions except for those local to the bonding sites where minor changes can follow from differences between the modulus of the original elastomer support and that of the target substrate. These mechanics calculations also provide insights into the minimum adhesion energy required to prevent delamination of the transferred structures. This energy increases in an approximate linear manner with the compressive strain associated with the 3D assembly process [equal to ε_pre/(1 + ε_pre), where ε_pre is the prestrain)], and reaches ∼12 mJ/m² at ∼80% prestrain for the table structure (SI Appendix, Fig. S11). This requirement, and similar ones for other 3D mesostructures, can be satisfied easily with various different choices of adhesives.

This type of 3D transfer process can be applied equally effectively to curvilinear substrates and biological tissues. In such cases, use of mechanically soft wax materials (e.g., paraffin wax) facilitates conformal contact via slight deformations induced during delivery to the target surface. Examples include a 3D table in Au–epoxy (thickness: 50 nm/7 μm, ribbon width: 50 μm) printed on a pen (∼10 mm in diameter, SI Appendix, Fig. S9C, PDMS as the adhesive), a 3D twisted table in Au–epoxy (thickness: 50 nm/7 μm, ribbon width: 50 μm) printed on the inner surface of a quartz tube (∼8 mm in inner diameter, SI Appendix, Fig. S9D, PDMS as the adhesive), a jellyfish-like structure in Au–PI (thickness: 50 nm/8 μm) printed onto a leaf from a butterfly orchid (∼5 μm in root-mean-square surface roughness, Fig. 2E, PDMS as the adhesive) and a table-tent mixed array in PI (thickness: 8 μm, ribbon width: 50 μm) printed onto a piece of chicken breast tissue [∼35 μm in root-mean-square surface roughness, Fig. 2F, N-butyl cyanoacrylate (Vetbond; 3M) as a biocompatible tissue adhesive]. This last example suggests promising potential in transplantable bioelectronic devices such as blood-flow sensors, mechanical actuators, and electronic tissue scaffolds, as described subsequently. The surface topology in these cases naturally affects the shapes of the 3D mesostructures, to an extent determined by the ratio of the radius of curvature to the lateral size of mesostructure. Evident changes in shape occur when this ratio approaches 1 (SI Appendix, Fig. S12 A and B).

Transfer can also deliver 3D structures onto surfaces that themselves serve as 2D precursors for an additional cycle of 3D assembly. The result yields unusual, hierarchical geometries that would be impossible to construct in a single step. Fig. 2G and SI Appendix, Fig. S13 highlight an example in which five 3D microstructures in PI (the cage in the center; thickness: 12 μm, ribbon width: 50 μm) and Au–PI (four structures that surround the cage; thickness: 50 nm/12 μm, ribbon width: 50 μm) with different shapes mount onto the surfaces of a box-like 3D kirigami structure in Cu–PI (thickness: 9 μm/12 μm). This example, and the one in SI Appendix, Fig. S9 E and F (3D structures with key feature sizes at 10 μm), also illustrate applicability across wide ranges of length scales. Here, and in all other cases, FEA results show good agreement with experiments (SI Appendix, Figs. S12C and S14). The observed failure mode is primarily due to debonding from the adhesive layers, with success rates at around 90%.

Three-Dimensional Mesostructures as Templates for Growth of Functional Materials at High Temperatures.

The collection of schemes summarized in Figs. 1 and 2 establishes many additional possibilities in geometries and applications of the 3D assembly process. A first example uses 3D structures integrated onto quartz and/or Si substrates for high-temperature templated growth of functional materials that have unique optical and electronic properties (Fig. 3 and SI Appendix, Figs. S15–S20). Here (SI Appendix, Figs. S15 and S16), conformal deposition of SiO₂ (2 μm in thickness) onto transferred 3D mesostructures of Si–epoxy followed by high-temperature (600 °C) annealing in air removes the polymer and converts the PDMS adhesive layers into SiO₂, leaving 3D structures made of Si–SiO₂ without any observable changes to the original shapes. SI Appendix, Fig. S17 illustrates three representative examples, including a 3D table of Si–SiO₂ (thickness: 50 nm/2 μm, ribbon width: 10 μm), a 3D helix of SiO₂ (thickness: 2 μm, ribbon width: 50 μm), and a 3D cage of Au–SiO₂ (thickness: 50 nm/2 μm, ribbon width: 50 μm).

Fig. 3.

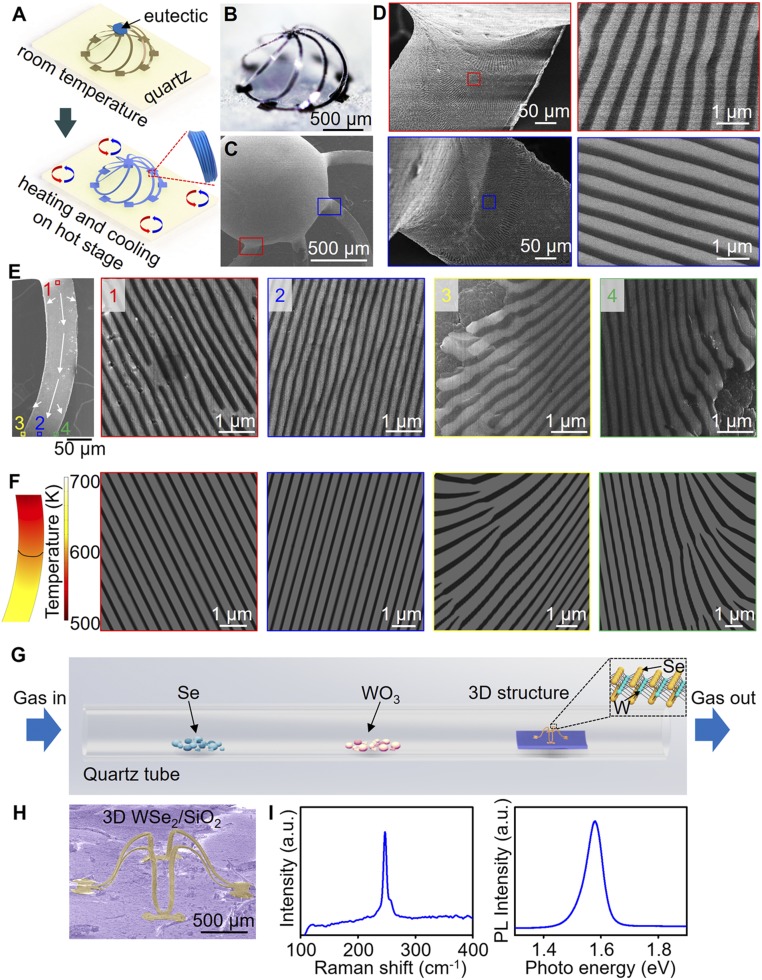
Three-dimensional mesostructures as templates for growth of functional materials at high temperatures. (A) Schematic illustration of the process of guided solidification of AgCl–KCl eutectic structures onto 3D cages of Si–SiO₂ bilayers on quartz. (B) Optical image of a 3D cage of Si–SiO₂ bilayers on quartz annealed in air for 3 h at 600 °C. (C and D) SEM images of the cage with solidified AgCl–KCl eutectic and magnified views of periodical lamellar structures. (E) SEM images of a ribbon component of the cage covered with solidified eutectic material (Left) and corresponding high-magnification views from the top center (red), bottom center (blue), bottom left (yellow), and bottom right (green) of the ribbon. (F) Heat-transfer and phase-field modeling of the solidification of AgCl–KCl eutectic features on one 3D ribbon, including the thermal profile (left frame) and simulated AgCl–KCl structures (right four frames) that correspond to SEM images above. The dark black line in the left frame represents the solidification front. (G) Schematic illustration of the CVD growth of atomic layers of WSe₂ on 3D structures of SiO₂ on a silicon wafer. (H) SEM image of a 3D structure after CVD growth of WSe₂. (I) Raman spectra and PL spectra of WSe₂ on a 3D structure.

One example of the use of these frameworks as 3D templates for material growth and processing involves geometrically guided phase separation in AgCl–KCl eutectics, of relevance partly due to the interesting optical properties that follow from controlled periodic variations in refractive index associated with this system, where length scales typically lie in the nanometer–micrometer range (38, 39). Specifically, directionally solidifying AgCl–KCl eutectic materials in 3D geometries could enable optical devices and metamaterials with unique characteristics difficult or impossible to realize using conventional fabrication schemes. In one example, 3D cages of Si–SiO₂ (thickness: 1.5 μm/2 μm, ribbon width: 50 μm) on quartz substrates yield controlled, AgCl–KCl submicrometer lamellae in 3D (Fig. 3 A–F) as a result of melting and solidification of AgCl–KCl powder (70 mol % AgCl and 30 mol % KCl, 80 mg) on top of the cage. During this process, the material flows downward along the constituent ribbons, such that cooling below the eutectic temperature (T_E ∼ 319 °C) drives solidification and formation of periodic architectures that are strongly influenced by the 3D geometry. SEM images in Fig. 3 C and D illustrate self-organized, periodic lamellar motifs with spacings of $\sim$400 nm (AgCl: bright in SEM image, KCl: dark in SEM image) oriented along the ribbons. Fig. 3E provides additional details on the eutectic structures along a single ribbon. In the center, the lamellar features exhibit long-range order and align to the tangent of the ribbon (red-squared region 1 and blue-squared region 2 in Fig. 3E). The lamellae tend to curve outside near the edges of the ribbon (yellow-squared region 3 and green-squared region 4 of Fig. 3E and SI Appendix, Fig. S18). Heat-transfer simulation results (the left frame in Fig. 3F) explain the outward curvature of the lamellae at the edges of the structures. Specifically, the lower thermal conductivity of the SiO₂ layer (1.3 Wm⁻¹⋅K⁻¹) compared with the Si layer (149 Wm⁻¹⋅K⁻¹) causes the solidification front to lag behind at these regions.

Phase-field simulations utilizing the thermal profile information from the heat-transfer simulations match the experimentally observed eutectic microstructures well (Fig. 3F and SI Appendix, Table S2 and note 5), further confirming the ability of these 3D structures to guide eutectic solidification. SI Appendix, Figs. S19 and S20 show the dimensions and thermal profiles in the simulations, with the phase of each point described by three nonconserved order parameters ($p_{\text{AgCl}}$, $p_{\text{KCl}}$, $p_L$). Each point is constrained ($p_{\text{AgCl}}+p_{\text{KCl}}+p_L=1$), and $p_{\text{AgCl}}=1$ corresponds to the solid AgCl phase, $p_{\text{KCl}}=1$ corresponds to the solid KCl phase, $p_L=1$ corresponds to the liquid phase. This level of control, together with versatility in 3D framework design, suggests unique opportunities in templated growth for optical devices and metamaterials that can operate in the visible and infrared wavelength regimes.

Another example of templated growth is in 2D materials such as graphene and transition-metal dichalcogenides, of interest due to their unusual electrical, optical, magnetic, mechanical, and thermal properties (13, 40, 41). Forming such materials on controlled 3D platforms might be of interest for fundamental or applied studies (13, 42, 43). As an illustration, growth of tungsten diselenide (WSe₂) atomic layers on pillar-like 3D structures of SiO₂ on quartz can be achieved by chemical vapor deposition (CVD). Fig. 3G illustrates the CVD process in a quartz tube furnace where powders of selenium (Se) and tungsten trioxide (WO₃) serve as the precursors for growth on a 3D structure, at set temperatures of 240, 850, and 850 °C, respectively, with argon (flow rate: 20 sccm) as the carrier gas. Vapors of Se and WO₃ react on the surface of the SiO₂ to form an atomic layer of WSe₂ in a conformal manner across the structure. The SEM image in Fig. 3H indicates negligible change in 3D geometry as a consequence of the CVD growth. Raman and photoluminescence (PL) spectra (Fig. 3I) collected from these 3D structures show good agreement with recent reports and confirm the formation of monolayer WSe₂ (44). Similar processes are applicable to other 2D materials and 3D templates.

Three-Dimensional Electronic Scaffolds for Engineered Dorsal Root Ganglion Neural Networks.

Transferred 3D frameworks can also be used for guided growth of biological systems. Sophisticated cellular scaffolds can leverage high-performance components, including various electronic and optoelectronic devices, formed in 2D planar designs, to allow interaction and communication with live cells and tissues in 3D. Potential consequences range from in vitro drug development to in vivo tissue repair (1–3). As a demonstration, 3D bilayer nested cages of epoxy (Fig. 4A) transferred onto optical-quality glass to enable high-resolution, in situ imaging (SI Appendix, Figs. S21–S23), serve as growth platforms for neural networks of dorsal root ganglion (DRG) cells dissociated from explants from rats. The DRG, located on the dorsal root of the spinal nerve, contains the cell bodies of pseudounipolar sensory neurons, along with other types of cells, including satellite glial cells and Schwann cells. From the DRG, sensory neurons project axons that bifurcate, connecting to the central nervous system (CNS) on one end and the periphery of the organism on the other (Fig. 4A, Left). The DRG is an interesting research target due to its relevance in peripheral nerve repair and to its connection to the nonregenerative CNS (45, 46). Presented here, the 3D bilayer cage structure is pretreated to promote cell adhesion with a modified form of poly-d-lysine (PDL) which includes peptides containing the integrin-binding sequence of amino acids, arginine–glycine–aspartic acid (RGD) (Fig. 4A, Right) (47). During the 35 d of cell culture development, the DRG cells organize into networks that exhibit two main modes of interaction with the scaffolds: following the 3D geometries of the scaffolds (left two frames in Fig. 4B and SI Appendix, Fig. S24) and forming “shortcuts” between ribbons (right two frames in Fig. 4B and SI Appendix, Fig. S25). The DRG cells are fixed and immunostained based on neuron-specific (MAP2, red) and glia-specific (GFAP, green) markers to show the organization of cells on the scaffolds by using confocal fluorescence microscopy. Corresponding phase-contrast images are also included in Fig. 4B to delineate the scaffold geometries. These experiments demonstrate that the scaffolds facilitate the reorganization of initially uniform dispersions of cells into hierarchical cellular constructs dictated in part by intrinsic cell properties.

Fig. 4.

Three-dimensional electronic scaffolds for engineered DRG neural networks. (A) Schematic illustration of rat DRG and the cell populations within them (Left), as cultured on 3D mesostructures (Right). (B) Confocal fluorescence micrographs immunostained with antiMAP2 (neurons, red), and antiGFAP (glia, green), and corresponding phase-contrast micrographs of DRG cells cultured on a 3D bilayer cage on a glass slide. (C) Schematic illustrate of the setup for GLIM imaging. “P” stands for polarizer and “NP” stands for Nomarski prism. (D) In situ observation of the migration of a DRG cell on a 3D ribbon. (E) Amira 3D rendering of interribbon DRG cell formations observed via GLIM. (F) Schematic illustration and optical image of a 3D cage with eight integrated and separately addressable electrodes for stimulation and recording. (Insets) Schematic illustration and SEM image of a representative electrode. (G) Impedance and phase measurements of these electrodes evaluated in cell culture medium. (H) Ferrocenecarboxylic acid oxidation test of the electrodes before and after protein treatment. (I) Extracellular action potential stimulation and recording of DRG neurons on 3D electrodes: data collected from one 3D electrode before (Top Left) and after electrical stimulation (Bottom Left), and magnified view of one spike (Right). (Scale bars, 100 μm.)

Gradient light interference microscopy (48) (GLIM, Fig. 4C) can capture the full 3D nature of both the scaffolds and the tissue constructs formed within them, along with intrinsic cell properties. This method offers label-free imaging by use of the gradient of the phase ($\mathrm{\Delta }{Ø}_{\gamma }={\nabla }_{\gamma }Ø$) rather than the phase itself. In situ GLIM time-lapse characterization, summarized in Fig. 4D, highlights the formation of the aforementioned shortcuts over the course of 27 h. Fig. 4E provides a 3D image rendered from the GLIM data (Amira, Inc.) of a single DRG cell bridging cellular structures on two different ribbons, providing information regarding the thickness of the cellular structures. Additional dynamic observations appear in Movie S1.

Integration of microelectrodes into such 3D constructs allows study of the electrophysiological behaviors of the growing DRG neural networks (Fig. 4 E–H and SI Appendix, Figs. S26–S28). Here, exposed circular gold pads (50 μm in diameter, 300 nm in thickness) patterned on 3D cages act as microelectrodes for noninvasive extracellular stimulation and recording of action potentials (Fig. 4F and SI Appendix, Fig. S26). A nanostructured, biocompatible layer of titanium nitride (TiN, 50 nm in thickness) deposited onto these gold pads increases the interfacial surface area and provides capacitive charge injection without generating/consuming chemical species during electric stimulation, thus promoting high-fidelity stimulation/recording. A circuit diagram for the neuron–electrode interface is in SI Appendix, Fig. S27. Electrochemical measurements in Fig. 4G indicate a low impedance (|Z|) for the electrodes in cell culture medium at room temperature. The phase response in Fig. 4G can be attributed to the complex impedance of the interface and the resistance (R_S) of the electrolyte, which is in series connection with the interface. Cyclic voltammetry curves in Fig. 4H demonstrate that the electrodes are electrochemically active, seen here as oxidation waves for a ferrocenecarboxylic acid test analyte measured with and without the RGD-modified PDL pretreatment (i.e., the presence of the TiN and adsorbed cell attachment protein modifies but does not block their electrical activities). The top left frame in Fig. 4I reveals no measurable signals after seeding and culturing DRG neurons for 7 d, consistent with silent behavior during this period (49). After stimulating DRG neurons using one electrode with a biphasic periodic voltage (frequency: 100 Hz, amplitude: 10 V, duration: 1 s), capacitive charging appears in the electrode–electrolyte double layer. The same electrode subsequently detects 12 spikes (the bottom left frame in Fig. 4I). Magnified views in Fig. 4I (right frame) and SI Appendix, Fig. S28 reveal that these spikes have triphasic waveforms with durations of ∼4 ms and amplitudes between 5 and 16 μV, consistent with shapes and durations reported from traditional studies using conventional 2D electrode structures (49, 50).

Transfer printing of 3D electrodes onto existing biological tissues (e.g., chicken, SI Appendix, Fig. S29) and integrating DRG neurons, or other classes of cells, with freestanding 3D mesostructures (SI Appendix, Figs. S30 and S31) represent additional possibilities. These types of 3D electronic scaffolds, as well as extensions of them that integrate other types of chemical, thermal, electrical, and/or optical sensors and actuators, have potential in many areas, including as vehicles to facilitate the development of in vitro models for drug discovery and toxicology and as tools to accelerate basic research on mechanisms by which stimuli can influence the development of cells, of particular relevance in the exploration of strategies to promote wound healing, tissue repair, disease treatment, and others.

Three-Dimensional Microswimmers with Controlled Motion Modes and Trajectories.

The use of freestanding 3D mesostructures integrated with biology suggests their possible role in micro/nanoscale robots for use in biomedicine and other areas. A proof-of-concept described in the following exploits 3D kirigami structures as self-propelled microswimmers with geometrically controlled dynamics and motion trajectories (Fig. 5). The structures include strategically patterned films of platinum (Pt, 100 nm in thickness) to catalyze the production of water and oxygen (O₂) at room temperature upon immersion into hydrogen peroxide (H₂O₂, 30% by weight). Bubbles of O₂ drive movements of the 3D structures in a controlled manner that depends on the placement of the Pt films and the 3D geometries (Movie S2). With Pt on one side of the 3D structure depicted in Fig. 5A, the microswimmer executes linear motions. By contrast, with Pt on four petals and one side of structure as shown in Fig. 5B, curvilinear motions result. SI Appendix, Fig. S32 presents an example of where purely rotational motions follow from Pt on four petals of the same type of system. Multibody dynamics simulations (SI Appendix, note 6) that model the forces induced by the O₂ bubbles as uniform pressures applied at the regions covered with Pt successfully capture the details, including the time-evolving gesture changes (Fig. 5 C and D). The predicted trajectories (Fig. 5 C and D) agree reasonably well with the experiments (Fig. 5 A and B), thereby establishing the models as predictive tools for design. These design possibilities extend the range of engineered motions that are possible in previous versions of related microswimmers but built with comparatively simple designs.

Fig. 5.

Three-dimensional microswimmers with controlled motion modes and trajectories. (A and B) Schematic illustrations, SEM images, and superimposed images of microswimmers designed for linear motion (A) and curvilinear motion (B). (Scale bars, 500 μm.) (C and D) Three-dimensional and top views of the trajectories and configurations of microswimmers predicted by multibody dynamics modeling.

Conclusions

In summary, the concepts in patterned, interfacial photopolymerization, mechanical plasticity, and physical transfer introduced here qualitatively expand the range of geometries and application possibilities available to schemes in 3D micro/nanomanufacturing by mechanical assembly. Broad, diverse collections of examples in 3D mesostructures, including those with sophisticated hierarchical and freestanding designs, both on and in varied substrate environments, hint at the scope of engineering options. Active, 3D templated control and sensing of growth processes in advanced, synthetic materials systems and living, biological tissues foreshadow some specific, promising opportunities in fundamental and applied research.

Methods

Fabrication of Freestanding 3D Mesostructures with Polymer Bases.

The process began with the assembly of 3D mesostructures with Al₂O₃ (50 nm in thickness) sacrificial layers deposited between the bonding sites and the elastomer substrates as described in SI Appendix, note 1. Drop casting photodefinable epoxy (SU8) with pipettes onto 3D mesostructures assembled on silicone substrates precoated with a thin layer of Al₂O₃ (50 nm in thickness) and then baking at 65 °C for 10 min and at 95 °C for 19 h created a solid encapsulation around the 3D geometry. Passing UV light through a photomask mounted on the back side of the substrates, followed by baking at 65 °C for 2 min and 95 °C for 2 min and immersion in developer, yielded a thin polymer base. The photomask defined the lateral geometries of this base; the UV exposure dose defined its thickness. Immersing the samples in HCl (37% by weight) for 19 h dissolved the Al₂O₃ sacrificial layers to form freestanding 3D structures.

Fabrication of Freestanding 3D Mesostructures Utilizing Plastic Deformation.

Fabrication began with spin coating a thin layer of PI (400 nm in thickness) onto the front side of a copper film (5 μm in thickness). The film was then laminated onto a PDMS-coated (10 μm in thickness) glass substrate, with PI side in contact with the PDMS. Photolithography, wet etching, and reactive ion etching (RIE) patterned the copper and PI layers in a matching geometry. Retrieving the structure onto water-soluble tape allowed deposition of Ti/SiO₂ (5 nm/50 nm in thickness) via electron beam evaporation through a shadow mask to define the bonding sites. The remaining steps followed the procedures described in SI Appendix, note 1. Preparation of freestanding 3D mesostructures of copper–polymer involved spin coating a thick layer of PI (7 μm in thickness) on the back side of a copper film to yield copper–polymer bilayers and then following the procedures described above, with extra photolithography and RIE steps to pattern the thick PI layer to cover the noncrease areas of copper. Preparation of freestanding 3D mesostructures of copper–silicon bilayers began with transfer printing 2D silicon structures (1.5 μm in thickness) onto a partially cured layer of PI (adhesive layer, 1.5 μm in thickness, baked at 110 °C for 1 min) spin casted on the back side of copper film. The subsequent procedures followed those described above, with the addition of steps for fully curing the PI adhesive layer, and photolithography and RIE to define silicon structures to match the noncrease areas of the copper patterns.

Transfer Printing of 3D Mesostructures.

Formation of 3D mesostructures followed previously reported schemes in mechanically guided 3D assembly, but with Al₂O₃ sacrificial layers deposited between the bonding sites and the elastomer substrates, as described in SI Appendix, note 1. Transfer printing of 3D mesostructures began with melting solid wax at elevated temperatures (125 °C for Crystalbond 509 or 90 °C for paraffin wax) and then casting this material onto the samples to cover the entire 3D mesostructures. Cooling to room temperature resolidified the wax to form a sacrificial carrier. Immersion in HCl (37% by weight) for 24 h removed the Al₂O₃ to release the structures embedded in wax. Transfer printing allowed delivery onto target substrates coated with one of three different types of adhesives: PDMS, silver conductive epoxy (CircuitWorks CW2400, ITW Chemtronics), or tissue adhesives (Vetbond, 3M). After curing the adhesive at room temperature, immersing the samples in an organic solvent (acetone for Crystalbond 509 and toluene for paraffin wax) at 70 °C dissolved the wax to complete the process.

Fabrication of 3D Hierarchical Structures.

The process started with the release of five first-order 3D structures embedded in wax (Crystalbond 509) using the steps described above. Transfer printing and dissolving the wax delivered these structures onto a patterned, PDMS-coated (10 μm in thickness) copper foil to yield a 2D–3D hierarchical precursor for a second buckling-induced assembly process. Defining bonding sites on this precursor through selective deposition of Ti/SiO₂ (5 nm/50 nm in thickness by electron beam evaporation) with a shadow mask, bonding it to a prestrained elastomer substrate, and releasing the prestrain transformed this hierarchical precursor into a corresponding 3D structure via procedures described in SI Appendix, note 1.

Fabrication of 3D Electronic Scaffolds.

Fabrication of 3D electronic scaffolds began with spin coating a sacrificial layer of poly(methyl methacrylate) (PMMA, 60 nm in thickness) on a silicon wafer. Spin casting, photolithography, and RIE formed a pattern of PI (4 μm in thickness) on top of the PMMA. Next, spin casting, photolithography, electron beam evaporation, wet etching, and lift-off patterned Cr/Au/TiN (10 nm/300 nm/50 nm in thickness) onto selected regions of the PI structure as the electrodes and conductive interconnections. Another layer of PI (3 μm in thickness) was patterned on top of the first, in a matching geometry but with circular openings to define the electrodes (50 µm in diameter). Dissolving the PMMA in acetone enabled transfer of the resulting 2D precursors to water-soluble tape. Electron beam evaporation of Ti/SiO₂ (5 nm/50 nm in thickness) through a shadow mask defined bonding sites. The remaining steps followed procedures described in SI Appendix, note 1.

Fabrication of 3D Microswimmers.

Preparation of 3D microswimmers started with thermal oxidation to form a layer of SiO₂ (800 nm in thickness) on a silicon wafer. Spin coating, photolithography, electron beam evaporation, and lift-off then formed strategically designed patterns of Ti/Pt/Cr (5 nm/50 nm/5 nm in thickness) as the catalysts. Next, spin coating and photolithography defined patterns of SU8 (7 μm in thickness). The remaining steps followed the procedures for fabrication of freestanding 3D mesostructures with polymer bases, as described above.

Guided Solidification of AgCl–KCl Eutectic Structures on 3D Cages of SiO₂–Si Bilayers.

Preparation of the eutectic AgCl–KCl involved mixing as-received AgCl (99.999%; Sigma Aldrich) and KCl (99.99%; Sigma-Aldrich) as per the eutectic composition (70 mol % AgCl and 30 mol % KCl), followed by melting in a glass vial at 470 °C for 2 h in a tube furnace. The air-cooled eutectic was broken into small pieces using agate mortar and pestle. A small piece (∼80 mg) was placed on top of the 3D mesostructure. The setup was heated to 450 °C on a Linkam THMS600 hot stage and held at that temperature for 5 min. The eutectic melted and flowed down along the ribbons of the 3D mesostructure. Deactivating the hot stage resulted in cooling at a rate of ∼140 °C/min, allowing the solidification to occur from top to bottom.

Thermal Profile and Phase-Field Modeling of Eutectics.

The temperature profile of one ribbon of the 3D cage structure during solidification was calculated using COMSOL. Dirichlet boundary conditions were applied to the top (300 K) and bottom (700 K) of the ribbon and the heat equation was solved, attaining the temperature profiles before equilibrium that represent the state during solidification. The shape of the solidification front (approximated by the eutectic temperature isocontour) was calculated to observe the effect of differing thermal conductivities in the component materials of the composite ribbon structure (Si, SiO₂, air). Solidification of the AgCl–KCl eutectic down the ribbon structure was simulated using the phase-field model developed by Folch and Plapp (51). Additional control over the nucleation of new lamellae at the solidification front was utilized to account for the lamellae that terminate at the edge of the ribbon. Simulations were conducted over computational domains representing the edge of the ribbon and the center of the ribbon, separately. Further details can be found in SI Appendix, note 5.

Adult Rat DRG Isolation.

All work with live animals was performed in full compliance with local and federal guidelines for the humane care and treatment of animals and in accordance with approval by the University of Illinois at Urbana–Champaign IACUC animal use protocol. Sprague-Dawley male rats were quickly decapitated using a sharp guillotine. Spine vertebrae were surgically cut on both side between pedicle and lamina in the area of the facet of superior articular process. This cut exposed the spinal cord, which was removed. Additional cuts on sides and in the middle of the ventral portion of the vertebral column created two chains of vertebra pieces with easily visualized DRGs. DRGs were removed using fine forceps and placed into the Hibernate A (Life Technologies) solution located on ice.

Scaffold Preparation for DRG Cell Seeding and Culture.

Transfer-printed 3D scaffolds were rinsed with ethanol, then sterilized by exposure to UV light (300-W lamp) in a laminar flow hood for 30 min. Scaffolds were immersed in a 100 µg/mL RGD-modified PDL solution for 60 min before seeding (47).

Primary Adult Rat DRG Dissociation and Seeding.

Approximately 20 lumbar and thoracic DRGs from an adult rat were collected and stored in Hibernate A up to 2 d before seeding. The Hibernate medium was then removed. The DRGs were treated with 0.25% collagenase in DRG physiological media for 1.5 h at 37 °C, and shaken a few times during incubation, strongly upon completion of the incubation period. The DRGs were centrifuged (200 × g) for 2–3 min to remove supernatant, and washed with HBSS. After another centrifugation to remove the HBSS, the DRG were incubated in 0.25% trypsin with EDTA for 15 min at 37 °C. The DRGs were centrifuged to remove supernatant, resuspended in DRG media + 1% FBS for 50 s to inactivate trypsin, and triturated. Once some of the pellet resettled, the supernatant was collected and centrifuged for 5 min at 200 × g. The resulting pellet was washed with HBSS and centrifuged to remove supernatant. Pelleted cells were resuspended in the desired amount of DRG media containing the glial inhibitor AraC, usually 1 mL per 10 original DRGs. After cell seeding, the scaffolds were incubated overnight at 37 °C to allow for cell attachment before an additional 2 mL per Petri dish (3 mm in diameter) of DRG media was added. The medium was changed twice every 7 d. The concentration of AraC in the DRG media was kept at 0.3 µM from the moment of cell seeding until the end of the culture.

Immunocytochemistry–Neuronal Extensions (MAP2)/Glia (GFAP)/Nuclei Staining.

After 7 d in culture, neurons were rinsed 3× with PBS (37 °C), immersed in 4% paraformaldehyde (37 °C) at ambient temperature (23–25 °C) for 20 min, and then rinsed again with PBS, five times (last time for 5 min on a shaking board). A PBS solution containing 0.25% Triton X-100 was added to the samples for 10 min to permeabilize cellular membranes, before rinsing again with PBS five times. The samples were incubated in a 5% Normal Goat Serum for 30 min before rinsing again with PBS five times. The samples were then exposed to primary rabbit anti-MAP2 antibody at a 1:1,000 dilution at 4 °C overnight and then rinsed five times with PBS. Next, the samples were exposed to primary chicken anti-GFAP (1:1,000 dilution) antibody at room temperature for 1 h and then rinsed five times with PBS. Secondary Alexa 594 anti-rabbit and Alexa 488 anti-chicken IgG antibodies (1:200) were added to the samples, which were allowed to incubate for 1 h (23–25 °C). The samples were then rinsed with PBS five times. Finally, the samples were incubated with 0.002% DAPI in PBS for 1 min and rinsed with deionized water for 30 s–1 min. The samples were covered with two to three drops of antifade mounting media and a coverslip was set on top of the mounted sample.

Confocal Fluorescence Imaging.

Tiled images of the entire scaffold were obtained using the 10× objective, were composed of either 2 × 2 tiles (927 µm × 927 µm) or 4 × 4 tiles (1,270 µm × 1,270 µm), depending on the scaffold architecture. These 10× magnification images required no immersion medium and were taken with an EC Plan-Neofluar N.A. = 0.3. In addition, single-frame and 2 × 2 tiled images (250 µm × 250 µm) were captured using a 40× objective for data analysis. The 40× magnification images were taken in Zeiss Immersol 518 immersion medium with refractive index n = 1.518 at 23 °C. Oversampling for all images was at least 2× as dictated by Nyquist sampling. Pinhole diameters for all images ranged from 1 to 2 airy unit (AU), with most measurements performed at ∼1.6 AU. A 20% tile overlap and online stitching permitted high-resolution large-area imaging of scaffold structures of interest. Confocal z stacks were reconstructed using ImageJ software.

Electrophysiological Recordings.

All extracellular recordings used an ac-coupled differential amplifier (model 1700; A-M Systems). Signals were filtered with a 300-Hz high-pass filter and a 1-kHz low-pass filter. Amplified signal was digitized by Digidata 1322A (Molecular Devices) at 6.7 kHz. Other methods related to three-dimensional electronic scaffolds for engineered DRG neural networks appear in SI Appendix, note 7.