TOUCHSTONE: An ab initio protein structure prediction method that uses threading-based tertiary restraints

Abstract

The successful prediction of protein structure from amino acid sequence requires two features: an efficient conformational search algorithm and an energy function with a global minimum in the native state. As a step toward addressing both issues, a threading-based method of secondary and tertiary restraint prediction has been developed and applied to ab initio folding. Such restraints are derived by extracting consensus contacts and local secondary structure from at least weakly scoring structures that, in some cases, can lack any global similarity to the sequence of interest. Furthermore, to generate representative protein structures, a reduced lattice-based protein model is used with replica exchange Monte Carlo to explore conformational space. We report results on the application of this methodology, termed TOUCHSTONE, to 65 proteins whose lengths range from 39 to 146 residues. For 47 (40) proteins, a cluster centroid whose rms deviation from native is below 6.5 (5) Å is found in one of the five lowest energy centroids. The number of correctly predicted proteins increases to 50 when atomic detail is added and a knowledge-based atomic potential is combined with clustered and nonclustered structures for candidate selection. The combination of the ratio of the relative number of contacts to the protein length and the number of clusters generated by the folding algorithm is a reliable indicator of the likelihood of successful fold prediction, thereby opening the way for genome-scale ab initio folding.

The inability to predict routinely the tertiary structure of a protein from its amino acid sequence remains one of the most challenging unsolved problems in biophysics. Contemporary approaches to this problem can be divided roughly into three categories of increasing complexity: (i) homology modeling (1, 2), (ii) threading (3, 4), and (iii) ab initio folding (5–9). The first two methods use the structures of already solved proteins as templates. The third, the ab initio method, does not require that an example of the fold of the protein of interest be previously solved. In principle, such an approach is very powerful; however, significant unresolved issues remain. First, there are problems with the search algorithms used to explore the protein's conformational space (10). Second, the energy functions used to evaluate the fitness of a given conformation cannot, in general, distinguish the native structure from alternative, protein-like decoys (11). To compensate for the imperfections in the energy functions, another way of selecting representative folds is required, with clustering of the structures being a promising approach (7–9). Finally, for a folding algorithm to be practical, one has to develop criteria that allow one to estimate the likelihood that a given prediction will be successful.

In this article, we address each of these issues and present the results on the application of our ab initio method to a representative 65-protein test set. To restrict the protein's conformational space, we employ the SICHO (SIde CHain Only) model (5) to represent the protein as a lattice chain connecting vertices, each vertex lying at the center of mass of a given residue's α-carbon and side chain heavy atoms. To restrict further the conformational search as well as to improve the correlation of energy with fold quality, we used both predicted secondary structure and tertiary contacts. Residue-based contacts are extracted from a threading protocol (3) for the generation of consensus contacts even when the proteins used to predict these contacts are not globally similar to the fold of the sequence of interest. Quite often, the number and accuracy of the predicted contacts is sufficient to guide the model into the neighborhood of the native fold. Another set of restraints that contains predicted distances of pairs of residues in local fragments also is used. To address the issue of fold selection, we combine the structure-clustering algorithm of Betancourt and Skolnick (12) with a knowledge-based heavy-atom pair potential selection procedure to select representative structures (13). This statistical potential is distance-dependent and is based on 167 types of residue-specific heavy atoms. Finally, to estimate the likelihood that the prediction is successful, we show that the number of predicted contacts and the number of obtained clusters from the simulations provide a confidence level for the prediction quality. We call the entire procedure TOUCHSTONE.

Methods

The SICHO Lattice Model.

The SICHO model is a 646-neighbor lattice embedded in an underlying cubic lattice grid with a spacing of 1.45 Å. The energy function consists of three types of terms: E_generic, E_specific, and E_rest. E_generic biases the model chain toward protein-like conformations and is independent of amino acid sequence (5). E_specific is a sequence-dependent potential that consists of three terms: a weak bias toward the predicted secondary structure (14, 15), a sequence-dependent short-range geometric bias for fragments (16), and a protein-specific pairwise potential (17). Homologous proteins are removed from the database when the latter two terms are calculated. As in threading discussed below, no proteins with an E value < 0.01 are considered. The last term, E_rest, is the newly derived restraint term extracted from threading (see below).

Prediction of Tertiary Restraints.

Two kinds of restraints are incorporated into our prediction scheme. The first type is the side chain contact predictions derived from the threading results. Here, a pair of residues predicted to be in contact must be at least five residues apart in the sequence. Quite often in threading, even when no template is hit with a significant Z score, common contacting substructures can be found in templates with weak Z scores from which the contacts can be predicted. Sometimes these common substructures that are in contact have a similar secondary structure and sometimes they do not, but they can experience similar interaction environments. In particular, our new threading algorithm, PROSPECTOR (3), uses four different scoring functions. For the top 20 scoring structures (the top 5 structures from each scoring function), whose Z scores are >1.3, a contact is predicted when it is present in 25% of the structures. These contacts are also converted to a protein-specific pair wise potential (17), which is used in the subsequent threading iteration. The consensus contacts are again collected, and the procedure is repeated for a third time. Then, all of the predicted contacts from all stages are used in the folding simulation. The restraint potential is not designed to satisfy all predicted contacts, because they are not exactly correct. This inaccuracy is because these contacts are sometimes collected from incorrect hits and also because of alignment problems in the threading algorithm. Therefore, a given structure has a preferable energy gain when a predicted contact is satisfied within plus or minus two residues. Furthermore, there is no energy penalty when at least 50% of all of the predicted contacts are satisfied. The 50% figure comes from the average accuracy of the contact prediction, which is 73.6% (see below). The threshold should be lower than this average accuracy to ensure that too many wrong contacts are not enforced. In practice, for 62 of the 65 proteins, the accuracy is better than 50%. Finally, local distance restraints are derived from multiple sequence alignments for short-sequence fragments no more than four residues in length.

We employ replica exchange Monte Carlo (18) to search conformational space. This protocol has been shown to be more effective than the conventional simulated annealing in a simple protein-like model (19). Fifty copies at different temperatures covering the entire folding transition region are used. Then, the conformations in trajectories at the three lowest temperatures are clustered (12). It takes about 100–150 days of computer time to perform 50 runs for a protein. Clustering is performed in two steps: (i) first, structures are clustered within each trajectory, and (ii) the resulting obtained centroids are clustered again among the different trajectories.

Structure Selection with an Atomic Potential.

A heavy-atom knowledge-based potential (13) is used to rank-order the structures generated from the Monte Carlo simulations; then, they are rebuilt at atomic detail (20). A scan-and-delete procedure is applied, in which the lowest energy structure is selected for each cluster, and then all of the higher-energy structures in the same cluster are removed. After this process, all of the nonclustered structures and the lowest energy structures from each cluster remain. The top five lowest energy structures are then selected.

Results and Discussion

The 65 test proteins, which cover a wide variety of protein types, are given in Table 1. There are 4 small proteins (which have little secondary structure), 21 α-proteins, 20 β-proteins, and 20 αβ-proteins, according to the CATH classification (21) obtained from the biomolquest server (22). The proteins range in length from 39 to 146 aa. The test set also includes 40 proteins randomly chosen from the paper by Simons et al. (7).

Table 1.

Predicted tertiary restraints and folding simulation results

ID	N (aa)	Npc	δ = 2	Nloc	Best (Å)	LowE (Å)	Noc	Clus (Å)	Atom (Å)	Simons
Small
1ixa	39	74	0.78	18	2.8	4.7	7	4.5 (2)	4.3
1fc2C	44	28	0.86	49	2.7	7.7	2	3.6 (2)	3.5
6pti	57	109	0.69	29	5.1	9.3	7	7.3 (5)	6.7
1rpo	61	22	0.55	222	2.8	11.9	4	3.7 (4)	3.6	92-40-27
α
1bw6A	56	86	0.91	99	3.5	4.9	7	5.0 (1)	4.9	1-1-1
2ezh	65	64	0.59	127	3.7	5.2	6	5.2 (2)	5.7	1-1-1, 17-14-14
1c5a	66	66	0.56	71	4.0	8.5	6	5.8 (3)	5.8
1hp8	68	23	0.91	219	3.2	4.0	2	4.9 (1)	4.7	*-3-1
2bby	69	77	0.84	148	3.1	4.9	5	4.9 (1)	4.9	*-1-1
1ftz	70	81	0.88	164	2.3	3.1	2	2.9 (1)	3.0
1pou	71	191	0.67	102	2.7	3.4	10	3.7 (1)	2.9	28-28-28
1lea	72	100	0.92	88	2.9	3.9	5	3.7 (1)	3.6	*-89-89
1kjs	74	40	0.63	212	3.7	6.7	6	4.5 (1)	4.6	1-1-1
1ner	74	101	0.71	131	3.0	4.6	6	4.1 (1)	4.0	*-60-25
1nkl	78	24	0.71	217	2.3	3.3	5	3.0 (1)	2.9	15-15-15
1aoy	78	144	0.97	120	3.3	4.5	5	4.5 (1)	4.4	*-*-1
1a32	85	98	0.28	272	5.0	7.3	4	7.4 (1)	5.6	1-1-1
1ngr	85	184	0.74	146	2.4	4.2	3	2.7 (1)	2.8	*-3-3
2af8	86	59	0.54	157	4.3	13.0	10	8.9 (2)	8.4	*-1-1
2ezk	93	14	0.71	193	8.6	14.3	8	10.4 (1)	11.2	210-210-210
2lfb	100	57	0.63	203	4.0	10.3	10	5.8 (5)†	5.1	*-*-*
256bA	106	91	0.87	175	2.8	4.0	3	3.4 (1)	3.1
1hmdA	113	143	0.83	151	2.3	3.1	5	2.6 (1)	2.8
1hlb	138	384	0.12	327	2.6	3.4	9	2.6 (1)	2.7	*-*-7
1mba	146	262	0.89	276	2.6	3.5	3	2.7 (1)	2.7
β
1tfi	50	58	0.88	18	2.4	6.2	5	4.4 (3)	4.1
1bq9A	53	67	0.96	67	4.1	9.4	8	6.9 (1)	6.5	*-72-2
1nxb	53	90	0.88	40	2.6	7.4	3	3.6 (3)	3.7	*-*-4
1shg	57	137	0.76	116	3.1	5.7	8	4.9 (1)	4.1
1vif	60	19	0.74	23	3.7	5.8	12	4.5 (1)	4.8	*-*-3
1fas	61	117	0.97	3	2.6	3.8	3	3.4 (1)	3.7
1csp	64	92	0.95	50	2.8	4.1	7	3.6 (1)	3.7	8-8-2
1sro	66	64	0.30	141	4.0	7.8	6	6.4 (2)	6.5	1-1-1
1pse	69	83	0.76	74	6.5	12.2	6	8.4 (4)	8.5	*-*-*
1ah9	71	113	0.78	76	6.8	9.8	8	9.9 (2)	8.4	*-*-*
1iyv	79	72	0.53	115	7.8	12.2	11	10.6 (3)	9.1	*-*-*
1rip	81	77	0.70	85	7.3	12.0	21	9.3 (5)	9.8	*-*-*
1tit	89	271	0.92	144	1.9	3.3	3	2.4 (1)	2.2	*-*-*
1wiu	93	224	0.97	158	2.5	3.3	3	2.6 (1)	2.9	*-*-*
2pcy	99	168	0.92	72	3.2	4.3	4	4.0 (1)	4.0
1ksr	100	162	0.91	126	3.8	7.4	9	5.1 (1)	5.9	*-*-*
1tlk	103	380	0.69	103	4.3	7.2	2	5.4 (1)	5.6
1thx	108	216	0.94	109	2.2	3.2	5	2.2 (1)	2.8
4fgf	121	162	0.84	103	7.6	8.3	5	9.7 (1)	9.2	*-*-*
2azaA	129	142	0.89	79	3.9	5.7	3	4.5 (1)	4.9
αβ
1gpt	47	71	0.96	4	2.2	5.6	4	4.4 (1)	3.3
2fdn	55	33	0.33	10	6.5	10.2	10	9.6 (4)	7.6	*-*-1
1pgx	56	61	0.30	54	1.9	2.8	4	2.3 (1)	2.2	13-1-1
2ptl	60	67	0.18	78	2.2	3.0	3	2.5 (1)	2.9	1-1-1
2fmr	65	82	0.83	89	3.3	4.3	2	3.7 (1)	3.6	2-2-2
1cis	66	112	0.82	46	3.6	4.7	6	4.8 (2)	4.6
1ctf	68	61	0.56	56	5.7	10.7	5	9.6 (2)	8.2	4-4-4
1stu	68	19	0.74	99	3.4	10.2	10	8.0 (4)	5.9	*-42-42
1ubi	76	147	0.92	75	2.3	4.2	8	3.6 (1)	2.9
1vcc	77	30	0.60	59	4.3	10.7	6	9.9 (1)	8.6	*-*-19
1poh	85	191	0.67	124	2.7	3.5	5	3.3 (1)	3.3
1ife	91	125	0.54	83	5.8	12.3	10	6.3 (3)	6.5
2sarA	96	123	0.96	50	3.5	4.9	6	4.1 (1)	4.8
1stfI	98	25	0.80	74	4.8	10.6	9	11.6 (3)	7.8
1tsg	98	156	0.63	100	7.3	9.3	7	8.7 (1)	8.1	*-*-*
1shaA	103	308	0.85	119	3.1	4.7	13	3.6 (1)	4.0
1erv	105	261	0.93	129	2.3	3.0	2	2.3 (1)	2.6	*-*-5
5fdl	106	54	0.52	86	8.3	14.0	5	9.7 (4)	10.2
1cewI	108	154	0.92	103	4.7	7.1	5	7.2 (1)	7.0
1pdo	121	181	0.74	203	4.0	7.7	2	6.5 (2)	6.2	*-*-3

ID, proteins that have a cluster in the top five lowest energy clusters equal to or below 6.5 Å rmsd from the native are emphasized in bold. N, the length of the protein chain. N_pc, the number of predicted contacts. δ = 2, accuracy of the predicted contacts allowing two residue shifts. N_loc, the number of predicted short-range distant restraints for local fragments. Best, the rmsd in angstroms of the best structure in the entire simulation trajectories. LowE, the rmsd of the lowest energy structure. N_oc, the number of obtained clusters. Clus, the rmsd of the best cluster centroids in the top five “lowest energy” clusters. Those cases ≤6.5 Å rmsd are in bold. The order of the cluster is written in the parentheses. Atom, the rmsd of the best structure selected in the top five by the atomic potentials where results better than the best cluster centroids are emphasized in bold. Simons, the results shown in table 1 of the paper by Simons et al. (7). Ranks of the cluster centers for three cutoffs are shown, from left, 5, 6, and 7 Å rmsd. The asterisks are used when no clusters are detected. Underlined numbers with a single line are those cases in which we considered our results to be better, whereas the ones with a double underline indicate those cases in which our results are worse. 

^† The ninth cluster is 4.9 Å rmsd. 

The tertiary restraints and the results of the folding simulations are also found in Table 1. The average accuracy of secondary structure predictions (Q₃) is 79.1%. On average, 33.0% of the long-range contacts are correctly predicted, and, on average, 73.6% are correct within plus or minus two residues. However, the average error in the rms deviation (rmsd) of the local fragment prediction was 0.38 Å. It also should be noted that the number of predicted contacts has substantially increased from our other study (6), where correlated mutation analysis was used.

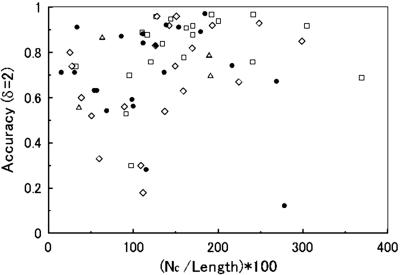
Fig. 1 shows that the prediction accuracy grows as the number of predicted contacts increases; accuracy reaches 70% for 34 of 45 cases where the number of restraints is larger than the number of protein residues. This improvement occurs because the enhancements of the number and the accuracy of the restraints occur at the same time when the threading algorithm detects significant common local structures.

Figure 1.

The number of the predicted long-range contacts and their accuracy (within onr or two residues) are shown. Proteins of the different structural type are plotted separately: ▵, small proteins; ●, α-helical proteins; □, β-proteins; ⋄, αβ-proteins. Nc, number of clusters.

For 47 of 65 proteins (72.3%), at least one cluster centroid (within the top five centroids, at most) with an rmsd 6.5 Å from native was successfully obtained (44 ≤ 6 Å, 39 ≤ 5 Å). 2lfb has the ninth cluster with an rmsd of 4.9 Å. All have the correct topology. When the atomic potential is used in the selection procedure, 50 proteins were successfully predicted (46 ≤ 6 Å, 39 ≤ 5 Å). If the best structure is counted, 58 proteins (89.2%) have a structure ≤6.5 Å. On the other hand, the lowest energy structures of only 36 proteins satisfy this criteria. This result shows the imperfections in the current folding potentials as well as the practical usefulness of selecting structures by populations with the clustering algorithm. In many cases, there are pairs of topological mirror-image structures (where the chirality of turns is reversed, but helices, if present, are right-handed) among the obtained cluster centroids. It is interesting to note that when one of the centroids has the proper fold, in most cases the mirror-image structure is also obtained.

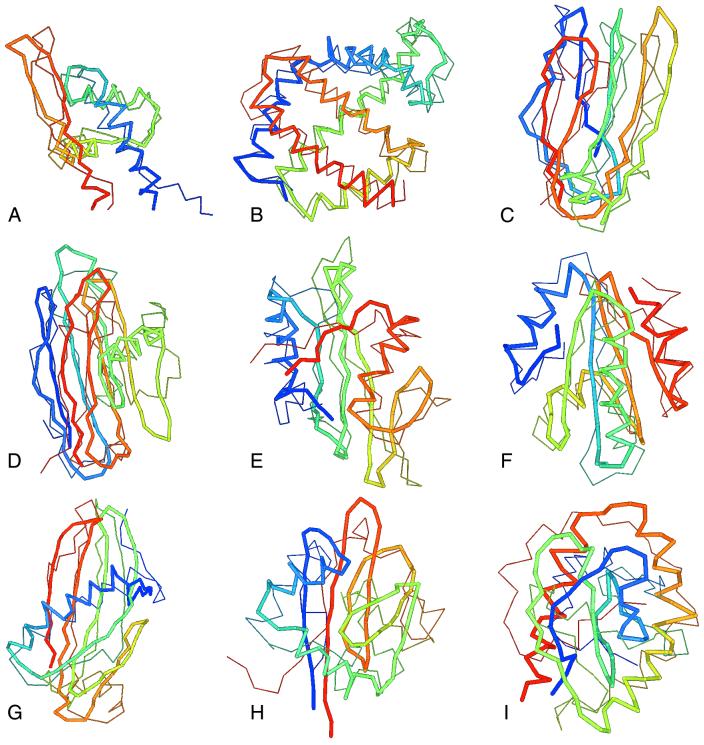
Fig. 2 shows some representative results for the superimposition of the experimental and predicted structures extracted from the native-like cluster. The predicted (experimental) structures are shown by thick lines and the native structures are shown by thin lines. Fig. 2A shows 1aoy, whose rmsd from native is 4.5 Å. Fig. 2B shows 1mba whose rmsd from native is 2.7 Å. Fig. 2C shows the best cluster centroid of 2pcy whose rmsd from native is 4.0 Å. Fig. 2D shows 2azaA, with an rmsd from native of 4.5 Å. Fig. 2E shows 1shaA with an rmsd from native of 3.6 Å. Fig. 2F shows 1erv whose rmsd from native is 2.3 Å. Fig. 2G shows 1cewI, whose rmsd from native is 7.2 Å. Fig. 2H shows 1tsg, whose rmsd from native is 8.7 Å, and Fig. 2I shows 5fd1 whose rmsd from native is rmsd 9.7 Å.

Figure 2.

Superimposition of representative experimentally observed and predicted structures. The predicted structures are shown by thick lines, and the native structures are shown by thin lines. (A) 1aoy, rmsd 4.5 Å. (B) 1mba, rmsd 2.7 Å. (C) 2pcy, rmsd 4.0 Å. (D) 2azaA, rmsd 4.5 Å. (E) 1shaA, rmsd 3.6 Å. (F) 1erv, rmsd 2.3 Å. (G) 1cewI, rmsd 7.2 Å. (H) 1tsg, rmsd 8.7 Å. (I) 5fd1, rmsd 9.7 Å.

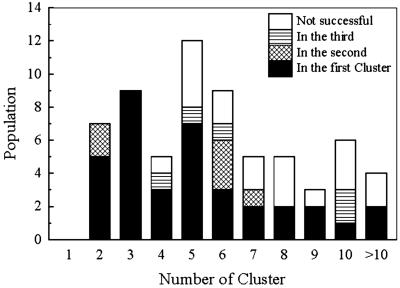
To make an ab initio folding algorithm practical, one has to establish the level of confidence of a given prediction. In the majority of the cases in Fig. 3 there is a proper fold when the number of obtained clusters is small. Indeed, if the number of clusters is equal to or less than five, a proper fold is obtained in 28 of 33 (84.8%) cases. Moreover, all 16 cases were successful when the number of the obtained clusters was two or three.

Figure 3.

The number of successful cases relative to the number of clusters. Black, the successful cluster (rmsd <6.5 Å) is obtained as the first cluster; crosshatch, the second cluster; horizontal hatch, one of the other clusters; white, successful cluster not obtained.

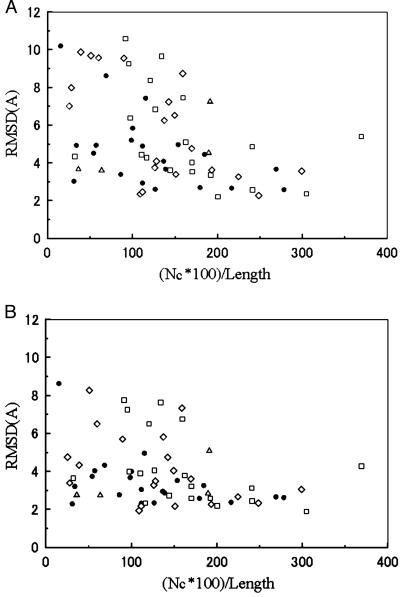
Fig. 4 shows the relationship between the quality of the simulation results and the number of the predicted contacts, which is another indication of how successful the simulation should be. When the number of restraints is more than the number of residues in the sequence, a cluster centroid closer than 6.5-Å rmsd to the native structure is obtained in 32 of 41 cases (78.0%). When the number of restraints is 150% or more relative to the sequence length, the success rate improves further to 88.0% (22 of 25 proteins). A proper fold is always obtained in either of two cases: (i) when the number of obtained clusters is equal to or less than three or (ii) as shown in Table 2, when the number of clusters is less than or equal to five, and the number of provided restraints is 150% or more of the sequence length.

Figure 4.

The number of long-range restraints and the quality of the clusters for each protein. (A) rmsd of the best cluster centroid. (B) rmsd of the best structure among all of the simulations. ▵, small proteins; ●, α-helical proteins; □, β-proteins; ⋄, αβ-proteins. Nc, number of clusters.

Table 2.

Summary of successful predictions with the number of clusters and restraints

Number of clusters	Number of restraints*
	100 or more	150 or more
3 or less	13 /13 (100%)	8 /8 (100%)
5 or less	23 /26 (88.5%)	13 /13 (100%)
7 or less	30 /36 (83.3%)	16 /18 (88.9%)

^*Ratio of the number of the predicted contacts to the number of amino acids in the protein. 

It is important to note that in contrast to other methods (7, 23), both the accuracy of contact prediction and the success rate when the number of predicted contacts is sufficiently large are completely independent of the type of secondary structure of the protein.

There are two situations in which our method failed to obtain a native-like cluster. In the first case, there are no proper structures below 6.5 Å in the predicted structure pool, so that there is no chance to get a resulting proper cluster centroid (eight cases: 2ezk, 1ah9, 1iyv, 1rip, 4fgf, 1ctf, 1tsg, and 5fd1). However, for 4fgf, 1tsg, and 5fd1, the global topology of the best cluster is almost correct (rmsds of 9.7 Å, 8.7 Å, and 9.7 Å, respectively). For 1ah9, the positions of the last two β-strands are exchanged, and the rest of the structure is correct in the seventh cluster centroid (rmsd of 7.5 Å). For 1ctf, even the best structure did not have the correct topology, although its rmsd was <6.5 Å. For the other proteins, global assembly of the correctly predicted local substructures went wrong.

The other undesirable scenario is when there are some proper folds below 6.5 Å in the pool. These folds were neglected or averaged out during the two steps of the clustering procedure because there were too few of them (10 cases: 6pti, 1a32, 2af8, 1bq9A, 1pse, 2fdn, 1stu, 1vcc, 1stfI, and 1cewI). However, for 1a32, the topology of the first cluster centroid is correct despite its poor rmsd. A small number of good structures are included in this cluster, but they are averaged out by a larger number of improper folds. As for 1stu, in the fourth cluster centroids, the direction of the C-terminal helix deteriorated because of the contamination of incorrect structures in the cluster, but the rest of its fold is correct. Interestingly, the eighth cluster centroid of 1stu is the mirror image of the native structure. As for 1cewI, in the first cluster centroid, a β-sheet with a large helix located over it are consensus and thus well reproduced, but the remaining fragment comprising residues 60–80 was distorted. For 1bq9A, structures with an rmsd <5 Å were neglected in the clustering process. For 1pse and 2fdn, there was only one proper structure (rmsd 6.5 Å) in the simulations, which was neglected in the clustering procedure.

Also, we have tried candidate selection by using the atomic potential to address the issue of rare but good quality structures. Furthermore, when the near-native structures do form a cluster, the atomic potential/cluster picking procedure can usually also pick those good candidates in the top five (see below). In each of 65 proteins, five structures are selected for final analysis. The best structures selected by the atomic potential also are shown in Table 1. In three cases, 1a32, 1stu, and 1bq9A, the atomic potential selected near-native structures that don't belong to any cluster, which are 2–3 Å better than cluster-selected ones. In 2fdn, the atomic potential picked a structure 7.6-Å rmsd from native, whereas the best cluster has an rmsd of 9.6 Å. For the rest of the cases, the two methods have comparable performance. With this procedure, we have successfully predicted the near-native structure in 50 of the 65 cases (76.9%), an improvement of 3 proteins.

In examining the 40 proteins also used by Simons et al. (7), our method clearly did better in 19 proteins and worse in 5. For the remaining 16 proteins, the results are almost the same or sufficiently similar; thus, it is hard to say which is better (because of differences in clustering methods).

Conclusions

We have demonstrated that ab initio structure prediction has become more feasible by using tertiary restraints derived from threading results, even when the threaded structures lack the global topology of the target protein. For 47 of 65 proteins, the simulated structures are clustered into a proper fold of less than 6.5-Å rmsd to the native structure. When the atomic potential is used, the number of correct predictions increases to 50 of 65. The resulting structure can be used for further analyses such as functional annotation by matching three-dimensional active-site motifs (24) or for low-resolution ligand docking (25).

Based on the present study, we can draw the following conclusions. First and foremost, by using predicted tertiary restraints of moderate accuracy, it is possible to predict protein structures of up to ≈150 residues in length. For example, 1mba, which is 146-residues long, has folded to 2.7-Å rmsd from native structure, which was not previously possible. Considering the moderate accuracy and abundance of predicted contacts, the restraints are implemented in such a way that only 50% of them need to be satisfied; yet, this is sufficient to guide the conformation toward native-like structures in many cases. Another important point is that this procedure facilitates the correct folding of proteins having any kind of secondary structure. Finally, we have established empirical indicators of successful prediction; these are the ratio of the number of contacts to the protein's size (the number and accuracy is highly correlated) and the number of clusters generated by the folding simulation. These indicators of when folding is successful should be quite useful in blind predictions.

Despite these significant improvements, almost all of the components of the algorithm may have to be revised to increase the fidelity and accuracy of this prediction engine further. For better or worse, the quality of the tertiary restraints dictates the success of our folding algorithm. Thus, additional work to improve their number and accuracy is still required; efforts to improve the threading-based contact prediction protocol as well as the evolutionary methods (6) will be necessary. Furthermore, both the energy function and the conformational search scheme need to be dramatically improved to reduce their reliance on the tertiary contacts. Nevertheless, the current study demonstrates that the methodology has reached a practical level. We note that this fully automated ab initio folding algorithm is one of the components of a unified approach for protein structure/function prediction (26, 27) that also includes generalized comparative modeling and that is applicable for large-scale prediction. Efforts to fold all of the small proteins in Mycoplasma genitalium are estimated to take a minimum of 8,500 CPU days on our cluster.

Abbreviation

rmsd

rms deviation