Summary
Objective
To compare general and disease-based modeling for fluid resuscitation and vasopressor use in intensive care units.
Methods
Retrospective cohort study involving 2944 adult medical and surgical intensive care unit (ICU) patients receiving fluid resuscitation. Within this cohort there were two disease-based groups, 802 patients with a diagnosis of pneumonia, and 143 patients with a diagnosis of pancreatitis. Fluid resuscitation either progressing to subsequent vasopressor administration or not was used as the primary outcome variable to compare general and disease-based modeling.
Results
Patients with pancreatitis, pneumonia and the general group all shared three common predictive features as core variables, arterial base excess, lactic acid and platelets. Patients with pneumonia also had non-invasive systolic blood pressure and white blood cells added to the core model, and pancreatitis patients additionally had temperature. Disease-based models had significantly higher values of AUC (p < 0.05) than the general group (0.82 ± 0.02 for pneumonia and 0.83 ± 0.03 for pancreatitis vs. 0.79 ± 0.02 for general patients).
Conclusions
Disease-based predictive modeling reveals a different set of predictive variables compared to general modeling and improved performance. Our findings add support to the growing body of evidence advantaging disease specific predictive modeling.
Keywords: Disease-based modeling, fluid resuscitation, intensive care units, decision modeling
1. Introduction
A body of literature already exists describing predictive modeling across a range of clinical outcomes in intensive care units. To date, much of this modeling has taken the approach of focusing on general intensive care unit (ICU) populations and an “average” patient [1]. One explanation for this is the tendency for clinical trials to enroll heterogeneous group of patients in order to maximize external validity of the findings, however, predictive models developed using this approach often perform poorly when applied to specific subsets of patients [2]. Another explanation for general population modeling is the lack of data supporting the application of these techniques to smaller subsets.
Recent advancements in modern ICUs have facilitated the capture of human signals with heightened resolution and an imperative to store them electronically. The burgeoning interest in and ability to capture large datasets provides predictive risk modelers with a substrate to apply tools and techniques to a study size that is now statistically robust. Where small groups of patients clustered together under disease headings previously might struggle for statistical robustness, large data sets now seem to be particularly fertile ground for analytics of this type to inform clinical guidelines.
Predictive modeling requires input variables and an outcome of interest [3, 4]. In this study, the chosen outcome is failed fluid resuscitation requiring subsequent vasopressor therapy. Fluid resuscitation therapy is often the first and mainstay treatment for correcting signs and symptoms synonymous with intravascular volume depletion. The goal of this therapy is to maximize preload and increase cardiac output. Effective intravascular pressure is the key for efficient perfusion at the cell level and thus treatment should ideally be started as soon as possible and subsequent therapy titrated against response [5–7]. Subsequent therapy for failed fluid resuscitation and blood pressure support often requires vasopressors. Fluid resuscitation and vasopressor administration are therefore common activities in ICUs and their management is important.
In this paper we compare fluid resuscitation and vasopressor administration predictive models for two disease-based conditions, pneumonia and pancreatitis, and compare these models to that for a general ICU population. We hypothesize that ICU patients with pneumonia and pancreatitis not only will have different models compared to general ICU patients, and that these models will have better performances in regards to prediction of non-response to fluid resuscitation.
2. Materials and Methods
2.1 Study Design and Population
This retrospective cohort study used data from the Multi-parameter Intelligent Monitoring for Intensive Care (MIMIC II) database [8]. This is a large database of ICU patients admitted to the Beth Israel Deaconess Medical Center (BIDMC), collected from 2001 to 2008, and that has been de-identified by removal of all Protected Health Information. The MIMIC II database currently contains more than 25,000 patients and includes high frequency sampled data of bedside monitors, clinical data and demographic data. BIDMC is a 621-bed teaching hospital with 28 medical, 25 surgical (including neurosurgical), 16 cardiothoracic surgical and 8 cardiology ICU beds.
The criteria for patients inclusion included: i) only medical and surgical ICU patients; ii) >15 yrs of age; iii) patients containing at least one measurement for all twenty-five variables from ► Table 2; iv) in the case of multiple ICU admissions, only the first stay was considered to exclude later developed complications; v) patients having at some point during the ICU stay, fluid resuscitation via normal saline or lactated Ringer’s solution at a 250 mL/hour rate, for more than one hour. The criteria for the outcome variable was the use of a vasopressor for more than two hours following initiation of the above-mentioned fluid resuscitation. Thus, we looked for patients who required additional fluid resuscitation in the ICU and predicted among these patients, which ones would respond and which ones would proceed to require vasopressors. A flowchart of the inclusion procedure is depicted in ► Figure 1.
Table 2.
List of variables considered and respective univariate regression analysis. All lab-related variables refer to serum measurements. OR – odds ratio; CI – confidence intervals.
| Variables (units) | All patients | Pneumonia | Pancreatitis | |||
|---|---|---|---|---|---|---|
| Odds Ratio (95% CI) |
p-value | OR (95% CI) |
p-value | OR (95% CI) |
p-value | |
| Heart Rate (beats/min) | 1.06 (1.02 – 1.10) |
0.0056 | 0.94 (0.88 – 1.01) |
0.16 | 0.69 (0.59 – 0.81) |
< 0.001 |
| Temperature (C) | 0.86 (0.82 – 0.89) |
< 0.001 | 0.77 (0.72 – 0.83) |
< 0.001 | 0.43 (0.37 – 0.51) |
< 0.001 |
| SpO2 (%) | 0.89 (0.86 – 0.93) |
< 0.001 | 0.86 (0.81 – 0.93) |
< 0.001 | 1.02 (0.87 – 1.21) |
0.770 |
| Respiratory Rate (breaths/min) | 0.92 (0.88 – 0.96) |
< 0.001 | 1.12 (1.04 – 1.20) |
0.0027 | 0.97 (0.82 – 1.13) |
0.662 |
| GCS Total | 0.62 (0.59 – 0.65) |
< 0.001 | 0.70 (0.65 – 0.76) |
< 0.001 | 0.57 (0.48 – 0.67) |
< 0.001 |
| Hematocrit (%) | 1.31 (1.25 – 1.37) |
< 0.001 | 1.28 (1.19 – 1.37) |
< 0.001 | 1.60 (1.36 – 1.89) |
< 0.001 |
| Platelets (103/μL) | 0.56 (0.53 – 0.59) |
< 0.001 | 0.46 (0.42 – 0.50) |
< 0.001 | 0.42 (0.34 – 0.51) |
< 0.001 |
| WBC – White Blood Cells (103/μL) | 1.69 (1.62 – 1.76) |
< 0.001 | 1.62 (1.50 – 1.74) |
< 0.001 | 1.85 (1.55 – 2.19) |
< 0.001 |
| Hemoglobin (g/L) | 1.37 (1.32 – 1.42) |
< 0.001 | 1.35 (1.26 – 1.45) |
< 0.001 | 1.93 (1.63 – 2.27) |
< 0.001 |
| RBC – Red Blood Cells (106/μL) | 1.28 (1.23 – 1.33) |
< 0.001 | 1.12 (1.04 – 1.21) |
0.0016 | 1.72 (1.45 – 2.03) |
< 0.001 |
| BUN – Blood urea nitrogen (mg/dL) | 1.02 (0.98 – 1.06) |
0.243 | 1.06 (0.99 – 1.14) |
0.089 | 0.73 (0.61 – 0.88) |
0.002 |
| Creatinine (mg/dL) | 1.58 (1.52 – 1.63) |
< 0.001 | 1.55 (1.47 – 1.65) |
< 0.001 | 1.36 (1.19 – 1.57) |
< 0.001 |
| Glucose (mg/dL) | 0.86 (0.82 – 0.90) |
< 0.001 | 1.05 (0.97 – 1.13) |
0.22 | 0.70 (0.59 – 0.84) |
0.001 |
| Potassium (mEq/L) | 1.40 (1.35 – 1.46) |
0.36 | 1.01 (0.94 – 1.09) |
0.67 | 1.06 (0.91 – 1.25) |
0.425 |
| Chloride (mEq/L) | 0.98 (0.94 – 1.02) |
< 0.001 | 1.22 (1.13 – 1.31) |
< 0.001 | 1.16 (0.91 – 1.25) |
0.07 |
| Sodium (mEq/L) | 0.52 (0.50 – 0.55) |
< 0.001 | 0.65 (0.60 – 0.70) |
< 0.001 | 0.69 (0.58 – 0.82) |
< 0.001 |
| Magnesium (mg/dL) | 1.15 (0.95 – 1.38) |
0.003 | 0.98 (0.91 – 1.06) |
0.74 | 1.31 (1.11 – 1.54) |
0.002 |
| NBP – Non-invasive systolic blood pressure (mmHg) | 0.39 (0.37 – 0.41) |
< 0.001 | 0.37 (0.33 – 0.40) |
< 0.001 | 0.54 (0.45 – 0.65) |
< 0.001 |
| NBP – Non-invasive mean blood pressure (mmHg) | 0.47 (0.45 – 0.49) |
< 0.001 | 0.45 (0.41 – 0.49) |
< 0.001 | 0.57 (0.48 – 0.67) |
< 0.001 |
| Arterial pH | 0.54 (0.52 – 0.57) |
< 0.001 | 0.47 (0.44 – 0.50) |
< 0.001 | 0.41 (0.34 – 0.48) |
< 0.001 |
| Arterial Base Excess (mEq/L) | 0.38 (0.36 – 0.40) |
< 0.001 | 0.32 (0.30 – 0.35) |
< 0.001 | 0.49 (0.39 – 0.61) |
< 0.001 |
| Lactic Acid (mg/dL) | 2.0 (1.97 – 2.11) |
< 0.001 | 2.18 (2.05 – 2.31) |
< 0.001 | 3.09 (2.69 – 3.58) |
< 0.001 |
| Urine Output (mL) | 0.73 (0.69 – 0.76) |
< 0.001 | 0.66 (0.60 – 0.72) |
< 0.001 | 1.25 (1.05 – 1.48) |
0.012 |
| Age (yr) | 1.19 (1.14 – 1.24) |
< 0.001 | 1.09 (1.02 – 1.17) |
0.015 | 1.23 (1.40 – 1.25) |
< 0.001 |
| SOFA | 1.62 (1.54 – 1.70) |
< 0.001 | 1.52 (1.40 – 1.65) |
< 0.001 | 0.77 (0.67 – 0.90) |
0.007 |
Figure 1.
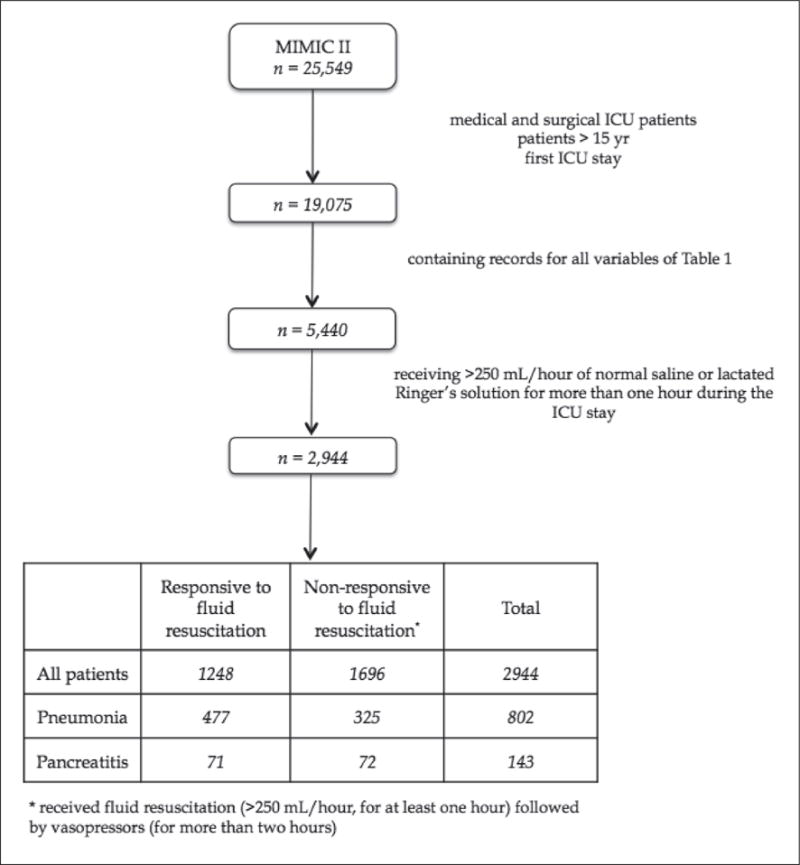
Patient selection flowchart
We addressed elements of data preprocessing as follows: 1) missing data was imputed consistent with the accepted last value carried forward method [9, 10]; 2) outliers were addressed using the inter-quartile range method [9]; 3) normalization of the data used the min-max procedure; and 4) data time points were rounded to closest heart rate samples using a gridding approach [12]. As previously mentioned, the primary outcome variable was vasopressor administration, and for modeling purposes this outcome was defined as binary: one if vasopressors were administered and zero if vasopressors were not administered (► Figure 2). For both outcomes, fluids were a prerequisite representing some attempt at fluid resuscitation, and we critiqued for normal saline and lactated Ringer’s solutions as the most commonly used infusions, and the infusions of choice for hypovolemic shock as recommended by the College of Surgeons [13, 14]. The list of vasopressors applicable to the data extraction and recommended by expert advisors included: phenylephrine, norepinephrine, dopamine, vasopressin, and epinephrine.
Figure 2.
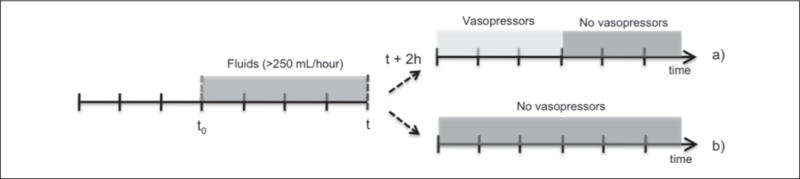
Two case scenarios: a) patient is non-responsive to fluid resuscitation (>250 mL/hour) and vasopressor therapy is required in the next two hours; b) patient is responsive to fluid resuscitation (>250 mL/hour) and does not require vasopressors in the next two hours (fluid resuscitation is maintained at >250 ml/hour, replaced by fluid management protocol at <250 mL/hour). t0 − initial time of analysis; t − current time; t + 2 h – prediction time.
The variables included represent time series, where the number of samples depends on the amount of time a patient received fluids. An example of the first scenario of ► Figure 2a would be a patient starting receiving fluids at 1 am and requiring vasopressors at 10 am. After 6 hours receiving vasopressors (4 pm) the patient no longer needs them and starts receiving fluids until 8 pm. From 8 pm on, the patient no longer needs fluids or vasopressors. For this patient, a total of 19 samples (8 pm – 1 am) for each of the variables from ► Table 1 are passed to the model. The outcome variable is also formed by 19 samples where from 1 am to 8 am (2 hour prediction window) they would take the value 0, from 8 am to 2 pm the value 1, and from 2 pm until the 8 pm again the value 0. Bringing together all samples for each variable and for all patients forms the complete dataset. This complete dataset is then randomly divided into two subsets: one for feature selection and another for model validation.
Table 1.
Baseline characteristics of the study populations of patients. Values were measured as median (interquartile range) or % (n/total). ICU – intensive care unit; LOS – length of stay; SOFA – Sequential Organ Failure Assessment.
| All | Pneumonia | Pancreatitis | p-value | |
|---|---|---|---|---|
| No. of patients, n | 2944 | 802 | 143 | n/a |
| Age, yr | 67 (12) | 68 (12) | 59 (12.3) | <0.01 |
| Male, % | 56.4 | 55.8 | 55.9 | n/a |
| Mortality, % | 46.1 | 58.7 | 50.3 | n/a |
| Hospital LOS, days | 13 (7.0) | 20 (10.5) | 19 (10.3) | NS |
| ICU LOS, days | 6.0 (4.9) | 12.0 (4.4) | 11.5 (3.9) | NS |
| Mean APACHE III* | 62(12) | 63 (13) | 63 (12) | NS |
| Mean SOFA | 9 (6.5) | 9 (6) | 10 (7) | NS |
| Time between admission and initiation of fluid resuscitation, hours | 6.5 (28.3) | 15(69) | 8.0 (45.1) | NS |
| Total time receiving fluid resuscitation, hours | 4.8 (7) | 5 (7) | 6.6 (10.8) | < 0.05 |
| Total volume of fluids received, ml | 3000 (4600) | 3000 (5000) | 4500 (5500) | <0.01 |
| Rate of fluids administration, mL/hour | 667 (510) | 576 (460) | 638 (606) | NS |
| Patients on vasopressors, % | 57.6 | 40.9 | 49.6 | n/a |
| Time between initiation of fluid resuscitation and initiation of vasopressors, hours | 4 (12.6) | 7 (16) | 4 (11) | NS |
| Total time receiving vasopressors, hours | 1.8 (8) | 5 (12) | 7 (14) | < 0.05 |
n/a – non applicable
NS – not statistically significant (p>0.05)
due to the lack of data neurologic abnormalities (0 – 48 points) and chronic health evaluation (0 – 23 points) were not added to the score
Our modeling was undertaken on two disease-based groups of patients, one with an ICD-9 diagnosis of pneumoniaa and another with an ICD-9 diagnosis of pancreatitisb. These two models were then compared to all subjects representing the general ICU population. The choice of pancreatitis and pneumonia reflected both good patient numbers, but also the belief that these two disorders are anatomically and pathologically distinct which would improve modeling performance and clinical applicability. The choice of ICD-9 codes for patient selection was based on the same approach used by Angus et al. [15] and Martin et al. [16]. However, as argued elsewhere [17], ICD-9 administrative data may not accurately reflect the true prevalence of comorbidities in hospitalized patients, so we also employed natural language processing (NLP) to supplement the identification of patient cohorts. This NLP was performed using a very simple word segmentation of the physicians and nurses’ notes, and identification of a set of keywords. Keywords for pneumomia included: “pneumonia”, “pneum” and “pna”; keywords for pancreatitis included: “pancreatitis”, “sap” and “pctt”.
For inputs to the model we utilized the twenty-five variables shown in ► Table 2. These were determined with expert advice and adhering to the following criteria: i) routinely acquired ICU variables (e.g., bedside monitors and laboratory tests); ii) pneumonia severity index and Ranson’s criteria for acute pancreatitis; iii) the variables selected as inputs were limited by patients with enough measurements; and iv) all chosen inputs should be independent with minimal correlation.
2.2 Model Definitions and Construction
Fuzzy modeling (FM) was selected as a modern approach with rules-based outcomes particularly suited to clinical scenarios. Fuzzy modeling is a tool that captures subjective clinical decision making in a non-linear algorithm that is then suitable for computer implementation [18]. This approach is appealing as it provides not only a transparent, non-crisp model, but also a linguistic interpretation in the form of if-then rules, which can potentially be embedded into clinical decision support processes [19, 20]. In this work, first-order Takagi-Sugeno (TS) fuzzy models [19] were used.
In this work, first-order Takagi-Sugeno (TS) fuzzy inference systems [19] were used, which are described by rules of the type:
Ri: If x1 is Ai1 and … and xM is AiM then y = ax + b, i = 1, 2,…, K where, K is the number of rules, x is the input vector, M is the number of inputs (features), AiM is the antecedent fuzzy set and y is the consequent function (output) for rule Ri. The overall output is determined through the weighted average of the individual rule outputs. Given that this is a classification problem, and that we have a linear consequent, a threshold t is required to turn the continuous output y ∈ [0, 1] into the binary output y ∈ {0, 1}. In this way, if y < t then y = 0, and if y ≥ t then y = 1. This threshold t was determined during the feature selection stage (by maximizing the value of AUC) and used during the model validation stage. The number of rules K, the antecedent fuzzy sets AiM and the consequent parameters are determined using fuzzy clustering in the product space of the input and output variables [20]. These models were developed based on the Matlab Fuzzy Logic Toolbox.
2.2.1 Feature Selection
Feature selection (FS), from the clinical point of view, is a process that reveals new predictive variables that had not been previously considered relevant to a given medical condition. From the engineering point of view, it is a crucial step in order to reduce model complexity and remove inputs that are redundant or do not improve the classification performance [20]. In Mendonça et al., a detailed description of the sequential forward selection search approach used here is reported [21]. Briefly, a model is built for each of the features in consideration and evaluated using a certain performance criterion. The feature that returns the best value of the performance criterion is the one selected. Then, other feature candidates are added to the previous best model, one at a time, and evaluated. Again, the combination of features that maximizes the performance criterion is selected. This procedure is repeated until the value of the performance criterion stops increasing. In the end, all the relevant features for the considered process should be obtained. Discrimination based on the area under the receiver-operating curve (AUC) [23, 24], was used as the performance criterion in our study. The main advantage of this technique relates to its simplicity, graphical representation, and transparent interpretation of the results, while the main disadvantage relates to fact that it is greedy and thus susceptible to finding local maxima [22].
2.2.2 Statistical Analysis
In the present work, we used the t-test as the test statistic to evaluate the hypothesis that the different between the means is significant. This test was applied to the means of the AUC, Specificity and Sensitivity, comparing each group of patients’ models in a pair-wise fashion.
2.2.3 Model Construction
To train and test the models, the dataset was initially randomly divided into two subsets of the same size: one for feature selection and the other for model assessment (MA). In the FS data subset, a combination of sequential forward selection with fuzzy modeling or logistic regression was performed to find the subset of features that produces the best AUC. The best model was selected after ten rounds of training and testing upon the FS data subset, using respectively 60% and 40% of the data. This 60/40 selection was random for each of the rounds.
In order to assess the validity and robustness of the discovered model, a 10-fold cross-validation was performed in the MA data subset [25]. Values of AUC, sensitivity, specificity and goodness of fit are reported for this validation step.
To further test our hypothesis and to assess the validation of the models, we have tested two additional scenarios. The first consisted of applying the general model generated using the all patient’s FS dataset, on the pneumonia and pancreatitis MA datasets, respectively. This scenario tests the performance of the models when similar patients populations are used. The second scenario tests the performance of the models when similar features are used. We have created two additional models on the MA dataset of the general population using the variables selected for the pneumonia and pancreatitis groups, and compare them with the specific models developed on their respective populations’ MA datasets.
3. Results
From the inclusion criteria, exclusion criteria, and preprocessing, a total of 2944 patients were selected. From these 2944 patients, 802 had an ICD9 diagnosis of pneumonia and 143 an ICD9 diagnosis of pancreatitis. Clinical and demographic characteristics of these groups are shown in ► Table 1. No significant differences were found between the pneumonia and pancreatitis subgroups with respect to hospital length of stay, ICU length of stay, APACHE III, or SOFA scores. Age (p < 0.05) was significantly different between the two subgroups.
Fluid and vasopressor administration is also shown in ► Table 1. Pancreatitis patients received both a greater overall volume of fluids and received vasopressors for longer periods than did patients with pneumonia.
The effect size and p-values obtained from the univariate logistic regression analysis of the initial set of variables is shown in ► Table 2. Correlation analysis between the variables showed three significantly correlated groups (p < 0.05). Firstly, hemoglobin, red blood cell count, and hematocrit; and secondly, mean non-invasive blood pressure and systolic non-invasive blood pressure, and thirdly arterial pH and arterial base excess. To strengthen the analysis we removed hemoglobin, red blood cell, mean non-invasive blood pressure, and arterial pH.
With regards to the number of rules generated, 4 rules (deriving from 4 clusters) were obtained for the general patients group while 3 rules were obtained for the pneumonia and pancreatitis groups.
► Figure 3 shows the cumulative stepwise performance contribution of each of the variables to the relevant models. From this figure, it is can be seen that only a few of the first variables significantly (p < 0.05) increase the value of AUC. In other words, the first variables selected by the forward selection approach have a significantly higher contribution to the models than the remaining variables. Arterial base excess, lactic acid, and platelets are common to all of the groups. Pneumonia patients add non-invasive systolic blood pressure and white blood cells, and pancreatitis patients add temperature to the models.
Figure 3.
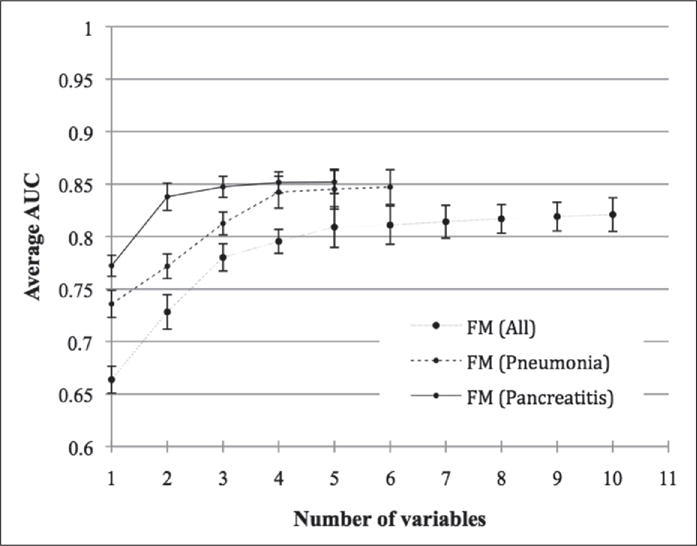
Evolution of area under receiver-operating curve (AUC) along with the stepwise inclusion of each of the variables pertaining to each best fitted fuzzy modeling (FM) for: a) All patients, b) Pneumonia and c) Pancreatitis patients.
Performance metrics in ► Table 4 show: i) satisfactory discrimination for all three groups of patients; and ii) significantly different (p < 0.05) values of AUC, specificity and sensitivity between different groups of patients. Pneumonia and pancreatitis patients returned an AUC of 0.82 ± 0.02 and 0.83 ± 0.03, while general patients re turned an AUC of 0.79 ± 0.02. Respective AUC curves are presented in ► Figure 4.
Table 4.
Results of the 10-fold cross validation step on the model assessment (MA) subset using, for each patients’ subgroup and modeling technique, the respective complete set of most predictive variables derived from the feature selection stage.
| All Patients | AUC | 0.79 ± 0.02 |
| Specificity | 0.78 ± 0.03 | |
| Sensitivity | 0.79 ± 0.02 | |
| Pneumonia | AUC | 0.82 ± 0.02 |
| Specificity | 0.81 ± 0.03 | |
| Sensitivity | 0.82 ± 0.04 | |
| Pancreatitis | AUC | 0.83 ± 0.03 |
| Specificity | 0.82 ± 0.04 | |
| Sensitivity | 0.84 ± 0.03 |
Figure 4.
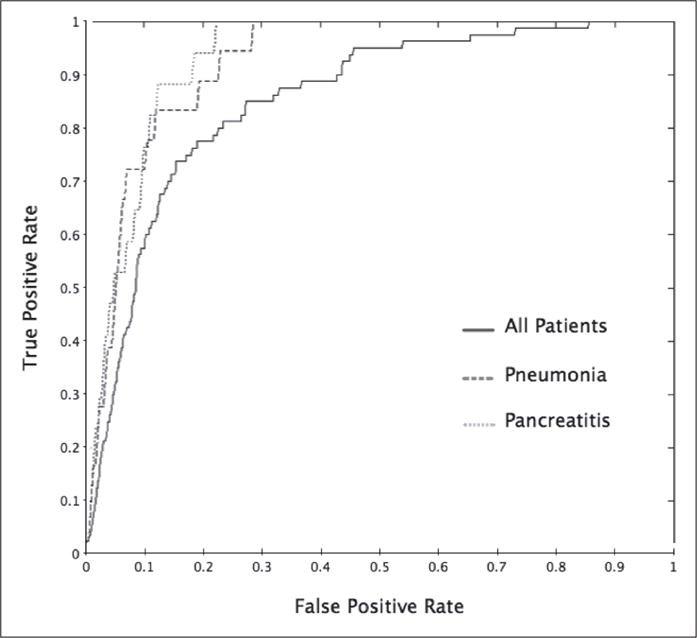
Receiver-operating curves (ROC) of the most predictive fuzzy model for all patients, pneumonia patients and pancreatitis patients
Given the risk of comparing mixed scenarios, i.e. combining comparison using different features with different patient populations, ► Table 5 and ► Table 6 present respectively the results corresponding to the performance of the models when similar patients populations are used, and when similar features are used.
Table 5.
Results of the 10-fold cross validation step on the model assessment (MA) subset of the pneumonia and pancreatic patients, using the general model developed in the feature selection stage
| Pneumonia patients (all patients’ features) |
Pancreatitis patients (all patients’ features) |
|
|---|---|---|
| AUC | 0.76 ± 0.02 | 0.78 ± 0.03 |
| Specificity | 0.74 ± 0.03 | 0.77 ± 0.02 |
| Sensitivity | 0.76 ± 0.03 | 0.78 ± 0.04 |
Table 6.
Results of the 10-fold cross validation step on the model assessment (MA) subset of the general population, using pneumonia and pancreatitis most predictive features from the feature selection stage
| All patients (pneumonia features) |
All patients (pancreatitis features) |
|
|---|---|---|
| AUC | 0.77 ± 0.03 | 0.75 ± 0.04 |
| Specificity | 0.77 ± 0.02 | 0.76 ± 0.03 |
| Sensitivity | 0.76 ± 0.03 | 0.73 ± 0.03 |
From ► Table 5 follows that general models perform significantly worse (p < 0.05) when applied to the pneumonia and pancreatitis MA datasets, as compared to using the best-fitted pneumonia and pancreatitis models in the same datasets. From Table 6 follows that using pneumonia and pancreatitis best features in the general patient population dataset leads to significantly inferior (p < 0.05) results than using this features in the respective patients’ populations.
To crosscheck our findings, we compared the models with a more traditional modeling approach using logistic regression. We observed the same phenomenon: namely, a core set of variables common to all three groups, and different variables added to the pneumonia and pancreatitis sub-groups. We note different variable selection between the fuzzy logic and logistic regression models, and this is explainable with a more detailed description of the modeling algorithms. However, this difference does not detract from the key findings and is not a key focus of this article. Similarly, during the feature selection step we also compared the performance of sequential forward selection with backward elimination. Backward elimination selected in general more features, however, the performance of the models did not significantly change.
4. Discussion
Our interest in this study was primarily to explore the consequences for predictive risk modeling of a group of patients aggregated together as general ICU patients, as compared to a more granular assessment of disease-based subsets of ICU patients. Our key finding is that variable selection is significantly different between general patient groups and disease-based groups. Furthermore, not only are the variables different, but the modeling performance is also improved in the disease-based groups. Pneumonia and pancreatitis patients returned, respectively, an AUC of 0.82 ± 0.02 and 0.83 ± 0.03, while general patients returned an AUC of 0.79 ± 0.02. The validation of these results was confirmed by the testing of two additional scenarios. The first tested the performance of the models when similar patients populations are used, and the second tested performance of the models when similar features are used. There are several implications from these findings.
Firstly, the trend towards large datasets and advanced analytics is opening new frontiers of knowledge discovery and creating opportunities for challenging existing models and paradigms. MIMIC II is one of the most complete ICU datasets. However, only recently we have been able to consider subsets of the data for specific conditions, such as we have studied here, with sample sizes that are robust enough to support clinical guidelines and new thinking.
Secondly, our purpose was not to make clinicopathological correlations between individual variables and the underlying pathology, but rather to draw attention to the utility inherent in our study design which, utilizes common and easily acquired ICU data such as temperature and heart rate. These features are likely to increase usability and have meaningful application in low resource environments.
Thirdly, these results could have implications for a number of generalized predictive index scores that are currently utilized in ICUs. Scoring tools such as SOFA and APACHE are generalized predictive instruments with more of a focus on physiological parameters that may indirectly imply disease. For example, impaired renal function is an input into some of these generalized formulae and may indirectly imply a chronic renal disease such as glomerulonephritis amongst all other renal pathology. In contrast, patient specific disease-based modeling can specifically use glomerulonephritis as an inclusion criteria, and bring with it into the model other associated and attendant variables that chronic renal disease may not. Current generalized index scores undoubtedly have a place as they are predicated on a few quick, easily-acquired assessments, as compared to disease-based predictive risk modeling which is more algorithmically intensive and time consuming. It is possible that generalized and focused predictive modeling can together serve valuable goals. Index scores may continue to provide excellent quick assessments, but when critical management decisions are being made at the edge of probabilities, disease-based models may more accurately inform decision-making.
There are some limitations to the analysis and interpretation of these results. First, several variables often referred to in the literature as being related to shock and vascular perfusion were not taken into account due to their inconsistent capture in the database. These variables include invasive arterial blood pressure and central venous pressure. However this is mitigated with the inclusion of other significant blood pressure measurements including systolic blood pressure and mean blood pressure. Second, despite the goal of maximizing sensitivity while maintaining specificity, a few false negatives were still present. This can be further explained as the non-detection of patients not responsive to fluid resuscitation (and thus more likely to require vasopressor therapy within 2 hours (false negatives)), and this may occur due to: i) patients simply deteriorated too fast (within the 2-hour window) to be caught by the algorithms; ii) additional information was available to the clinician but not to the algorithms, and the clinicians intervened due to patients’ conditions other than hemodynamic instability. Expert opinion and review of the data suggests the numbers of cases in this category is low. Finally, our findings findings of improved accuracy with patient subset-specific models were demonstrated in only two clinical conditions from a single center, and these findings may need to be validated in other scenarios using data from multiple ICUs.
5. Conclusions
Improved technology means that larger amounts of data can be captured daily at the point of care, turning specific groups of patients representative enough for researchers to explore them. These patient-specific data, together with modern predictive modeling tools, allow challenging existing generalized guidelines and models of care.
In this work we bring together both the tools and the clinical data environment to demonstrate the power of disease-based modeling compared to general modeling – the gold standard in clinical practice. We recommend further work be done to revisit some of the existing ICU risk models and that disease-based modeling across a range of pathologies be explored.
Table 3.
List of variables selected and area under receiver-operating curve (AUC) for the best fitted fuzzy modeling (FM), for each patient group, model after the forward selection procedure, using the feature selection (FS) subset.
| Number of variables selected | Variables selected | AUC | |
|---|---|---|---|
| All Patients | 10 | Arterial base excess Lactic Acid Platelets Sodium Non-invasive systolic blood pressure White blood cells SOFA BUN Creatinine SpO2 |
0.83 ± 0.01 |
| Pneumonia | 6 | Arterial base excess Platelets Non-invasive systolic blood pressure Lactic acid Sodium White blood cells |
0.85 ± 0.01 |
| Pancreatitis | 5 | Lactic acid Platelets Temperature Arterial base excess Sodium |
0.89 ± 0.01 |
Acknowledgments
The authors would like to acknowledge the help and space provided by the Division of Clinical Informatics of the Beth Israel Deaconess Medical Center and the Massachusetts Institute of Technology. Both human and technical resources were available through them and were critical for the development of this work. This work is supported by the Portuguese Government under the following programs: project PTDC/SEMENR/100063/2008, Fundação para a Ciência e Tecnologia (FCT), and by the MIT-Portugal Program and FCT grants SFRH/BPD/65215/2009, SFRH/43043/2008 and SFRH/43081/2008, Ministério da Educação e da Ciência, Portugal.
Footnotes
Pneumonia ICD-9 codes: 003.22; 020.3; 020.4; 020.5; 021.2; 022.1; 031.0; 039.1; 052.1; 055.1; 073.0; 083.0; 112.4; 114.0; 114.4; 114.5; 115.05; 115.15; 115.95; 130.4; 136.3; 480.0; 480.1; 480.2; 480.3; 480.8; 480.9; 481; 482.0; 482.1; 482.2; 482.3; 482.30; 482.31; 482.32; 482.39; 482.4; 482.40; 482.41; 482.42; 482.49; 482.8; 482.81; 482.82; 482.83; 482.84; 482.89; 482.9; 483; 483.0; 483.1; 483.8; 484.1; 484.3; 484.5; 484.6; 484.7; 484.8; 485; 486; 513.0; 517.1
Pancreatitis ICD-9 codes: 577.0; 577.1; 577.2; 577.8; 577.9; 579.4
References
- 1.Celi LAG, Tang RJ, Villarroel MC, et al. A Clinical Database-Driven Approach to Decision Support: Predicting Mortality Among Patients with Acute Kidney Injury. Journal of Healthcare Engineering. 2011;2:97–110. doi: 10.1260/2040-2295.2.1.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Strand K, Flaaten H. Severity Scoring in the ICU: A Review. Acta Anaesthesioogical Scandinavica. 2008;52(4):467–478. doi: 10.1111/j.1399-6576.2008.01586.x. [DOI] [PubMed] [Google Scholar]
- 3.Bellazzi R, Diomidous M, Sarkar IN, Takabayashi K, Ziegler A, McCray AT. Data Analysis and Data Mining: Current Issues in Biomedical Informatics. Methods Inf Med. 2011;50(6):536–544. doi: 10.3414/ME11-06-0002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Peek N, Combi C, Tucker A. Biomedical Data Mining. Methods Inf Med. 2009;48:225–228. [Google Scholar]
- 5.Alam HB. Advances in resuscitation strategies. Int J Surg. 2011;9(1):5–12. doi: 10.1016/j.ijsu.2010.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Alam HB, Rhee P. New developments in fluid resuscitation. Surg Clin North Am. 2007;87(1):55–72. doi: 10.1016/j.suc.2006.09.015. [DOI] [PubMed] [Google Scholar]
- 7.Boluyt N, Bollen CW, Bos AP, Kok JH, Offringa M. Fluid resuscitation in neonatal and pediatric hypovolemic shock: a Dutch Pediatric Society evidence-based clinical practice guideline. Intensive Care Med. 2006;32(7):995–1003. doi: 10.1007/s00134-006-0188-4. [DOI] [PubMed] [Google Scholar]
- 8.Saeed M, Lieu C, Mark R. MIMIC II: A massive temporal ICU database to support research in intelligence patient monitoring. Computers in Cardiology. 2002;29:641–644. [PubMed] [Google Scholar]
- 9.Clifford GD, Long WJ, Moody GB, et al. Robust parameter extraction for decision support using multimodal intensive care data. Philosophical transactions, Series A, Mathematical, physical, and engineering sciences. 2009;367:411–429. doi: 10.1098/rsta.2008.0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Allison PD. Missing Data. 2001. (Sage University Papers Series on Quantitative Applications in the Social Sciences). [Google Scholar]
- 11.Hoaglin D, Mosteller F, Tukey J, editors. Understanding Robust and Exploratory Data Analysis. New York: John Wiley & Sons; 1983. [Google Scholar]
- 12.Cismondi F, Fialho A, Vieira S, Sousa J, Reti S, Howell M, et al. 2011 IEEE Symposium on Computational Intelligence and Data Mining (CIDM) Paris: 2011. New methods to processing misaligned, unevenly sampled time series containing missing data; pp. 224–231. [Google Scholar]
- 13.Committee on Trauma. Advanced Trauma Life Support, Student Course Manual. 6th. Chicago: American College of Surgeons; 1997. Shock; pp. 87–107. [Google Scholar]
- 14.EAST. Clinical Practice Guidelines: Endpoints of Resuscitation NGC:003293. Eastern Association for the Surgery of Trauma; 2003. p. 28. [Google Scholar]
- 15.Angus DC, Linde-Zwirble WT, Lidicker J, Clermont G, Carcillo J, Pinsky MR. Epidemiology of severe sepsis in the United States: analysis of incidence, outcome, and associated costs of care. Crit Care Med. 2001;29:1303–1310. doi: 10.1097/00003246-200107000-00002. [DOI] [PubMed] [Google Scholar]
- 16.Martin GS, Mannino DM, Eaton S, Moss M. The epidemiology of sepsis in the United States from 1979 through 2000. N Engl J Med. 2003;348:1546–1554. doi: 10.1056/NEJMoa022139. [DOI] [PubMed] [Google Scholar]
- 17.Quan H, Parsons GA, Ghali WA. Validity of information on comorbidity derived from ICD-9 — Critical care medicine administrative data. Med Care. 2002;48:675–685. doi: 10.1097/00005650-200208000-00007. [DOI] [PubMed] [Google Scholar]
- 18.Bates JHT, Young MP. Applying Fuzzy Logic to Medical Decision Making in the Intensive Care Unit. Am J Respir Crit Care Med. 2003;67(7):948–952. doi: 10.1164/rccm.200207-777CP. [DOI] [PubMed] [Google Scholar]
- 19.Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modelling and control. IEEE Transactions on Systems, Man and Cybernetics. 1985;15:116–132. [Google Scholar]
- 20.Sousa JMC, Kaymak U. Fuzzy Decision Making in Modeling and Control. Singapore: World Scientific Pub Co; 2002. [Google Scholar]
- 21.Mendonça LF, Vieira SM, Sousa JMC. Decision tree search methods in fuzzy modeling and classification. Int J Approx Reason. 2007;44:106–123. [Google Scholar]
- 22.Vieira SM, Sousa JMC, Runkler TA. Two cooperative ant colonies for feature selection using fuzzy models. Expert Systems with Applications. 2010;37(4):2714–2723. [Google Scholar]
- 23.Hadorn DC, Keeler E, Rogers W, et al. Assessing the Performance of Mortality Prediction Models. Santa Monica, CA: Rand; 1993. [Google Scholar]
- 24.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 25.Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Proceedings of International Joint Conference on AI 1995. :1137–1145. [Google Scholar]


