Generalized Scalar-on-Image Regression Models via Total Variation

Abstract

The use of imaging markers to predict clinical outcomes can have a great impact in public health. The aim of this paper is to develop a class of generalized scalar-on-image regression models via total variation (GSIRM-TV), in the sense of generalized linear models, for scalar response and imaging predictor with the presence of scalar covariates. A key novelty of GSIRM-TV is that it is assumed that the slope function (or image) of GSIRM-TV belongs to the space of bounded total variation in order to explicitly account for the piecewise smooth nature of most imaging data. We develop an efficient penalized total variation optimization to estimate the unknown slope function and other parameters. We also establish nonasymptotic error bounds on the excess risk. These bounds are explicitly specified in terms of sample size, image size, and image smoothness. Our simulations demonstrate a superior performance of GSIRM-TV against many existing approaches. We apply GSIRM-TV to the analysis of hippocampus data obtained from the Alzheimers Disease Neuroimaging Initiative (ADNI) dataset.

1 Introduction

The aim of this paper is to develop generalized scalar-on-image regression models via total variation (GSIRM-TV) with scalar response and imaging and/or scalar predictors. This new development is motivated by studying the predictive value of ultra-high dimensional imaging data and/or other scalar predictors (e.g., cognitive score) for clinical outcomes including diagnostic status and the response to treatment in the study of neurodegenerative and neuropsychiatric diseases, such as Alzheimer’s disease (AD)(Mu and Gage 2011). For instance, the growing public threat of AD has raised the urgency to discover and validate prognostic biomarkers that may identify subjects at greatest risk for future cognitive decline and accelerate the testing of preventive strategies. In this regard, prior studies of subjects at risk for AD have examined the utility of various individual biomarkers, such as cognitive tests, fluid markers, imaging measurements, or some individual genetic markers (e.g., APOE4 gene), to capture the heterogeneity and multifactorial complexity of AD (reviewed in Weiner et al. 2012).

Our GSIRM-TV considers the use of imaging predictor X and/or scalar predictors Z to predict scalar response Y. In practice, imaging data are often represented in the form of 2-dimensional matrix or 3-dimensional array. Assume that X ∈ ℝ^N×N is a 2-dimensional matrix of size N × N which is observed without error and Z ∈ ℝ^p is a p × 1 vector with the first component being constant one. Our GSIRM-TV assumes that Y given (X, Z) follows

$$Y\mid (X,Z)~\text{Exponential}\text{Family}(\mu ,\varphi )\text{and}g(\mu )={\theta }_0^{T}Z+\langle X,{\beta }_0\rangle ,$$ (1)

where μ and ϕ are, respectively, canonical and scale parameters, 〈U, V〉 = Σ_i,ju_i,jv_i,j for U = (u_i,j) ∈ ℝ^N×N and V = (v_i,j) ∈ ℝ^N×N, and g(·) is a known link function. Moreover, θ₀ and β₀(·) are unknown parameters of interest and β₀(·) is called the coefficient image/function. Throughout the paper, assume that images are observed without error. We may deal with such measurement errors in images by applying some smoothing methods to reduce error in images (Li et al. 2010).

GSIRM-TV can be regarded as an extension of the well-known functional linear model (FLM) and the high-dimensional linear model (HLM) that have been extensively studied in the literature. If we regard 〈U, V〉 as an approximation of a two-dimensional integral, then GSIRM-TV is an approximated version of FLM. The literature on FLM is too vast to summarize here. Please see the well-known monographs Ramsay and Silverman (2005) and Ferraty and Vieu (2006). The functional principal component analysis (fPCA) and various penalization methods have been developed to estimate the coefficient function. For example, the fPCA method has been discussed by James (2002), Müller and Stadtmüller (2005), Hall and Horowitz (2007), Reiss and Ogden (2007, 2010), James et al. (2009), and Goldsmith et al. (2010) and the penalized method has been studied by Crambes et al. (2009), Yuan and Cai (2010), and Du and Wang (2014). On the other hand, if we vectorize X and β₀(·) as N² × 1 vectors, model (1) takes the form of the high dimensional generalized linear regression. To achieve sparsity in β₀, various penalization methods, such as Lasso or SCAD, have been developed. Please see Tibshirani (1996), Chen et al. (1998), Fan and Li (2001), and references therein.

Compared with FLM and HLM, a key novelty of GSIRM-TV is that the coefficient image β₀(·) in model (1) is assumed to be a piecewise smooth image with unknown jumps and edges. Such assumption not only has been widely used in the imaging literature, but also is critical for addressing various scientific questions, such as the identification of brain regions associated with AD. As an illustration, we consider a data set with n = 300 subjects simulated from a functional linear model which is a special case of (1). The first row of Figure 1 presents the true 64 × 64 image matrix β₀, X, and Y from the left to the right. We have vectorized X, used fPCA for FLM, Lasso for HLM, and GSIRM-TV to estimate the coefficient image and presented the estimated coefficient images in the second row of Figure 1. Unfortunately, both FLM and HLM fail to capture the main feature of the true coefficient image due to their key limitations. First, fPCA requires that β₀ be well presented by the eigenfunctions of X, whereas it is not the case according to Figure 1. Second, the existing regularization methods can have difficulty in recovering β₀, since the true coefficient image is non-sparse. Moreover, most regularization methods for FLM assume that the unknown coefficient function is one-dimensional and belongs to a smoothed function space, such as the Sobolev space, and thus they will not be able to preserve edge and boundary information for the data set presented in Figure 1. In contrast, our GSIRM-TV estimate developed in this paper can truly preserve the sharp edge of the original image.

Figure 1.

Results from a simulated data set. The top row includes the true 64 × 64 coefficient image β₀ in the left panel, one realization of a 64 × 64 image predictor X in the middle panel, and the responses Y from n = 300 in the right panel. The bottom row includes the estimated coefficient functions obtained from fPCA (left), Lasso (middle), and Total Variation (right).

In this paper, we make two important contributions including a new estimation method based on the total variation analysis and non-asymptotic error bounds on the risk under the framework of GSIRM-TV. The total variation analysis plays a fundamental role in various image analyses since the path-breaking works of Rudin and Osher (1994) and Rudin, Osher and Fatemi (1992). The total variation penalty has been proved to be quite efficient for preserving the boundaries and edges of images (Rudin et al. 1992). Michel et al. (2011) proposed a similar total variation method for image regression and image classification, but they focus on the development of different algorithms for the TV optimization problem. According to the best of our knowledge, this is the first paper on the development of statistical analysis of the total variation method for GSIRM-TV. The fused lasso (Tibshirani et al. 2005; Friedman et al. 2007) uses a similar penalty function. But for the 2-dimensional parameter, the fused lasso and the TV penalty can be quite different. For example, the isotropic total variation penalty uses the Euclidean norm of the first differences of the parameter, rather than the sum of the absolute values of the first differences. There are a few papers on the use of two-dimensional or three-dimensional imaging predictors in FLM (Guillas and Lai 2010; Reiss and Ogden 2010; Zhou et al. 2013; James, et al. 2009; Goldsmith et al. 2010; Gertheiss et al. 2013; Wang et al. 2014; Reiss et al. 2015), but none of them consider the piecewisely smoothed function with jumps and edges and the total variation analysis. We also derive nonasymptotic error bounds on the risk for the estimated coefficient image under the total variation penalty. We are able to obtain finite-sample bounds that are specified explicitly in terms of the sample size n, the image size N × N, and the image smoothness.

The rest of the paper is organized as follows. Section 2 considers linear scalar-on-image regression model and proposes the TV optimization framework to estimate the unknown coefficient image. We also establish the nonasymptotic error bound for the prediction error. Section 3 extends linear scalar-on-image regression model to generalized scalar-on-image regression models. Section 4 examines the finite-sample performance of GSIRM-TV and compares it with several state-of-the-art methods, such as regularized matrix regression (Zhou and Li 2014). Section 5 applies GSIRM-TV to the use of the hippocampus imaging data for a binary classification problem. Future research directions are discussed in Section 6. The technical proofs of main theorems are given in the Appendix.

2 Linear scalar-on-image regression model

We start with considering a linear scalar-on-image regression model, which is the simplest case of GSIRM-TV (1), as follows:

$$Y=\langle X,{\beta }_0\rangle +\epsilon ,$$ (2)

where ε is the random error with 𝔼(ε|X) = 0 and 𝔼(ε²|X) = σ², and without loss of generality, both X and Y are assumed to be centered with 𝔼(Y) = 𝔼(X) = 0. Model (2) may be treated as a special case of FLM since discrete images are isometric to the space of piecewise-constant functions defined as

$$\mathcal{X}=\{x\in L^2(\mathrm{\Omega }):x(u,v)=N{X}_{jk},\frac{j-1}{N}\le u<\frac{j}{N},\frac{k-1}{N}\le v<\frac{k}{N}\text{for}1\le j,k\le N\},$$

where X_jk is the (j, k)–th pixel value of the image X and Ω = [0, 1]². By treating β₀ as an integrable function in Ω, that is, β₀ ∈ L²(Ω), model (2) can be rewritten as

$$Y={\int }_0^1{\int }_0^{1}x(u,v){\beta }_0(u,v)\mathit{dudv}+\epsilon .$$

2.1 The space of bounded variation

Throughout the paper, it is assumed that β₀ is a function of bounded variation in Ω if the total variation of β₀ in Ω, denoted by ||β₀||_TV, is finite and defined as follows:

$${\Vert {\beta }_0\Vert }_{TV}=sup\left\{{\int }_{\mathrm{\Omega }}{\beta }_0(u,v)\text{div}f(u,v)\mathit{dudv}:f\in C_c^{\infty }(\mathrm{\Omega };R^2),{\mid f\mid }_{\infty }\le 1\right\},$$

where |f|_∞ = sup_(u,v)∈Ω |f(u, v)| and $C_c^{\infty }(\mathrm{\Omega };R^2)$ denotes the vector field with value in R², which is infinitely differentiable and has compact support in Ω. Moreover, f(u, v) = (f₁(u, v), f₂(u, v)) and div f(u, v) = ∂_uf₁(u, v) + ∂_vf₂(u, v), where ∂_u = ∂/∂u and ∂_v = ∂/∂v. The vector space of functions of bounded variation in Ω is denoted by BV(Ω). For example, if β₀ is differentiable in Ω, then ||β₀||_TV reduces to ${\int }_{\mathrm{\Omega }}\sqrt{{({\partial }_u{\beta }_0)}^2+{({\partial }_v{\beta }_0)}^2}\mathit{dudv}$. In this case, β₀ belongs to the Sobolev space W^1,1(𝒟), i.e., functions with integrable first order partial derivatives. However, the power of total variation in image analysis arises exactly from the relaxation of such constraints. The BV(Ω) is much larger than W^1,1(𝒟) and contains many interesting piecewise continuous functions with jumps and edges. This is exactly the advantage of using TV regularization over other familiar regularization methods used in the nonparametric literature. For example, the smoothing spline penalty term is not sensitive enough to capture sharp edges and jumps.

There are at least two additional advantages of using bounded variation functions in model (2). First, many real images with edges have small total variation since image edges usually reside in a low-dimensional subset of pixels. As an illustration, in Figure 2, the left panel displays the Shepp-Logan phantom image, while the middle and right panels show the two components of the discrete gradient of the phantom image, which have obvious sparse patterns. Second, BV(Ω) is mathematically tractable even though it contains many more functions with edges and jumps compared with W^1,1(𝒟).

Figure 2.

Left: the Shepp-Logan phantom image; Middle and Right: the two components of the discrete gradient of the phantom image.

2.2 Estimation

On the basis of model (2) and BV(Ω), we propose to solve the following TV minimization:

$$\begin{array}{ll}\text{minimize}\hfill & {\Vert \beta \Vert }_{TV}\hfill \\ \text{subject}\text{to}\hfill & {\sum }_{i=1}^n{(Y_i-\langle X_i,\beta \rangle )}^2\le {\lambda }^2,\hfill \end{array}$$ (3)

where λ is a smoothing parameter, which controls the noise level. It is known that the above minimization problem is equivalent to the penalized optimization

$$\sum _{i=1}^n{(Y_i-\langle X_i,\beta \rangle )}^2+\stackrel{⌣}{\lambda }{\Vert \beta \Vert }_{TV},$$ (4)

where λ̌ is a different smoothing parameter. The TV optimization has been widely used to reconstruct images in the compressive sensing literature (see e.g., Candès et al. 2006a; Candès et al. 2006b; Needell and Ward 2013). Using the TV optimization for one-dimensional regression has been studied by Mammen and van de Geer (1997) and Tibshirani (2014). Michel et al. (2011) discussed some algorithms to solve a similar optimization problem. To the best of our knowledge, nothing has been done on the statistical properties of the TV estimator for scalar-on-image regression models.

To solve the TV minimization (3) (or (4)), we treat β = (β_jk) ∈ ℝ^N×N as an N × N block of pixels with β_jk as its (j, k) element. Then, we define the discrete total variation of β = (β_jk) ∈ ℝ^N×N. For any β ∈ BV(Ω), the discrete gradient ∇ : BV(Ω) → ℝ^N×N×2 is defined by

$${(\nabla \beta )}_{jk}=\{\begin{array}{ll}({\beta }_{j+1,k}-{\beta }_{jk},{\beta }_{j,k+1}-{\beta }_{jk}),\hfill & 1\le j,k\le N-1,\hfill \\ (0,{\beta }_{j,k+1}-{\beta }_{jk}),\hfill & j=N,1\le k\le N-1,\hfill \\ ({\beta }_{j+1,k}-{\beta }_{jk},0),\hfill & 1\le j\le N-1,k=N,\hfill \\ (0,0),\hfill & k=j=N.\hfill \end{array}$$

Based on (∇β)_jk = ((∇β)_jk,1, (∇β)_jk,2)^T, the anisotropic version of the total variation norm ||β||_TV can be rewritten as

$${\Vert \beta \Vert }_{TV}^{\mathit{aniso}}={\Vert \nabla \beta \Vert }_1=\sum _{jk}\left\{\mid {(\nabla \beta )}_{jk,1}\mid +\mid {(\nabla \beta )}_{jk,2}\mid \right\}.$$

On the other hand, its isotropic version is defined by

$${\Vert \beta \Vert }_{TV}^{\mathit{iso}}=\sum _{jk}{\Vert {(\nabla \beta )}_{jk}\Vert }_2=\sum _{jk}\sqrt{{(\nabla \beta )}_{jk,1}^2+{(\nabla \beta )}_{jk,2}^2}.$$

The anisotropic and isotropic induced total variation norms are equivalent up to a factor of $\sqrt{2}$, i.e.,

$$\frac{1}{\sqrt{2}}{\Vert \beta \Vert }_{TV}^{\mathit{iso}}\le {\Vert \beta \Vert }_{TV}^{\mathit{aniso}}\le \sqrt{2}{\Vert \beta \Vert }_{TV}^{\mathit{iso}}.$$

We will write all results in terms of the anisotropic total variation seminorm, but our results also extend to the isotropic version.

Let A_X be an n × N² design matrix such that the ith row is the vectorized X_i. With a slight abuse of notation, we use β to denote the coefficient matrix and its corresponding vector. We may rewrite (3) as the matrix form given by

$$\widehat{\beta }=argmin{\Vert \beta \Vert }_{TV}\text{subject}\text{to}{\Vert Y-A_X\beta \Vert }_2\le \lambda .$$ (5)

We adapt an algorithm called TVAL3 based on the augmented Lagrangian method (Hestenes 1969; Powell 1969; Li 2013). Specifically, we solve an equivalent optimization problem given by

$$\underset{w,\beta }{min}\sum _{l=1}^{N^2}{\Vert w_l\Vert }_1\text{subject}\text{to}{\Vert Y-A_X\beta \Vert }_2\le \lambda \text{and}{D}_l\beta =w_l\text{for}\text{all}l,$$

where D_l is an 2 × N² vector of constants associated with the discrete gradient. As an illustration, we consider a simple case with N = 2. In this case, we have β = (β₁₁, β₁₂, β₂₁, β₂₂)^T. We may choose

$$\begin{array}{l}{D}_1=\left[\begin{array}{llll}-1\hfill & 1\hfill & 0\hfill & 0\hfill \\ -1\hfill & 0\hfill & 1\hfill & 0\hfill \end{array}\right],D_2=\left[\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 1\end{array}\right],\\ D_3=\left[\begin{array}{rrrr}\hfill 0& \hfill 0& \hfill -1& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0& \hfill 0\end{array}\right],\text{and}{D}_4=\left[\begin{array}{llll}0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right],\end{array}$$

so that we have D₁β = (∇β)₁₁, D₂β = (∇β)₁₂, D₃β = (∇β)₂₁, and D₄β = (∇β)₂₂.

Its corresponding augmented Lagrangian function is given by

$${\mathcal{L}}_A(w,\beta )=\sum _{l=1}^{N^2}\left\{{\Vert w_l\Vert }_1-{\mathbf{v}}_l^T(D_l\beta -w_l)+\frac{{\alpha }_l}{2}{\Vert D_l\beta -w_l\Vert }_2^2+\frac{\gamma }{2}{\Vert A_X\beta -Y\Vert }_2^2\right\},$$

where v_l, α_l, and γ are tuning parameters. We may find the minimizer iteratively, and then the subproblem at each iteration of TVAL3 becomes min_wl,β ℒ_A(w_l, β). In our algorithm, v_l is updated at each iteration. Moreover, α_l’s and γ as smoothing parameters can be selected by using either the C_p criterion or the K-fold cross-validation (CV). However, its computational time can be long even under current computing facilities. In our numerical examples, we pre-fix the tuning parameters by setting α_l = 2⁵ for l = 1, …, N² and γ = 2⁸. The simplest way to choose γ is to try different values from 2⁴ up to 2¹³ and compare the recovered images. The value of α_l is much less sensitive to the choice of γ. We leave tuning parameter optimization for our future research topic.

We describe the complete algorithm as follows.

• Step 1. Initialize β⁽⁰⁾ and ${\mathbf{v}}_l^{(0)}$;

• Step 2. Given β = β^(k) and ${\mathbf{v}}_l={\mathbf{v}}_l^{(k)}$, we solve for ${\omega }_l^{(k+1)}$, l = 1, …, N², by minimizing

  $${\Vert {\omega }_l\Vert }_1-{\mathbf{v}}_l^T(D_l\beta -{\omega }_l)+\frac{{\alpha }_l}{2}{\Vert D_l\beta -{\omega }_l\Vert }_2^2.$$
  The explicit solution (component-wise) is given by

  $${\omega }_l=\{\begin{array}{ll}{D}_l\beta -\frac{{\mathbf{v}}_l+1}{{\alpha }_l},\hfill & \text{if}{D}_l\beta >\frac{{\mathbf{v}}_l+1}{{\alpha }_l};\hfill \\ 0,\hfill & \text{if}\frac{{\mathbf{v}}_l-1}{{\alpha }_l}\le D_l\beta \le \frac{{\mathbf{v}}_l+1}{{\alpha }_l};\hfill \\ D_l\beta -\frac{{\mathbf{v}}_l-1}{{\alpha }_l},\hfill & \text{if}{D}_l\beta <\frac{{\mathbf{v}}_l+1}{{\alpha }_l}.\hfill \end{array}$$
• Step 3. Given ${\omega }_l={\omega }_l^{(k+1)}$ and ${\mathbf{v}}_l={\mathbf{v}}_l^{(k)}$, l = 1, …, N², we solve for β^(k+1) by minimizing

  $$\sum _{l=1}^{N^2}\left\{-v_l^T{D}_l\beta +\frac{{\alpha }_l}{2}{\Vert D_l\beta -{\omega }_l\Vert }_2^2+\frac{\gamma }{2}{\Vert A_X\beta -Y\Vert }_2^2\right\}.$$
  The explicit solution is given by

  $${\beta }^{(k+1)}={\left\{\sum _{l=1}^{N^2}({\alpha }_l{D}_l^T{D}_l+\gamma A_X^T{A}_X)\right\}}^{-1}\left\{\sum _{l=1}^{N^2}({\mathbf{v}}_l^T{D}_l+{\alpha }_l{D}_l^T{\omega }_l+\gamma A_X^{T}Y)\right\}.$$
• Step 4. Given β = β^(k+1), ${\omega }_l={\omega }_l^{(k+1)}$, update ${\mathbf{v}}_l^{(k+1)}$ by using

  $${\mathbf{v}}_l^{(k+1)}={\mathbf{v}}_l^{(k)}={\alpha }_l\left(D_l{\beta }^{(k+1)}-{\omega }_l^{(k+1)}\right).$$

• Step 5. Iterate Steps 2–4 until convergence.

2.3 The error bound

In this subsection, we establish the nonasymptotic error bound for the TV estimator β̂ based on model (2). We consider two types of distances to measure the error. The first one is a weighted L₂ distance such that

$${\Vert \widehat{\beta }-{\beta }_0\Vert }_{X,2}={\left\{{\mathbb{E}}^{\ast }({\langle X_{n+1},\widehat{\beta }-{\beta }_0\rangle }^2)\right\}}^{1/2},$$

where 𝔼^* represents taking expectation with respect to (Y_n+1, X_n+1) only. The second one is the TV distance between β̂ and β₀, ||β̂ − β₀||_TV.

We derive both error bounds by means of Haar wavelet basis. Various wavelet bases are commonly used to effectively represent images and the Haar wavelet is the simplest possible wavelet. The bivariate Haar wavelet basis for L₂(Ω) can be constructed as follows. Let ϕ⁰(t) = I_[0,1) be the indicator function, and the mother wavelet ϕ¹(t) = 1 for t ∈ [0, 1/2) and −1 for t ∈ [1/2, 1). Starting from the multivariate functions

$${\varphi }^d(s,t)={\varphi }^{d_1}(s){\varphi }^{d_2}(t),d\in \{(0,1),(1,0),(1,1)\},$$

the bivariate Haar basis functions include the indicator function I_[0,1)² and other functions

$${\varphi }_{j,k}^d(u,v)=2^j{\varphi }^d(2^{j}x-k),d\in \{(0,1),(1,0),(1,1)\},x=(u,v),j\ge 0,k\in {\mathbb{Z}}^2\cap 2^j{[0,1)}^2.$$

The bivariate Haar wavelet basis is an orthonormal basis for L₂[0, 1)². Note that discrete images are isometric to the space ℐ_N ⊂ L₂[0, 1)² of piecewise constant functions ${\mathcal{I}}_N=\{f\in L_2{[0,1)}^2:f(s,t)=c_{jk},\frac{j-1}{N}\le s<\frac{j}{N},\frac{k-1}{N}\le t<\frac{k}{N}\}$ via the identification c_jk = NX_jk. Letting N = 2^J, the bivariate Haar basis restricted to the N² basis functions {I_[0,1)², ${\varphi }_{j,k}^d$, j ≤ J −1, d ∈ {(0, 1), (1, 0), (1, 1)}, k ∈ ℤ² ∩ 2^j[0, 1)²} forms an orthonormal basis for ℝ^N×N. Denote by Φ the discrete bivariate Haar transformation and {ϕ_l} the Haar basis, in which Φβ ∈ ℝ^N×N contains the bivariate Haar wavelet coefficients of β. Next, we review a theoretical result of Petrushev et al. (1999), who proved a deep and nontrivial result on BV(Ω). Specifically, it states that the Haar wavelet coefficients of β₀ ∈ BV(Ω) are in weak ℓ₁. That is, if the Haar coefficients are sorted decreasingly according to their absolute values, then the l–th rearranged coefficient is in absolute value less than c||β₀||_BV/l with c being an absolute constant.

Invoking Haar wavelets is only for theoretical investigation and we do not estimate the Haar coefficients directly. We now introduce the main assumptions of this paper:

• A1Assume that the coefficient image β₀ in the space of N × N blocks of pixel values with bounded variation. Assume that the error ε is sub-Gaussian.
• A2Assume that the discrete Haar representation of the image predictor X is $X={\sum }_l{\rho }_l^{1/2}{\xi }_l{\varphi }_l$, where ρ_l are positive constants and ξ_l are independently and identically distributed sub-Gaussian random variables with zero mean and unit variance.
• A3For any β ∈ BV(Ω), write β = Σ_lγ_lϕ_l, where the γ_l are the Haar basis coefficients of β. We arrange γ_l in a decreasing order according to their absolute values and denote the sorted coefficients as γ_(l). Assume that the corresponding sorted ρ_(l) associated with the same basis function satisfies c₁s^−2q ≤ ρ_(s) ≤ c₂s^−2q with q > 1/2 for each s and two positive constants c₁, c₂.

Assumption A2 on the wavelet representation of X is reasonable because the discrete wavelet transformation approximately decorrelates or “whitens” data (Vidakovic 1999). Although we might use the Karhunen-Loève expansion of X, we do not adopt this approach in order to avoid additional complexity associated with the estimation of eigenfunctions. When we sort the Haar wavelet coefficients of both β and X, the corresponding basis functions may not follow the same order. Assumption A3 specifies the decay rate of the Haar wavelet coefficients of X. From A2, the predictor images X_i can be written as $X_i={\sum }_l{\rho }_l^{1/2}{\xi }_{il}{\varphi }_l$. Let à be an n × N² matrix with the (i, l)-th element being ${\xi }_{il}/\sqrt{n}$. It is well-known that à satisfies the restricted isometry property (RIP) with a large probability (Candès et al. 2006a, 2006b). Specifically, if n ≥ C⁻²s log(N²/s), then with probability exceeding 1 − 2e^−Cn, we have

$$(1-\delta ){\Vert u\Vert }_2^2\le {\Vert \stackrel{\sim }{A}u\Vert }_2^2\le (1+\delta ){\Vert u\Vert }_2^2$$ (6)

for all s-sparse vectors u ∈ ℝ^N2 with a small RIP constant δ < C.

Let {γ̂_l} and {γ_l} be, respectively, the wavelet coefficients of β̂ and β₀. It turns out that ||β̂ − β₀||_X,2 = {Σ_lρ_l(γ̂_l − γ_l)²}^1/2, which is the weighted L₂-norm of the wavelet coefficient difference. On the other hand, since ||ϕ_l||_TV ≤ 8 (Needell and Ward, 2013),

$${\Vert \widehat{\beta }-{\beta }_0\Vert }_{TV}\le \sum _l\mid {\widehat{\gamma }}_l-{\gamma }_l\mid {\Vert {\varphi }_l\Vert }_{TV}\le 8{\Vert {\widehat{\gamma }}_l-{\gamma }_l\Vert }_1,$$

which is bounded by the L₁-norm of the wavelet coefficient difference. We obtain the following theorem, whose detailed proof can be found in the Appendix.

Theorem 2.1

Assumptions A1-A3 hold. Let C be an absolute constant and λ = Cn^1/2. If n ≥ Cs^2q+1 log(N²/s^2q+1) and δ < 1/3 in (6), then with probability greater than 1 – 2 exp(−Cn), we have

$${\Vert \widehat{\beta }-{\beta }_0\Vert }_{X,2}\le C\left\{\sigma +\frac{1}{{(\mathit{s}logN)}^{q+\frac{1}{2}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_s\Vert }_1\right\},$$ (7)

and

$${\Vert \widehat{\beta }-{\beta }_0\Vert }_{TV}\le Clog\left(\frac{N^2}{s}\right)\left\{{(\mathit{s}logN)}^{q+\frac{1}{2}}\sigma +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right\},$$ (8)

where (∇β₀)_s = arg min_u:s-sparse ||∇β₀ − u||₁ is the best s-sparse approximation to the discrete gradient ∇β₀.

Theorem 2.1 provides non-asymptotic error bounds for ||β̂ − β₀||_X,2 and ||β̂ − β₀||_TV, which are specified explicitly in terms of sample size n and image size N × N, and the underlying smoothness of the true coefficient image based on the discrete gradient.

Remark 2.1

We call a prediction “stable” if ||β̂ − β₀||_X,2 ≤ Cσ holds with a high probability. Assume that the coefficient image has the sparse discrete gradient, i.e., ∇β₀ is supported on S₀ with |S₀|₀ ≤ s. If λ = Cn^1/2, then Theorem 2.1 shows that ||β̂ − β₀||_X,2 ≤ Cσ, which indicates that our prediction procedure is stable. Furthermore, for the extreme case with noiseless data, our prediction procedure is exact. The required sample size n is of order s^2q+1 log(N²/s^2q+1), which depends on the smoothness of the true coefficient image β₀, the relative smoothness between β₀ and X, and the image size N × N.

Remark 2.2

The parameter q characterizes the decay rate of the wavelet coefficients of X. The larger the q, the more the required sample size. Theorem 2.1 also shows that the larger q is, the smaller the prediction error is. When q = 0, this gives the special case discussed in Needell and Ward (2013).

3 Generalized scalar-on-image regression models

In this section, we extend all developments for model (2) to GSIRM-TV (1). Given X ∈ ℝ^N×N and Z ∈ R^p, the response variable Y is assumed to follow an exponential family distribution as

$$exp(\{Y\eta (X,Z;{\theta }_0,{\beta }_0)-b(\eta (X,Z;{\theta }_0,{\beta }_0))\}/a(\psi )+c(y,\psi )),$$ (9)

where a(·), b(·), and c(·) are known functions, and ψ is either known or considered as a nuisance parameter. Our GSIRM-TV also assumes β₀ ∈ BV(Ω). It can be shown (Nelder and Wedderburn, 1972) that

$$\mathbb{E}(Y\mid X)=\mu (X,Z;{\theta }_0,{\beta }_0)=\stackrel{.}{b}(\eta (X,Z;{\theta }_0,{\beta }_0))\text{and}\text{Var}(Y\mid X)=a(\psi )\ddot{b}(\eta (X,Z;{\theta }_0,{\beta }_0)),$$

where ḃ(η) and b̈(η) are, respectively, the first and second derivatives of b(η) with respect to η. Moreover, $\eta (X,Z;{\theta }_0,{\beta }_0)={\stackrel{.}{b}}^{-1}(g^{-1}({\theta }_0^{T}Z+\langle X,{\beta }_0\rangle )))$ is the canonical parameter of (9). A Gaussian distribution with variance σ² has a(ψ) = σ² and b(η) = η²/2, a Bernoulli distribution has a(ψ) = 1 and b(η) = log(1 + e^η), and a Poisson distribution has a(ψ) = 1 and b(η) = e^η.

3.1 Estimation

Let ξ = (θ, β) ∈ R^p×BV(Ω). Given the observed data, we propose to find estimates ξ̂ by minimizing a penalized likelihood function given by

$$n^{-1}\sum _{i=1}^n\left\{Y_i\eta (X_i,Z_i;\theta ,\beta )-b(\eta (X_i,Z_i;\theta ,\beta ))\right\}+\lambda {\Vert \beta \Vert }_{TV}.$$ (10)

We use an algorithm, which is a standard iteratively reweighted least squares for GLMs, modified to add a TV penalty, to calculate ξ̂ = (θ̂, β̂). Given a trial estimate of ξ, denoted by ξ̂_I, we introduce the iterative weights and the working dependent variable as

$${\widehat{w}}_{i,I}=\ddot{b}({\widehat{\eta }}_{i,I})\text{and}{\widehat{Y}}_{i,I}=g({\widehat{\mu }}_{i,I})+(Y_i-{\widehat{\mu }}_{i,I})\stackrel{.}{g}({\widehat{\mu }}_{i,I}),$$ (11)

where μ̂_i,I = μ(X_i, Z_i; ξ̂_I), ġ(μ) = dg(μ)/dμ, and η̂_i,I = η(X_i, Z_i; ξ̂_I). Then, we can calculate the next estimate of ξ, denoted by ξ̂_I+1, by minimizing

$${\widehat{\xi }}_{I+1}={\text{argmin}}_{\xi }\left\{\sum _{i=1}^n{\omega }_{i,I}{[{\widehat{Y}}_{i,I}-{\partial }_{\xi }{\mu }_{i,I}({\widehat{\xi }}_I)\xi ]}^2+\lambda {\Vert \beta \Vert }_{TV}\right\},$$ (12)

where ∂_ξ = ∂/∂ξ. The optimization in (12) can be effectively solved by using TVAL3 algorithm discussed in Section 2. Finally, we can iteratively solve ξ̂_I until convergence.

We provide the complete algorithm as follows.

• Step 1. Initialize ξ⁽⁰⁾ = (θ⁽⁰⁾, β⁽⁰⁾).

• Step 2. For each k, define the weights and the working dependent variable in (11), and define the objective function in (12). Use TVAL3 algorithm to solve for ξ^(k+1) = (θ^(k+1), β^(k+1)).

• Step 3. Iterate Steps 2 and 3 until convergence.

We consider the logistic scalar-on-image regression model as an example. Specifically, Y_i given (X_i, Z_i) follows a Bernoulli distribution with the success probability p_i and $\text{logit}(p_i)=\langle X_i,{\beta }_0\rangle +{\theta }_0^T{Z}_i$ for i = 1, …, n. Given the current estimate ξ̂_I, it is easy to obtain the iterative weight and effective response variable, respectively, given by

$${\widehat{\omega }}_{i,I}=\frac{e^{{\widehat{\eta }}_{i,I}}}{{(1+e^{{\widehat{\eta }}_{i,I}})}^2}\text{and}{\widehat{Y}}_{i,I}={\widehat{\eta }}_{i,I}+\frac{Y_i-{\widehat{\mu }}_{i,I}}{{\widehat{\mu }}_{i,I}(1-{\widehat{\mu }}_{i,I})}.$$

Therefore, the estimate ξ̂_I+1 can be obtained by solving a weighted penalized least squares in (12).

3.2 The error bound

We establish an non-asymptotic prediction error bound for GSIRM-TV. We need some additional assumptions as follows.

• B1Assume η(X, Z; β₀, θ₀) is bounded almost surely. Given (X, Z), the response Y is sub-Gaussian, i.e., 𝔼{exp(t[Y − ḃ(η(X, Z; β₀, θ₀))])|X} ≤ exp(t²σ̃²/2) for some σ̃² > 0 and all t ∈ ℝ.
• B2The function ḃ(·) is monotonic with inf_t b̈(t) ≥ c₃ and sup_t b̈ (t) ≤ c₄ for two positive constants c₃ and c₄.

The sub-Gaussian assumption B1 holds for many well-known distributions, such as Gaussian. The assumption B2 requires that the second derivative of b(·) is bounded above and away from zero.

Theorem 3.1

Assumptions A1–A3 and B1–B2 hold. Let λ = Cn^−1/2, where C is a positive constant. If n ≥ Cs^2q+1 log (N²/s^2q+1) and δ < 1/3 in (6), with probability greater than 1 − 2 exp(−Cn), we have ||θ̂ − θ₀||₂ ≤ Cn^−1/2,

$${\Vert \widehat{\beta }-{\beta }_0\Vert }_{X,2}\le C\left\{1+\frac{1}{{(\mathit{s}logN)}^{q+\frac{1}{2}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_s\Vert }_1\right\},$$ (13)

and

$${\Vert \widehat{\beta }-{\beta }_0\Vert }_{TV}\le Clog\left(\frac{N^2}{s}\right)\left\{{(\mathit{s}logN)}^{q+\frac{1}{2}}\sigma +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right\}.$$ (14)

The conditional mean of Y_n+1 given X_n+1 is ḃ(η(X_n+1, β₀)). We may measure the accuracy of β̂ by 𝔼^*[ḃ(η(X_n+1, β̂)) − ḃ(η(X_n+1, β₀))]². Under B1, this risk is bounded by ${\Vert \widehat{\beta }-{\beta }_0\Vert }_{X,2}^2$ and thus, it is reasonable to study the non-asymptotic behavior of ||β̂ − β₀||_X,2. Theorem 2.1 is a special case of Theorem 3.1 if it is assumed in Theorem 2.1 that responses follow a normal distribution. If assuming that the coefficient image has the sparse discrete gradient, Theorem 3.1 shows that ||β̂ − β₀||_X,2 is bounded by a constant, which is proportional to σ under the assumption of Theorem 2.1. This shows that our prediction procedure is stable for GSIRM-TV.

4 Simulation Studies

In this section, we conducted a set of Monte Carlo simulations to examine the finite sample performance of the TV estimate β̂ and compare it with five competing methods. The first approach (Lasso) is to calculate the Lasso estimates of β₀. The second one (Lasso-Haar) is to calculate the Lasso estimates of the Haar coefficients of β₀ and use the inverse discrete wavelet transform to calculate the estimates of β₀. The third one (Matrix-Reg) is to estimate β₀ by using a recent development called regularized matrix regression (Zhou and Li 2014), which treats the coefficient image as a matrix and penalizes the nuclear norm of this matrix. The fourth one (FPCR) is the functional principal component regression approach (Reiss and Ogden 2007, 2010) by using tensor product cubic B-splines to approximate the coefficient function. The fifth one (WNET) is to perform scalar-on-image regression in the wavelet domain by naive elastic net (Zhao et al. 2014). Among these six approaches, the TV, Lasso, Lasso-Haar, and Matrix-Reg methods have been implemented by Matlab and the FPCR and WNET methods have been implemented in the R packages ‘refund’ and ‘refund.wave’ (see Reiss et al. 2015), respectively. For the FPCR and WNET methods, we have used the default settings of both packages. The choice of wavelet basis in WNET is the Daubechies basis.

We present some results based on linear scalar-on-image regression model (2). Specifically, X_i were simulated from a 64×64 phantom map with N = 64 and 4, 096 pixels according to a spatially correlated random process X_i = Σ_l l^−q/2ξ_ilϕ_l with q = 0, 0.5, and 1, where the ξ_l are standard normal random variables and the ϕ_l are bivariate Haar wavelet basis functions. We consider four different β₀ images including triangle, oval, T-shape, and checkerboard shapes (Figure 3). Among them, the triangle and oval images are convex, while the other two are not. Errors ε_i were independently generated from N(0, 1). We set n₁ = 300 for the training set and n₂ = 100 for the test set. We repeated each setting 100 times. We calculated the root mean squared prediction error (RMSPE) to compare the finite sample performance of the six different estimation methods. Let β̂ be the estimated coefficient image from the training set and Ŷ_i = 〈β̂, X_i〉 be the predicted responses for the test set. For each test set, RMSPE is defined by

Figure 3.

The true coefficient images used for the simulation study.

$$\text{RMSPE}=\sqrt{n_2^{-1}\sum _{i=1}^{n_2}{({\widehat{Y}}_i-Y_i)}^2}.$$

We also calculated the means and standard errors of RMSPEs for the 100 testing datasets.

Figures 4 and 5 present the estimated β₀ from a randomly selected training dataset with q = 0 and q = 0.5, respectively, for the sample size n = 300. For all four different shapes, our TV estimates can capture the sharp boundaries of the underlying shapes. In contrast, the Lasso method fails for all shapes, since the predictor images X_i are highly correlated. The Lasso estimates of the Haar coefficients can roughly capture the true shapes. However, this method cannot faithfully recover the sharp boundaries of the triangle, oval, and T shapes, whereas it does work very well for the checkerboard shape, since this checkerboard shape is exactly one of the bivariate Haar wavelet basis functions. The matrix regression approach can roughly capture the true shapes when q = 0, and unfortunately this method fails for the case when q = 0.5, for which the entries of X are spatially correlated. The PCR approach uses splines to approximate the predictor images, and it cannot preserve the sharp edges of coefficient estimator for our examples. The WNET method fails for the case when q = 0 but it can capture the shapes of the true coefficient image when the predictors are more spatially correlated.

Figure 4.

The estimated coefficient images from six estimation methods when q = 0 and n = 300: TV (Top row); Lasso (Second row); Lasso-Haar (Third row); Matrix regression (fourth row); FPCR (Fifth row); and WNET(Sixth row).

Figure 5.

The estimated coefficient images from six methods when q = 0.5 and n = 300: TV (Top row); Lasso (Second row); Lasso-Haar (Third row); Matrix regression (fourth row); FPCR (Fifth row); and WNET(Sixth row).

Table 1 presents the RMSPEs of all six methods across all shapes. Overall, our TV method has significantly smaller prediction errors, in particular for q = 0. It is expected that the Lasso method leads to the largest prediction error. For all these methods, the larger q is, the smaller are their RMSPEs. For a larger q which means the predictor images are more spatially correlated, the performances of the TV, Lasso-Haar, FPCR, and WNET are similar to each other.

Table 1.

The RMSPEs of six methods including TV, Lasso, Lasso-Haar, Matrix-Reg, FPCR, and WNET for four different shapes: the numbers in brackets are the corresponding standard errors of those RMSPEs.

	TV			Lasso			Lasso-Haar
q	0	0.5	1	0	0.5	1	0	0.5	1
Triangle	3.20 (0.70)	1.53 (0.12)	1.18 (0.08)	34.02 (2.25)	13.12 (0.95)	3.96 (0.32)	18.76 (1.43)	5.08 (0.52)	1.98 (0.17)
Oval	1.69 (0.22)	1.49 (0.13)	1.22 (0.09)	31.16 (2.00)	11.83 (0.95)	3.57 (0.25)	14.99 (1.24)	3.82 (0.28)	1.67 (0.15)
T-shape	2.04 (0.51)	1.47 (0.09)	1.23 (0.10)	30.10 (2.41)	18.81 (0.81)	3.34 (0.28)	19.65 (1.84)	4.62 (0.46)	1.69 (0.16)
Checkerboard	6.27 (1.09)	1.45 (0.11)	1.10 (0.08)	49.00 (3.54)	25.46 (1.65)	9.08 (0.83)	1.43 (0.14)	1.06 (0.08)	1.05 (0.07)
	Matrix-Reg			FPCR			WNET
q	0	0.5	1	0	0.5	1	0	0.5	1
Triangle	23.13 (1.78)	6.46 (0.55)	4.00 (0.34)	10.89 (0.76)	2.27 (0.18)	1.19 (0.09)	28.42 (2.45)	2.10 (0.17)	1.28 (0.10)
Oval	18.81 (1.58)	5.58 (0.37)	3.41 (0.30)	9.28 (0.68)	2.12 (0.15)	1.19 (0.09)	24.74 (2.40)	2.03 (0.16)	1.26 (0.10)
T-shape	20.97 (1.45)	5.49 (0.38)	3.57 (0.33)	11.69 (0.82)	3.42 (0.26)	1.64 (0.12)	24.41 (2.18)	2.52 (0.21)	1.46 (0.13)
Checkerboard	35.33 (2.89)	12.80 (0.95)	6.35 (0.38)	10.70 (0.83)	3.05 (0.22)	1.14 (0.10)	44.24 (3.23)	5.41 (0.55)	2.03 (0.15)

5 Real data analysis

To illustrate the usefulness of our proposed model, we consider anatomical MRI data collected at the baseline by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study, which is a large scale multi-site study collecting clinical, imaging, and laboratory data at multiple time points from healthy controls, individuals with amnestic mild cognitive impairment, and subjects with Alzheimer’s disease (AD). “Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year publicprivate partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California, San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.”

Alzheimer’s disease as an age-related neurodegenerative brain disorder is often characterized by progressive loss in memory and deterioration of cognitive functions (De La Torre 2010; Weiner et al. 2012). Important neuropathological hallmarks of AD are the gradual intraneuronal accumulation of neurofibrillary tangles formed as a result of abnormal hyperphosphorylation of cytoskeletal tau protein, extracellular deposition of amyloid-β (Aβ) protein as senile plaques, and massive neuronal death. These pathologies are evident in the hippocampus, which is located in the medial temporal lobe underneath the cortical surface, and other vulnerable brain areas. The hippocampus belongs to the limbic system and plays important roles in the consolidation of information from short-term memory to long-term memory and spatial navigation (Colom et al. 2013; Fennema-Notestine et al. 2009; Luders et al. 2013).

Given the MRI scans, hippocampal substructures were segmented with FSL FIRST (Patenaude et al. 2011) and hippocampal surfaces were automatically reconstructed with the marching cube method (Lorensen and Cline 1987). We adopted a surface fluid registration based hippocampal subregional analysis package (Shi et al. 2013), which uses isothermal coodinates and fluid registration to generate one-to-one hippocampal surface registration for surface statistics computation. It introduced two cuts on a hippocampal surface to convert it into a genus zero surface with two open boundaries. The locations of the two cuts were at the front and back of the hippocampal surface. By using conformal parameterization, it essentially converts a 3D surface registration problem into a two-dimensional (2D) image registration problem. The flow induced in the parameter domain establishes high-order correspondences between 3D surfaces. Finally, various surface statistics were computed on the registered surface, such as multivariate tensor-based morphometry (mTBM) statistics (Wang et al. 2010), which retain the full tensor information of the deformation Jacobian matrix, together with the radial distance (Pizer et al. 1999). This software package and associated image processing methods have been adopted and described by various studies (Shi et al. 2014).

We applied GSIRM-TV to the hippocampus data set calculated from ADNI. The sample in our investigation includes n = 403 subjects: 223 healthy controls (HC) (107 females and 116 males) and 180 individuals with AD (87 females and 93 males). We consider binary disease status with 0 being HC and 1 being AD as responses. The image predictor X_i is the 2D representation of left hippocampus. The covariate vector Z_i includes constant(=1), gender (Female=0 and Male = 1), age (55–92), and behavior score (1–36). Given (X_i, Z_i), Y_i is assumed to follow a Bernoulli distribution with the success probability p_i satisfying

$$\text{logit}(p_i)=\langle X_i,{\beta }_0\rangle +{\theta }_0^T{Z}_i\text{for}i=1,\dots ,n.$$

We used the iterative reweighted algorithm described above to estimate the unknown parameters.

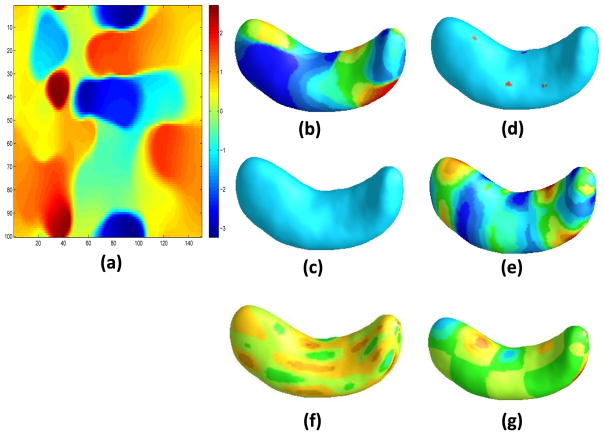
Table 2 presents the estimates of θ₀ and their corresponding standard deviations, which were calculated by using the bootstrap method. Figure 7 shows the estimated coefficient images by using the five estimation methods. The effects around pixels (5, 40), (40, 40), (95, 40) seem to be captured well by our TV estimate. The confidence band for the coefficient image can also be obtained by using the bootstrap method. We randomly partitioned the hippocampus data set into a training set with n₁ = 203 and a test set with n₂ = 200. We repeated this random partition for 100 times and computes 100 classification errors. The average classification error of TV is 8.13% with a standard error 1.56%. We also obtain the average classification errors for other five methods. The average classification errors are 12.23%(7.36%), 21.65%(15.56%), 12.03%(11.55%), 17.13%(3.27%), 16.45%(15.57%), respectively, for Lasso, Lasso-Haar, matrix regression, FPCR, and WNET. For the WNET method, since the R code requires the image size to be a power of 2, we have added zeros to make the image size of 256 × 256 as suggested by one of the referees. Inspecting Table 2 reveals that sex and age are not significant in GSIRM-TV. We run the same procedure without sex and age and obtained a similar classification result as the full model, which is omitted from the paper.

Table 2.

ADNI hippocampus data set: the estimated coefficients of the four scalar covariates and their standard deviations in parentheses.

	intercept	sex	age	behavior score
θ̂	−1.807 (3.186)	−0.533 (0.590)	−0.093 (0.043)	0.869 (0.111)

Figure 7.

Estimated coefficient images for hippocampus data based four methods: the 2d-representation of TV estimator (a) and the surface representation of TV estimator (b), Lasso estimator (c), Lasso-wavelet estimator (d), matrix regression estimator (e), FPCR estimator (f), and WNET estimator (g).

6 Conclusion

We have developed a class of GSIRM-TVs for scalar response and imaging and/or scalar predictors, while explicitly assuming that its slope function belongs to BV(Ω). We have developed an efficient penalized total variation minimization to estimate the coefficient image. We have used simulations and real data analysis to show that GSIRM-TV is quite efficient for estimating the slope function, while preserving its edges and jumps. We have established the nonasymptotic error bound of the TV estimate for the excess risk.

It is known that many image data have small total variation and are compressible with respect to wavelet transform. Therefore, we may generalize our approach to include both total variation penalty and Lasso penalty on the wavelet coefficients. Specifically, let Φ be the wavelet transformation operator and γ be the wavelet coefficients of the coefficient image β₀. We may calculate γ by minimizing

$$\sum _{i=1}^n{\left(Y_i-\langle X_i,{\mathrm{\Phi }}^{-1}\gamma \rangle \right)}^2+{\lambda }_1{\Vert {\mathrm{\Phi }}^{-1}\gamma \Vert }_{TV}+{\lambda }_2{\Vert \gamma \Vert }_1,$$ (15)

where Φ⁻¹ is the inverse discrete wavelet transform, and β = Φ⁻¹γ. In (15), there are two smoothing parameters λ₁ and λ₂ which need to be selected. Efficient algorithm is also needed to be developed to solve (15). We leave this as further research work.

We have so far focused on two-dimensional (2-D) images. It would be interesting to extend our method to analyze k–dimensional (k-D) images for k ≥ 2 (Zhou et al., 2013; Zhu et al., 2014). For example, consider a 3-D image f ∈ ℝ^N3, where f = (f_e), in which e = (e₁, e₂, e₃) ∈ {1, 2, 3}³. The inner product can be defined as

$$\langle f,g\rangle =\sum _{e\in {\{1,2,3\}}^3}{f}_e·g_e.$$

For ℓ = 1, 2, and 3, the discrete derivative of f in the direction of r_ℓ is f_rℓ ∈ ℝ^{Nℓ−1×N×N3−ℓ},

$${(f_1)}_e=f_{(e_1+1,e_2,e_3)}-f_{(e_1,e_2,e_3)},{(f_2)}_e=f_{(e_1,e_2+1,e_3)}-f_{(e_1,e_2,e_3)},{(f_3)}_e=f_{(e_1,e_2,e_3+1)}-f_{(e_1,e_2,e_3)},$$

and the 3-D discrete gradient is (∇f)_e = (f_rℓ)_e for e_ℓ ≤ N − 1 and zero elsewhere. Hence the 3-D anisotropic and isotropic total variation seminorm can be defined similarly. We may consider a similar total variation optimization (4) to estimate the 3-D coefficient image. This research is currently under investigation and will be presented in another report.

Figure 6.

Observed left hippocampus images.

7 Appendix

In this appendix, we provide proofs of Theorems 2.1 and 3.1. The constant C represents a universal constant independent of everything else, but it may be different from different lines.

7.1 Proof of Theorem 2.1

We prove the theorem by extending the arguments from Candès, Romberg, and Tao (2006a, 2006b) and Needell and Ward (2013). In the following, a ≲b means that there exists a constant C such that a ≤ Cb.

Recall that {ϕ_l} is a set of discrete bivariate Haar wavelet basis functions. Write $X_i={\sum }_l{\xi }_{il}{\rho }_l^{1/2}{\varphi }_l$, β₀ = Σ_l γ_lϕ_l, and β̂ = Σ_l γ̂_lϕ_l. We aim to derive the error bounds of Σ_l ρ_l(γ_l − γ̂_l)² and Σ_l |γ_l − γ̂_l|. Denote by α = β₀ − β̂ and write α = Σ_l h_lϕ_l, where the h_l = γ_l − γ̂_l are the wavelet coefficients of the difference between the true coefficient image and the estimated coefficient image. We may sort h_l in descending order according to their absolute values. Denote the sorted coefficients by h_(l). The corresponding ρ_l with the same basis function with h_l is denoted by ρ_(l). Note that the ρ_(l) are not necessarily sorted, but it is assumed to satisfy Condition A3.

Let S denote the support of s largest entries in the absolute values of α. As shown in Lemma 9 of Needell and Ward (2013), the set K of wavelets which are non-constant over S has cardinality at most 8s log N. With an abuse of notation, let K = 8s log N. Lemma 7.1 derives cone constraints for the wavelet coefficients h_(j) and the weighted wavelet coefficients ${\rho }_{(j)}^{1/2}{h}_{(j)}$.

In the following, we focus on ${\rho }_{(l)}^{1/2}{h}_{(l)}$ for l = K + 1, …, N². Let

$$\stackrel{\sim }{s}=c{s}^{2q+1}{(logN)}^{2q+1},d=\lfloor N^2/(4\stackrel{\sim }{s})\rfloor .$$

We may write K^c = K₁ ∪ K₂ ∪ ⋯ ∪ K_d, where K₁ consists of 4s̃ largest |h_(l)| within K^c, K₂ consists of next 4s̃ largest-magnitude of |h_(l)|, and so on. Since ρ_(l) is of order l^−2q and the magnitude of each ${\rho }_l^{1/2}\mid h_l\mid$ in K_j−1 is larger than that in K_j up to a constant, we have

$${\left(\sum _{l\in K_j}{\rho }_l{\mid h_l\mid }^2\right)}^{1/2}\lesssim \frac{1}{2\sqrt{\stackrel{\sim }{s}}}\sum _{l\in K_{j-1}}{\rho }_l^{1/2}\mid h_l\mid \text{for}j=2,3,\mathrm{....}$$

Combining this result with Lemma 7.1 yields

$$\begin{array}{l}\sum _{j=2}^d{\left(\sum _{l\in K_j}{\rho }_l{\mid h_l\mid }^2\right)}^{1/2}\lesssim \frac{1}{2\sqrt{\stackrel{\sim }{s}}}\sum _{l=K+1}^{N^2}{\rho }_{(l)}^{1/2}\mid h_{(l)}\mid \\ \lesssim \frac{1}{2\sqrt{\stackrel{\sim }{s}}}\left\{s^q{(logN)}^q\sum _{l=1}^K{\rho }_{(l)}^{1/2}\mid h_{(l)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right\}\\ \lesssim \frac{1}{2\sqrt{K}}\sum _{l=1}^K{\rho }_{(l)}^{1/2}\mid h_{(l)}\mid +\frac{1}{2\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\\ \le \frac{1}{2}{\left(\sum _{j=1}^K{\rho }_{(l)}{\mid h_{(l)}\mid }^2\right)}^{1/2}+\frac{1}{2\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1.\end{array}$$ (16)

Recall that β̂ is calculated by solving (5). Let à be an n × N² matrix with the (i, l)th element being n^−1/2ξ_il, ρ be a diagonal matrix with the l-th diagonal element ρ_l, and γ and h be the wavelet coefficients of β₀ and α, respectively. Therefore, $A_X{\beta }_0=\sqrt{n}\stackrel{\sim }{A}{\rho }^{1/2}\gamma$ and $A_X\delta \beta =\sqrt{n}\stackrel{\sim }{A}{\rho }^{1/2}h$. Let $\lambda =C\sqrt{n}\sigma$. With probability more than 1 − e^−Cn, ${\Vert Y-A_X{\beta }_0\Vert }_2\le C\sqrt{n}\sigma$. This gives

$$\sqrt{n}{\Vert \stackrel{\sim }{A}{\rho }^{1/2}h\Vert }_2={\Vert A_X\alpha \Vert }_2={\Vert A_X{\beta }_0-A_X\widehat{\beta }\Vert }_2\le {\Vert Y-A_X{\beta }_0\Vert }_2+{\Vert Y-A_X\widehat{\beta }\Vert }_2\lesssim \sqrt{n}\sigma .$$ (17)

Following the argument in Candès et al. (2006a, 2006b), if n ≥ C⁻²s log(N²/s), then à satisfies the restricted isometry property (RIP) with a large probability: with probability exceeding 1 − 2e^−Cδ2n,

$$(1-\delta ){\Vert u\Vert }_2^2\le {\Vert \stackrel{\sim }{A}u\Vert }_2^2\le (1+\delta ){\Vert u\Vert }_2^2,$$ (18)

for all s-sparse vector u ∈ ℝ^N2. Therefore,

$$\begin{array}{l}\sqrt{n}\sigma ⊳\sqrt{n}{\Vert \stackrel{\sim }{A}{\rho }^{1/2}h\Vert }_2\ge \sqrt{n}{\Vert \stackrel{\sim }{A}{({\rho }^{1/2}h)}_K+\stackrel{\sim }{A}{({\rho }^{1/2}h)}_{K_1}\Vert }_2-\sqrt{n}\sum _{j=2}^d{\Vert \stackrel{\sim }{A}{({\rho }^{1/2}h)}_{K_j}\Vert }_2\\ \ge \sqrt{n(1-\delta )}{\Vert {({\rho }^{1/2}h)}_K+{({\rho }^{1/2}h)}_{K_1}\Vert }_2-\sqrt{n(1+\delta )}\sum _{j=2}^d{\Vert {({\rho }^{1/2}h)}_{K_j}\Vert }_2\\ \ge \sqrt{n(1-\delta )}{\Vert {({\rho }^{1/2}h)}_K+{({\rho }^{1/2}h)}_{K_1}\Vert }_2-\sqrt{n(1+\delta )}\left(\frac{1}{2}{\Vert {({\rho }^{1/2}h)}_K\Vert }_2+\frac{1}{2\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right)\\ \ge (\sqrt{1-\delta }-\frac{\sqrt{1+\delta }}{2})\sqrt{n}{\Vert {({\rho }^{1/2}h)}_K+{({\rho }^{1/2}h)}_{K_1}\Vert }_2-\frac{\sqrt{n(1+\delta )}}{2\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1.\end{array}$$

Since δ < 1/3, we have

$$\sqrt{n}{\Vert {({\rho }^{1/2}h)}_K+{({\rho }^{1/2}h)}_{K_1}\Vert }_2\lesssim 5\sqrt{n}\sigma +\frac{3\sqrt{n}}{\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1.$$ (19)

Further, it follows from (16) and (19) that

$${\Vert \sum _{j=2}^d{({\rho }^{1/2}h)}_{K_j}\Vert }_2\le \sum _{j=2}^d{\Vert {({\rho }^{1/2}h)}_{K_j}\Vert }_2\le \frac{1}{2}{\Vert {({\rho }^{1/2}h)}_K+{({\rho }^{1/2}h)}_{K_1}\Vert }_2+\frac{\sqrt{n}}{2\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1.$$

We arrive at

$$\sqrt{n}{\Vert {\rho }^{1/2}h\Vert }_2\lesssim 8\sqrt{n}\sigma +\frac{5\sqrt{n}}{\sqrt{\stackrel{\sim }{s}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\lesssim \sqrt{n}\sigma +\frac{\sqrt{n}}{{(\mathit{s}logN)}^{q+\frac{1}{2}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1.$$

This gives

$${\Vert {\rho }^{1/2}h\Vert }_2\le C\left\{\sigma +\frac{1}{{(\mathit{s}logN)}^{q+\frac{1}{2}}}{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right\},$$

which provides the weighted L₂ error bound.

Finally, because

$$\begin{array}{l}\sqrt{n}\sigma ⊳\sqrt{n}{\Vert \stackrel{\sim }{A}{\rho }^{1/2}h\Vert }_2\ge \sqrt{n(1-\delta )}{\Vert ({\rho }^{1/2}h)\Vert }_2\\ \ge \sqrt{n(1-\delta )}{\Vert {({\rho }^{1/2}h)}_K\Vert }_2\ge \sqrt{n(1-\delta )}{K}^{-q}{(\sum _{j=1}^K{\mid h_{(j)}\mid }^2)}^{1/2},\end{array}$$

we have

$${\left(\sum _{j=1}^K{\mid h_{(j)}\mid }^2\right)}^{1/2}\lesssim {(\mathit{s}logN)}^q\sigma .$$

Combining this with (20) leads to the L₁ error bound since

$$\begin{array}{l}\sum _{j=1}^{N^2}\mid h_{(j)}\mid \le (1+log(\frac{N^2}{s}))\sum _{j=1}^K\mid h_{(j)}\mid +log\left(\frac{N^2}{s}\right){\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\\ \le (1+log(\frac{N^2}{s}))K^{1/2}{(\sum _{j=1}^K{\mid h_{(j)}\mid }^2)}^{1/2}+log\left(\frac{N^2}{s}\right){\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\\ \lesssim (1+log(\frac{N^2}{s}))K^{q+\frac{1}{2}}\sigma +log\left(\frac{N^2}{s}\right){\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\\ \lesssim log\left(\frac{N^2}{s}\right)\left\{{(\mathit{s}logN)}^{q+\frac{1}{2}}\sigma +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right\}.\end{array}$$

This completes the proof of the theorem.

Lemma 7.1

Let K = 8s log N. Then

$$\sum _{j=K+1}^{N^2}\mid h_{(j)}\mid \lesssim log\left(\frac{N^2}{s}\right)\left(\sum _{j=1}^K\mid h_{(j)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right),$$ (20)

$$\sum _{j=K+1}^{N^2}{\rho }_{(j)}^{1/2}\mid h_{(j)}\mid \lesssim s^q{(logN)}^q\sum _{j=1}^K{\rho }_{(j)}^{1/2}\mid h_{(j)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1.$$ (21)

Proof

Let α = β₀−β̂. We first derive a cone constraint for α. Let S̃ be the support of the largest s elements of ∇β₀. Observe that

$${\Vert \nabla \widehat{\beta }\Vert }_1\le {\Vert \nabla {\beta }_0\Vert }_1={\Vert {(\nabla {\beta }_0)}_{\stackrel{\sim }{S}}\Vert }_1+{\Vert {(\nabla {\beta }_0)}_{{\stackrel{\sim }{S}}^c}\Vert }_1,$$

and on the other hand,

$$\begin{array}{l}{\Vert \nabla \widehat{\beta }\Vert }_1={\Vert {(\nabla {\beta }_0)}_{\stackrel{\sim }{S}}-{(\nabla \alpha )}_{\stackrel{\sim }{S}}\Vert }_1+{\Vert {(\nabla {\beta }_0)}_{{\stackrel{\sim }{S}}^c}-{(\nabla \alpha )}_{{\stackrel{\sim }{S}}^c}\Vert }_1\\ \ge {\Vert {(\nabla {\beta }_0)}_{\stackrel{\sim }{S}}\Vert }_1-{\Vert {(\nabla \alpha )}_{\stackrel{\sim }{S}}\Vert }_1-{\Vert {(\nabla {\beta }_0)}_{{\stackrel{\sim }{S}}^c}\Vert }_1+{\Vert {(\nabla \alpha )}_{{\stackrel{\sim }{S}}^c}\Vert }_1.\end{array}$$

Combining these two inequalities yields

$${\Vert {(\nabla \alpha )}_{{\stackrel{\sim }{S}}^c}\Vert }_1\le {\Vert {(\nabla \alpha )}_{\stackrel{\sim }{S}}\Vert }_1+2{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_{\stackrel{\sim }{S}}\Vert }_1.$$ (22)

The cone constraint on the discrete gradient can be transferred to a cone constraint on the wavelet coefficients. Write

$$\alpha =\sum _{j\in S}{h}_j{\varphi }_j+\sum _{j\in S^c}{h}_j{\varphi }_j,$$

where the wavelet coefficients are nonconstant over S which has cardinality at most K = 8s log N. Recall that |h_j| ≤ Cj⁻¹||∇α||₁. From (22) we have

$$\begin{array}{l}\sum _{j=K+1}^{N^2}\mid h_{(j)}\mid \le \sum _{j=s+1}^{N^2}\mid h_{(j)}\mid \lesssim log\left(\frac{N^2}{s}\right){\Vert \nabla \alpha \Vert }_1\\ =log\left(\frac{N^2}{s}\right)\left({\Vert {(\nabla \alpha )}_{\stackrel{\sim }{S}}\Vert }_1+{\Vert {(\nabla \alpha )}_{{\stackrel{\sim }{S}}^c}\Vert }_1\right)\\ \lesssim log\left(\frac{N^2}{s}\right)\left(2{\Vert {(\nabla \alpha )}_{\stackrel{\sim }{S}}\Vert }_1+2{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_{\stackrel{\sim }{S}}\Vert }_1\right)\\ \lesssim log\left(\frac{N^2}{s}\right)\left(\sum _{j=1}^K\mid h_{(j)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\right),\end{array}$$

where the last inequality holds because ||∇ϕ_j||₁ ≤ 8 (Needell and Ward, 2013), and

$${\Vert {(\nabla \alpha )}_{\stackrel{\sim }{S}}\Vert }_1={\Vert \nabla (\sum _{j\in \stackrel{\sim }{S}}{h}_{(j)}{\varphi }_{(j)})\Vert }_1\le \sum _{j\in \stackrel{\sim }{S}}\mid h_{(j)}\mid {\Vert \nabla {\varphi }_{(j)}\Vert }_1\le 8\sum _{j\in \stackrel{\sim }{S}}\mid h_{(j)}\mid \le 8\sum _{j=1}^K\mid h_{(j)}\mid .$$

Furthermore, since ρ_(j) is of order j^−2q for q > 0 from A3, we have

$$\begin{array}{l}\sum _{j=K+1}^{N^2}{\rho }_{(j)}^{1/2}\mid h_{(j)}\mid \lesssim \sum _{j=K+1}^{N^2}{j}^{-q}{j}^{-1}{\Vert \nabla \alpha \Vert }_1\le {\Vert \nabla \alpha \Vert }_1\\ \lesssim \sum _{j=1}^K\mid h_{(j)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\\ \lesssim K^q\sum _{j=1}^K{\rho }_{(j)}^{1/2}\mid h_{(j)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1\\ =s^q{(logN)}^q\sum _{j=1}^K{\rho }_{(j)}^{1/2}\mid h_{(j)}\mid +{\Vert \nabla {\beta }_0-{(\nabla {\beta }_0)}_S\Vert }_1,\end{array}$$ (23)

which completes the proof of the lemma.

7.2 Proof of Theorem 3.1

Write ξ = (θ, β), W = (X, Z), and W_i = (X_i, Z_i), i = 1, …, n. Denote η_i(ξ) = η(W_i; ξ), η_W(ξ) = η(W; ξ), and

$$M_n(\xi )=-\frac{1}{n}\sum _{i=1}^n\left\{Y_i{\eta }_i(\xi )-b({\eta }_i(\xi ))\right\},{\overline{M}}_n(\xi )=-\frac{1}{n}\sum _{i=1}^n\left\{\stackrel{.}{b}({\eta }_i(\xi )){\eta }_i(\xi )-b({\eta }_i(\xi ))\right\}.$$

Recall that ξ̂ minimizes −M_n(ξ) + λ||β||_TV. We have

$$0\le M_n(\widehat{\xi })-M_n({\xi }_0)-\lambda {\Vert \widehat{\beta }\Vert }_{TV}+\lambda {\Vert {\beta }_0\Vert }_{TV}.$$

Direct calculation yields

$$\begin{array}{l}{M}_n(\xi )-M_n({\xi }_0)=-\frac{1}{n}\sum _{i=1}^n\left(Y_i-\stackrel{.}{b}({\eta }_i({\xi }_0))\right){\eta }_i(\xi -{\xi }_0)+\stackrel{.}{b}({\eta }_i({\xi }_0)){\eta }_i(\xi -{\xi }_0)-\left(b({\eta }_i(\xi ))-b({\eta }_i({\xi }_0))\right)\\ =H_n(\widehat{\xi })-\frac{1}{2n}\sum _{i=1}^n\ddot{b}({\eta }_i^{\ast }){\eta }_i^2(\xi -{\xi }_0).\end{array}$$ (24)

where η_i(ξ − ξ₀) = (θ − θ₀)^TZ + 〈X,β − β₀〉, and

$$H_n(\xi )=-\frac{1}{n}\sum _{i=1}^n\left(Y_i-\stackrel{.}{b}({\eta }_i({\xi }_0))\right){\eta }_i(\xi -{\xi }_0),$$ (25)

and ${\eta }_i^{\ast }$ is a number between η_i(ξ) and η_i(ξ₀). Therefore,

$$\begin{array}{l}\frac{1}{2n}\sum _{i=1}^n\ddot{b}({\eta }_i^{\ast }){\eta }_i^2(\xi -{\xi }_0)\le H_n(\widehat{\xi })-\lambda {\Vert \widehat{\beta }\Vert }_{TV}+\lambda {\Vert {\beta }_0\Vert }_{TV}\\ \le \underset{\xi }{sup}\mid H_n(\xi )\mid -\lambda {\Vert \widehat{\beta }\Vert }_{TV}+\lambda {\Vert {\beta }_0\Vert }_{TV}\\ \lesssim n^{-1/2}+\lambda ,\end{array}$$

where the last inequality is because of Lemma 7.2.

Let $g^{\ast }={(g_1^{\ast }(X_1,\dots ,X_n),\dots ,g_n^{\ast }(X_1,\dots ,X_n))}^T$ be the least favorable direction such that, for any g = (g₁(X₁,…, X_n), …, g_n(X₁, …, X_n))^T, we have

$$\frac{1}{n}\sum _{i=1}^n{\left(Z_i-g_i^{\ast }(X_1,\dots ,X_n)\right)}^T{g}_i(X_1,\dots ,X_n)=0.$$

Note that

$$\begin{array}{l}\frac{1}{n}\sum _{i=1}^n{\eta }_i^2(\widehat{\xi }-{\xi }_0)=\frac{1}{n}\sum _{i=1}^n{\left({(\widehat{\theta }-{\theta }_0)}^T{Z}_i+\langle X_i,\widehat{\beta }-{\beta }_0\rangle \right)}^2\\ =\frac{1}{n}\sum _{i=1}^n{\left({(\widehat{\theta }-{\theta }_0)}^T(Z_i-g_i^{\ast })+{(\widehat{\theta }-{\theta }_0)}^T{g}_i^{\ast }+\langle X_i,\widehat{\beta }-{\beta }_0\rangle \right)}^2\\ ={(\widehat{\theta }-{\theta }_0)}^T\left(\frac{1}{n}\sum _{i=1}^n(Z_i-g_i^{\ast }){(Z_i-g_i^{\ast })}^T\right)(\widehat{\theta }-{\theta }_0)+\frac{1}{n}\sum _{i=1}^n{\left({(\widehat{\theta }-{\theta }_0)}^T{g}_i^{\ast }+\langle X_i,\widehat{\beta }-{\beta }_0\rangle \right)}^2.\end{array}$$

Assuming that $n^{-1}{\sum }_{i=1}^n(Z_i-g_i^{\ast }){(Z_i-g_i^{\ast })}^T$ is non-singular, we conclude that ||θ̂ − θ₀||₂ ≲ n^−1/2 by choosing λ = Cn^−1/2, and ${\Vert A_X\widehat{\beta }-A_X{\beta }_0\Vert }_2\lesssim \sqrt{n}$, which gives an equation similar to (17). The following proofs will go through with the same arguments as for the proof of Theorem 2.1. This completes the proof of Theorem 3.1.

Lemma 7.2

Assume B1–B2 hold. Let r = q − 1/2 > 0. Let B_δ = {ξ: δ/2 ≤ d_W(ξ, ξ₀) ≤ δ}, where

$$d_W^2(\xi ,{\xi }_0)={\Vert \theta -{\theta }_0\Vert }_2^2+{\mathbb{E}}_X\left({\langle X,\beta -{\beta }_0\rangle }^2\right)$$

Then,

$$\underset{\xi \in B_{\delta }}{sup}\left|H_n(\xi )\right|=O_p\left(n^{-\frac{1}{2}}{\delta }^{\frac{2r+1}{2(r+1)}}\right).$$ (26)

Proof

Recall that H_n(ξ) = − (P_n − ℙ) f_ξ(W, Y), where

$$f_{\xi }(W,Y)=\left(Y-\stackrel{.}{b}({\eta }_W({\xi }_0))\right){\eta }_W(\xi -{\xi }_0).$$

Consider ℳ_δ = {f_ξ(W, Y) : ξ ∈ B_δ}, with L₂(P) norm, i.e., for any f ∈ ℳ_δ, ${\Vert f\Vert }_{P,2}^2={\mathbb{E}}_{W,Y}{f}^2(W,Y)$.

Let ${\mathbb{G}}_n=\sqrt{n}(P_n-\mathbb{P})$ and ||G_n||_ℳδ = sup_f∈ℳδ |𝔾_nf|. Then,

$$\underset{\xi \in B_{\delta }}{sup}\left|H_n(\xi )\right|=n^{-1/2}{\Vert G_n\Vert }_{{\mathcal{M}}_{\delta }}.$$

Therefore, it suffices to show that

$${\Vert {\Vert {\mathbb{G}}_n\Vert }_{{\mathcal{M}}_{\delta }}\Vert }_{P,2}=O({\delta }^{\frac{2r+1}{2(r+1)}}).$$

We prove this result by using Theorem 2.14.1 of van der Vaart and Wellner (1996) and exploiting the covering numbers of ℳ_δ. For statistical applications of covering numbers, please see Chapter 2 of van der Vaart and Wellner (1996). This result can be achieved by showing that

$$log\mathcal{N}\left(\epsilon ,{\mathcal{M}}_{\delta },{\Vert ·\Vert }_{P,2}\right)\lesssim {\epsilon }^{-1/r}log(\frac{4\delta +\epsilon }{\epsilon }).$$

Suppose that there exist ξ₁, …, ξ_m ∈ B_δ such that, for any ξ ∈ B_δ, min_1≤i≤m ||ξ − ξ_i||_P,2 ≤ ε. Observe that

$$\underset{1\le i\le m}{min}{\mathbb{E}}_{W,Y}{\left[\left(Y-\stackrel{.}{b}({\eta }_W({\xi }_0))\right){\eta }_W(\xi -{\xi }_0)-\left(Y-\stackrel{.}{b}({\eta }_W({\xi }_0))\right){\eta }_W({\xi }_i-{\xi }_0)\right]}^2\le C{\epsilon }^2.$$

Therefore, the cover number for ℳ_δ is of the same order of that for B_δ, and specifically,

$$\mathcal{N}\left(\epsilon ,{\mathcal{M}}_{\delta },{\Vert ·\Vert }_{P,2}\right)=\mathcal{N}\left(\frac{\epsilon }{C},B_{\delta },d_W\right).$$

Write β = Σ_k γ_kϕ_k, ${\beta }_0={\sum }_k{\gamma }_k^0{\varphi }_k$, and $X={\sum }_k{\rho }_k^{1/2}{\xi }_k{\varphi }_k$. Hence, $d_W^2(\xi ,{\xi }_0)={\Vert \theta -{\theta }_0\Vert }_2^2+{\sum }_k{\rho }_k{({\gamma }_k-{\gamma }_k^0)}^2$. For any β = Σ_k γ_kϕ_k, ∈ B_δ, let β^* =Σ_k≤M γ_(k)ϕ_(k) with M = ε^−1/(r+1). Since ρ_(l) is of order l^−2q, Σ_ℓ>s ρ_(ℓ) is of order s^−2r with r = q − 1/2 > 0. Therefore,

$$\mathbb{E}\left({\langle X,\beta -{\beta }^{\ast }\rangle }^2\right)=\sum _{k>M}{\gamma }_{(k)}^2{\rho }_{(k)}\lesssim \frac{1}{M^2}{M}^{-2r}=M^{-2(r+1)}={\epsilon }^2.$$

So if we can find ${\beta }_1^{\ast },\dots ,{\beta }_m^{\ast }\in B_{\delta }^{\ast }$, where $B_{\delta }^{\ast }=\{\beta ={\sum }_{k\le M}{\gamma }_{(k)}{\varphi }_{(k)}:{\sum }_{k\le M}{\rho }_{(k)}{({\gamma }_{(k)}-{\gamma }_{(k)}^0)}^2\le {\delta }^2\}$, satisfying for all ${\beta }^{\ast }\in B_{\delta }^{\ast }$,

$$\underset{1\le k\le m}{min}\mathbb{E}\left({\langle X,{\beta }^{\ast }-{\beta }_k^{\ast }\rangle }^2\right)\le {\epsilon }^2,$$

it also guarantees that, for any β ∈ B_δ,

$$\underset{1\le k\le m}{min}\mathbb{E}\left({\langle X,\beta -{\beta }_k^{\ast }\rangle }^2\right)\lesssim \underset{1\le k\le m}{min}\left\{\mathbb{E}\left({\langle X,\beta -{\beta }^{\ast }\rangle }^2\right)+\mathbb{E}\left({\langle X,{\beta }^{\ast }-{\beta }_k^{\ast }\rangle }^2\right)\right\}\lesssim {\epsilon }^2.$$

In addition, since θ ∈ Θ which is a bounded subset of ℝ^p, we may find θ₁, …, θ_m̃ such that, for any θ ∈ Θ, ${min}_{1\le k\le \stackrel{\sim }{m}}{\Vert \theta -{\theta }_k\Vert }_2^2\le {\epsilon }^2$.

Since it is known that the covering number for a ball in ℝ^M is $\mathcal{N}(\epsilon ,B_{\delta }^{\ast },d_X)\lesssim {\{(4\delta +\epsilon )/\epsilon \}}^M$, it follows from the above arguments that

$$log\mathcal{N}\left(\epsilon ,{\mathcal{M}}_{\delta },{\Vert ·\Vert }_{P,2}\right)\lesssim (M+p)log\left(\frac{4\delta +\epsilon }{\epsilon }\right)\lesssim {\epsilon }^{-\frac{1}{r+1}}log\left(\frac{4\delta +\epsilon }{\epsilon }\right).$$

We calculate J(1, ℳ_δ) by

$$J(1,{\mathcal{M}}_{\delta })={\int }_0^1\sqrt{1+log\mathcal{N}\left(\epsilon ,{\mathcal{M}}_{\delta },{\Vert ·\Vert }_{P,2}\right)}d\epsilon \lesssim {\delta }^{\frac{2r+1}{2(r+1)}}.$$

It follows from Theorem 2.14.1 in van der Vaart and Wellner (1996), we have ${\Vert {\Vert {\mathbb{G}}_n\Vert }_{{\mathcal{M}}_{\delta }}\Vert }_{P,2}=O({\delta }^{\frac{2r+1}{2(r+1)}})$, which completes the proof of the lemma.