Comparison of Tenofovir Plasma and Tissue Exposure Using a Population Pharmacokinetic Model and Bootstrap: A Simulation Study from Observed Data

Abstract

Sparse tissue sampling with intensive plasma sampling creates a unique data analysis problem in determining drug exposure in clinically relevant tissues. Tissue exposure may govern drug efficacy, as many drugs exert their actions in tissues. We compared tissue area-under-the-curve (AUC) generated from bootstrapped noncompartmental analysis (NCA) methods and compartmental nonlinear mixed effect (NLME) modeling. A model of observed data after single-dose tenofovir disoproxil fumarate was used to simulate plasma and tissue concentrations for two destructive tissue sampling schemes. Two groups of 100 data sets with densely-sampled plasma and one tissue sample per individual were created. The bootstrapped NCA (SAS 9.3) used a trapezoidal method to calculate geometric mean tissue AUC per dataset. For NLME, individual post-hoc estimates of tissue AUC were determined, and the geometric mean from each dataset calculated. Median normalized prediction error (NPE) and absolute normalized prediction error (ANPE) were calculated for each method from the true values of the modeled concentrations. Both methods produced similar tissue AUC estimates close to true values. Although the NLME-generated AUC estimates had larger NPEs, it had smaller ANPEs. Overall, NLME NPEs showed AUC under-prediction but improved precision and fewer outliers. The bootstrapped NCA method produced more accurate estimates but with some NPEs >100%. In general, NLME is preferred, as it accommodates less intensive tissue sampling with reasonable results, and provides simulation capabilities for optimizing tissue distribution. However, if the main goal is an accurate AUC for the studied scenario, and relatively intense tissue sampling is feasible, the NCA bootstrap method is a reasonable, and potentially less time-intensive solution.

INTRODUCTION

Determining antiretroviral (ARV) concentrations in tissues that may act as sites of HIV transmission or as viral reservoirs is critical to pre-exposure prophylaxis (PrEP) and achieving cure. The majority of HIV transmission occurs by exposure of the virus to vulnerable cells in anogenital tissues (cervical and vaginal tissue in receptive women, rectal tissue in receptive men and women) through sexual contact (1); adequate drug exposure at the tissue site of viral transmission has demonstrated efficacy in preventing infection, in vitro(2, 3) and in vivo(4, 5). The gastrointestinal tract contains gut-associated lymphoid tissue (GALT), a well-described mucosal reservoir of viral persistence (6) that potentially limits the ability to achieve cure if those therapies do not achieve effective concentrations in the GALT.(7) Structures within both the male and female genital tracts may also serve as viral reservoirs (reviewed in (8)).

Pharmacokinetic (PK) sampling of these tissues presents several logistical and ethical challenges, as invasive procedures are required to obtain biopsy specimens from the gastrointestinal, rectal, or female genital tract tissues. Individual subjects cannot contribute multiple samples from these matrices in short time frames, and cost constrains enrollment of large numbers of subjects to construct densely-sampled concentration-time profiles. Hence, sparse sampling in tissue, with pooled data analysis, has been used to compare exposures in plasma and tissue, essentially borrowing methods developed for destructive sampling in laboratory animals.(9)

Several other, more computationally intense methods have been developed for these purposes, but have several limitations, chiefly: a) only providing area under the curve (AUC) estimates over the dosing interval (AUCt), rather than to infinity (AUC_∞); b) relying on linear-trapezoidal methods, known to be less accurate than log-linear trapezoidal methods, for calculating AUC estimates; and c) the inability to provide estimates of variances in these AUC estimates. Several proposed methods address one or more of these issues, such as the sparse-sample option available in Phoenix-WinNonlin, based on Bailor(9) and Nedelman(10), which does provide a pooled-sample estimate of terminal elimination rate (lambda z), AUC_t,, and AUC_∞, but relies on linear trapezoidal methods. Other more complex methods have been proposed, but are not widely used.(10–12)

Nonlinear mixed-effects (NLME) modelling (13, 14) and bootstrapping NCA methods (15, 16) have been advocated to address these issues. NLME requires the development of a structural model of drug disposition as well as a statistical model of variability, which is inherently more difficult in the setting of sparse sampling. Bootstrap-based NCA methods for PK parameter estimation is an alternative model-independent method that can provide estimates of variance around AUC estimates, if desired, and offers an alternative to compartmental modeling of sparse data. Further, published experience comparing bootstrap to traditional NCA, against both a theoretical estimate (i.e., known true value) and actual clinical or animal study data, has been quite encouraging.(15, 17–19)

Our aim here was to test, on ARV concentration data obtained from a tissue PK study in healthy volunteers (20), which method, NLME or NCA-based bootstrap, is optimal for determining measures of exposure in tissues. Tenofovir (TFV), an orally administered antiretroviral approved for use (combined with other agents) for both HIV treatment and prevention, with a complex distribution profile, was chosen as the test case.

METHODS AND MATERIALS

Clinical Study Data and Model Development

For this exercise, plasma and rectal tissue concentrations of TFV were used from an investigation which sampled plasma and several tissue sites in 15 healthy volunteers for 14 days after administration of a single 300mg oral dose of tenofovir disoproxil fumarate.(20) The TAIL study was conducted at the University of North Carolina at Chapel Hill, with the goal of characterizing the wash-out of drug in tissue. The tissue data were collected in a unique design given the length of the study: each subject contributed two tissue samples, spaced 5–7 days apart. For this exercise, tenofovir concentrations in the plasma and rectal tissue homogenates from 8 male participants were used. The intracellular metabolite of tenofovir, tenofovir diphosphate was also measured in tissue homogenates as part of the original study, and was not considered here for reasons of parsimony. Participants also received 200mg of emtricitabine with tenofovir, as this combination is approved for both HIV treatment and prevention, and 7 female participants provided cervical and vaginal tissue samples. All subjects provided full plasma profiles, although the plasma sampling was sparse in the first 24 hours after administration. To supplement these data, TFV concentration-time data over 24 hours was used from a similar study conducted by the same research group with a similar design, but with more intensive sampling immediately post-administration.(13) This allowed accurate recovery of distribution-phase parameters, and a more accurate calculation of the AUC.

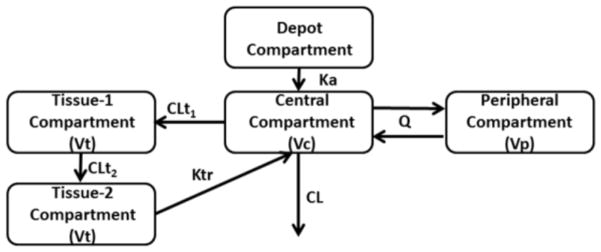
NLME modelling using NONMEM 7.3 was used to fit these data, using the First Order Conditional Estimation Method with Interaction (FOCE-I). Parameters were assumed to have a log-normal distribution and the residual error models (plasma and tissue) were assumed to be proportional and log normal respectively, after testing several residual error model possibilities, including additive and additive/proportional. This “true” model was built by fitting data from the terminal tissue and plasma compartments from the Patterson et al study (20) and plasma data from Cottrell et al study.(21) This model consisted of a four compartment model, as seen in Figure 1. A standard two-compartment model described the plasma concentrations, with an additional compartment to describe drug transfer from plasma to tissue and a compartment to describe drug transfer from the rectal tissue to a transit compartment (tissue compartment 2) then back to the plasma (central compartment). Tissue compartment 2 served as a delay in transfer of the drug back to the central compartment, and could represent metabolite formation, degradation, and recycling. Tissue concentrations analyzed here are sampled from the 1^st tissue compartment. The parameter estimates of the true model along with inter-individual variability on those parameters are located in Table 1. Tenofovir plasma parameters are consistent with the literature (22, 23), which generally describes tenofovir disposition as a two-compartment model. For tissue parameters, no direct comparators are available in the literature, though estimates are similar in magnitude to those of Cottrell et al.(21) Standard diagnostic plots are included in the Supplement.

Figure 1.

Pharmacokinetic model used simulate plasma and tissue data for 100 data sets used in the method comparison. Plasma data was simulated from the central compartment, and tissue data from the tissue-1 compartment. Parameters are defined in Table 1.

Table 1.

Pharmacokinetic Parameters and associated variability used to simulate the 100 datasets (Full Model).

Parameter	Value	%CV
Clearance: CL (L/hr)	47.3	21.1
Central Volume: Vc (L)	144
Intercompartmental Clearance: Q (L/hr)	186
Peripheral Volume: Vp (L)	971
Absorption Rate Constant: Ka (hr-1)	0.741
Clearance In, Tissue-1: CLt1 (L/hr)	1.83	25
Clearance, Tissue-1 to Tissue-2: CLt2(L/hr)	0.0924	64.5
Transfer Rate, Tissue-2 to Central: Ktr (hr-1)	0.0152	36.7
Tissue Volume: Vt(L)	0.749
Residual Variability
Plasma Proportional Error	7.8%
Tissue-1 Exponential Error	56%

Simulation of Method Comparison Data Sets

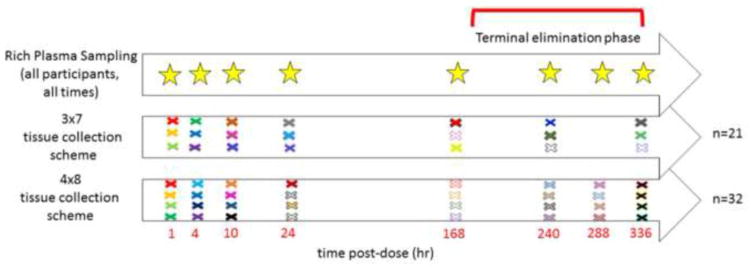
This model was used to simulate a data repository of 4000 participants from which to construct the 2 groups of 100 datasets. Plasma and tissue concentrations for each individual were simulated at the following time points: 1, 2, 4, 10, 20, 24, 48, 120, 168, 240, 288, and 336 hours post-dose. This approach allowed for the investigation of different sampling schemes while maintaining consistent individuals for comparison between sampling schemes. Parameters used to generate these profiles were assumed to be log-normally distributed. A proportional residual error model was used in plasma, and a log-normal residual error model in the tissue. From this database of virtual subjects, participants were sampled without replacement to create 2 groups of 100 data sets for the following two scenarios. The first sampling scheme consisted of 32 participants having nine sampling times from plasma (representing a rich sampling scheme, at 1, 2, 4, 10, 24, 168, 240, 288, and 336), and each participant contributing one tissue sample at one of eight sampling times (representing a sparse sampling scheme in tissue, at 1, 4, 10, 24, 168, 240, 288, and 336 hours post dose; Figure 2a). Four of these tissue sampling times occurred during the TFV terminal elimination phase. This design provided 4 tissue concentrations per tissue sampling time from unique participants. From the 100 data sets created in sampling scheme one (hereafter called “4×8 sampling scheme”), one sample time (288 hours) in its entirety was removed from each data set, and one concentration from each tissue sample time was removed, to create sampling scheme two (called “3×7 sampling scheme”). This scheme consisted of 21 participants with rich plasma sampling and seven sampling times in tissue. Each participant contributed one sample at specified sampling times (Figure 2b), with three concentrations (participants) per sampling time. Three of the sampling times occurred in the terminal phase. The true tissue exposure for each participant was determined from the parameter estimates in the structural model used to generate those participants. This exposure was determined analytically using Laplace transforms of the differential equations and then evaluating the limit of the transform as s→0 (derivations provided in Supplemental Material). Using this approach the expression for plasma exposure and tissue exposure are as follows:

$$\begin{gathered} {\mathit{AUC}}_{\mathit{plasma}}=\frac{\mathit{Dose}}{CL} \\ {\mathit{AUC}}_{\mathit{Tissue}}=\frac{\mathit{Dose}}{CL}\ast \frac{\mathit{CLt}1}{\mathit{CLt}2} \end{gathered}$$

Figure 2.

Rich plasma and sparse tissue sampling times for the 3×7 and 4×8 designs. Each colored × represents a different participant’s tissue sampling time. For the 3×7, there are 21 participants total, and 32 for the 4×8 design. All participants (represented by the stars) provided 9 plasma samples over the 336 hour sampling.

Where Dose represents the dose of TFV given, CL (L/h) represents the systemic clearance, CLt1 (L/h) represents the clearance of TFV into the tissue compartment 1, and CLt2 represents the clearance of TFV out of tissue compartment 1. Participants’ true AUC based on their parameters were known, so in each dataset a “true” geometric mean for that dataset could be calculated and used as a basis for comparison between sparse-sampling analysis methods.

Analysis of Simulated Datasets

The 100 datasets from the two different sparse sampling schemes were then evaluated using both bootstrapping NCA methodology and refitted using a reduced model in NONMEM. The reduced NLME model differed from the simulation model in that inter-individual variability in tissue clearance (CLt2) could not be estimated with a single tissue sample per individual, and thus was fixed to zero. The residual error term for the tissue concentrations was also fixed to two different estimates at the low and high end of estimated analytical error, to assess any potential interaction of residual error and AUC estimates, in the reduced model.

Analysis of Simulated Datasets: Reduced NLME Modeling

Initially, one dataset from the one hundred simulated datasets was fit to one of three plausible structural models. This was done to evaluate if other plausible structural models would yield a reasonable model structure that could describe the data. These three models included the fitted model as shown in Figure 1; a version with the Ktr leaving the system rather than transferring drug back into the central compartment; and a 3 compartment model version. The initial parameters for structural model assessment were adjusted by 20–30% from original values. Estimated inter-individual values with shrinkage estimates greater than 30% were dropped from the fitting. Standard goodness of fit plots and visual predictive checks were employed to verify the appropriateness of the model, and Akaike’s Information Criterion (AIC) used to differentiate between structural models.(24) When the model fit was designated as appropriate for this first dataset, this model was then fit to the remaining 99 datasets. Once all models had been refit and new individual post-hoc parameter estimates were determined, individual AUC in plasma and tissue could be calculated based on the AUC equations above. The geometric mean AUCs (both tissue and plasma) of the each dataset were calculated and compared to the true value for that dataset.

Analysis of Simulated Datasets: NCA with Bootstrapping

Bootstrap analyses were performed using SAS software version 9.3 (SAS Institute, Cary, NC), using Proc Survey-Select for bootstrapping, with stratification for sampling times.(25) The bootstrap method used for this experiment, with minor modifications, is similar to the “pooled bootstrap” method used for PK analysis as described by Mager & Goller.(15, 16) SAS code was written for the mathematical functions to derive standard PK parameters.(26) Thus, the compiled SAS programs were designed to generate NCA estimates for plasma and tissue concentrations based on a bootstrap resampling method, which permitted model-independent estimates of PK parameters and their corresponding estimates of variance.

AUC was used as the primary outcome measure. Trapezoidal AUC values were based on a “linear-up/log-down” method of calculation, and estimates of the terminal elimination rates (lambda z) were generated using SAS Proc Robustreg to reduce the impact of outlier values on lambda z estimation. For the 1000 replicate estimates (for each of the total 100 simulation-datasets), the regression line-based estimate of geometric-mean C_t for that replicate was divided by the estimated lambda z to calculate AUC_tail, and added to AUC_t to estimate AUC. The assumptions of this method and a description of the validation process are included in Appendix A.

Comparison of Methods for AUC estimates from simulated data

For both of the 4×8 and 3×7 sampling schemes, three sets (4 sets for 3×7) of AUC values were generated for each of the 100 datasets (i.e., simulated studies), representing: 1) true, 2) NLME (Low and High Residual Error for 3×7), and 3) bootstrap estimates. Normalized prediction error (NPE) and absolute normalized prediction error (ANPE) were calculated for each method vs. the true values from the modeled concentrations. Due to right skewing of the prediction error data, comparison of the two methods were based on nonparametric methods by Sheiner & Beal.(27),

The median values for NPE and ANPE and their minimum and maximum values were calculated using the following equations, where i represents each of the hundred data sets:

$$\begin{gathered} {\mathit{NPE}}_i=\frac{{\mathit{FittedAUC}}_i-{\mathit{TrueAUC}}_i}{{\mathit{TrueAUC}}_i} \\ {\mathit{ANPE}}_i=\frac{|{\mathit{FittedAUC}}_i-{\mathit{TrueAUC}}_i|}{{\mathit{TrueAUC}}_i} \end{gathered}$$

Since each sparse sampling scenario relied on the same simulated plasma concentrations, the resulting AUC data for method comparisons were assumed to be correlated.

RESULTS

Reduced vs. Full NLME Model

Of the three plausible structural models, the reduced model similar to the model used to simulate the data performed the best on the initial dataset, and thus was used to analyze all other data sets. This NLME model performed well in predicting the population parameter estimates for the two sparse sampling schemes, with volume terms exhibiting the highest parameter variability of the hundred datasets, likely due to lack of sampling around peak concentrations in both compartments. Clearance parameters and their variability were well estimated over the simulated sample designs. The sparse sampling scheme in tissue did not to support estimations of inter-individual variability on the clearance of the parent drug out of the tissue compartment 1 (CL_t2 parameter, Figure 1), and thus the eta term on this parameter was fixed to zero. Additionally, as a single tissue sample was taken for each participant in the simulated data sets, it was not possible to estimate inter- and intra-individual variability on parameters associated with the tissue compartment. Thus, the residual variability was fixed to 25% CV in the tissue compartment (low end of estimated analytical error).(14) The 3×7 scheme data were also re-run with the residual variability of the model fixed at 45% CV in the tissue compartment (high end of estimated analytical error). Of several error models tested during initial model development, proportional error in plasma and log-normal error in tissue were found to give reasonable characterization of the residual error.

Plasma AUC Comparisons

Both methods estimated the true plasma AUC values of the 100 datasets for 4×8 sampling scheme well (data not shown), and thus the plasma AUC values for the 3×7 sampling scheme were not further investigated, since the focus of the study was to compare the effects in tissue compartment between sampling schemes

Rectal Tissue AUC Comparisons

Given the high variability observed in tissue concentrations, both sampling schemes produced some simulated individual datasets with log-mean concentrations in tissue (but not plasma) that increased rather than fell during the tissue terminal elimination phase, resulting in physiologically implausible positive elimination slopes. This made a bootstrap estimate impossible for that particular individual. To avoid removing these data from the bootstrap analyses, the next available earlier tissue sampling time (24 hours) was systematically included in the batch fits of the regression lines, and analyzed using robust regression. Table 2 shows the nonparametric summary measures of bias and precision (expressed as percentage values) for the two methods based on NPE and ANPE for all 100 datasets, including results with 45% CV fixed residual error in the 3×7 sampling design. For the 4×8 sampling design, the bootstrap method median NPE was quite close to the true value, however the range of both NPE and ANPE values is wide, and 20 of the data sets had ANPE values of 30% or higher, with half of those having ANPE values of 50% or higher. For the 3×8 sampling scheme, the bootstrap NCA method displays similar results, with even wider NPE and ANPE ranges, and additional data sets with ANPE values of at least 30%. In contrast, the NLME method NPE values of −8.7% and −9.3% for the 4×8 and 3×7 sampling designs, respectively, reflected AUC estimates that systematically were slightly lower than the true AUC estimates. There was some improvement in NPE (−7.1% for 3×7 design) when residual error was fixed to larger assay uncertainty. This illustrates that a reasonable attempt to accurately assess the magnitude of the residual error is needed to prevent bias in parameter estimates. However, the range of ANPE values was narrower than the bootstrap NCA method, and there were fewer datasets resulting in high (≥30%) ANPE values. NPE and ANPE values for the 100 datasets for the bootstrap method showed greater variability and were much more highly skewed (Figures 2 & 3) than those observed with the NLME method.

Table 2.

Summary of normalized prediction error (NPE) and absolute normalized prediction error (ANPE) expressed as a percentage value for both estimation methods.

Sample Design	Method	NPE: Median [Min, Max] (%)	ANPE : Median [Min, Max] (%)	ANPE ≥ 30% (% of dataset)	ANPE ≥ 50% (% of dataset)
4×8	NLME	−8.7 [−35, 30]	13.1 [0.1, 35]	7	0
	Bootstrap	−0.1 [−36, 115]	17.1 [0.4, 115]	20	10
3×7	NLME (25%CV Residual Error)	−9.3 [ −45, 52]	14.7 [0.7, 52]	12	1
	NLME (45% CV Residual Error)	−7.1 [−47,76]	17.0 [0.7,76]	16	1
	Bootstrap	3.5 [−48, 119]	17.2 [0.1, 119]	26	11

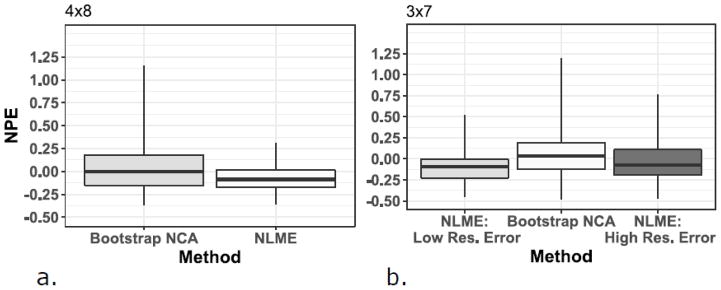
Figure 3.

Figure 3a and 3b. Boxplots of the normalized prediction error (NPE) by estimation method and sparse tissue sampling design. NLME results are divided into low and high residual error (Res.) for the 3×7 design. Data are presented as median (midpoint), interquartile range (box), and range (whiskers). NLME: Nonlinear Mixed Effects Modeling; NCA: noncompartmental analysis

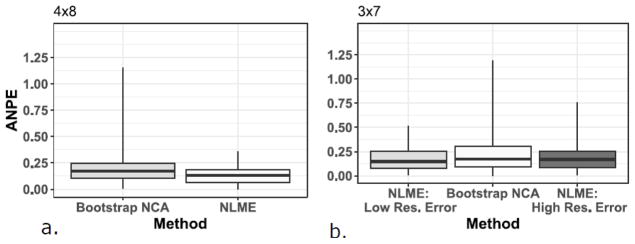
Figures 3a & 3b and Figures 4a & 4b show boxplots of the NPE and ANPE, respectively, by estimation method and sparse tissue sampling design. Data are presented as median (midpoint line), interquartile range (box), and range (whiskers). These figures visually show the smaller variability in NPE with NLME modeling than with the bootstrapping method, and for the 3×7 sampling design, the influence of different residual error values on the NPE and ANPE values.

Figure 4.

Figure 4a and 4b. Boxplots of the absolute normalized prediction error (ANPE) by estimation method and sparse tissue sampling design. NLME results are divided into low and high residual error (Res.) for the 3×7 design. Data are presented as median (midpoint), interquartile range (box), and range (whiskers). NLME: Nonlinear Mixed Effects Modeling; NCA: noncompartmental analysis

DISCUSSION

Here, two modestly different tissue sampling strategies for characterizing TFV PK in rectal tissue, selected to be in the range of clinically and ethically feasible sampling in humans, were analyzed using NLME and bootstrap, and their AUC estimates compared. While both methods provided reasonable estimates of AUC in the 100 simulated studies (i.e., median values within 10% of true AUCs), estimations by bootstrap were somewhat closer than NLME to true values for both sampling schemes in this small simulation study. However, bootstrap had significantly greater variability in AUC estimates than NLME, particularly in the 3×7 sampling scheme. This result was attenuated when the residual error was fixed to a larger value in the 3×7 NLME analysis, resulting in more variability in the AUC estimates.

The primary advantages of the bootstrap-NCA method includes speed of analysis, ready interpretation of output, and fewer assumptions associated with model development. However, a significant disadvantage includes its reliance upon relatively greater amounts of (and more precisely collected) sparse data. If bootstrap alone is to be used for analysis, for drugs with complex PK such as TFV, 4 or more tissue samples per time-point and at least 9 tissue sampling times would be recommended. Ideally, there also should be at least 4 time-points during the terminal elimination phase, since a reliable estimate of lambda z is crucial for estimating AUC_tail, and thus total AUC, half-life, and other PK parameters. As seen here, use of 3 tissue observations per time and 7 tissue sampling times can be done with bootstrap using geometric means, but the estimates are sensitive to outliers and data with missing replicates at these sparsely-sampled intervals. Because sample time is a strata in the bootstrap-NCA method, if tissue samples are collected at times that deviate significantly from the study protocol, as may occur in complex clinical studies, either the resulting concentrations or the resulting time deviations would have to be ignored.

With NLME, these time deviations may actually confer an advantage, by providing more information across the time interval under study. Using NLME methods allow for sparse samples to be taken at different time within a clinical study, which can be advantageous for invasive sampling such as tissue biopsy. A second advantage to NLME methods are that the totality of all data can be used, as was the case here where plasma concentration drives the tissue concentration. Finally using NLME/compartmental methods allows for simulations to be performed to investigate other dosing scenarios, dosing regimens, or what-if scenarios, that can be more difficult with non-compartmental methods. The disadvantage in use NLME/compartmental methods is development of the underlying model, as well as assumptions that may have to be made, such as the magnitude of the residual error in sparse, independent samples, and model qualification/validation steps required before using the model.

Bootstrap estimates of AUC overall were reasonably close to the true sample estimates. However, TFV concentrations during the 168 to 336 hour sampling times were quite variable (e.g., 100 to 250 percent CV). In many individual fits, inclusion of the next available earlier tissue sampling time (24 hours) was needed with bootstrap analyses (serving as a restricting hinge) to estimate a negative slope for the elimination phase and avoid exclusion of those AUC estimates by program criteria. Since runs for this investigation were done in batch, it was necessary to include the extra earlier sample time for all fits. Although robust (iterative re-weighted) regression was used to limit the impact of deviate values, this approach may still have resulted in overestimation of lambda z, and subsequently underestimation of AUC_tail. For this drug, the true AUC_tail made a very small contribution to overall AUC, thus, the likely bias was limited; however, this also is a potential limitation of the bootstrap-NCA approach for other agents. In other studies, a larger spread in sampling times during terminal elimination (if feasible) would mitigate against this problem.

The individual calculated AUC values in tissue were right skewed, consistent with the assumption that the AUC values were log-normally distributed. In the NLME analysis, the estimates of the simulated geometric mean AUC tended to be biased low from the true value, whereas the median of the data set tended to better estimate the true value. On the whole, the 100 data sets geometric means were well-clustered, suggesting that in this study, this measure of central tendency was biased low, with high precision. The cause of this under-estimation is unclear, although is partially related to fixing the residual error in the tissue model. Hing & Woolfrey (13) investigated this with a relatively small number of simulations based on animal data and showed that there was very little difference when changing the fixed error value. In this study, the magnitude of the residual variability affected the model parameter estimates. The overall NPE was improved as residual variability was fixed to a larger value, but variability associated with NPE slightly increased. When this error was estimated by NLME, the overall exposure was closer to the true value of the sample, but the ability to estimate inter-individual variability was sacrificed. Analytical replicates of destructive samples has been suggested as a method to overcome this limitation.(28), and thus using a fixed estimate of 45% CV in the 3×7 design, derived from internal data available in the UNC Clinical Pharmacology and Analytical Chemistry Laboratory (Mackenzie Cottrell, personal communication), we did observe an improvement in the NPE, but not the ANPE. A second possible cause of bias in the tissue compartment is use of the FOCE algorithm. With two data points per individual in a two compartment model, the best FOCE clearance estimates were within 10% of the true value, in line with our experience.(29) These factors support our observation that the precision and magnitude of the bias were relatively unchanged by reducing both the number of samples per time point and the number of time points. To test this, expectation-maximization algorithms could be used.(29, 30)

This simulation study represents some strengths previous lacking in this research area. This is to our knowledge the first simulation study based on actual data from a clinical study linking plasma with sparse tissue samples, and accounting for the high variability observed in such data. In most other simulation studies in this area variability was only up to 30% CV. When high variability was encountered, extreme values were commonly trimmed or discarded in prior work, while essentially all data in this study was utilized.

A number of limitations are also present. First and foremost, although this was based on a model from clinical data, it did involve simulated concentrations, introducing the potential for error. The modeler (JWC) who simulated the 100 clinical datasets was also the individual who did the re-optimizing in NLME for the two sparse scenarios, and thus the process was not blinded. We addressed this by going through the modeling process on one sparse dataset to determine which of three biologically plausible models (the simulated model and two others) best fit the data,

Further, neither method was optimized for each of the 100 datasets, since they were run as batch. To get a more accurate measure of the variability in NPE and ANPE, additional datasets for each scenario could be analyzed. Finally, only a single drug underwent investigation.

In conclusion, while each method had its advantages, overall NLME analysis was preferred, since this method is more versatile, can integrate information from the plasma concentrations as well as other matrices, and also allows the inclusion of covariates. Particularly when there are at least 4 observations per sampling time, first use of NCA via bootstrap to generate initial estimates may be a useful strategy to take advantage of the strengths of both methods. Although not studied, generating bootstrap-based NCA plasma and tissue parameter estimates and their variances, may improve the ability of the modeler to formulate the NLME model, improve convergence rates, and ideally, improve the robustness of the tissue estimates resulting from a subsequent NLME analysis.

Achieving robust estimates of tissue exposure will allow better tissue pharmacodynamics and permit more clinically accurate dosing, based not only on plasma concentrations, but now on target tissue exposure. This was recently demonstrated in the HIV prevention field where NLME analysis was used to combine in-vivo tissue concentrations with in-vitro efficacy data to simulate and predict probabilities of protection given various patterns of non-adherence. (21) The predicted probabilities are consistent with clinical trial results in the field, several of which failed to show a positive effect of tenofovir/emtricitabine on HIV transmission rates due mainly to non-adherence. This exercise also suggests that the degree of adherence needed to have a high probability of protection differs based on the site of tissue exposure to the virus through sexual intercourse. Several other examples in both infectious diseases (cefazolin dosing in obese pregnant women undergoing Cesarean delivery (31), distribution of liposomal amphotericin B(32)), antibody design(33), and oncology ((34)) demonstrate the clinical utility of establishing tissue target concentrations or exposures and then using those to optimize drug dosing. This improvement in pharmacotherapy should be one more step in our ultimate goal of achieving full HIV prevention and cure. As treatments for HIV cure advance from the bench to animal and finally human studies, it will likely be critical to assess the ability of these agents to penetrate reservoir tissues to reverse HIV latency, as well as ensuring that adequate antiretroviral concentrations are present in these sites, so that reactivated virus does not propagate further and can be cleared by the immune system. Based on our simulation exercise presented here, and our own experience in conducting clinical studies involving invasive sampling techniques, we recommend the use of NLME techniques to create PK/PD models of drug exposure and variability at the site of therapeutic action.

Supplementary Material

10928_2017_9554_MOESM1_ESM

Supplemental Figures 1–8. Diagnostic plots for the model fitted to the observed clinical study tenofovir concentrations for plasma (Figures 1–4) and rectal tissue (Figures 5–8). Plots include the observed concentrations vs. the population predicted concentrations (Figures 1 and 5, for plasma and tissue, respectively); the observed concentrations vs. the individual predicted concentrations (Figures 2 and 6); the Conditional Weighted Residuals (CWRES) vs time (Figures 3 and 7); and Visual Predictive Checks (VPCs), including the 90% prediction interval for the model (Figures 4 and 8). For Figure 4, the inset depicts the plasma VPC during the first 24 hours post-dose.

APPENDIX

Appendix A- NCA bootstrap internal validation

Since the original simulation datasets represented approximately log-normal plasma and tissue concentration data, and there were a small number of tissue samples per simulation dataset, geometric mean concentrations at each time-point were generated, and geometric mean PK parameter estimates were used. Estimates of positive slopes were excluded from the individual bootstrap estimate, as per Mager & Goller. (7, 8).

As part of a validation process for the bootstrap method, SAS-derived bootstrap results from our lab were compared with published data from Bailer (9) using linear trapezoidal methods for AUCt. In addition, comparisons were made with 100 random sample sets generated for a previously cited orally administered drug with known PK parameters and one-compartment model characteristics and 10 sampling times.(35) In this case, concentration-time data were generated using Monte-Carlo simulations of log-normal concentration-time profiles with added 30% proportional error (first 500 observations/time-point ×10 sampling times, then n=4 observations/time-point × 10 sampling times). These experiments allowed results to be compared to these known PK parameters with both rich and sparse data. Good agreement also was shown with these true reference values, with good accuracy with n=500 observations per time-point and an only a 1% positive bias when n=4 observations per time-point were analyzed. Finally, PK parameters from Mager & Goller were compared using the tissue data from their example #3.(15) Parameter estimates generated using the current bootstrap program were similar to that reported by Mager & Goller using “pseudo profiles,” and traditional NCA.