A Residue Resolved Bayesian Approach to Quantitative Interpretation of Hydrogen Deuterium Exchange from Mass Spectrometry: Application to Characterizing Protein-Ligand Interactions

Abstract

Characterization of interactions between proteins and other molecules is crucial for understanding the mechanisms of action of biological systems and, thus, drug discovery. An increasingly useful approach to mapping these interactions is measurement of hydrogen/deuterium exchange (HDX) using mass spectrometry (HDX-MS), which measures the time-resolved deuterium incorporation of peptides obtained by enzymatic digestion of the protein. Comparison of exchange rates between apo- and ligand-bound conditions results in a mapping of the differential HDX (ΔHDX) of the ligand. Residue-level analysis of these data, however, must account for experimental error, sparseness and ambiguity due to overlapping peptides. Here, we propose a Bayesian method consisting of a forward model, noise model, prior probabilities, and a Monte Carlo sampling scheme. This method exploits a residue-resolved exponential rate model of HDX-MS data obtained from all peptides simultaneously, and explicitly models experimental error. The result is the best possible estimate of ΔHDX magnitude and significance for each residue given the data. We demonstrate the method by revealing richer structural interpretation of ΔHDX data on two nuclear receptors: vitamin D-receptor (VDR) and retinoic acid receptor gamma (RORγ). The method is implemented in HDX Workbench and as a standalone module of the open source Integrative Modeling Platform.

Graphical abstract

INTRODUCTION

Decision-making in the development of drug molecules relies on robust interpretation of subtle changes in biophysical signals. Hydrogen/deuterium exchange (HDX) is one such method that reports on the lability of backbone amide hydrogens, providing a qualitative measure of stability at various sites in the system.^1,2 Increasingly, ligand binding to proteins and protein-protein interactions have been quantified by differential Hydrogen Deuterium Exchange (ΔHDX), observed via Mass Spectrometry (MS).³ Briefly, ΔHDX is the calculated difference between two independent HDX experiments, one performed on a baseline system, such as an apoenzyme, and one performed with a perturbant, such as a ligand. Applications of ΔHDX include antibody-antigen classification,^4,5 probing the molecular basis of lipid signaling enzymes^6–10 and for providing structural insights into these interactions over the entire protein.^8,10–14 This technique is uniquely suited to probing larger, more complex systems that are inaccessible to conventional methods, such as NMR spectroscopy and X-ray crystallography. The increasing importance of the ΔHDX analysis in drug discovery and development generates a need for a robust, objective method that maximizes the information content extracted for downstream interpretation.

HDX-MS data, however, is typically measured in segments of multiple residues, not single residues, resuslting in ambiguities when attempting to interpret HDX at the residue level. The measured ²D exchange of each peptide is the convoluted signal from each exchangeable site in the peptide; rapid back-exchange of sidechain sites means that this can be assumed to be only the backbone amide residues.¹⁵ In addition, overlapping peptides will often have different magnitudes of exchange, exacerbating the problem of assignment of an exchange state at a single site. The most robust approaches fit a residue-resolved exchange model to the HDX-MS data sampling a small number of finite exchange rates using a combinatorial approach.¹⁶ This approach was later improved by constructing a two-stage sampling method to produce quantitative rate constants.¹⁷ Finally, the program HDSite introduces further improvements, such as adding information from the shape of the MS envelope.¹⁸

In all cases, the methods take advantage of overlapping peptides, which result in independent sectors, where a sector is defined as a linear sequence of residues observed by a unique set of peptides. Analysis at the sector level, however, introduces two additional ambiguities. First, determination of a single hydrogen exchange rate model at an individual residue or sequence of residues requires combining the data for each peptide that samples that residue. Secondly, the expected error at each site is highly influenced by the number of times it is sampled, among other intrinsic experimental parameters. Robust modeling of these data must account for these ambiguities, as well as potentially include information from multiple experiments conducted on different instruments under different conditions.

Here, we describe a Bayesian framework and realistic exponential kinetic model to extract the maximum information from HDX-MS experiments by combining all available data and prior information from any experimental protocol [Fig 1]. First, we develop a scoring function that compares a residue-resolved exponential model to the exchange of all peptides, while accounting for and explicitly modeling experimental error and ambiguities. Second, we develop a sampling scheme and an analysis pipeline that evaluates and returns an ensemble of good scoring models (not only the best scoring one), and reports the estimated value and the standard deviation for the exchange at each residue position, increasing the spatial resolution of HDX up to two-fold. Third, we build on the Bayesian approach to quantify both the magnitude and significance of ΔHDX in a macromolecule due to a perturbation event, such as ligand binding, point mutation or change in experimental conditions.

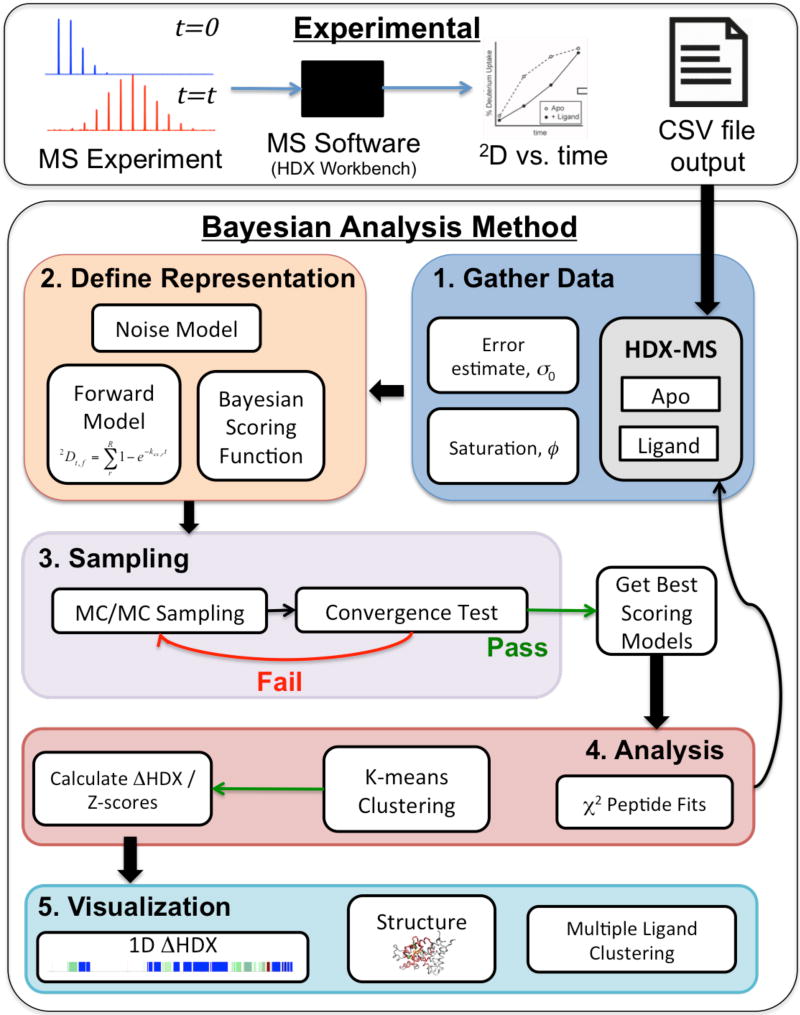
Figure 1. Method Flowchart.

Experimental: The method uses MS data that is analyzed by instrument-specific software, such as HDX Workbench, to produce ²D incorporation data vs. time. The resulting .csv files or modified .csv files are used as input into the Bayesian method. Bayesian Method: Step 1; Data (information) is gathered, including the HDX-MS ²D incorporation data for both apo and liganded (or perturbed) states as well an estimate for the error, σ₀, and deuterium saturation level, ϕ, and the prior probabilities chosen for these two parameters (as described in the text). Step 2: The representation of the system is defined, beginning with the Forward Model, which, for this implementation is defined by the residue-resolved exchange rate chosen from a finite grid of values. The Noise model is defined as described in the text. This model defines the scoring function for each peptide. The Bayesian scoring function is then constructed by combining the scoring functions for all peptides, the noise model and prior probabilities. Step 3: A MC algorithm is used to sample the landscape of the Bayesian scoring function until a convergence criteria is passed. From this, a set of the best scoring models from each state are passed to Step 4. Analysis; where the individual experimental data points are compared to the top scoring models and clustering is performed to identify potential multi-state solutions. Analysis may show that more data need to be collected (if results are too imprecise) or that certain data points are inconsistent with the rest of the data. Finally, the ΔHDX and Z-scores are calculated between each state and visualized in Step 5 via a 1D plot, and on a 3D structure if available. Also, downstream analysis such as multiple ligand clustering can be performed.

Application to Ligand Binding in Nuclear Receptors

The nuclear receptor superfamily consists of a broad class of transcription factors whose functions vary both qualitatively and quantitatively according to the structure of a bound ligand. Many members of the nuclear receptor family have highly flexible ligand binding domains that can adopt and envelope ligands of various molecular dimensions. In turn, these different ligands produce varying expression profiles, broadly classified as agonists (activators), antagonists (competitive inhibitors which ablate the response to an agonist), inverse agonists (which produce a negative response) and degraders (which induce receptor degradation) and these responses have been utilized to design novel therapeutics.¹⁹ The expression profile of a certain receptor-ligand pair reports on the binding affinity of the complex to certain areas of DNA and the recruitment of other coactivators and corepressors that control gene expression. Thus, modulation of the conformational dynamics plays a critical role in determining the overall activity of a ligand. Recently, differential hydrogen exchange has been extensively utilized to probe ligand and other perturbation interactions in nuclear receptors and other systems.^5–8,11 The specific changes in structure and dynamics that govern these changes, however, are largely unknown.²⁰ We show the increased interpretive ability of our method by analyzing data from two such nuclear receptors.

First, we apply the method to the vitamin D-receptor (VDR) – 25-hydroxy vitamin D3 (25-OH VD3) complex,²¹ showing that the increased spatial resolution identifies a small area of deprotection in the critical helix 10 that is absent in standard analyses. Second, we analyze the ΔHDX of the retinoic acid receptor-gamma (RORγ) in complex with three ligands. We have chosen these ligands because all of them have also been observed crystallographically in complex with the target, and thus we can compare the ΔHDX results with the structural information available. Compound T01091317 (PDB: 4nb6) shows inverse agonist activity in contrast to its role as an agonist for the liver-X receptor^23,24 and many other NRs.^25,26 Crystal structures of RORγ in complex with T01091317 and two known agonists, referred to as Genentech (PDB: 4wpf)²⁷ and GSK (PDB:4nie)²⁸, show little overall structural differences in the receptor beyond specific interactions in the binding site. We demonstrate here that our Bayesian method resolves differences in the ΔHDX that provide additional structural insight at the single residue level.

METHODS

HDX-MS of Nuclear Receptors

Deuterium incorporation as a function of time for the apo and liganded states of VDR were gathered as previously reported²¹ and data for a 6His-SUMO-RORγ construct was obtained as previously described.²⁹ Briefly, HDX was measured at six time points from 10s to 3600s. Digested and quenched sample was measured in triplicate at each time point. Peptide identification and deuterium incorporation was performed in HDX Workbench³⁰ using peak centroid difference with respect to unlabeled peptide and a fully deuterated control sample to quantify the deuterium incorporation. The data finally reported were selected by the experimentalist using standard criteria as generated in the HDX Workbench software. The HDX Workbench output CSV files for the apo and liganded states were utilized as the starting point for ΔHDX analysis [Fig 1, top].

Bayesian model of HDX data

The Bayesian approach³¹ estimates the probability of a particular model, given all information about the modeled system, including prior knowledge on the system, experimental data on the system and models of experimental noise. For HDX-MS, the model M consists of the exchange rate constant for each backbone amide hydrogen {k_i} as well as extra parameters. Using Bayes theorem, the posterior probability p(M|D,I) of model M, given data D and prior information I, is defined as

$$p(M|D,I)\propto p(D|M,I)\cdot p(M|I)$$

The likelihood function p(D|M,I) gives the probability of observing data D, given M and I. The prior p(M|I) defines the probability of model M, given I. The data D = {d_f,t,n} is the set of measured ²D incorporation for each timepoint, t, each peptide, f, and replicate, n. Peptides that ionize with different charge states are treated as independent replicates (n). To relate the model to the data point n, one needs a forward model f({k_i}) that predicts the data point generated from a given set of modeled amide rate constants {k_i} and a noise model, which reflects our uncertainties about the experimental measurements and the forward model. The score and the likelihood score are defined as the negative logarithm of p(D|M,I) · p(M|I) and p(D|M,I), respectively.

Forward model

The forward model (fmod) calculates the deuterium uptake $(D_{f,t}^{\mathit{\text{fmond}}})$ of peptide f after exchange time t and approximated by a unimolecular first-order reaction. It is expressed as

$$D_{f,t}^{\mathit{\text{fmod}}}=F_{f,t}(\{K_i\},\varphi )=\varphi (N_f-\sum _{i=n_{f,\mathit{\text{beg}}}}^{n_{f,\mathit{\text{end}}}}{\partial }_i{e}^{-k_{i}t})$$

where ø is the deuterium fraction of the exchange buffer; N_f is the number of observable amides for peptide f, defined as the total number of residues, minus the number of prolines (which contain no amide), minus two to account for fast back exchange in the two N-terminal residues;³² n_f,beg and n_f,end are the beginning and ending residues of peptide f; and ∂_i is a delta function whose value is one if residue i has an observable amide and zero if otherwise.

Noise Model

The theoretical deuterium incorporation at a given site is bound to be between 0 and 1, scaled by the fraction of deuterium in the exchange buffer, ϕ thus, we modeled the error in the experimental data using a truncated Gaussian, resulting in the probability of observing a single data point, $D_{f,t,n}^{\mathit{\text{exp}}}$ for peptide f at time t and replicate n.

$$P(D_{f,t,n}^{\mathit{\text{exp}}}|M,{\sigma }_{f,t,}A,B)=\frac{e\frac{{(D_{f,t,n}^{\mathit{\text{exp}}}-D_{f,t}^{\mathit{\text{fmod}}})}^2}{2{\sigma }_{f,t}^2}}{{\left(2\pi \right)}^{1/2}{\sigma }_{f,t}}\cdot \frac{1}{2\left[\mathit{\text{erf}}\right(\frac{A-D_{f,t,n}^{\mathit{\text{exp}}}}{\sqrt{2}{\sigma }_{f,t}})-\mathit{\text{erf}}(\frac{B-D_{f,t,n}^{\mathit{\text{exp}}}}{\sqrt{2}{\sigma }_{f,t}}\left)\right]}$$

where is the σ_f,t is the point error estimate for peptide f at timepoint t. The model, M = ({k_i}, ø) consists of the set of residue resolved exchange rates, {k_i}, and saturation level, ø. A and B are the bounds of the truncated Gaussian. For this work, the bounds of the noise model were chosen as A = −0.1ϕ and B = 1.2ϕ to allow for ²D incorporation data that is both negative and higher than the theoretical number of amides.

Likelihood function

The likelihood function (P(D^exp|M,{σ}))for the entire dataset (D^exp) is a product of likelihood functions $(P(D_{f,t,n}^{\mathit{\text{exp}}}|M,{\sigma }_{f,t})))$ for each data point, $D_{f,t,n}^{\mathit{\text{exp}}}:$

$$P(D^{\mathit{\text{exp}}}|M,\{\sigma \})={\prod }_f^{N_f}{\prod }_t^{N_t}{\prod }_n^{N}P(D_{f,t,n}^{\mathit{\text{exp}}}|M,{\sigma }_{f,t})$$

where the uncertainty σ_f,t scales the probability of generating the data point d_n when the expected data point value is f_n(M). To account for varying levels of noise in the data, every time point from each peptide has an individual σ_f,t.

Prior Information

An uninformative Jeffrey’s prior³³ is applied to each individual hydrogen exchange constant, k_i, in our model to represent a lack of information of the bounds and distribution of this parameter. A Gaussian prior is chosen for the deuterium fraction in the exchange buffer, $p(\varphi |{\varphi }_0,{\sigma }_{\varphi })=\text{exp}(-\frac{{[d_n-f_n(M)]}^2}{2{\sigma }_{\varphi }^2}).$ A unimodal distribution was chosen as a prior for the uncertainty σ_n:³⁴ $p({\sigma }_{f,t}|{\sigma }_0)=\frac{2{\sigma }_0}{\sqrt{\pi {\sigma }^2}}\mathit{\text{exp}}(-\frac{{\sigma }_0^2}{{\sigma }^2}),$ where the expected uncertainty σ₀ is derived from the standard deviation of ²D incorporation from observations at t = 0; the heavy tail of the distribution allows for outliers.

Sampling

The main computational cost of the method consists of searching the space of exchange rates for each residue site. To reduce the complexity of the search, a finite grid of exchange rates is chosen with the minimum and maximum values of exchange determined from the range of experimental time points.

For small systems (proteins with <30 exchangeable amides), the number of available exchange states can be enumerated. In the case of larger systems, sampling is performed by a Metropolis Monte Carlo (MC) algorithm³⁵ to generate models of HD exchange rates, {k_i}, for each condition and sampled parameters from the posterior distribution. Each MC move proposes an increment/decrement step along the grid of exchange values. The dependence of the experimental uncertainty parameters, σ_f,t, was eliminated by integrating the likelihood and prior probabilities with respect to σ_f,t.³⁶

Two independent sampling instances are initialized, with each amide exchange rate set to a random value on the sampling grid. A simulated annealing step is first performed at high temperature (T) and this MC temperature gradually decreased for the production run. Periodically, a test for sampling convergence was performed using a Bernoulli-related statistic to compare the distribution of clustering results between the two independent runs.³⁷ Upon satisfaction of the sampling test, the two independent runs are merged for subsequent analysis.

Analysis

The best scoring solutions found during sampling for each target state are clustered according to the exponential model using a k-means algorithm³⁸ as implemented in the scikit-learn package.³⁹ In the event of multiple significant clusters, one may consider a multistate model for a specific target condition, where the observed HDX signal may arise from a linear combination of two or more dominant states. The best scoring models for each cluster are then used to recapitulate the target data using the forward model and report a χ² score for the fit of the model to each individual data point, which can be used to identify observations that may be erroneous or warrant further scrutiny.

The mean value x̄ and standard deviation σ for the log(k_i) of each site i in the peptide is calculated from the ensemble of best scoring models for each target state. The ΔHDX is then reported as the difference between the mean values of each state, while the significance can be reported using a two-sample Z-score:

$$Z=({\overline{x}}_1-{\overline{x}}_2)\cdot {\left(\frac{{\sigma }_1^2+{\sigma }_2^2}{N}\right)}^{-1/2}$$

where N is the number of best scoring models chosen from each state. Alternatively, the result can be transformed into a probability, Q , that the HDX observations for the two conditions are different by integrating along the normal distribution.

$$Q(Z)=\frac{2}{\sqrt{\pi }}{\int }_0^Z{e}^{-x^2}\mathit{\text{dx}}$$

In cases where the modeled exchange rate for one or more of the states is outside the experimental design (either too fast or too slow to be observed on the experimental timescale), a flag is noted in the output to represent the uncertainty in the reported exchange rates of the resulting ambiguity in the modeled exchange rate is noted with a flag in the output.

Visualization of Results

The ΔHDX model is plotted as a colorbar with hue representing the mean difference between the two populations (red as protection, white as no difference and blue as deprotection), and color saturation representing one of the two confidence metrics.

The information can also mapped onto a 3D structure, reporting the mean ΔHDX in the B-factor column of a PDB file (transformed into a color gradient for each residue). The confidence, Q, is reported in the occupancy column using the formula 0.5 + 1.5 * Q, which can be visualized as the Cα radius.

Nuclear Receptor Test Cases

HDX-MS data for VDR and RORγ were modeled using a grid of twenty exchange rates spanning the range of log(k_ex) from 0 to −6, to span the range of experimental time points. All simulations of VDR and RORγ were found to equilibrate following 250 MC steps at T = 10, followed by 50 steps each at T = 4, 3, 2 and 1 and a production run of 5000 steps at T = 1. The time to complete each apo-ligand ΔHDX dataset was 2–4 hours on two 2.2GHz processors (one for each independent run). From the combined ensemble of 10000 models, the 1000 best scoring models for each condition were used to calculate the mean and standard deviation of the log(k_ex) at each sector.

Comparison to Delta Percent Deuterium Method

As a comparison, we compare our results to those generated by the delta percent deuterium method (Δ%²D), as implemented in HDX Workbench.³⁰ Briefly, for a set of HDX-MS data, the average percent ²D (%²D) incorporation for a peptide over all time points is calculated. The Δ%²D for the peptide is calculated by subtracting the apo %²D from the perturbed (in our case, ligand bound) state %²D. To produce a single value at each residue, the maximum Δ%²D among all peptides sampling that site is reported. Similar analysis was performed using the average Δ%²D and minimum Δ%²D among all peptides, which both give slightly different quantitative results, while not changing our conclusions.

Illustration of Joint Likelihood

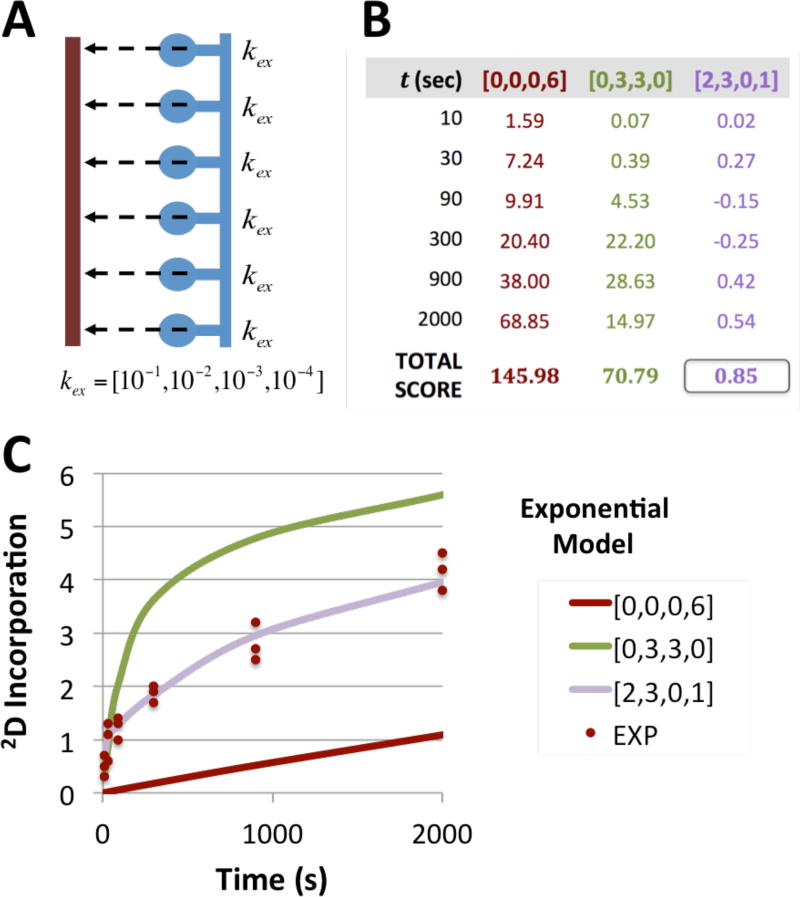
Data from a peptide with six observable and exchangeable amides was simulated with two amides of rate k_ex = 10⁻¹s⁻¹, three with k_ex = 10⁻²s⁻¹ and one amide with rate k_ex = 10⁻⁴s⁻¹ [Fig 2], assuming a ²D saturation, ø, of 1.0. The expected ²D incorporation at time = 10, 30, 90, 300, 900 and 2000 seconds was calculated and three observations at each time point created by adding 5% Gaussian noise. To fit the simulated data, an exchange grid of log(k_ex) = [−1,−2,−3,−4] was used and three models created: [0, 0, 0, 6], representing a peptide with six amides exchanging at 10⁻⁴s⁻¹, and similarly [0, 3, 3, 0] and [2, 3, 0, 1], the latter being the exchange rates used to create the simulated data. For each model, the Bayesian scoring function was applied and the log likelihood at each time point calculated. The total score of each model to the simulated data is the sum of the score for all time points.

Figure 2. Illustration of Joint Likelihood.

A) Schematic of a system consisting of a single MS peptide (brown) covering six observable amides (blue) and the model consisting of a grid where k_ex is chosen from the set of unimolecular rate constants (in s⁻¹ units). B) Three prospective exchange models are scored against simulated data for the model peptide using the scoring function. The noise parameter, σ_ν, is set as 5% of the mean of the simulated experimental data. The purple model, containing two amides exchanging at 10⁻¹/s, three at 10⁻²/s and one at 10⁻⁴/s provides the best fit for all the data, resulting in the lowest combined score. C) Plot of simulated data for the model peptide (brown points) consisting of three replicates at six time points is plotted along with three exchange models for the simulated system.

RESULTS AND DISCUSSION

Developed is a robust method to convert hydrogen/deuterium exchange data, measured by Mass Spectrometry on overlapping peptides into a residue-resolved model that accounts for data and method uncertainties. Four key points emerge from this work. First, the successful application of a Bayesian method allows for robust statistical consideration of many aspects of the input data. Second, the method increases the information content of the data interpretation by improving the accuracy and spatial resolution of the resulting models. Third, the coalescence of heterogeneous, differentially sampled data, potentially from multiple experiments into a single residue-resolved model allows for easier downstream comparison and clustering of results among high-throughput screening results of multiple ligands, variants or experimental conditions. Fourth, the method reports quantitative exchange rate constants, as log (k_ex), at each site, which are expected to be linearly related to the free energy of activation of the exchange event. These values are then comparable with results obtained from other conditions or other methods that report on dynamic behavior.

Bayesian method resolves 25-OH VD3 stabilization of Helix 10 in VDR

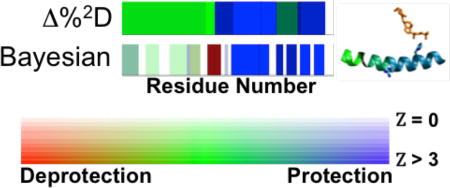
The HDX-MS data on VDR with and without 25-OH VD3 each contained 36 peptides, which, analyzed by the Δ%²D method, results in a model of 26 independent observations, while the Bayesian method reports 45 independent sectors of sequence, resulting in a 73% increase in spatial resolution [Fig. 3A]. The reported ΔHDX of the two methods are qualitatively similar, with 25-OH VD3 found to confer large degrees of protection throughout the area close to the binding pocket and most significantly in the ligand binding helix 3 [Fig 3B].

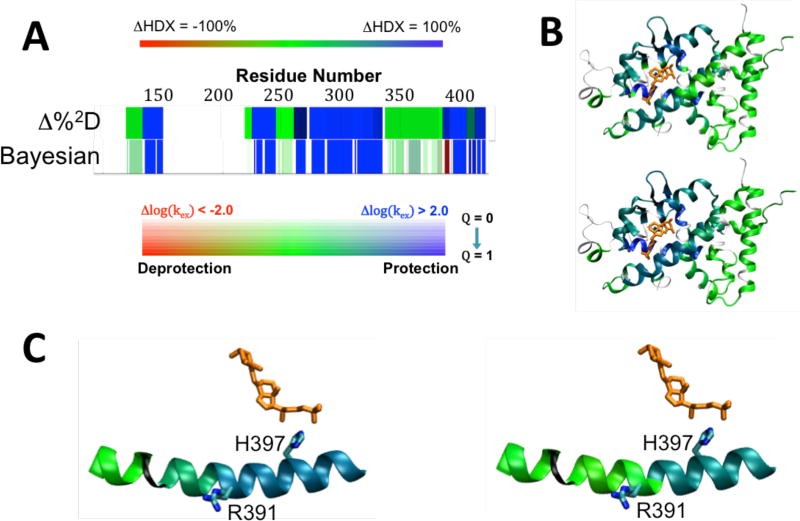
Figure 3. Analysis of ΔHDX data from VDR-25-OH VD3 complex.

A) Comparison of ΔHDX plots for 25-OH VD3 with VDR using Δ%²D (top) and Bayesian (Bottom) analysis methods. Δ%²D is colored by %protection, with blue representing 100% protection, red representing 100% deprotection, green signifying no difference with white indicating no data. The magnitude of Bayesian ΔHDX is represented with blue indicating Δlog(k_ex) > 2.0 and red = Δlog(k_ex) < −2.0, with green indicating no change. The significance of the difference is represented by the color saturation with full color applied for Q = 1 (Z > 3.0) and zero saturation (white) for Q = 0 Z( = 0). B) ΔHDX mapped on crystal structure trace of VDR (PDB 1DB1) for Δ%²D method (top) and Bayesian method (bottom). Thin black lines represent no HDX-MS data. 25-OH VD3 is shown in orange. D) Close-up of helix 10 interaction with VDR, with the peptide colored by ΔHDX analyzed by the Δ%²D (left) and Bayesian method (right). The Bayesian method shows slight deprotection in the N-terminal side ofhelix 10, which is absent in the Δ%²D method.

Both the Bayesian and Δ%²D methods show protection in helix 10; however, Δ%²D indicates a similar degree of protection along the entire helix, while the Bayesian method reports finer details [Table 1]. First, only the C-terminal side of the helix (residues 393–403) is highly protected upon binding 25-OH VD3, with a Δlog (k_ex) of −1.98 and high significance. The high average exchange rate for the apo condition, log(k_ex) = −0.87, which is close to the average random coil rate of this region, log(k_ex) = −0.24, in this region suggests intrinsic disorder in the absence of ligand and order upon ligand binding, which is fully consistent with the crystal structure that shows a hydrogen bond between 25-OH VD3 and H397 [Fig. 3C].

Table 1.

Δ%²D vs. Bayesian log (k) for VDR Helix 10.

Res	Δ%2D	Bayesian
		Δlog(k)	Z	Apo log(k)
K386	−35.9	0.52	2.8	−4.16
L387	−35.9	0.52	2.8	−4.16
A388	−35.9	0.52	2.8	−4.16
D389	−35.9	0.52	2.8	−4.16
L390	−49.8	−0.03	0.1	−5.02
R391	−57.3	−0.47	0.8	−0.39
S392	−57.3	0.09	0.2	−0.67
L393	−57.3	−1.98	21.3	−0.87
E394	−57.3	−1.98	21.3	−0.87
E395	−57.3	−1.98	21.3	−0.87
H396	−57.3	−1.98	21.3	−0.87

The N-terminal side of the helix, however, shows more subtle changes in ΔHDX upon ligand binding using the Bayesian analysis than by Δ%²D, with residues 386–390 having a slight degree of deprotection. The slow rate of hydrogen exchange in the apo state (log(k_ex) = −4.15) suggests that secondary structure is present in both the bound and unbound conditions. The observed fast exchange in the Bayesian model of R391 and S392 in both the apo and liganded states indicates a potential break in the helix that is not observed in the crystal structure. R391C and R391S are familial mutations that block the heterodimerization of VDR to the retinoic X receptor that is required to activate vitamin-D response elements.^40,41 The mutations do not affect 25-OH VD3 binding, which is consistent with the small ΔHDX effects in this area observed with the Bayesian analysis, but not with the larger effects reported by the Δ%²D method.

Identification of potential single residue determinants of ligand activity in RORγ

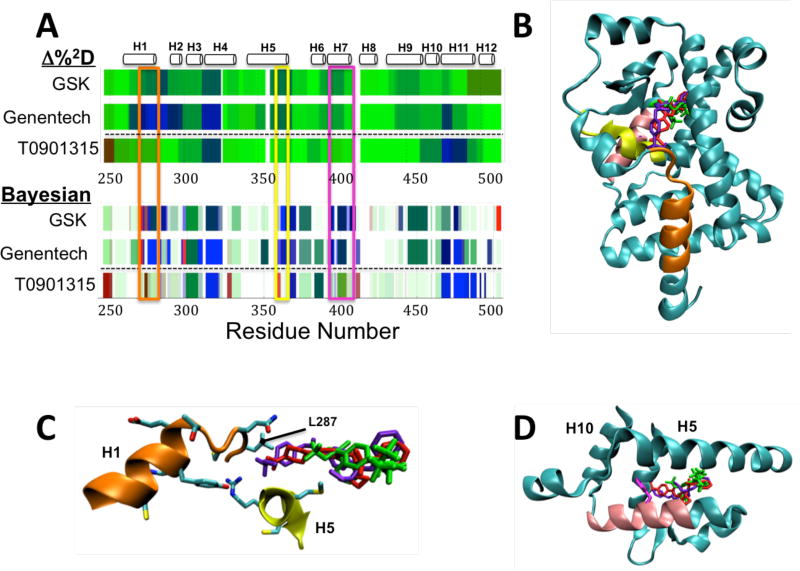
The HDX-MS datasets for RORγ in complex with the three ligands (T0901317, Genentech and GSK) show greater interpretive power when analyzed by the Bayesian method over Δ%²D [Fig 4A]. Major differences between the two classes of compound, the inverse agonist T0901317 [bottom rows in Fig 4A] and the Genentech and GSK agonists [top two rows in Fig 4A], are seen throughout the LBD using both methods. In particular, differences between the two classes are observed at residues 276–287 at the C-terminus of helix 1 [orange box], residues 365 to 373 in helix 5 [yellow box] and residues 399 to 410 in helix 7 [pink box]. Each of these regions, predictably, map to helices that flank the ligand-binding site [Fig 4B].

Figure 4. ΔHDX of ligands of RORγ.

A) ΔHDX of agonists GSK and Genentech and inverse agonist T0901315 with respect to RORg as analyzed by the Δ%²D method (top) and Bayesian method (bottom). Areas of major difference between the two classes of compound are seen in residues 276 to 287 (orange box), 365 to 373 (yellow box) and residues 399 to 410 (pink box). B) Visualization of the three ligands bound to RORg, T0901315 (green, PDB: 4NB6), GSK (red, PDB: 4NIE) and Genentech (blue, PDB: 4WPF) on the structure of RORγ (from PDB 4NIE). Areas of peptide with major ΔHDX differences highlighted in part A are colored. C) Close up of orange and yellow areas and the side chain interactions with the ligand binding site, showing the difference in interactions in this area between T0901315 (green) and the two agonists. D) Close up of pink region in helix 7 with the side chain of F403 in magenta showing its positioning just outside the ligand binding site at the junction of helices 5 and 10.

The Bayesian method reveals several residue-resolution features hidden in the peptide-resolution MS data that are not observed in the Δ%²D method. First, in helices 1 and 5, the inverse agonist shows significant deprotection, while the agonists confer significant protection to these regions. The smaller aliphatic tail of T0901317 [Fig 4C, green] does not interact with the side chains of H1, unlike the two agonists [Fig 4C, blue and purple]. The fast exchange for L287 (~100% exchange by the first time point) in the apo state predicted by the Bayesian model, implicates that this loop is disordered. The Bayesian ΔHDX model of both of the agonists shows significant difference, but not for the inverse agonist, implicating that a discriminant between the two types of ligands may be a stabilization of this disordered loop.

Secondly, the Bayesian method reveals that F403 in helix 7 shows a large and significant protection effect (Δlog(k_ex) = −0.73) with the inverse agonist, while the two agonists show 10 fold smaller effects at low significance, in contrast to the rest of helix 7, where the two agonists have significant protection throughout and T0901317 has little effect. This model is consistent with the crystal structure, which shows that F403 is centrally positioned at the interface of helix 7 and helices 5 and 10 [Fig 4D]. This leads to the hypothesis that this residue may be critical for the propagation of dynamics that affect corepressor/coactivator binding and that ΔHDX in this region could be a predictor of ligand activity.

Downstream Applications in SAR

The ability to resolve individual exchange factors allows comparing quantitative HDX-MS measurements of numerous ligands to a single target, and thus facilitate their use in screening compounds with higher spatial resolution than traditional HDX-MS methodology. As exhibited in the RORγ example, and in other work⁴², HDX-MS can be used as a footprinting method to predict ligand activity in nuclear receptors. A distance metric can be calculated among numerous ligands utilizing the calculated ensembles of log(k_ex) at each residue. The consolidation of peptide data by the Bayesian method allows for clustering among different ΔHDX experiments regardless of peptide coverage. Additionally, principal component analysis could be performed to identify portions of sequence and structure that vary in ΔHDX in response to certain changes in ligand chemistry.

Extension to structural interpretation of HDX

Various methods have been proposed to predict hydrogen exchange rates from 3-dimensional structure^43–45. These methods exclusively use the residue resolved rates determined via NMR to correlate local structural features with observed HDX. The consolidation of overlapping peptide data into residue resolved rates allows for HDX-MS data to improve this type of structural characterization, both by increasing the amount of data available to train potential models and expanding the application of the structural models to those systems only approachable by HDX-MS.

Model Limitations and Other Considerations

The method was developed making a number of approximations and assumptions, which limit its application to specific, yet very common, conditions. First, the forward model maps the residue resolved exchange model to HDX-MS data that has been processed into ²D incorporation values based on peptide centroid differences. The entire MS peak envelope, however, contains information about the ensemble of exchange rates in the peptide,¹⁸ which can be leveraged by explicitly modeling the peak envelope. The modularity of the Bayesian approach, however, allows for fairly straightforward modification of the forward and noise models to predict MS peak envelopes from a model of residue resolved HDX rates, or incorporate other information obtained from current and future innovations in experimental protocols.

Our model makes a number of assumptions about the nature of HDX-MS, in addition to the prior probabilities described above. First, it is assumed that observed exchange events occur in the EX2 regime,¹ where the exchange reaction is the rate-limiting step, resulting in a single unimolecular rate constant, as described in the forward model. Secondly, we assume fast back exchange for both side chain labile protons,¹⁵ and the two N-terminal amides in each peptide³², resulting in quantification of backbone amide sites from only residue three onward in each peptide. Back exchange of amide hydrogens is not considered as test cases in this work are scaled using fully deuterated controls. In the absence of this information, however, reported ΔHDX values will be slightly lower, due to the loss of ²D at a rate proportional to the total incorporation. Thirdly, we assume the rates of hydrogen and deuterium exchange on a free amide site is identical. In practice, equilibrium fractionation experiments have shown up to 2 fold difference in these rates.⁴⁶ Because of the paucity of equilibrium exchange data, it is difficult to correct for this effect. Because the methods for observing equilibrium exchange are nearly identical to the HDX method, a single experiment that observes both effects is feasible and could potentially lead to a significantly more informative exchange model. Modifying any of these assumptions in practice can likely be achieved by straightforward changes to the forward model.

The most robust analysis methods are limited by the amount and quality of the input data. The subtle ΔHDX effects observed in the nuclear receptors utilized a data-rich experimental protocol containing multiple time points observed in triplicate. Fewer time points and single replicates will result in less precise estimates of the exchange constant at each site, blurring small differences. Thus, in the case of imprecise results, increasing the number of replicates and/or time points may improve the interpretability of the data.

Traditionally, HDX-MS has been used to qualitatively assess the flexibility in certain areas of the protein and the ligand- or variant-induced perturbation of this flexibility via ΔHDX-MS. The application of the method to data for VDR and RORγ show that HDX-MS can be utilized to provide residue resolved interpretation where information content is sufficient. In cases where information is not sufficient, our reporting of a wide distribution of potential HDX rates, rather than just the mean, cautions against over-interpretation. The experimentalist can then potentially target these poorly resolved areas to increase information content by increased peptideation, number of replicates or number of time points.

The time-scale of measurement also induces ambiguity in ΔHDX analysis. Hydrogens with an exchange rate of 10^−0.33 or faster will be >99% exchanged within 10 seconds. Thus, sites in a system where both the initial and perturbed exchange events are faster than 10^−0.33 cannot be resolved if the first timepoint is 10 seconds or slower. The same is true for very slow exchange events. For both instances, rather than report a ΔHDX of zero or close to zero, we report is that the difference cannot be resolved because the events are outside of the experimental timescale. If these scenarios occur in important areas of the system, this information informs the user that additional timepoints or a change in conditions may allow these areas to be resolved.

Availability of Software

The software is distributed as part of the open source Integrative Modeling Platform, available at www.github.com/salilab/imp and as a standalone library, available at www.github.com/salilab/hdx. Additionally, the method is incorporated as a post-processing technique using HDX Workbench. A webserver is currently in construction and will be hosted at www.salilab.org.

The analysis scripts and data used for this work are downloadable at www.github.com/salilab/bayesian_dhdx.

CONCLUSIONS

We have developed a Bayesian method to interpret HDX-MS and specifically ΔHDX-MS. The method provides a robust interpretation of ²D incorporation data by explicitly accounting for noise and using residue-resolved exchange rates to simultaneously fit data collected at multiple time points from all overlapping peptides and multiple replicates. The method is a significant improvement over deterministic techniques. The probability distribution of exchange rates inferred for each residue are used to assign the statistical significance of the deviations observed in ΔHDX experiments. The more accurate and precise exchange rate estimates, together with a better estimate of their uncertainty, have a potential impact on downstream analysis in SAR and structural modeling.