Abstract
Purpose
To establish a continuous relationship between the size of various antibody fragments and their systemic clearance (CL) in mice.
Methods
Two different orthogonal approaches have been used to establish the relationship. First approach uses CL values estimated by non-compartmental analysis (NCA) to establish a correlation with protein size. The second approach simultaneously characterizes the PK data for all the proteins using a 2-compartment model to establish a relationship between protein size and pharmacokinetic (PK) parameters.
Results
Simple mathematical functions (e.g. sigmoidal, power law) were able to characterize the CL vs. protein size relationship generated using the investigated proteins. The relationship established in mouse was used to predict rat, rabbit, monkey, and human relationships using allometric scaling. The predicted relationships were found to capture the available spares data from each species reasonably well.
Conclusions
The CL vs. protein size relationship is important for establishing a robust quantitative structure-PK relationship (QSPKR) for protein therapeutics. The relationship presented here can help in a priori predicting plasma exposure of therapeutic proteins, and together with our previously established relationship between plasma and tissue concentrations of proteins, it can predict the tissue exposure of non-binding proteins simply based on molecular weight/radius and dose.
Keywords: Monoclonal Antibody (mAb), Antibody Fragments, Systemic Clearance, QSPKR, Compartmental Modeling
INTRODUCTION
Understanding the pharmacokinetics (PK) of large molecules is critical to guide their preclinical and clinical drug development. While the PK of antibodies is relatively well studied (1, 2), PK of antibody derived molecules remain under-investigated. In addition, how changes in the physiochemical properties of these molecules (e.g. size, charge etc.) affect their PK is not well understood. Consequently, we have initiated an effort to establish quantitative structure-PK relationships (QSPKR) for biologics. We have begun by investigating how the size of a protein affects its systemic PK. Previously we have established a quantitative relationship between the size of proteins and their extent of tissue distribution (represented as the Biodistribution Coefficient), to help predict the exposure of a protein in a non-target expressing tissue just based on its plasma PK (3),(4). In this report we have investigated how the size of antibody fragments affects their systemic clearance (CL).
The CL of proteins is mainly determined by three pathways: (i) non-metabolic elimination pathway like renal clearance, (ii) non-specific metabolic pathway like proteolysis in extracellular environment or inside the cells following pinocytosis, and (iii) specific metabolism pathway that involves receptor mediated endocytosis and degradation of proteins into specific cells. Several physicochemical properties of proteins determine which of these pathways will be the dominant pathway for the elimination of a given protein. This involves, the size of the protein, charge state of the protein, glycosylation pattern of the protein, presence of FcRn binding region in the protein, and the ability of the protein to bind to a specific internalizing receptor. Out of which, here we are mainly focusing on the size of the protein. It is assumed that if the protein does not bind specifically to any receptor, the smaller size proteins will mainly follow renal elimination pathway and very big proteins will undergo non-specific uptake and elimination by specialized cells (e.g. kupffer cells). As such, the effect of size on CL of proteins is obvious, and serves as a prominent starting point for building QSPKR for clearance of proteins. Nonetheless, while building this relationship, it is important to keep in mind that proteins that expresses FcRn binding domain (e.g. intact antibody) and bind to specific receptors would deviate from the true protein size vs. CL relationship. A true protein size vs. CL relationship can only be established if size is the only factor that changes between different proteins. Thus, our efforts should be considered aimed towards developing a preliminary relationship between the size of antibody fragments and their CL.
Here we have used published PK data of various antibody fragments in mice to establish the relationship between protein size and CL. The size of proteins range from 13 kDa (nanobody) to 150 kDa (IgG). Two approaches have been utilized to build the CL vs. protein size relationship. In the first approach, non-compartmental analysis (NCA) is used to calculate CL of each antibody fragments, and the calculated CL vs. molecular weight/radius relationship is characterized using a modified sigmoidal function. In the second approach, plasma PK data from all the proteins is characterized simultaneously using a 2-compartmental PK model, and CL along with other PK parameters is modeled as a function of protein molecular weight (MW) using a power function. In the end, the CL vs. protein size relationship established for mice was used to predict the same relationship for rat, rabbit, monkey, and human using allometric scaling. The quality of allometrically scaled relationships was evaluated by superimposing the clearance values of different size proteins in each of the animal species onto the respective CL vs. protein size relationships.
MATERIALS AND METHODS
Molecular library
Published PK of antibody fragments and IgGs in mice were collected from numerous biodistribution studies. Eight different types of antibody fragments were included, which are: nanobody (13 kDa, n=2), scFv (27 kDa, n=13), diabody (50 kDa, n=2), Fab (50 kDa, n=6), scFv2 (55 kDa, n=2), minibody (80 kDa, n=3), F(ab)2 (100 kDa, n=6), scFv-Fc (105 kDa, n=2), along with the PK of IgG in FcRn KO mice (150 kDa, n=1). A detailed list of each published biodistribution study is provided in Supplementary Table-1. Data was digitized using the software ‘Grab It! XP’. All digitized concentration data were converted to nM before analysis.
Non-compartmental analysis (NCA)
Concentration vs. time profiles of each antibody fragment were pooled together following dose-normalization. NCA was conducted for each type of protein using WinNonlin (version 6.3, Pharsight Corp., Mountain View, CA). Typical clearance (CL) was calculated as the reciprocal of dose normalized AUC0-inf.
Establishing CL vs. molecular size (molecular weight and radius) relationship following NCA analysis
In order to establish a continuous relationship between CL and protein size, CL vs. molecular weight relationship was generated using NCA calculated CL values of all but three proteins. Fab, scFv-Fc, and IgG PK in wild type mice were not included for establishing the relationship. Mathematical relationship was characterized using several equations (e.g. exponential, polynomial, power law, and sigmoidal) with the help of ADAPT 5 software, and the equation with the best goodness-of-fit (determined using AIC value, visual inspection, and %CV of parameter estimates) was finalized. The final equation for CL vs. molecular weight relationship was:
| (Eq.1) |
In order to establish a relationship between CL and molecular radius (ae), the radius of each protein was estimated from its molecular weight using a published mathematical relationship between molecular weight and radius (5):
| (Eq.2) |
The final equation used to mathematically characterize the CL vs. protein radius relationship is:
| (Eq.3) |
Parameters for Equation-3 were derived from Equation-1 and Equation-2.
Two-compartment fitting approach
The concentration vs. time profiles for each protein were pooled together following dose-normalization. A two-compartment PK model was used to simultaneously characterize all the data together. Model equations are provided below:
| (Eq.4) |
| (Eq.5) |
A total of four system parameters were estimated. V1 represents central volume, which was considered to represent plasma volume and assumed to be similar for all proteins. Other three parameters, V2, CL, and CLD, represent peripheral volume, systemic clearance, and distributional clearance, respectively. The value of these three parameters were assumed to be related to the molecular weight of a protein. These relationships were described using following parsimonious equations, which were finalized based on goodness-of-fit criteria:
| (Eq.6) |
| (Eq.7) |
| (Eq.8) |
| (Eq.9) |
α can be interpreted as V2 of a hypothetical protein with molecular weight approaching 0. β and γ can be interpreted as the values of CL and CLD for a hypothetical protein with a molecular weight equal to 1 kDa. κ, λ, and μ describes how fast V2, CL, and CLD decreases with increasing molecular weight.
All the relationships were fitted using maximum likelihood method in ADAPT-5, and goodness-of-fit was assessed by visual inspection, %CV of parameter estimates, and AIC values. The relationship between CL and radius (shown in Equation-9) was derived from Equation-8 and Equation-2.
Allometric scaling of CL vs. protein size relationship
The CL vs. molecular weight relationship established for mouse based on the NCA derived CL values (equation 1) was scaled to rat, rabbit, monkey and human using the following allometric equation:
| (Eq.10) |
The value of scaling coefficient used for clearance was 0.75 (6). The body weight used for scaling the clearance were 0.028, 0.28, 1.2, 6.2, and 70 kg for mouse, rat, rabbit, monkey, and human, respectively. The final equations for the CL vs. molecular weight relationship for each species are provided below:
| (Eq.11) |
| (Eq.12) |
| (Eq.13) |
| (Eq.14) |
The validity of the mouse and allometrically scaled CL vs. molecular weight relationship for each species was evaluated by superimposing the predicted relationship onto the observed clearance values of different size proteins in the respective animal species. The observed data available from the literature on the clearance of different proteins in different animal species was sparse, and a detailed list of each publication from which the clearance values were obtained is provided in the Supplementary Table-2. Of note, the validation dataset was completely separate from the dataset used for building the relationship. The model building dataset was created at University at Buffalo and the model validation dataset was created independently at Hoffmann-La Roche.
RESULTS
Non-compartmental analysis of protein PK
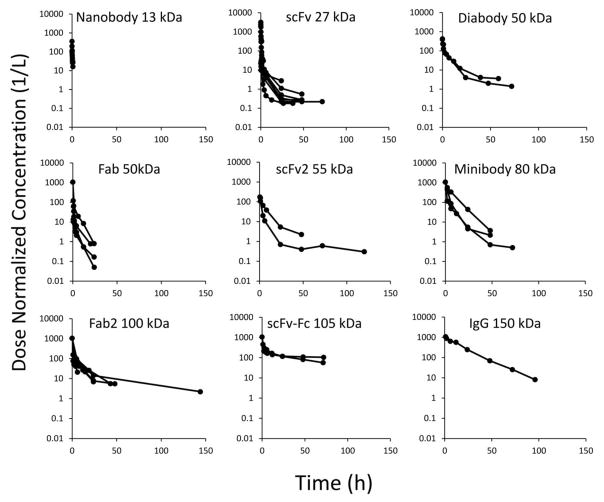
The dose normalized plasma concentration vs. time profiles for each class of protein are shown in Figure-1. It was observed that plasma PK of most proteins followed a bi-exponential profile, except for nanobody and Fab, for which no clear trend was visible, probably because of short sample collection timeframe post dosing. Plasma PK profiles collected from different published studies for each protein molecule class were pooled and subjected to non-compartmental analysis using WinNonlin. Calculated CL values for each protein molecule are summarized in Table-1. It is apparent from Table-1 that increasing molecular weight generally resulted in decreased clearance of antibody fragments.
Figure 1.
Digitized plasma PK data for nanobody (13 kDa, n=3), scFv (27 kDa, n=13), diabody (50 kDa, n=2), Fab (50 kDa, n=6), scFv2 (55 kDa, n=2), minibody (80 kDa, n=3), F(ab)2 (100 kDa, n=6), scFv-Fc (105 kDa, n=2), and IgG in FcRn KO mice (150 kDa, n=1).
Table 1.
NCA estimated CL values for each antibody fragments and IgGs in mice
| MW (kDa) | CL (L/h) | CL (mL/min) | Radius (nm) | |
|---|---|---|---|---|
| Nanobody | 13 | 1.44E-02 | 2.41E-01 | 1.87 |
| scFv | 27 | 1.64E-03 | 2.74E-02 | 2.48 |
| Fab | 50 | 2.72E-03 | 4.53E-02 | 3.14 |
| Diabody | 50 | 8.10E-04 | 1.35E-02 | 3.14 |
| scFv2 | 55 | 9.80E-04 | 1.63E-02 | 3.26 |
| Minibody | 80 | 3.34E-04 | 5.57E-03 | 3.77 |
| Fab2 | 100 | 4.40E-04 | 7.33E-03 | 4.11 |
| scFv-Fc | 105 | 6.38E-05 | 1.06E-03 | 4.19 |
| IgG (WT mouse) | 150 | 1.66E-05 | 2.77E-04 | 4.81 |
| IgG (FcRn KO) | 150 | 5.21E-05 | 8.68E-04 | 4.81 |
Building the relationship between protein size and CL estimated via NCA
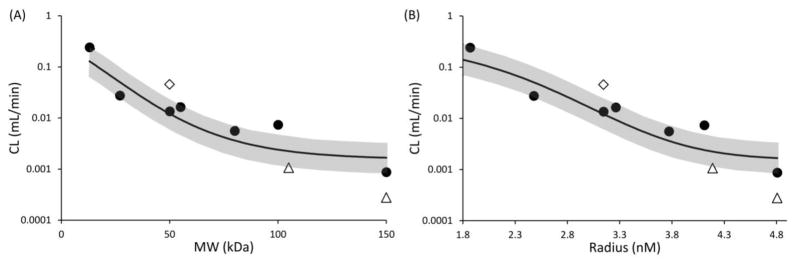
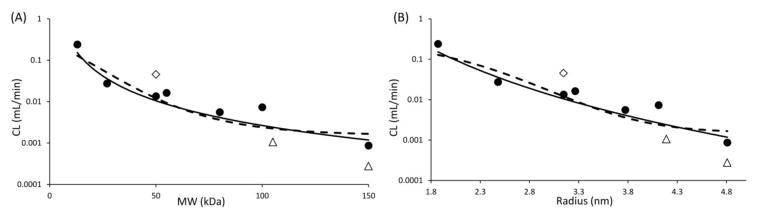
We further established a quantitative relationship between NCA calculated CL values of antibody fragments and their size, represented as molecular weight or radius. Fab was excluded from building the quantitative relationship because none of the PK profiles for Fab obtained from the literature collected plasma samples for long enough time to capture the beta phase of the bi-exponential PK profile, resulting in overestimation of CL calculated via NCA. The PK of scFv-Fc and IgG in wild type mice was excluded from building the relationship because it is well known that Fc-containing proteins can exploit the FcRn-mediated salvage pathway to prolong their systemic circulation (7, 8), resulting in lower CL than size matched non-Fc containing proteins. Resultant CL vs. molecular weight and CL vs. molecular radius plots are provided in Figure-2. Both the relationships were quantitatively characterized using modified sigmoidal functions (Equation-1 and Equation-3 shown in Materials and Methods section).
Figure 2.
(A) Clearance vs. molecular weight, and (B) clearance vs. radius relationships. Solid circles represent CL values calculated using NCA for all proteins, except Fab, scFv-Fc, and IgG in wild type mice. Solid diamond represents Fab, and solid triangles represent scFv-Fc and IgG. Solid line represents fitted relationships, and the gray area represent the two-fold error envelop.
Three independent variables, a, b and c, were estimated as model parameters. Estimated values of these parameters, as well as resultant %CV value of the fittings, are provided in Table-2. The fitted relationships are shown in Figure-2 as solid lines, along with two fold error envelop shown as gray zone. As evident from Figure-2 and Table-2, CL vs. molecular weight and CL vs. radius relationships were reasonably well captured by the modified sigmoidal equations. All the proteins utilized for building the relationship, except F(ab)2, fell within the two-fold error envelope.
Table 2.
Estimated model parameters for NCA based CL (mL/min) vs. size relationship
| a | b | c | |
|---|---|---|---|
| Estimated value | 23.24 | 0.03618 | 7.47 |
| %CV | 9.39 | 10.48 | 2.51 |
Simultaneous fitting of all PK data using 2-compartment model
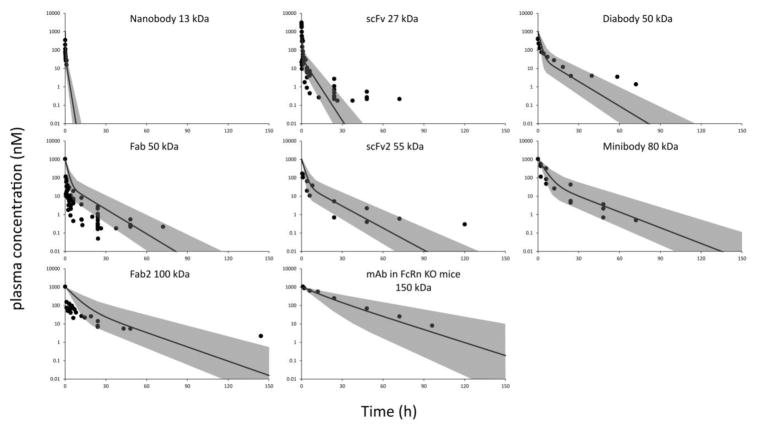
PK data for all antibody fragments and IgG PK in FcRn knock-out mice were fitted simultaneously using a 2-compartment PK model. Central compartment volume (V1) was assumed to represent plasma volume, and hence was considered to be the same for all the molecules. Whereas peripheral compartment volume (V2), distributional clearance (CLD), and clearance from the central compartment (CL), were all assumed to correlate with the molecular weight of proteins. These parameters were modeled as functions of molecular weight using power equations, which are shown in Equation-6, 7, and 8. Model fitting results are shown in Figure-3 and the values of fitted parameters are shown in Table-3. As evident from Figure-3, the PK data of several proteins were captured well by the 2-compartment model. The estimated model parameters were further used to establish a relationship between CL and protein size.
Figure 3.
Observed and model predicted PK profiles for nanobody (13 kDa), scFv (27 kDa,), diabody (50 kDa), Fab (50 kDa), scFv2 (55 kDa), minibody (80 kDa), F(ab)2 (100 kDa), and IgG in FcRn KO mice (150 kDa). Solid circles represent digitized raw PK data, and solid lines represent 2-compartment model fitted PK profiles. The gray area represent the zone obtained by changing the systemic clearance two-fold.
Table 3.
Estimated model parameters for CL (mL/min) vs. size relationship obtained following simultaneous fitting approach, along with CV% for each parameter
| Parameter | Estimate | %CV |
|---|---|---|
| V1 (mL) | 1.15 | >50 |
| α (mL) | 3.44 | >50 |
| κ | 2.33E-02 | 0.909 |
| γ (mL/min) | 37.50 | >50 |
| μ | 2.48 | 0.297 |
| β (mL/min) | 24.98 | >50 |
| λ | 1.97 | 6.37E-02 |
| B (mL/min) | 3.90 | NA |
| L | 5.10 | NA |
Building the relationship between protein size and CL estimated via 2-compartment model
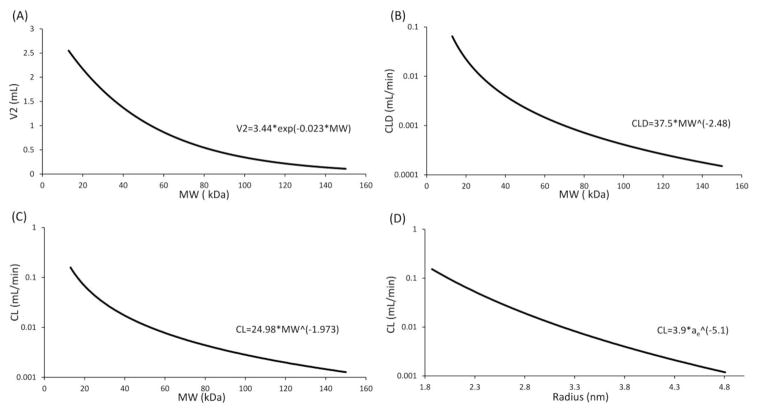
Estimated parameters of Equation-8 and 9 (see Materials and Methods section), were used to generate the mathematical relationship between protein size and CL. Figure-4 shows the model simulated V2 vs. molecular weight, CLD vs. molecular weight, CL vs. molecular weight, and CL vs. radius relationships as solid lines, along with equations characterizing each relationship.
Figure 4.
Simulated, (A) V2 vs. MW, (B) CLD vs. MW, (C) CL vs. MW, and (D) CL vs. ae profiles, generated using parameters estimated by simultaneously fitting all the protein PK data using a 2-compartment model.
The CL values obtained by 2-compartment model fitting were further compared with the CL values obtained using NCA. Figure-5 shows the CL vs. molecular weight and CL vs. radius relationships obtained by the 2-compartment model fitting and NCA based approaches superimposed over the CL values calculated for each protein using NCA. It is evident that both the methods provide similar estimates of systemic clearance for given protein molecules. The sigmoidal shape relationship derived based on the NCA approach suggests an upper limit of increasing CL with decreasing molecular weight, while the simple power law equation derived from 2-compartment model fitting approach predicts unusually high CL values for low molecular weight proteins (MW<10).
Figure 5.
(A) CL vs. MW, and (B) CL vs. radius relationships generated by the two different approaches superimposed over each other. Solid circles represent NCA calculated CL values for all proteins except Fab, scFv-Fc, and IgG in wild type mice. Solid diamond represents NCA calculated CL for Fab, and solid triangles represent NCA calculated CL for scFv-Fc and IgG in wild type mice. Solid line represents continuous relationship between CL and MW/radius obtained using compartmental modeling fitting approach. Dashed line represents continuous relationship between CL and MW/radius obtained using NCA approach.
Extension of CL vs. protein size relationship to other species
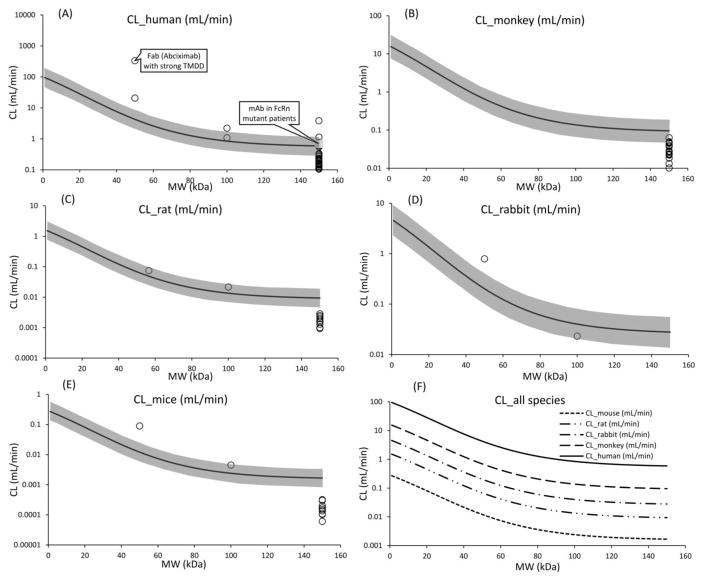
The main objective behind this analysis was to evaluate if the CL vs. protein size relationship established in mice can be extended to other animal species using the principles of allometric scaling. Figure-6 provides the allometrically scaled CL vs. molecular weight relationships for rat, rabbit, monkey, and human, which is superimposed over literature derived clearance values for different size proteins in the respective species. The mouse relationship was also superimposed over the observed clearance values for few more proteins that were not included while building the relationship. While the data obtained from literature for validation is very sparse and variable, in general the allometrically scaled relationships were found to capture the available data from each species reasonably well. It was found that the observed clearance of antibody in all species was lower than the one predicted by the CL vs. protein size relationship for ~150 kDa protein, which is due to the role of FcRn in extending the half-life of antibodies. This reasoning can be further validated by comparing the observed clearance of antibody in patients with FcRn mutation (9) with the one predicted by the allometrically scaled human CL vs. protein size relationship, which were very close to each other (Figure 6A). When comparing the observed clearance values of proteins with the predicted relationships it is also important to understand the role of Target Mediated Drug Disposition (TMDD) (10). For example, it was observed that the clearance of Abciximab, a Fab fragment that binds to the glycoprotein (GP) IIb/IIIa receptor, was much higher in the clinic than the one predicted by the human CL vs. protein size relationship for a ~50 kDa protein. However, this discrepancy can be explained by the fact that Abciximab demonstrates very strong affinity for its receptor on the platelets, which leads to unusually rapid elimination of this molecule from the system (11). Figure 6F provides a superimposition of CL vs. protein size relationships predicted for each animal species.
Figure 6.
CL vs. molecular weight relationships for antibody and antibody fragments. The lines represent the relationships generated using equations and the symbols represent the observed clearance values. The proteins at 150 kDa are monoclonal antibodies. Panels A, B, C, D, and E represent human, monkey, rabbit, rat, and mouse. The gray area in those panels represent twofold error envelop. Panel F superimposes the CL vs. molecular weight relationships for all the animal species.
DISCUSSION
Availability of QSPKRs can significantly improve preclinical and clinical development of protein therapeutics. These relationships can help a priori predict preclinical and clinical PK of protein therapeutics, which can eliminate the need for unnecessary in vivo biodistribution studies and can guide the implementation of first-in-human studies. In our previous work (3, 12) we have established a simple method to infer tissue concentrations of antibody and antibody fragments in target-free tissues based on the plasma concentrations, using Biodistribution Coefficient (BC), which is an invariant ratio of tissue and plasma concentrations for a protein. We were further able to expand the concept of BC to develop a QSPKR for the extent of protein distribution, by establishing a continuous quantitative relationship between BC values and the size of proteins. Here, we have continued our efforts to establish QSPKRs for protein therapeutics by investigating how the size of proteins affect their systemic clearance (i.e. CL). We have established the QSPKR by performing meta-analysis of a number of published biodistribution studies of biologics in mice, and have used two different approaches to establish a quantitative relationship between CL and protein size.
The first approach utilized NCA to estimate CL of various antibody fragments, and developed CL vs. MW and CL vs. radius (ae) relationships using modified sigmoidal function. Since NCA assumes that the drug is eliminated solely from the blood space, one needs to bear in mind that the estimated CL values based on this approach inherently assume that all the proteins are cleared from the central compartment. It is also important to note that three molecules were excluded while building the relationships. Fab was excluded because there was insufficient data to capture the beta-phase of its bi-exponential profile, which could lead to overestimation of CL. ScFv-Fc and IgG were excluded because they can bind to FcRn and demonstrate reduced CL compared to non-FcRn binding size matched protein (7, 8). Figure-2 shows the fitted CL vs. molecular weight and CL vs. radius relationships along with two-fold error envelops. Modified sigmoidal equations was able to fit the dataset reasonably well. Both the relationships showed a clear trend towards decreasing the CL of proteins with increasing size, suggesting protein size is a major determinant for the systemic CL of proteins. As expected, scFv-Fc and IgG showed unusually lower CL in wild type mice. While the NCA based approach provided a clear CL vs. protein size relationship using CL values calculated by a method that is agnostic of any compartmental distribution of proteins, formation of the relationship required 2 separate fittings. Therefore, we further attempted to establish CL vs. protein size relationship using a 2-compartmental PK model fitting approach.
The second approach involved simultaneous fitting of all protein PK data using a two-compartment mammalian PK model. We assumed that all the proteins have the same value for the central compartment volume (V1), representing the plasma volume of mice. Conversely, we assumed that the other three parameters of the model (i.e. V2, CLD, and CL) correlate with the molecular weight of the proteins. This approach was able to simultaneously capture the plasma PK of most protein molecules reasonably well (Figure-3). The plasma PK of scFv and diabody were overpredicted, and the PK of Fab was underpredicted by the model. This can be either due to the limited number of studies included in the analysis for these low molecular weight proteins, or misspecification of the relationship between protein size and CL (or other PK parameters) in the low molecular weight range. The parameters that determined how fast CL changes with changing molecular weight, such as λ, κ and μ, were estimated with high confidence (Table-3), whereas the parameters that determined the intercept, such as β, V1, α and γ, were estimated with low confidence (CV% >50). This suggests that we have high confidence in evaluating how the CL of protein decreases with increasing size, however we do not have enough data in the lower molecular weight range to confidently estimate the CL of very small protein molecules (<10 kDa). Thus, there is a need to generate more PK and biodistribution data for proteins with lower molecular weight to reinforce the proposed relationships.
Since the second approach uses a mammillary PK model to establish CL vs. protein size relationships, it inherently assumes that the clearance of proteins occur from the central compartment. Nonetheless, this approach helps in establishing the relationship between protein size and two more PK parameters (i.e. V2 and CLD) indirectly (Figure-4), which would require further verification. The relationship between V2 and molecular weight suggest that even for very small proteins the peripheral volume of distribution will not go beyond ~3.5 mL, which is very close to the interstitial fluid volume reported for mouse (~4.5 mL)(13). The relationship between CLD and molecular weight suggest that for very small proteins the distributional clearance can go to a value higher than plasma flow of a mouse (~6 mL/min), suggesting the relationship maybe overpredicting the CLD values at these molecular weight range. Thus, there is a need for more PK data from proteins in the lower molecular weight range to further refine this relationship.
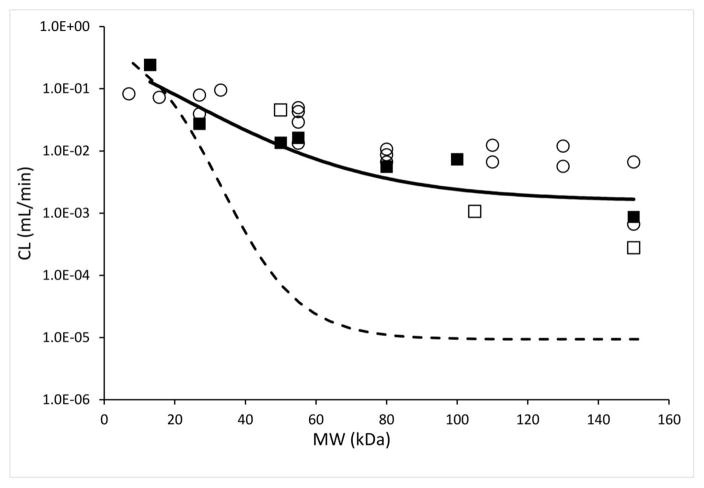
Figure-7 provides a comparison of the ‘systemic CL vs. molecular weight’ relationships we have obtained in this paper with relevant previously reported data. Schmidt and Wittrup have provided data on the ‘terminal slope’ of the PK profile of various proteins in mice, which we have used to obtain the systemic clearance values of those proteins in mice using equation-9 reported in their paper (14). The CL values derived from their study were close to the CL values obtained in this paper for mid-to-lower molecular weight range proteins, however for larger proteins CL values derived from their study were higher than what we found. This discrepancy maybe because of the presence of target-mediated drug elimination of proteins in the PK studies employed by Schmidt and Wittrup, as most of their studies were conducted in tumor bearing mice, and target-mediated effect is more prominent for molecules with inherently low systemic clearance. We further dissected the contribution of renal vs. non-renal routes of elimination towards determining the total systemic elimination of different size proteins. We calculated renal clearance of proteins by multiplying the sieving coefficient of proteins with glomerular filtration rate in mice (0.278 ml/min) (15). A ‘sieving coefficient vs. molecular weight’ relationship for proteins reported by Norden et al. was used to generate the ‘renal clearance vs. molecular weight’ relationship shown in Figure-7 (16). It is evident that as the size of a protein becomes smaller the renal elimination component becomes the major contributor towards overall elimination of proteins. The renal clearance profile also suggests that the NCA derived modified-sigmoidal shape relationship between CL and protein size may be more realistic than the simplistic power law relationship obtained from compartmental fitting. One can also derive a relationship between non-renal clearance and protein size, however correlating this relationship with a physiological process may be difficult since our understanding about the physiological determinants driving this process is poor.
Figure 7.
This figure compares various CL vs. MW relationships. Solid line represents fitted CL vs. MW relationship established using NCA based CL values calculated in the current study. Dashed line represents calculated renal CL vs. MW relationship in mice, obtained using sieving coefficient vs. MW relationship reported by Norden et al. (16) Renal clearance was obtained by simply multiplying the sieving coefficients with glomerular filtration rate (GFR). Close squares represent NCA calculated CL for proteins from the current study, except for Fab, scFv-Fc, and IgG in wild type mice, which are shown as open squares. Open circles represent CL values for various proteins that are derived from kclear values reported by Schmidt and Wittrup.(14)
We also evaluated if the CL vs. molecular weight relationship established from mice data can be extrapolated to other animal species. As mentioned above, renal and non-renal pathways both account for the elimination of protein therapeutics. Thus, in order to predict the clearance of protein therapeutics based on mice data we need to employ a strategy that can account for the changes in both the elimination pathways between different species. In the absence of any other universally accepted strategy to do so, we employed the allometric scaling approach, which has been widely accepted as a reliable approach to scale physiological processes across different species. Figure-6 (panels A–D) shows the CL vs. molecular weight relationship generated for rat, rabbit, monkey, and human, after allometric scaling of the mouse relationship. The quality of these allometrically scaled relationships was evaluated by superimposing the observed CL data for different size proteins onto the predicted relationship curves. The quality of mouse CL vs. protein size relationship was also evaluated by comparing it with the observed clearance values of few more proteins that were not included while building the relationship (Figure 6E). While the validation data points were close enough to the predicted relationships, the observed data is too few and too variable to make any robust claims about the quality of the CL vs. molecular weight relationships, especially for rat, rabbit, monkey, and human. It is also important to add that the shape of the CL vs. protein size relationship discovered by us should be taken as an approximation of the true relationship, and this relationship should become more robust as we generate more data (especially in the extreme molecular weight ranges) in multiple animal species going forward. Nonetheless, it was found that the intercept of the CL vs. molecular weight relationship for each animal species (0.27 ml/min for mouse, 1.52 ml/min for rat, 4.53 ml/min for rabbit, 15.5 ml/min for monkey, and 96 ml/min for human) was very close to the reported GFR values for each animal species (0.28 ml/min for mouse (15), 1.6 ml/min for rat (17), 5.1 ml/min for rabbit (18), 19 ml/min for monkey (19), and 126 ml/min for human (17)). This suggests that the clearance values predicted by the CL vs. molecular weight relationship are realistic and physiologically relevant for all the animal species evaluated.
The protein size vs. CL relationships proposed here can be valuable for protein engineers and drug development scientist who is looking for a guidance on selecting the size of an antibody fragment to accomplish desired drug exposure in plasma or a given tissue. The relationships shown in Figure-6 can help approximate systemic clearance of a protein in several animal species and human based on its size. This CL value can provide a way to calculate the expected systemic exposure (i.e. area under the concentration-time profile or AUC) of the protein when divided from the dose. When the systemic exposure values of a protein is multiplied by a specific Biodistribution Coefficient value for that protein in a given tissue (can be obtained from reference 12), it provides an estimate of tissue exposure for a protein. Thus, just based on the size of a protein, one may be able to estimate its plasma and tissue exposures, provided the protein does not show significant aberrations in its physicochemical properties and does not contain FcRn or receptor binding properties. It is also important to keep in mind that while the exposure can be predicted, accurate prediction of concentration vs. time profiles for proteins is still challenging, mainly because we still don’t have robust relationships between the size of protein and other PK parameters (e.g. rate and extent of distribution) that is required to predict the PK profiles with accuracy. Consequently, development of a platform PBPK model for protein therapeutics (13, 20) may be more appropriate if the goal is to a priori predict plasma and tissue PK of proteins.
CONCLUSION
In this study, we have established a continuous quantitative relationship between CL and protein size (represented as molecular weight or radius) using two different approaches. Both the approaches were able to capture published PK data of antibody fragments well, and resulted in similar CL vs. protein size relationships characterized by power law or modified-sigmoidal equations (Figure-5). In general, the NCA method is quick and easy to use, but the fitted result would be highly dependent on the quality of the dataset (richness of data and duration of sampling time). On the other hand, the simultaneous fitting method provides a more mechanistic view and could be used to explore multiple relationships at once. However, this approach requires better understanding of mathematical PK modeling, and may yield relationships that can be too simplified. Our analysis suggests that more PK and disposition data is needed for proteins with lower molecular weight range to further refine the relationships proposed here. Exploratory analysis also suggest that the proposed CL vs. molecular weight relationship in mice can be used to roughly predict similar relationships for other animal species using the principles of allometric scaling.
Supplementary Material
Acknowledgments
This work was in part supported by NIH grant GM114179 to DKS, and the Center for Protein Therapeutics at the University at Buffalo. We thank the members of the Quantitative and Systems Pharmacology Group at Roche pRed for valuable discussion regarding clearance of large molecules.
ABBREVIATIONS
- BC
Biodistribution Coefficient
- CL
Systemic clearance
- NCA
Non-compartmental analysis
- PK
Pharmacokinetics
- QSPKR
Quantitative structure-PK relationship
- MW
Molecular weight
- TMDD
Target Mediated Drug Disposition
References
- 1.Lobo ED, Hansen RJ, Balthasar JP. Antibody pharmacokinetics and pharmacodynamics. Journal of pharmaceutical sciences. 2004;93(11):2645–68. doi: 10.1002/jps.20178. [DOI] [PubMed] [Google Scholar]
- 2.Wang W, Wang E, Balthasar J. Monoclonal antibody pharmacokinetics and pharmacodynamics. Clinical Pharmacology & Therapeutics. 2008;84(5):548–58. doi: 10.1038/clpt.2008.170. [DOI] [PubMed] [Google Scholar]
- 3.Shah DK, Betts AM. Antibody biodistribution coefficients: inferring tissue concentrations of monoclonal antibodies based on the plasma concentrations in several preclinical species and human. MAbs. 2013;5(2):297–305. doi: 10.4161/mabs.23684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Clayton NS, Emery NJ. What do jays know about other minds and other times? In: Berthoz A, Christen Y, editors. Neurobiology of Umwelt: How Living Beings Perceive the World. Research and Perspectives in Neurosciences. Berlin: Springer-Verlag Berlin; 2009. pp. 109–23. [Google Scholar]
- 5.Venturoli D, Rippe B. Ficoll and dextran vs. globular proteins as probes for testing glomerular permselectivity: effects of molecular size, shape, charge, and deformability. American Journal of Physiology-Renal Physiology. 2005;288(4):F605–F13. doi: 10.1152/ajprenal.00171.2004. [DOI] [PubMed] [Google Scholar]
- 6.Huh Y, Smith DE, Rose Feng M. Interspecies scaling and prediction of human clearance: comparison of small-and macro-molecule drugs. Xenobiotica. 2011;41(11):972–87. doi: 10.3109/00498254.2011.598582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ober RJ, Martinez C, Vaccaro C, Zhou J, Ward ES. Visualizing the site and dynamics of IgG salvage by the MHC class I-related receptor, FcRn. The Journal of Immunology. 2004;172(4):2021–9. doi: 10.4049/jimmunol.172.4.2021. [DOI] [PubMed] [Google Scholar]
- 8.Glassman PM, Abuqayyas L, Balthasar JP. Assessments of antibody biodistribution. The Journal of Clinical Pharmacology. 2015;55(S3):S29–S38. doi: 10.1002/jcph.365. [DOI] [PubMed] [Google Scholar]
- 9.Waldmann T, Terry W. Familial hypercatabolic hypoproteinemia. A disorder of endogenous catabolism of albumin and immunoglobulin. Journal of Clinical Investigation. 1990;86(6):2093. doi: 10.1172/JCI114947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mager DE, Jusko WJ. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. Journal of pharmacokinetics and pharmacodynamics. 2001;28(6):507–32. doi: 10.1023/a:1014414520282. [DOI] [PubMed] [Google Scholar]
- 11.Mager DE, Mascelli MA, Kleiman NS, Fitzgerald DJ, Abernethy DR. Simultaneous modeling of abciximab plasma concentrations and ex vivo pharmacodynamics in patients undergoing coronary angioplasty. Journal of Pharmacology and Experimental Therapeutics. 2003;307(3):969–76. doi: 10.1124/jpet.103.057299. [DOI] [PubMed] [Google Scholar]
- 12.Li Z, Krippendorff B-F, Sharma S, Walz AC, Lavé T, Shah DK. Influence of molecular size on tissue distribution of antibody fragments. MAbs. 2016;8(1):113–9. doi: 10.1080/19420862.2015.1111497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shah DK, Betts AM. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. Journal of pharmacokinetics and pharmacodynamics. 2012;39(1):67–86. doi: 10.1007/s10928-011-9232-2. [DOI] [PubMed] [Google Scholar]
- 14.Schmidt MM, Wittrup KD. A modeling analysis of the effects of molecular size and binding affinity on tumor targeting. Molecular cancer therapeutics. 2009;8(10):2861–71. doi: 10.1158/1535-7163.MCT-09-0195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bivona BJ, Park S, Harrison-Bernard LM. Glomerular filtration rate determinations in conscious type II diabetic mice. American Journal of Physiology-Renal Physiology. 2011;300(3):F618–F25. doi: 10.1152/ajprenal.00421.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Norden AG, Lapsley M, Lee PJ, Pusey CD, Scheinman SJ, Tam FW, et al. Glomerular protein sieving and implications for renal failure in Fanconi syndrome. Kidney international. 2001;60(5):1885–92. doi: 10.1046/j.1523-1755.2001.00016.x. [DOI] [PubMed] [Google Scholar]
- 17.Paine SW, Ménochet K, Denton R, McGinnity DF, Riley RJ. Prediction of human renal clearance from preclinical species for a diverse set of drugs that exhibit both active secretion and net reabsorption. Drug Metabolism and Disposition. 2011;39(6):1008–13. doi: 10.1124/dmd.110.037267. [DOI] [PubMed] [Google Scholar]
- 18.Michigoshi Y, Katayama R, Yamagishi N, Kato M, Saito J, Satoh H, et al. Estimation of glomerular filtration rate in rabbits by a single-sample method using iodixanol. Laboratory animals. 2012;46(4):341–4. doi: 10.1258/la.2012.011065. [DOI] [PubMed] [Google Scholar]
- 19.Iwama R, Tsubasa S, Sakurai K, Takasuna K, Ichijo T, Furuhama K, et al. Estimation of glomerular filtration rate in cynomolgus monkeys (Macaca fascicularis) The Journal of Veterinary Medical Science. 2014;76(10):1423. doi: 10.1292/jvms.14-0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shah DK. Pharmacokinetic and pharmacodynamic considerations for the next generation protein therapeutics. Journal of pharmacokinetics and pharmacodynamics. 2015;42(5):553–71. doi: 10.1007/s10928-015-9447-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.