A recurrent neural model for proto-object based contour integration and figure-ground segregation

Abstract

Visual processing of objects makes use of both feedforward and feedback streams of information. However, the nature of feedback signals is largely unknown, as is the identity of the neuronal populations in lower visual areas that receive them. Here, we develop a recurrent neural model to address these questions in the context of contour integration and figure-ground segregation. A key feature of our model is the use of grouping neurons whose activity represents tentative objects (“proto-objects”) based on the integration of local feature information. Grouping neurons receive input from an organized set of local feature neurons, and project modulatory feedback to those same neurons. Additionally, inhibition at both the local feature level and the object representation level biases the interpretation of the visual scene in agreement with principles from Gestalt psychology. Our model explains several sets of neurophysiological results (Zhou et al, 2000; Qiu et al, 2007; Chen et al, 2014), and makes testable predictions about the influence of neuronal feedback and attentional selection on neural responses across different visual areas. Our model also provides a framework for understanding how object-based attention is able to select both objects and the features associated with them.

1 Introduction

Gestalt psychologists recognized the importance of the whole in influencing perception of the parts when they laid out several principles (“Gestalt laws”) for perceptual organization (Wertheimer, 1923; Koffka, 1935). Contour integration, the linking of line segments into contours, and figure-ground segregation, the segmenting of objects from background, are fundamental components of this process. Both require combining local, low-level and global, high-level information that is represented in different areas of the brain in order to segment the visual scene. The interaction between feedforward and feedback streams carrying this information, as well as the contribution of top-down influences such as attentional selection, are not well understood.

The contour integration process begins in primary visual cortex (V1), where the responses of orientation selective neurons can be modulated by placing collinear stimuli outside the receptive fields (RFs) of these neurons (Stemmler et al, 1995; Polat et al, 1998). Contextual interactions between V1 neurons have often been summarized using a “local association field,” where collinear contour elements excite each other and noncollinear elements inhibit each other (Ullman et al, 1992; Field et al, 1993). Results from neuroanatomy lend support to these ideas, as the lateral connections within V1 predominantly link similar-orientation cortical columns (Gilbert and Wiesel, 1989; Bosking et al, 1997; Stettler et al, 2002). Computational models based on these types of local interactions have successfully explained the ability of V1 neurons to extract contours from complex backgrounds (Li, 1998; Yen and Finkel, 1998; Piëch et al, 2013). While some of these models also incorporate feedback connections, the mechanisms by which higher visual areas construct the appropriate feedback signals and target early feature neurons are not clearly specified. One of the main purposes of the present study is to introduce concrete neural circuitry that makes this recurrent structure explicit, thereby allowing us to make quantitative predictions and compare model predictions with experimental data.

Segmenting an image into regions corresponding to objects requires not only finding the contours in the image but also determining which contours belong to which objects. This is part of what is known as the binding problem, as it is unclear how higher visual areas “know” which features belong to an object (Treisman, 1996). One solution involves differential neural activity, where the neurons responding to the features of an object show increased firing compared with neurons responding to the background. Such response enhancement was first observed in V1 for texture-defined figures (Lamme, 1995). Alternatively, it has been proposed that binding is implemented by neurons that represent features of the same object firing in synchrony while neurons representing features of different objects firing asynchronously (“binding by synchrony;” for review see Singer, 1999). While this is an attractive and parsimonious hypothesis, experimental evidence is controversial (Gray et al, 1989; Kreiter and Singer, 1992; de Oliveira et al, 1997; Thiele and Stoner, 2003; Roelfsema et al, 2004; Dong et al, 2008).

Border-ownership selective cells that have been found in early visual areas, predominantly in secondary visual cortex (V2), appear to be dedicated to this task (Zhou et al, 2000). Border-ownership selective cells encode where an object is located relative to their RFs. When the edge of a figure is presented in its RF, a border-ownership cell will respond with different firing rates depending on where the figure is located. For example, a vertical edge can belong either to an object on the left or on the right of the RF. A border-ownership selective cell will respond differently to these two cases, firing at a higher rate when the figure is located on its “preferred” side, even though the stimulus within its RF may be identical. For a more detailed operational definition of how border-ownership selectivity is determined experimentally, see Section 2.4. Border-ownership coding has been studied using a wide variety of artificial stimuli, including those defined by luminance contrast, color contrast, figure outlines (Zhou et al, 2000), motion (von der Heydt et al, 2003), disparity (Zhou et al, 2000; Qiu and von der Heydt, 2005), and transparency (Qiu and von der Heydt, 2007) as well as, more recently, with faces (Hesse and Tsao, 2016) and within complex natural scenes (Williford and von der Heydt, 2014).

To explain this phenomenon, some computational models assume that image context integration is achieved by propagation of neural activity along horizontal connections within early visual areas. Border-ownership information could be generated from the asymmetric organization of surrounds (Nishimura and Sakai, 2004, 2005; Sakai et al, 2012) or from a diffusion-like process within the image representation (Grossberg, 1994, 1997; Baek and Sajda, 2005; Kikuchi and Akashi, 2001; Pao et al, 1999; Zhaoping, 2005). However, these models have difficulties explaining the fast establishment of border ownership which appears about 25ms after the first stimulus response (Zhou et al, 2000). Propagation along horizontal fibers over the distances used in the experiments would imply a delay of at least ≈ 70ms (Girard et al, 2001, based on the conduction velocity of horizontal fibers in primate V1 cortex; we are not aware of corresponding data for V2). Furthermore, such models are difficult to reconcile with the observation that the time course of border-ownership coding is largely independent of figure size (Sugihara et al, 2011).

An alternative computational model involves populations of grouping (G) cells which explicitly represent (in their firing rates) the perceptual organization of the visual scene (Schütze et al, 2003; Craft et al, 2007). These cells are reciprocally connected to border-ownership selective (B) neurons through feedforward and feedback connections. The combination of grouping cells and the cells signaling local features represents the presence of a “proto-object” (Rensink, 2000), resulting in a structured perceptual organization of the scene. Among the operations that can be performed efficiently in the organized scene are tasks that require attention to objects. In our model, attention to an object targets the grouping neurons representing it, rather than, e.g., all low-level features within a visual area that is defined purely spatially (like everything within a certain distance from the center of attention). Therefore attention is directed to proto-objects, resulting in the modulation of B cell activity through feedback from grouping cells (Mihalas et al, 2011). This proto-object based approach is consistent with psychophysical and neurophysiological studies (e.g. Duncan, 1984; Egly et al, 1994; Scholl, 2001; Kimchi et al, 2007; Qiu et al, 2007; Ho and Yeh, 2009; Poort et al, 2012).

Similar to our approach, several other studies also make use of recurrent connections between different visual areas. Zwickel et al (2007) studied the influence of feedback projections from higher areas in the dorsal visual stream on border-ownership coding. Feedback in their model is only to the border-ownership selective neurons, so they did not test their model on contour integration tasks. Domijan and Šetić (2008) proposed a model involving interactions between the dorsal and ventral visual streams for figure-ground assignment. In their model, there is no explicit computation of border ownership, but instead different surfaces are represented by different firing rates. Jehee et al (2007) proposed a model of border-ownership coding involving higher visual areas, including areas TE and TEO. In their model, border-ownership assignment depends on the size of the figure, which is directly correlated to the specific level in the visual hierarchy of the model at which an object is grouped. They did not test their model on stimuli with noise, or study the effect of object-based attention. Sajda and Finkel (1995) proposed a complex neural architecture involving contour, surface, and depth modules that performs temporal binding through propagation of neural activity within and between populations of neurons. Tschechne and Neumann (2014) proposed a model quite similar to ours. Their model requires a repeated sequence of filtering, feedback, and center-surround normalization that is solved in an iterative manner. Unlike in our model, V4 neurons in their model do not respond to straight, elongated contours. Also, their model only provides a coarse picture of the timing of contour integration and border-ownership assignment across visual areas. Layton et al (2012) also proposed a model that performs border-ownership assignment. Their model introduces an additional neuron class (“R cells”) that implements competition between grouping cells of different RF sizes (similar to a model by Ardila et al (2012)), and the feedback to B cells is by means of shunting inhibition instead of the gain-modulation that we use in our model.

Previous experimental studies have suggested the involvement of multiple visual areas in contour integration and figure-ground segregation (Poort et al, 2012; Chen et al, 2014). The purpose of the present paper is to extend previous models of perceptual organization (Craft et al, 2007; Mihalas et al, 2011) to explain how feedback grouping circuitry can implement the mechanisms necessary to accomplish both contour integration and figure-ground assignment. Most models mentioned above reproduce results restricted to a single set of experiments (e.g. contour integration or figure-ground segregation). In contrast, our model is able to reproduce results from at least three sets of experiments using the same set of network parameters. Our model provides a general framework for understanding how features can be grouped into proto-objects useful for the perceptual organization of a visual scene. In addition, our model also allows us to explain effects of object-based attention and the role of feedback in parsing visual scenes, areas of research which have not been extensively studied.

2 Materials and methods

2.1 Model Structure

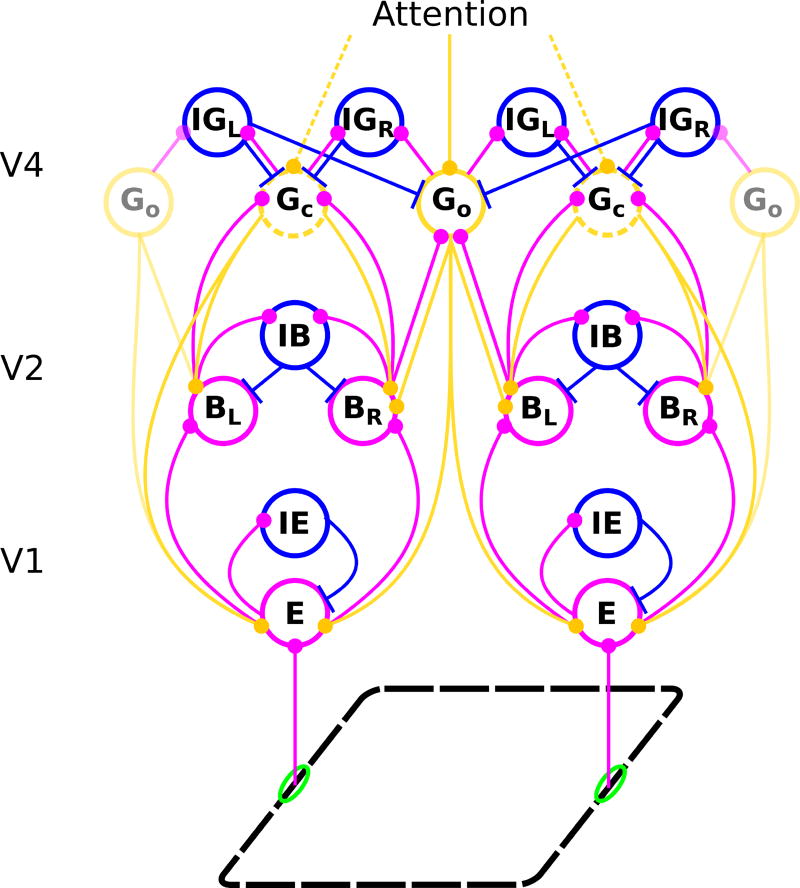
The model consists of areas V1, V2, and V4 (Figure 1). Input comes from a binary-valued orientation map with four orientations (0, π/4, π/2, and 3π/4 relative to the horizontal). The input signal is first represented in V1 and then propagated to V2 and V4 by feedforward connections. Area V4 provides feedback to lower areas (see Supplementary Material for equations). Neurons in higher areas have larger RFs and represent the image at a coarser resolution. Linear RF sizes in area V4 are four times larger than in V2, which, in turn, are twice as large as those in V1.

Fig. 1.

Structure of the model network. Each circle stands for a population of neurons with similar receptive fields and response properties. Magenta, blue, and orange lines represent feedforward excitatory, lateral inhibitory, and feedback excitatory projections, respectively. Edges and other local features of a figure (black dashed parallelogram) activate edge cells (E) whose receptive fields are shown by green ellipses. Edge cells project to border ownership cells (B) that have the same preferred orientation and retinotopic position as the E cells they receive input from. However, for each location and preferred orientation there are two B cell populations with opposite side-of-figure preferences, in the example shown B_L whose neurons respond preferentially when the foreground object is to the left of their receptive fields and B_R whose members prefer the foreground to the right side of their receptive fields. E cells also excite other E cells with the same preferred orientation (connections not shown), as well as a class of inhibitory cells (IE) which, in turn, inhibit E cells of all preferred orientations at a given location. Only E cells of one preferred orientation are shown. B cells have reciprocal, forward excitatory and feedback modulatory connections with two types of grouping cells, G_c and G_o, which integrate global context information about contours and objects, respectively. E cells receive positive (enhancing) modulatory feedback from these same grouping cells. Opposing border ownership cells compete directly via IB cells and indirectly via grouping cells, which bias their activity and thus generate the response differences of opposing border ownership selective neurons. G cell populations also directly excite inhibitory grouping cells (IG; again with the indices L and R), which inhibit G_c cells nonspecifically and G_o cells in all orientations except the preferred one. Top-down attention is modeled as input to the grouping cells and can therefore either be directed towards objects (solid lines) or contours (dashed lines) in the visual field (top).

To achieve contour integration, we implement mutual excitatory lateral connections between V1 edge (E) cells with the same orientation preference. These connections are similar to the local association fields used in other models (Li, 1998; Piëch et al, 2013). Background suppression is carried out through a separate population of inhibitory (IE) cells. The input from V1 edge cells activates border-ownership (B) cells in V2. The B cells inherit their orientation preferences from their presynaptic E cells and for each orientation, there are two B cell populations with opposing side-of-figure preferences. A combination of lateral connections within V2 and feedback connections from V4 (described below) is used to generate border-ownership selectivity. Inhibitory (IB) cells in V2 cause competition between B cells that have the same location and same orientation preference and opposite side-of-figure preference.

In V4, two different types of grouping cells exist. Contour grouping cells (G_c) integrate local edge information and are selective for oriented contours (Figure 2A). Object grouping cells (G_o) are sensitive to roughly co-circular arrangements of edges, thus implementing Gestalt laws of good continuation, convexity of contour, and compact shape (Figure 2B). Competition between separate contours and objects is carried out by a population of inhibitory (IG) cells. Grouping (G_c and G_c) cells project back reciprocally to those B cells from which they receive input, and also to the E cells that project to those B cells. This feedback enhances the activity of E cells along contours and biases the competition between B cells to correctly assign border ownership along object boundaries. Importantly, feedback connections are modulatory, rather than driving, such that the feedback does not modify activities of cells that do not receive sensory input. Biophysically, this can be achieved if the feedback projections employ glutamatergic synapses of the NMDA type (Wagatsuma et al, 2016).

Fig. 2.

Spatial distribution of border ownership cell to grouping cell connectivity; darker pixels indicate stronger connection weights. A) Contour grouping neurons integrate features along oriented contours (horizontal line shown in black), emphasizing the Gestalt principle of good continuation. B) Object grouping neurons integrate features in a co-circular pattern (square figure shown in black), emphasizing the Gestalt principles of convexity and proximity.

To model the effect of object-based attention, we assume that areas higher than V4 provide additional excitatory input to those grouping cells whose activity represents the presence of objects or contours in the visual scene, as shown in Figure 1. This attentional input is driving (as opposed to modulatory) but it is relatively weak; we select its strength as 7% of that of the driving input to the sensory (E) cells. In one part of this study (section 3.2), we model the effect of a lesion in V4 that removes the feedback completely by setting the weight of feedback connections from V4 to lower areas to zero.

Our approach is an extension of the proto-object-based model of perceptual organization proposed by Mihalas et al (2011). Different from their approach, we include a new population of contour grouping neurons (the G_c cells) to explain recent results on cortico-cortical interactions during contour integration (Chen et al, 2014). As a result, top-down attention in our model can either be directed to contours or to objects. Our model is also able to reproduce the time course of neural responses in different visual areas, while the Mihalas et al (2011) model only explains mean neural activities. In order to create more complex input stimuli, we also increased the number of model orientations from two to four. As a simplification to their model, we only include one scale of grouping neurons since we focus on mechanisms that do not require multiple scales.

2.2 Model Implementation

Model neuronal populations (usually referred to as “neurons” in the following) are represented by their mean activity (rate coding). The activity is determined by a set of coupled, first-order nonlinear ordinary differential equations which was solved in MATLAB (Math-Works, Natick MA) using standard numerical integration methods. The mean firing rate is necessarily positive, therefore units are simple zero-threshold, linear neurons which receive excitatory and inhibitory current inputs with their dynamics described by,

$$\tau f\prime (t)=-f+{[\sum W]}_{+}$$ (1)

where f represents the neuron’s activity level and τ its time constant, chosen as τ = 10⁻² s for all neurons. The sum is over all W which are the neuron’s inputs, f′ is the first derivative of f with respect to time, and []₊ means half-wave rectification.

All simulations were performed on a 300-core CPU cluster running Rocks 6.2 (Sidewinder), a Linux distribution intended for high-performance computing. A total of 100 simulations were performed for each experimental condition, and our results are based on the mean neural activities averaged over these simulations with different randomly selected stimulus noise patterns, see sections 2.3 and 2.4.

To constrain our model parameters, we used three sets of neurophysiological data. The first comes from recent contour grouping results (Chen et al, 2014), and our model was able to largely reproduce the magnitude and time course of contour integration at both the V1 and V4 levels. The second comes from studies of border-ownership coding (Zhou et al, 2000) and we show that our model not only explains the emergence of border ownership selectivity but also its approximate time course as reported in that study. The third set of experimental data constraining our model is from the study by Qiu et al (2007) of the interaction between border-ownership selectivity and selective attention. In order to fit the model parameters, we started from the parameters given by Mihalas et al (2011), and modified them to fit the larger body of experimental results to include contour integration, border-ownership selectivity, and attentional selection.

2.3 Contour integration experiments

For the contour integration experiments reported by Chen et al (2014), awake behaving monkeys were trained to perform a two-alternative forced-choice task using two simultaneously presented patterns, one containing a contour embedded in noise and one that was noise only (see Figure 3 for examples). The patterns were composed of 0.25° by 0.05° bars distributed in 0.5° by 0.5° grids. The diameter of the patterns was 4.5°, and the number of bars in the embedded contour was randomly set to 1, 3, 5, or 7 bars within a block of trials in order to control the saliency of the contour. To obtain a reward, the monkey had to saccade to the pattern that contained the contour. When the number of bars was set to 1, both presented stimuli were noise patterns, and the monkey was rewarded randomly with a probability of 50%. While the animals were performing the task, simultaneous single- or multi-unit recordings were made in area V1 and V4 neurons with overlapping receptive fields.

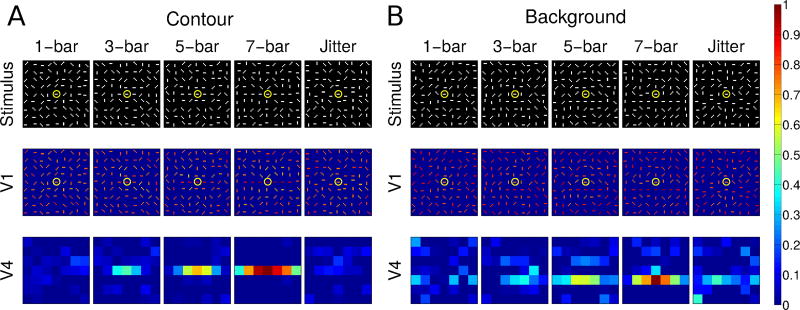
Fig. 3.

Normalized V1 E cell and V4 G_c cell population responses to contours of varying lengths in either the contour (A) or the background (B) condition. In (A), the “recorded” neuron is on the contour; in (B), it is offset from the contour. The top row shows stimuli, the second and third rows show activity in model areas V1 and V4, respectively. Yellow circles mark the RFs of the V1 neurons whose activity is shown in Figure 4. Activity from model area V2 is not shown because a single contour does not produce clear border ownership selectivity, and the activity in V2 is essentially the same as that in V1, but with reduced spatial resolution due to the lower number of neurons. Columns in each condition show, from left to right, increasing contour length, with the right-most column showing a jittered stimulus configuration (see text). Neural activity is color coded and normalized to the 7-bar stimulus in both contour and background conditions, with warmer colors representing higher activity (see color bar at right). To avoid unbalanced inputs near the boundaries of the visual field we use periodic boundary conditions. We crop this and all other maps of population activity by one pixel on each side to remove artifacts related to using periodic boundary conditions.

We modeled these experiments by creating visual stimuli contained in a 4.5° by 4.5° area. We “recorded” from the V1 receptive field that was at the center of the stimulus (marked by the yellow circles in Figure 3), as well as from the corresponding V4 neuron. Input from this area was projected onto a V1 layer of 64 × 64 neurons, each with a receptive field size of ~ 0.7° so the receptive fields overlapped ten-fold at each location in the visual field. We divided the input field into a 9 × 9 grid (each grid point at the center of a 0.5° by 0.5° area) and we placed at each grid location a stimulus bar consisting of three adjacent pixels, corresponding to a size ~ 0.21° by ~ 0.07°. Each stimulus bar had one of four orientations, 0, π/4, π/2, or 3π/4. As in the Chen et al (2014) experiment, contours consisted of 1, 3, 5, or 7 adjacent stimulus bars. We positioned the contour either at the center of the visual field so that the center element of the contour was in the RF of the “recorded” cell (Contour condition, Fig. 3A), or offset from the center of the visual field, such that the “recorded” neuron was next to the contour (Background condition, Fig. 3B). We changed the length of the contour by adding bars to both ends of the contour. Due to their size, V4 receptive fields basically enclosed the entire contour. For more details on the stimulus configuration, see Section 3.1.

2.4 Figure-ground segregation experiments

For the figure-ground segregation experiments (Zhou et al, 2000; Qiu et al, 2007; Zhang and von der Heydt, 2010), awake, behaving monkeys were trained on a fixation task. Receptive fields of each recorded neuron in areas V1 and V2 were first mapped to determine the optimal stimulus properties for that neuron. Afterwards, in some experiments, a square shape was presented on a uniform gray background with one edge of the square centered on the receptive field of the neuron at the neuron’s preferred orientation. In other experiments (results shown in Figures 9 and S3) the stimulus consisted of two partially overlapping squares, and again the receptive field of the recorded neuron was centered at its preferred orientation on one edge of one of the squares. The size of the square varied between experiments but it was always chosen such that the closest corner was far away from the classical receptive field of the recorded neuron. The square was presented in two positions between which it was “flipped” along the long axis of the neuron’s receptive field. For instance, if the preferred orientation was vertical, the square was presented either to the left or the right of the cell’s receptive field (we used this example in the choice of the indices in Figure 1). The difference in the firing rate of the neuron for when the square appears on one side versus the other side is defined as the border-ownership signal. Importantly, in all stimulus conditions, local contents within the receptive field of the neuron remained the same between these two conditions; only global context changed, so the neuron had to integrate information from outside its classical receptive field.

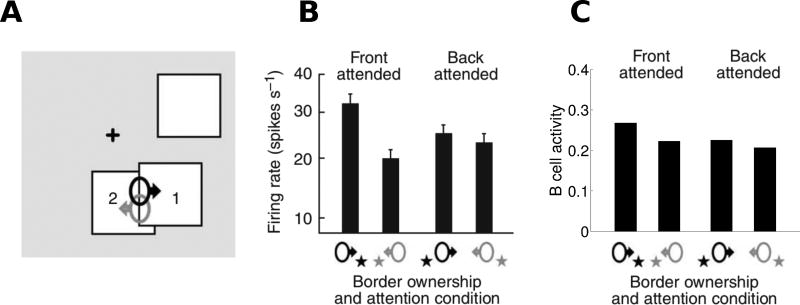
Fig. 9.

Quantitative comparison of model performance to neurophysiological findings (Qiu et al, 2007) for border-ownership coding of overlapping figures. (A) The stimulus configurations used are shown, with neurons coding right border ownership (black) and left border ownership (gray) when attention was focused on either foreground square 1 (front attended) or on background square 2 (back attended). (B) The responses of border ownership selective cells recorded in V2 are shown: bars indicate the average firing rate for each stimulus condition. (C) Model B cell responses to analogous stimulus conditions. For both the model and the experiments, border-ownership modulation was strong when attention was on foreground but weak when attention was on background. Panels A and B are modified from Figure 3 of Qiu et al (2007).

We modeled these experiments by creating visual stimuli that were projected onto the V1 layer. The input to the simulation was either a single square of a size that maximally activated G_o grouping cells of the size chosen in our model, or two partially overlapping squares, as shown in Figure S3, with each of these squares having the same optimal size. In other models (Craft et al, 2007; Mihalas et al, 2011; Russell et al, 2014), grouping cells of many scales are present, covering the range of possible objects in the input. We calculated border-ownership selectivity at the V2 level using the vector modulation index defined in section 2.5. In order to create noisy versions of the single square image (Figure 7), we followed a similar approach as in the contour integration experiments, section 2.3. We again divided the visual field into a 9 × 9 grid and we positioned horizontal and vertical bars at specific grid points to generate a square. We then placed a stimulus bar at all other grid points, with their orientations randomly chosen from four possibilities, 0, π/4, π/2, and 3π/4.

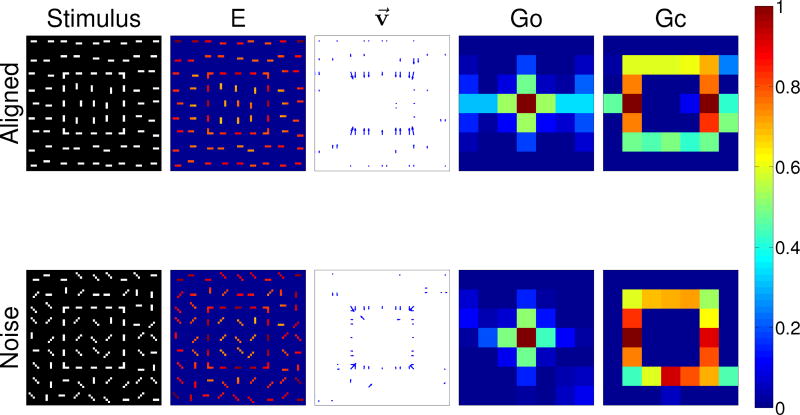
Fig. 7.

Figure-ground segregation of a square object with aligned contour elements (top row) and with noise contour elements (top row). Shown are (left to right) the input stimulus, the edge cell activity (E), the border ownership assignment along edges (shown as the vector modulation index v⃗, section 2.5), the object grouping neuron activity (G_o) and the contour grouping activity (G_c). Activities are normalized within each map, and warmer colors indicate higher activity (see color bar at right).

2.5 Quantitative assessment of border ownership selectivity: Vector modulation index

While the border ownership signal discussed in the previous section (the difference in firing rates between presentations of a figure on the two sides of a a neuron’s RF) is useful to characterize border-ownership selectivity for that particular neuron, description of population behavior requires a more general measure. We use the vector modulation index, introduced by Craft et al (2007) and defined by the expression

$$\overrightarrow{\mathbf{v}}(x,y)=m_{\hat{i}}(x,y)\hat{i}+m_{\hat{j}}(x,y)\hat{j}$$ (2)

where î and ĵ are unit vectors along the horizontal and vertical image axis, respectively, and the components m_î(x, y) and m_ĵ(x, y) are the usual modulation indices along their respective axes, defined as

$$m_{\hat{i}}(x,y)=\frac{{\sum }_{\theta }{B}_{\theta }(x,y)\text{ cos }\theta }{{\sum }_{\theta }|B_{\theta }(x,y)\text{ cos }\theta |}$$ (3)

$$m_{\hat{j}}(x,y)=\frac{{\sum }_{\theta }{B}_{\theta }(x,y)\text{ sin }\theta }{{\sum }_{\theta }|B_{\theta }(x,y)\text{ sin }\theta |}$$

Here, B_θ(x, y) is the border ownership signal (difference between the activities of the two opposing B neurons) at the preferred orientation θ at position (x, y), and θ runs over all angles taken into account in the model (four directed orientations in our case, namely 0, π/4, π/2, and 3π/4, each with both side-of-figure preferences). Vertical bars in the sums in the denominators indicate absolute values.

Both components in Eq. 3 are limited to values between +1 and −1. For the x-component, for instance, a positive value of m_î(x, y) signifies that the figure is to the right of position (x,y) and a negative value signifies that the figure is to the left. Its absolute value indicates the “strength” of the border-ownership signal, with zero being equivalent to ambivalence between left and right. Corresponding comments apply to the y-component, m_ĵ(x, y), regarding the figure’s position upward or downward of (x,y). The direction of the vectorial modulation index v⃗(x, y) defined in Eq. 2 indicates the position of the foreground figure in the two-dimensional image plane relative to the point (x,y). For instance, positive values in both components [m_î(x, y) > 0, m_ĵ(x, y) > 0] indicate that the figure is located upwards and to the right of (x,y).

3 Results

3.1 Contour enhancement in V1 and V4

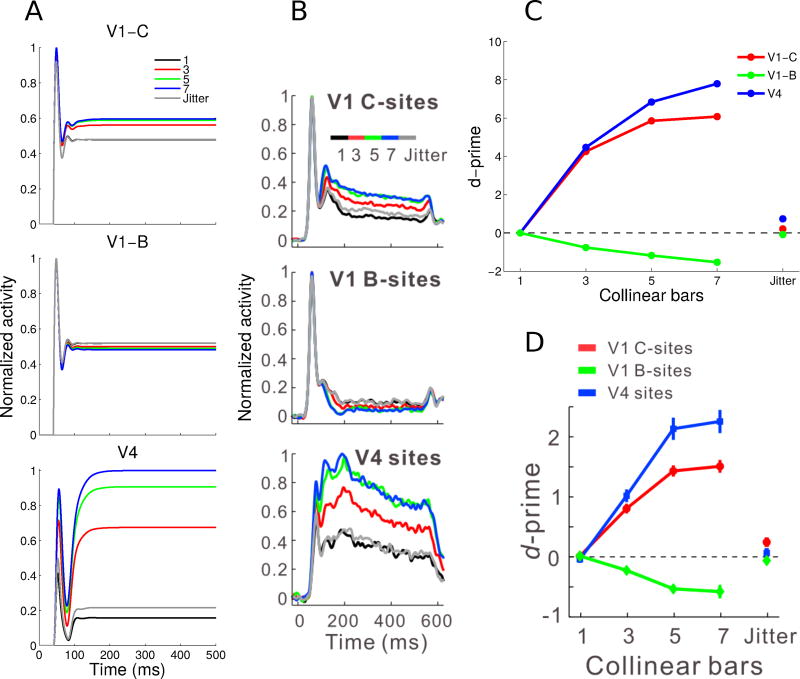
We examined contour-related responses in our model using visual stimuli composed of collinear bars among randomly oriented bars (Figure 3), closely matching the stimuli used in the physiological experiments by Chen et al (2014). The number of collinear bars constituting an embedded contour was set to either 1, 3, 5, or 7 bars, determining the length of the embedded contour, which also controlled its saliency. When the number of collinear bars was one, the stimulus was identical to a noise pattern. We compared the activity of model neurons whose RFs are centered on the contours or in the noise background (but close to contours) with that obtained in the analogous positions during neurophysiological recordings.

V1 responses were split into those of neurons on contour sites (C-sites) and background sites (B-sites). For contour sites (Figure 3A), the embedded contour was centered on the RF of a neuron with a preferred orientation matching that of the contour. For background sites, the contour was laterally placed 0.5° away from the RF center of the recorded neuron, and a background bar was placed in the RF (Figure 3B), with the contour orientation again matching the preferred orientation of the recorded neuron. Both V1 and V4 neurons along the contour showed increased activity with contour length. Neurons on the background showed increased suppression with contour length. Correspondingly, we show in Figure 4 the responses of neurons whose preferred orientations align with the contours (yellow circles in Figure 3).

Fig. 4.

Normalized V1 E cell (contour and background sites) and V4 G_c cell neuronal activity and contour-response d′ to contours of varying lengths. (A) V1 contour (top) and background (middle) sites and V4 sites (bottom) showed facilitation followed by saturation with increasing contour length (see legend). V1 background sites showed greater suppression with longer contours. The jitter condition involved a 7-bar pattern where each bar was laterally offset to disrupt collinearity. (B) Corresponding experimental results showing normalized and averaged PSTHs from the Chen et al (2014) study. (C) Contour-response d′ was higher for the V4 sites compared to the V1 contour sites, and was facilitated by increasing contour length. V1 background sites had increasingly negative d′ with longer contours, indicating background suppression. The jitter condition reduced the absolute value of the d′ values to close to zero, making it similar to the baseline noise condition. (D) Corresponding experimental observations, showing the mean contour-response d′ from the Chen et al (2014) study. Panels B and D are modified from Figure 2 of Chen et al (2014). All model results (Panels A and C) are averages for a single neuron over 100 simulations.

Except for an input delay of 40ms corresponding to the duration of visual processing from the retina to V1, we did not add any time delays in the feedforward or feedback connections of our model, as we were not attempting to reproduce any specific latency effects. Nevertheless, our model generally reproduced the dynamics of neural responses to contours in both V1 and V4 observed in the Chen et al (2014) experiment (Figure 4A). The most salient feature of the neuronal responses is that the levels of sustained activity differ based on the number of bars in the embedded contour. This is observed both for contour sites and for background sites but, importantly, this effect went in opposite directions for these two cases. As the number of collinear bars increased from one to seven, V1 contour sites centered on the contour showed increased activity, with response saturation after five bars. In contrast, V1 background sites that were offset from the embedded contour showed a decrease in activity with increasing number of bars in the background (response suppression). Similar to V1 contour sites, V4 sites showed saturating responses with increasing contour lengths (Figure 4A, bottom). These results were qualitatively similar to those obtained in the Chen et al (2014) experiments which are reproduced in Figure 4B (their Figure 2A).

The model data also showed strong onset transients in both (contour and background) V1 populations (Figure 4A, top and center), again in good agreement with experimental results (Figure 4B, top and center). Transients in V4 neurons were weaker, in both model and experimental data, and nearly absent in the experimental data (though not the model) for longer contours (Figure 4B, bottom). The transient peak observed in the model results is due to a sharp suppression of the activity level for a short (< 50ms) period which is not observed in the empirical data. We believe that this suppression is due to the strong inhibition at the V4 level between G and IG cells, without equivalent excitation between different G cells.

Following Chen et al (2014), we quantitatively analyzed the contour responses using the d-prime (d′) metric from signal detection theory (Green and Swets, 1966), which quantifies the difference in distributions of mean neuronal firing rates between a contour pattern and the noise pattern integrated over the whole interval shown in Figure 4A,B, i.e. 0–500 ms. Neuronal responses to the 1-bar pattern (the noise pattern) were the baseline for examining contour-related responses in V1 and V4, this pattern therefore had a contour-response d′ of zero. The contour-response d′ increased with contour length for both the V1 contour and V4 sites, and d′ decreased with contour length for the V1 background sites, Figure 4C.

The agreement between model (Figure 4C) and experimental results (Figure 4D) is striking. One difference we note is that the absolute values of all model d′ substantially exceed the corresponding experimental values. This is to be expected since no noise was included in the model (other than the random orientation of input stimulus bars which is also present in the experimental approach) while there are surely multiple sources of noise in the biological system. We have not thoroughly investigated this question but it is highly likely that addition of noise to the model will decrease the d′ values.

At first sight, it seems possible that V4 neurons respond with a higher firing rate to longer contours than to shorter ones simply as a consequence of the large size of RFs in V4. In this view, the enhanced responses in V4 with increasing contour length is due to the spatial summation of many bars within the RF at the optimal orientation, independent of their precise location in the RF. To investigate this possiblity, Chen et al (2014) introduced a “jitter” condition to the 7-bar contour, where alternating collinear bars were laterally offset by a small amount (much less than the receptive field size) in order to disrupt the collinearity of the original contour. They showed that jittering disrupted the contour integration process and reduced the neural responses in V1 and V4 close to baseline levels (Figure 4B, gray lines). We found the same result in our model, Figure 4A, gray lines. Furthermore, in the jitter condition, contour-response d′ approached baseline for the V1 and V4 sites, as shown in the rightmost points for Figure 4D for experimental data and Figure 4C for model results. In both cases, no substantial difference between the jitter condition and the baseline noise condition was observed.

We also investigated the orientation and position dependence of contour-related responses in V1 and V4, and found close agreement of our model results with experimental data (Chen et al, 2014). Due to space constraints, these results are presented in the Supplementary Material. The results for V4 are presented in Supplementary Figure S1 and the results for V1 are presented in Supplementary Figure S2.

3.2 The role of feedback and attention in contour grouping

While different forms of attention exist that can be flexibly used for different tasks, we choose here to focus only on the mechanisms of object-based attention (Egly et al, 1994; Scholl, 2001; Kimchi et al, 2007; Ho and Yeh, 2009). We postulate that attention to objects acts at the level of grouping neurons, in agreement with the Mihalas et al (2011) model. As shown in that study, modulation of the activity of grouping cells bypasses the need for attentional control circuitry to have access to detailed object features. Instead, grouping neurons are used as “handles” of the associated objects and it is in their interaction with feature-coding neurons that features are assigned to objects. One of the consequences of this mechanism is that the spatial resolution of attentional selection is coarser than visual resolution since the smallest “unit” of spatial attentional deployment is the size of the receptive (and projective) field of grouping cells, which is considerably larger than the receptive fields of feature-coding neurons at the same eccentricity. Behavioral results show strong evidence in favor of this coarse attentional resolution (Intriligator and Cavanagh, 2001).

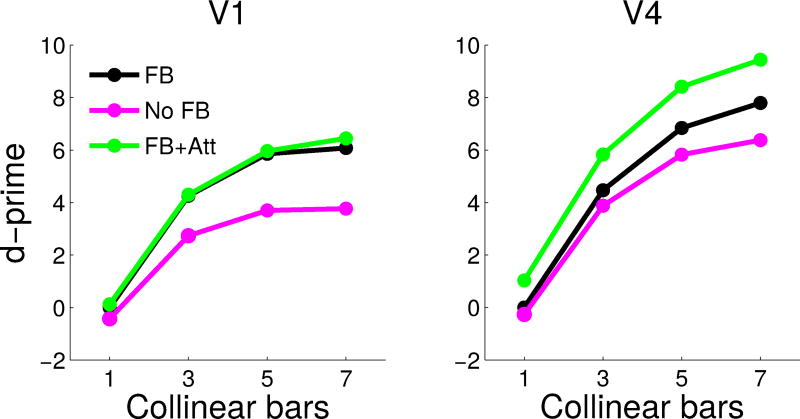
In our model, attention can be directed to objects, including contours. For the contour integration experiments, this is implemented as a top-down input to all contour grouping neurons at the attended location, but, importantly, there was no direct input to the feature-coding edge (E) cells. As we have seen before (Figure 4), d′ in V1 and V4 populations increases with the number of collinear bars, even in the absence of attention. In addition, we now show that attention increases the contour-response d′ for both V1 and V4 neurons, with the additive effect being much larger in V4 than in V1 (Figure 5). For the 7-bar contours, attention increases the contour-response d′ in V1 from 6.08 to 6.66 and in V4 from 7.80 to 11.59. This is consistent with findings that attention has a much larger effect on higher-level neurons compared to early sensory neurons (review: Treue, 2001).

Fig. 5.

Contour-response d′ in V1 E cells (A) and V4 G_c cells (B) for the model with (green) and without attention (black), and for the model with feedback removed (magenta). Attention strongly increased contour-response d′ in V4 (B), while the lack of feedback strongly decreased contour-response d′ in V1 (A).

One of the advantages of computational modeling is that it allows the study of scenarios that are difficult to implement empirically. One question that is difficult to answer experimentally is how removal of feedback from V4 to lower visual areas would change neuronal responses in V1 and V4, structures that are known to be connected bidirectionally (Zeki, 1978; Ungerleider et al, 2007). While it is possible to study the influence of feedback on V2 (and other areas) by cooling (Hupé et al, 1998) or pharmacological inactivation (Jansen-Amorim et al, 2012) of area V4, such manipulations only allow limited control of the effect on multiple brain structures. In contrast, a computational model allows the study of interactions between different areas with perfect control. In the model, we can eliminate all feedback from area V4 simply by “lesioning” the connections from the grouping neurons to the V2 and V1 neurons (setting their strength to zero), thus turning the model into a feedforward network. We found that this has the opposite effect of applying attention on the d′ metric: the decrease in contour response d′ was much larger in V1 compared to V4. Removing feedback reduced the 7-bar contour-response d′ in V1 from 6.08 to 3.77, and in V4 from 7.80 to 6.38 (Fig. 5). We note that the contour-response d′ in V1 is above zero even without feedback from grouping neurons because of the contribution of local excitatory connections to contour integration. This asymmetric effect in contour response d′ in the two areas (V1 and V4) may point to the different roles of feedforward and feedback processing in early vision. We are not aware of any experimental manipulations that completely remove feedback from area V4 without changing the circuitry in other ways, so our results are a prediction awaiting experimental falsification.

3.3 Border-ownership assignment and highlighting figures in noise

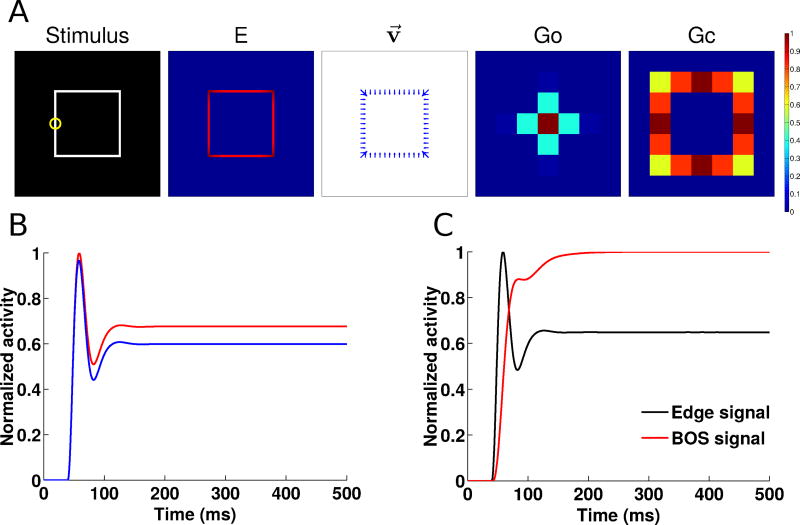
We next apply our model to understanding border-ownership assignment, discussed in Section 2.4. We focus first on the standard square figure frequently used in neurophysiological studies of this function (Zhou et al, 2000; Qiu et al, 2007; Sugihara et al, 2011; Williford and von der Heydt, 2013, 2014; Martin and von der Heydt, 2015). In Figure 6A, we show the input stimulus, the edge cell activity from area V1 of our model, the border-ownership vector modulation field from V2 (defined in Section 2.5), and the object and contour grouping cell activity from V4. Our model enhances V1 activity along the edges of the square, correctly assigns border ownership in V2 neurons (in agreement with Zhou et al, 2000), and enhances activity of V4 neurons at the center of the square and the edges of the square (object and contour grouping neurons, respectively).

Fig. 6.

Figure-ground segregation of a square object as in the Zhou et al (2000) experiments. (A) Shown left to right are the input stimulus, the edge cell activity (E), the border ownership assignment along edges (shown as the vector modulation index v⃗, section 2.5), the object grouping neuron activity (G_o) and the contour grouping activity (G_c). Activities are normalized within each map, and warmer colors indicate higher activity (see color bar at right). (B) Time course of normalized border-ownership cell activity for the preferred side-of-figure (red) and non-preferred side-of-figure (blue) for the receptive field marked by the yellow circle in panel A. Here, the preferred side-of-figure is to the right. (C) Timing of the normalized border-ownership signal (red) and the edge signal (black). The BOS signal is defined as the difference in activities of the two opposing pairs of border-ownership cells in panel B. The edge signal is defined as the sum of the activities of the two border-ownership cells. The curves are normalized to the same scale (0–1) to show the time course of the responses.

We also show the time course of the border-ownership signal for a RF located along the left edge of the figure (indicated by the yellow circle in Figure 6A). The firing rate of a border-ownership selective neuron depends on which side the figure is presented on with respect to its RF. In Figure 6B, the preferred neuron has a side-of-figure preference to the right (red), while the non-preferred neuron has a side-of-figure preference to the left (blue). The firing rate difference is the border-ownership signal, whose steady-state value is used to compute the vector modulation index v⃗ (Section 2.5). In Figure 6C, we show that the border-ownership signal (red) appears rapidly and with short latency compared to the onset of the edge signal (black). Experimental data show that the border-ownership signal appears ~20 ms after the onset of edge responses (Zhou et al, 2000). In our model, the border-ownership signals appears almost instantly. We believe that in addition to visual input, border-ownership cells also receive grouping feedback and that this takes additional time which is not included in our model (see Craft et al, 2007, as an example of a model with latencies).

We then extend this approach by adding additional oriented bars to the stimulus, see Figure 7. In the top row of the figure, results are shown when the bar orientation within the figure differs from that of the background, similar to the texture-defined figures used in the Lamme (1995) experiments. In the bottom row, bars within and outside the figure are all oriented randomly, similar to the noise stimuli used in the Chen et al (2014) study. As in Figure 6, we again show the responses of different populations of neurons in our model. For both types of stimuli, the edges of the square, even when broken up into different bars, are still enhanced while the background bars are suppressed, especially within the square. Interestingly, for the aligned stimulus (top row), only the top and bottom edges of the square show border ownership modulation. This may be an artifact of our modeling procedure, where the edges of our figure are defined by contour elements instead of texture discontinuities. For the noise stimuli (bottom row), border ownership is still assigned correctly along the edge of the square, but the noise results in occasional nonzero border-ownership cell activity at other points in the image as well. For both types of stimuli, grouping cell activity is still centered on the square, and contour grouping neurons still highlight the edges of the squares, but there is also noticeably increased noise.

3.4 Interaction between border ownership assignment and attention

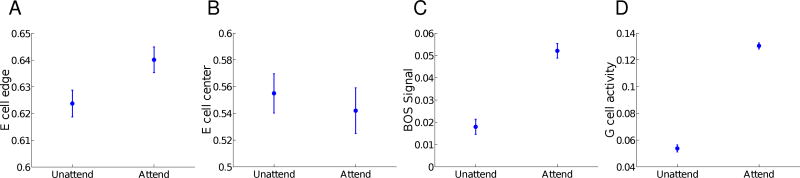
Although border ownership selectivity emerges independently of attention (Qiu et al, 2007), attention may help to facilitate figure-ground segregation in the presence of noise. For the square figure with noise, we found that in our model, attention increases the responses of neurons along the edge of the figure (unpaired t-test, p = 2.32 × 10⁻⁵⁹) and suppresses those in the center (unpaired t-test, p = 3.42 × 10⁻⁸). In addition, attention increases border-ownership modulation along the edge of the figure (unpaired t-test, p = 1.37 × 10⁻¹⁴³) and increases the activity of object grouping neurons in the center of the figure (unpaired t-test, p = 1.53 × 10⁻²³⁹). All effects were small but highly significant, and were based on the differences in summed activity of neurons along the edge or center of the figure over a total of 100 simulations. Figure 8 shows the average neural activity in the different populations of neurons in our model, with and without the effect of attention.

Fig. 8.

Attentional modulation of different neuronal populations aids figure-ground segregation in the presence of noise. Each panel (A–D) shows the means and standard deviations of neural activity with and without added attention over 100 different simulations. (A) Edge cell activity along the contour of the object shows enhancement with attention. (B) Edge cell activity in the center of the figure shows suppression with attention. (C) The BOS signal along the contour of the object shows enhancement with attention. (D) Object grouping cell (Go) activity centered on the object shows enhancement with attention

Attention must also operate in cluttered environments where multiple objects may be present. Qiu et al (2007) studied border-ownership responses in area V2 when two overlapping squares were presented and attention was directed either to the foreground or background square. Mihalas et al (2011), using a model closely related to ours but without G_c cells, reproduced the experimental finding that border-ownership modulation was strong when attention was on the foreground figure but weak when attention was on the background figure. Our model reproduces this finding, see Supplementary Figure S3. The quantitative effect on border-ownership selectivity is shown in Figure 9. Our model also reproduces the experimental finding that border-ownership modulation is strong when attention is on the foreground figure (Figure 9C, “Front attended”) and weak when attention is on the background figure (Figure 9C, “Back attended”).

These results demonstrate that the object and contour grouping neurons are able to assist with early level segmentation of objects in noise and clutter. Previous experimental studies have only tested squares without noise, although the effect of figures defined by broken contours has been investigated before (Zhang and von der Heydt, 2010). Our results predict that border ownership assignment and grouping are robust even in the presence of noise, clutter, and interruptions in figure borders, and that attention may further aid this process.

4 Discussion

In this study, we use computational models to elucidate the role of attention and feedback in contour and object processing. Different from many models that are tailor-made to reproduce one set of experimental results, we demanded that our model explain data from at least three sets of experimental approaches, (1) contour integration, (2) figure-ground segregation, (3) attention to objects. We hypothesize that these processes are fundamentally linked in terms of the larger goal of image understanding. Using the same set of model parameters, we reproduced several experimental findings and generated non-trivial predictions.

4.1 Model predictions

Our model predicts that attentional modulation is specific to the attended contour or object, rather than being defined purely spatially. This is possible because, in our model, attention modifies firing rates of grouping cells, rather than of elementary feature-coding cells. Attending to the contour increases contour-response d′ in both V1 and V4, consistent with experimental results showing increased contour-related responses after animals had been trained to perform a contour detection task, compared to when they performed a separate set of tasks in which the contour was behaviorally irrelevant (Li et al, 2008). We note that Li et al (2008) only studied neural responses in V1, while our model makes predictions about attention-related changes to contour-response d′ in both V1 and V4. We also find that attention modulates border ownership activity in V2 in an object-based manner. As a result, our model makes predictions about neural activity in visual areas V1, V2, and V4 across different stimuli and tasks.

We predict that the interaction of modulatory feedback from grouping cells with local inhibition enhances the representation of the figure and suppresses the representation of the background. Indeed, our model produces background suppression for isolated contours as well as for figures embedded in noise. We note that this prediction is different from what others have observed in texture-defined figures (Lamme, 1995; Lee et al, 1998), where there is generally response enhancement of the center of the figure. This difference may be due to how the figure is defined, by its contour in our experiment and by texture in Lamme (1995) and Lee et al (1998). It is possible that if feedback from object grouping neurons is to the center of the figure instead of its edges, we may observe enhancement of activity at the center of the figure. Understanding how border-ownership assignment interacts with filling-in of surfaces is a future direction of research. Furthermore we predict that attention, in addition to enhancing the figure in an object-based manner, also helps to suppress noise in the background.

We also predict that removing feedback from V4 to lower visual areas reduces neural responses in V1, while having a smaller effect in V4. The activity of V4 neurons is also affected due to the recurrency of the network model. This could be tested experimentally by the same contour detection task used by Chen et al (2014), and measuring the contour-response d′ in V1 and V4 from reversible inactivation of feedback connections. Although complete and selective deactivation of V4 feedback to areas V1 and/or V2 is technically challenging, there have been attempts to study the effect of this type of feedback either through extra-striate lesions (Supér and Lamme, 2007) or reversible inactivation (Jansen-Amorim et al, 2012). Anesthesia presumably also decreases top-down influences, and indeed reduces contour-related V1 responses (Li et al, 2008) and figure-ground segregation (Lamme et al, 1998).

4.2 Comparison to other models

Many have argued that contour integration and figure-ground segregation are largely local phenomena that rely on lateral connections (Grossberg, 1994, 1997; Li, 1998; Zhaoping, 2005; Piëch et al, 2013). While some of these models include a role for top-down influences (Li, 1998; Piëch et al, 2013), they do not offer a specific mechanism by which higher visual areas representing object-level information selectively feed back to lower visual areas containing feature-level information about the object. In contrast, our model is explicit in that feedback connections from higher visual areas modulate the responses of early feature-selective neurons involved in the related processes of contour integration and figure-ground segregation. Our model thus is a member of a broad class of theoretical models that achieve image understanding through bottom-up and top-down recurrent processing (Ullman, 1984; Hochstein and Ahissar, 2002; Roelfsema, 2006; Epshtein et al, 2008). In comparison to similar models, our model is able to reproduce experimental findings from two traditionally separate fields of study– contour integration and figure-ground assignment. Importantly, using the same set of network parameters, the grouping cells in our model are able to represent proto-objects (both contours and extended objects) and provide a perceptual organization of the scene. We show that this perceptual organization is critical for interfacing with top-down attention, and that it provides a general theoretical framework for understanding how feedback connections and an hierarchy of visual areas can be used to group together the features of an object.

4.3 Roles of V1 and V4 in visual processing

While V1 neurons have small RFs that accurately code for orientation, V1 also shows strong background inhibition off the contour. This property allows V1 neurons to enhance contours and suppress noise in the image at a high spatial resolution. V4 neurons, on the other hand, have large RFs that integrate local feature information over large areas of visual space and provide a coarse, proto-object representation of contours and objects. Feedback from V4 can then be refined by the lateral connections present within early visual areas, which aids in the enhancement of the figure and its edges in the image.

Even when V1 neurons receive no feedback from V4, there is an increase in contour-response d′ with contour length (Figure 5). This contour facilitation is solely due to the excitatory lateral connections present in V1, and is weaker without feedback. As a result, feedback from V4 may not be necessary for contour facilitation, but it interacts with local lateral connections in a push-pull manner – neurons along the contour are enhanced, while elements on the background are suppressed. Not surprisingly, removing this type of feedback has a larger effect on V1 neurons compared to V4 neurons, although the activity of V4 neurons is also affected due to the recurrency of the network model.

4.4 Contour and object grouping neurons

Contour grouping neurons have direct experimental support through the recent neurophysiological experiments published by Chen et al (2014). In our model, relatively few numbers of grouping neurons (both contour and object) are required. The spatial resolution of the grouping process does not need to be very high, as grouping cells only provide a coarse template of the contours and objects present in the scene. Assuming that the activity of grouping cells represents proto-objects with a similar resolution as attention, the total number of grouping cells may be less than 2% of the number of border-ownership cells (Craft et al, 2007). In the contour integration experiments (Chen et al, 2014), many V4 neurons were found to respond to straight, elongated contours, while in our model, only a subset of the grouping neurons are selective for contours. One possible explanation for this is overtraining – monkeys performed the task a very large number of times each day for many months, and neural plasticity may have generated many V4 neurons which respond to contours.

There is no unambiguous neurophysiological evidence for object grouping neurons yet, although previous studies have found neurons in V4 that respond to contour segments of various curvatures (Pasupathy and Connor, 2002; Brincat and Connor, 2004). The receptive fields of these neurons are similar to those proposed by Craft et al (2007). Other types of grouping neurons may also exist, including those that respond to gratings (Hegdé and Van Essen, 2007), illusory surfaces (Cox et al, 2013), or 3D surfaces (He and Nakayama, 1995; Hu et al, 2015). We do not attempt to model the whole array of grouping neurons that may exist, but only those necessary for reproducing the neurophysiological experiments referred to here.

In our model, orientation-independent attentional input to contour grouping cells was used to enhance neural responses to a contour at a given location. We note that this form of attention is analogous to the size- and location tolerant attentional selection process proposed by Mihalas et al (2011). The local circuitry of their model was able to sharpen a relatively broad and nonspecific attentional input to match the size and location of a figure in the visual scene. Similarly, the local circuitry of our model transforms the orientation-independent attentional input such that it only enhances the contour of the correct orientation. We note that attention also has a suppressive effect in our model, essentially inhibiting unattended objects and locations. There is physiological support for this mechanism (Wegener et al, 2004; Hopf et al, 2006; Sundberg et al, 2009; Tsotsos, 2011). Furthermore, previous results show suppression of border-ownership activity along the shared edge of overlapping squares when the back square was attended, but not the front square (Qiu et al, 2007). Finally, psychophysical experiments demonstrate an “object superiority effect,” where reaction times are fastest when attention is directed to targets that are part of the cued object, and slowest when targets are outside of an object (Egly et al, 1994; Kimchi et al, 2007).

Complementarily, feature-based attention acts broadly across the visual scene and increases the responses of all components that share similar feature attributes (e.g. color, orientation, or direction of movement) with the attended component (Motter, 1994; Treue, 1999). Orientation-specific forms of attention can enhance neural responses in V1 and V4, but do not significantly alter tuning curves or selectivity (McAdams and Maunsell, 1999). Our model may be able to reproduce similar results by essentially changing the form of the attentional input to be orientation-specific, i.e. top-down attention targets a single population of contour grouping neurons with the same orientation preference. We expect that both object-based and feature-based forms of attention exist and can be flexibly used for different tasks.

4.5 Scope and limitations of the model

Our model seeks to reproduce two different sets of experimental results, while making testable predictions for future experiments. We only included one scale of grouping neurons for simplicity, although multiple scales of grouping neurons are needed to account for the diversity in the scale of objects in the real world. Our model also assigns distinct roles to the different visual areas, edge processing in V1, border ownership assignment in V2, and grouping of contours and objects in V4. However, the physiological properties of neurons in early visual areas have not been fully characterized, and neurons in these different areas may have additional ranges of selectivity than the ones we assign them in our model. Finally, our model operates on artificial images composed of simple shapes such as contours or square figures. In order to truly understand grouping mechanisms in natural vision, our model must also be able to operate on natural images as input, where the number of potential objects and features are much richer. We are currently working on the construction of such a model.