Broadband W-band Rapid Frequency Sweep Considerations for Fourier Transform EPR

Abstract

A multi-arm W-band (94 GHz) electron paramagnetic resonance (EPR) spectrometer that incorporates a loop-gap resonator (LGR) with high bandwidth is described. A goal of the instrumental development is detection of free induction decay (FID) following rapid sweep of the microwave frequency across the spectrum of a nitroxide radical at physiological temperature, which is expected to lead to a capability for Fourier transform (FT) EPR. Progress toward this goal is a theme of the paper. Because of the low Q-value of the LGR, it was found necessary to develop a new type of automatic frequency control, which is described in an appendix. Path-length equalization, which is accomplished at the intermediate frequency of 59 GHz, is analyzed. A directional coupler is favored for separation of incident and reflected power between the bridge and the LGR. Microwave leakage of this coupler is analyzed. An oversize waveguide with hyperbolic-cosine tapers couples the bridge to the LGR, which results in reduced microwave power and signal loss. Benchmark sensitivity data are provided. The most extensive application of the instrument to date has been the measurement of T₁ values using pulse saturation recovery. An overview of that work is provided.

1. INTRODUCTION

A number of electron paramagnetic resonance (EPR) spectrometer designs have been described for use at W-band (1,2). Sidabras et al. (3) extended loop-gap resonator (LGR) technology to W-band in 2007, and compared the LGR with a TE₀₁₁ cavity resonator. Sensitivities were about the same. However, the LGR had a much lower Q-value and a much higher resonator efficiency parameter Λ (G/W^1/2) (4), which enabled development of the concept of W-band broadband EPR. The LGR greatly facilitated two previous papers from the Medical College of Wisconsin group. The first paper described sinusoidal microwave frequency modulation as an alternative to sinusoidal magnetic field modulation (5). The second, entitled “W-band frequency-swept EPR,” was published in 2010 (6). It provides a framework of ideas that motivate the work described here.

The 2010 paper established that it was feasible to tip the magnetization of a nitroxide radical spin label in fluid solution by rapid sweep of the microwave frequency across the spectrum, and that the signal could then be observed by detection of the free induction decay (FID). This may be the first EPR report of FID detection following sweep of the microwave frequency rather than magnetic field—noting that frequency and field sweeps are linked by the gyromagnetic ratio: ω = γH. Fourier transform (FT) of the FID to produce a spectrum was not accomplished, presumably because of the insufficient frequency sweep rate. It was concluded, however, that feasibility for FT EPR by frequency sweep broadband W-band technology had been established.

The 2010 paper offered a new approach to time-domain EPR spectroscopy in contrast with the pulse FT method of nuclear magnetic resonance (NMR), where a short and intense pulse of radio frequency (RF) energy tips the magnetization of substantially all spins in the spectrum by 90 degrees in the rotating frame. The temporal evolution of the spins results in a response to the RF pulse that can be Fourier transformed to obtain a spectrum. We note that other investigators have explored the direct EPR analogy to the NMR FT experiment using intense microwave pulses (1,2). It is also noted that Doll et al. (7) report the use of microwave frequency sweep to invert the magnetization in a context of double electron-electron resonance (DEER).

Detailed comparison of manipulation of the magnetization by sweeps of frequency or field through the resonance condition with manipulation by well-timed true microwave pulses is a subject for the future. FIDs are expected to be more broadly of interest in EPR because of the relatively short phase-memory times at physiological temperatures. There is an important primary benefit of the sweep approach in time-domain EPR spectroscopy: the required peak power is much lower and much less costly to generate. The combination of frequency-swept FIDs and high resonator efficiency LGRs with a 1 GHz resonator bandwidth provide the enabling technologies for broadband FT EPR.

In comparison of field sweep with frequency sweep, several technical issues will immediately come to mind. Rapid sweep of the magnetic field induces eddy currents in the resonators and consequent forces and heating. Rapid microwave frequency sweep leads to baseline issues arising from microwave reactance of the bridge itself. Off-resonance sample resonator reflections generally require baseline subtraction. In frequency-swept experiments, automatic frequency control (AFC) could occur at the beginning of each frequency sweep. The correction voltage would be held by a sample-and-hold (S/H) circuit used during sweep when signal averaging of successive sweeps is employed. In principle, sweep of the microwave frequency can be much faster than sweep of the magnetic field, providing the ability to generate adiabatic conditions over the entire nitroxide spectrum without the need for high-current coil drivers.

A technical issue in the W-band FT frequency sweep idea lies in complications presented by complex additions of signals from multiple paths arising from imperfections of the microwave circuitry. One such imperfection is known as “leakage” from the irradiating microwave source to the receiver. When a reflection resonator is used, leakage arises from imperfections in the circulator or directional coupler as well as from imperfections of waveguide components in the transmission line to and from the sample resonator. In this work, we have come to prefer use of a directional coupler rather than a circulator because of reduced leakage. The problem of leakage at high microwave frequencies such as W-band was first recognized by Krymov and Gerfen in 2003 (8). That citation is the only one known to us in the EPR literature on this subject.

Trapezoidal sweep of the microwave frequency was investigated in the 2010 paper (6). FID signals were observed during sweep of the frequency and also when the frequency was static. Problems arising from leakage affect the baseline of the FID during sweep, but only cause a fixed offset during the portion of the sweep cycle where the frequency was static.

Information is presented in this paper concerning phase noise of the microwave source, although that subject is incomplete. Phase noise was very troublesome in the work reported in our 2007 paper (5), which apparently arose from use of a commercial source at 59 GHz as an intermediate frequency (IF). It was replaced by a self-designed Gunn diode oscillator strongly coupled to a TE₀₁₁ resonator, modeled after (9), to achieve low phase noise. In the work reported here, phase noise was not evident in absorption EPR signal even at a frequency offset from the carrier of as low as 433 Hz. It is noted that phase or frequency noise in the source could, in principle, affect the quality of the frequency sweep that is applied to the sample. No such effects have been found to date.

In Section 2 of the paper, the status of the instrument in its present configuration is reviewed and possible categories of experiments are listed in Table 1. In addition, Appendix C describes the mechanical assembly. A description of a novel AFC circuit is included together with additional detail in Appendix A. The paper addresses the main theme in Section 3: troublesome effects from leakage that become apparent when the microwave frequency is swept. In Section 4, sensitivity data for conventional W-band EPR spectroscopy are given. From time to time, the overall status of the instrument is checked by measurement of the signal-to-noise ratio (SNR) of 1 micromolar TEMPO in water. The sensitivity of the instrument has been improved by an estimated factor of 10 relative to the previous published report. Saturation recovery (SR) considerations are also examined in Section 4 (10,11), which historically have been a principal application of the instrument. The paper concludes with Section 5: Discussion.

Table 1.

Modes of operation of the W-band bridge Field modulation with magnetic field sweep

Frequency modulation with magnetic field sweep

Frequency sweep (equivalent to non-adiabatic rapid sweep [NARS])

Frequency sweep with free induction decay (FID) readout

Multi-quantum (MQ) EPR

Saturation recovery (SR)

Pulse electron-electron double resonance (ELDOR)

2. OVERVIEW OF THE SPECTROMETER

2.1. Brief Description of the W-band Bridge

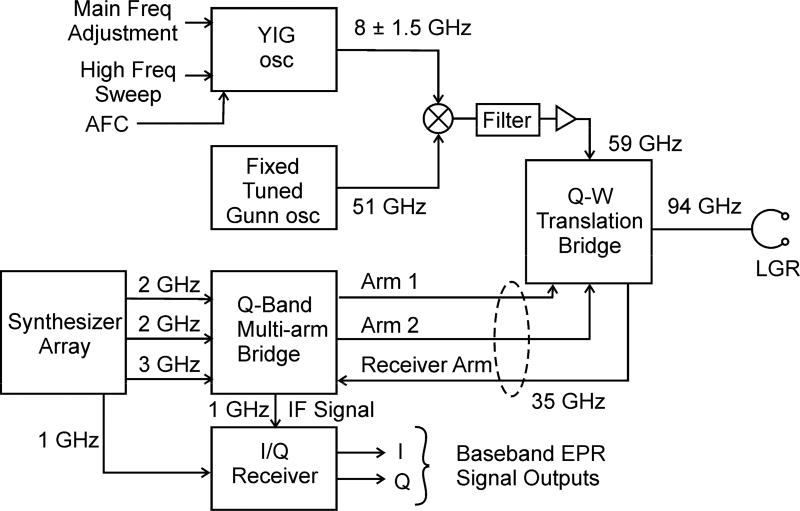
A block diagram of the W-band spectrometer is shown for context in Fig. 1. The signal translation details are described in Ref. (6). Briefly, time-locked synthesizers, nominally 2 GHz, mix with a low phase noise 33 GHz Gunn diode oscillator (9) output in the Q-band multi-arm bridge to produce a nominal 35 GHz in Arms 1 and 2. The output of a low phase noise yttrium iron garnet (YIG)-tuned oscillator (YTO), nominally at 8 GHz, mixes with a 51 GHz Gunn diode oscillator (6) output to produce a nominal 59 GHz. In upconversion (UC), these 35 GHz and 59 GHz inputs to the Q-W Translation Bridge mix to produce the nominal 94 GHz incident power. In down-conversion (DC), the 94 GHz EPR signal mixes with the same 59 GHz input to produce 35 GHz. This input to the receiver arm of the Q-band multi-arm bridge mixes with 36 GHz, which is derived from a 3 GHz synthesizer being mixed with the 33 GHz Gunn diode oscillator, to produce a 1 GHz IF signal output. We have found that the methodology of low-order mixing at a nominal frequency of 35 GHz is well suited for continuous-wave and other experiments where the phase noise of the system is crucial to the EPR signal integrity.

Figure 1.

Block diagram of the multi-arm W-band EPR spectrometer

During bridge operation, the phase of the observing incident power relative to the phase of the reference 1 GHz synthesizer can be adjusted at either synthesizer in order to symmetrize the LGR mode display. Fine phase adjustments permit separation of the I and Q baseband displays into pure absorption and dispersion detection.

A synthesized function generator (DS345) applied to the High Frequency Sweep input in Fig. 1 drives the frequency modulation (FM) coil in the YIG oscillator and it allows numerous experiments. Sinusoidal, square wave, triangular, and sawtooth modulation or sweep of the microwave frequency are available. Magnetic field modulation and lock-in detection are available but are not shown in Fig. 1.

Experiments enabled by this configuration are listed in Table 1. The experiments that use sweep of the microwave frequency are particularly dependent on the work presented in this paper.

2.2. The AFC

The significant advantage of the LGR that arises from the broadband frequency characteristics at high microwave frequency such as W-band presents a disadvantage in development of an effective AFC system. Not only is the separation between 3 dB points of the resonator very great, but also, because of the short wavelength at W-band, there is increased need for an effective AFC to correct for thermal drift. The availability of quadrature detection of the real and imaginary components of the resonator reflection coefficient of an LGR is incorporated in the AFC system developed for use at W-band. At 1 GHz in a properly phased mixer chain from W-band down to baseband, the Q-channel display of the complex valued reflection of the LGR has a discriminator characteristic. AFC information is derived from this characteristic, which goes to zero and changes sign as a function of frequency as in a Pound-type AFC (12). The error signal in the feedback loop of the AFC is the reflected Q-channel voltage relative to zero value voltage. This signal is zero if the incident microwave frequency is the same as the LGR resonant frequency. This information is collected in short time durations of the order of 100 nanoseconds and held in a S/H circuit where it stretched to form a square wave, followed by lock-in detection. The resulting baseband error voltage is filtered, conditioned, and introduced to the AFC feedback loop. The details of this new AFC system are described in Appendix A.

2.3. Path Equalization

A path-length equalizer (delay line) in the reference arm was introduced to EPR microwave bridges by Varian in the 1960s. The purpose of this equalizer was to compensate for the long pathway from the circulator to the resonator and back to the circulator. A survey is provided in Ref. (13). Further translation to the 3 mm wavelength of W-band exacerbates the path equalization problem. Insertion of an equalizer at 94 GHz is problematic because of high insertion loss and the short wavelength in WR-10 rectangular waveguide. We implemented a path-length equalizer at the IF of 59 GHz (V-band) within the W-Q Translation Bridge. The delay line length can be determined from the measured phase response dθ/df, described as (see Appendix B)

$${\ell }_{\text{DL}}=\frac{-c\sqrt{{f_{\text{LO}}}^2-{f_{c\text{LO}}}^2}}{2\mathrm{\pi }{f}_{\text{LO}}}\frac{d\mathrm{\theta }}{\mathit{\text{df}}},$$ (1)

where ℓ_DL is the length of the delay line at the intermediate conversion frequency f_LO, nominally 59 GHz in this bridge, f_cLO is the cutoff frequency of the rectangular waveguide for this IF, and c is the speed of light.

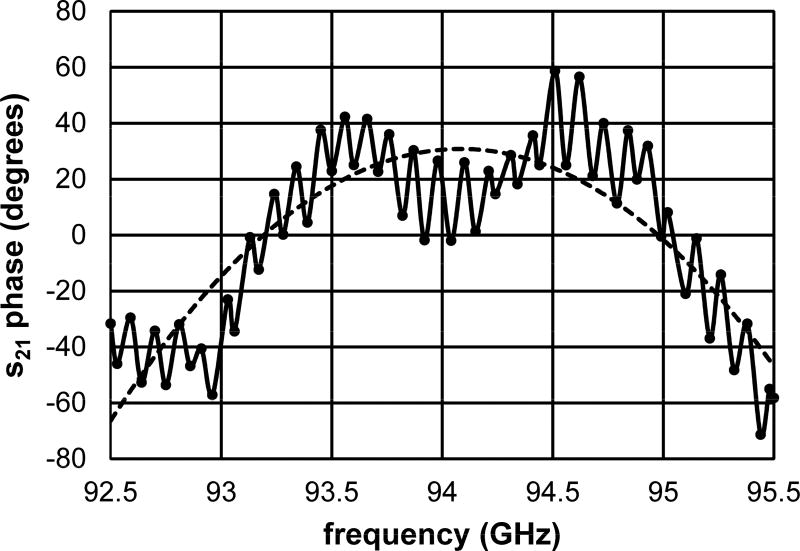
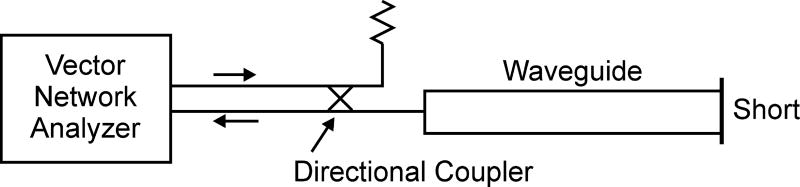
This measurement was performed on our W-band bridge using the Agilent Technologies (now Keysight Technologies, Santa Rosa, CA) PNA model E8363C vector network analyzer by connecting the transmitting port of the analyzer to a Q band input of the Q-W Translation Bridge (Arm 1 or 2 in Fig. 1), and the receiving port of the analyzer to the Q-band output (Receiver Arm). A short is placed at the resonator port for this evaluation of path-length equalization. A transmission phase shift (scattering parameter s₂₁) measurement was performed as a function of tuning the local oscillator (LO) frequency (nominal f_LO = 59 GHz). A total phase shift of 1310 degrees was measured over a span of 3 GHz centered on 59 GHz. The length of WR-15 rectangular waveguide required to balance these arms was determined from Eq. (1) to be 0.268 m shorter than the V-band delay line already in the LO DC path. We removed this length (within an estimated ±4 mm) and measured the phase shift over a span of 3 GHz, data shown in Fig. 2. A quadratic trend line shows that the peak in the dispersive phase response is about 94.1 GHz. Two variations relative to the trend line are evident: a lower-frequency variation that repeats about once per GHz and a higher-frequency variation that repeats about 10 times per GHz. These variations were traced to standing waves in the LO microwave circuit path and to leakage in the resonator coupler, respectively. The latter is the topic of Section 3.

Figure 2.

Measured phase response after equalization (solid) and quadratic trend line (dashed). The resonator port is shorted. The frequency between local peaks is about 100 MHz, which corresponds to about a 35 G field span.

2.4. Hyperbolic Cosine Oversize Waveguide Probe

Another technical advance is the use of an oversize waveguide section with hyperbolic cosine tapers to connect the LGR to the spectrometer. It was formed using commercially available WR-28 waveguide as well as a pair of specially designed tapers with a hyperbolic-cosine shape from WR-28 to WR-10 waveguide (14,15). Oversize waveguide is distinguished from corrugated waveguide, overmoded waveguide, or quasi-optic techniques by minimal coupling to higher-order modes. Only the TE₁₀ mode of the parent WR-10 waveguide is propagated. The preservation of the main mode throughout the structure with minimal mode coupling is the reason for its broadband behavior. Hyperbolic-cosine tapers minimize reflection of the main mode and the excitation of unwanted propagating waveguide modes. In the present work, an oversize assembly with a gradual 90 degree twist was implemented. The oversize waveguide assembly has a broadband one-way insertion loss of 0.78 dB over a measured 4 GHz bandwidth and shows minimal amplitude distortion of approximately 0.15 dB. For comparison, a straight length of WR-10 waveguide has a one-way insertion loss of 3.15 dB. The measured phase response of the twisted oversize waveguide assembly relative to an ideal distortionless transmission line is reduced by a factor of two compared to a straight length of WR-10 waveguide. Oversize waveguide with hyperbolic cosine transitions is an effective way to increase incident power and the return signal amplitude for broadband EPR experiments.

3. LEAKAGE

In frequency-swept experiments, the precession of spins that gives rise to the FID begins to be observable as the swept microwave frequency first approaches EPR. It continues to develop in complexity as the frequency sweeps through the spectrum. When trapezoidal sweep is used, the precession may continue to evolve even though the incident microwave frequency is stationary as shown in the 2010 paper (6). In this case, the FID time-varying signal consists of two parts: decay during spectral passage followed by continued evolution during the stationary period. Leakage and microwave frequency-dependent standing waves contaminate the first portion of the signal, but not the second. An analysis of this leakage follows.

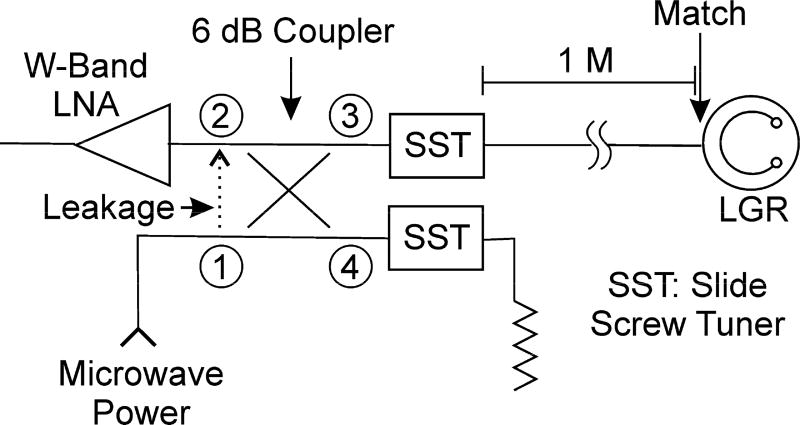
A general problem associated with microwave leakage in the directional coupler (or circulator) which separates the incident microwave power to the sample resonator from the reflected signal arises at high microwave frequencies. Figure 3 shows a zoomed-in drawing of the “resonator coupler” section of the microwave circuit. The leakage of concern is from port 1 of the directional coupler to port 2. Any mismatch that occurs at the LGR and waveguide flanges leads to the reflection of microwave power, which leads to complex (phase-dependent) summation with this leakage at the input to the low-noise microwave amplifier. Whether or not this summation is positive or negative (in the extremes) depends on the path-length difference between power that reaches the low-noise amplifier (LNA) by leakage and by resonator mismatch.

Figure 3.

Resonator coupler signal and leakage paths

Krymov and Gerfen analyzed this problem in a D-band bridge (130 GHz), showing that one can generally solve the problem at a particular frequency with careful tuning (8). In Ref. (8), they considered a relatively high-Q resonant cavity, whereas the instrument under consideration here has an LGR of a high Λ-value and low Q-value. In addition, the use of a two-arm bridge allows multiple new experiments and the impact of the leakage problem depends on the experiment. The LGR ameliorates the leakage problem because of high Λ- and low Q-values.

The nature of the leakage problem is made apparent by a straightforward calculation. Assume +10 dBm of microwave power at the input of the 6 dB coupler in Fig. 3 and 30 dB isolation between ports 1 and 2. Then, 1 mW of power is present at the output of the LNA (20 dB gain) due to leakage. Furthermore, assume that the LGR is matched to 30 dB. The power that is incident on the LGR is +4 dBm assuming zero insertion loss in the transmission line. The microwave power that is reflected from the LGR is −26 dBm, corresponding to −6 dBm at the output of the LNA, or 250 µW, which is smaller than the leakage. If we assume a path length to the LGR of about 1 m, the path-length difference is about 500 waveguide wavelengths round-trip. The separation of the 3 dB points of the LGR is about 500 MHz, or 0.5 percent of the W-band frequency. In this example, the constructive/destructive pattern repeats about four times as the microwave frequency sweeps between the 3 dB points of the LGR. Each repetition corresponds to about 125 MHz. This frequency range corresponds to an interval of 45 G of the spectrum for free radicals if the magnetic field is swept. The detailed waveform of the repetition pattern depends on the relative phases and also on which of the two interfering microwave signals is larger in amplitude.

The leakage shown in Fig. 3 affects the amplitude and phase of the 1 GHz microwave carrier at the in-phase/quadrature (I/Q) mixer (Fig. 1). All magnetic field modulation experiments generate sidebands and intermodulation frequencies, following the work of Anderson (16). These are different microwave frequencies, and the phenomena of constructive or destructive summation do not occur. However, the leakage contributes to the microwave carrier. Detection to baseband occurs in the I/Q mixer. If this carrier can be assumed to be much less than the power at the I/Q mixer from the 1 GHz synthesizer, ordinary W-band EPR spectroscopy will proceed in the usual way. However, frequency-swept experiments as well as frequency-modulation experiments can be affected by the leakage.

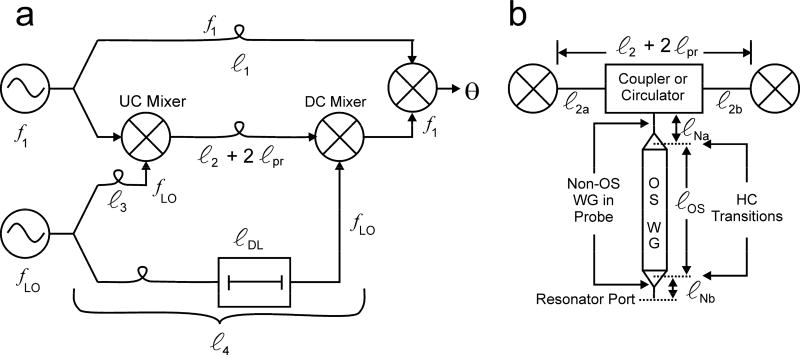
The amplitude and phase variations due to leakage through the resonator coupler can be analyzed using transmission line theory. The amplitude and phase effects of active components and filters and the phase shift though the coupling region of the resonator coupler from one arm to another are not considered in this analysis beyond accounting for the physical length of these components. The insertion loss of the bridge waveguide in ℓ₂ (Fig. 4) is also ignored—it is the same for both the signal and leakage. The input to the DC mixer is designated as the reference location for the leakage-signal interaction. Let IL_pr be the insertion loss of the waveguide probe. A portion of this loss is in standard WR-10 waveguide and the remainder is in oversize waveguide, as shown in Fig. 4b. The input power into the resonator coupler suffers a loss due to the coupling factor, CF, and waveguide probe insertion loss IL_pr up to the sample resonator. The loss due to the reflection coefficient of the resonator is

$${\mathrm{\Gamma }}_{\text{res}}(f)=\frac{{\mathrm{\beta }}_o-1-{\mathit{\text{iQ}}}_{o}2\frac{f-f_o}{f_o}}{{\mathrm{\beta }}_o+1+{\mathit{\text{iQ}}}_{o}2\frac{f-f_o}{f_o}}=|{\mathrm{\Gamma }}_{\text{res}}(f)|e^{+i\text{ arg}[{\mathrm{\Gamma }}_{\text{res}}(f)]},$$ (2)

where Q_o is the unloaded quality factor of the resonator, f_o is the resonant frequency, f is the operating frequency, and β_o is the coupling factor of the resonator (as opposed to the phase constant β). The signal then suffers the return path loss through the probe to the coupling region of the resonator coupler, IL_pr, and the insertion loss through the coupler, IL_DC. When all insertion losses and the coupling factor are expressed in dB, the total loss of the signal in Nepers (Np), (αx)_sig, exclusive of the resonator reflection coefficient, is

$${(\mathrm{\alpha }x)}_{\text{sig}}=\frac{\mathit{\text{CF}}+2({\mathit{\text{IL}}}_{\text{pr}})+{\mathit{\text{IL}}}_{\mathit{\text{DC}}}}{8.686}.$$ (3)

Figure 4.

Two-path circuit for phase change analysis. (a) Bridge delay line analysis model; loops in the transmission paths represent delays; ℓ₂ = ℓ_2a + ℓ_2b. (b) Detail for the signal arm; ℓ_pr = ℓ_Na + ℓ_Nb + ℓ_OS.

The phase shift of the signal ϕ_sig from the W-band UC mixer must include the phase shift in the LO signal path. Assume the bridge arms are balanced. The phase of the V-band LO does not contribute to the phase at the DC mixer output because it is added to both the signal and leakage during UC and subtracted during DC. The phase shift from the V-band LO to the UC mixer, through the two-way waveguide probe path, to the DC mixer input is

$${\mathrm{\varphi }}_{\text{sig}}=-{\mathrm{\beta }}_{\text{LO}}{\ell }_3-{\mathrm{\beta }}_2{\ell }_2-2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}-2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}},$$ (4)

with the notation of Appendix B being utilized, that is, all βs are phase constants except β_o. The voltage signal at the DC mixer input, normalized to a 1 W input power to the resonator coupler, is obtained by combining the factors in Eqs. (2), (3), and (4),

$${\stackrel{\sim }{V}}_{\text{sig}}=\sqrt{Z_o(f)}{e}^{-{(\mathrm{\alpha }x)}_{\text{sig}}+i{\mathrm{\varphi }}_{\text{sig}}}{\mathrm{\Gamma }}_{\text{res}}(f),$$ (5)

where Z_o(f) is the rectangular waveguide characteristic impedance (17), WR-10 in this case. The tilde over the variable denotes that it is a complex number representing the magnitude and phase of the sinusoidal voltage.

The leakage from the input to the output of the resonator coupler bypasses the path to and from the sample resonator, resulting in a phase shift that is less than the phase shift of the signal by the term (−2β₂ℓ_N − 2β_OSℓ_OS). Phase shift in the leakage through the coupler is ignored. The leakage power level is primarily due to the coupling factor, the directivity D of the coupler, and reflection from the coupler-waveguide probe flange interface. The latter two effects are consolidated into D. Although the leakage path length through a coupler with finite directivity is different than the leakage path length due to reflection at the flange interface, they are much closer together than to the two-way path length of the waveguide probe. Hence, the leakage voltage normalized to a 1 W input power at the DC mixer input is

$${\stackrel{\sim }{V}}_{\text{leak}}=\sqrt{Z_o(f)}{e}^{-{(\mathrm{\alpha }x)}_{\text{leak}}+i{\mathrm{\varphi }}_{\text{leak}}},$$ (6)

where ${(\alpha x)}_{\text{leak}}=\frac{(\mathit{\text{CF}}+D)}{8.686}$, D is expressed in dB, and ϕ_leak = −β_LOℓ₃ −β₂ℓ₂. The directivity can be highly frequency dependent. The worst-case (minimum) directivity is normally utilized. The total signal at the DC mixer input is the complex sum of the signal and leakage voltages,

$${\stackrel{\sim }{V}}_T={\stackrel{\sim }{V}}_{\text{sig}}+{\stackrel{\sim }{V}}_{\text{leak}}.$$ (7)

Substituting Eqs. (5) and (6) into (7) and factoring out the phase term (−β_LOℓ₃ −β₂ℓ₂ − 2β₂ℓ_N −2β_OSℓ_OS, because it is part of the phase equalization condition, results in

$${\stackrel{\sim }{V}}_T=\sqrt{Z_o(f)}{e}^{i[-{\mathrm{\beta }}_{\text{LO}}{\ell }_3-{\mathrm{\beta }}_2{\ell }_2-2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}-2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}}]}[|{\mathrm{\Gamma }}_{\text{res}}(f)|e^{-{(\mathrm{\alpha }x)}_{\text{sig}}+i\text{ arg}[{\mathrm{\Gamma }}_{\text{res}}(f)]}+e^{-{(\mathrm{\alpha }x)}_{\text{leak}}+i(2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}+2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}})}].$$ (8)

The factor in square brackets represents the signal-leakage complex summation. If (αx)_leak is increased by higher coupler directivity, then the leakage is decreased relative to the signal.

The power at the input of the DC mixer normalized to 1 W of power at the resonator coupler input,

$$P_{\mathit{\text{Tn}}}=10\text{log}\left[\frac{{|{\stackrel{\sim }{V}}_T|}^2}{Z_o(f)}\right],$$ (9)

is sufficient to plot the amplitude response.

The phase response at the bridge output is incomplete without incorporating phase shift in the LO DC path. The input signal Ṽ_T mixes with the phase-shifted LO signal Ṽ_LO at the DC mixer,

$${\stackrel{\sim }{V}}_{\text{LO}@\text{DCmix}}={\stackrel{\sim }{V}}_{\text{LO}}{e}^{-i{\mathrm{\beta }}_4{\ell }_4}.$$ (10)

The phase at the output of the DC mixer is the difference of the phases of the input and LO signals,

$${\mathrm{\varphi }}_{\text{DCmix}-\text{out}}=\text{arg}({\stackrel{\sim }{V}}_T)-\text{arg}({\stackrel{\sim }{V}}_{\text{LO}@\text{DCmix}})=-{\mathrm{\beta }}_{\text{LO}}{\ell }_3-{\mathrm{\beta }}_2{\ell }_2-2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}-2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}}+\text{arg}[|{\mathrm{\Gamma }}_{\text{res}}(f)|e^{-{(\mathrm{\alpha }x)}_{\text{sig}}+i\text{ arg}[{\mathrm{\Gamma }}_{\text{res}}(f)]}+e^{-{(\mathrm{\alpha }x)}_{\text{leak}}+i2({\mathrm{\beta }}_2{\ell }_{\mathrm{N}}+{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}})}]+{\mathrm{\beta }}_4{\ell }_4.$$ (11)

The sum of the terms −β_LOℓ₃ − β₂ℓ₂ − 2β₂ℓ_N − 2β_OSℓ_OS + β₄ℓ₄ = −β₂ℓ₂ − 2β₂ℓ_N − 2β_OSℓ_OS + β_LOℓ_DL is recognized to be constant when the bridge is balanced (dθ/df = 0) per the analysis in Appendix B. Hence, the term {arg[|Γ_res (f)|e^{−(αx)_sig+i arg[Γ_res(f)]} + e^{−(αx)_leak+i(2β₂ℓ_N+2β_OSℓ_OS)}]} represents the phase variation due to complex summation of the leakage and signal. If |Γ_res (f)|e^−(αx)_sig>> e^{−(αx)_leak}, the leakage is negligible, and ϕ_DCmix-out reduces to arg[Γ_res (f)], that is, the change of angle at the DC mixer output due to a frequency change matches the change of angle of the sample resonator reflection coefficient, as ideally desired.

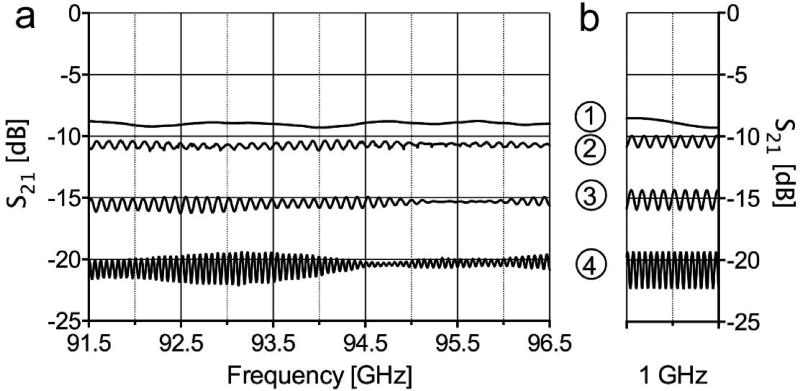
Test cases were measured on the Agilent PNA-X model N5242A vector network analyzer with an Agilent N5262A millimeter head controller, two OML, Inc. (Morgan Hill, CA), V10VNA2 T/R 75 to 110 GHz millimeter wave extenders, and an OML V10-CAL calibration kit. A Terabeam (Harvard, MA) HBC10-03/387 3 dB W-band directional coupler and four different waveguides were connected to the analyzer, as shown in Fig. 5. The four cases were 1) 25.4 mm-long WR-10 waveguide, 2) 941 mm oversize waveguide assembly (14), 3) 940 mm WR-10 waveguide, and 4) 1778 mm WR-10 waveguide, each terminated with a waveguide short. The coupler has an approximate worst-case leakage of 36 dB, a through-arm insertion loss of 4.5 dB, and a coupling factor of 4.2 dB (including losses).

Figure 5.

Coupler/waveguide measurement setup

The round-trip path insertion loss measurements are shown in Fig. 6A. The 25.4 mm WR-10 waveguide (trace 1) adds about 0.1 dB loss (one-way). Thus, the major portion of the nominal 9 dB loss is the coupling and insertion loss of the coupler. There is ripple in the response from summation of the signal and leakage in the coupler, but there are fewer ripple variations due to the short path length from the coupling region of the coupler to the short. The oversize waveguide test assembly consists of 102 mm in WR-10 waveguide and 840 mm in oversize waveguide (14) (trace 2). The insertion loss of the assembly is about 1 dB (one-way), which gives an 11 dB round trip insertion loss, 2 dB more than (trace 1). The ripple in the response is about 1 dB peak-to-peak. Frequency regions of higher coupler directivity have lower ripple because the leakage is lower. The 940 mm WR-10 (trace 3) waveguide adds about 3.2 dB loss (one-way), which gives a 15.5 dB round-trip insertion loss, 6.5 dB more than (trace 1). The 1.5 dB peak-to-peak ripple in the response is larger than in (trace 2) because of greater signal attenuation and the leakage is relatively larger. The complex summation of the signal and leakage results in larger extremes. The number of variations per GHz in (trace 3) is somewhat larger than in (trace 2), despite almost equal mechanical lengths. This is because most of the length in (trace 2) is oversize waveguide, which has a lower phase change per unit frequency since it is farther from cutoff relative to standard rectangular waveguide. The 1778 mm WR-10 waveguide (trace 4) adds about 6 dB loss (one-way), which gives a 21 dB round-trip insertion loss, 12 dB more than (trace 1). The 3 dB peak-to-peak ripple in the response is larger than in (trace 3) because the signal is attenuated even more relative to the leakage. For all cases, the number of variations per GHz and the worst-case peak-to-peak ripple correspond to the ripple patterns calculated using Eq. (9), as frequency is varied when the leakage is 36 dB, shown in Fig. 6B. The agreement between Eq. (9) and measured data is noteworthy.

Figure 6.

Frequency response of a 3 dB coupler with various waveguides (a) measured, (b) worst-case as predicted by Eq. (9). Circled numbers 1–4 correspond to 25.4 mm WR-10, 941 mm oversize waveguide assembly, 940 mm WR-10, and 1778 mm WR-10.

The frequency regions of lower peak-to-peak ripple in Fig. 6, nominally at 95.5 GHz, correspond to lower leakage in the resonator coupler. To minimize the leakage over a finite bandwidth, we connect a low reflection termination (load) in place of the LGR and adjust the slide screw tuner (SST) on port 4 of the coupler in Fig. 3. The SST on port 3 is utilized only if the LGR match changes significantly during the course of the experiment. We have found that leakage can be significantly suppressed over a span of 50 to 100 MHz using this approach.

4. SELECTED RESULTS

4.1. Sensitivity

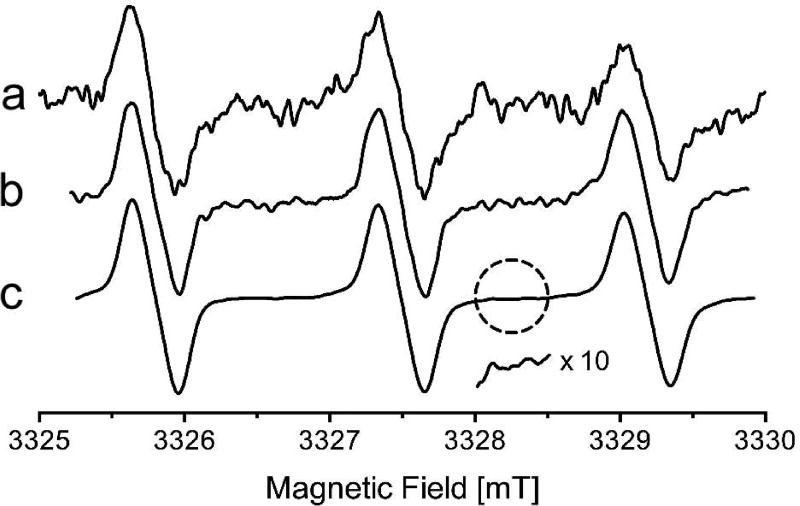
Continuous wave experiment results are shown in Fig. 7 for data collected from a 1 µM TEMPO sample at 25°C in a 0.15 mm inner diameter and 0.25 mm outer diameter quartz capillary. Comparative data were taken from Ref (3), shown in Fig. 7A. In Ref (3), a cylindrical TE₀₁₁ cavity was used and total sample volume was 30 nL. Spectrometer parameters were 3 G peak-to-peak field modulation at 100 kHz, 0.5 mW microwave power, 50 ms time constant, and 128 averages at 30 s per scan. Each scan has 1024 points with a sweep of 5 mT. Figures 7B and 7C were taken with the current W-band system, including the AFC system described in Appendix A, using a five-loop—four-gap LGR using the same capillary and sample volume. Spectrometer parameters were 3 G peak-to-peak field modulation at 433 Hz, 0.5 mW microwave power, 50 ms time constant. Each scan was 1024 points over 4.75 mT. The five-loop—four-gap LGR has no modulation slots, and, therefore, a low audio frequency (433 Hz) was used for field modulation. A single scan was taken over 1 min and 30 s, and a five-point moving average filter was used to remove high frequency noise, shown in Fig. 7B. Finally, a spectrum was collected using 128 averages at 1 min and 30 s per scan for a total scan time of 3 hr and 45 min, shown in Fig. 7C. Success in this long scan is attributed to use of the AFC system introduced in this paper. A five-point moving average filter was used to remove high-frequency noise. The noise profile of the spectra with 128 averages is shown in the inset.

Figure 7.

Sensitivity data at 1 µM TEMPO. From Ref. (3): (a) 128 scans. New benchmark spectra: (b) single scan, 1 min 30 s, five-point moving average filter. (c) 128 scans, 3 hr 45 min, five-point moving average filter, with 10× noise inset. Samples were not degassed.

The noise of the spectrum of Fig. 7A is dominated by the microwave source, which at the time the spectrum was acquired was that of a commercially available varactor-tuned 59 GHz oscillator. Figure 7B has a reduced noise level of about a factor of 3 relative to Fig. 7A. This improvement is attributed to introduction of a microwave Gunn-diode oscillator at 51 GHz (Fig. 1) with markedly lower phase noise. Figure 7C establishes that a useful spectrum can be obtained at spin label concentrations as low as 10⁻⁷ molar.

It is remarkable that high-quality EPR data can be obtained using a field modulation frequency of 433 Hz. The noise figure of the LNA is of the order of 6 dB and is independent of the choice of field modulation frequency. Apparently, the role of phase noise is below the noise figure of the receiver under conditions of the experiments of Fig. 7. It is possible that amplified thermal noise arising in the microwave power amplifiers dominates the noise seen in Figs. 7B and 7C. It is also possible that environmental noise contributes to the noise levels. These figures are the current state-of-the-art with respect to the SNR. The spectra of Fig. 7 were obtained using a magnetic field modulation amplitude that yielded the maximum signal intensity, which is customary when comparing sensitivities. Some modulation broadening is apparent.

4.2. Saturation Recovery

Saturation recovery of nitroxide radical spin labels in various biological preparations at W-band has become an important class of applications of the instrument described here. In a series of four papers (11,18–20), the sample handling problems were addressed, and the rationale for SR experiments on spin-label probes at W-band was developed. Two resonators of the LGR class have been used. The relatively low Q-values and high efficiency parameters, Λ, of W-band LGRs were found to be highly advantageous. The configuration and operation of our W-band bridge for SR is described in Ref. (10). The SR signals acquired at W-band were of about the same SNR as at X-band, but the volume of sample was greatly reduced at W-band. Reported sample volumes at W-band ranged from 30 to 150 nL, compared with typical LGR sample volumes at X-band of 3 µL. Thus, the concentration-sensitivity of SR was found to be reasonably independent of microwave frequency. Measured T₁ values were found to be somewhat shorter than at Q-band, which is an anomalous result requiring further research. A new application of SR was discovered: the measured T₁ values of spin-labeled lipids provide a relative measure of membrane fluidity that complements order-parameter analysis (18). Bimolecular collisions of spin labels with oxygen to measure oxygen transport across lipid bilayers was a subject of particular interest in these papers (11). Control of the oxygen partial pressure over the sample through use of gas permeable sample tubes at W-band was developed. It was also much faster than at X-band because of the thinner sample-tube walls and smaller sample-tube diameter (20).

Table 2 summarizes major results of T₁ measurements as a function of microwave frequency. These values change drastically with microwave frequency, increasing more than five times between 2.54 and 34.6 GHz before decreasing at 94 GHz. Table 2 also contains values of the oxygen transport parameter, which is defined as W(x) = T₁⁻¹(air,x) − T₁⁻¹ (N₂,x), where T₁ values are the spin-lattice relaxation times of the nitroxide in samples equilibrated with atmospheric air and nitrogen, respectively. W(x) is proportional to the product of the local translational diffusion coefficient and the local concentration of oxygen at a “depth” x in the lipid bilayer that is in equilibrium with atmospheric air (21). The data of Table 2 lead to the conclusion that the effect of bimolecular collisions of oxygen on observed spin label relaxation rates is independent of microwave frequency even at W-band, where spin-lattice relaxation times behave anomalously.

Table 2.

Spin-lattice relaxation time and oxygen transport parameter (W(x))^a vs. microwave frequency obtained from 16-SASL in DMPC bilayers at 27°C

Freq. (GHz)	S1(2.54)	S2(3.45)	X(9.2)	K(18.5)	Q(34.6)	W(94)
T1(µs)	0.69	0.94	2.54	3.46	3.69	2.05
W(x)(µs−1)	2.68	2.71	2.67	2.54	2.68	3.02

^aW(x) = T₁⁻¹(air,x) – T₁⁻¹ (N₂,x), where T₁ values are the spin-lattice relaxation times of the nitroxide in samples equilibrated with atmospheric air and nitrogen, respectively. W(x) is proportional to the product of the local translational diffusion coefficient and the local concentration of oxygen at a “depth” x in the lipid bilayer that is in equilibrium with atmospheric air.

At X-band, our research on human eyes necessitated preparation of samples from the eye bank that were pooled from many human donors in order to acquire significant SR data. The small sample volume at W-band allows experiments on a single eye. The individual (single donor) experimental approach is critical because the health history of the donor is a major factor in analysis of data. In this series of papers, the small sample volume, which permitted experiments on small and precious samples, was found to be the principal benefit of W-band.

5. DISCUSSION

5.1. Noise

Microwave phase noise is seldom an issue for spectrometers designed for use at cryogenic temperatures because the long T₁ values of the sample require low incident microwave power. Our thrust has been primarily toward nitroxide-radical spin labels at room temperature, where microwave phase noise can be a limiting noise source.

Most source noise that is close to the carrier is suppressed in a reflection bridge through use of a well-matched sample resonator. Source noise is reduced with use of a low Q-resonator. The high resonator efficiency parameter Λ of an LGR (4) results in the need for a lower incident power level, relative to other resonators, for the same H₁ at the sample. Thus, the source noise is proportionately reduced in detection. The noise detected from phase noise demodulation by a resonator in a bridge circuit is proportional to the sample resonator Q, the offset from the center frequency, and the incident signal voltage, and is inversely proportional to the center frequency (22). Thus, this W-band bridge generally has an inherent advantage over lower frequencies due to the lower resonator Q, the higher center frequency, and a larger Λ-value of the LGR. Although source noise intrinsically increases with microwave frequency, this discussion and the data of Fig. 7 suggest that the effect of source noise on the overall spectrometer performance at W-band when using a low field modulation frequency is not as great as expected.

Phase noise can also appear directly at the signal mixer due to leakage. It has not been enhanced by sample resonator discrimination, but can still be demodulated in the dispersion channel in a delay line demodulation manner which depends on the degree of imbalance in the reference arm and the leakage path in the signal arm, about 2 m. Note that this scenario is another reason to move the resonator coupler adjacent to the resonator. Quantifying this aspect of phase noise would require further analysis.

The white noise power from the power amplifiers in the incident arms will appear in both the absorption and the dispersion channels. This noise also occurs through leakage and by reflection from the sample resonator, typically 30 to 35 dB lower than the incident noise power density. This noise, along with the EPR signal, is amplified by the LNA with its associated noise figure. This noise is potentially considerable. For illustration purposes, if the noise power density at the W-band power amplifier outputs is roughly −120 dBm/Hz (−174 dBm/Hz + 44 dB power amplifier gain + 10 dB noise figure), a noise power density at the input of the W-band to Q-band DC mixer is about −140 dBm/Hz (−120 dBm/Hz − 13 dB circuit loss − 30 dB leakage and residual resonator reflection + 23 dB LNA gain), about 34 dB above thermal noise at room temperature.

Oscillator noise may not be the dominant noise source at 433 Hz offset from the carrier. The phase noise of the 51 GHz Gunn diode oscillator is dominant and is estimated to be −50 dBc/Hz at 433 Hz offset (−120 dBc/Hz at 100 kHz offset + 60 dB going to 100 Hz offset + 10 dB for 1/f noise effects). The phase noise sideband levels at the DC mixer can be estimated by calculating sideband suppression due to the resonator. Using Ondria’s carrier suppression filter formula (23), the phase noise sidebands at 433 Hz offset from 94 GHz, with a loaded sample resonator Q of 100, are suppressed about 120 dB. The resultant phase noise sidebands reflected from the resonator would be on the order of −173 dBm/Hz for a −3 dBm carrier, which is virtually at room temperature thermal noise and below the noise floor of the LNA. Ondria’s formula assumes a matched resonator. In practice, the mismatch of the sample resonator produces greater reflections, but these reflections are not frequency-discriminated by the resonator. Thus, the incident arm power amplifier thermal noise could easily be the dominant source of noise at 433 Hz offset in this W-band bridge.

The apparent masking of phase noise by the amplified thermal noise of the incident arm power amplifiers is in general agreement with noise measurements that were performed as an instrumental check on bridge operation. Initially, the noise out of the I and Q baseband receiver channels was measured with a termination on the resonator port and maximum attenuation of the incident arm power amplifiers. This noise was about −114 dBm/Hz from each channel in the range of 330 Hz to 500 kHz and was flat versus frequency, although spurs were present below 1 kHz. This noise level is the receiver noise floor. Then the noise measurement was repeated with the LGR with sample in place at −3 dBm incident power, the same power that was used in the experimental data of Fig. 7. Similar noise levels were observed in both channels from 2 kHz to 500 kHz. It was difficult to measure below 2 kHz with the presence of spurs, particularly 60 Hz harmonics. Additional noise characterization is required to confirm in the data of Fig. 7 that amplified thermal noise from the incident arm power amplifiers dominated. Possible studies of microwave noise using the existing W-band spectrometer include comparison with similar data obtained using a TE₀₁₁ cavity in an attempt to characterize phase noise close to the carrier. In addition, progressive mismatch should yield information on AM noise. However, we may indeed be at a limit that is imposed by instabilities in the environment.

Benefits of the use of oversize waveguide with hyperbolic-cosine tapers can be expected to vary with specific experiments. For FID and SR, increase in H₁ as well as in EPR signal will each be advantageous. However, if the limiting noise is determined by the microwave source in a CW EPR experiment, performance of the oversize waveguide will depend on the stability of the match of the resonator to the waveguide.

5.2. Leakage

In EPR bridges that use reflection resonators, it is necessary to separate the microwave power that is incident on the sample resonator from the microwave power that is reflected. A circulator, magic tee, or directional coupler can be used. At low microwave frequencies, circulators have been preferred because of minimal insertion loss. Moreover, complex summation of the signal and leakage, which depends on the difference of the leakage pathway and the pathway to and from the slightly mismatched resonator, expressed in wavelengths, does not vary much across the bandwidth. However, at W-band, use of a circulator becomes problematical in broadband EPR due to leakage concerns.

A general approach to overcome the frequency dependence of the leakage is placement of the directional coupler adjacent to the sample resonator. In this paper, we demonstrated the efficacy of this approach on a test bench. A conventional magic tee is hardly possible in the confined space of the bore of the superconducting magnet, but 3 dB-hybrid combiners as well as 6 and 10 dB directional couplers are feasible. The 3 dB-hybrid combiner sacrifices half of the input power and half of the signal power. The directional couplers can be used in two ways: minimal loss of incident power at a cost of decreased signal power, or minimal signal-power loss at a cost of lowered incident power. The latter is preferred in most experiments because of the high Λ value of the LGR and because power amplification is generally feasible.

For experiments using swept microwave frequency, there is a possible spectral acquisition alternative to a hardware solution of the leakage problem. One could sweep the microwave frequency over a significant fraction of the spectral width using a triangular modulation waveform and step the polarizing magnetic field in small steps across the entire spectrum. The data could be combined properly in a computer. In this way, every spectral point is sampled by the swept microwave frequency in the same way, and variation of the signal/leakage summation pattern across the triangular sweep is averaged. This methodology is similar in concept to that which is used in nonadiabatic rapid sweep spectroscopy (24), where triangular modulation of the magnetic field is stepped across the spectrum.

5.3. Broadband EPR Spectroscopy

The four synthesizers in the 1 to 3 GHz range (Fig. 1) have a common time base. These instruments are on continuously to avoid thermal drift during warm-up. The sensitivity data, Fig. 7, was acquired in 3 hours. Our goal in this project has been to achieve sufficient system stability that scans as long as 24 hours are feasible.

A well-designed AFC system will always pull the source microwave frequency to a value where the absorption spectrum is in one channel of the I/Q mixer and the dispersion is in another. In the presence of leakage, the AFC will pull the microwave frequency to a value that depends on the interference pattern. In this situation, the signal amplitude can change slightly, but the EPR absorption and dispersion modes are expected to remain pure.

High microwave frequency leads to an intrinsically high bandwidth of microwave components. These bandwidths, expressed in MHz, can exceed the overall spectral bandwidth (based on 2.8 MHz/G) of the immobilized nitroxide at W-band. However, because of leakage the useful bandwidth in a frequency-swept experiment of the microwave-bridge assembly, including the transmission line from the bridge to the resonator at the center of the magnet, is reduced. Leakage causes interference and standing-wave patterns to occur, making the goal of broadband EPR spectroscopy difficult to achieve. Each waveguide flange can be troublesome. Quality WR-10 flange connections, such as precision flat flanges suggested in the ALMA memos (25,26), generally have a return loss of 30 dB or more. Minimization of the number of flange connections between the resonator coupler and the resonator, especially close to the resonator coupler, reduces such reflections. In addition, microwave power loss in waveguide increases as the wavelength decreases in a frequency-dependent manner.

Nevertheless, a certain level of success has been achieved in microwave frequency-sweep experiments (6). The introduction of the LGR to W-band is the main technical reason for this success, because of the low Q-value and high Λ-value. Other technical advances include the use of oversize waveguide with hyperbolic cosine tapers to connect the LGR to the bridge because carefully designed tapers reduce standing waves (14). Analysis of the leakage at the directional coupler that separates incident microwave power from residual reflected microwave power as well as EPR-signal power is reported here. The analysis suggests a possible cure: position the directional coupler in the magnet close to the LGR.

Frequency sweep experiments performed thus far make use of a digital function generator to drive the frequency modulation (FM) coil in the YTO. Work in progress will replace at least one of the low-frequency synthesizers in the frequency-mixer chain with an arbitrary waveform generator (AWG). The AWG will allow more rapid frequency sweeps over larger ranges with much higher accuracy. More rapid sweep of the microwave frequency will enable further development of the use of resonant frequency sweeps across a spectrum as an alternative to delivery of intense true microwave pulses.

Appendix A. The AFC for Broadband EPR

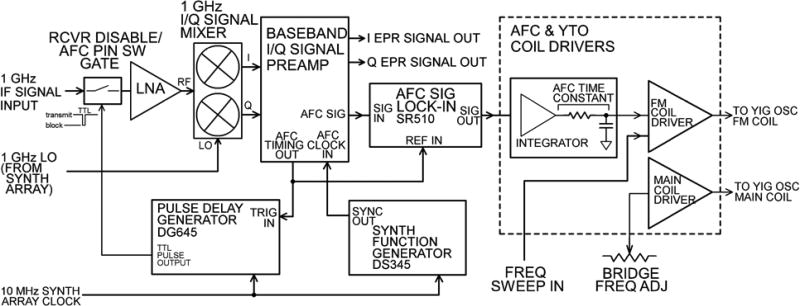
The block diagram of the AFC system shown in Fig. A1, and the accompanying basic timing diagram in Fig. A2, illustrate the operation of the AFC circuit. They are referred to in the following description. The time intervals on the timing diagram are not shown to scale for ease of display. The 1 GHz IF signal from the Q-band multi-arm bridge shown in Fig. 1 feeds the AFC system. The Q-channel of the 1 GHz I/Q signal mixer functions as a phase discriminator in the AFC system when the 1 GHz LO phase is adjusted to give a 90 degree phase difference between the RF and LO inputs of the mixer and the incident power is at the resonant frequency of the sample resonator. The complex nature of the sample resonator reflection coefficient results in a change in the phase of the reflected signal incident on the input of the I/Q signal mixer as the source frequency and resonator frequency drift apart.

The down-converted reflected signal from the resonator at the 1 GHz IF is first gated by the receiver disable PIN switch. A low off-time duty cycle ratio (250 ns off) transistor-transistor logic pulse from the Stanford Research DG645 Pulse Delay Generator controls the PIN switch. The DG645 is triggered by the Stanford Research DS345, the AFC clock source. These components are shown in Fig. A1. The switch control waveform is shown by trace a in Fig. A2. In the SR mode of operation, this gating pulse is synchronized and timed with the pump pulse to protect the LNA and successive stages in the receiver chain from the higher power pump pulse by preventing pump transmission into the receiver. Signal gating is at a frequency up to 100 kHz settable by the user, and should be at a frequency far removed from the field modulation frequency in the field modulation mode of bridge operation so as to avoid interference. In the SR mode of operation, this frequency is the repetition frequency of the pulse experiment. The gated signal is down-converted to baseband in the 1 GHz I/Q signal mixer. The post mixer preamplifier circuit interfaces the I/Q signal mixer with other signal conditioning circuitry both for the EPR signal and for the AFC signal. Both of these components are also shown in Fig. A1.

The signal output of the Q channel of the preamplifier is shown by trace b in Fig. A2. The output waveform of the preamp shows the effect of the signal gating. The zero amplitude portion of the waveform is the time interval when the receiver disable switch is in the isolation state. The portion of the mixer output sensitive to the frequency/phase of the reflected signal from the sample resonator is the interval when the receiver disable switch is transmitting. The polarity and amplitude of this portion of the signal determine the frequency of the microwave source relative to the resonator when the phase of the LO of the I/Q signal mixer is properly adjusted.

Logic in the preamplifier produces the control waveform shown by trace c in Fig. A2 from the input AFC sample clock supplied by the DS345. The pulse width of the sample portion of the sample/hold (S/H) control waveform is 100 ns, the acquisition time for the S/H amplifier, also located in the preamplifier. The hold time of the S/H amplifier is the logic zero portion of the S/H control waveform. The logic waveform in trace c shows that sampling occurs in both the on and off portions of the gated signal of trace b, converting the shorter (250 ns) switch-off portion of the signal waveform and the longer remaining portion into a square-wave, shown in trace d. This is the AFC signal from the preamplifier that feeds the AFC lock-in amplifier (Stanford Research, SR510). The signal from the S/H amplifier is then synchronously detected by the AFC lock-in amplifier at the same gating frequency as the PIN switch. The frequency range of the lock-in amplifier determines the maximum clock set frequency of the AFC system (100 kHz). After synchronous detection, the signal is integrated, low-pass filtered, and interfaced to the YTO FM coil.

This AFC system provides a very stable and dependable lock, even at low (< −30 dBm) microwave power levels with the low-Q W-band LGR (Sample loaded Q<100). Because of its robust performance, this AFC is also used in CW EPR experiments. The chopping frequency is adjusted so as not to interfere with the EPR field modulation signal. For most experiments, the AFC clock is 40 kHz, and due to the low duty cycle of the off-time sampling, has minimal effect on the S/N of the EPR signal.

Figure A1.

AFC system for broadband EPR. The S/H amplifier is within the Baseband I/Q Signal Preamp.

Figure A2.

AFC system timing diagram

Appendix B. Path Equalization Analysis

An analysis of the phase shift at the signal mixer output due to LO frequency changes follows. The analysis incorporates the dispersive nature of waveguide transmission media. Consider the general two-path circuit shown in Fig. 4a. The small “loops” in the connecting lines between components represent delays due to transmission line lengths. Component time delays beyond the path length time delay are not considered in this first-order analysis. The microwave source output at frequency f₁ is divided, and the upper (reference) arm is fed directly to the signal mixer. The frequency in the signal arm (with the UC and DC mixers), however, is translated to frequency f₂, routed to and from the sample resonator, and mixed back to f₁. The details of the signal arm are shown in Fig. 4b.

The path ℓ₂ + 2ℓ_pr consists of bridge circuit waveguide plus twice the length of the probe, the latter being due to the round-trip path. The waveguide probe partially consists of the same waveguide size as the W-band bridge circuit, WR-10, that is, non-oversize waveguide (non-OS WG), over the ℓ_Na and ℓ_Nb lengths, where ℓ_N = ℓ_Na + ℓ_Nb, and partially of oversize waveguide (OS WG) (14). If f₁ is constant, and if the phase change as a function of the LO frequency f_LO is zero at the output of the DC mixer, then the phase at the signal mixer θ will be constant. The bridge arms are equalized. This condition is theoretically possible over a frequency range for transverse electromagnetic wave transmission lines, but dispersion in waveguide will perturb the arm balance to some extent.

The phase shift of the transmission line from the LO source to the DC mixer is −β₄ℓ₄, and the phase shift of the transmission line from the LO source to the UC mixer is −β₃ℓ₃, where β = 2π / λ = 2πf / v is the phase constant (wave number) in rad/m, v is the phase velocity, and λ is the guide wavelength in the waveguide transmission medium. Assume the delay line is length ℓ_DL, where ℓ₄ = ℓ₃ + ℓ_DL. The phase shift in path ℓ₃ from the LO to the UC mixer adds to whatever occurs over the path ℓ₂ + 2ℓ_pr. The phase shift in path ℓ₄ from the LO to the DC mixer is subtracted. Hence, the phase at the signal mixer output is the difference of the phases of the two input signals to the DC mixer (assuming f₁ is constant),

$$\mathrm{\theta }=-{\mathrm{\beta }}_3{\ell }_3-{\mathrm{\beta }}_2{\ell }_2-2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}-2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}}-(-{\mathrm{\beta }}_4{\ell }_4)=-{\mathrm{\beta }}_3{\ell }_3-{\mathrm{\beta }}_2{\ell }_2-2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}-2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}}+{\mathrm{\beta }}_4({\ell }_3+{\ell }_{\text{DL}}).$$ (B1)

The waveguide in the LO circuit is the same in both the UC and DC paths. The phase constants are identical, β₃ = β₄ = β_LO, leaving

$$\mathrm{\theta }=-{\mathrm{\beta }}_2{\ell }_2-2{\mathrm{\beta }}_2{\ell }_{\mathrm{N}}-2{\mathrm{\beta }}_{\text{OS}}{\ell }_{\text{OS}}+{\mathrm{\beta }}_{\text{LO}}{\ell }_{\text{DL}}.$$ (B2)

Waveguide is dispersive, so when the operating frequencies relative to cutoff in two different waveguide sizes are unequal, the velocities are different. The criterion for minimal phase variation as a function of frequency, dθ/df = 0, requires differentiation of βℓ for waveguide with respect to frequency. The cutoff wavelength λ_c in TE₁₀ rectangular waveguide is λ_c = 2a = c / f_c, where a is the internal waveguide width, c is the speed of light, and f_c is the cutoff frequency. We start with

$$\nu ={\mathrm{\lambda }}_{g}f=\frac{{\mathrm{\lambda }}_o}{\sqrt{1-{\left(\frac{{\mathrm{\lambda }}_o}{2a}\right)}^2}}f=\frac{c}{\sqrt{1-{\left(\frac{f_c}{f}\right)}^2}},$$ (B3)

where the waveguide wavelength λ_g is designated specifically to distinguish it from the free-space wavelength λ_o. The phase constant is

$$\mathrm{\beta }=\frac{2\mathrm{\pi }f}{\nu }=\frac{2\mathrm{\pi }}{c}\sqrt{f^2-{f_c}^2}.$$ (B4)

Then

$$\frac{d(\mathrm{\beta }\ell )}{\mathit{\text{df}}}=\frac{2\mathrm{\pi }f\ell }{c\sqrt{f^2-{f_c}^2}}.$$ (B5)

Taking the derivative of Eq. (B2) and substituting Eq. (B5) results in

$$\frac{d\mathrm{\theta }}{\mathit{\text{df}}}=\frac{-2\mathrm{\pi }{f}_2{\ell }_2}{c\sqrt{{f_2}^2-{f_{c2}}^2}}-2\frac{2\mathrm{\pi }{f}_{2}2{\ell }_{\mathrm{N}}}{c\sqrt{{f_2}^2-{f_{c2}}^2}}-2\frac{2\mathrm{\pi }{f}_{2}2{\ell }_{\text{OS}}}{c\sqrt{{f_2}^2-{f_{c\text{OS}}}^2}}+\frac{2\mathrm{\pi }{f}_{\text{LO}}{\ell }_{\text{DL}}}{c\sqrt{{f_{\text{LO}}}^2-{f_{c\text{LO}}}^2}}.$$ (B6)

In the arm-balanced condition with the delay line, dθ/df = 0. In the arm-unbalanced condition without the delay line (ℓ_DL = 0), dθ/df ≠ 0 and can be measured on a vector network analyzer as a function of changing the LO frequency. Subtracting equations that correspond to these two conditions, the delay line length can be determined from the measured dθ/df,

$${\ell }_{\text{DL}}=\frac{-c\sqrt{{f_{\text{LO}}}^2-{f_{c\text{LO}}}^2}}{2\mathrm{\pi }{f}_{\text{LO}}}\frac{d\mathrm{\theta }}{\mathit{\text{df}}},$$ (B7)

where the negative sign is present because dθ/df is negative without the delay line per Eq. (B6).

Appendix C. Physical Layout of the Spectrometer

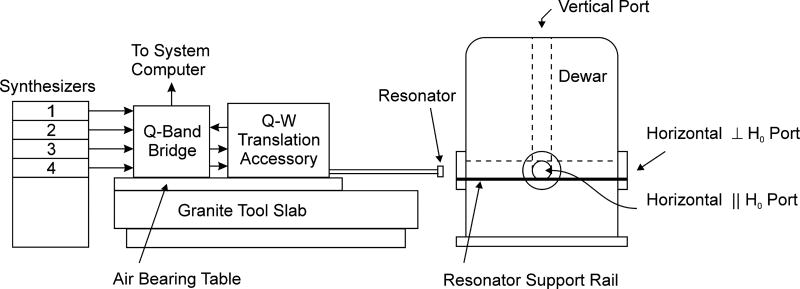
The overall assembly of the microwave components and magnet of the W-band spectrometer is shown in Fig. C1. The mechanical support system for moving the microwave bridge, along with the waveguide probe, resonator, and sample, into the side port of a Magnex/Bruker superconducting magnet consists of a granite slab 250 cm long by 50 cm wide by 20 cm thick, with an air-bearing-supported slide floating on a cushion of dry nitrogen. The system allows vibration-free insertion of the probe without disrupting the sample or resonator, which is adjusted for microwave coupling outside the magnet. An early description of the system developed here is provided in Ref. (27). Use of a granite slab for achieving stability of a high-frequency microwave bridge was also reported in Ref. (28).

The granite slab was ground flat along the top and two sides to within 250 microns. A box-like aluminum-frame structure was fabricated using 2 cm by 4 cm aluminum rails; 2 cm linen phenolic plates support the rails and wrap around the sides of the granite, providing directional stability while sliding the bridge assembly along the granite slab.

The granite slab is supported at the three points that were used during grinding. Support at these three points ensures that the slab remains flat. Each support consists of a 3.75 cm diameter brass-threaded sleeve that makes contact with the slab. Stainless steel threaded inserts are attached to vibration-damping swivel leveling mounts. Each mount provides isolation from floor vibrations transmitted to the large mass of the granite slab (about 2 metric tons). The supports are designed for this weight and are stabilized by a 10 cm by 10 cm fir wood subframe on large castors, allowing movement with respect to the magnet. The slab is laser-aligned to the magnet bore. It is raised to the proper level at the three support points, and the wheels are raised. The vibration damping mounts rest on double brass plates that slide sideways by an adjustable screw, allowing precise alignment while raised.

The in-house designed gas-bearing system consists of four 5 cm × 23 cm × 30 cm granite plates, one at each corner of the sliding table. A bolt at the center of each plate allows the height to be adjusted. Each granite plate was ground flat, and a pattern of air distribution grooves was machined into this surface. Dry nitrogen gas is fed into each pattern of grooves, which forms a cushion above the smooth granite slab.

The sliding table that rests on the gas bearings is 2 cm-thick plastic-coated fiberboard. The sides of the granite slab align the structure parallel to the magnet bore. Nylon-tipped adjustable screws provide a low-friction alignment guide, since little force is involved. With about 150 kg weight of the microwave assembly and table, vibration-free movement is obtained at a pressure of 15 psi. Tests show an estimated 450 kg of lift at 15 psi with approximate lift height of 0.1 mm.

Special attention has been paid to support of the waveguide probe that slides into the center of the magnet. The sliding table is precision drilled, which provides a mounting surface to which the probe is bolted. The waveguide passes through a fiberglass tube filled with expanded urethane foam to dampen vibrations and provide thermal isolation from the environment. A silicone rubber disc at the end of the probe makes a resilient contact with a smooth fiberglass tube inserted in the magnet bore. A water-cooled modulation coil system is installed between the tubes of a double concentric fiberglass-tube assembly in the magnet bore. The entire coil assembly is encapsulated in epoxy and machined to size. There is a slight press fit to the outer tube that stiffens the assembly. The outer tube is supported by round plates that compress an O-ring seal to give additional acoustic dampening to the tube support.

Figure C1.

Overall assembly of the W-band spectrometer