F-RAG: Generating Atomic Coordinates from RNA Graphs by Fragment Assembly

Abstract

Coarse-grained models represent attractive approaches to analyze and simulate RNA molecules, for example for structure prediction and design, as they simplify the RNA structure to reduce the conformational search space. Our structure prediction protocol RAGTOP (RNA-As-Graphs Topology Prediction) represents RNA structures as tree graphs, and samples graph topologies to produce candidate graphs. However, for a more detailed study and analysis, construction of atomic from coarse-grained models is required. Here we present our graph-based fragment assembly algorithm (F-RAG) to convert candidate 3D tree graph models, produced by RAGTOP into atomic structures. We use our related RAG-3D utilities to partition graphs into subgraphs and search for structurally similar atomic fragments in a dataset of RNA 3D structures. The fragments are edited and superimposed using common residues, full atomic models are scored using RAGTOP’s knowledge based potential, and geometries of top scoring models is optimized. To evaluate our models, we assess all-atom RMSDs and Interaction Network Fidelity (a measure of residue interactions) with respect to experimentally solved structures, and compare our results to other fragment assembly programs. For a set of 50 RNA structures, we obtain atomic models with reasonable geometries and interactions, particularly good for RNAs containing junctions. Additional improvements to our protocol and databases are outlined. These results provide a good foundation for further work on RNA structure prediction and design applications.

Graphical abstract

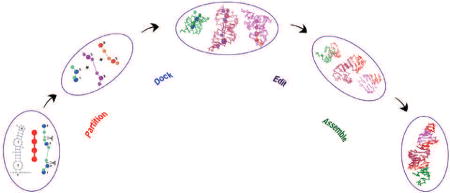
Introduction

Ribonucleic acid (RNA) molecules play a myriad of crucial and essential roles in cellular biology, from their traditional roles as mRNAs, tRNAs, and rRNAs [1] to catalysis as ribozymes [2], and gene regulation as miRNAs and siRNAs [3, 4]. Single-stranded RNA chains can adopt complex three-dimensional (3D) structures composed of single and double stranded regions that dictate their biological functions. Naturally, their structure-function relationships are of crucial importance to interpret their activities. Such information can be utilized for RNA design, with tremendous potential for therapeutic, industrial, and biomedical applications.

The availability of high-quality RNA 3D structures is a prerequisite for RNA structural studies and analysis. The process of RNA structure determination using experimental methods like X-ray crystallography, Nuclear Magnetic Resonance (NMR), and more recently cryo-EM, is challenging and laborious. In addition, a large percentage of available RNA structures are far from perfect in terms of structural validation criteria like steric-clashes, sugar pucker, and other geometry measures [5]. The study of RNA structure using complementary computational approaches is an exciting area of research that has the potential to greatly improve our understanding of the fundamental forces behind RNA structure-function relationships [6, 7, 8, 9, 10, 11, 12].

One effective approach to study RNA structure, folding, and dynamics is to use coarse-grained models to represent RNA structures [13]. Instead of working with the atomic representation of RNA molecules, the representation of the RNA structure is simplified to reduce the number of degrees of freedom. Most coarse-grained approaches model each residue in the RNA structure by one [14, 15], three [16, 17, 18, 19, 20, 21] or multiple beads [22, 23, 24, 25, 26, 27], followed by molecular dynamics (MD), energy minimization (EM), or Monte Carlo (MC) simulations. They may use knowledge-based (derived from known RNA structures) or force-field based potentials to score the candidate conformations. Employing coarse-grained approaches reduce the RNA conformational search space and makes the problem of sampling different topologies and conformations of the RNA structure more tractable.

However, the compactness of the RNA representation and reduced conformational search space also necessitates another step: generation of atomic models from the simplified candidate RNA structures. Fragment assembly is a common approach used in modeling, and is widely used for molecular systems, for example in Rosetta [28]. Specialized programs for RNA, like iFoldRNA [16, 17, 18], SimRNA [22, 23], HiRe-RNA [26, 27], and the method by Ren and coworkers [24, 25] derive atomic models residue by residue by using the coarse-grained beads to map atomic units of individual nucleotides, followed by energy minimization. Vfold3D [20, 21] uses sequence and secondary (2D) structure information to build a coarse-grained model of the RNA molecule from fragments of helices and loops from a template library, and then converts this coarse-grained model into an atomic model residue by residue as above. C2A [29] builds atomic models using fragments of single and double stranded 2D structure regions from an RNA 3D reference structure database. This database contains fragments in both coarse-grained and atomic formats; fragments are selected from this database based on structural similarity to the given RNA candidate (in coarsegrained form), and the energy of the assembled fragments is minimized.

Apart from the above coarse-grained methods, other fragment assembly based approaches also build RNA 3D structure from sequence and/or 2D structure. FARNA/FARFAR [30, 31] uses MC simulations and knowledge-based energy functions to assemble 3-residue fragments into atomic models. Program 3dRNA [32] builds atomic models from fragments of smallest 2D structure elements (base pairs, hairpins, internal loops, junctions, and pseudoknots) derived from the SCOR and RNA junction database, followed by energy minimization. The MC-fold/MC-sym pipeline [33, 34] identifies nucleotide cyclic motifs (NCM) for a given RNA molecule and builds atomic models by assembling the NCM fragments from a dataset of RNA structures. RNAComposer [35, 36] divides the given RNA sequence and 2D structure into helices, hairpins, internal loops, and junctions and uses best matching fragments from the RNA Frabase dictionary to build the atomic model.

Our coarse-grained approach relies on the RNA-As-Graphs (RAG) library that represents RNA 2D structures as planar, undirected tree graphs [37]. Unpaired regions or loops in the RNA structure correspond to vertices of the tree graph, and helical regions connecting the loops correspond to edges of the graph. Graphs for RNA were introduced in the 1970s by Waterman [38], Nussinov [39, 40], Shapiro [41], and others; see recent reviews [8, 42, 43]. This simplified representation of the RNA structure reduces the conformational search space drastically, and allows us to study RNA structure using methods and algorithms from graph theory [11]. We have successfully applied RAG to predict RNA junction stacking and orientations using a data-mining, random forest approach [44, 45, 46], simulate in vitro selection of RNA molecules [47, 48], and partition graphs to define recurrent RNA motifs [49].

Recently, we have developed a hierarchical graph sampling methodology, called RAGTOP (RNA-As-Graphs Topology Prediction), to predict RNA 3D graph topologies corresponding to a given RNA 2D structure [50]. Our Junction-Explorer data mining program [44, 45] is first used to determine the junction orientation (co-axial stacking and family) of the candidate sequence and 2D structure, as classified in our junction analysis work. The resulting 2D RNA tree-graph is converted to a 3D graph, followed by Monte Carlo/Simulated Annealing (MC/SA) sampling of 3D graph topologies using a knowledge-based scoring function. This function includes bend and twist terms for internal loops as well as a radius of gyration term. The former terms for internal loop geometry were recently enhanced to distinguish internal loops that contain kink-turn motifs [51]. The candidate graphs selected after the MC/SA simulations show good performance with respect to other RNA prediction algorithms in predicting RNA structure topologies. RAGTOP has also been successfully applied to predict tertiary structures of riboswitches [52].

In this paper, we present the next step in the RAGTOP methodology called F-RAG (Fragment-Assembly for RNA-As-Graphs): automatic generation of atomic coordinates of RNA structures from coarse-grained candidate graph topologies. This task is performed using fragment assembly, where the candidate graph is partitioned into subgraphs, and the best matching atomic fragments are assembled using common graph vertices. This assembly is made possible by our program RAG-3D that employs tree graph partitioning techniques [49], and contains a search tool (also available as a web-server) for finding similar 3D structural fragments for a given RNA molecule or motif from a database of RNA structures and substructures [53]. In our fragment assembly, the atomic models are edited to match sequences and lengths of the candidate graphs. The generated models are then scored according to the knowledge-based potential, and the geometries of the top 20 models are optimized.

Here, we apply F-RAG to build 3D structures for 50 RNA 2D structures, ranging from 17 to 111 nucleotides. These RNAs contain different numbers and types of hairpins, internal loops, and junction motifs. We assess our atomic models with respect to the experimentally determined structures by calculating the all-atom Root Mean Square Deviations (RMSD) and Interaction Network Fidelity (INF) [54]. The latter is a measure of how accurately the computed 3D structure captures various canonical and non-canonical interactions present in the reference structure. We also compare our results to the Vfold3D program that combines coarse-grained modeling with fragment assembly, and the 3dRNA program that uses fragment assembly to combine atomic fragments of elemental 2D structural motifs. For this RNA test set, F-RAG produces best atomic models (chosen from the top 20 scoring models) with RMSDs less than 10 Å for 46 out of the 50 structures. On average, our models have better geometries and less steric-clashes compared to structures generated using Vfold3D and 3dRNA. These results show good potential for our RAG approach for the study and analysis of RNA structures, especially for junction structures due to good initial junction orientation prediction using JunctionExplorer [44, 45]. Further improvements can be envisioned by additional structure refinement to deal with chain breaks, improving our RNA structure databases, and adding missing residues to 5′ and 3′ ends and to junctions motifs.

Results

Computational experiments

To assess the results of F-RAG, we generated 3D atomic models for 50 RNA structures, with 17 to 111 nucleotides, and compared our results to the experimentally solved structures, i.e., the reference structures obtained from the PDB. Our representative RNA set includes structures with hairpin loops, internal loops, junctions and dangling ends of various sizes. For RNA structures solved using Nuclear Magnetic Resonance (NMR), the first model was considered as the reference structure. Table 1 provides the list of 50 RNA structures, along with a description of their structural complexity.

Table 1.

List of 50 RNA PDB files whose 3D structures were generated in this paper

PDB	Residues	Molecule	Structure
2M4W	17	HEV Genome Bulge	Hairpin, Internal Loop
2MEQ	19	Helix 60 of 23S rRNA	Hairpin
2M5U	22	P4 hairpin of CPEB3 ribozyme	Hairpin
2N7X	23	miRNA 20bd element	Hairpin, Internal Loop
1RLG	25	C/D box sRNP	Hairpin, Internal Loop
2MIS	26	VS Ribozyme	Hairpin, Internal Loop
2N0J	27	Neomycin riboswitch	Hairpin, Internal Loop
2NCI	28	Metal binding loop	Hairpin, Internal Loop
3SIU	28	U4atac snRNA	Hairpin, Internal Loop
1OOA	29	Protein binding RNA Aptamer	Hairpin, Internal Loop
2IPY	30	H IRE RNA	Hairpin, Internal Loop
2OZB	33	U4 snRNA	Hairpin, Internal Loop
2XEB	33	U4 snRNA	Hairpin, Internal Loop
1MJI	34	5S rRNA fragment	Hairpin, Internal Loop
2M57	35	Domain 5 of group II intron	Hairpin, Internal Loops
4PCJ	35	CUG repeats	Hairpin, Internal Loop
2HW8	36	mRNA bound to L1 protein	Hairpin, Internal Loop
2N6S	36	CssA mRNA thermometer	Hairpin
5KQE	36	Telomerase RNA P2ab	Hairpin, Internal Loop
1I6U	37	16S rRNA fragment	Hairpin, Internal Loop
1F1T	38	Malachite green aptamer	Hairpin, Internal Loops
1ZHO	38	mRNA with L1 protein	Hairpin, Internal Loop
2MXL	39	Hairpin from Influenza A	Hairpin, Internal Loop
2N6T	42	CssA mRNA thermometer top	Hairpin, Internal Loops
2N6X	43	CssA mRNA thermometer middle	Hairpin, Internal Loop
5BTM	43	AUUCU repeats	Hairpin, Internal Loops
1S03	47	spc Operon mRNA	Hairpin, Internal Loop
1XJR	47	s2M element of SARS virus	Hairpin, Internal Loops
2MTJ	47	Junction from VS ribozyme	Hairpins, 3-way junction
2VPL	48	mRNA with L1 protein	Hairpin, Internal Loop
1U63	49	mRNA with L1 protein	Hairpin, Internal Loop
2PXB	49	SRP from E.coli	Hairpin, Internal Loops
2N4L	53	HIV-1 Intron Splicing Silencer	Hairpin, Internal Loops
2HGH	55	55-mer 5S rRNA fragment	Hairpins, Internal Loop, 3-way junction
1DK1	57	rRNA fragment bound to S15	Hairpins, Internal Loop, 3-way junction
1MMS	58	58-mer fragment from 23S rRNA	Hairpins, Internal Loop, 3-way junction
1Y39	58	58-mer fragment from 23S rRNA	Hairpins, Internal Loop, 3-way junction
2N3Q	62	Three-way junction from VS ribozyme	Hairpin, Internal Loops, 3-way junction
2MQT	68	U5-PSB domain of leukemia virus	Hairpin, Internal Loops
2N6W	68	CssA thermometer	Hairpin, Internal Loops
1KXK	70	Domain of ai5g group II intron	Hairpin, Internal Loops
2OIU	71	L1 ribozyme RNA Ligase	Hairpins, Internal Loop, 3-way junction
4LCK	75	tRNA-Gly	Hairpins, 4-way junction
1P5O	77	HCV IRES Domain II	Hairpin, Internal Loops
3D2G	77	TPP Specific riboswitch	Hairpins, Internal Loops, 3-way junction
2HOJ	79	thi-box riboswitch	Hairpins, Internal Loops, 3-way junction
2GDI	80	TPP riboswitch	Hairpins, Internal Loops, 3-way junction
2GIS	94	SAM-I riboswitch	Hairpins, Internal Loops, 4-way junction
1LNG	97	7S.S SRP RNA	Hairpins, Internal Loops, 3-way junction
2LKR	111	Yeast U2/U6 snRNA complex	Hairpins, Internal Loops, 3-way junction

We apply F-RAG to candidate graph models predicted by RAGTOP [50, 51]. RAGTOP uses the 2D structure as input (here determined by RNAView [55] using the reference structure). JunctionExplorer is then applied to predict the junction co-axial stacking and family. Graph sampling by MC/SA is performed for 50,000 steps (“random moves”, as recently optimized [51]). The lowest scoring graph is taken as the candidate graph (see the subsection titled “Junction prediction and graph-topology sampling” in Materials and Methods). This candidate graph is partitioned into subgraphs by RAG-3D, and the top 10 fragments for each subgraph are computed. For each candidate graph, we run RAG-3D both with and without the additional requirement on the atomic fragment to have the same loop types as the target graph (see the subsection titled “Graphpartitioning and RAG-3D search” in Materials and Methods). Next, F-RAG is performed separately for each combination of 1, 2 or 3 subgraphs assembled to form the complete graph, and atomic models are generated for each subgraph decomposition.

Starting from a candidate 3D tree graph predicted by RAGTOP, the computational time required by F-RAG scales with the number of associated subgraphs used in F-RAG. For 1 subgraph (generating a maximum of 10 atomic models), F-RAG requires 1–2 minutes. For 2 subgraphs (generating a maximum of 100 atomic models), F-RAG requires 5–7 minutes. For 3 subgraphs (generating a maximum of 1000 atomic models), F-RAG requires 20–30 minutes.

Among all the candidate models, we select all models with the highest number of residues, and sort them in increasing order based on scores using our knowledge-based RAGTOP potential described in [51]. The geometries of the 20 top models (lowest scores) are optimized using PHENIX [56] (version 1.10.1, with sugar-pucker specific geometry parameters).

The Root Mean Square Deviations (RMSDs) for all non-hydrogen atoms computed with respect to the reference structure for each of the top 20 models are calculated using PyMOL [57]. Base-pairing and base-stacking interactions are determined using MC-Annotate [58].

Besides RMSD, we also use other metrics for comparing RNA structures, as described by Parisian et. al. in [54], as also used in the RNA-Puzzles exercise [59, 60, 61]: Specificity (PPV), Sensitivity (STY), Interaction Network Fidelity (INF), and Deformation Index (DI). In brief, PPV is the percentage of base pairing and stacking interactions in the predicted atomic model that are found in the reference structure; STY is the percentage of interactions in the reference structure that are found in the predicted atomic model. These measures are calculated as PPV = |TP|/(|TP| + |FP|), and STY = |TP|/(|TP| + |FN|). |TP|, |FP|, and |FN| define the number of base pairing and stacking interactions present in: both the reference and the predicted structure (|TP|), predicted structure but absent in the reference structure (|FP|), reference structure but absent in the predicted structure (|FN|). INF combines PPV and STY to describe the interaction prediction accuracy of the atomic model ( $\text{INF}=\sqrt{\mathit{\text{PPV}}\ast \mathit{\text{STY}}}$). PPV, STY, and INF take values between 0 and 1, with a higher number indicating better prediction accuracy. DI combines the atomic (RMSD) and interaction prediction accuracy (DI = RMSD/INF), with smaller values indicating better prediction. The clashscore (calculated as the number of steric clashes per 1000 atoms [62, 63]), and bond-length and bond-angle outliers were calculated using PHENIX [56].

Comparison with reference structure

When using fragments from RAG-3D without the additional requirement of same type of loops, F-RAG generated atomic models for 49 of the 50 RNA structures (see Table S1 in Supplementary Information for the lowest RMSD and lowest DI atomic models). For the L1 ribozyme RNA ligase (PDB ID: 2OIU), none of the top atomic fragments from RAG-3D had the same type of dangling end loop as required by the target (3 strands and 2 adjacent helices), so they could not be used by F-RAG. However, when using fragments produced by RAG-3D with the additional requirement of same types of loops, our fragment assembly procedure generated atomic models for all 50 structures, with better RMSD and DI values on average. The atomic models with the lowest DI have an average RMSD of 4.46 Å, and an average DI of 5.90 Å, which is better than the average RMSD (4.60 Å) and DI (6.20 Å) values generated by the former run. Hence, we use the results from the second run for comparison.

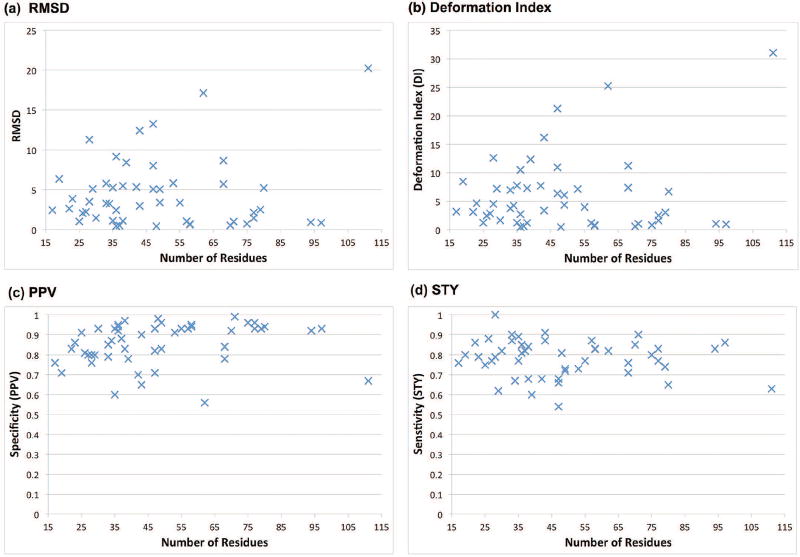
Figure 1 shows the RMSD, DI, and other metrics for the lowest DI (of the top 20) atomic model generated by F-RAG (see Table S2, Figures S2 and S3 in Supplementary Information for comparison metrics for the top scoring models). For 45 of the 50 structures, the lowest DI model has an RMSD of less than 10 Å. We also see that the metrics for structure comparison of atomic models with the reference structure do not depend on the total number of residues in the RNA molecule, but rather on the structural similarity between the fragment and the reference structure. For example, for the yeast U2/U6 snRNA complex (PDB ID: 2LKR), the RMSD is very high (20.26 Å) because the fragment used to generate the atomic model had 2 residues missing from one of the strands of the 3-way junction, and extra residues in the other two strands. Similarly, for the 3-way junction from the VS ribozyme (PDB ID: 2N3Q), the RMSD is high (17.13 Å) because the fragment used has 1 residue missing from the dangling end, and has extra residues in the junction strands. Moreover, most of the atomic models that have low RMSDs (between 0–4 Å) with respect to the reference structure use fragments from related RNA structures found by the RAG-3D search. This highlights RAG-3D’s ability to locate fragments containing similar submotifs as the target structure, using just 3D tree graphs. Table S3 in Supplementary Information illustrates the candidate graph and the lowest DI atomic model generated for 50 RNA structures by F-RAG.

Figure 1. Statistics for lowest DI models generated by F-RAG for 50 RNA structures.

(a) Number of residues vs. RMSD (in °A) (b) Number of residues vs. Deformation Index (in °A) (c) Number of residues vs. Specificity (PPV) (d) Number of residues vs. Sensitivity (STY). See the main text for definitions of these measures.

The average INF values for the lowest DI atomic models is 0.82, but the INF value is as low as 0.62 for some structures (see Figure S1 in Supplementary Information). This is is partly due to missed interactions present in the reference structure (indicated by low STY values). These missing interactions are both canonical and non-canonical in nature. Some of the missing interactions are single base pairs and interactions involving residues in the internal loop and bulges that are ignored in the 2D tree representation of the RNA 2D structure. Note that single base pairs are also ignored in the 3D tree graph. The best atomic model for 11 RNA structures with large chain breaks (> 5 Å distance between O3′ and P atoms of consecutive residues) are not resolved by optimizing the geometry.

Of the 50 structures, reference structures of 25 of them are also a part of the RAG-3D database, i.e., RAG-3D selects fragments from the reference structures as part of the top 10 fragments, that are then used as input to FRAG. Table 2 lists the best RMSD and DI values when we remove such models from consideration, re-calculate the top 20 atomic models, and then select the best models with lowest RMSD and DI values. We see that the lowest DI values change for 11 out of the 25 structures, with a significant change (> 2 Å) for 6 structures.

Table 2.

Lowest RMSD and DI models for 25 structures with and without models generated using fragments from the reference structures.

PDB	Lowest RMSD Model		Lowest DI Model
	With reference fragments	Without reference fragments	With reference fragments	Without reference fragments
1RLG	1.034	9.267	1.25	16.14
3SIU	3.480	3.480	4.55	4.55
1OOA	5.005	5.005	7.22	7.22
2OZB	3.291	3.291	3.76	3.76
1MJI	3.246	3.246	4.27	4.27
2HW8	0.450	0.450	0.50	0.50
1I6U	0.532	2.137	0.63	2.59
1F1T	5.060	5.060	7.30	7.30
1ZHO	1.089	1.315	1.21	1.46
1S03	5.088	5.186	6.38	6.66
1XJR	8.025	8.025	10.97	10.97
2VPL	0.428	10.427	0.48	12.55
1U63	3.408	3.408	4.37	4.37
2PXB	5.065	5.065	6.10	6.10
1DK1	1.008	1.060	1.18	1.18
1MMS	0.647	0.647	0.73	0.73
1Y39	0.717	1.018	0.81	1.15
1KXK	0.544	5.759	0.62	7.65
2OIU	1.004	17.768	1.06	23.20
4LCK	0.729	22.498	0.83	30.54
3D2G	1.460	1.460	1.64	1.64
2HOJ	2.504	2.504	3.03	3.03
2GDI	4.976	4.976	6.71	6.71
2GIS	0.919	0.947	1.05	1.07
1LNG	0.858	14.362	0.96	19.43

The bold values indicate a change in the lowest RMSD or DI when models using fragments from the reference structure are removed.

Comparison with Vfold3D and 3dRNA

We also compare our generated atomic models to two other RNA 3D structure prediction programs, Vfold3D [20, 21] and 3dRNA [32]. Vfold3D uses sequence and 2D structure information to build coarse-grained models of RNAs from fragments of helices and loops from a template library, and then converts this coarse-grained model into an atomic model, one residue at a time, using coarse-grained beads to map to atomic models of individual residues. 3dRNA builds atomic models from fragments of small 2D structural elements (base pairs, hairpins, internal loops, junctions, and pseudoknots) derived from SCOR and RNA junction databases, followed by energy minimization. We provide the same sequence and 2D structure information to Vfold3D and the 3dRNA server as to RAGTOP and F-RAG. We ran the Vfold3D program using default parameters, and 3dRNA with fragment assembly and optimization. All structures generated by the Vfold3D webserver were considered, and the models with the lowest RMSD and DI were selected for comparison. Vfold3D generated between 1 and 50 structures for each RNA. The 3dRNA webserver generates 5 structures by default, and the models with the lowest RMSD and DI were selected for comparison.

Table 3 lists the best RMSD and DI atomic models generated by the three fragment assemblies for all 50 RNA structures. Out of 50 structures, F-RAG and 3dRNA generated atomic models for all 50 structures, whereas Vfold3D generated atomic models for 44 structures. The six structures that Vfold3D fails to generate atomic models are: 3-way junction from the VS ribozyme (PDB ID: 2MTJ), L1 ribozyme RNA ligase (PDB ID: 2OIU) with a dangling end with 3 strands and 2 adjacent helices, U4 snRNA (PDB ID: 2XEB) with one residue hairpin, a 3-way junction from VS ribozyme (PDB ID: 2N3Q), SAM-I riboswitch (PDB ID: 2GIS) with a 4-way junction, and yeast U2/U6 snRNA complex (PDB ID: 2LKR). For the 44 common structures, F-RAG generates the lowest DI atomic model for 25 structures, Vfold3D for 10 structures, and 3dRNA for 9 structures. For the 6 structures for which Vfold3D does not generate atomic models, both F-RAG and 3dRNA generate the lowest DI atomic model for 3 structures each. Overall, F-RAG generated the atomic model with lower DI values for a larger number of structures (28 structures) than Vfold3D (10 structures) and 3dRNA (12 structures).

Table 3.

Comparison of lowest RMSD and DI models generated using F-RAG, Vfold3D, and 3dRNA.

PDB	Lowest RMSD Model			Lowest DI Model			PDB	Lowest RMSD Model			Lowest DI Model
	F-RAG	Vfold3D	3dRNA	F-RAG	Vfold3D	3dRNA		F-RAG	Vfold3D	3dRNA	F-RAG	Vfold3D	3dRNA
2M4W	2.439	3.957	2.16	3.19	4.86	3.45	5BTM	2.906	4.932	2.303	3.37	5.18	2.63
2MEQ	6.367	7.319	0	8.49	9.71	0	1S03	5.088	3.356	5.911	6.38	3.98	7.86
2M5U	2.635	3.078	0	3.12	3.61	0	1XJR	8.025	5.442	9.216	10.97	6.61	14.23
2N7X	3.588	4.94	5.106	4.68	6.29	5.96	2MTJ	13.255	N/A	2.288	21.27	N/A	2.88
1RLG	1.034	1.544	2.637	1.25	1.7	3.76	2VPL	0.428	4.069	1.766	0.48	4.39	2.1
2MIS	2.087	2.311	1.392	2.46	3	1.53	1U63	3.408	4.295	4.119	4.37	4.93	5.44
2N0J	2.170	1.845	3.889	2.86	2.13	4.68	2PXB	5.065	1.728	1.145	6.10	1.85	1.2
2NCI	9.916	8.229	11.815	12.62	10.82	15.25	2N4L	5.843	3.801	10.898	7.15	4.06	13.08
3SIU	3.480	1.554	1.832	4.55	1.69	1.94	2HGH	3.375	4.045	5.079	3.99	4.38	5.55
1OOA	5.005	5.228	5.455	7.22	6.73	7.16	1DK1	1.008	2.317	3.025	1.18	2.51	3.43
2IPY	1.461	2.353	3.933	1.67	2.64	4.48	1MMS	0.647	2.145	2.746	0.73	2.52	3.82
2OZB	3.291	4.059	6.178	3.76	4.54	8.14	1Y39	0.717	2.733	8.183	0.81	3.2	13.5
2XEB	5.798	N/A	3.456	6.97	N/A	4.07	2N3Q	17.006	N/A	4.528	25.25	N/A	6.56
1MJI	3.246	2.201	4.332	4.27	2.65	5.63	2MQT	8.665	6.129	4.311	11.24	6.93	4.83
2M57	5.169	1.949	2.057	7.75	2.17	2.45	2N6W	5.722	5.86	8.988	7.40	7.45	12.06
4PCJ	1.116	4.514	2.701	1.23	5.47	3.1	1KXK	0.544	5.116	6.561	0.62	5.57	8.46
2HW8	0.450	1.627	1.639	0.50	1.75	1.68	2OIU	1.004	N/A	12.472	1.06	N/A	15.65
2N6S	2.436	3.024	2.685	2.75	3.46	3.16	4LCK	0.729	2.772	7.27	0.83	3.2	9.74
5KQE	8.803	7.793	5.503	10.51	8.97	7.17	1P5O	2.148	4.095	7.353	2.53	4.99	9.96
1I6U	0.532	1.458	2.65	0.63	1.7	3.15	3D2G	1.460	3.916	3.538	1.64	4.36	5.08
1F1T	5.060	6.503	6.484	7.30	9.12	11.4	2HOJ	2.504	17.084	4.703	3.03	20.55	6.45
1ZHO	1.089	1.757	2.033	1.21	1.94	2.16	2GDI	4.976	16.959	3.887	6.71	21.66	4.57
2MXL	8.419	4.116	3.602	12.37	4.72	4.52	2GIS	0.919	N/A	4.224	1.05	N/A	5.17
2N6T	5.351	3.892	6.51	7.72	5.6	8.97	1LNG	0.858	4.86	6.966	0.96	5.82	8.71
2N6X	12.312	14.652	12.411	16.20	20.16	16.54	2LKR	20.262	N/A	19.553	31.07	N/A	32.65

The bold numbers indicate the program that had the lowest value of RMSD or DI. N/A entry in the Vfold3D column indicates that it was not able to generate an atomic model for that structure.

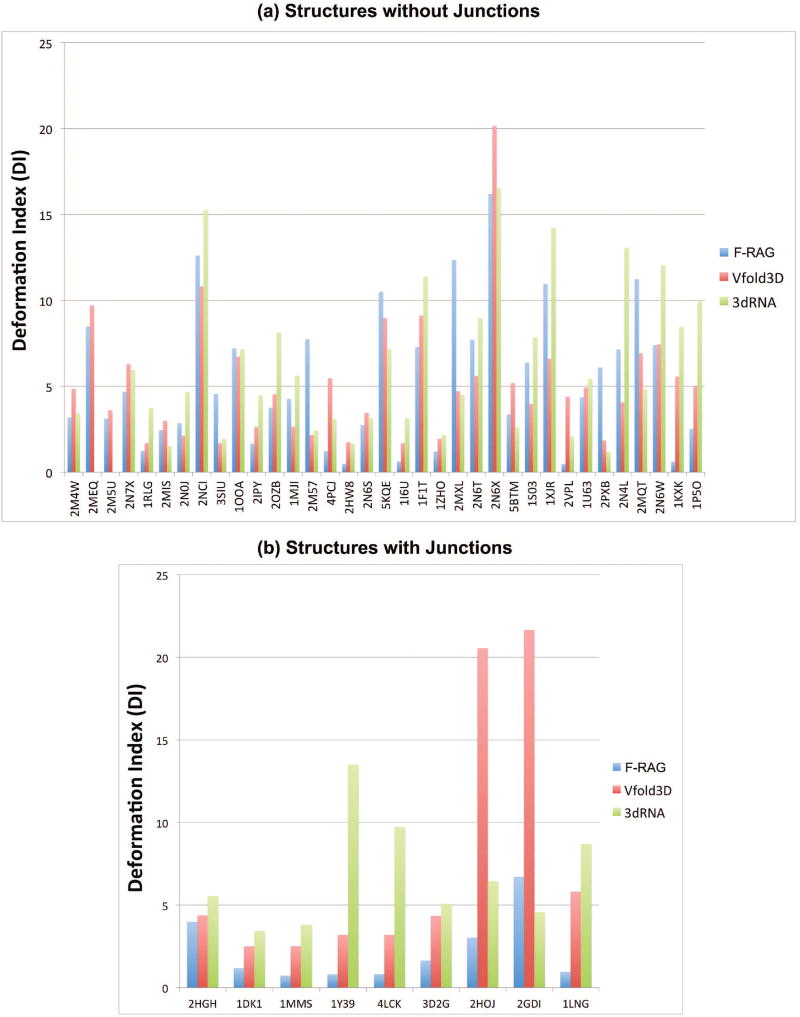
Figure 2 compares the lowest DI atomic models generated by all three programs for the 44 RNA structures generated by all. Recall that DI combines RMSD and interaction measures. Figure 2a compares RNA structures with only internal loops and hairpins, and Figure 2b compares RNA structures with junctions. For structures with only internal loops and hairpins, the lowest DI F-RAG and Vfold3D atomic models have DI values within 1.5 Å of each other for 14 of 35 RNAs; Vfold3D performs better than F-RAG (> 1.5 Å) for 12 structures, and F-RAG performs better than Vfold3D for 9 structures. Comparing F-RAG to 3dRNA, the lowest DI F-RAG and 3dRNA atomic models have DI values within 1.5 Å of each other for 13 of 35 RNAs; 3dRNA performs better than F-RAG for 8 structures, and F-RAG performs better than 3dRNA for 14 structures. However, F-RAG performs significantly better than other programs for RNAs with junctions, with F-RAG generating atomic models with lower DI values for 9 structures compared to Vfold3D, and for 8 structures compared to 3dRNA.

Figure 2. Comparison of lowest DI models generated for 44 RNA structures by F-RAG, Vfold3D, and 3dRNA.

(a) Structures with hairpins and internal loops (b) Structures with hairpins, internal loops, and junctions.

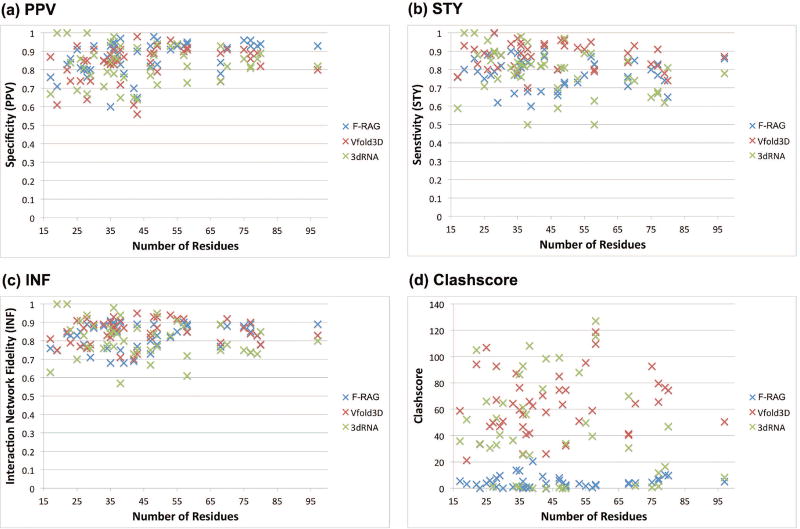
Figure 3 compares the PPV, STY (both are interaction measures, with higher values better), and clashscore values for the atomic models with lowest DI values for the 44 structures generated by all the three fragment assembly approaches. On average, all three programs have similar PPV values, but F-RAG and 3dRNA have lower STY values (0.79) as compared to Vfold3D (0.87), indicating more missed base-pairing and stacking interactions. However, atomic models generated using F-RAG have significantly less steric clashes as compared to atomic models generated using Vfold3D and 3dRNA. Most of the steric clashes in the atomic models generated by Vfold3D and 3dRNA come from bond-length outliers. That is, two atoms of a covalent bond are far enough that their vdW spheres overlap is considered a steric clash. Thus, our models have better covalent bond geometry, likely due to optimizing the geometry with PHENIX.

Figure 3. Comparison metrics for lowest DI models generated for 44 RNA structures by F-RAG, Vfold3D, and 3dRNA.

(a) Number of residues vs. Specificity (PPV). (b) Number of residues vs. Sensitivity (STY). (c) Number of residues vs. Interaction Network Fidelity (INF) (d) Number of residues vs. Clashscore. See the main text for definition of these measures.

Discussion

In this work we have presented our RNA graph-based procedure for generating atomic models from RAGTOP’s predicted coarse-grained 3D graph candidates using fragment assembly. The fragment assembly relies on available tools, such as RAG-3D’s search for common motifs and RAG-3D’s partitioning into subgraphs. Our F-RAG procedure works well compared to other available tools, especially for RNAs with junctions. Its limitations include a dependence on the input 2D structure and treatment of pseudoknots, which are not represented in tree graphs. However, pseudoknots could be part of the atomic fragments of the experimental subgraph substructures in the RAG-3D database and hence our final atomic model. Furthermore, the RAG-3D database may not contain atomic fragments to match every subgraph for any given 2D structure. However, we have not encountered this problem for the 152 different subgraph decompositions used for 50 RNA structures in this paper.

To improve performance of F-RAG further, improvements can be considered to our scoring functions, energy minimization, and fragment library (greater variety of loop types and number of residues). We also could improve residue number editing for junctions and dangling ends. For example, the lowest DI atomic model generated for a 3-way junction structure from VS ribozyme (PDB ID: 2N3Q) has 1 residue missing from the dangling end; the atomic models generated for another 3-way junction from the VS ribozyme (PDB ID: 2MTJ) and for the yeast U2/U6 snRNA (PDB ID: 2LKR) have 3 and 2 missing residues as compared to the reference structure respectively. None of the top fragments for these structures had the same number of residues as the target structure. Replacing the junction or the dangling end motifs with a new motif from the non-redundant dataset that has the required number of residues is not yet implemented in F-RAG. This is more difficult for junctions, because in addition to the number of residues, we have to preserve the co-axial stacking and family of the target junction. The combination of all three requirements makes junction motif fitting more restrictive. Implementing the ability to fill in the missing residues one at a time (rather than replacing the entire loop) is a better solution and will likely lead to better results for structures with various loop types. In addition, we need to implement better ways to remove extra residues from the junction strands so that they do not leave chain breaks, which is also true for the above three examples.

On average, the DI and RMSDs for atomic models generated by F-RAG are better when using fragments selected by RAG-3D with the additional requirement for the atomic fragment containing the same number and types of loops as the target subgraph. However, there are a few structures where this is not the case. For example, for the structure of a hairpin from the influenza A virus (PDB ID: 2MXL), the lowest RMSD increases from 5.25 Å to 8.42 Å when using fragments with this additional requirement. Thus, less similar fragments, with the additional ability to substitute loop types during the fragment assembly procedure can lead to models with better scores. As of now, the RAG-3D fragments are treated as input to F-RAG. Implementation of a feedback mechanism between the RAG-3D search and F-RAG should lead to better integration between the two components so that we do not miss fragments that can potentially lead to better results.

Improvements to our MC/SA procedure and knowledge-based scoring potential can also be envisioned. The MC/SA simulation currently samples only the bend and torsion angles at internal loop vertices. Addition of junction flexibility (while preserving the co-axial stacking and family) during the MC/SA simulation and terms to score different junction topologies will likely lead to better graph RMSDs and better atomic fragments. Adding more structural diversity to the non-redundant dataset of hairpins and internal loops, and using only high-quality atomic fragments and a non-redundant RAG-3D database could lead to better atomic models, and eliminate the potential bias of RAG-3D search to return structurally similar fragments. However, the final model may contain chain breaks, and thus further refinement may be needed before subjecting the atomic models to energy minimization or molecular dynamics simulations by standard biomolecular programs. Minimizing the energy of the atomic models may lead to better STY values and can resolve chain breaks in the atomic model that are too large to be fixed by optimizing only the geometry.

Conclusion

We have described an efficient fragment assembly approach, F-RAG, to generate atomic models from coarse-grained 3D tree graph candidates generated by our program RAGTOP. F-RAG relies on our RAG-3D graph partitioning and search utilities to obtain structurally similar atomic fragments. The combined atomic models are scored by our statistical scoring function, and the covalent bond geometry is optimized using PHENIX. Overall, F-RAG works well when compared to other programs, especially for RNAs with junctions due to our initial application of JunctionExplorer to predict the relevant coaxial stacking and junction family [44]. The favorable performance on junctions combined with the modularity of our programs provide good foundations for further work on RNA structure prediction as well as design applications.

Materials and Methods

This section provides the definitions and background information on the RNA-As-Graphs (RAG) resource, including details of our hierarchical approach for sampling RNA 3D graph topologies (RAGTOP), graph-partitioning, RAG-3D search tool and database, template loop library created from the non-redundant database obtained from NDB, and our F-RAG procedure.

RAG 2D and 3D tree graphs

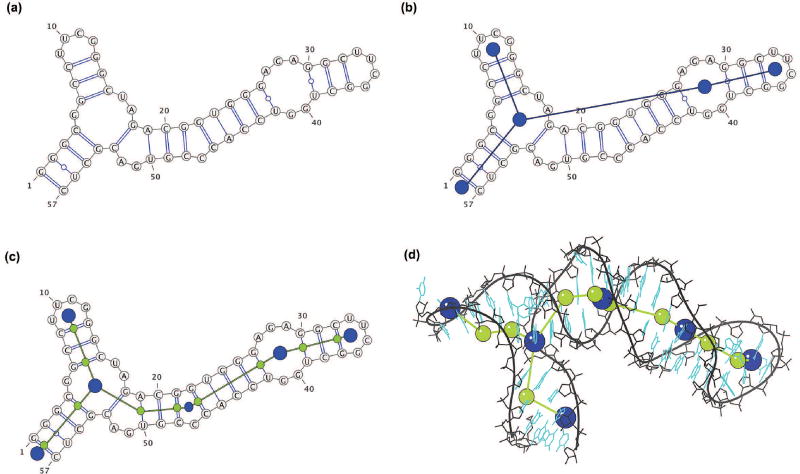
RNA bases form hydrogen bonds with each other upon folding of the ribonucleotide chain. The canonical base pairs are GC, AU, and GU wobble. Base pairs stack on one another to form stems or helices that are interrupted by single-stranded regions of unpaired bases called loops. The connectivity of stems and helices is called the secondary structure (2D) of the RNA molecule (Figure 4a). The 2D structure can be represented in the form of an undirected tree graph G = (V,E) [64]. The vertices V correspond to different loops: hairpin loops, internal loops and bulges (with at least two nucleotides in either strand), junctions, and dangling ends. A dangling end refers to an exterior loop that includes unpaired residues at the 5′ and the 3′ ends of the RNA sequence. The edges E correspond to helical stems, with at least two base pairs. Figure 4b shows a 2D tree graph with 5 vertices for a 57-residue fragment of rRNA (PDB ID: 1DK1). Our RAG resource enumerates and catalogs all possible graph topologies for graphs up to 13 vertices (≈ 260 nucleotides) [65], and each unique 2D graph topology is given a RAG ID by order of the Laplacian second eigenvalue [66]. In addition, the graphs associated with known RNA structures are classified as “existing RNA”. The remaining, hypothetical graphs are classified as “RNA-like”, or “non RNA-like” by clustering techniques [67].

Figure 4. 2D and 3D tree graphs for a fragment of ribosomal RNA (PDB ID: 1DK1).

(a) Secondary structure. (b) Corresponding 2D tree graph topology. (c) 3D tree graph constructed from the 2D tree graph by adding extra vertices for internal loop with one nucleotide (smaller blue vertex) and helical ends (green vertices) (d) 3D tree graph corresponding to the experimentally solved tertiary structure.

To weigh the graphs by their residue content and incorporate additional features, we convert the 2D tree graph into a 3D tree graph with additional vertices and edges (Figure 4c). Two vertices are added to represent the 5′ and 3′ ends for each helix, along with vertices for internal loops and bulges that contain less than two nucleotides in either strand. Isolated single base pairs are ignored. The vertex set V now consists of vertices representing loop and helical ends. The edges of the graph now connect the two vertices representing each helix, or the loop vertices to the proximal end helical vertices. The lengths of each edge are scaled by the number of residues in the corresponding helices and loops [50]. (Note that while the initial 3D graph is in 2D space, the MC sampling moves transform the tree graph into 3D space). An atomic RNA 3D structure can also be represented using a 3D tree graph (Figure 4d), by assigning 3D coordinates to the 3D graph vertices using the coordinates of the C1′ atom, the C6 atom for pyrimidine residues, and the C8 atom for purine residues as specified in [50].

Junction prediction and graph-topology sampling

The co-axial stacking and family for helical arrangements for RNA junctions are predicted using data mining tools by JunctionExplorer [44] and modeled as graphs by RNAJAG [45]. The JunctionExplorer algorithm consists of training decision trees of a random forest procedure [44] on 3-way and 4-way junction data derived from known RNA structures. The decision criteria are based on the number of residues in the junction strands, adenine content, and free energy of the proximal base pairs. JunctionExplorer classifies a 3-way junction into one of three families [68], and a 4-way junction into one of nine families [69].

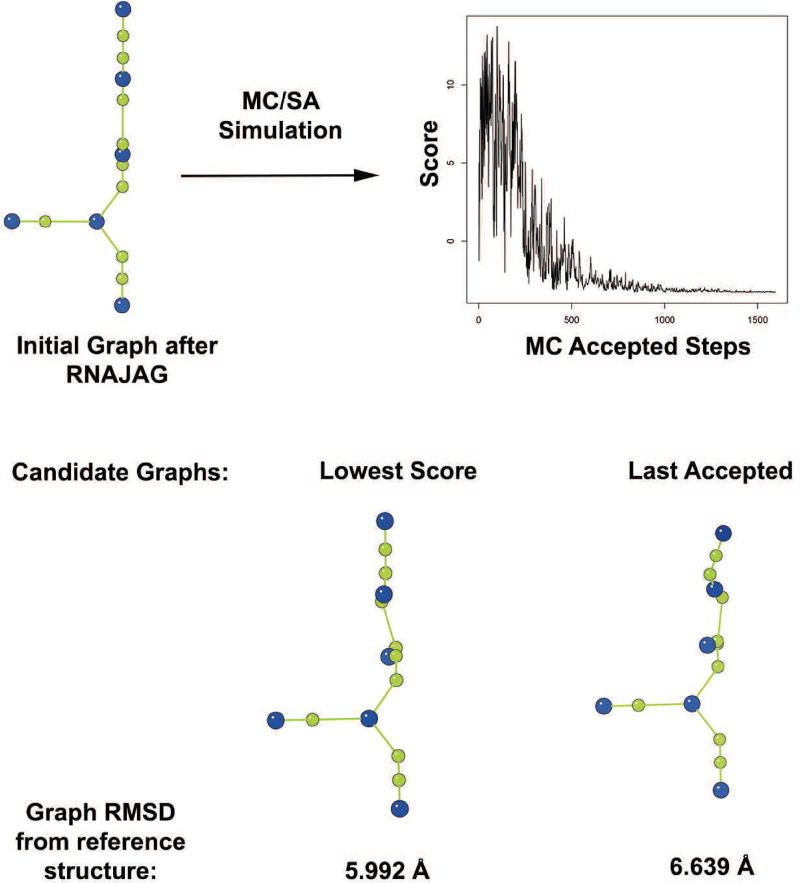
The next step in the RAGTOP hierarchical approach is the sampling and selection of candidate graph topologies that will serve as a target for atomic coordinates generation [50]. Monte Carlo/Simulated Annealing (MC/SA) sampling is performed at flexible internal loop vertices of the 3D tree graph. For each move, an internal loop and one of its adjacent helices is randomly selected for rotation along a randomly selected axis (x, y, or z). For local or restricted moves, the angle range is reduced gradually from 360° to 10°. For random moves, the range of angle is always full (i.e., 360°). The SA protocol involves cooling the ‘system temperature’ by the effective term T_i = c/log₂(1 + i/s), where c = 1/(20 * log₂(10)), i is the iteration number, and s is the total number of MC moves specified a priori. The junction orientation is kept fixed during the MC/SA simulation to preserve the co-axial stacking and the junction family predicted by JunctionExplorer. All sampled graph topologies are scored by a knowledge-based scoring function derived from known RNA structures. Terms include bend and twist potentials of helices around internal loops, and radius of gyration measurements. We have recently enhanced our scoring potentials by distinguishing internal loops that contain kink-turns, by identifying kink-turn sequence patterns [51]. Following the MC/SA sampling, candidate graphs are selected from the accepted graphs as either the graph with the lowest score or the last accepted graph. Figure 5 shows the candidate graphs (lowest scored and last accepted graph using the random moves SA protocol) selected after the MC/SA protocol on a fragment of the ribosomal RNA (PDB ID: 1DK1).

Figure 5. Results of the MC/SA simulation on a fragment of ribosomal RNA (PDB ID: 1DK1).

The initial graph constructed after junction family and stacking prediction is subjected to MC/SA simulation. The graph shows convergence of the MC/SA simulations. The two potential candidate graphs are shown, along with their graph RMSDs from the 3D tree graph of the reference crystal structure.

Graph partitioning and RAG-3D search

Representing RNA structures as graphs allows us to use graph-theory algorithms to partition RNA structures. The RNA 2D and 3D graphs can be partitioned into subgraphs to study submotifs in RNA structures. The Laplacian spectrum of the 2D graph of an RNA structure can be used to represent RNA graph topology, and graph-partitioning algorithms use the eigenvector associated with the second smallest eigenvalue of the Laplacian matrix to partition the graph into subgraphs [49]. We have found the gap-cut method (described in [49]) to be most effective in partitioning the graph into topologically distinct subgraphs. By design, we do not modify the junctions and the neighboring loops.

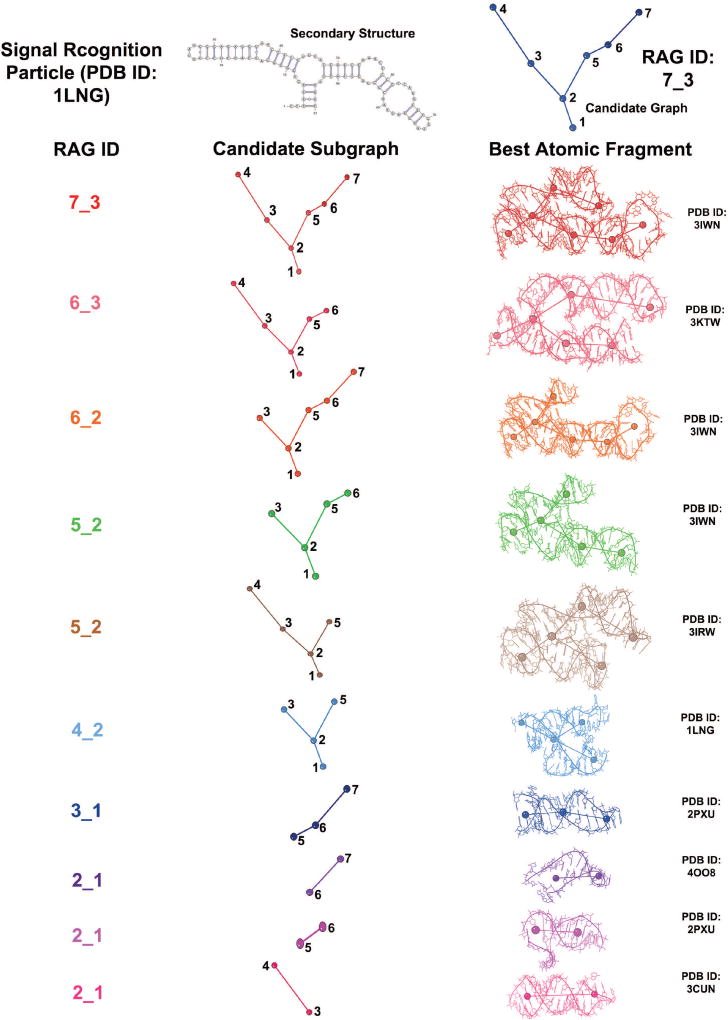
Graph partitioning is used in our context of fragment assembly. The RAG-3D database [53] is a set of all substructures (with associated graph and atomic fragments) for 1500 representative RNA structures (obtained from the PDB as of March 2014). It consists of 7169 graph and atomic fragments corresponding to 51 different RAG topologies. The RAG-3D database and search tool can be used to search for similar substructures of any given RNA [53]. A 3D graph is constructed for the query RNA, and all its subgraphs are aligned with every 3D graph fragment in the RAG-3D database with the same RAG ID. The resulting graph RMSD is measured between the query subgraph and the graph fragment in the database. For each query subgraph, the RAG-3D search provides ten graph fragments with corresponding atomic fragments in order of increasing graph RMSDs. In this paper, the query to the RAG-3D search is the candidate 3D tree graph obtained by RAGTOP. When searching for matching fragments, RAG-3D as reported previously [53] takes into account the graph topology and the graph RMSD, but not the loop type and number of strands in the loops. Thus, for example, a hairpin loop vertex is indistinguishable from an internal loop vertex at the end of a subgraph, and the dangling end loop vertex with three strands and two adjacent helices is indistinguishable from an internal loop vertex. Therefore, we added a criterion to RAG-3D to identify atomic fragments with the same number and same loop types as the target subgraph. Figure 6 illustrates RAG-3D’s partitioning of the candidate graph selected after MC/SA simulation for the 7S.S SRP RNA (PDB ID: 1LNG), and the top atomic fragments provided by RAG-3D search.

Figure 6. RAG-3D partitioning for 7S.S SRP RNA (PDB ID: 1LNG).

Subgraphs and best matching (lowest graph RMSD) atomic fragments for the candidate graph of the signal recognition particle (PDB ID: 1LNG) are shown as obtained by our RAG-3D graph partitioning and search (with added requirement for the fragment to have matching loop types).

Non-redundant dataset for template loops

In addition to the RAG-3D database described above, we also use the non-redundant database obtained from the Nucleic Acid Database (NDB) to create a library of template loops to be used in the F-RAG procedure. The non-redundant database was first cited in [50] in connection to our derived statistical potential, and an updated version was used to develop statistical potentials for k-turn motifs [51]. For the purpose here to create a library of template hairpins and internal loops, the non-redundant list of RNA structures obtained from the NDB was filtered to remove structures with incomplete and modified residues. Duplicate chains and multiple models within the same PDB file were also removed. All hairpins and internal loops from the remaining 880 structures were classified into categories based on the number of residues and strand sequence (555 hairpin categories and 395 internal loop categories). One loop is selected from each category to form the library of template loops used in F-RAG.

For the F-RAG procedure, one template loop (from the template loop library constructed above) with the same number of residues and sequence is selected for each hairpin and internal loop in the target structure. If a loop with the same sequence does not exist, then a score is given to each loop with the same number of residues (0 for every nucleotide match, 1 for every pyrimidine-pyrimidine and purine-purine mismatch, 2 for every purine-pyrimidine mismatch), and the loop with the lowest score is selected as the template loop. Note that such a template loop is only used in F-RAG if the atomic fragments provided by the RAG-3D search do not meet all the requirements listed in the section below.

With the above tools, our F-RAG procedure can be described as follows:

Details of the F-RAG procedure

The target graph is defined as the candidate graph obtained from the RAG-TOP MC/SA simulation. For each target graph, we generate atomic models as follows:

Input and Output

We apply RAG-3D partitioning and search utilities to the target graph to divide it into subgraphs and obtain the top 10 matching atomic fragments for each subgraph from the RAG-3D database. For each hairpin and internal loop in the target 2D structure, a template loop that best matches its number of residues and sequence is extracted from the non-redundant dataset (as described above). The secondary structure, target graph, subgraphs, top 10 fragments obtained by RAG-3D, and best matching template loops from the non-redundant dataset all serve as input to F-RAG (sketched in Figure 7). The output of F-RAG consists of the atomic models generated by combining the different atomic fragments, each with a 3D graph, graph RMSD from the target 3D graph, and score according to the knowledge-based potential described above.

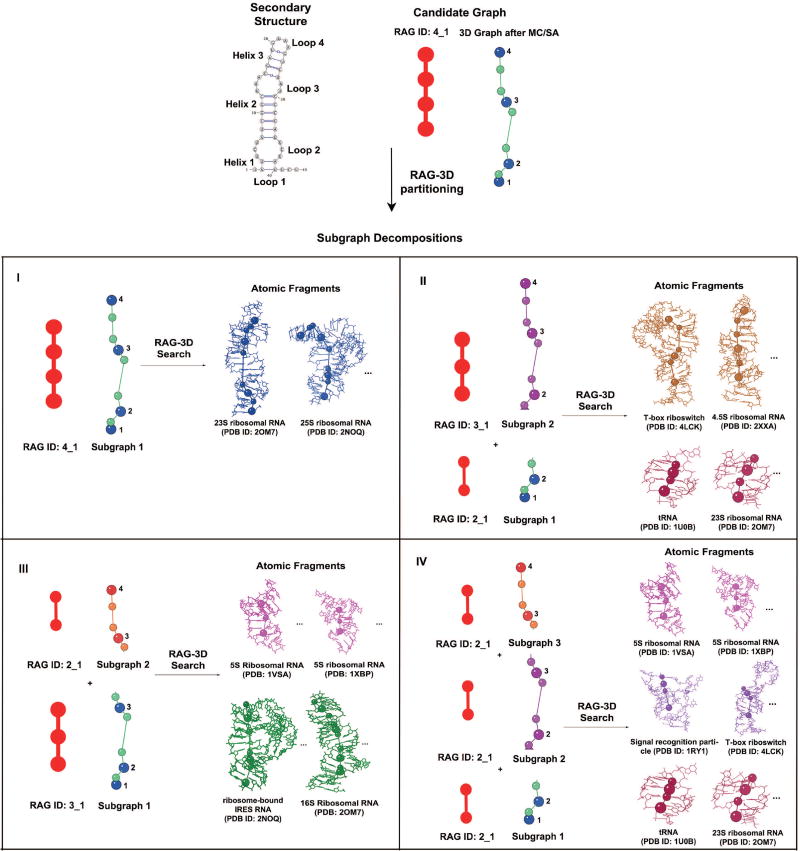
Figure 7. Sample F-RAG Input for the pentanucleotide AUUCU repeat expansion RNA (PDB ID: 5BTM).

The 2D structure, candidate graph, corresponding subgraphs, and associated atomic fragments from the RAG-3D search that serve as input to F-RAG are shown. For this 4 1 target, we obtain 4 subgraph decompositions as shown. For each subgraph decomposition, we run F-RAG using the 10 lowest graph RMSD atomic fragments for each target subgraph, to obtain many atomic models. We then select all atomic models that have the same number of residues as the target structure (or the highest number of residues in case of missing residues), sort them in increasing order of their score (based on our knowledge-based statistical potential), and select the top scoring models for geometry optimization with PHENIX. In Figure 8, we illustrate the steps of F-RAG for one subgraph decomposition, namely III.

Algorithm description

Let the subgraphs of the target 3D graph be numbered in increasing order from the 5′ to the 3′ direction. The algorithm proceeds by calling the recursive procedure below for each subgraph starting from the 5′ direction to generate atomic coordinates for that subgraph. The following steps describe the procedure to generate atomic coordinates for each subgraph and to connect its atomic coordinates to the partially built atomic model. Figure 8 illustrates the different steps in the procedure.

1. Identify the common subgraph vertex

   Determine the vertex of this subgraph that is common to previous subgraphs, to serve as the link between this subgraph and the previous subgraphs. For the first subgraph, there is no such vertex.

2. Identify the main subgraph vertex

   Determine the main vertex for the subgraph. For a subgraph that contains a junction, the main vertex is the first junction vertex. For a subgraph without junctions, the main vertex is the first internal loop vertex. If neither junctions nor internal loops exist, the main vertex is the hairpin loop vertex. Note that the common vertex identified in step 1 cannot be the main vertex.

   Next, divide the vertices of the subgraph into two sets, the first containing all subgraph vertices that are 5′ of the main vertex, and the second set containing all subgraph vertices that are 3′ of the main vertex.

   Then for each atomic fragment of this subgraph, perform the following steps:

3. Identify the main fragment vertex

   Determine the loop vertex in the fragment graph that corresponds to the main vertex of the target subgraph, i.e., the vertex in the fragment graph that is of the same loop type (junction, internal loop, or hairpin loop) as the main target loop vertex. If there is more than one loop of the same type in the fragment graph, choose the vertex with the least difference in the number of loop residues between the fragment and the target loop. Similar to the target main vertex, divide the fragment graph vertices into two sets, the first containing all fragment vertices that are 5′ of the main fragment vertex, and the second set containing all fragment vertices that are 3′ of the main fragment vertex.

4. Check fragment type

   Compare the two sets of target subgraph vertices calculated in step 2 to the corresponding set of fragment graph vertices calculated in step 3 to determine whether the fragment has the same 5′ to 3′ order of loops as the target subgraph. If the fragment does not match the target subgraph, remove the current fragment from consideration and go to step 3 for the next fragment. If the fragment matches the target subgraph, proceed to the next step.

5. Dock fragment graph onto the target subgraph

   Dock the fragment graph, along with the the corresponding atomic fragment, onto the target subgraph, using three corresponding vertices from the fragment graph and the target subgraph. The three corresponding vertices used for docking are the main loop vertex, and the loop vertices 5′ and 3′ of the main loop vertex in both the target subgraph and the fragment graph. If the target subgraph contains only two loop vertices, then the third vertex is chosen to be the 5′ helix vertex of the main loop vertex in both the target subgraph and the fragment graph.

6. Generate atomic coordinates for loop vertices

   Generate the coordinates for loop vertices in the target subgraph using the atomic coordinates of the corresponding loops from the fragment by the following steps. The atomic coordinates are generated for subgraph loops in the 5′ to 3′ direction to maintain connectivity of the atomic model.

   1. Edit the number and identities of base pairs in the 5′ helix
      Adjust the length of the helix 5′ of the fragment loop (remove or add base pairs) to match the length of the helix 5′ of the target loop. To preserve the connectivity of this helix with the previously built model, overlap the 5′ base pair of this helix with the corresponding base pair in the partially built model. The base pairs are overlapped using three atoms from both base pairs: C1′ atom of base 1, C1′ atom of base 2, and the C6/C8 atom of base 1 (depending on whether the first base is a pyrimidine/purine). Edit the bases in the helix to match the sequence of the corresponding target helix.
   2. Edit the number and identity of the loop residues
      Compare the number of residues in each strand of the fragment loop to the corresponding strand of the target loop. If the number of residues is equal, edit the fragment residue to match the corresponding target residue. If the number of residues in the fragment loop is less than the target loop, select the template loop for hairpins and internal loops (taken as input from the non-redundant dataset) and overlap this new loop on the 5′ helix generated above. (For junctions, the atomic model generated will have missing residues.) If the number of residues in the fragment loop is greater, remove extra residues for internal loops and junctions. For hairpin loops, select the template hairpin loop. Edit the residues in the fragment loop to match the target loop sequence.
   3. Edit the identity of base pairs in the 3′ helices
      For each 3′ helix of the target loop (there can be more than one if the loop is a junction), edit the identity and length of the corresponding 3′ helices of the fragment loop to match the sequence of the corresponding target helix. If any adjustment to the number of loop residues was made in step 6b, or a template loop was used, overlap the 5′ base pair of this helix on the 3′ base pair of the loop to maintain connectivity.

7. Apply the recursive procedure to the next target subgraph

   Unless the subgraph is last, go to step 1 for the next subgraph. For the last subgraph, a full atomic model for the target 3D graph has been generated. Construct a 3D tree graph for this full atomic model (using coordinates of the C1′ atom, C6 atom for pyrimidines, and C8 atom for purines), and calculate its graph RMSD from the target 3D graph, and its score according to the knowledge-based potential. Produce the full atomic model, graph RMSD, and associated score.

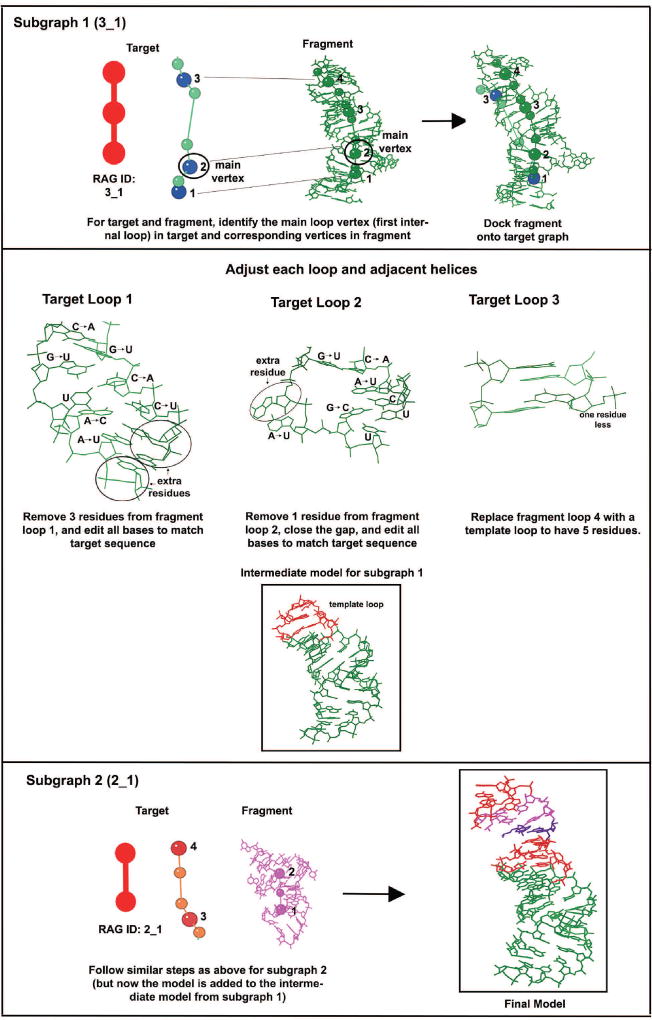
Figure 8. Steps of the F-RAG procedure for a sample application to subgraph decomposition III (shown in Figure 7) for the pentanucleotide AUUCU repeat expansion RNA (PDB ID: 5BTM).

The steps of F-RAG illustrated for the two subgraphs are: main vertex for the target subgraph is identified, respective vertices for docking the fragment graph onto the target graph are identified, fragments are docked onto the target graphs, and base types and numbers are edited in all loops and helices. Atomic fragments are superimposed to produce the final model. The colors in the final model indicate the segment’s source: green - fragment of subgraph 1; red - template loops; purple - extra base pair added; magenta - fragment of subgraph 2.

Highlights.

1. Graph-based fragment assembly method to generate atomic from coarse-grained RNA models

2. Good results, compared to two fragment-assembly based programs, especially for RNA junctions

3. Good foundation for future work on RNA structure prediction and design with compact representations

List of Abbreviations

RNA

Ribonucleic acid

RAG

RNA-As-Graphs

RAGTOP

RNA-As-Graphs Topology Prediction

F-RAG

Fragment-Assembly for RNA-As-Graphs

PDB

Protein Data Bank

NMR

Nuclear Magnetic Resonance

MC

Monte Carlo

MD

Molecular Dynamics

SA

Simulated Annealing

PHENIX

Python-based Hierarchical Environment for Integrated Xrytallography

RMSD

Root Mean Square Deviation

PPV

Specificity

STY

Senstivity

INF

Interaction Network Fidelity

DI

Deformation Index