The Healthy Worker Survivor Effect: Target Parameters and Target Populations

Abstract

Purpose of Review

We offer an in-depth discussion of the time-varying confounding and selection bias mechanisms that give rise to the healthy worker survivor effect (HWSE).

Recent Findings

In this update of an earlier review, we distinguish between the mechanisms collectively known as the HWSE and the statistical bias that can result. This discussion highlights the importance of identifying both the target parameter and the target population for any research question in occupational epidemiology. Target parameters can correspond to hypothetical workplace interventions; we explore whether these target parameters’ true values reflect the etiologic effect of an exposure on an outcome or the potential impact of enforcing an exposure limit in a more realistic setting. If a cohort includes workers hired before the start of follow-up, HWSE mechanisms can limit the transportability of the estimates to other target populations.

Summary

We summarize recent publications that applied g-methods to control for the HWSE, focusing on their target parameters, target populations, and hypothetical interventions.

Introduction

Determination of exposure limits to protect workers’ health requires accurate estimates of the risks of occupational exposures. Assessments of workplace risk are generally based directly on observational studies of occupational cohorts [1]. Estimates from these studies, however, are often subject to bias due to the Healthy Worker Survivor Effect (HWSE), a ubiquitous process that results in the healthiest workers accruing the most exposure over their lifetimes [2–7]. It is therefore critical to attempt to control for the potential downward bias caused by the HWSE [1,8].

The HWSE can be conceptualized as bias due to either time-varying confounding or a selection process [5,7,9–11]. In a previous review, Buckley et al. detail recent applications of analytical approaches that control for the HWSE [8]. To emphasize the resultant loss of study validity, Buckley refers to the phenomenon as Healthy Worker Survivor Bias. In the epidemiologic literature, bias is used to refer to the mechanisms that cause results to deviate from the truth [12,13]. However, we want to preserve the distinction between the mechanisms we refer to collectively as the Healthy Worker Survivor Effect, and the statistical bias that it often causes, for which we will reserve the terminology Healthy Worker Survivor Bias. These two ideas are discussed in more detail below.

In this paper, we expand on Buckley’s review by discussing the mechanisms that give rise to the bias in more depth [8]. We highlight the role that identification of both target parameters and target populations plays in allowing occupational epidemiologists to estimate unbiased exposure effects from cohorts affected by the HWSE mechanism. We then review recent applied papers published since Buckley’s review (Table 1) that attempt to remove Healthy Worker Survivor Bias, focusing on their target parameters and populations [14–22].

Table 1.

Target Populations and Target Parameters for Selected Recent Applications of G-Methods to Control for Bias due to Mechanisms of the Healthy Worker Survivor Effect

Study Reference	Target Population		Target Parameter
	Study Population	Inception Cohort	Reported Target Parameter	Estimation Method	Measured Time Varying Confounders	True Value of Target Parameter Affected by HWSE Mechanism
Neophytou et al 2014	Aluminum smelter and fabrication workers	No	Hazard ratio for ischemic heart disease while at work, comparing hypothetical intervention in which all workers were always exposed above the cutoff for PM2.5 to one in which all workers were always exposed below the cutoff	IPTW	Composite health score	Yes
Keil & Richardson 2016	Copper smelter workers	No	Cumulative incidence for respiratory cancers, heart disease, and other causes under each intervention on arsenic exposure, compared to the natural course of each disease	G-computation	Employment status	Yes
Neophytou et al 2016	Underground non-metal miners	Yes*	Risk ratio/difference and attributable fraction of lung cancer under interventions eliminating occupational exposure to diesel exhaust	G-computation	Employment status Job location	Yes
Brown et al 2015	Aluminum smelter and fabrication workers	No	12-year cumulative incidence of ischemic heart disease under hypothetical intervention in which all workers remained at work and were exposed above the median PM2.5 compared to one in which all workers were always exposed below median	TMLE	Composite health score Co-morbidities	No
Keil et al 2015	Uranium miners	No	Ratio of median survival times for lung cancer mortality corresponding to a 100 working-level month increase in cumulative radon exposure	G-estimation	Employment status	No
Björ et al 2015	Iron ore miners	No	Hazard ratio for mortality not known to be related to dust exposure, comparing hypothetical intervention in which all workers were exposed above the cutoff for respirable dust during the first 15 years of follow-up to one in which all workers were never exposed above the cutoff	G-estimation	Employment status Sick leave/Time off Job Location	No
Picciotto et al 2015	Autoworkers	Yes	Total number of person-years of life lost in the cohort due to cardiovascular disease that could have been saved by enforcing various exposure limits on certain metalworking fluids	G-estimation	Employment status Intermittent time off Other metalworking fluids	Yes╪
Picciotto et al 2016	Autoworkers	Yes	Average number of years of life lost due to cardiovascular disease that could have been saved per person among the ever-exposed workers by enforcing a ban on exposure to certain metalworking fluids	G-estimation	Employment status Intermittent time off Other metalworking fluids	Yes╪
Costello et al 2016	Aluminum smelter workers	Yes	Hazard ratio for ischemic heart disease while at work, comparing hypothetical intervention in which all workers were always exposed above the cutoff for PM2.5, to one in which all workers were always exposed below the cutoff	IPTW	Composite health score	Yes
	Aluminum fabrication workers	Yes	Ratio of risk within a population of workers who were hired and then assigned to specific jobs by the employer thereby defining their exposure histories to PM2.5 without intervention	Cox Model	Composite health score	Yes

HWSE: Healthy Worker Survivor Effect IPTW: Inverse Probability Weighting TMLE: Targeted Maximum Likelihood Estimation

PM_2.5: Particulate Matter <2.5μm in diameter

^*Follow-up started at dieselization at each mine so the cohort was an inception cohort with respect to diesel exhaust exposure, though not with respect to employment.

^╪Estimate of model coefficient that is unaffected by HWSE mechanism was combined with data and assumptions to obtain an estimate of a target parameter that is affected by HWSE mechanism.

Target Parameters

Epidemiologic studies try to answer questions about the relationship between an exposure and a health outcome in a population. Target parameters provide answers to those questions; they summarize the relationship of interest with a single number, or a series of numbers [23]. Familiar target parameters include standardized mortality ratios, odds ratios, hazard ratios, and regression slopes.

The directed acyclic graph (DAG) presented in Figure 1a describes the data generating process for a simplified occupational cohort study with two time points. Researchers use this study design to estimate the effect that long term workplace exposure has on an adverse health outcome, with the ultimate goal of evaluating limits to mitigate lifetime risk in the workforce [9,11,13,24]. Measured variables for these data are: exposure assessed at the two time points (A₁ and A₂), time-varying health status measured at the end of time point 1 (H), and an outcome measured at the end of time point 2 (Y). There also are unmeasured shared predictors (U) of underlying health status and the outcome, representing differences in susceptibility or other risk factors within the population.

Figure 1.

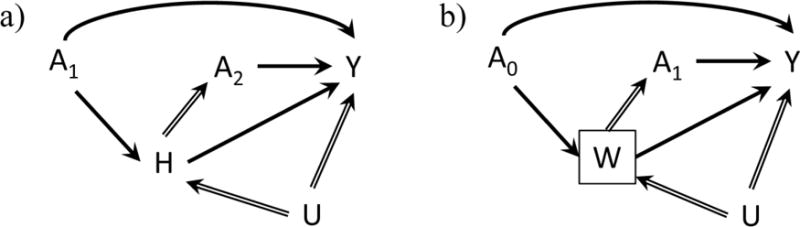
Directed acyclic graphs describing the data generating processes for theoretical occupational health cohort studies of exposure (A) on an outcome (Y). The subscripts under A represent the time point of the exposure, so A1 is exposure that occurs in the first year of follow-up, A2 represents exposure in the second year, and A0 represents exposure that occurs at time 0 prior to the start of follow-up. U represents an unmeasured covariate affecting either an adverse health status (H) or work status (W) and the outcome (Y). Solid arrows represent the relevant causal effect of exposure on the outcome unmediated by future exposure, while hollow arrows represent pathways that constitute the Healthy Worker Survivor Effect mechanisms. a) Displays the time-varying confounding on the causal pathway that occurs via adverse health status (H). b) Displays the selection process that occurs when researchers condition on work status (W) by choosing a population of active workers for follow-up.

There are two direct pathways by which exposure causes the outcome: A₁ → Y and A₂ →Y. There are also two indirect pathways by which exposure causally affects the outcome: A₁ → H → Y and A₁ → H → A₂ → Y. We represent the pathways in the DAG that constitute the Healthy Worker Survivor Effect mechanism using hollow arrows.

One of the basic processes by which the Healthy Worker Survivor Bias perpetuates itself is via the arrow between H and A₂. Workers in poorer health tend to accrue less exposure, whether by reducing the amount of time that they work, by switching to lower exposed jobs, or by leaving the workforce entirely. The workers who tend to survive in the active workforce and to accrue the most exposure, conversely, are the healthiest ones. The variable H acts as a time-varying confounder on the causal pathway: it both contains a portion of the effect of past exposure (A₁ → H → Y) and acts as a confounder of the future exposure-response relationship (A₂ ← H → Y). Estimation of unbiased causal effects of exposure from data structures including these pathways requires the use of a class of modern statistical estimation approaches known collectively as g-methods [25–28].

Researchers can apply most g-methods with standard software using the traditional tools of epidemiologic research: standardization, weighting, and regression. Each of the g-methods (including inverse probability weighted estimation of marginal structural models, g-computation, targeted maximum likelihood based estimation (TMLE), and g-estimation of structural nested models) can be applied to estimate different target parameters. These parameters are often defined using the language of interventions to articulate questions that, if answered, capture the causal relationship between exposure and outcome. Target parameters for these methods are structured as answers to questions about disease occurrence under counterfactual scenarios. They estimate the outcome(s) in a target population if the specified intervention(s) had been imposed. The ability of researchers to estimate these parameters from their observed data relies on the key assumptions of consistency, conditional exchangeability, and positivity [11,29].

Consider two possible interventions on the system described in Figure 1a. In each intervention, all workers experience the same fixed level of exposure: in the first, exposure is always high, and in the second, exposure is always low. If these two interventions were implemented, health status would not act as a time-varying confounder in the resulting data. Workers who in reality would tend to transfer to jobs with more or less exposure as a function of this health status would instead remain at their original exposure level for the entire study period. The effect of exposure could be inferred from the comparison of the outcomes experienced by the same worker cohort under each intervention. By defining these structural parameters with reference to an intervention of interest, epidemiologists can identify questions that isolate the causal effect of the exposure under study [30]. To be clear, some of these interventions are not intended to be implemented; they are clearly infeasible due to both practical and ethical considerations. Rather they are chosen because, if they were to be implemented, their resulting data would provide an easily interpretable way to estimate the causal effect of the exposures under study.

By contrast, target parameters from traditional approaches, such as Standardized Mortality Ratios or Cox proportional hazards, evaluate risk by comparing observed groups who actually experienced different exposure histories [11,13]. The risk among the highest exposed subset is evaluated among a select group of the healthiest and most robust workers. It is no surprise, therefore, that these estimands underestimate the risk for the entire population.

We define bias as an expected difference between an estimand ( $\widehat{\xi }$) and the true value of its target (ξ₀). For an unbiased estimand, the two values are equivalent ( $\widehat{\xi }$=ξ₀). Counterintuitively, some estimation targets (i.e. some ξ₀s) are affected by the mechanisms of the HWSE. Thus, a parameter can be unbiased, in that $\widehat{\xi }$=ξ₀, even though the value of ξ₀ might depend on the strength of the HWSE mechanisms (for example, the causal relationship between H and A₂).

We distinguish between two types of causal parameters corresponding to interventions. A causal contrast that corresponds to the biologic effect of exposure on an outcome is an example of a target parameter whose true value is not affected by the HWSE mechanisms. A valid way to evaluate this etiologic effect would be to compare the outcomes of two hypothetical interventions, one with high exposure, and one with low exposure, in a working population. All workers would remain at work for the duration of both interventions and receive their assigned exposure. In an occupational context, the controlled direct effect [31] estimated by contrasting the outcomes under these two interventions would represent the etiologic effect of exposure.

By contrast, a target parameter corresponding to a more realistic intervention might be affected by the HWSE mechanisms. For example, researchers may be interested in interventions that reduce occupational exposure limits to specific levels. These interventions are typically of the nature ‘if at work then exposure is set at or below the exposure limit’. These are dynamic interventions dependent on a subject’s employment status, in contrast to static ‘always at work and always exposed’ interventions [32,33]. These realistic interventions allow workers to leave work and be unexposed if not at work, as would be expected in a real world setting where workers can opt to leave work (the interventions may be unrealistic in other ways). The counterfactual outcomes under these realistic interventions can be compared to the observed outcome (under the natural course of events), and causal parameters such as the risk difference can be obtained. Under such interventions and comparisons, the true value of the estimand is affected by the strength of the associations denoted by the hollow arrows in the DAG in Figure 1a.

If exposure is an irritant, some workers might leave work earlier under a high exposure scenario, become subsequently unexposed, and as a result accumulate less exposure than they would have under a low exposure scenario. The higher exposure scenario may then result in lower risk for the population than the lower exposure scenario even though exposure is harmful. Assessment of such interventions is therefore aimed not necessarily at estimating the etiologic effect of exposure on an outcome, but rather at estimating what would happen in a realistic or real-world intervention on the target population.

Target Populations

A group of people who all start work on the same day may include workers with varying degrees of susceptibility to the health effects of exposure. If workers who are more susceptible leave work and/or experience the outcome prior the start of follow-up, then the subset of workers who remain eligible for the study at the start of follow-up will have a greater proportion of “immune” workers, or survivors, than the population of workers from which they came. If the study population is then defined to include only the workers who were still employed at the start of follow-up, the study population consists of all surviving workers: those who do not yet have the exposure-related outcome of interest. One could use these data to obtain an unbiased estimate of the target parameter for a population of workers culled of the susceptible, but the estimate would likely not be generalizable to a population of all workers, potentially dampening its utility in guiding health-based exposure limits. If, instead, the target population is all workers ever employed in that workplace, then a study population of surviving workers may be a biased sample of the target population, and any resulting target parameter will suffer from selection bias.

Many occupational cohorts are defined to include a cross-sectional sample of workers already employed at the start of follow-up [14–16,18,21,22,34,35]. These workers constitute a left-truncated cohort [34,36–39]. The DAG in Figure 1b demonstrates how this choice of analytical cohort, in combination with the HWSE mechanisms, can result in bias due to selection. The DAG includes a conditioning on active employment at the start of follow-up. This defines a cohort based on a cross-sectional sample of the workers who began employment prior to the start of follow-up. The variable W, an indicator representing active employment, serves as the time-varying confounder on the causal pathway between exposure at time 0 and the outcome. The box around W represents the selection criterion for entry into the cohort (only workers with W = 1 are included in the study population). This conditioning opens up a pathway from previous exposure through the unmeasured confounder to the outcome (A₀ →W← U → Y) and, without additional assumptions, prevents identification of the causal effect of exposure prior to start of follow-up [9]. That is, conditioning on a descendent of exposure usually results in selection bias that affects any estimates derived from the resultant cohort [10]. In reality, many occupational cohorts include those still at work at the beginning of follow-up as well as any workers hired during follow-up, and therefore will only be proportionally affected by this mechanism.

We can also view this effect as an instructive example of the concept of transportability, or external validity. Bareinboim and Pearl have given transportability a formal definition and demonstrated the use of DAGs to identify systems whose measured effects are transportable to each other [40]. If we apply this principle to our DAG in Figure 1b, we can see that the unblocked pathway between exposure prior to follow-up start (A0) and the outcome prevents simple transportability, or generalizability, between the left-truncated cohort and the original group of workers from which they were selected. This implies that effect measures estimated in the left-truncated cohort will not necessarily be the same as might be observed from the original ‘inception’ population. A clear discussion of the target population should acknowledge that any cross-sectional cohort may have been subject to a selection process that distinguishes it from the original full cohort from which it was sampled.

The question of external validity is fundamental to all epidemiologic research [13,41]. We emphasize it here to highlight the fact that the same HWSE structural mechanisms (cf Figures 1a and 1b) that cause time-varying confounding can also cause bias due to sample selection. Despite the commonalities in their origins, successfully addressing both biases requires distinct epidemiologic approaches. In the following sections, we discuss the roles that identification of target parameters and target populations played in addressing potential bias due to the HWSE mechanisms in recent published research.

Methods for estimating exposure effects in cohorts with Healthy Worker Survivor Effect present

Using recent applications in the literature (summarized in Table 1), we describe several different estimation approaches used to address Healthy Worker Survivor Bias and focus on how the applications relate to the key ideas of target parameters and target populations developed above.

Inverse probability of treatment weighting (IPTW)

IPTW estimation reweights observed data using weights that are inversely proportional to the probability that each subject received their observed exposure history, creating a pseudo-population in which measured confounders no longer predict exposure [42–44]. Exposure effects can then be estimated from this re-weighted population using marginal structural models that include exposure as the only predictor for the outcome.

In a cohort of actively employed aluminum manufacturing workers, Neophytou et al. 2014 used marginal structural Cox models to estimate the effect of exposure to particulate matter <2.5μm in diameter (PM_2.5) on the incidence of ischemic heart disease while still employed, adjusting for time-varying confounding by a composite health score [14]. The target parameter was the ratio of the average hazard of heart disease during follow-up that would have been observed if all workers in the target population were always exposed above the PM_2.5 cutoff while at work, to the average hazard that would have been observed if all workers were always exposed below the cutoff while at work. Results from this analysis were protected from potential bias caused by time-varying confounding by the health risk score. The analytic cohort was a population of surviving workers and new hires. The results are considered unbiased if the target population is defined as this analytic cohort, but may have limited transportability to all workers. Results based on the survivor population vs. the inception population were explored further in Costello et al., discussed below [19].

G-computation/the parametric g-formula

G-computation, or the parametric g-formula, is an extension of standardization for time-varying exposures. G-computation allows the estimation of the risk of an outcome as a weighted sum (or integral) of the probability of the outcome conditional on its risk factors. The parametric g-formula relies on parametric models to predict the probabilities of the outcome and all other risk factors.

Keil & Richardson apply the parametric g-formula to estimate the effect of hypothetical interventions modifying occupational exposures to arsenic in a cohort of copper smelter workers [21]. Cumulative incidences (from age 20 onwards) for respiratory cancers, heart disease, and other causes were estimated under each intervention and compared to the natural course (observed cumulative incidence). The interventions of interest allowed workers to leave work, so the true value of the target parameter was affected by the strength of the relationship between exposure and leaving work and the association between leaving work and the outcomes. However, this does not mean that the findings were biased due to time-varying confounding by employment status, as the realistic target parameter of interest was identifiable from the observed data. Both the analytic population and target population included workers hired before start of follow-up. Thus their results may have limited generalizability to the population of all workers at this smelter.

Neophytou et al. 2016 use a similar approach to estimate risk of lung cancer under interventions modifying occupational exposure to diesel exhaust in a cohort of underground non-metal miners [22]. The authors report risk differences and risk ratios comparing each intervention to the natural course of each disease, as well as the attributable fraction of lung cancer cases for the exposure of interest. The intervention of interest allowed workers to leave work, so the true value of the effect being estimated was affected by the strength of the relationship between exposure and leaving work, but again, the findings are not affected by bias resulting from time-varying confounding by employment status. Start of follow-up in the analytic population coincided with dieselization of participating mines, but included workers hired before start of follow-up. Although this may be considered as an ‘inception’ cohort from the point of view of the exposure of interest, the results may still not be transportable to a population of all underground non-metal miners.

Targeted maximum likelihood estimation

Targeted maximum likelihood estimation is a generalized methodology for performing causal inference introduced by van der Laan and colleagues [45]. Applied to a longitudinal cohort, TMLE uses a sequential estimation process to remove the time-varying confounding at each time point, allowing the estimation of intervention-based target parameters [46,47]. Each sequential estimation is targeted to the parameter of interest, providing efficient estimation and double robustness.

Brown et al. studied the effects of airborne exposure to PM_2.5 on the development of ischemic heart disease while employed in an active cohort of aluminum workers [18]. They estimated the marginal 12-year cumulative incidence of heart disease under different exposure interventions. The target parameter compared the incidence that would have been observed if all workers had remained at work and were continuously exposed above the median PM_2.5 compared to what would have been observed if each worker were continuously exposed below the median PM_2.5 and remained at work. They adjusted for potential time-varying confounding of the exposure assignment and employment termination processes by the underlying health risk score, hypertension, dyslipidemia, and diabetes. The cohort included previously hired workers, thereby limiting the transportability of the results to the cohort of all workers ever employed.

G-estimation of structural nested (accelerated failure time) models

Instead of combining exposures over time to compute cumulative exposure and then estimating its composite effect on the outcome, g-estimation of a structural nested accelerated failure time model removes time-varying confounding by estimating the effect of exposure at each time separately, adjusting only for past covariates, and then combining those effects together over time. In this way, the effect estimate is free from confounding by measured time-varying covariates [48,49].

This approach assumes that the effect of exposure (if such exposure could occur) would be the same after leaving employment as it is during employment: employment status is not an effect measure modifier [50]. This allows us to estimate an etiologic effect, and avoid considering interventions on employment status. In the papers discussed below, the models chosen assume that there is no effect measure modification by any covariate. These applications of structural nested accelerated failure time models yield a parameter corresponding to the ratio of median survival times comparing what would have happened under two counterfactual exposure interventions. The exact nature of the scenarios depends on the model and exposure metric. Because this ratio compares two interventions on exposure, ignoring employment status, the true value of the target parameter does not depend on the observed strength of the relationship between employment status (or other variables H) and later exposure. Nevertheless, estimation of this target parameter still requires correct adjustment for time-varying covariates.

Keil et al. use this approach to assess effect of occupational exposure to radon on lung cancer mortality in a cohort of male uranium miners in Colorado [15]. The authors estimated the ratio of median survival times that would have been observed for an increase in cumulative exposure equivalent to 100 working level months, assuming the relationship between exposure and survival time to be linear. The analysis adjusted for employment status as the main time-varying confounder. The analytic population included workers hired before study initiation, possibly limiting generalizability of the results to a population of all workers in these mines.

The estimate of the primary parameter of an accelerated failure time model has also been used to derive estimates of other target parameters. Examples include (a) the hazard ratio comparing everyone being exposed for the first 15 years of follow-up to everyone never being exposed [15] and (b) the total and/or average number of person-years of life that could have been saved in the cohort by enforcing various exposure limits [16,17,20]. These other target parameters generally require additional assumptions and depend on other properties of the observed data, such as the distribution of survival time or exposure; those listed under (b) compare what would have happened under an intervention to what actually happened, and are therefore affected by the HWSE mechanisms in the observed data.

Excluding workers hired before start of follow-up

If the target population is all workers, one would ideally study an inception cohort (a group of workers followed from their very first day at work) in order to completely eliminate the selection bias induced by the HWSE. Such a cohort emulates features of a randomized controlled trial where follow-up time, exposure, and eligibility all start at the same time [51–53]. In some situations, study design or statistical power considerations may prohibit analysis of an inception cohort; nevertheless, the inception cohort from which the study sample was drawn is often the target population.

In a recent paper, Costello et al. analyzed data from a cohort of aluminum manufacturing workers exposed to PM_2.5 and followed for ischemic heart disease while still employed [19]. When follow-up started, most workers in the cohort were currently employed; 38% were hired after the start of follow-up. Results were presented for the full cohort, for the sub-cohort hired after the start of follow-up, and for those hired 10 and 25 years prior to start of follow-up. Restriction to those hired after the start of follow-up yielded the strongest hazard ratios for PM_2.5 and heart disease incidence, consistent with reduced selection bias. Results suggest that restriction by hire date also reduces the magnitude of the selection bias. Thus, even if restriction to an inception cohort is not feasible, partial restriction can help alleviate the bias if the target population includes all workers.

Discussion

Due to their common structural origins, time-varying confounding affected by prior exposure and the potential for left truncation bias generally co-occur in occupational studies. In several of the works we discussed above in the context of one of these issues, both were actually addressed to a degree. Picciotto et al. 2015 and 2016 used g-estimation to address confounding by both employment status and intermittent time off work; the study population was also restricted to create an inception cohort, thus addressing both aspects of the problem [17,20]. Similarly, Costello et al. used ITPW to address time-varying confounding affected by prior exposure and cohort restriction to address left truncation in the aluminum smelter worker sub-cohort in which both processes were operating [19].

There are cases in which the target population is not an inception cohort, but rather includes workers hired before the start of follow-up. For example, a reasonable research question might be to quantify the impact an intervention would have had if implementation had occurred on a particular date and affected all current employees, similar to the interventions discussed in Keil & Richardson [21] and Neophytou et al. 2016 [22]. This question concerns a realistic workplace intervention that would have impacted both those workers employed prior to start of follow-up and those hired afterwards. The transportability of such a parameter to other worker populations including future workers, and its utility for guiding the development of occupational exposure limits, should be carefully evaluated in future research.

There are several steps that researchers can undertake in order to best address concerns about bias arising from the HWSE. First, identify the target population and evaluate whether it differs from the observed cohort. Determine if an incident cohort is a viable analytical sample and if there is any information about workers who left prior to the start of follow-up. Second, identify the target parameter, which might correspond to an intervention on workers’ exposure and possibly employment status, and choose an analytic approach that can estimate that target parameter in the particular dataset available. No single analytic approach is sufficient to ensure unbiased estimation in every occupational setting. Each of the estimation approaches we discuss above offers the ability to control for the time-varying confounding that characterizes the HWSE.

IPTW estimation is the simplest to implement, and has generally been used when there are no concerns about structural non-positivity, such as when all follow-up time occurs among employed workers. When follow-up extends past employment termination, g-computation or longitudinal TMLE can be used, although the intervention definition should carefully consider the role of leaving work. G-estimation also offers the ability to use follow-up time after leaving work, but has thus far been applied only with a limited class of models. Extensions of any of these estimation approaches to different target parameters should be explored more in future research for various target populations. Deciding which to use may come down to ease of implementation and the researcher’s willingness to make modeling assumptions.

Conclusion

The HWSE has resisted easy classification because of its multifaceted origins. In this review, we distinguish between the mechanisms of HWSE and the bias it can cause through discussion of target populations and target parameters in the context of recent applications of g-methods. We conclude with the hope that more occupational epidemiologists will structure their research around these concepts and thereby better estimate the risks associated with workplace exposures.