A common microstructure in behavioral hearing thresholds and stimulus-frequency otoacoustic emissions

Abstract

Behavioral hearing thresholds and otoacoustic emission (OAE) spectra often exhibit quasiperiodic fluctuations with frequency. For behavioral and OAE responses to single tones—the latter referred to as stimulus-frequency otoacoustic emissions (SFOAEs)—this microstructure has been attributed to intracochlear reflections of SFOAE energy between its region of generation and the middle ear boundary. However, the relationship between behavioral and SFOAE microstructures, as well as their presumed dependence on the properties of the SFOAE-generation mechanism, have yet to be adequately examined. To address this, behavioral thresholds and SFOAEs evoked by near-threshold tones were compared in 12 normal-hearing female subjects. The microstructures observed in thresholds and both SFOAE amplitudes and delays were found to be strikingly similar. SFOAE phase accumulated an integer number of cycles between the frequencies of microstructure maxima, consistent with a dependence of microstructure periodicity on SFOAE propagation delays. Additionally, microstructure depth was correlated with SFOAE magnitude in a manner resembling that predicted by the intracochlear reflection framework, after assuming reasonable values of parameters related to middle ear transmission. Further exploration of this framework may yield more precise estimates of such parameters and provide insight into their frequency dependence.

I. INTRODUCTION

Behavioral hearing thresholds from sensitive ears often fluctuate quasiperiodically with small changes in test frequency (Elliott, 1958; van den Brink, 1970; Thomas, 1975). These fluctuations, termed microstructure or fine structure, are idiosyncratic to individual ears, relatively stable over time, and correlated with fluctuations in loudness judgements for low-level tones (Elliott, 1958; Long, 1984). Similar microstructure patterns are also observed in the amplitudes, phases, and delays of otoacoustic emissions (OAEs) (e.g., Kemp, 1980; Zwicker and Schloth, 1984), sounds recorded in the ear canal which originate from vibrations within the cochlea (Kemp, 1978). For behavioral and OAE responses to single tones—the latter referred to as stimulus-frequency otoacoustic emissions (SFOAEs)—microstructure is thought to be at least partially attributed to multiple intracochlear reflections of the waves that give rise to SFOAEs, specifically between their region of generation and the middle ear boundary (Kemp, 1979a; Talmadge et al., 1998; Konrad-Martin and Keefe, 2003; Epp et al., 2010). The microstructures observed in behavioral thresholds and SFOAEs are therefore presumed to have a common origin, if not to also be highly similar in their frequency periodicity and morphology. However, such relationships have yet to be unequivocally demonstrated.

According to the aforementioned “intracochlear reflection framework,” the microstructures observed in thresholds and SFOAE responses explicitly depend on the mechanisms underlying SFOAE generation. SFOAEs are predominantly thought to arise via scattering of forward-traveling cochlear waves by micromechanical impedance irregularities that are randomly distributed along the cochlear partition (Zweig and Shera, 1995; Talmadge et al., 1998; Shera, 2003). Reflections from near the peak of the traveling wave excitation pattern are thought to contribute strongly to the net reflected wave, such that SFOAEs (and therefore, microstructure) are presumed to be highly sensitive to the active, outer hair cell-mediated processes responsible for traveling wave amplification. Regardless of the precise details of their origin, the resulting waves travel to the cochlear base, where they drive the stapes to produce an SFOAE in the ear canal. Additionally, due to the impedance mismatch at the middle ear, these waves are partially reflected back in the forward direction, thus modulating the input to the cochlear partition.

Depending on their relative phases, the additional forward-traveling waves that result from reflections at the stapes can interfere constructively or destructively with the primary stimulus-driven wave. Maximal constructive interference occurs at frequencies for which the round-trip phase accumulation due to wave propagation from the cochlear base to the SFOAE generation region and back is a whole number of cycles. Such frequencies are presumably associated with local peaks in behavioral sensitivity (i.e., threshold minima) and SFOAE amplitude spectra, as well as SFOAE delays.¹ Provided sufficient amplification of the forward- and reverse-propagating waves, such that the round-trip gain exceeds any losses, self-sustaining cochlear oscillations may also occur at these frequencies, resulting in spontaneous otoacoustic emissions (SOAEs) in the ear canal (Kemp, 1979a,b; Shera, 2003).

Consistent with this framework, SOAEs are almost always accompanied in frequency by threshold minima (e.g., Wilson, 1980; Schloth, 1983; Zwicker and Schloth, 1984; Long, 1984; Baiduc et al., 2014; Dewey et al., 2014) and peaks in transient- or tone-evoked OAEs (Probst et al., 1986; Bergevin et al., 2012), though SOAEs are not necessarily measurable at the frequencies of all threshold minima or evoked-OAE peaks. While a strong correspondence between the microstructures of thresholds and evoked OAEs may also be assumed on this basis, such a relationship has yet to be clearly demonstrated nor studied in more than a few subjects. For instance, threshold minima have been shown to correspond to some, but not all, peaks in the amplitudes of OAEs evoked by transient stimuli (Horst et al., 1983; Zwicker and Schloth, 1984) and to be essentially misaligned with the peaks in chirp-evoked OAE spectra (Uppenkamp and Neumann, 1996). This is despite the finding that OAEs evoked by clicks and continuously-swept tones are nearly spectrally-equivalent to SFOAEs evoked by discrete tones (Kalluri and Shera, 2007a, 2013) and are thought to share the same underlying generation mechanisms. Perhaps surprisingly, the spectral structures of behavioral thresholds and discrete-tone-evoked SFOAEs have not been explicitly compared and analyzed quantitatively.

The present report addresses this by comparing pure-tone thresholds and SFOAE responses obtained at identical, discrete frequencies in normal-hearing individuals. We find that these measures indeed share a common microstructure. This relationship was evident even in frequency regions with no strong SOAEs, which were avoided so as to limit the possible influence of perceptual effects related to their presence (e.g., beating, roughness, or masking; Long, 1998; Long and Tubis, 1988a,b; Smurzynski and Probst, 1998) as well as effects that they may have on SFOAE measurement (e.g., entrainment or suppression). Additionally, the measurements demonstrate that the periodicity and strength of this common microstructure are related to SFOAE delay and magnitude, respectively, consistent with a dependence of microstructure on the underlying SFOAE generation mechanism. As our analyses were motivated in part by the equations that more formally describe the intracochlear reflection framework, these are outlined in an appendix. However, the logic, nomenclature, and equations presented are largely adapted from Talmadge et al. (1998) and Shera (2003) (see also Shera and Zweig, 1993b; Zweig and Shera, 1995), and the basic ideas are no different than those first proposed by Kemp (1979a), such that the reader is directed to these sources for more in-depth treatment.

II. METHODS

A. Subjects

Subjects included 12 female adults ages 18–32 [mean ± 1 standard deviation (SD) = 22.1 ± 3.8 yrs]. All subjects had clinically-normal pure-tone audiograms, with thresholds less than 20 dB hearing level at octave frequencies from 0.25 to 8 kHz, and at 3 and 6 kHz, as measured with an Interacoustics Audio Traveller AA220 (Interacoustics, Assens, Denmark). Differences between thresholds for air- and bone-conducted stimuli did not exceed 10 dB at more than one frequency between 0.25 and 4 kHz. Subjects had normal otoscopic and tympanometric findings, and reported no history of ear pathology or surgery that would influence cochlear or middle ear function. One subject was associated with the laboratory and volunteered her time. The others provided written, informed consent and were compensated monetarily. All procedures were approved by the Institutional Review Board at Northwestern University.

The study was limited to female subjects to reduce potential sources of variability related to cochlear and/or middle ear function. In preliminary measurements, we also found that female subjects typically performed the threshold measurement procedure faster and more reliably than male subjects, and were quieter during the SFOAE measurements. Recruitment of only female subjects was therefore intended to improve the feasibility of obtaining complete data sets, as well as to improve the quality and interpretability of the collected data.

B. Equipment

All measurements were made in a sound-attenuating audiometric booth with the subject seated in a recliner. Signals were generated and recorded using custom software written in C++, MATLAB (The MathWorks Inc., Natick, MA), and MaxMSP (cycling74.com) and run on an Apple Macintosh computer. Digital-to-analog and analog-to-digital conversions were performed with a MOTU 828 mkII FireWire interface (Mark of the Unicorn, Cambridge, MA) using 24-bit resolution and sampling rates of 44.1 or 48 kHz. Outgoing stimulus signals were amplified (ER H4C; Etymotic Research Inc., Elk Grove Village, IL) and presented via MB Quart 13.01 HX speakers (Maxxsonics, Chicago, IL) coupled to an Etymotic Research ER-10B+ OAE probe with flexible plastic tubing. All acoustic measurements were made with the ER-10B+ microphone and preamplifier (set to +20 dB gain), and were compensated for the magnitude and phase of the microphone transfer function (Siegel, 2007; Rasetshwane and Neely, 2011a). Following insertion of the ER-10B+ in the ear canal, silicone earmold material (Insta-mold Products Inc., Oaks, PA) was injected around the probe to seal it in place. Examination of the ear canal half-wave resonance frequency obtained from repeated in situ calibrations (described below) at the beginning, middle, and end of each session confirmed the stability of the probe position over time.

C. Calibration

Stimuli were referenced to the forward pressure level (FPL) in the ear canal (e.g., Scheperle et al., 2008; Souza et al., 2014) using methods described previously (Dewey and Dhar, 2017). Calibration in terms of FPL was preferable to simply using the sound pressure level (SPL) measured by the probe, as using the latter results in insertion-depth dependent errors resulting from interference between the forward- and reflected-pressure components at the plane of the probe, particularly in the 2–5 kHz region where we focused our measurements (Souza et al., 2014). Briefly, FPL calibration requires calculation of the Thévénin-equivalent pressure and impedance of the acoustic assembly, which was performed on a weekly basis using pressure measurements with the probe inserted into a set of known acoustic loads. These quantities were then used to decompose the pressure measured by the probe in the ear canal into its forward- and reverse-going components, such that compensation factors could be derived to achieve the target FPL across frequency.

For comparison with studies using other calibration methods, we inserted the probe into an ear simulator (IEC 60318‐4; Ear Simulator Type 4157, Brüel & Kjær, Nærum, Denmark) and found that the SPL measured by the simulator microphone at its terminal end was 2–4 dB higher than the nominal FPL for the 2–5 kHz range. Thus, to the extent that any individual ear was similar to the simulator, we estimate that the SPL near the eardrum of our subjects was ∼3 dB higher than the nominal FPL. In contrast, the SPL measured by the probe at the entrance of the simulator (or a human ear canal) was typically 2–8 dB below the nominal FPL, as the result of destructive interference between the forward and reflected pressures at the probe.

D. Threshold measurement

Pure-tone thresholds were obtained with a modified, fixed-frequency Békésy tracking procedure (Lee et al., 2012). Stimuli were 250 ms, including 25 ms rise/fall times, and were pulsed twice per second with an interstimulus interval of 250 ms. Subjects were instructed to press and hold a button as long as the stimulus was audible and release the button once it became inaudible. Each press or release of the button marked a “reversal.” The stimulus level was stepped by 6 dB per presentation prior to the second reversal, and by 2 dB per presentation thereafter. After six “ascending” runs, with the stimulus level crossing from below to above threshold, the stimulus levels at the midpoints between reversals were calculated, excluding the first two. The average midpoint level was taken as the threshold if the standard error was less than 1 dB. Otherwise, additional ascending runs were completed until this criterion was met. The total tracking time at each frequency was typically 30–60 s. We have found that thresholds estimated with this method are typically repeatable within a few dB both within and across sessions, at least when using an in situ calibration method that accounts for the depth of probe insertion (e.g., Souza et al., 2014).

E. SFOAE measurement

SFOAEs were evoked by discrete tones presented at near-threshold probe levels (L_p) and extracted from the total ear canal pressure via the “suppression method” (Kemp and Chum, 1980; Kalluri and Shera, 2007b). For a given probe frequency (f_p), each 250 ms presentation of the probe tone alone was followed by a 250 ms presentation of both the probe and a 56 dB FPL suppressor tone with frequency 47 Hz below f_p. During the response to the probe alone, the pressure at f_p contained contributions from both the probe stimulus and any evoked SFOAE. In the presence of the suppressor, which was presumed to largely eliminate the SFOAE,² the pressure at f_p was that contributed primarily by the probe stimulus. Each response to the probe-plus-suppressor was therefore subtracted from the response to the probe alone to cancel the stimulus pressure and yield a residual waveform for which the pressure at f_p was dominated by the evoked SFOAE (or noise). In practice, the probe tone was presented continuously and the suppressor was pulsed on (via a separate sound source) for 250 ms during the latter half of each 500 ms interval, with 5 ms cosine squared ramps applied to the onset and offset of each presentation. Ramps were also applied to the beginning and end of the total probe stimulus waveform. Each 500 ms presentation pair (probe alone, probe-plus suppressor) was repeated 32 times for a total measurement time of 16 s at each f_p. Stimulus frequencies were rounded to multiples of 4 Hz so that an integer number of stimulus cycles were included in each 250 ms presentation window.

The amplitude and phase at f_p were estimated using a least-squares fit (LSF) analysis (Long and Talmadge, 1997) applied to the average SFOAE residual. The analysis was applied after removing the first and last 5 ms of the response and Hann windowing the remaining 240 ms interval. The probe stimulus phase was estimated from the average response to the probe-plus-suppressor and subtracted from the SFOAE phase at each frequency. SFOAE phase-gradient delays were then computed as the negative slope of the unwrapped phase curve over the three-point, 1/50-octave span centered on each f_p.

To calculate the noise floor amplitude, the polarity of every other residual was reversed prior to averaging and applying the LSF analysis. Due to limitations of the recording software, no automatic online artifact rejection was performed. Instead, the total ear canal pressure was continuously monitored and recording intervals were manually paused and restarted when excessive noise from the subject or measurement system was detected. To minimize noise during the measurements, subjects were given 10 s breaks (cued by a short 250 Hz tone) after every 32 s of measurement time, and were instructed to restrict swallowing or movement to these intervals. These procedures yielded noise floor amplitudes consistently below −20 dB SPL.

F. SOAE measurements

Three-minute ear canal recordings were made in quiet to determine the presence of SOAEs. Recordings were typically made in the middle of the threshold measurements and at the very end of the session, if not also in the middle of the SFOAE measurements when time allowed. A fast Fourier transform was performed on each second of the recording, and the median amplitude (across all 180 spectra) for each 1-Hz-wide frequency bin was used to construct the final ear canal spectrum. The spectrum of the microphone signal was also continuously monitored throughout each test session to ensure that any SOAEs within the frequency range of the measurements did not exceed a peak spectral amplitude of −10 dB SPL.

G. Screening protocol

Ten of the 12 subjects were selected from a group of recruits who participated in a 2-h screening session. The screening was used to identify subjects who (1) met the audiometric, tympanometric, and otoscopic criteria, (2) could perform the threshold measurements in a reasonable amount of time (less than 1 min per frequency), and (3) had measurable SFOAEs for an L_p of 18 dB FPL but no strong SOAE activity (i.e., SOAEs with peak amplitudes > −10 dB SPL) for at least a one-half-octave span between 2 and 5 kHz. During the screening session, thresholds and SFOAEs were obtained for a single test ear, which was selected either randomly or so as to avoid strong SOAE activity in the frequency range of interest. SFOAE measurements during the screening were typically made between 1412 and 5708 Hz in 1/100-octave steps, though alternatively narrower or wider frequency ranges were used for some of the earlier recruits. Thresholds were obtained with a coarser resolution (∼1/10-octave steps) over the same range, primarily to orient the subject to the threshold measurement procedure. Two additional subjects were selected based on having approximately met the same screening criteria via other preliminary measurements, which used different methods for calibrating and/or SFOAE measurement.

H. Test protocol

The 12 subjects who met the screening criteria and were willing to participate further completed two additional 3-h testing sessions, typically separated by a week (mean ± 1 SD = 7.5 ± 2.97 days; range = 3–14 days). Measurements in the two sessions were identical, such that the responses could be averaged across sessions. Test ears (8 left, 4 right) were the same as those used in the screening measures.

In each session, thresholds and SFOAEs were measured at the same 47 frequencies over a ∼0.46-octave span, achieving a resolution of ∼1/100-octave. The center frequency ($f_{\mathrm{c}}$) of each span was individually determined so that the test range included at least one SFOAE amplitude peak exceeding −10 dB SPL for an L_p of 18 dB FPL. Test spans were further adjusted to exclude any SOAEs with peak amplitudes exceeding −10 dB SPL. Measurements were focused between 2 and 5 kHz to take advantage of the lower measurement system noise floor in this frequency range, as well as to avoid low-frequency physiological noise due to heartbeat or breathing. Additionally, preliminary measurements suggested that average threshold and SFOAE levels were relatively constant between 2 and 5 kHz, whereas lower thresholds and larger SFOAE responses were often observed between ∼0.75 and 2 kHz. Since this frequency dependence may be related to cochlear and/or middle ear properties, an $f_{\mathrm{c}}$ of 4 kHz was used whenever possible, thus minimizing such sources of variability. However, this was feasible for only half of the subjects due to their SFOAE and SOAE profiles, thus $f_{\mathrm{c}}$ fell between 2.2 and 4.312 kHz. Across all subjects, test frequencies ranged from 1.876 to 5.108 kHz, with a mean of 3.576 kHz and median of 3.672 kHz.

Threshold measurements were split between two uninterrupted 20–30 min blocks, with thresholds obtained for either the lower or higher 25 frequencies of the total 47 frequency span within each block. Test frequency order was randomized within a measurement block. Thresholds at the three frequencies overlapping the two frequency lists were averaged together to create a smoother final threshold curve. Subjects were given a short break between the measurement blocks, during which an SOAE recording was made.

Following the threshold measurements, SFOAEs were obtained for probe levels of 0, 6, 12, and 18 dB FPL at the same 47 frequencies, as well as two additional frequencies 1/100-octave below and above the 0.46-octave span. This allowed for the calculation of the SFOAE phase-gradient delay at the first and last frequencies tested in the threshold measurements. SFOAE responses at all f_p's were obtained for one L_p at a time. While f_p was presented in a fixed order, from low to high frequencies, the ordering of L_p was randomized for each test session. During the SFOAE measurements, subjects were instructed to remain awake while watching a subtitled movie.

I. Analysis

1. Microstructure extraction

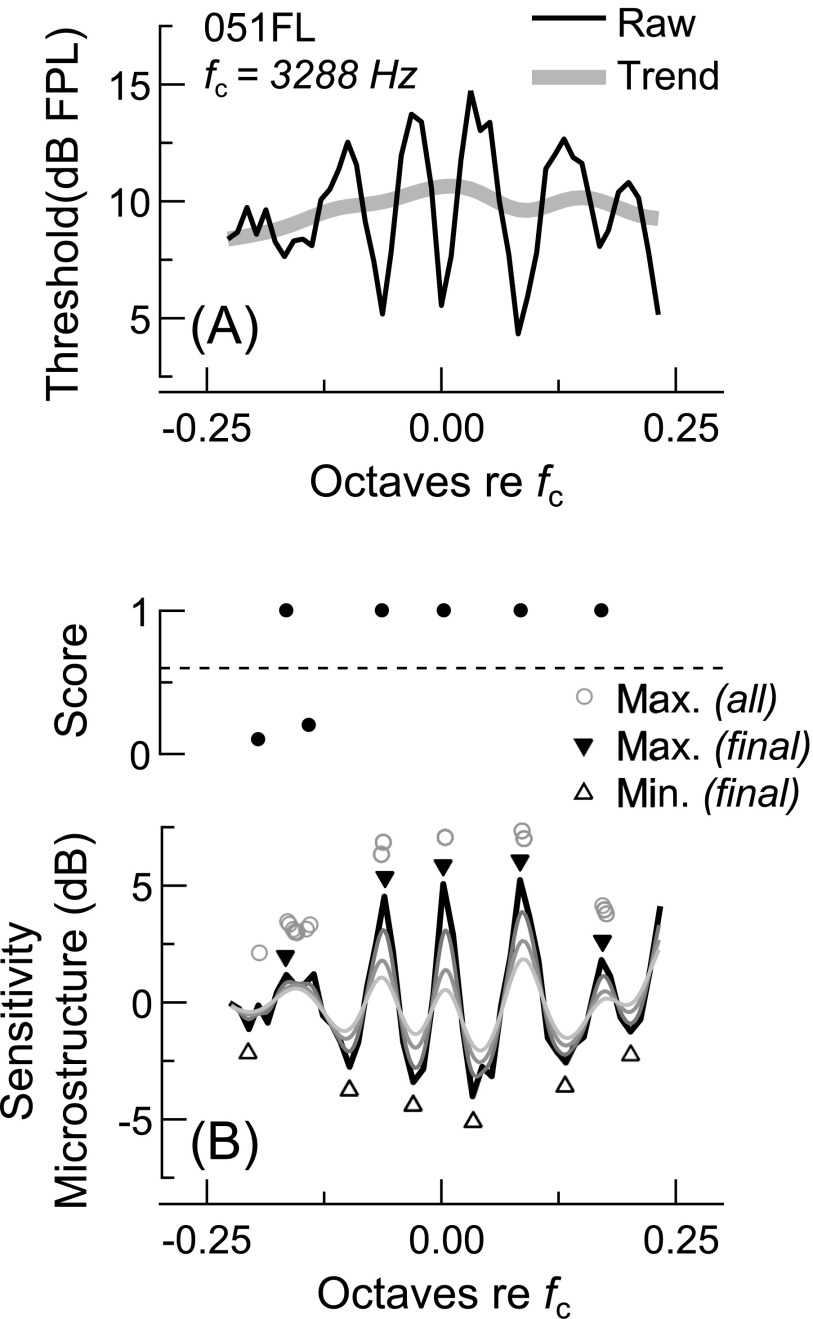
After averaging measurements across the two test sessions, microstructures were extracted from the thresholds, SFOAE amplitudes, and SFOAE delays so that their morphologies could be explicitly compared. Microstructure extraction was achieved by removing the more slowly varying background trends from the raw data, as illustrated in Fig. 1. Trends were estimated by twice-filtering the raw data using a fourth-order, low-pass Butterworth filter with a cutoff frequency of 7 cycles per octave (using the filtfilt.m function in Matlab to perform zero-phase filtering). As threshold microstructure has a periodicity of approximately 10–20 cycles per octave [see Heise et al. (2008) for a review], low-pass filtering with these parameters largely removed the microstructure, leaving just the trend.

FIG. 1.

Microstructure extraction and analysis for subject 051FL. (A) Raw threshold measurements (thin line) were low-pass filtered with a fourth-order Butterworth filter (cutoff frequency = 7 cycles/octave) to determine the background trend (thick line). The trend was then subtracted from the raw thresholds to yield the microstructure. The threshold microstructure was then, was inverted and referred to as the sensitivity microstructure. (B) Sensitivity maxima and minima were determined by low-pass filtering the microstructure ten times (with cutoff frequency = 40 cycles/octave) and finding the zero-crossings in the derivative of the curve resulting from each filtering operation (thin dark-to-light curves show the microstructure filtered 2, 6, and 10 times). Each maximum identified after the first round of filtering was scored for robustness to further smoothing by calculating the fraction of the ten filtering operations after which an extreme was identified within 1/100-octave of its original frequency (all maxima identified after each filtering procedure are shown with circles). Maxima with scores greater than 0.6 [dashed line in top part of (B)] were kept in the analysis. The final frequency and magnitude of each maximum were taken as those of the maximum in the unfiltered microstructure curve occurring within 1/40-octave of its smoothed, filtered frequency (solid triangles). The most negative points occurring 1/10–1/80-octave below or above the maximum were identified as the associated low- and high-side minima (open triangles).

For thresholds and SFOAE amplitudes, trends were extracted from data expressed in dB FPL or SPL, respectively, rather than in linear units, with the microstructure then obtained by subtracting the trend from the raw data (both in dB units). This was not the case for the SFOAE delays, which remained in linear units for the filtering procedure, after which the microstructure was obtained by taking the ratio of the raw delays to the trend. These different approaches were used as they more accurately recovered the trends in SFOAE data synthesized using a highly simplified model (see the appendix). Delay microstructure ratios were converted to dB after eliminating any negative delay ratios, and both the SFOAE amplitude and delay microstructures were clipped to fall between ±14 dB, so as to prevent subsequent analyses from being overly influenced by data with low signal-to-noise-ratio (SNR). The threshold microstructure was inverted to be of the same sign as the SFOAE microstructures, and is therefore referred to as sensitivity microstructure throughout the text.

2. Microstructure analysis

Microstructures extracted from the different measurements were first compared using simple Pearson product-moment correlations. In a second approach, we identified maxima and minima in the sensitivity microstructure curve and then compared the microstructure depth, or level difference in dB, for each maximum-minimum pair with that of the nearest maximum-minimum pair in the SFOAE amplitude or delay microstructures. An objective but necessarily arbitrary procedure was used to identify “true” sensitivity maxima and minima (as opposed to random fluctuations), as described in Fig. 1(B). Extrema in the SFOAE amplitude and delay microstructure curves were then identified within 1/50-octave of those in the sensitivity microstructure, and depths were computed for each maximum-minimum pair. This approach therefore allowed for slight frequency shifts between the microstructures, and reduced the influence of random measurement noise in the comparisons.

Identifying extrema in the microstructure curves was also necessary to determine how microstructure periodicity (i.e., the frequency distance between adjacent maxima) and depth related to SFOAE delays and magnitudes, respectively. These analyses are described in more detail in Sec. III.

3. SFOAE response interpolation

While the above analyses were initially performed using SFOAE data collected at each L_p, we found it useful to also analyze SFOAE responses estimated for an L_p of 0 dB sensation level (SL), which we defined as the level of the threshold trend at each frequency. Using a constant SL probe facilitated comparison across subjects and frequency ranges, as a fixed-FPL L_p could be somewhat below or above threshold for a given subject and test frequency (the average threshold for each subject ranged from 3.54 to 18.40 dB FPL). Additionally, responses for a 0 dB SL probe should presumably best approximate the SFOAEs elicited during the threshold measurements. Responses were estimated via linear interpolation of the measured SFOAE amplitudes and phases. Noise floor amplitudes were taken as the higher of the two that would have been used in the interpolation.

III. RESULTS

A. Individual measurements

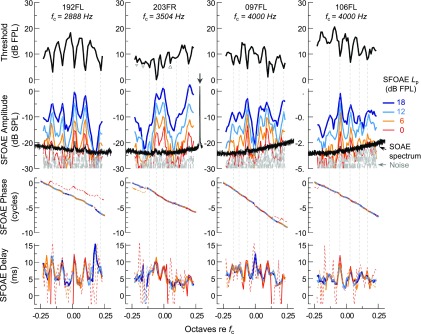
Thresholds and SFOAE amplitudes, phases, and delays are shown for four representative subjects in Fig. 2. All measures exhibited a degree of quasiperiodic microstructure superimposed on a more slowly varying background trend, with both the trends and microstructures being idiosyncratic to each ear. As indicated by the dashed vertical lines, fluctuations in thresholds were closely mirrored by those in the SFOAE responses from the same ear, with threshold minima aligning well in frequency with peaks in SFOAE amplitudes and delays. Since SFOAE delays were computed from the negative slope of the SFOAE phase curve, delay peaks also correspond to downward ripples in the phase curve, though such phase fluctuations are not obvious at the scale shown. Low-level SOAEs also occurred at some threshold minima frequencies. These are evident as small peaks in the ear canal spectrum measured in quiet (black trace shown with the SFOAE amplitudes).

FIG. 2.

(Color online) Behavioral thresholds and SFOAE amplitudes, phases, and delays for four subjects. Subject identifiers and the center frequency ($f_{\mathrm{c}}$) of each 0.46-octave range are shown at the top of each column. Dashed vertical lines illustrate the close frequency correspondence between threshold minima and peaks in SFOAE amplitudes and delays. Low-level SOAE peaks (black spectra) were also occasionally observed at these frequencies, though each $f_{\mathrm{c}}$ was adjusted to avoid larger SOAEs (see arrow for subject 203FR in the second column). Vertical lines were not drawn for threshold minima with depths of less than 2 dB (open triangles) or for one minimum not meeting the criterion of the automated, objective microstructure-identification procedure (closed triangle) described in Fig. 1. Such frequencies were not associated with strong fluctuations in SFOAE amplitudes or delays. Dashed portions of the phase curves indicate data with SNR < 6 dB. For the delay curves, dashed portions indicate where the SNR was less than 6 dB at two or more of the three frequencies used to compute the delay. These plotting conventions are maintained in all subsequent figures.

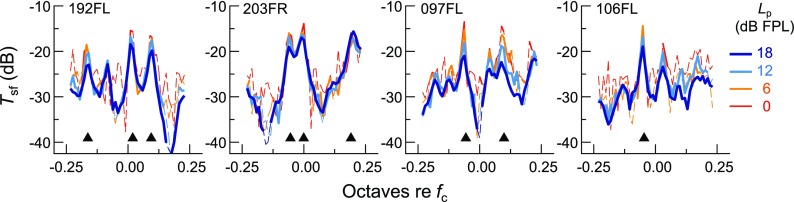
SFOAE microstructure was generally stable across probe level due to the near-linear amplitude growth and phase stability with increasing L_p. However, compressive growth was often observed at amplitude peaks, such that the amplitude microstructure became less pronounced at higher L_p. This is illustrated in Fig. 3, which shows the SFOAE amplitudes normalized to the stimulus level, or what is referred to as the SFOAE transfer function ($T_{\text{sf}}$) magnitude. Between the lowest and highest L_p, T_sf peak magnitudes typically decreased by 3–6 dB, but could be reduced by as much as 9 dB. While low-level SOAEs were often present at the magnitude peaks (triangles indicate SOAE frequencies), their presence and/or spectral level did not explain the degree of nonlinearity observed. An overall decline in T_sf magnitude at frequencies other than those of maxima was only occasionally observed at an L_p of 18 dB FPL. Changes in the SFOAE delay microstructure with L_p were less clear, though SFOAE delays were sometimes more peaked at the lowest L_p. SFOAE delays also exhibited more erratic fluctuations and negative values at low probe levels, presumably due to noise in the phase estimates (thin dashed portions of the phase curves indicate SNR < 6 dB).

FIG. 3.

(Color online) SFOAE transfer function ($T_{\text{sf}}$) magnitudes for each subject in Fig. 2, illustrating the similarity of the SFOAE amplitude microstructures across L_p. SFOAE amplitude growth was near-linear at many frequencies, as evidenced by constant $T_{\text{sf}}$ magnitude across L_p. However, growth was sometimes more compressive near amplitude peaks, particularly those associated with SOAEs (black triangles), such that $T_{\text{sf}}$ magnitudes decreased with increasing L_p at these frequencies. Thin dashed portions of each curve indicate data with SNR < 6 dB.

In addition to the more rapid fluctuations observed in the SFOAE amplitudes across frequency, which typically did not exceed 15 dB in magnitude, much deeper (>20 dB) and/or wider notches in SFOAE amplitude were also occasionally observed. Such notches are evident at ∼0.18 octaves re f_c for subject 192FL, −0.15 and 0.07 octaves re f_c for 203FR, and 0 and 0.17 octaves re f_c for 097FL. The narrow notches for subjects 192FL and 097FL were associated with a brief steepening of the phase curve and thus a peak in SFOAE delay, while the broader valleys for subject 203FR were associated with relatively shallow phase slopes. These amplitude and phase fluctuations did not correlate with any features in the threshold curve. Whether such variations should be considered part of the microstructure or the background trend is somewhat arbitrary, and their presence slightly complicated efforts to separate the two.

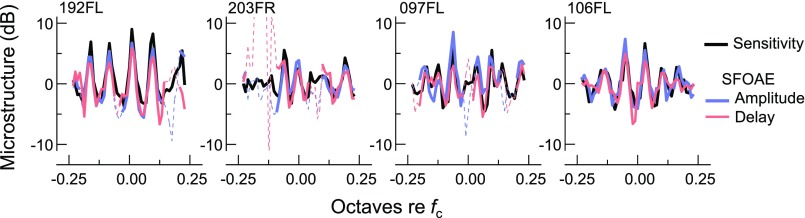
B. A common microstructure

For a more explicit comparison, microstructures were extracted from the raw data by removing the underlying background trend, which was computed via low-pass filtering (see Sec. II I 1). As illustrated in Fig. 4, microstructures extracted from the threshold curves—here inverted and referred to as the sensitivity microstructure—were strikingly similar to the SFOAE amplitude and delay microstructures, both in the frequency locations of their maxima and in their overall morphology. Discrepancies between microstructures primarily occurred when the SFOAE SNR was low (indicated by thin dashed lines). To facilitate comparison across subjects, the SFOAE microstructures shown here were extracted from SFOAE responses estimated for an L_p of 0 dB SL (see Sec. II I 3), though similar results were observed when comparing microstructures from the SFOAEs measured at the different fixed-FPL probe levels.

FIG. 4.

(Color online) Microstructure comparisons for the four subjects in Fig. 2. The morphology of the sensitivity microstructure curves (black lines) was highly similar to those of the SFOAE amplitude and delay microstructures, shown here for data estimated for an L_p of 0 dB SL. Dashed portions of the SFOAE microstructures indicate where the SNR was less than 6 dB.

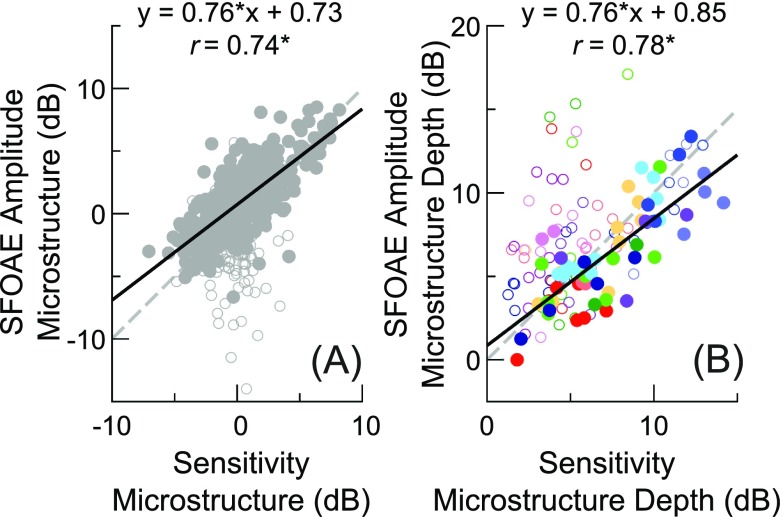
Pearson product-moment correlations between sensitivity and either SFOAE amplitude or delay microstructure magnitudes were significant (p < 0.05) for 11 of the 12 subjects when using SFOAE responses estimated for an L_p of 0 dB SL and excluding data with SNR < 6 dB. Individual correlation coefficients could exceed 0.9, with average coefficients of 0.67 and 0.68 found for comparisons of sensitivity vs SFOAE amplitude and delay microstructures, respectively. When compared across all subjects and frequencies, highly significant correlations were found between the magnitudes of the sensitivity microstructure and the microstructures of both SFOAE amplitudes ($r=0.74;p<0.0001$) and delays ($r=0.70;p<0.0001$) estimated for an L_p of 0 dB SL. Sensitivity and SFOAE amplitude microstructure magnitudes are compared in Fig. 5(A) (comparisons with SFOAE delay microstructures not shown for simplicity). Note that the spread of SFOAE microstructure magnitudes could be quite large, particularly at frequencies where sensitivity microstructure magnitudes were low. Such discrepancies could be due to subtle frequency shifts between the microstructures, larger measurement noise in the SFOAE responses (even after applying an SNR criterion of 6 dB), and/or the presence of deep notches or valleys in the SFOAE amplitudes, which were sometimes still present in the microstructure curves.

FIG. 5.

(Color online) (A) Comparison of sensitivity and SFOAE amplitude microstructure magnitudes across all frequencies and subjects (n = 564), using SFOAE data estimated for an L_p of 0 dB SL. Pearson correlation coefficients and linear regression fits (black lines) were computed only for data where the SFOAE SNR was at least 6 dB (filled symbols; n = 400). Open symbols indicate data not meeting the SNR criterion. (B) As in (A), but instead only showing the depth (level difference) for each identified sensitivity maximum-minimum pair versus the corresponding depth in the SFOAE amplitude microstructure ($n=157$). The correlations and linear regression fit were computed only for data where the SNR at both the SFOAE maximum and minimum was at least 6 dB (n = 57). Asterisks indicate a significant ($p<0.0001$) linear correlation and the dashed lines show unity slope. Symbol shades are used to distinguish data from different subjects in (B).

To further evaluate the similarity of the microstructure magnitudes, the depth, or level difference, for each adjacent maximum-minimum pair in the sensitivity microstructure was calculated and compared with the depth of the corresponding maximum-minimum pair in the SFOAE microstructure, as shown in Fig. 5(B). An automated procedure was used to identify extrema in the microstructures extracted from thresholds and SFOAE responses estimated for an L_p of 0 dB SL (see Sec. II I 2). This analysis allowed for a small amount of shift between the minima and maxima frequencies identified in the sensitivity and SFOAE amplitude/delay curves, and thus is distinct from that shown in Fig. 5(A), which compared the magnitudes of the microstructure curves at each and every test frequency. Nevertheless, while highly significant correlations were found between the microstructure depths observed in threshold sensitivity and both SFOAE amplitudes ($r=0.78;p<0.0001$) and delays ($r=0.72;p<0.0001$), this approach only marginally improved the correlations beyond those obtained between the raw microstructure magnitudes. As indicated by the regression line slope falling below 1, sensitivity microstructure depths tended to exceed the corresponding SFOAE microstructure depths by several dB, at least for data points where the SNR was at least 6 dB at both the SFOAE maximum and minimum (filled circles). The difference in depths is likely due to the compressive growth of SFOAE amplitudes at microstructure maxima, which was observed even at near-threshold levels (Fig. 3).

Despite such discrepancies, the data overall support the conclusion that there is a common microstructure in the behavioral thresholds and SFOAE responses to near-threshold-level tones. The following analyses assess whether the frequency periodicity and depth of this microstructure are related to SFOAE phase-gradient and magnitude in a manner consistent with the intracochlear reflection framework. While the microstructures extracted from the behavioral or SFOAE responses could each be analyzed independently, we focused our analysis on the sensitivity microstructure, so as to take advantage of the wider range of depths and the reduced influence of measurement noise.

C. Relationship between microstructure periodicity and SFOAE phase accumulation

If the common microstructure described above is due to intracochlear reflection of the waves that give rise to SFOAEs, its frequency periodicity should be inversely correlated with SFOAE phase vs frequency gradients, i.e., phase-gradient delays (Kemp, 1979a). This is because the microstructure frequency periodicity is theoretically determined by the round-trip delay associated with the propagation and reflection of waves traveling from the base to the SFOAE generation region and back to the stapes. Microstructure peaks occur at frequencies where the phase accumulation associated with this round-trip delay is a whole number of cycles. Assuming that delays due to reflection at the stapes and transmission through the middle ear and ear canal are relatively small, the round-trip phase accumulation is essentially that of the SFOAE measured in the ear canal. Thus, the SFOAE phase should accumulate one cycle between the frequencies of adjacent microstructure peaks, as has been shown previously for adjacent SOAEs (Bergevin et al., 2012).

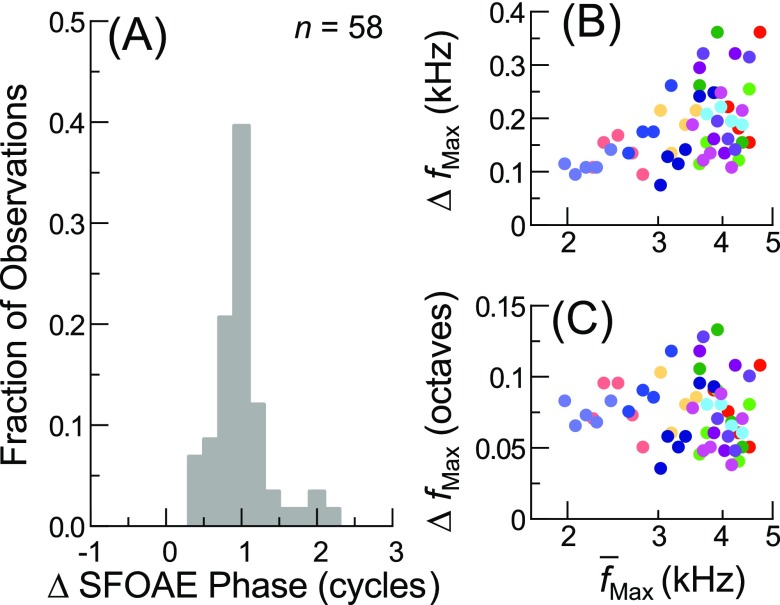
Consistent with this, the SFOAE phase accumulated between frequencies of adjacent threshold sensitivity maxima was typically close to one cycle, as shown in the histogram in Fig. 6(A). Phase accumulations were determined using responses for an L_p of 18 dB FPL, after subtracting the estimated phase accumulated due to round-trip travel through the middle ear [194 μs, the sum of the forward and reverse middle ear delays previously estimated from data in Puria (2003), by Dong and Olson (2006)] and ear canal [140 μs, from Rasetshwane and Neely (2011b)]. Not compensating for these additional delays only slightly reduced the fraction of observations occurring within the 0.9–1.1 cycle bin (from 0.40 to 0.36). Histograms produced using SFOAE phase data for lower L_p were also centered around one cycle but less strongly peaked. Variability in SFOAE phase vs frequency gradients across frequency and ears can therefore explain some of the variation in both the absolute and relative frequency spacings of microstructure maxima, shown in Figs. 6(B) and 6(C).

FIG. 6.

(Color online) (A) Histogram of the SFOAE phase accumulated between sensitivity microstructure maxima, using the phases from SFOAE responses for an L_p of 18 dB FPL (bin width = 0.2 cycles; n = 58 pairs of adjacent maxima). There is a clear peak at one cycle of phase accumulation. (B) and (C) The frequency difference ($\Delta f_{\text{Max}}$) between adjacent sensitivity maxima in Hz (B) or octaves (C) plotted as a function of their geometric mean frequency. The absolute frequency difference increased with frequency, thus maintaining a relative spacing of roughly 10–20 cycles/octave, though both the absolute and relative spacings were variable overall, presumably due in part to variation in SFOAE phase gradients across frequency and ears.

Slight deviations from one cycle of SFOAE phase accumulation per microstructure period likely resulted from imprecise determination of the sensitivity maxima frequencies, as the phase difference between adjacent test frequencies was typically 0.1 to 0.2 cycles. Additionally, two cycles of SFOAE phase were sometimes accumulated between sensitivity maxima frequencies. This was observed for the fourth and fifth sensitivity maxima of subject 192FL and for the third and fourth maxima of subject 097FL (see first and third columns of Fig. 2). For both subjects, the absence of a threshold minimum at a frequency in between was associated with a deep null in SFOAE amplitude. This suggests that while there may be a set of potential maxima frequencies determined by the intracochlear SFOAE delay, additional conditions must be satisfied for maxima to be strong—namely, the generation of a sufficiently large SFOAE.

After subtracting the nearest integer number of cycles from the SFOAE phase accumulations, so as to reduce the influence of potentially “skipped” microstructure maxima, the mean and median phases accumulated between adjacent maxima were −0.013 and −0.0018 cycles (re one cycle), respectively. The distribution of phase accumulations was significantly different from uniform (Kolmogorov-Smirnov test; $D=0.69,p<0.0001$). Similar results were found when using data for other L_p.

D. Relationship between microstructure depth and SFOAE magnitude

The relationship between microstructure depth and evoked OAE magnitude has not been examined previously in any detail. At least a gross correlation between microstructure depth and SFOAE amplitude is anticipated, given that both should depend on the strength of the reflections that give rise to the SFOAE. However, as explored below, such a relationship should only be observed if the reflectance at the stapes and the influence of middle ear transmission on SFOAE amplitudes are similar across frequency and ears.

Microstructure depth is theoretically determined by the ratio of the maximum constructive and destructive effects of intracochlear reflection. As outlined in the appendix, these effects can be described formally in terms of the more apical SFOAE-generating “reflectance,” here termed $R_{\mathrm{a}}$, and the basal reflectance at the stapes, $R_{\mathrm{b}}$. Briefly, $R_{\mathrm{a}}$ is defined as the ratio of the net backward-propagating wave (resulting from backscattering of the forward-going wave as it travels along the cochlear partition) to the forward-propagating wave, as evaluated at the cochlear base. Likewise, $R_{\mathrm{b}}$ is the ratio of the reflected to incident waves at the stapes. Following Eq. (A1) in the appendix, the microstructure depth is given (in dB) by

$$20\hspace{0.17em}{\text{log}}_{10}\left(\frac{1+\left|R_{\mathrm{a}}{R}_{\mathrm{b}}\right|}{1-\left|R_{\mathrm{a}}{R}_{\mathrm{b}}\right|}\right),$$ (1)

as long as $R_{\mathrm{a}}$ and $R_{\mathrm{b}}$ are linear and $\left|R_{\mathrm{a}}{R}_{\mathrm{b}}\right|<1$. Note that this description only approximately holds, since $R_{\mathrm{a}}$ may depend on the stimulus level even near threshold, as evidenced by the nonlinearities observed in $T_{\text{sf}}$ magnitudes (Fig. 3). Additionally, even the presence of small SOAEs could suggest that the round-trip gain associated with intracochlear reflection ($\left|R_{\mathrm{a}}{R}_{\mathrm{b}}\right|$) approaches or exceeds 1, such that reflections become self-sustaining. Stabilization of the amplitudes of these self-sustaining oscillations also requires that $R_{\mathrm{a}}$ be nonlinear, as they would otherwise continue to grow with each round of reflection. Nevertheless, to the extent that this simplified, linear formulation holds, and if $R_{\mathrm{b}}$ is held constant, then microstructure depth should grow exponentially with increasing $R_{\mathrm{a}}$ magnitude when both are expressed in dB, as shown in Fig. 7(A).

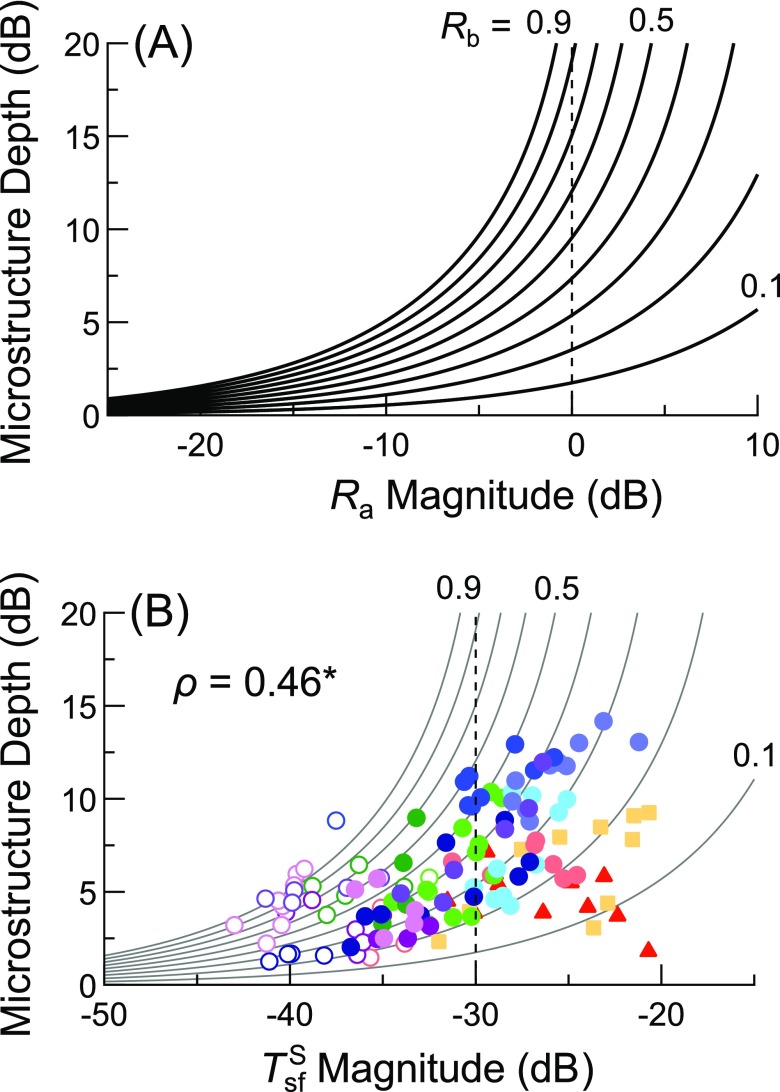
FIG. 7.

(Color online) (A) Theoretical dependence of microstructure depth on the magnitude of $R_{\mathrm{a}}$, as defined in Eq. (1), for values of $\left|R_{\mathrm{b}}\right|$ ranging from 0.1 to 0.9 in 0.1 steps (values of 0.1, 0.5, and 0.9 are noted next to the appropriate curves). (B) Microstructure depth for each pair of adjacent sensitivity maxima and minima plotted versus the $T_{\text{sf}}^{\mathrm{S}}$ magnitude calculated at their geometric mean frequency, using SFOAE responses for an L_p of 0 dB SL. The Spearman's rank correlation coefficient (ρ) is shown for all points with an SFOAE SNR of at least 6 dB (filled symbols); asterisk indicates p < 0.0001. The curves from (A) are also shown after horizontally shifting them by −30 dB, an estimate of $|G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})|$ from Puria (2003). Vertical dashed lines indicate where $\left|R_{\mathrm{a}}\right|=1$ (i.e., 0 dB).

To determine whether a similar relationship exists between the measured microstructure depths and SFOAE amplitudes, we derived a quantity that should be roughly proportional to $R_{\mathrm{a}}$. This was achieved by first normalizing SFOAE amplitudes to the stimulus level (thus obtaining $T_{\text{sf}}$), and then smoothing this transfer function to remove the microstructure. In other words, we assumed that the background trend in the SFOAE amplitudes was proportional to the magnitude of the SFOAE-generating reflectance. From the equation describing the SFOAE pressure given in the appendix [Eq. (A2)], removing the terms for the stimulus pressure and the microstructure yields the smoothed SFOAE transfer function

$$T_{\text{sf}}^{\mathrm{S}}=G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})R_{\mathrm{a}},$$ (2)

where $G_{\text{me}}^{\text{RT}}$ is the round-trip pressure gain due to forward and reverse middle ear transmission (as measured in human cadaveric temporal bones by Puria, 2003) and the term $1+R_{\mathrm{b}}$ accounts for the fact that the total pressure driving the middle ear in reverse is the sum of the incident and reflected pressure waves at the stapes. Since $T_{\text{sf}}^{\mathrm{S}}$ is proportional to $R_{\mathrm{a}}$, microstructure depth should therefore increase exponentially with increasing $T_{\text{sf}}^{\mathrm{S}}$ magnitude, as long as $R_{\mathrm{b}}$ and $G_{\text{me}}^{\text{RT}}$ are assumed to be similar across frequency and ears.

Though the validity of this assumption is questionable, microstructure depth was in fact positively correlated with $T_{\text{sf}}^{\mathrm{S}}$ magnitudes (Spearman's $\rho =0.46;p<0.0001$ for data with SNR > 6 dB; $\rho =0.56;p<0.0001$ for all data), as shown in Fig. 7(B). Here the depth for each maximum-minimum pair identified in the sensitivity microstructure curves is plotted against the $T_{\text{sf}}^{\mathrm{S}}$ magnitude computed at the geometric mean frequency of the maximum and minimum, using SFOAE responses estimated for an L_p of 0 dB SL.³ The distribution of the data, though somewhat variable, was roughly consistent with the theoretical form of the relationship, with an upward curvature evident for the central cluster of points. Two subjects with particularly large SFOAE amplitudes but little microstructure (data indicated by squares and triangles) fell somewhat outside of this trend.

Since $T_{\text{sf}}^{\mathrm{S}}$ is equivalent to $R_{\mathrm{a}}$ scaled by $G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})$, the theoretical curves [from Fig. 7(A)] are shown in Fig. 7(B) after translation along the x axis by −30 dB, an estimate of the magnitude of this latter term from the data of Puria (2003) at 3.576 kHz, the mean test frequency across all of our measurements. Assuming this value of $G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})$, the data are largely accommodated by the theoretical curves assuming that $\left|R_{\mathrm{b}}\right|$ falls between 0.2 and 0.5, a range of values similar to that also reported by Puria (2003) for frequencies between 2 and 5 kHz. Thus, the data are consistent with reasonable estimates of middle ear parameters, and a small amount of variation in $R_{\mathrm{b}}$ and/or $G_{\text{me}}^{\text{RT}}$ across frequency and/or ears could readily account for the variability observed in the data. Note that using SFOAE responses for a constant SL probe likely reduced variability related to differences in calibration accuracy or forward middle ear transmission across frequency or subjects. This is supported by the fact that computing $T_{\text{sf}}^{\mathrm{S}}$ from SFOAE responses for any fixed-FPL L_p resulted in weaker correlations (Spearman's $\rho \le 0.32$ for data with SNR > 6 dB, with significant correlations found only for an L_p of 12 and 18 dB FPL). It is also worth noting that, regardless of the L_p used to compute $T_{\text{sf}}^{\mathrm{S}}$, most of the data points fell to the right of the vertical line indicating where $\left|R_{\mathrm{a}}\right|=1$ when assuming a $G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})$ magnitude equivalent to −30 dB, suggesting that the data were associated with high values of $R_{\mathrm{a}}$.⁴

Unfortunately, the magnitudes of $R_{\mathrm{b}}$ or $G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})$ could not be confidently estimated for any given ear, as the individual data were typically sparse and/or did not form a well-defined distribution. Nevertheless, an increase in microstructure depth with increasing $T_{\text{sf}}^{\mathrm{S}}$ magnitude was often observed for individual ears. Using SFOAE data for an L_p of 0 dB SL, significant (p < 0.05) Spearman's rank correlations were obtained between $T_{\text{sf}}^{\mathrm{S}}$ magnitude and microstructure depth in 6 of the 12 subjects (mean ± 1 SD for $\rho =0.47\pm 0.43$ for all subjects), significant Pearson's product moment correlations were found in eight subjects ($r=0.46\pm 0.49$ for all subjects), and linear regression slopes were positive in ten subjects (slope $=0.38\pm 0.38$ for all subjects). Thus, both the individual and group data suggest a positive association between SFOAE magnitudes and microstructure depth, consistent with a dependence of both quantities on the strength of the underlying SFOAE generating mechanism.

IV. DISCUSSION

A. A common microstructure

The present report confirms the frequency correspondence among threshold sensitivity maxima, SOAEs, and peaks in the amplitudes of evoked OAEs (e.g., Horst et al., 1983; Zwicker and Schloth, 1984; Long, 1984) and further demonstrates that peaks in OAE delays also occur at the same frequencies. Moreover, the microstructures extracted from the behavioral and SFOAE measures were highly similar not only in their frequency periodicity, but in their morphologies and magnitudes. Thus, the data provide strong evidence that threshold and SFOAE responses share a common microstructure.

Previous examinations of the relationships among threshold and evoked OAE microstructures have been relatively few in number, have presented data from only a few subjects in a largely qualitative manner, and have not explicitly compared the microstructures of thresholds and SFOAEs evoked by discrete tones. For instance, Horst et al. (1983) demonstrated a frequency correspondence between certain sensitivity maxima and large transient-evoked otoacoustic emission (TEOAE) amplitude peaks, but did not note whether other maxima corresponded to lower-level TEOAE peaks, nor whether any such peaks were dominated by SOAE activity synchronized to the stimulus.⁵ In a more compelling example, Zwicker and Schloth (1984) showed a close correspondence between most sensitivity maxima and TEOAE amplitude peaks in a single ear without measurable SOAE activity. While sensitivity maxima with depths exceeding 10 dB coincided well with TEOAE maxima, five out of the nine sensitivity maxima with depths between 5 and 10 dB fell either at TEOAE amplitude minima or between amplitude minima and maxima, and one fairly large TEOAE amplitude peak was not associated with a sensitivity maximum (see their Figs. 6 and 7). Similarly, Uppenkamp and Neumann (1996) found (also in a single ear) that the microstructures in sensitivity and chirp-evoked SFOAE amplitudes shared a common periodicity but were essentially misaligned by 0.25–0.5 cycles.

Given the near-equivalence of the spectra of OAEs evoked by discrete tones, swept tones, and clicks (Kalluri and Shera, 2007a, 2013), the origin of the discrepancies between sensitivity and OAE microstructures in previous studies is unclear. It is possible that responses to transient or swept-frequency stimuli presented at near-threshold levels are more subject to nonlinear and dynamic interactions, particularly when there are multiple, long-lasting response components, such as synchronized SOAEs. For instance, Kalluri and Shera (2007a) found that certain synchronized SOAE components could alternatively enhance or decrease click-evoked OAE amplitudes measured repeatedly from the same ear. Such interactions could conceivably result in differences in the spectra of OAEs evoked by clicks or chirps vs single tones.

Though the sensitivity and SFOAE microstructures were highly similar, sensitivity microstructure was often several dB deeper than the associated SFOAE amplitude and delay microstructures. This difference was likely related to the compressive SFOAE growth observed at microstructure peaks, and the comparison of an iso-response (threshold) to an iso-input (SFOAE) measurement. Microstructure magnitudes may be more similar when using SFOAE data for lower L_p, where SFOAE amplitude growth is less compressive, though such comparisons would be compromised by poor SNR. Alternatively, SFOAE “thresholds” could be obtained, though the wide variation in overall SFOAE magnitudes would make it difficult to establish a single response criterion for all subjects and frequencies.

Other discrepancies between the microstructures could be attributed to measurement noise, artifacts of the microstructure extraction procedure, or additional sources of spectral fluctuations idiosyncratic to the behavioral and OAE measures. For instance, the deep, widely-spaced notches observed in SFOAE spectra were not associated with similar fluctuations in sensitivity. Such notches occurred even at frequencies where microstructure maxima were expected based on the SFOAE phase accumulation, and were likely due to interference between reverse-going waves arising from different SFOAE reflection sites and/or sources. Destructive interference would diminish the net reverse-propagating wave (and thus, the magnitude of the wave reflected at the stapes) without influencing the forward-propagating, stimulus-driven wave.

B. Comparison with ripples in ear canal pressure

It is important to note that the common microstructure described here was only observed after SFOAE responses were appropriately separated from the evoking stimulus pressure using the suppression method. In some previous reports, SFOAEs have been investigated by simply quantifying the ripples in the total ear canal pressure as the frequency of the stimulus tone is swept (e.g., Zwicker and Schloth, 1984; Lutman and Deeks, 1999). The ripples result from interference between the stimulus and evoked SFOAE at the plane of the probe microphone, such that the ripple magnitude and periodicity is determined by the relative amplitudes and delays of the stimulus and SFOAE. Since maximal constructive interference occurs when the SFOAE phase has accumulated an integer number of cycles relative to the stimulus phase, the ripple periodicity is similar to that of threshold microstructure. However, the sign, magnitude, and precise frequency location of the ripples are typically not equivalent to the threshold fluctuations (Wilson, 1980; Long, 1984; Lutman and Deeks, 1999). This is because the presence of ripples in the total pressure implies only that the phase of the SFOAE rotates rapidly relative to that of the stimulus, and does not require that the evoked SFOAE exhibit strong microstructure.

Discrepancies in the sign of the ripples in ear canal pressure and the sensitivity/SFOAE microstructure are also likely due to the fact that the SFOAE phase reflects not only the intracochlear delay but also delays associated with ear canal and middle ear transmission. In the present study, SFOAE maxima were noted to interfere either constructively or destructively with the stimulus pressure, in a manner that was variable across frequency and ears (not shown). Most often, however, the ear canal pressure and sensitivity/SFOAE microstructures were in phase near 3 kHz and out of phase closer to 4 kHz. This difference in sign is consistent with the influence of the round-trip ear canal and middle ear delay (estimated to be 334 μs, see Sec. III C), as such a delay would produce an additional 1 or 1.34 cycles of SFOAE phase accumulation at 3 and 4 kHz, respectively, relative to the intracochlear delay.

C. Comparison with DPOAE microstructure

The common microstructure described here is also anticipated to be related, but not identical, to that observed in distortion product (DP) otoacoustic emission (DPOAE) spectra (see Talmadge et al., 1998, for review). DPOAEs are evoked by two tones with frequencies f₁ and f₂ and measured at frequencies ($f_{\text{dp}}$) that are arithmetic combinations of f₁ and f₂. For the $2f_1-f_2$ DPOAE (and perhaps other DPOAEs), quasiperiodic amplitude and phase fluctuations are attributed to interference between two components. The first is generated near the f₂ tonotopic location and propagates basally, while the second arises from distortion product (DP) energy propagating apically to its own characteristic place, thus eliciting an SFOAE at $f_{\text{dp}}$ (Kalluri and Shera, 2001). While the phase-gradient of the first component (often referred to as the “distortion” component) is practically flat with frequency, the phase of the second, “reflection” component rotates rapidly. Interference between the two components occurs with a periodicity that is primarily determined by the delay of the reflection component, and therefore resembles that of threshold and SFOAE microstructure. Though multiple reflections of DP energy between the stapes and its sites of origin may also contribute to DPOAE microstructure (e.g., Dhar et al., 2002), the overall microstructure morphology is primarily determined by the relative amplitudes and phases of the two reverse-propagating component sources. This is consistent with the finding that microstructures extracted from DPOAEs and thresholds are not strongly correlated (Lutman and Deeks, 1999).

D. Relationship with SOAEs

Frequency regions containing strong SOAEs were avoided in this study primarily to minimize any perceptual interference resulting from their presence. In addition, SOAEs are thought to result from conditions which violate the assumptions of the equations relating microstructure depth to $R_{\mathrm{a}}$ and $R_{\mathrm{b}}$ (the presence of an SOAE suggests that $\left|R_{\mathrm{a}}{R}_{\mathrm{b}}\right|$ approaches 1, and that $R_{\mathrm{a}}$ is nonlinear), thus limiting the applicability of this formulation. Nevertheless, our measurements support the notion that SFOAE and threshold microstructure are inextricably linked to the mechanisms underlying SOAE generation. In our screening measurements, the largest fluctuations in SFOAE amplitudes and delays for a given ear were typically observed near the frequencies of prominent SOAEs. Our test measurements also revealed that pronounced threshold and SFOAE microstructure could be observed even in the presence of only small humps in the ear canal spectra recorded in quiet. The majority of the 12 subjects possessed at least one such low-level SOAE in the test range, and the microstructure was generally weaker in the absence of such humps. It is unclear whether these humps reflect truly self-sustained activity (where the gain associated with round-trip intracochlear reflection must approach or exceed 1) or if they are in fact emissions evoked by semi-continuous background or physiological noise which are slightly enhanced via the multiple intracochlear reflection process (such that the round-trip gain need not approach 1). At the very least, the observation that large SFOAEs could be evoked at nearby frequencies suggests that these humps were not primarily limited in amplitude by inefficiencies in reverse middle ear transmission.

Note that the presence of large SFOAEs was not sufficient for the observation of SOAEs or microstructure. In fact, the subject with the largest SFOAE amplitudes (triangles in Fig. 7) had relatively weak microstructure and no measurable SOAEs within the frequency range tested. If microstructure and SOAEs arise from reflections of outgoing-SFOAE energy at the stapes, then the latter observation could be explained by a reduced stapes reflectance, which may also be associated with increased reverse middle ear transmission. In other words, less reflection at the middle ear boundary could reduce microstructure and SOAE incidence, while being associated with an increase in the SFOAE pressure produced in the ear canal.

E. Origins of microstructure

Consistent with the intracochlear reflection framework, microstructure periodicity and depth were related to SFOAE phase-gradient delay and magnitude, respectively. To our knowledge, the present report is the first to explicitly demonstrate the accumulation of one cycle of SFOAE phase between adjacent sensitivity microstructure maxima. However, this finding is perhaps unsurprising, as SFOAE phase accumulates an integer number of cycles of phase between SOAE frequencies (Bergevin et al., 2012), and a roughly reciprocal relationship has long been noted between the delays of tone-evoked OAEs or TEOAEs and the frequency spacing between adjacent threshold minima, evoked OAE maxima, and SOAEs (Kemp, 1979a; Zwicker and Schloth, 1984; Konrad-Martin and Keefe, 2003; Shera, 2003).

A relationship between microstructure magnitude and evoked OAE amplitudes has not previously been demonstrated, however. For instance, Horst et al. (1983) reported that no straightforward relationship existed between threshold microstructure depth and the amplitude of the associated TEOAE, though no quantification was provided. In contrast, the present analysis revealed that microstructure depth is positively correlated with SFOAE amplitude—or more specifically, with the magnitude of the smoothed SFOAE transfer function ($T_{\text{sf}}^{\mathrm{S}}$). The form of this relationship, though somewhat variable, was consistent with a dependence of microstructure depth on the magnitude of the underlying SFOAE-generating reflectance, which should be proportional to $T_{\text{sf}}^{\mathrm{S}}$. Variability in this relationship could easily be accounted for by small differences in middle ear transmission and/or $R_{\mathrm{b}}$ across frequency and ears. Some variability may have also been eliminated a priori via the criteria used to select the subjects and frequency regions of study (i.e., measurable SFOAEs but minimal SOAE activity), as well as using SFOAE responses estimated for an L_p of 0 dB SL to compute $T_{\text{sf}}^{\mathrm{S}}$, which likely reduced the influence of any variability in stimulus calibration or forward middle ear transmission.

While consistent with the intracochlear reflection framework, the present data do not rule out other explanations for microstructure. At least in the context of SOAE generation, the more “global” intracochlear reflection or “standing wave” framework (e.g., Shera, 2003) contrasts with an alternative class of models in which active, “local” oscillators (i.e., hair cells) are capable of producing spontaneous vibrations, either alone or via coupling to their neighbors (e.g., Vilfan and Duke, 2008; Wit and van Dijk, 2012; Wit et al., 2012). Such models have primarily been used to explain SOAE generation in nonmammals in which the role of basilar membrane-based traveling waves is uncertain. Despite morphological differences, the inter-relationships among SOAEs and SFOAEs are similar in both mammals and nonmammals such as lizards and barn owls, with SFOAE phase accumulating roughly an integer number of cycles between SOAE frequencies (Bergevin et al., 2015). These details have been reproduced in a model employing locally-coupled oscillators (Wit et al., 2012) rather than intracochlear reflection. However, since the basic requirements of SFOAE generation and a cochlea-middle ear boundary are also met in these species, it is possible that intracochlear reflections may account for the generation of SOAEs and SFOAE microstructure in all cases. Importantly, the precise details regarding how SFOAEs are generated and propagate are not critical to this explanation for microstructure, which merely requires that the SFOAE generation process produces a form of delayed feedback to the cochlea.

F. Estimation of middle ear parameters and their frequency dependence

The intracochlear reflection framework may be further validated and/or explored by independently manipulating $R_{\mathrm{a}}$ and $R_{\mathrm{b}}$ (to the extent that this is possible) and studying how microstructure is affected. Such manipulations may provide insight into the precise form of the relationship between $T_{\text{sf}}^{\mathrm{S}}$ magnitude and microstructure depth. Assuming that the intracochlear reflection framework is applicable in humans, further description of this relationship could yield noninvasive estimates of properties related to middle ear transmission, in particular $R_{\mathrm{b}}$ and $G_{\text{me}}^{\text{RT}}$, or at least offer insight into how these properties change with frequency.

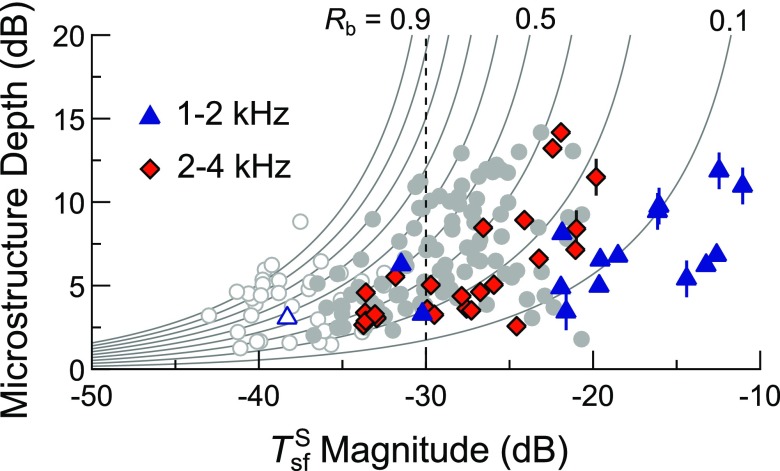
While the present data do not permit precise estimates of any such quantities, the relationship between $T_{\text{sf}}^{\mathrm{S}}$ and microstructure depth was consistent with values of $G_{\text{me}}^{\text{RT}}$ and $R_{\mathrm{b}}$ taken from Puria's (2003) measurements in human temporal bones (approximately −30 dB and 0.2–0.5, respectively) for the 2–5 kHz range. Since the values of $G_{\text{me}}^{\text{RT}}$ and $R_{\mathrm{b}}$ reported by Puria (2003) vary across frequency, the relationship between $T_{\text{sf}}^{\mathrm{S}}$ magnitude and microstructure depth is anticipated to shift to lower or higher values of $T_{\text{sf}}^{\mathrm{S}}$ depending on the frequency range examined. For instance, $G_{\text{me}}^{\text{RT}}$ is least attenuating near 1 kHz, such that a given microstructure depth is expected to be associated with larger SFOAE magnitudes at 1 kHz than those observed at higher frequencies.

Support for this possibility is provided in Fig. 8, which compares microstructure depth and $T_{\text{sf}}^{\mathrm{S}}$ magnitude for all sensitivity maxima observed in a set of preliminary data obtained from 1–4 kHz in one subject.⁶ While the distribution of the data associated with sensitivity maxima frequencies above 2 kHz (diamonds) was comparable to that previously shown in Fig. 7 (gray circles), data associated with maxima below 2 kHz (triangles) tended toward higher $T_{\text{sf}}^{\mathrm{S}}$ magnitudes for a similar range of microstructure depths. The latter data could therefore be better accommodated by the theoretical curves (shown here as in Fig. 7) by assuming less attenuating values of $G_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})$ (perhaps 10 dB less horizontal shift of the theoretical curves) and lower $R_{\mathrm{b}}$ magnitudes, so as to fit the less steeply-sloping form of the distribution. Nevertheless, due to the anecdotal nature of the data and the possible influence of SOAEs in this subject, further examination of these relationships in a larger group of subjects is required. Future work could also evaluate the frequency dependence of the relationship between microstructure depth and $T_{\text{sf}}^{\mathrm{S}}$ magnitude at very low and high frequencies, where middle ear transmission is expected to differ more substantially from that at 1 kHz.

FIG. 8.

(Color online) Microstructure depth vs $T_{\text{sf}}^{\mathrm{S}}$ magnitude (for an L_p of 0 dB SL) for all maximum-minimum pairs observed between 1 and 4 kHz for one subject. The different distributions of data for maxima falling below and above 2 kHz (triangles and diamonds, respectively) suggest that the relationship between depth and $\left|T_{\text{sf}}^{\mathrm{S}}\right|$ varies with frequency, perhaps due to differences in $R_{\mathrm{b}}$ and $G_{\text{me}}^{\text{RT}}$. Symbols marked with vertical lines indicate data for maxima associated with SOAEs greater than −10 dB SPL in amplitude. The data and theoretical curves from Fig. 7(B) (gray circles/curves) are shown for comparison. Dashed vertical line indicates where $\left|R_{\mathrm{a}}\right|=1$.

V. CONCLUSIONS

Similar quasiperiodic fluctuations were observed in behavioral hearing thresholds and the amplitudes and delays of SFOAE responses to near-threshold tones when obtained from adult, female subjects. The periodicity and magnitude of this common microstructure were related to the SFOAE phase-gradient and amplitude, respectively. Such relationships are consistent with a framework that attributes microstructure to intracochlear reflections of SFOAE energy between its region of generation and the middle ear boundary. While the relationship between microstructure depth and SFOAE magnitude was roughly similar across ears for the mid-frequency range examined here, it is possible that this relationship differs at lower and higher frequencies, due to changes in middle ear transmission and the reflectance at the stapes.

Appendix: Intracochlear reflection framework

The effects of multiple intracochlear reflections on thresholds and SFOAEs can be formally understood in terms of the more apical, SFOAE-generating reflectance, here termed $R_{\mathrm{a}}$ (as in Talmadge et al., 1998, also termed R in Shera and Zweig, 1993a, and elsewhere), and the basal reflectance encountered at the middle ear boundary, $R_{\mathrm{b}}$ (as in Kemp, 1979a; Talmadge et al., 1998, and also termed $R_{\text{stapes}}$ in Shera, 2003). The apical reflectance, $R_{\mathrm{a}}$, is defined as the ratio of the total reverse-propagating pressure wave to the incident, forward-going wave, as evaluated at the cochlear base. Likewise, $R_{\mathrm{b}}$ is defined as the ratio of the reflected to incident pressure waves at the stapes. Both $R_{\mathrm{a}}$ and $R_{\mathrm{b}}$ are complex-valued functions of stimulus frequency, and for the purposes of the following equations, assumed to be linear (though as described in the main text, $R_{\mathrm{a}}$ is likely input-dependent even at near-threshold levels, such that the below formulations are only approximate).

Following stimulation of the ear and initiation of a forward-traveling wave, reflections from the SFOAE-generating region are then re-reflected at the stapes, producing an additional forward-propagating component proportional to $R_{\mathrm{a}}{R}_{\mathrm{b}}$. The sum of the additional forward-going waves due to multiple (n) rounds of reflection ($R_{\mathrm{a}}{R}_{\mathrm{b}}+R_{\mathrm{a}}^2{R}_{\mathrm{b}}^2+\cdots +R_{\mathrm{a}}^n{R}_{\mathrm{b}}^n$) results in the modulation of the initial, stimulus-driven forward-going wave by a factor that converges to

$$\frac{1}{1-R_{\mathrm{a}}{R}_{\mathrm{b}}}.$$ (A1)

Since the total reverse-going wave is simply the total forward-going wave scaled by $R_{\mathrm{a}}$, the interference described by Eq. (A1) also influences the SFOAE pressure in the ear canal ($P_{\text{sf}}$), which, for a given stimulus pressure ($P_{\text{stim}}$), is described by

$$P_{\text{sf}}=P_{\text{stim}}{G}_{\text{me}}^{\text{RT}}(1+R_{\mathrm{b}})\left(\frac{R_{\mathrm{a}}}{1-R_{\mathrm{a}}{R}_{\mathrm{b}}}\right).$$ (A2)

Here the term $1+R_{\mathrm{b}}$ accounts for the effect of the basal reflectance on the total pressure driving the stapes in reverse (the total pressure is the sum of the incident and reflected pressures, e.g., Shera, 2003), and $G_{\text{me}}^{\text{RT}}$ describes the round-trip pressure gain due to middle ear transmission. The latter is the product of the forward pressure gain from the eardrum to the cochlear vestibule and the pressure gain going in the reverse direction (as has been estimated in human cadaveric temporal bones by Puria, 2003) and describes the net effect of middle ear transmission on an OAE evoked and measured at the same frequency, as is the case for SFOAEs.

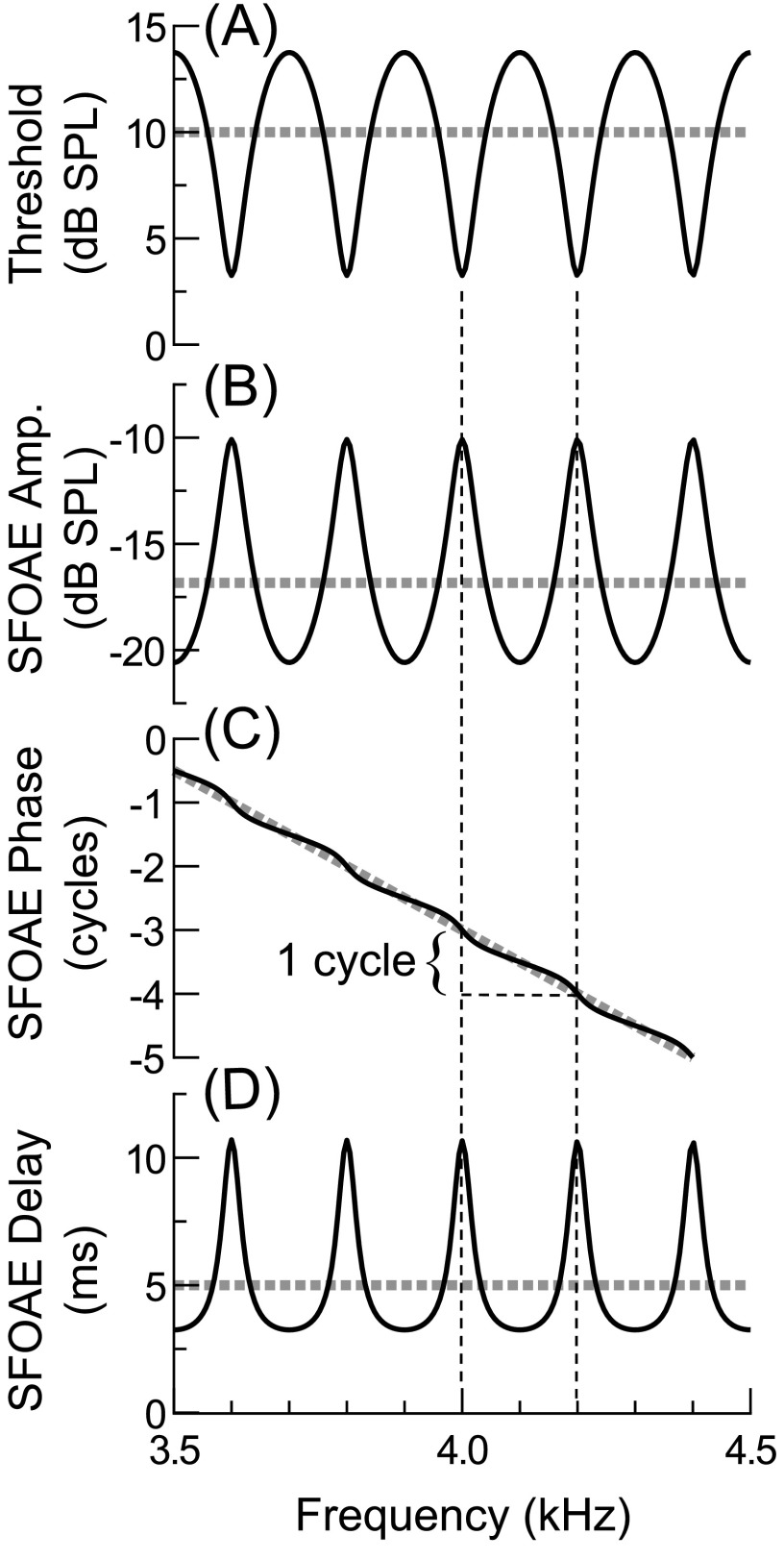
From the above equations, behavioral thresholds and SFOAEs are predicted to have a common microstructure with a periodicity and magnitude determined by $R_{\mathrm{a}}{R}_{\mathrm{b}}$. This common microstructure is illustrated in Fig. 9, which compares synthesized threshold and SFOAE responses assuming fixed values of the terms given in Eqs. (A1) and (A2) over a narrow frequency range. Peaks in behavioral sensitivity (i.e., threshold minima) and both SFOAE amplitudes and delays occur at frequencies for which the round-trip phase accumulation associated with is a whole number of cycles [$\angle (R_{\mathrm{a}}{R}_{\mathrm{b}})=2\pi n$, where n is any integer]. If it is assumed that the phase and magnitude of $R_{\mathrm{b}}$ vary slowly across frequency (e.g., Puria, 2003), then microstructure periodicity and magnitude are primarily determined by $R_{\mathrm{a}}$. Microstructure periodicity and magnitude should therefore be related to SFOAE delay and amplitude, assuming that the latter are largely determined by $R_{\mathrm{a}}$, and that $R_{\mathrm{b}}$ and/or $G_{\text{me}}^{\text{RT}}$ are similar across frequency and ears. These relationships are examined in further detail in Sec. III.

FIG. 9.

Theoretical relationships among threshold and SFOAE microstructures given Eqs. (A1) and (A2), with values for each term fixed across a ∼0.5 octave span centered on 4 kHz. Here $R_{\mathrm{a}}$ was given a magnitude of 0.9 and delay of 5 ms (the approximate SFOAE delay near 4 kHz) and $R_{\mathrm{b}}$ was given a magnitude of 0.6 and delay of 0 ms (the delay associated with $R_{\mathrm{b}}$ is presumed negligible, for simplicity). For the purposes of this simplified illustration, thresholds [in (A)] were synthesized by scaling the inverse of Eq. (A1) by a nominal threshold level of 10 dB SPL, thus assuming a linear relationship between the steady-state forward-traveling-wave magnitude and the neural excitation required for behavioral threshold, and ignoring any complex spatio-temporal effects resulting from intracochlear reflection. The SFOAE pressure [the amplitude, phase, and delay of which are shown in (B)–(D)] was calculated with $P_{\text{stim}}$ equivalent to 10 dB SPL, and $G_{\text{me}}^{\text{RT}}$ with magnitude equivalent to −30 dB, and, for convenience, a negligible delay (0 ms). Thick dashed lines indicate the nominal threshold and SFOAE response values (i.e., trends) without the influence of the microstructure term, $1/(1-R_{\mathrm{a}}{R}_{\mathrm{b}})$.