AIC identifies optimal representation of longitudinal dietary variables

Abstract

Objectives

The Akaike Information Criterion (AIC) is a well-known tool for variable selection in multivariable modeling as well as a tool to help identify the optimal representation of explanatory variables. However, it has been discussed infrequently in the dental literature. The purpose of this paper is to demonstrate the use of AIC in determining the optimal representation of dietary variables in a longitudinal dental study.

Methods

The Iowa Fluoride Study enrolled children at birth and dental examinations were conducted at ages 5, 9, 13, and 17. Decayed or filled surfaces (DFS) trend clusters were created based on age 13 DFS counts and age 13–17 DFS increments. Dietary intake data (water, milk, 100 percent-juice, and sugar sweetened beverages) were collected semiannually using a food frequency questionnaire. Multinomial logistic regression models were fit to predict DFS cluster membership (n= 344). Multiple approaches could be used to represent the dietary data including averaging across all collected surveys or over different shorter time periods to capture age-specific trends or using the individual time points of dietary data.

Results

AIC helped identify the optimal representation. Averaging data for all four dietary variables for the whole period from age 9.0 to 17.0 provided a better representation in the multivariable full model (AIC= 745.0) compared to other methods assessed in full models (AICs =750.6 for age 9 and 9–13 increment dietary measurements and AIC = 762.3 for age 9, 13, and 17 individual measurements). The results illustrate that AIC can help researchers identify the optimal way to summarize information for inclusion in a statistical model.

Conclusions

The method presented here can be used by researchers performing statistical modeling in dental research. This method provides an alternative approach for assessing the propriety of variable representation to significance-based procedures, which could potentially lead to improved research in the dental community.

Introduction

Model selection is a common challenge across research in all empirical scientific disciplines. Different fields have gravitated toward different standard model selection approaches. The fields of computer science and data science often use complex algorithms such as tree-based models including random forests and boosting, which improves predictive accuracy at the cost of interpretation (1). In genetics and genomics, regularization methods such as least angle regression and the LASSO (2) have become increasingly popular, since they allow investigators to identify a potentially small set of important traits among an initial collection that is often very large. Many other disciplines frequently utilize straightforward step-wise techniques, such as backward elimination, which are understandable and can be implemented using computationally efficient algorithms, yet can lead to potentially biased solutions (3,4). Recently, the American Statistical Association, the world’s largest community of statisticians, released an official report warning against the overuse of P-values and P-value based methods (5,6). P-values are particularly problematic for variable selection, although they tend to be pervasively used for this purpose.

In most published applied work where model selection techniques are employed, the focus is primarily to identify the optimal subset of potential predictors to use in a final model. Even in the statistical literature, there have been relatively few articles discussing the optimal way to represent predictors in the model.

In standard regression modeling, variables can be represented in many ways: for example, quantitative and continuous, quantitative and discrete, qualitative with multiple levels, qualitative with two levels. Quantitative skewed explanatory variables may have a large influence on parameter estimates, while categorical explanatory variables with multiple levels (e.g., Likert scale) may produce many parameter estimates. A common approach to address such modeling issues is to categorize the variable values into two or three groups, although oftentimes there are many possibilities for categorization. These decisions frequently are based on convenience or discipline-governed logic rather than statistical reasoning. Similar dilemmas about the optimal representation of explanatory variables arise in longitudinal studies when such variables are collected over time. Researchers need to identify the optimal ways to represent these variables (e.g., through some form of averaging over the time points or the inclusion of measurements at separate time points). In this paper, we demonstrate the use of the Akaike information criterion (AIC) in determining the optimal representation of explanatory variables with data collected in the Iowa Fluoride Study. When modeling an outcome, enriching the characterization of the mean structure by incorporating a large collection of pertinent explanatory variables may reduce inferential bias yet will also increase variability. Conversely, simplifying the characterization by relying on a parsimonious collection of variables will decrease variability yet may inflate bias. AIC is a statistical method that helps determine the optimal variance-bias tradeoff.

Methods

Iowa fluoride study background

The Iowa fluoride study (IFS) team has published numerous articles modeling dental caries prevalence and incidence during childhood and adolescence for participating Iowa children (7–13). Detailed descriptions of different parts of the study have been published previously, so only a brief description of the study is presented here. The IFS recruited a birth cohort at 8 Iowa hospital post-partum wards during 1992–1995. Dental examinations for dental caries and fluorosis took place at about ages 5, 9, 13, and 17 by a team of trained and calibrated examiners. Questionnaires were sent every 6 months during adolescence to obtain dietary intakes and behavioral variable information and measurements. Additional details on the questionnaires are provided in the “candidate predictor variables” section below.

Outcome variable

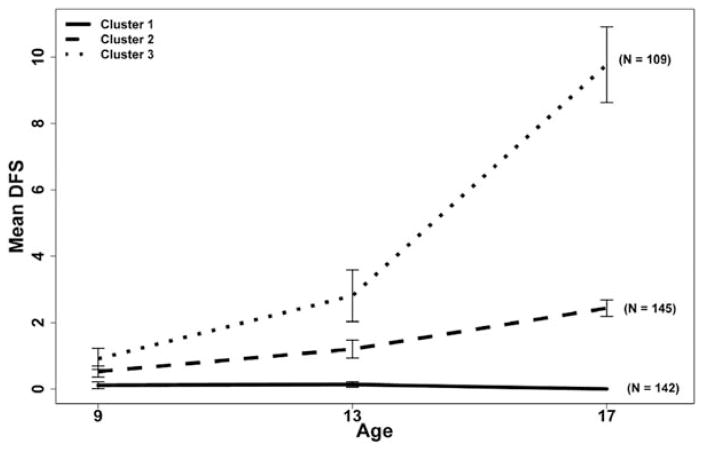
Decayed and filled surface (DFS) counts were calculated for individuals for all dental exams using criteria that distinguished cavitated from non-cavitated lesions (9–11,13). For the present analyses, only cavitated and/or filled tooth surfaces were included in the DFS counts. Three DFS count cluster groups were created from 396 subjects using the age 13 dental exam DFS counts and the DFS increments between the age 13 dental exam and the age 17 dental exam (Figure 1).

Figure 1.

DFS clusters created from age 13 DFS count and 13–17 DFS incidence of the Iowa Fluoride Study cohort. The age 9 DFS counts were not used in the creation of the clusters (n = 396).

Clustering is a descriptive statistical technique used to combine individuals into similar groups based on prescribed variables of interest. In this study, age 13 DFS counts and age 13–17 DFS increments served as the clustering variables. While the clustering methodology and results will be the focus of another paper, in brief, we used Ward’s (ward.D2) clustering (14) with the “stats” package in R (64–bit Version R–3.0.2) to create three clusters. Ward’s clustering creates groups that maximize the squared Euclidean distance between cluster centers, creating groups that are internally homogeneous and externally heterogeneous. It should be noted that the distribution of DFS counts and increments is highly discrete and right skewed, and cannot be viewed as approximately normal. Subjects with large counts and increments, which could be deemed as outliers, were not removed prior to clustering. The authors felt that such high-risk individuals should be captured in our analyses. Several different numbers of cluster groups were considered; however, cluster sizes greater than three produced small sample sizes for cluster membership. Thus, three clusters were used, as shown in Figure 1 below. In Figure 1, the error bars surrounding the means represent the 95 percent confidence intervals for the mean. The age 9 values are included in the figure for reference, but they were not included in the clustering algorithm. The method discussed in this paper requires a complete set of data with no missingness. While there were 396 participants who had caries outcomes and satisfied the aforementioned questionnaire criteria, only the 344 participants who had complete data were used in the modeling analyses. In order to best capture the observed trends, we formed our clusters based on the most complete set of information available. Therefore, we determined the representation method with the clusters created from the full population (n = 396).

Candidate predictor variables

We were interested in predicting cluster membership using data collected with the semiannual questionnaires. It has been shown that childhood beverage intakes are associated with adolescent caries (12,15,16). In order to capture childhood and adolescent beverage intake amounts, information from questionnaires from ages 9.0 to 17.0 years was considered. With the abundance of dietary data collected over this time span, we needed to identify the optimal representation of these data when predicting cluster membership. The questionnaires assessed individuals’ beverage intakes, fluoride exposures, and brushing habits. For these analyses, we focused only on dietary variables (i.e., fluoride exposures and behavioral variables such as brushing frequency were not included) and estimated the total ounce intakes per day for water and other sugar-free beverages, milk, sugar-sweetened beverages (SSB), and 100 percent juice. Since the purpose of this model selection technique was to identify the best dietary beverage variable representation, other important variables (e.g., sociodemographic, oral hygiene variables) were not included in this study. In a related analysis to be published in a separate paper, such variables were incorporated into the final model selection once the optimal variable representation was determined. The term predict in this manuscript is used in the traditional sense where we predict cluster membership for a new individual based on a hypothetical set of covariates rather than forecasting future caries trajectories.

In order to initially be considered in the analysis, we required individuals to have returned at least one questionnaire during at least four of the following five periods:

• Period 1: 9, 9.5, and 10 years,

• Period 2: 10.5, 11, 11.5, and 12 years,

• Period 3: 12.5, 13, and 13.5 years,

• Period 4: 14, 14.5, 15, and 15.5 years, and

• Period 5: 16, 16.5, and 17 years.

For the purpose of illustration, a sampled participant’s questionnaire data for the four dietary variables of interest is shown in Table 1. With the large amount of information available across the different ages, summarization of the data was needed. To help understand the research problem, we provide a simple example here. Assume the individual represented in Table 1 belonged to DFS Cluster 3 (high DFS cluster). When predicting this cluster membership, we might believe that incorporating the substantial increase in SSB intake from the age 11.5 questionnaire would be useful in the model. If we included the age 11.5 questionnaire data as a predictor, a traditional complete-case analysis would remove all individuals who did not return this specific questionnaire. In order to accommodate potential missingness in questionnaires, we considered several forms of averaging (e.g., creating a new variable that averages questionnaires across ages 10.0, 10.5, 11.0, 11.5, providing for missing questionnaires). This allows for individuals to have missed questionnaires, but still have observed averages.

Table 1.

Example of One Iowa Fluoride Study Subject’s (ID 36) Dietary Responses from Ages 9.0 to 17.0 for the Four Dietary Categories–Ounces per Day

Questionnaire at child’s age	Water and other sugar-free beverages	Milk	Sugar-sweetened beverages	100% juice
9.0	5.1	6.9	11.1	0.0
9.5	6.0	6.9	17.1	0.0
10.0	5.0	12.0	14.3	7.1
10.5	8.0	9.1	12.0	0.0
11.0	40.0	16.0	15.4	0.0
11.5	10.0	12.0	26.1	0.0
12.0	20.0	18.3	9.7	0.0
12.5	12.0	16.0	15.7	0.0
13.0	71.4	24.0	26.7	0.0
13.5	10.0	20.6	10.3	0.0
14.0	30.0	24.0	29.7	0.0
14.5	11.1	24.0	15.1	0.0
15.0	45.7	24.0	3.4	0.0
15.5*	–	–	–	–
16.0	16.0	22.9	3.4	0.0
16.5*	–	–	–	–
17.0	32.0	32.0	0.0	0.0
Calculated values
Method 1
“9–17”†	21.5	17.9	14.0	0.5
Method 2
“9”‡	5.6	6.9	14.1	0.0
“9”‡ to “13”¶	25.6	13.3	3.5	0.0
Method 3
“9”‡	5.6	6.9	14.1	0.0
“13”¶	31.1	20.2	17.6	0.0
“17”§	32.0	32.0	0.0	0.0

^*The questionnaires were not returned at ages 15.5 and 16.5.

^†The questionnaires were averaged between ages 9.0 and 17.0, inclusive.

^‡The questionnaires were averaged at ages 9.0 and 9.5.

^¶The questionnaires were averaged at ages 12.5, 13.0, and 13.5.

^§The questionnaires were averaged at ages 16.5, 17.0, and 17.5.

Several different averaging periods were considered for the questionnaire dietary data variables, but four different averaging periods are presented here for demonstration:

• “9–17”: averaged questionnaire data collected at ages 9.0–17.0,

• “9”: averaged questionnaire data collected at ages 9.0, and 9.5,

• “13”: averaged questionnaire data collected at ages 12.5, 13.0, and 13.5, and

• “17”: averaged questionnaire data collected at ages 16.5 and 17.0, and 17.5.

The questionnaires starting at age 9.0 changed wording, so the questionnaire at 8.5 was not used in the “9” measurement. Using these different averages, three different questionnaire representation methods were considered in predicting DFS cluster group:

• Method 1: “9–17” capturing average dietary intakes,

• Method 2: “9” intake and the difference from “9” to “13” capturing changes in dietary intakes, and

• Method 3: “9”, “13”, and “17” as three separate periods capturing dietary intakes close to the dental examination ages.

Method one neglects all information pertaining to fluctuations across the 8-year time period and attempts to summarize the dietary intake variables for each individual through their own average measurements across the adolescent period. The second method uses dietary beverage intakes near the dental examination at age 9, along with the changes in dietary intakes between the average intake around age 9 and the average intake around age 13. Incorporation of either changes in dietary intakes or dietary intakes measured at multiple times allows for the model to capture behavioral changes in beverage intakes. Method three uses dietary beverage intake averages near all three targeted dental examinations. The dietary intake changes could be important predictors of DFS cluster; these changes would be lost if we averaged over the entire adolescent period (i.e., Method 1). For the sampled participant, the calculated variable values for the three methods are presented in Table 1.

In regression models, the degrees of freedom associated with the model fit can be interpreted as a measure of the information needed for the estimation of the model parameters (3). Every covariate parameter we estimate corresponds to one degree of freedom. The greater the model degrees of freedom, the less precise our parameter estimates and predicted outcomes; this concept is often referred to as the “estimation cost.” However, each additional covariate included in the model potentially reduces inferential bias (e.g., estimators of the mean response, predictors of new outcomes). Since increased model complexity inflates variability while potentially reducing bias, an optimal statistical model must provide an adequate balance between fidelity to the data (a requirement for low bias) and parsimony (needed to control variability). Such a model can be identified by using a penalized measure of model fit.

For this analysis, we need to determine if the extra information provided through explicit representation of the dietary variables at several different and separate ages is worth the additional parameter estimation cost. For this assessment, we will use the Akaike Information Criterion to help identify the optimal penalized model fit corresponding to different explanatory variable representations.

Akaike information criterion

The AIC is a statistical technique introduced by Hirotugu Akaike (17), who reformulated the problem of selecting an optimal model among a candidate collection as a decision problem as opposed to a hypothesis testing problem. AIC and other non-significance-based model selection criteria have been gaining popularity in statistical modeling over hypothesis testing and traditional automated model selection techniques such as backward elimination (18). Extensive theoretical results about the derivation and performance of AIC have been published, so only a brief introduction is provided here (19–21).

AIC is a well-known tool for variable selection in multivariable modeling, yet it is also a useful tool to help identify the optimal representation of explanatory variables collected. AIC provides a measure of penalized fit, incorporating both the empirical likelihood and the number of parameters in the model. The empirical likelihood (L) is a measure that reflects how effectively the model predicts the data used in its own construction. In other words, the better the fit, the larger the likelihood. The formula for the calculation of AIC is

$$\text{AIC}=-2{\text{log}}_e(L)+2p,$$

where L is the empirical likelihood, log_e is the natural log function, and p is the number of parameters in the model. In the formula, larger likelihoods (better fit) produce larger values of log_e (L) resulting in smaller values of −2log_e (L). More parameters (larger p) in the model produce a larger penalty. The first term, the goodness-of-fit term, will decrease in accordance with improvements in model fit, while the second term, the penalty term, will increase with additional model complexity. Lower AIC values are preferable; such models ideally provide an optimal compromise between adherence to the data and simplicity. AIC, therefore, helps determine which variables are necessary for prediction without overfitting the model. AIC may be perceived as a measure that gauges the separation between the fitted candidate model and the model that presumably generated the data; thus, models corresponding to lower values of AIC are perceived as being closer to the “truth” (21).

It is generally recommended that a decrease of 2 or more AIC units between two competing models indicates a meaningfully improved penalized fit (19). Models within 2 AIC units of each other are deemed to have similar penalized fit, with one model no worse than the others. Adapted from Burnham and Anderson (19), the AIC difference between model i and the lowest observed AIC model can be interpreted as follows:

• ΔAIC between 0 and 2: Essentially no advantage of lowest AIC model compared to model i

• ΔDAIC between 4 and 7: Advantage of lowest AIC model compared to model i

• ΔDAIC between >10: Substantial advantage of lowest AIC model compared to model i

To maintain comparable AIC values, the likelihood should be calculated from identical datasets for the different models. In other words, the user must have a complete dataset for every representation considered before performing analyses. Prior to modeling, we created a subset of the original data keeping only participants who had averaging of dietary variable measurements for the three time points, for the increment from 9 to 13, and for the averaging over questionnaires from ages 9 to 17.

Modeling

We fit a full multinomial logistic regression model with a generalized logit link predicting caries cluster group with the four dietary variables (water and other sugar-free beverages, milk, SSB, and 100 percent juice), constrained to the same representation format, using PROC LOGISTIC in SAS Version 9.4. Multinomial models using a generalized logit require (k–1) equations, where k is the number of outcome levels. One group is used as reference and each outcome comparison to the reference will have its own equation and set of parameters. For this example, DFS Cluster 1 is the reference group, while DFS Cluster 2 and DFS Cluster 3 will have their own equations and parameter estimates comparing these two groups to DFS Cluster 1 (see Appendix). We will use AIC to identify which method best predicts cluster membership, by appropriately balancing goodness-of-fit and parsimony. Method 1 provides a proxy for the cumulative intake over the adolescent period by averaging the questionnaires. Method 2 incorporates each dietary variable by capturing dietary intake at the age 9 dental examination, as well as the change in dietary intake from ages 9 to 13, through two separate measurements. This doubles the number of dietary parameters we are estimating compared to Method 1. In Method 3, we incorporate the dietary intake during three separate time periods to capture the different fluctuations over the adolescent years. This method has triple the number of estimated dietary parameters compared to Method 1.

Results

Participant demographic and cluster dietary summary statistics

Demographic information for these 344 participants is presented in Table 2. Demographic variables are allowed to be missing, since only dietary variables are assessed in the current analysis. Summary statistics of the four dietary variable intakes for the three clusters are shown separately for the three representation methods in Table 3. Considering the 100 percent juice variable, for Method 1, we observed a decrease in average total ounces per day of juice intake from the low DFS cluster (Cluster 1, average intake: 2.72 oz) to the medium DFS cluster (Cluster 2, average intake: 2.17 oz) and the high DFS cluster (Cluster 3, average intake: 1.72 oz). With Method 2, we observed a similar decrease in average total ounces per day of juice intake around the age 9 dental examinations. The medium DFS cluster (Cluster 2) had a larger negative net increment in average juice intake from ages 9 to 13 compared to the low DFS cluster (Cluster 1) (average decrease for Cluster 1: −0.13 oz; average decrease for Cluster 2: −0.36 oz). In the high DFS cluster (Cluster 3), we note an increased average juice intake from ages 9 to 13 (average increase Cluster 3: 0.18 oz). When modeling cluster membership, this decrease in juice intake could be an important factor in separating individuals from the low DFS cluster (Cluster 1) and the medium DFS cluster (Cluster 2). Averaging over the age 9–17 period would not capture these deviations in intake. In Method 3, we see the similar decreases in intake across the clusters over the three different age ranges.

Table 2.

Demographic Information from 344 Participants of the Iowa Fluoride Study with Complete Outcome and Dietary Data

Variable	Category	N (%)
Sex	Females	178 (51.7)
	Males	166 (48.3)
Race	Caucasian	331 (96.2)
	Other	13 (3.8)
Mother’s education	<4-Year Degree	171 (50.6)
	4-Year Degree or More	165 (48.8)
	No Female Head of Household	2 (0.6)
Family income	<$60,000	105 (30.5)
	$60,000 or More	225 (65.4)
	Refused to Answer	14 (4.1)

Table 3.

Summary Statistics for Iowa Fluoride Study Dietary Beverage Intakes for Three Representation Methods (Total oz/day) (n = 344)

Variable	DFS cluster	Method 1		Method 2				Method 3
		9.0 to 17.0 average		“9”*		“9”* to “13”† increment		“9”*		“13”†		“17”‡
		Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
100% Juice	1 – Low	2.72	2.29	2.77	3.00	−0.13	3.68	2.77	3.00	2.63	3.29	1.94	3.19
	2 – Medium	2.17	2.22	2.28	3.12	−0.36	2.43	2.28	3.12	1.92	3.06	1.49	2.11
	3 – High	1.72	1.44	1.66	2.10	0.18	2.50	1.66	2.10	1.84	2.17	1.17	2.31
	Combined	2.25	2.10	2.29	2.86	−0.13	2.97	2.29	2.86	2.16	2.95	1.57	2.62
Milk	1 – Low	13.50	6.54	12.34	6.36	1.92	7.16	12.34	6.36	14.26	8.43	13.52	9.82
	2 – Medium	11.64	7.13	11.81	7.71	−0.73	7.86	11.81	7.71	11.08	8.13	11.60	10.43
	3 – High	12.07	7.59	10.95	7.34	1.72	11.53	10.95	7.34	12.67	11.95	11.44	9.39
	Combined	12.44	7.08	11.77	7.14	0.90	8.84	11.77	7.14	12.68	9.48	12.26	9.95
Sugar-sweetened beverages	1 – Low	10.33	6.31	7.72	5.84	3.73	7.82	7.72	5.84	11.45	8.68	12.27	12.17
	2 – Medium	11.29	7.41	8.94	6.20	3.29	7.83	8.94	6.20	12.23	8.72	12.59	12.75
	3 – High	12.07	7.59	9.79	8.66	2.50	7.76	9.79	8.66	12.29	9.30	13.09	11.15
	Combined	11.15	7.09	8.72	6.87	3.24	7.80	8.72	6.87	11.96	8.85	12.61	12.09
Water and other sugar-free beverages	1 – Low	18.66	9.77	12.30	9.87	7.69	11.43	12.30	9.87	19.99	12.31	24.99	15.93
	2 – Medium	16.64	9.37	10.21	7.87	7.32	12.09	10.21	7.87	17.53	13.91	25.34	22.86
	3 – High	15.76	8.63	10.91	8.80	5.63	13.51	10.91	8.80	16.54	12.70	23.93	15.76
	Combined	17.14	9.38	11.17	8.91	7.00	12.25	11.17	8.91	18.16	13.06	24.83	18.66

^*“9”: Averaged questionnaire data collected at ages 9.0 and 9.5.

^†“13”: Averaged questionnaire data collected at ages 12.5, 13.0, and 13.5.

^‡“17”: Averaged questionnaire data collected at ages 16.5, 17.0, and 17.5.

Modeling results

Summary statistics about the model fit for the three different models are reported in Table 4. We notice the fit to the data improved (−2log_e (L). decreased) with the additional parameters in the more explicit representation methods. This was expected because the additional information allowed for more precise estimates of cluster membership for the sample at hand. In terms of AIC, this better fit was not worth the estimation cost of the additional parameters. Averaging dietary questionnaire data over the entire adolescent period from ages 9 to 17 provided a better penalized fit in describing DFS cluster membership compared to the use of multiple, separate dietary intake variables at the different ages. Both modeling approaches with more period-specific variables yielded AIC values at least 2 units higher than Method 1 (~ 6 units higher for Method 2 and ~ 17 units higher for Method 3).

Table 4.

AIC Values for Three Methods of Representing Longitudinal Beverage Intake Data in the Iowa Fluoride Study (n = 344)

Method*	# Dietary parameters estimated (k)	−2log (likelihood)	AIC	Difference from minimum AIC	Level of empirical support for method compared to lowest AIC model
Method 1	8	729.0	745.0	0.0	–
Method 2	16	718.6	750.6	5.6	Less support
Method 3	24	714.3	762.3	17.3	Substantially less support

^*Method 1 represents beverage intake variables through an average of questionnaires between 9.0 and 17.0 years of age; Method 2 represents beverage intake variables through questionnaires around 9 and the change of beverage intake between 9 and 13 years of age; Method 3 represents beverage intake variables through three specific time points around 9, 13, and 17 years of age.

The parameter estimates, confidence intervals, and P-values for the model containing the four beverage variables using the chosen representation method are presented in Table 5. An increase in 100 percent juice, water and other sugar-free beverages, and milk intake was associated with higher odds of being in the low DFS cluster (Cluster 1) compared to the other two clusters; while a decrease in sugar-sweetened beverages was associated with higher odds of being in the low DFS cluster (Cluster 1). Only the 100 percent juice intake association was statistically significant at the 0.05 level (P < 0.004); the association for water and other sugar-free beverages was nearly significant (P = 0.067). It is known that other factors besides beverage intake (e.g., brushing frequency, gender) are confounders of caries trajectories, so these results should not be taken as definitive conclusions. Using the established representation method, we can incorporate the confounders in an appropriate statistical model to identify overall factors associated with caries trajectories.

Table 5.

Parameter Estimates from Chosen Representation Method in Iowa Fluoride Study Predicting Caries Clusters (n = 344)

Variable*	Cluster	Odds ratio	95% CI	P-value
100x% juice	1	1.00	–	0.004
	2	0.90	0.80, 1.01
	3	0.78	0.68, 0.91
Milk	1	1.00	–	0.267
	2	0.97	0.94, 1.01
	3	0.98	0.95, 1.02
Sugar-sweetened beverages	1	1.00	–	0.355
	2	1.02	0.98, 1.06
	3	1.03	0.99, 1.07
Water and other sugar-free beverages	1	1.00	–	0.067
	2	0.98	0.95, 1.01
	3	0.97	0.94, 1.00

^*Beverage intake variables (total oz/day) were averaged from questionnaires between 9.0 and 17.0 years of age.

Discussion

Statistics methods for modeling are evolving; P-values in modeling applications are commonly misused and misinterpreted, as noted by the recent report of the American Statistical Association (5). With this in mind, alternative approaches for model formulation and selection need to be considered and discussed in all fields, including dental research. One of these alternative, underutilized methods is AIC. The proper incorporation of tools such as AIC in the modeling of observational data could improve adherence to the STROBE guidelines, and render inferential conclusions that are more defensible and reproducible.

Even though we demonstrated variable representation through longitudinal data, AIC can be used with any type of data to help identify the optimal representation (e.g., determining whether we should leave age as continuous or categorize it in a cross-sectional study). In addition, hypothesis-testing based comparisons usually require nested models; AIC can be used to compare non-nested models (19). Finally, AIC can be employed to consider models based on all possible subsets of explanatory variables, unlike certain other model selection techniques that only consider a few potential models among the entire candidate collection (e.g., backward elimination, forward selection).

For this analysis, questionnaire data were self-reported, which can result in potential recall bias. In addition, only full models containing all four dietary variable types were compared among the three methods instead of allowing a subset of variables in each model. In modeling, we required all four dietary variable types to have the same representation within a model (e.g., water could not be averaged over questionnaire years 9.0–17.0, while milk used all three time points). In dental longitudinal studies, analyses of other datasets without relative stability of dietary intake patterns could produce different results.

In this paper, AIC was used to identify whether averaging the dietary questionnaires over ages 9–17 provided the optimal representation for penalized fit compared to the two other methods considered. This technique helped provide statistical justification for variable representation. AIC could subsequently be used to help identify a subset of the predictors for the final model from a full set of potential variables using this chosen representation method for the dietary variables.

AIC is only one of many criteria that can be used for the selection of a model or for the determination of variable representations. There are several other measures that work well in various situations, including variants of AIC based on different complexity penalizations. Hurvich and Tsai (22) refined AIC by developing a “corrected” AIC, AICc, which improves the performance of the criterion in applications involving small sample sizes. AICc revises the penalty of AIC by incorporating a factor based on the relationship between the sample size and the number of parameters. When the number of parameters is large in comparison to the sample size, the revised penalty term is larger. It should be noted that AICc has only been justified for certain modeling frameworks, and that the refined penalty term is only exact in the setting of Gaussian linear models.

The Bayesian Information Criterion (BIC) (also called the Schwarz Bayesian Criterion) was introduced by Schwarz (23) in 1978. In large-sample settings, BIC is designed to select the model with the highest Bayesian posterior probability. This criterion is similar to AIC except it incorporates the sample size into the penalty term (AIC penalty term is p * 2 BIC penalty term is p * log_e (n)). With the larger penalty term compared to AIC, BIC is traditionally stricter when incorporating variables into a “favored” model. In large-sample settings, AIC is often advocated for predictive modeling whereas BIC is more appropriate for descriptive modeling. AIC may be more defensible for traditional frequentist analyses since its development is closely tied to likelihood-based inferential modeling techniques. In our particular application, we have considered both AIC and BIC and they have produced the same results, in terms of favoring Method 1 over Method 2, and Method 2 over Method 3. This should not be surprising, since BIC emphasizes parsimony to a greater degree than AIC. Further descriptions of AIC, BIC, and AIC variants, as well as other model selection criteria, can be found in model selection papers and textbooks (18).

The use of model selection criteria avoids the potential problems of hypothesis testing and the reliance on P-values for the determination of variable inclusion and variable representation. In hypothesis testing, we consider nested models, and assume that the larger model is the “true” model. We then test whether a variable or collection of variables may be omitted. In practice, the “true” model is never known; thus hypothesis testing is not usually appropriate in modeling applications. While hypothesis testing as well as automated techniques can provide a flawed yet tractable method for variable selection (24,25), these techniques are not designed to address the problem of variable representation. This problem is ideally tailored to the use of model selection criteria, since it intrinsically involves an evaluation of the competing objectives of goodness-of-fit and parsimony.

As discussed in this paper, utilizing model selection methods such as AIC that do not prioritize significance levels, will be important to incorporate into the evolving dental research field. Ultimately, the variable representation problem can be viewed as a special case of the more pervasive bias-variability tradeoff problem, which is endemic to statistical modeling. AIC and related criterion-based selection methods are better designed to address this problem than P-values and traditional tests of significance.

Appendix: Equations of three considered models

Equations:

• Method 1: averaged all the questionnaire data from 9 to 17 representing it as one predictor for each dietary variable:

  $$\begin{array}{l}\mathit{logit}(\text{Cluster}=2\text{versus}1)={\beta }_0\\ +{\beta }_{W2,1}\ast \mathit{Water}(\text{Average}9\text{to}17)\\ +{\beta }_{M2,1}\ast \mathit{Milk}(\text{Average}9\text{to}17)\\ +{\beta }_{S2,1}\ast \mathit{SSB}(\text{Average}9\text{to}17)\\ +{\beta }_{J2,1}\ast 100\%\mathit{Juice}(\text{Average}9\text{to}17)\\ \mathit{logit}(\text{Cluster}=3\text{versus}1)={\beta }_0\\ +{\beta }_{W3,1}\ast \mathit{Water}(\text{Average}9\text{to}17)\\ +{\beta }_{M3,1}\ast \mathit{Milk}(\text{Average}9\text{to}17)\\ +{\beta }_{S3,1}\ast \mathit{SSB}(\text{Average}9\text{to}17)\\ +{\beta }_{J3,1}\ast 100\%\mathit{Juice}(\text{Average}9\text{to}17)\end{array}$$
• Method 2: used age ~9 dietary intake measurement and age 9–13 dietary intake increment as two separate predictors for each dietary variable:

  $$\begin{array}{l}\mathit{logit}(\text{Cluster}=2\text{versus}1)={\beta }_0\\ \begin{array}{ll}+{\beta }_{W2,1}\ast \mathit{Water}(\text{Age}9)\hfill & +{\beta }_{W2,2}\ast \mathit{Water}(\text{Ages}9\text{to}13\text{Increment})\hfill \\ +{\beta }_{M2,1}\ast \mathit{Milk}(\text{Age}9)\hfill & +{\beta }_{M2,2}\ast \mathit{Milk}(\text{Ages}9\text{to}13\text{Increment})\hfill \\ +{\beta }_{S2,1}\ast \mathit{SSB}(\text{Age}9)\hfill & +{\beta }_{S2,2}\ast \mathit{SSB}(\text{Ages}9\text{to}13\text{Increment})\hfill \\ +{\beta }_{J2,1}\ast 100\%\mathit{Juice}(\text{Age}9)\hfill & +{\beta }_{J2,2}\ast 100\%\mathit{Juice}(\text{Ages}9\text{to}13\text{Increment})\hfill \end{array}\\ \\ \mathit{logit}(\text{Cluster}=3\text{versus}1)={\beta }_0\\ \begin{array}{ll}+{\beta }_{W3,1}\ast \mathit{Water}(\text{Age}9)\hfill & +{\beta }_{W3,2}\ast \mathit{Water}(\text{Ages}9\text{to}13\text{Increment})\hfill \\ +{\beta }_{M3,1}\ast \mathit{Milk}(\text{Age}9)\hfill & +{\beta }_{M3,2}\ast \mathit{Milk}(\text{Ages}9\text{to}13\text{Increment})\hfill \\ +{\beta }_{S3,1}\ast \mathit{SSB}(\text{Age}9)\hfill & +{\beta }_{S3,2}\ast \mathit{SSB}(\text{Ages}9\text{to}13\text{Increment})\hfill \\ +{\beta }_{J3,1}\ast 100\%\mathit{Juice}(\text{Age}9)\hfill & +{\beta }_{J3,2}\ast 100\%\mathit{Juice}(\text{Ages}9\text{to}13\text{Increment})\hfill \end{array}\end{array}$$
• Method 3: used age ~9 dietary intake measurement, age ~13 dietary intake measurement, and age ~17 dietary intake measurement as three separate predictors for each dietary variable:

  $$\begin{array}{l}\mathit{logit}(\text{Cluster}=2\text{versus}1)={\beta }_0\\ \begin{array}{lll}+{\beta }_{W2,1}\ast \mathit{Water}(\text{Age}9)\hfill & +{\beta }_{W2,2}\ast \mathit{Water}(\text{Age}13)\hfill & +{\beta }_{W2,3}\ast \mathit{Water}(\text{Age}17)\hfill \\ +{\beta }_{M2,1}\ast \mathit{Milk}(\text{Age}9)\hfill & +{\beta }_{M2,2}\ast \mathit{Milk}(\text{Age}13)\hfill & +{\beta }_{M2,3}\ast \mathit{Milk}(\text{Age}17)\hfill \\ +{\beta }_{S2,1}\ast \mathit{SSB}(\text{Age}9)\hfill & +{\beta }_{S2,2}\ast \mathit{SSB}(\text{Age}13)\hfill & +{\beta }_{S2,3}\ast \mathit{SSB}(\text{Age}17)\hfill \\ +{\beta }_{J2,1}\ast 100\%\mathit{Juice}(\text{Age}9)\hfill & +{\beta }_{J2,2}\ast 100\%\mathit{Juice}(\text{Age}13)\hfill & +{\beta }_{J2,3}\ast 100\%\mathit{Juice}(\text{Age}17)\hfill \end{array}\\ \mathit{logit}(\text{Cluster}=3\text{versus}1)={\beta }_0\\ \begin{array}{lll}+{\beta }_{W3,1}\ast \mathit{Water}(\text{Age}9)\hfill & +{\beta }_{W3,2}\ast \mathit{Water}(\text{Age}13)\hfill & +{\beta }_{W3,3}\ast \mathit{Water}(\text{Age}17)\hfill \\ +{\beta }_{M3,1}\ast \mathit{Milk}(\text{Age}9)\hfill & +{\beta }_{M3,2}\ast \mathit{Milk}(\text{Age}13)\hfill & +{\beta }_{M3,3}\ast \mathit{Milk}(\text{Age}17)\hfill \\ +{\beta }_{S3,1}\ast \mathit{SSB}(\text{Age}9)\hfill & +{\beta }_{S3,2}\ast \mathit{SSB}(\text{Age}13)\hfill & +{\beta }_{S3,3}\ast \mathit{SSB}(\text{Age}17)\hfill \\ +{\beta }_{J3,1}\ast 100\%\mathit{Juice}(\text{Age}9)\hfill & +{\beta }_{J3,2}\ast 100\%\mathit{Juice}(\text{Age}13)\hfill & +{\beta }_{J3,3}\ast 100\%\mathit{Juice}(\text{Age}17)\hfill \end{array}\end{array}$$

Table A1.

STROBE Statement – Checklist of Items that Should Be Included in Reports of Observational Studies

	Item No	Recommendation
Title and abstract	1	(a) Indicate the study’s design with a commonly used term in the title or the abstract The data used for the demonstration of the methodology is from a cohort study. The Iowa Fluoride Study (IFS) recruited a birth cohort at eight Iowa hospitals. The IFS followed this cohort, collecting regular dietary and beverage intakes as well as completing dental examinations at about ages 5, 9, 13, and 17 (b) Provide in the abstract an informative and balanced summary of what was done and what was found This has been completed.
Introduction
Background/rationale	2	Explain the scientific background and rationale for the investigation being reported We explain that statistical modeling is evolving and that modeling approaches beyond P-values need to be understood and adopted (pages 4–5).
Objectives	3	State specific objectives, including any prespecified hypotheses The objective is to demonstrate the use of a statistical method in the context of a dental study. There are no prespecified hypotheses.
Methods
Study design	4	Present key elements of study design early in the paper NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study.
Setting	5	Describe the setting, locations, and relevant dates, including periods of recruitment, exposure, follow-up, and data collection NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study.
Participants	6	(a) Cohort study – Give the eligibility criteria, and the sources and methods of selection of participants. Describe methods of follow-up Case-control study – Give the eligibility criteria, and the sources and methods of case ascertainment and control selection. Give the rationale for the choice of cases and controls Cross-sectional study – Give the eligibility criteria, and the sources and methods of selection of participants NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study. (b) Cohort study – For matched studies, give matching criteria and number of exposed and unexposed Case-control study – For matched studies, give matching criteria and the number of controls per case NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study.
Variables	7	Clearly define all outcomes, exposures, predictors, potential confounders, and effect modifiers. Give diagnostic criteria, if applicable The outcome is described in the “Outcome Variable” section under “Methods.” The candidate predictors are described in the “Candidate Predictor Variables” section under “Methods.”
Data sources/measurement	8*	For each variable of interest, give sources of data and details of methods of assessment (measurement). Describe comparability of assessment methods if there is more than one group The source and details of methods assessment for the outcome data (dental examinations) are described in the “Outcome Variable” section under “Methods.” The source and details of methods assessment for the predictor variables are described in the “Candidate Predictor Variables” section under “Methods.”
Bias	9	Describe any efforts to address potential sources of bias NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study
Study size	10	Explain how the study size was arrived at NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study.
Quantitative variables	11	Explain how quantitative variables were handled in the analyses. If applicable, describe which groupings were chosen and why Three different representation methods are considered for the longitudinal dietary variables of interest. Since this paper serves as a demonstration of a methodology, we felt three representation methods were sufficient for illustrative purposes.
Statistical methods	12	(a) Describe all statistical methods, including those used to control for confounding We did not control for confounding in this analysis. The purpose was to introduce a methodological approach. The statistical method is described in the “Akaike Information Criterion (AIC)” section under “Methods.” (b) Describe any methods used to examine subgroups and interactions Subgroups and interactions are not considered. (c) Explain how missing data were addressed We averaged over time points which will allow for missing observations. This is described in the “Candidate Predictor Variables” section under Methods. Missing averages were removed prior to the analyses in order to use the presented methodology. (d) Cohort study – If applicable, explain how loss to follow-up was addressed Case-control study – If applicable, explain how matching of cases and controls was addressed Cross-sectional study – If applicable, describe analytical methods taking account of sampling strategy NA (e) Describe any sensitivity analyses NA – In a different manuscript where we use this methodology, such an analysis is presented.
Results
Participants	13*	(a) Report numbers of individuals at each stage of study – for example, numbers potentially eligible, examined for eligibility, confirmed eligible, included in the study, completing follow-up, and analyzed This is described in the “Iowa Fluoride Study Background” section under “Methods.” There were 396 participants with data, but only 344 participants were used in the final analysis due to missingness. (b) Give reasons for nonparticipation at each stage NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study. (c) Consider use of a flow diagram NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study.
Descriptive data	14*	(a) Give characteristics of study participants (e.g., demographic, clinical, social) and information on exposures and potential confounders NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study. (b) Indicate number of participants with missing data for each variable of interest This is described in the “Iowa Fluoride Study Background” section under “Methods.” (c) Cohort study – Summarise follow-up time (e.g., average and total amount) NA – This project does not focus on the Iowa Flouride Study, but rather it describes a methodology that can be used in the modeling of the data from the study.
Outcome data	15*	Cohort study – Report numbers of outcome events or summary measures over time This is described in the “Outcome Variable” section under “Methods.” There were 344 participants who were categorized into three different caries trajectories groups. Case-control study – Report numbers in each exposure category, or summary measures of exposure Cross-sectional study – Report numbers of outcome events or summary measures
Main results	16	(a) Give unadjusted estimates and, if applicable, confounder-adjusted estimates and their precision (e.g., 95% confidence interval). Make clear which confounders were adjusted for and why they were included NA – The presented methodology does not focus on the unadjusted estimates, but rather focuses on variable selection through penalized fit. (b) Report category boundaries when continuous variables were categorized NA – Continuous predictor variables were not categorized. (c) If relevant, consider translating estimates of relative risk into absolute risk for a meaningful time period NA
Other analyses	17	Report other analyses done – for example, analyses of subgroups and interactions, and sensitivity analyses The modeling methodology is employed in another manuscript that focuses on analyses, results, and conclusions as opposed to the presentation of a methodological approach. Sensitivity and other analyses are not applicable here.
Discussion
Key results	18	Summarise key results with reference to study objectives This is described in the “Discussion” section.
Limitations	19	Discuss limitations of the study, taking into account sources of potential bias or imprecision. Discuss both direction and magnitude of any potential bias Limitations are discussed in a paragraph in the “Discussion” section.
Interpretation	20	Give a cautious overall interpretation of results considering objectives, limitations, multiplicity of analyses, results from similar studies, and other relevant evidence This is described in the “Discussion” section.
Generalisability	21	Discuss the generalizability (external validity) of the study results This is covered in the both the “Introduction” and “Discussion” sections. The methodology presented here can be applied to many statistical modeling frameworks.
Other information
Funding	22	Give the source of funding and the role of the funders for the present study and, if applicable, for the original study on which the present article is based This information is included in a “Funding” passage at the end of the manuscript.

^*Give information separately for cases and controls in case-control studies and, if applicable, for exposed and unexposed groups in cohort and cross-sectional studies.

Note: An Explanation and Elaboration article discusses each checklist item and gives methodological background and published examples of transparent reporting. The STROBE checklist is best used in conjunction with this article (freely available on the Web sites of PLoS Medicine at http://www.plosmedicine.org/, Annals of Internal Medicine at http://www.annals.org/, and Epidemiology at http://www.epidem.com/). Information on the STROBE Initiative is available at www.strobe-statement.org.