Charge-Transfer Analysis of 2p3d Resonant Inelastic X-ray Scattering of Cobalt Sulfide and Halides

Abstract

We show that with 2p3d resonant inelastic X-ray scattering (RIXS) we can accurately determine the charge-transfer parameters of CoF₂, CoCl₂, CoBr₂, and CoS. The 160 meV resolution RIXS results are compared with charge-transfer multiplet calculations. The improved resolution and the direct observation of the crystal field and charge-transfer excitations allow the determination of more accurate parameters than could be derived from X-ray absorption and X-ray photoemission, both limited in resolution by their lifetime broadening. We derive the crystal field and charge-transfer parameters of the Co²⁺ ions, which provides the nature of the ground state of the Co²⁺ ions with respect to symmetry and hybridization. In addition, the increased spectral resolution allows the more accurate determination of the atomic Slater integrals. The results show that the crystal field energy decreases with increasing ligand covalency. The L₂ edge RIXS spectra show that the intensity of the (Coster–Kronig induced) nonresonant X-ray emission is a measure of ligand covalency.

1. Introduction

The ground-state electronic configuration influences the intrinsic chemical and physical properties of a system, including conductivity, magnetism, and chemical bonds. In the ligand–metal charge-transfer (LMCT) model, the 3d states of a transition-metal ion are assumed to be strongly correlated, where the Co²⁺ ions are approximated with a 3d⁷ ionic configuration. The 3d⁷ configuration is affected by the crystal field interaction, and it interacts with the 3d⁸L configuration via LMCT. The LMCT model has been introduced to classify the 3d transition-metal compounds into different types of insulators or conductors according to values of the Hubbard energy (U) and the LMCT energy (Δ).¹ The electronic structure can be investigated with infrared spectroscopy (IR),² optical absorption spectroscopy,³⁻⁶ Raman spectroscopy,⁷ and X-ray photoemission spectroscopy (XPS).⁸

2p3d resonant inelastic X-ray scattering (RIXS) is a bulk-sensitive, state- and element-selective measurement able to accurately investigate atomic, crystal field, and charge-transfer information.⁹⁻¹¹ Earlier 2p3d RIXS experiments had energy resolutions in the range of 200–500 meV,¹⁰⁻¹⁶ but this has improved to 30–200 meV in recent years.¹⁷⁻¹⁹ The increased resolution implies that dd-excitations and charge-transfer excitations can be analyzed in more detail.²⁰ In addition, the low-energy excitations (phonons, magnons) become visible, but this is not analyzed in the present paper. We have chosen cobalt dihalides and CoS as prototype materials to investigate the power of 2p3d RIXS experiments. These systems have been investigated by XPS.^8,21−24 The charge-transfer parameters influence the Neel temperature (T_N) and are correlated with the crystal structure.²⁵⁻²⁹ Cobalt chalcogenides are widely used as electrodes of pseudocapacitors,^30,31 hydrogen production catalyst,^32,33 and quantum dot-sensitized solar cells.³⁴ The understanding of its essential characteristics, such as local atomic structure, oxidation state, or chemical composition, is complicated by various amorphous and nanostructures. Recently, Kornienko et al. used Raman spectroscopy and X-ray absorption spectroscopy (XAS) to investigate the amorphous cobalt sulfide catalysts,³² but the electronic structure of the cobalt ions were not discussed in detail. We note that, unlike the cobalt dihalides, cobalt sulfides show metallic behavior.^34,35

In this study, the 2p3d RIXS spectra of CoF₂, CoCl₂, CoBr₂, and CoS compounds are analyzed systematically using the LMCT model. Although all the crystal structures are different,²⁵⁻²⁷ the cobalt ions in these compounds are surrounded by six ligands in an (distorted) octahedral geometry.^21,23 From the LMCT analysis, we derive relations between covalency, crystal field strength, and peak positions in 2p XAS and 2p3d RIXS.

2. Methodology

2.1. Experimental Details and Sample Preparation

Cobalt(II) fluoride (powder, >99%, ρ = 4.43 g·cm^–3), anhydrous cobalt(II) chloride (beads, −10 mesh, 99.999% trace metals basis, ρ = 3.36 g·cm^–3) and anhydrous cobalt(II) bromide (beads, −10 mesh, 99.99% trace metals basis, ρ = 4.91 g·cm^–3) were obtained from Sigma-Aldrich. Cobalt sulfide (powder, 99.5%, ρ = 5.45 g·cm^–3) was obtained from City Chemical LLC. The powders were applied on carbon tape, attached to the sample holder in an argon atmosphere glovebox, and transferred in an anaerobic environment to the RIXS measurement chamber using a dedicated transfer tool designed for the ADRESS beamline.³⁶

XAS and RIXS spectra were measured at the ADRESS beamline of the Swiss Light Source (SLS).¹⁷ The Co L_2,3 edge (2p) XAS spectra were measured through the drain current and by a photodiode for total electron yield (TEY). The incident energy scale was calibrated measuring the cobalt 2p XAS spectra of the cobalt monoxide powder and comparing it with literature values.³⁷ The 2p3d RIXS spectra were measured with the use of the high-resolution Super Advanced X-ray Emission Spectrometer (SAXES)³⁸ of the ADRESS beamline.¹⁷ A scattering geometry was used in which the angle between the incoming light vector and the outgoing one was 90°. The incoming light was polarized in linear parallel mode (linear horizontal; LH) to the scattering plane with a grazing incident angle of 20°. The total resolution of the 2p3d RIXS spectra were calibrated by measuring the elastic scattering of a noncobalt containing and amorphous reference with the incoming energy from 765 to 785 eV. The combined energy resolution of the RIXS zero-loss peak was found to be 160 meV of full width at half-maximum (fwhm) at the Co L₃ edge (780 eV). The experiments were performed at room temperature and with a pressure below 10^–9 mbar. The spectra were summed over 6–15 partial spectra that were acquired from 40 to 120 s each (varying to avoid detector saturation). The spot size of the beam was 4 × 52 μm², and the incident flux was estimated as 5 × 10¹² ph/s. Using the spectral acquisition times given in Table S1 of the Supporting Information and the freely available Matlab script XASskindose,³⁹ the skin doses for each CoF₂, CoCl₂, CoBr₂, and CoS spectrum were estimated to vary between 2.0 and 4.5, 1.9–4.9, 0.9–3.8, and 2.5–7.8 teragray (TGy), respectively. The accumulated skin doses will be three times higher because typically two different sample spots were used to acquire spectra at six excitation energies. Sample integrity was confirmed by repeated measurements of the 2p XAS spectral shape.

2.2. Theory and Simulations

The 2p3d RIXS spectra are calculated with the Kramers–Heisenberg formula:^10,40

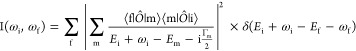1

Here, ω_i and ω_f are the energies of the incident and the emitted photons; Ei, E_f, and E_m are the eigenvalues of the initial state |i⟩, the final state |f⟩, and the intermediate state |m⟩, respectively; Γ_m gives the lifetime broadening of the intermediate state, and Ô is the transition operator, for which the dipole transitions were implied for the case of the 2p3d X-ray absorption and the 3d2p X-ray emission channels. In 2p3d RIXS, |i⟩, |m⟩, and |f⟩ refer to the configurations 2p⁶3dⁿ, 2p⁵3dⁿ⁺¹, and 2p⁶3dⁿ, respectively. In addition, if the LMCT hybridization is included, the initial state |i⟩ becomes the linear combination between the ionic configuration (3dⁿ) and configuration with ligand hole (3dⁿ⁺¹L). By tuning the 2p3d absorption energy, the resonance conditions can emphasize different intermediate states.

Two important phenomena are correlated with the LMCT hybridization within a 3d transition-metal ion: (a) the ligand hybridization influences the metal t_2g and e_g states differently;⁹ and (b) bonding and antibonding states between original ionic states |dⁿ⟩ and ligand hole states |dⁿ⁺¹L⟩ are created that give rise to the dd-excitations and charge-transfer excitations, respectively.^9,10 These two phenomena will be discussed in terms of (a) the crystal field energy 10Dq and (b) the charge-transfer energy Δ. Using incident energies at various energies of the L₃ edge, it is possible to analyze the details of the dd-excitations and the charge-transfer excitations in the 2p3d RIXS spectra.⁹⁻¹¹ The theoretical details are discussed in section 2 of the Supporting Information.

The beam polarization was defined as LH (LV) as the light was polarized linear parallel (linear perpendicular) to the scattering plane. The experimental 2p3d RIXS spectra were measured with a LH polarization incident beam and a 90° scattering geometry. This experimental setting was simulated as the sum of [LV_in to LH_out] and [LH_in to LV_out] polarizations for powder samples. In order to study the 2p XAS and 2p3d RIXS spectral shapes, charge-transfer multiplet (CTM) calculations were used.^9,41,42 A modified version of the code was applied to obtain exact solutions of the charge-transfer Hamiltonian.⁴³ XAS calculations were performed with CTM4XAS.⁴⁴ The charge-transfer RIXS calculations were performed with the use of a dedicated Matlab program.⁴⁵ CTM4DOC was used to project the states to their individual basis and to analyze the expansion coefficients in terms of different basis sets.⁴⁶

In a CTM calculation, the following interactions are used: atomic electron–electron interactions, spin–orbit coupling, the crystal field potential, the charge-transfer hybridization, and the broadening parameters. The Slater integrals (F_dd², F_dd, F_pd², G_pd, and G_pd³) describe the atomic electron–electron interactions in the initial, intermediate, and final states. Alternatively one can use the Racah parameters B and C that are linear combinations of F_dd and F_dd⁴ (B = (9 F_dd – 5 F_dd⁴)/441 and C = 5 F_dd/63).^47,48 The LMCT effect is included by the single impurity Anderson model,^49,50 considering the interactions between dⁿ and dⁿ⁺¹L configurations, where an electron has been transferred from the ligand valence band while preserving spin and symmetry.⁹ The LMCT energy (Δ) is the ionic energy difference between the two configurations, and the electron hopping integrals (T) describe their coupling.⁹ The resulting ground-state wave function is a mixture of the dⁿ and dⁿ⁺¹L configurations, which is given as |φ_GS⟩ = α |dⁿ⟩ + β |dⁿ⁺¹L⟩ with an eigen energy E_GS.

3. Results

3.1. 2p3d RIXS Experiments

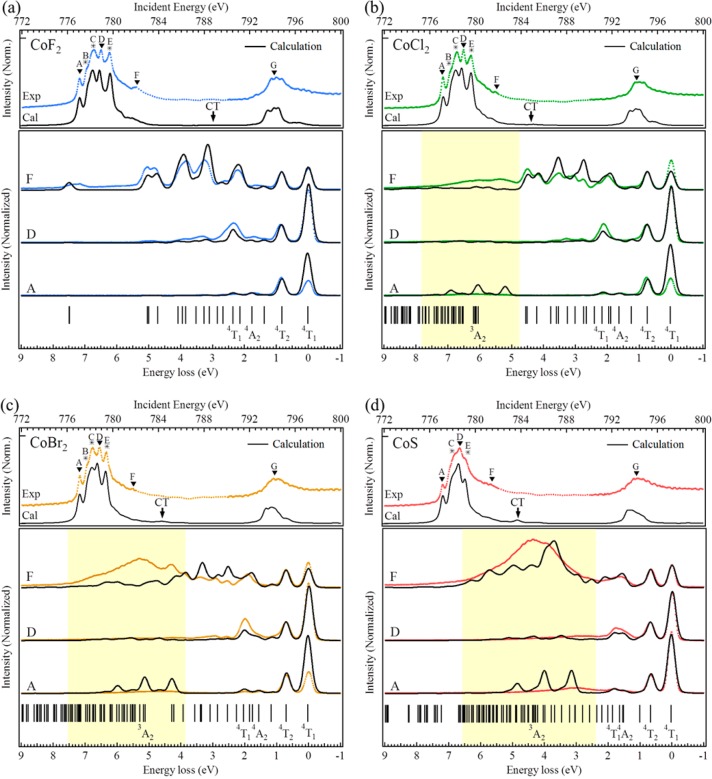
The top panel in Figure 1 shows the 2p (L_2,3) XAS spectra of CoF₂, CoCl₂, CoBr₂, and CoS. All four spectra show the clear signature of a ⁴T₁ high-spin Co²⁺ ground state, equivalent to CoO.^10,51 One can observe that the multiplet states are more and more compressed in the series CoF₂ < CoCl₂ ∼ CoBr₂ < CoS. To measure the 2p3d RIXS spectra, the incident photon energies were selected in the 2p XAS spectra and labeled with capital symbols A–G (top panels of Figure 1). The chosen incident energies correspond to the different peaks and features of the XAS spectra, as indicated. The incident energies A–F correspond to the 2p_3/2 edge. At the 2p_1/2 edge, only the highest peak energy G was selected for the 2p3d RIXS measurements. In the case of CoS, the multiplet states are compressed, which makes peak B invisible; therefore, no 2p3d RIXS was measured at energy B for CoS.

Figure 1.

Experimental and simulated 2p XAS (top panels) and the RIXS (bottom panels) spectra of (a) CoF₂, (b) CoCl₂, (c) CoBr₂, and (d) CoS. The capital labels A–G indicate the incident energies of the RIXS spectra. The yellow blocks indicate the excitation regions of the charge-transfer excitations.

The bottom panels in Figure 1 present both the experimental and the LMCT-simulated 2p3d RIXS spectra (section 3 of the Supporting Information), where the intensity of the simulation was normalized to the first dd-excitation at approximately 0.7 eV. For CoF₂, a series of sharp features are observable over the whole energy range from 0.0 to 9.0 eV. In fact the peaks continue above 9.0 eV, but the spectra are limited to this energy range to make the low-energy peaks better visible. CoBr₂ and CoS also contain the same series of sharp peaks, but they are limited to the range between 0.0 and 3.0 eV. Between 3.0 and 7.0 eV, broader features are visible. The 2p3d RIXS final states relate to excitations of the ⁴T₁ Co²⁺ ions. One can make a direct comparison to optical spectroscopy and relate the sharp peaks with dd-excitations and the broad peaks with charge-transfer excitations. A difference with optical spectroscopy is that the dd-excitations are dipole-forbidden in direct optical absorption, which makes them weak in intensity.³⁻⁶ Because 2p3d RIXS is a dipole excitation plus dipole decay transition, the dd-excitations are strong. In fact, for CoF₂ and CoCl₂ the dd-excitations are stronger than the charge-transfer excitations. Experimentally we conclude that in 2p3d RIXS we reach equivalent final states as in optical absorption with an inverted intensity strength where dd-excitations are stronger than charge-transfer excitations.

3.2. 2p3d RIXS Simulations

The spectral features are calculated with the Kramers–Heisenberg equation using the incident photon energies from the experiments. The general procedure in the 2p3d RIXS calculations is the following:

• (1)We calculate the atomic parameters for the Co²⁺ ion, using the common approach in CTM4XAS of using 80% of the Hartree–Fock calculated values for the Slater integrals plus the spin–orbit couplings as calculated for the free ion.
• (2)We use the 2p3d RIXS spectra of each compound to determine the value of 10Dq.
• (3)We use the 2d3p RIXS spectra of each compound to determine Δ.
• (4)Keeping the optimized 10Dq and Δ, the atomic parameters were optimized to obtain the best fit for both the 2p XAS and all 2p3d RIXS spectra, where the same parameters are used for all four systems.

First we describe the comparison with the 2p3d RIXS experiments. In section 3.3 we describe the procedure to determine the value of 10Dq. In section 3.4 we describe the procedure to determine the value of Δ and the consequence of charge transfer on the crystal field splitting.

All CTM calculations were performed in C₄ symmetry at 300 K using a small exchange field (M ∼ 2 meV) to take the antiferromagnetic order (T_N ∼ 10–40 K) into account.²⁷⁻²⁹ The 300 K results were calculated by considering the first six energy states and summing them with a Boltzmann distribution weighting. Because of the contraction of the 3d wave function due to the core hole, the 10Dq value is reduced with 15% for the intermediate state.⁵² The charge-transfer parameters include the charge-transfer energy Δ, the Hubbard Coulomb repulsion between the 3d electrons U_dd (U), the core hole potential U_pd (Q), and the electron hopping parameters T. In this article, the parameters were fixed by using U = 6 eV, Q = 7 eV, T_t2g = 1 eV, and T_eg = 2 eV. Note that 2p XAS and 2p3d RIXS are not sensitive to the values of U and Q, but only to their energy difference. For Co²⁺, only 3d⁷ and 3d⁸L configurations were considered in the calculations. The 3d⁹L² and 3d¹⁰L³ configurations were neglected when reproducing the 2p XAS and the 2p3d RIXS spectral shapes.⁵³

As described above, the initial calculations were performed with atomic Slater integrals, defined as 80% of their Hartree–Fock value. 2p3d RIXS allows for a refinement of the atomic parameters: The combination of (a) its 160 meV resolution, (b) the multiple resonant spectra, and (c) the large number of spectral features allows for a further refinement of the atomic interactions. The optimized values of the Slater integrals are given in Table 1 (see section 4d of the Supporting Information), where we note that in O_h symmetry the exchange interaction for e_g and t_2g states is not exactly the same.⁵⁴ The F_dd² and F_dd are not necessarily reduced by the similar reduction values. The lifetime of the 2p core states is approximately constant for the L₃ edge.^55,56 The lifetime broadening (L) of the 2p core hole was set to 0.4 eV fwhm,^10,57 and we add the experimental resolution with a Gaussian value of 0.16 eV fwhm. The final states of 2p3d RIXS relate to dd-excitations that are known from optical spectroscopy.³⁻⁶ The lifetime of the dd-excitations varies depending on the spin state. We use a broadening of 50 meV fwhm for lifetime of dd-excitations and the Gaussian broadening of 160 meV for simulating both incoming and outgoing beams. Because the elastic ⁴T₁ peak is split into 12 individual states spread over 100 meV,⁵¹ its overall broadening is ∼250 meV.

Table 1. Slater Integral and Spin–Orbit Coupling Energies in the Simulation (in eV)^a.

	Fdd2	Fdd4	Fpd2	Gpd1	Gpd3	ζp	ζd
2p63d7	9.470	6.805	–	–	–	–	0.066
2p63d8L	8.512	6.072	–	–	–	–	0.059
2p53d8	10.115	7.276	6.389	4.318	2.701	9.748	0.083
2p53d9L	–	–	5.83	3.895	2.435	9.750	0.075

^aThe slater integrals values F_dd², F_dd, F_pd², G_pd, and G_pd³ are 82%, 94%, 88%, 80%, and 88% of the Hartree–Fock values, respectively.

We analyzed the nature of the lowest-lying states of 3d⁷ configuration that are given with their ⁴T₁, ⁴T₂, and ⁴A₂ Mulliken symbols in Figure 1 and listed in Table 2. The yellow block indicates the region of the charge-transfer excitations, where a large charge-transfer energy Δ shifts them to higher excitation energies. The charge-transfer peaks provide a determination for the hybridization information and will be further discussed in section 3.4. In general, the energy and shape of the excitations are well-reproduced, especially in the first 2 eV. The peaks at higher excitation energies above 3.0 eV were not simulated as accurately, which is related to the approximations to the 3d⁸L charge-transfer band due to limitations in computer power. The full charge-transfer band has been approximated with three charge-transfer states that yield features that are too sharp at energies above 3.0 eV.

Table 2. RIXS-Derived State Symmetry Term Symbols and Energies (in eV) and Their Comparison to Calculations.

	CoF2	CoCl2	CoBr2	CoS
	exptl/calcd	exptl/calcd	exptl/calcd	exptl/calcd
Quartet
4T1	0.00/0.00	0.00/0.00	0.00/0.00	0.00/0.00
4T2	0.85/0.81	0.77/0.72	0.71/0.68	0.67/0.65
4A2	1.71/1.76	1.60/1.61	1.52/1.54	1.44/1.51
4T1	2.27/2.35	2.11/2.14	1.98/2.02	1.79/1.83
Charge Transfer
3A2 (CT)	11.50/11.26	6.12/6.11	5.30/5.30	3.94/4.20

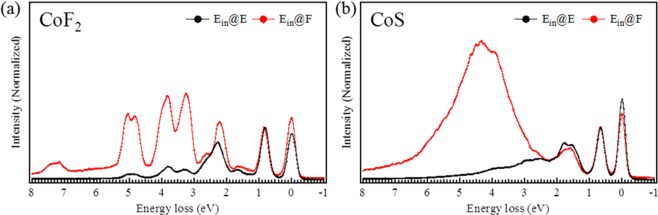
With Figure 2 we emphasize the excitation selectivity. At incident energies A–E, the 0–2 eV excitations dominate, but at incident energy F, more intensity is found at the higher excitation energies. In the case of CoF₂, the spectra at energy F gives dd-excitations in the whole energy loss region between 0 and 8 eV (Figure 2a). The spectra at energy F of CoS shows a large and broad feature at about 4 eV (Figure 2b) that can be assigned to charge-transfer excitations.

Figure 2.

Experimental results at incident energies E and F of (a) CoF₂ and (b) CoS.

3.3. Determination of the Crystal Field Value 10Dq from 2p3d RIXS Experiments

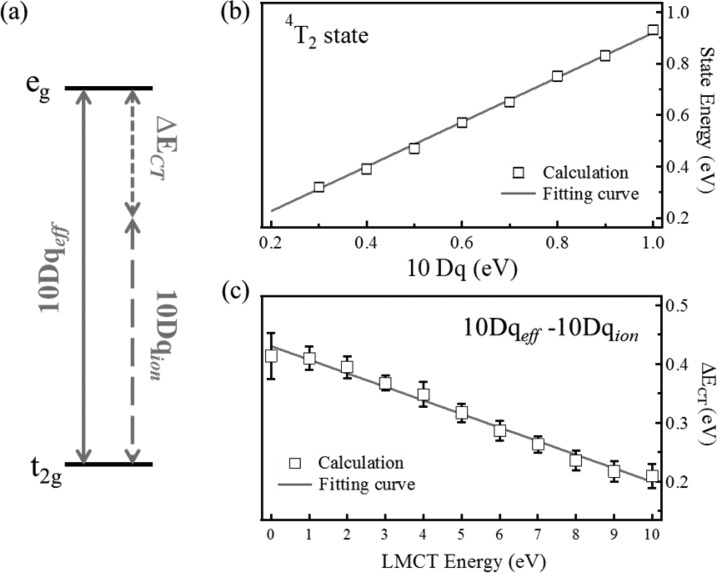
In our CTM simulation, 10Dq and Δ are the only two free parameters that are used in addition to the fixed atomic parameters. From the Tanabe–Sugano diagram³ it is known that the effective value of 10Dq is close to the splitting between the ground state and the first dd-excitations. In other words, the first peak in the dd-excitations will be close to the value of 10Dq. We will investigate the relation between the first dd-excitation energy and 10Dq. In the Co²⁺ (3d⁷) high-spin Tanabe–Sugano diagram (Figure S5), the energy difference between the ⁴T₁ and ⁴T₂ states is linear in 10Dq between 0.2 and 1 eV. This energy difference corresponds to the first dd-excitation in the 2p3d RIXS spectra. As such, one can track the 10Dq value by locating the first dd-excitation peak, which is more reliable than fitting the 2p XAS spectrum.⁵³ The energy difference between the ⁴T₁ and ⁴T₂ sates has been collected in Figure 3b. From these data points, the following relation regarding the crystal field splitting was derived (see section 4 of the Supporting Information for more details):

2

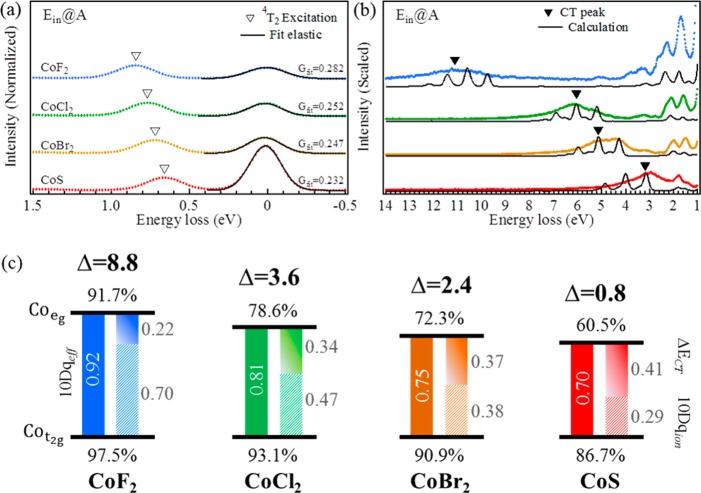
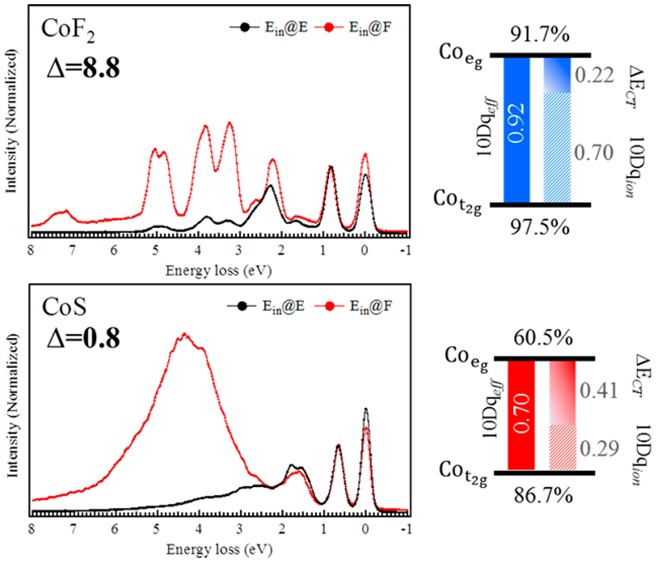
This equation shows that the difference between ⁴T₁ and ⁴T₂ states is not exactly equal to 10Dq, but they are correlated with a linear relationship. From this relation we can determine the 10Dq value experimentally from the first dd-excitation of the 2p3d RIXS spectra. The peak maxima of the first dd-excitations are 0.85, 0.77, 0.71, and 0.67 eV for CoF₂, CoCl₂, CoBr₂, and CoS, respectively (the ⁴T₂ state in Figure 4a). In all cases the first peak relates to the ⁴T₂ state.^3−7,10,51 The 10Dq values of the compounds were converted using eq 2, and they are 0.92, 0.81, 0.75, and 0.70 eV for CoF₂, CoCl₂, CoBr₂, and CoS, respectively. This relates to an increase with respect to first dd-excitation by 0.07, 0.04, 0.04, and 0.03 eV, respectively.

Figure 3.

(a) Conceptual contributions of 10Dq_eff. (b) Energy difference between the ground state (⁴T₁) and the first dd-excitation (⁴T₂) as a function of 10Dq without LMCT effect. (c) ΔE_CT correlation with respect to LMCT energy Δ. The fitted straight lines in panels b and c provide the values given in eqs 2 and 3, respectively. The error in panel c is the error of different calculation sets to the their average point (details in section 4c of the Supporting Information).

Figure 4.

Zoom of the 2p3d RIXS spectra at incident energy A in (a) the low-energy loss region (between −0.5 and 2 eV) and (b) the charge-transfer excitation region. (c) Graphical representation of the conceptual effective crystal field energy splitting and the cobalt ionic orbital covalence in a function of Δ.

3.4. Ionic and Covalent Contribution to the Crystal Field Splitting

When the LMCT effect is considered, the charge transfer contributes to the e_g–t_2g splitting, i.e., the overall effective crystal field is caused by both ionic and charge-transfer contributions. The total crystal field splitting (10Dq_eff) should be reconsidered as the effect from two components:

• 1.The ionic crystal field value (10Dq_ion)
• 2.The charge-transfer contribution (ΔE_CT)

Figure 3a shows the ionic and charge-transfer contributions of the crystal field splitting. In the simulations we relate the first dd-peak to the total crystal field splitting, which implies that after the determination of the charge-transfer energy Δ, we have to adjust 10Dq_ion. Figure 3c shows the results for a series of calculations as a function of Δ. One can observe a linear trend between the value of Δ and (10Dq_eff – 10Dq_ion). This implies that there is a linear relation between the charge-transfer contribution (ΔE_CT) and Δ (cf. Figure 3c):

3

We optimized the Δ values by comparing the calculated charge-transfer peak to the experimental spectra. In Table 3 the Δ and ΔE_CT values are given, and after eq 3 was applied, the ionic crystal energy 10Dq_ion was obtained. Figure 4c summaries the contributions of 10Dq_eff (filled bars), 10Dq_ion (striped bars), and ΔE_CT (slide bars) in a graphical presentation.

Table 3. Experimental First dd-Excitation and its Relation to Different 10Dq Values and Δ.

	first dd	10Dqeff	10Dqion	ΔECT	Δ
CoF2	0.85	0.92	0.70	0.22	8.8
CoCl2	0.77	0.81	0.47	0.34	3.6
CoBr2	0.71	0.75	0.38	0.37	2.4
CoS	0.67	0.70	0.29	0.41	0.8

4. Discussion

4.1. Width of the Elastic Peak

An interesting observation is that the width of the elastic peak in CoF₂ (fwhm ∼280 meV) is larger than that in CoS (fwhm 230 meV), whereas the experiment resolution was 160 meV with an uncertainty of less than 10 meV. In other words, the observed elastic peak broadenings are larger than the experiment resolution. This implies that there are additional broadening mechanisms due to (1) 3d spin–orbit coupling, (2) magnetic exchange, (3) symmetry distortions, and/or (4) vibrations. The effects 1–3 split the ⁴T₁ ground state.⁵¹ Infrared spectroscopy results² show that the highest energy of the spin–orbit coupling peak (interacting with the exchange field) is 0.173 eV for CoF₂, while the energies for CoCl₂ and CoBr₂ are 0.148 and 0.143 eV, respectively, confirming the 0.03 eV broadening difference in Figure 4a. One possible reason for this effect is that when the Δ value is smaller, the dⁿ and dⁿ⁺¹L configurations are more hybridized, leading to an effective reduction of the 3d spin–orbit coupling. An alternative scenario is that the more ionic the compound, the larger the effect of a crystal field distortion.

4.2. Ground-State Analysis and Differential Orbital Covalency

The LMCT energies listed in Table 3 were determined according to the charge-transfer excitations as emphasized in Figure 4b. A trend of the charge-transfer excitations is visible as a function of Δ. The obtained Δ values were 8.8, 3.6, 2.4, and 0.8 eV with respect to the CoF₂, CoCl₂, CoBr₂, and CoS samples. The center of the features were extracted from the spectra and are given in Table 2. A smaller Δ value leads to a stronger hybridization of ground state between the 3d⁷ and 3d⁸L configurations, in which the ground state can be described by |φ_GS⟩ = α|3d⁷⟩ + β|3d⁸L⟩ with the population coefficient values α and β. This gives the hybridization percentages of the original multiplet (|α|²) and the ligand hole multiplet configuration (|β|²).

To obtain the hybridization percentages, the microstates of the ground state are projected into separate 3d⁷ and 3d⁸L configurations of specific orbitals derived from symmetry (in octahedral symmetry, for example, in terms of e_g and t_2g orbitals).⁴⁶ The results are shown in Table 4. It is observed therein that the percentage of the |3d⁷⟩ states on the cobalt ion decreases with decreasing Δ. The percentage of ligand-hybridized |3d⁸L⟩ states for CoS is ∼30%. From these numbers, the metal covalency of the e_g and t_2g orbitals can be estimated. Here we consider only one-electron hopping from the ligand to the metal ion e_g or t_2g orbitals. Hence, only the 3d⁷ ground state |t_2g⁵e_g²⟩ and the ligand hole e_g |t_2g⁵e_g³L⟩ and t_2g |t_2g⁶e_g²L⟩ states are taken into account. The covalence fraction of cobalt within e_g orbitals is then given by

4

where 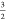is a renormalization factor (2 out of 3 holes in the d⁷ configuration are in e_g orbitals) and P_t2g^xeg^y are the percentages for configuration t_2g^xe_g as given in Table 4. This implies that the covalence fraction of cobalt within the e_g orbitals is reduced from 100% by the corresponding fraction of ligand character within these e_g orbitals. Similarly, the covalence fraction of cobalt in the t_2g orbitals is then given by

5

Table 4. Orbital Occupation and Covalency Analysis of CoF₂, CoCl₂, CoBr₂, and CoS.

	|d7⟩		|d8L⟩			metal covalency
	|t25e2⟩	|t24e3⟩	|t25e3L⟩	|t26e2L⟩	|t24e4L⟩	T2g	Eg	DOC	⟨n⟩
CoF2	85.3	8.6	5.1	0.8	0.3	97.5	91.7	5.8	7.06
CoCl2	75.7	8.3	12.9	2.1	1.0	93.1	78.6	14.4	7.16
CoBr2	71.0	8.1	16.7	2.7	1.4	90.9	72.3	18.6	7.21
CoS	62.5	7.4	23.8	4.0	2.3	86.7	60.5	26.2	7.30

It follows that, when going through the series from CoF₂ to CoS, the cobalt ion character in the e_g orbitals decreases faster than that in the t_2g orbitals (Figure 4c). In octahedral symmetry, the ligand 2p orbitals overlap strongly with the cobalt 3d e_g (d_x²–y² and d_z²) orbitals; thus, ligand hybridization is affecting e_g orbitals more than t_2g orbitals. By subtracting the e_g from the t_2g orbital covalency one obtains the differential orbital covalency (DOC)⁵⁸ as given in Table 4. The DOC values are dependent on crystal field symmetry and strength, as well as charge-transfer hopping energies. Note that we obtain a similar DOC value for CoS as obtained for [FeCl₆]^3– with similar symmetry and charge-transfer settings:⁵⁸ CoS (Δ = 0.8 eV; T_eg:T_t2g = 2:1) and [FeCl₆]^3– (Δ = 0.1 eV; T_eg:T_t2g ∼ 2:1) have DOC values of 25–27%.

4.3. Charge-Transfer Parameters Derived from 2p3d RIXS Compared with 2p XPS

When the Δ values in Table 2 are compared with XPS-derived Δ values,⁸ only the value for CoF₂ is found to be equal (RIXS, 8.8 eV vs XPS, 8.6 eV). CoCl₂ (RIXS, 3.6 eV vs XPS, 4.5 eV) and CoBr₂ (RIXS, 2.4 eV vs XPS, 3.5 eV) show less agreement. For CoS, a small Δ value (0.8 eV) was found, which is related to the sample exhibiting metallic behavior.^1,34 First, a simulation including the third configuration 3d⁹L² has been tested (Figure S11). In the case of CoBr₂, the three-configuration calculation shifts the charge-transfer excitation ∼0.3 eV lower than the two-configuration calculation with the same Δ value. In other words, the Δ value should be ∼2.7 eV (2.4 + 0.3) for CoBr₂ when we consider the third configuration. This brings the Δ value a bit closer to, but smaller than, the XPS value (3.5 eV).

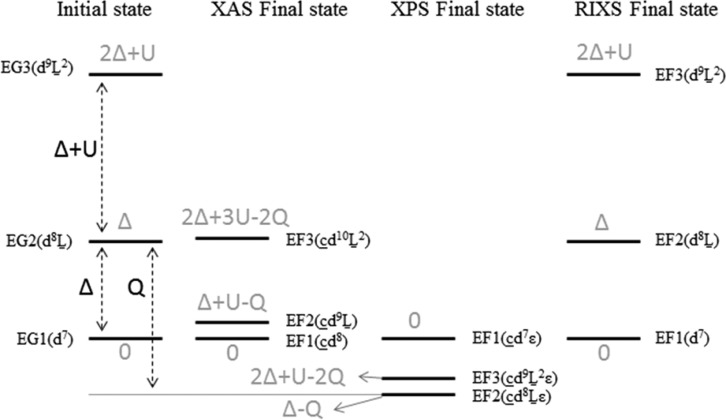
Figure 5 displays the final state configurations of the XAS, XPS, and RIXS processes. It shows the energy differences between the ionic configuration and the two charge-transfer configurations. The notations EG and EF refer to ground and final states, respectively. The numbers 1, 2, and 3 refer to configurations with zero, one, and two ligand hole(s), respectively. The charge-transfer configurations show that the core–hole potential (Q) needs to be taken into account in the case of XAS and XPS spectra. This implies that we have to optimize Q (in addition to Δ) to simulate the XAS and XPS spectra. Because of the larger screening effects, at least three charge-transfer configurations need to be taken into account for XPS spectra.^21,59 On the other hand, the relative final state energy of the first LMCT configuration in valence RIXS is Δ. Being independent of Q, the core–hole will not contribute to the relative configuration energy in 2p3d RIXS, where we note that via its influence on 2p XAS Q could influence the intensities. We ignore the second LMCT configuration in the RIXS calculations. As indicated in Figure 5, the relative initial and final state energies of the second LMCT configuration are 2Δ + U in RIXS. In the vast majority of cases, its relative energy will be significantly higher than that of the first LMCT configuration and will play a negligible role in the spectral shape. Finally, we note that our Δ and 10Dq_ion determinations are in line with CTM analysis of CoO 2p3d RIXS by Magnuson et al.¹⁰

Figure 5.

Initial ground and final state energy configurations of XAS, XPS, and RIXS.

We conclude that RIXS is more accurate for the determination of Δ due to (1) the sharper experimental features and (2) the smaller (nonlocal) screening effects. Note that the uncertainty in the atomic parameters (and in 10Dq) is also present in XPS, but because of the absence of spectral features it is not possible to gain experimental information regarding their exact values. Because 2p XAS and 2p3d RIXS are not sensitive to the separate values of U and Q, a full electronic structure determination would ideally consist of 2p3d RIXS combined with 2p XPS, or another (resonant) photoemission/Auger experiment.

4.4. Use of the Coster–Kronig Auger Channel to Determine the Covalency

In this section, the L₂ (2p_1/23d) edge RIXS spectra are discussed. In comparison with the L₃ (2p_3/23d) edge RIXS spectra, the L₂ edge RIXS spectra give the resonant spectra of L₂ (3d2p_1/2) emission and in addition the nonresonant spectra of L₃ (3d2p_3/2) emission. Figure 6 shows the experimental and calculated results. Between 0 and 10 eV the spectra show the dd-excitations and the charge-transfer excitations, reproduced with the same procedure as discussed above. New features were observed in the high energy loss region. These features relate to X-ray emission from the 3d2p_3/2 channel. The integrated intensity ratio between nonresonant (9–25 eV) and resonant (−2 to 8.5 eV) emissions (L₃/L₂) are ∼0.55, 1.06, 1.22, and 1.71 for CoF₂, CoCl₂, CoBr₂, and CoS, respectively.

Figure 6.

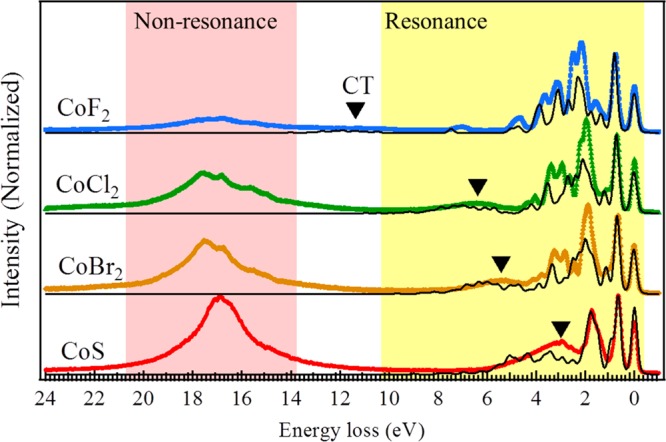
Experimental (colored traces) and simulated (black lines) RIXS spectra at incident energy G.

In order to explain these features, the core hole decay was simplified in two groups: radiative decay (X-ray emission) and nonradiative or electronic decay (Auger). In the case of 2p core holes in 3d transition-metal ions, the electronic decay channels constitute more than 99% of the total decay, and they dominate the lifetime.^11,20,56 These Auger channels are dominated by the 2p3p3p, 2p3p3d, and 2p3d3d decays. In the resonant 2p_1/23d X-ray emission, the RIXS signal follows the process

The scattering cross section is proportional to the radiative decay. In the case of the nonresonant channel, a Coster–Kronig Auger channel is involved in the first step of the decay process:²⁰

The 3d2p_3/2 X-ray emission intensity is proportional to the strength of the Coster–Kronig Auger channel, where the other Auger channels are equivalent in strength for the L₃ and the L₂ edges.^18,49,55 The large L₃ X-ray emission for CoS implies that the Coster–Kronig channel is strong, which is correlated with the large charge-transfer effects. This behavior has also been studied on cobalt clusters in SiO₂⁴⁹ and iron-based superconductors.⁶⁰⁻⁶² Our conclusion is that the intensity of the Coster–Kronig induced nonresonant X-ray emission is a measure of the covalency of a system, where further study is required to quantify this effect for different elements.

5. Conclusions

We have measured high-resolution 2p3d RIXS results of CoF₂, CoCl₂, CoBr₂, and CoS. Charge-transfer multiplet calculations are able to accurately reproduce the spectral shapes. The analysis revealed accurate values of the charge-transfer energy Δ and the crystal field value 10Dq, where the crystal field is split into ionic and charge-transfer contributions. In comparison with XPS, 2p3d RIXS is a more accurate method to determine the charge-transfer energy (Δ). In addition, it is more precise regarding the crystal field value 10Dq and also in determining the atomic electron–electron interactions (Slater integrals).

From the simulations, the orbital occupancies of the different states are given, and the corresponding differential orbital covalency analysis confirms that CoS is significantly more covalent than CoF₂. It is observed experimentally that the broadening of the quasi-elastic peak become gradually smaller while going from ionic CoF₂ to covalent CoS, due to either an effective reduced 3d spin–orbit coupling and/or symmetry distortions.

The L₂ edge RIXS spectra are analyzed with respect to the integrated intensity ratio between resonant (2p_1/23d) and nonresonant (2p_3/23d) X-ray emissions, which are ∼0.55, ∼1.06, ∼1.22, and ∼1.71 for CoF₂, CoCl₂, CoBr₂, and CoS, respectively. These numbers show that the Coster–Kronig channel is stronger in CoS, and we conclude that the ratio between resonant and nonresonant decay is a potential tool to probe the effects of electron delocalization.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.7b06882.

• Applied X-ray skin doses, charge-transfer multiplet calculation and single-impurity Anderson model, details on the experimental and simulated results, Tanabe–Sugano diagrams and the effects of charge transfer (PDF)

The authors declare no competing financial interest.