Solving Immunology?

Abstract

Emergent responses of the immune system result from integration of molecular and cellular networks over time and across multiple organs. High-content and high-throughput analysis technologies, concomitantly with data-driven and mechanistic modeling, hold promise for systematic interrogation of these complex pathways. However, connecting genetic variation and molecular mechanisms to individual phenotypes and health outcomes has proven elusive. Gaps remain in data, and disagreements persist about the value of mechanistic modeling for immunology. Here, we present the perspectives that emerged from the NIAID workshop “Complex Systems Science, Modeling and Immunity” and subsequent discussions regarding the potential synergy of high-throughput data acquisition, data-driven modeling and mechanistic modeling to define new mechanisms of immunological disease and to accelerate the translation of these insights into therapies.

The Complexities of Immune Dysregulation

Dysregulation of immune and inflammatory pathways is at the core of many diseases facing citizens of the 21^st century. These diseases are multi-factorial, exhibit great patient-to-patient variability, and are often intractable to both traditional therapy and reductionist insight. Immune regulation in healthy individuals is orchestrated by highly complex, massively- and dynamically-interacting gene networks, immune signaling pathways, cellular networks, host-pathogen interactions, and nutrition-microbiota-host interplay. Immune-mediated diseases, such as those that stem from the response to viral or bacterial infection, as well as trauma-induced inflammation, Crohn’s disease (CD), type 1 diabetes (T1D), or multiple sclerosis (MS), result when these homeostatic immunoregulatory mechanisms deviate or fail.

Recent decades have brought tremendous progress in the application of “omics” and associated bioinformatics methods to several immunological diseases. Genome and disease mapping consortia have helped elucidate how genetic variation influences disease risk, and consortia over the last 15 years have provided progressively finer resolution of immune disease-associated genetic variation [1, 2]. Multi-dimensional and high-throughput technologies are facilitating a comprehensive and systematic interrogation of complex immune pathways and the identification of relationships among their components at both the cellular and molecular levels, in both healthy individuals and those with infections or immune-mediated diseases. Moreover, computational analyses in genome-wide association studies (GWAS) are identifying increasing numbers of candidate immune disease-modulating genetic elements. For example, over 60% of the genetic variation predicting MS onset has been elucidated; these genetic variants largely overlap with other autoimmune diseases [3].

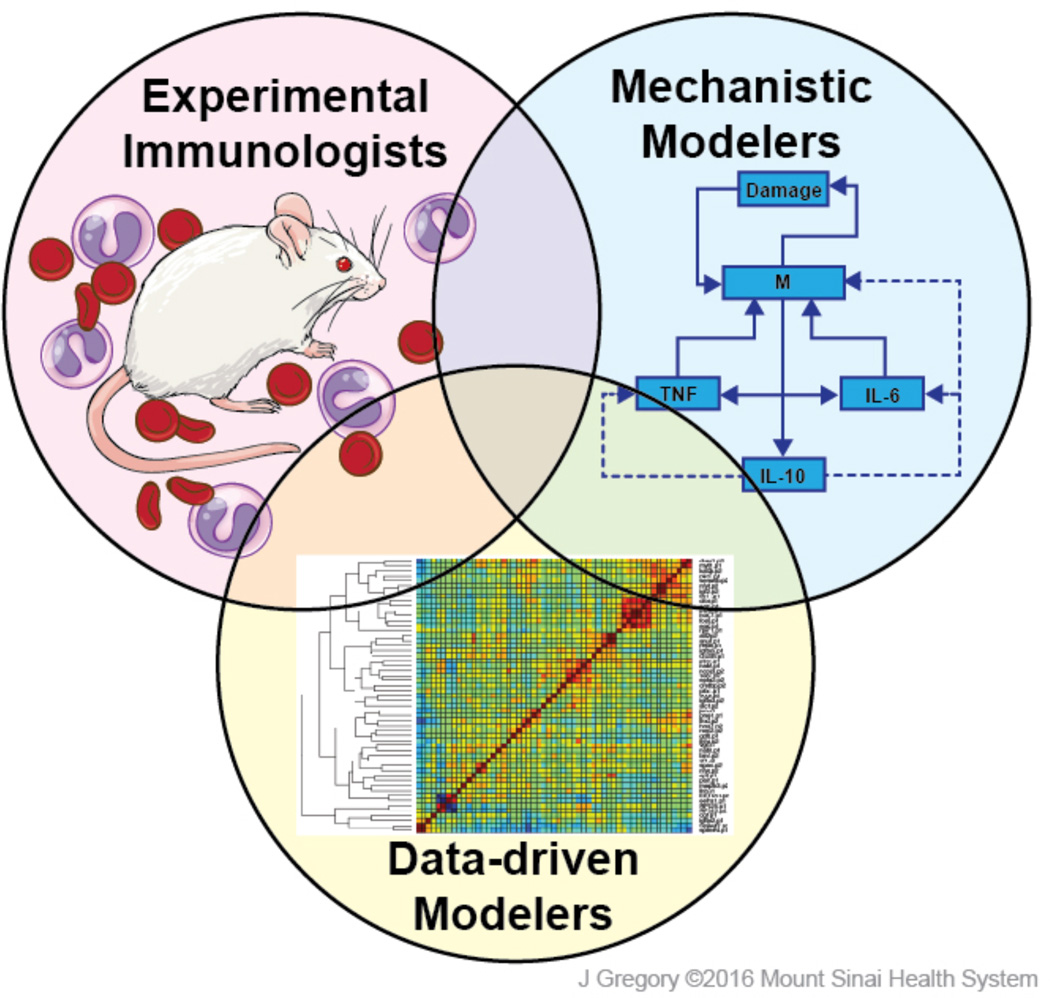
A fundamental challenge for immunology is how to extend this rapidly growing, individualized data acquisition. More specifically: what is the optimal way to leverage focused, hypothesis-driven immune research to understand how immune system behavior in health and disease emerges from molecular, genetic, epigenetic, cellular, and environmental modulatory elements? The National Institute of Allergy and Infectious Disease (NIAID) convened a workshop of computational and experimental immunologists in October 2015 to address this challenge. At the workshop and in subsequent discussions, different viewpoints separated experimental immunologists, data-driven modelers, and mechanistic modelers (Fig. 1). Although researchers from divergent backgrounds approach fundamental questions in immunology from different and sometimes clashing perspectives, they share a common interest in reducing the burden of immune disease by improving the predictability of immunological responses.

Figure 1. Different Perspectives of Immunology Researchers.

Generally, immunologists seek to understand the role of immune system in health and disease, focusing on how genetic, epigenetic, and environmental variations affect immune function and influence individual disease expression and response to treatment. Data-driven modelers seek to map predictive relationships between multiple data variables and disease in individuals, reconstructing and examining how molecular and celluar networks change in health and disease. Mechanistic modelers seek to define how a defined set of molecular and cellular interactions can lead to complex outcomes in health and immunological disease. This latter group utilizes abstractions of biological mechanisms encoded into computational models, and seek to define how diverse, complex health and disease phenotypes emerge from a defined set of immune interactions, set in motion by defined initial biological conditions.

A further common view shared by experimental and computational immunology researchers is that despite the explosion of “omics” and related techniques such as mass cytometry (CyTOF) in experimental immunology, a dearth of key data is a major impediment to an improved mechanistic and predictive understanding of immunology. The ability to infer novel interactions, principal drivers, and interconnected networks using data-driven modeling, including approaches such as bioinformatics, machine learning classifiers, or mathematical modeling of signaling networks or cell dynamics, is now well accepted [4]. However, mechanistic mathematical modeling has been incorporated less well into experimental immunology research. Some researchers are skeptical that mechanistic models can provide predictive power, especially in the absence of key quantitative data to anchor the model fully. However, modelers point out that even relatively simple mathematical models can improve insight from existing data, and better integration of mechanistic modeling approaches into immunology research can optimize the choice of what and when to measure, sharpen hypothesis testing, and help make the resulting data sets more informative (See Text Box 1).

TEXT BOX 1: SMALL VS. BIG MODELS.

Small or reduced models help select among alternative mechanistic hypotheses and provide qualitative predictions. In contrast, highly detailed models can lead to specific, quantitative predictions of behavior over time. Model complexity can be a double-edged sword. An increase in the number of model parameters increases both model resolution and the risk of overfitting the experimental data.

Small models/qualitative insights

As an example, the host innate immune response to bacterial sepsis was simulated using a reduced model [80]. In this study, a mechanistic model consisting of three ordinary differential equations accounted for a bacterial pathogen population, an early pro-inflammatory mediator derived from the initial activation of macrophages/neutrophils, and the later production of damage-associated molecular pattern molecules (also a surrogate for the damage sustained by the host in the course of infection and inflammation). Each equation represents the rate of change of each of these components (pathogen, composite early immune response, composite damage response) relative to the levels of the other components and simulation of the model provides the predicted level of each component over time. This highly abstracted model reproduced both a healthy outcome and diverse negative outcomes that are observed in sepsis patients, depending on initial conditions and parameter values. Simulation supported the hypothesis that the clinical condition of sepsis can arise from several distinct physiological states, each of which requires a different treatment approach.

Large models/quantitative insights

Large, detailed models can integrate data, procedural knowledge, and theory into information processing representations of innate and adaptive immune responses to simulate complex immunological systems. An example is an inflammatory bowel disease (IBD) model [27]. The modeling platform used incorporates mathematical modeling and machine learning methods to allow clinical trial data integration, including subjects’ Crohn’s disease (CD) activity index (CDAI), endoscopic measures of mucosal healing, data from electronic medical records, preclinical data from animal models, and cellular and molecular signatures. Simulating such models can guide clinical plans, predict results of clinical trials, and suggest new therapeutics. Through this modeling and experimental validation, a novel Lanthionine Synthetase C-like 2 (LANCL2)-based oral therapeutic for CD was identified and is being developed [81]. Model simulations will be used to help guide the design of Phase 2 and 3 clinical studies [72].

The initial process of formally developing a simple and perhaps initially incorrect model that includes only a few entities often proves invaluable in revealing hidden assumptions, formalizing hypotheses, and identifying key missing measurements and experiments. Importantly, data mining and mechanistic modeling are synergistic approaches that are not intended to replace experimentation, but rather to each serve a complementary role in an iterative cycle of data exploration, hypothesis exploration, and experiment. In this regard, one motivator for the NIAID conference was the concern that academic immunology research is lagging industry and other medical research fields in incorporating modeling approaches. In adapting to the high rate of failure and the more than $2.6 billion total R & D costs involved in the approval of a new drug or biologic [6], industry has turned increasingly to computational modeling at all levels, from modeling drug-receptor interactions to pharmacokinetic and pharmacodynamic modeling, to in silico clinical trials [7, 8]. The FDA’s Critical Path initiative has further stimulated the incorporation of mathematical modeling in drug discovery [9]. Recent NIH requests for applications in many areas, such as cancer research, specifically call for integration of modeling approaches http://grants.nih.gov/grants/guide/rfa-files/RFA-CA-15-014.html. These trends are applicable to immunology.

We suggest that immunology research needs to evolve more rapidly from a paradigm of experiment, data analysis, and interpretation, to a more integrative approach that incorporates formal computational modeling and prediction. The fruitful application of this type of complementary, iterative approach to the question of how the T cell response is scaled to the level of the antigenic signal has recently been reviewed [5]. We explain the complementary role and limitations of both data-driven and mechanistic modeling, and review successes of computational immunology in both basic and translational settings. Finally, we lay out a roadmap for bridging the immunologist-modeler divide to accelerate insight into emergent mechanisms of immune system function and the translation of data into individualized treatment for infectious and immune-mediated diseases.

Modeling Approaches and Applications in Immunology

One likely reason for the narrow adoption of mathematical modeling by the immunology community – similar to the broader biomedical research community – is the sheer diversity of methods and approaches broadly encompassed within this discipline, as well as the lack of formal computational, mathematical, and statistical training of most immunologists. Below, we review briefly major types of computational modeling and their application to immunology.

Various data-driven modeling or data mining approaches are an essential element of large-scale systems immunology research. These methods share a grounding in rich experimental datasets, providing quantitative measurements of molecular concentrations, biochemical reactions, or cellular and tissue-level parameters. These data are then combined with topologies and injected into computational approaches that seek to determine the multivariate relationships among objects in the networks, and how the system as a whole responds to perturbation [10]. This type of modeling iterates between prediction, experimental testing via perturbation, and refinement of the model based on the new data [4].

Unsupervised analysis approaches, such as hierarchical clustering, principal component analysis, and more classical statistical analyses, are considered data-driven modeling, as are various network inference algorithms that can provide information on the correlation, and, in some instances, causal structure among variables [11, 12]. These approaches have been used in modeling and simulation of the mono- (e.g. folding) or bi-molecular interactions (e.g. MHC-TCR-Ag complexes), of signal transduction cascades, of CyTOF data representing T cell phenotypes, of genetic regulatory networks, or of cellular behavior (e.g. [13]). Some studies use regression techniques that build models predictive within the conditions of the data upon which they were trained [14], as well as predictive classifiers [15]. These methods can provide insight into the molecular circuits underlying immunological phenomena, such as switching between immune cell subsets [16]. As an adjunct to this type of endeavor, resources such as a user-friendly, web accessible, 38,000 public experiment-based resource to predict immune-system and disease relevant gene-gene relationships supports big data mining and hypothesis development by immunology researchers without computational training [17]. A potential limitation of data-driven modeling is that, at least in some cases, predictions are based on correlations, making generalizable mechanisms difficult to infer from the resulting model.

Mechanistic modeling (sometimes called hypothesis-based modeling [18]) is based on specific mechanistic hypotheses, and uses mathematical equations and computer simulations to describe abstractions of complex biological systems that are, in essence, hypotheses about the core functions or processes that govern the system [4, 19–21]. Data-driven and mechanstic modeling have commonalities and can complement each other. However, whereas data-driven modeling is based on obtaining data and inferring relationships among entities and/or differences among groups, mechanistic modeling typically starts with an initial picture of how things work that, after abstraction into mathematics, can then be played forward in time and compared against experimental or clinical results. Mechanistic modeling has provided non-intuitive mechanistic insight into many areas of immunology, ranging from molecular systems, such as how analog signals from TCR engagement become digital further downstream and the basis for non-linearities in the system [22–25] to clinical responses in disease, as described below. A major rationale for pursuing modeling in immunology (and systems biology more generally) is that complex networks with cooperativity and feedback (which broadly describes biological systems at every scale) exhibit complex, nonlinear relationships (a characteristic that can be inferred from, but not tested explicitly with, data-driven modeling [13, 26]). Simply put, it is difficult to predict how a given perturbation at the molecular level will affect system behavior at higher scales over time or at homeostasis without the aid of a mechanistic model that can be “played forward in time” under a variety of conditions that would be impractical to test only using experimentation.

Perhaps the most fundamental difficulty when pursuing mechanistic modeling concerns the appropriate level of abstractions/complexity for the model (e.g. do we study at the molecular or cellular level, at the second-, minute-, or days-long time scale, how few or many components and relationships should be included?) relative to the underlying biological system and the scientific questions being posed (See Text Box 1). Defining the optimum balance of modeling simplicity versus complexity for the problem at hand benefits from interdisciplinary interactions between modeling experts and experimentalists. The development of user-friendly software tools (see Text Box 2) facilitates both formal modeling by experimentalists and this interaction between experimental immunologists and modelers. Some platforms, such as ENISI MSM integrate mechanistic modeling at the intracellular scale and data-driven modeling at tissue level and population levels [27] (Text Box 2).

TEXT BOX 2: IMMUNOLOGY-FRIENDLY COMPUTATIONAL MODELING SOFTWARE.

There are a variety of user-friendly platforms that faciliate immunological modeling without detailed understanding of the mathematical considerations “under the hood”. These include:

COPASI

Complex Pathway Simulator (COPASI) enables researchers to construct biochemical and immunological ODE models that help them understand how a system works. Model parameters can be adjusted as necessary to reproduce experimental results. https://nimml.org/tools/copasi-suite

ENISI MSM

ENteric Immunity Simulator (ENISI) MultiScale Modeling (MSM) platform is designed for modeling complex mucosal immune responses. ENISI MSM can simulate in silico experiments from signaling pathways to tissue level events, and in silico clinical trials. It integrates agent based modeling (ABM), ordinary differential equations (ODE), and machine learning methods. https://www.nimml.org/tools/enisi-suite

Simmune

Simmune provides an intuitive visual interface guided modeling of molecular interactions to provide cellular, spatial and time-dependent simulations of immune processes. https://www.niaid.nih.gov/research/simmune-software

MCell

Monte Carlo Cell (MCell) is a program that uses spatially realistic 3-D cellular models and specialized Monte Carlo algorithms to simulate the movements and reactions of molecules within and between cells, supported by extensive training tutorials. http://mcell.org

RuleBender

This tool helps the collaborative development of diagram-based models, usable by immunologists who are not necessarily experts in mathematical modeling, while providing the deeper insights into the simulation process that are needed for such tasks as model and simulation debugging, and overall understanding of molecular systems. http://visualizlab.org

VCell

Virtual Cell (VCell) is a comprehensive platform for modeling cell biological systems that is built on a central databse and disseminated as a web application. http://vcell.org

The following sections briefly highlight some of the major common approaches to mechanistic modeling, and the diverse areas of immunology to which they have been applied.

Systems of Ordinary Differential Equations (ODEs) remain one of the most flexible, widespread approaches for mechanistic modeling in immunology. Each distinct “species” of interest in an ODE model, whether it be an organism, cell type, virus, bacterium, or biomolecule, is represented by a continuous-time variable. These variables often interact with each other in a recursive manner that precludes “solving” the system of equations in the manner familiar from traditional mathematics courses; rather, these systems of equations are simulated using a numerical integration algorithm, yielding predicted trajectories for each variable (i.e. a graph of their predicted levels over time). ODE models almost always describe system dynamics (that is, behavior over time). Individual terms in the equations express how rates-of-change of each species depend on population sizes, interactions among species, and external factors. Even when time-course data are not available, ODE models can be useful for analyzing the steady-state behavior of a system.

Classical applications of simple ODE models simulated interacting virus and lymphocyte populations in HIV infection [28, 29]. These relatively simple models involving few species revealed an unexpectedly dynamic interplay between the virus and immune system during latent infection. Quantitative estimates of staggeringly large daily rates of HIV-1 production helped identify the need for combinatorial antiretroviral therapy regimes and spurred their development and implementation. These studies also paved the way for detailed mathematical studies of lymphocyte dynamics in infection and homeostasis, in conjunction with experiments. A few recent examples of immunological insights contributed by this type of ODE modeling are the differences in maintenance of peripheral naïve T cells between mice and humans [30], the phenotype-specific dynamics of antigen-stimulated CD8+ T cells in SIV [31], and the balance between immunopathology and protection in T-cell based vaccines [32].

At the sub-cellular scale, ODE models have been successfully applied to elucidate dynamic control mechanisms governing signaling and gene regulation in the immune system. An example of iterative experiments and model development leading to new insights is found in the NF-κB signaling system [33]. In another example, a detailed model involving approximately 50 biomolecular species and hundreds of reactions was used to study control of dendritic cell (DC) maturation [34]. The model enabled zeroing-in on cell-specific regulation of the RelB protein in mouse embryonic fibroblasts (MEF) and dendritic cells. Differences in two biochemical rate constants were identified as being able to account for qualitatively different, cell-type-specific responses in silico. These predictions were confirmed by altering these rates through genetic engineering of MEFs, producing DC-like control. Emerging advanced applications of ODE modeling include landscape and flux theory [35], which may hold the potential to define and quantify homeostatic vs. pathological immune system states, as well as the barriers to transition between states.

Whereas an ODE model typically predicts average population sizes or concentrations over time, an Agent-Based Model (ABM) explicitly represents each individual model entity (often cells with distinct attributes) in a computer simulation. The “rules-of-engagement” are defined in advance, and events occur probabilistically. ABMs are typically spatial (meaning, for example, that cells must be in proximity to interact), and are useful for exploring how local interactions influence larger-scale behavior [20]. In immunology, ABMs were introduced to study lymphocyte antigen-specific recognition and activation [36]. Representations of receptor-ligand interactions which represent unoccupied/occupied sites as zeros-ones bit strings has enabled ABMs to go some way towards modeling the combinatorial diversity of immune repertoires. ABMs have been applied to the study of granuloma formation in Mycobacterium tuberculosis [37, 38]; germinal center formation [39]; thymic selection [40]; multiscale modeling of mucosal immune responses to IBD and gastroenteric infection using ENISI, which recapitulate the relationship between mucosal immune responses and inflammatory lesions in the gastrointestinal (GI) tract [41, 42]; and spatial dynamics of infection [43]. Folcik et al. have also generated a multiscale ABM that recapitulates the interactions between the cells of the innate and adaptive immune system, ultimately resulting in immune memory for an antigen following infection [44].

Logical models allow researchers to model network dynamics in the absence of detailed information about parameters governing interactions (the general paucity of this information is a perennial challenge for many types of mathematical modeling). In a logical model, network species are categorized according to a small number of discrete states (e.g., “active” or “inactive”) and interactions such as “X activates Y” govern updates to the system state at each timestep. As such, only qualitative information about interactions, rather than quantitative rate parameters, is required in the building of the model [45]. Examples of applications of logical models include T cell receptor signaling [46, 47] and T cell specification [48, 49].

Models can either be deterministic or stochastic

A deterministic model, such as an ordinary differential equation described above, will always give the same result each time it is simulated with the same parameters. When studying responses at the single cell level, however, the small number of molecules involved may lead to large differences in behavior that is truly random. In stochastic models, the behavior of a system is affected by random uncertainty. “Stochastic modeling” is an umbrella term: a number of different mathematical frameworks and simulation methods are available for stochastic modeling, including stochastic differential equations, diffusion-type equations, stochastic biochemical network models, reaction-diffusion models, and probabilistic Boolean networks, among others. Agent-based models are also typically stochastic. By accounting for individual molecules and biochemical reactions, stochastic models have revealed how lymphocytes respond sensitively to small amounts of antigen. For example, a synergistic modeling/experimental study showed that feedback regulation in a particular T cell receptor signalling module gives rise to a digital (“on” or “off”) activation response at the single-cell level (Das et al., 2009). Other examples of stochastic modeling applied to immunology include studies of stochastic cytokine expression [46, 50]; dynamics of lymphocyte differentiation and expansion [51]; cellular response to infection [51–54]; lymphocyte repertoire development [55]; and affinity maturation [56, 57].

All models, at some level, aim to describe and predict complex systems. Mechanistic models, particularly ODE-based deterministic models, lend themselves to further practical applications, such as the dynamic control of a given complex system [58]. This application is at the heart of a field known as Control Theory, which has been applied in the context of immunology for nearly four decades [59, 60]. The immune system can be viewed as consisting of interlocked and finely tuned homeostatic and regulatory mechanisms, which must achieve an appropriate, proportional and dynamic defense against infection and autoimmunity. Mathematical control theory is central to the design of engineered systems, and core concepts such as feedback control are clearly at work in the immune system [61]. Increased application of control theory to immunology will shed light on how natural immune responses work, and how therapies can be designed to tailor immune responses in specific disease contexts. A complementary role of control theory is in the rigorous formulation and solution of optimal immunotherapy drug infusion regimes [62], as well as in identifying patient-specific therapeutic strategies for the acute inflammatory response to severe infection [63]

Clinical Trial Simulations in Immune-mediated and Inflammatory Diseases

In silico clinical trials, in which mechanistic models are carried out over a broad range of parameter values and initial conditions, using advanced machine learning methods, or using stochastic simulation methods such as ABMs have been applied for over a decade in the setting of acute inflammation and immunity [64–71]. We highlight two examples of in silico clinical trials in the settings of Crohn’s Disease (CD) and trauma-induced inflammation.

ABM and ODE models, in combination with supervised machine learning methods, have been used to create virtual CD patients [27, 42]. In a recent study [72],10,000 virtual CD patients were created using information from clinical trials where both individual response to treatment and aggregated data were combined with expert knowledge with the goal of comparing current and investigational treatments. Virtual treatment strategies were designed based on changes of immunological parameters that drive response to treatment. These virtual CD patients provide a diversified population to generate novel non-intuive hypotheses regarding treatment response to novel therapeutics (see Text Box 1). Another example of virtual patients based on mechanistic modeling involves inflammation and critical illness caused by traumatic injury. A recent study describes a multi-compartment ODE model that represents a virtual trauma patient [68]. This mathematical model was used to create both Individual-specific variants as well as a cohort of 10,000 virtual trauma patients [68]. The model was able to predict trauma-induced mortality as well as a non-intuitive role for interleukin-6 which was validated with single nucleotide polymorphisms (SNP) data [68].

These examples indicate that the outcome and process of clinical trials in complex immune and inflammatory diseases are becoming computationally tractable. In silico clinical trials can have their pitfalls, as well [73]. They carry the risk of de-prioritizing therapies that might have been valuable, or of being unsuccessful because the pathophysiological knowledge that underlies the model remains incomplete (and hence the model is overfitting to the sparse data that are typically available). For instance in the case of T1D, the identity of effector or inhibitory molecules and cells, the impact of beta-cell regeneration, the role of viruses or other environmental triggers that conspire to provoke autoimmune diabetes are poorly understood, let alone their quantitative or dynamic parameters (and there are likely to be several patient subtypes and instigating causes). While a plausible quantitative model of T1D [74] could readily be programed to simulate immuno-modulatory trials of T1D in thousands of patients, its results would only be as good as the assumptions underlying the model.

Integrating Modeling and Experimentation for 21^st Century Immunology

The successes of immunology-focused modeling suggest that computational, mechanistic modeling should be at the heart of interdisciplinary research to optimize the translational impact of the immunology research portfolio, from highly focused, hypothesis-driven research, to large-scale team science, to bedside applications. Our core contention is that rather than a relatively linear process of hypothesis➔experiment➔data, a better approach to the complexity of immunology might be data➔model➔experiment➔validation➔refined model, leading to both novel hypotheses, data/theory integration, streamlined experimentation, and prediction of translation to humans and therapeutic impact of fundamental biological mechanisms. Both data-driven and mechanistic modeling would serve the immunology community in this revised workflow. Data-driven modeling would allow for inference of novel interrelationships, feedback architectures, and principal characteristics; this type of modeling is already a mainstay of large, collaborative consortia focused on “omics” studies. Mechanistic modeling could be a major “equalizer” for many labs in an environment of limited grant funding because it would help target key experiments in a resource-constrained environment. Alternatively, mechanistic modeling could help delineate key datasets and help with design and interpretation in large, systems-oriented studies.

A major role for modeling that needs to be better utilized by the immunology research community is as a customized data analysis tool for the extraction of new, and perhaps non-intuitive, mechanistic hypotheses from experimental data. Fitting an experimental dataset that provides dynamics, i.e. measurements obtained over time, using a simple model often highlights features in the data that are poorly fit to the predictions of the model. This leads to thoughtful exploration of the cause of the discrepancy between data and simulation: are there experimental errors? measurement noise? a mechanism not included in the model? This process can lead to model revision to test whether a novel mechanism is a plausible explanation for the discrepancy, and to further experiments to test the hypothesis. Modeling thus allows us to better take advantage of otherwise discarded information in the experimental data that actually reflect important novel mechanisms, which in turn can have a major influence on subsequent experimental work or therapeutic development. This type of modeling, illustrated by classical HIV work of Perelson and colleagues described above [28, 29], is most useful when it is anchored not only in the data, but also in the biology and immunology that underlies the assumptions of the model. Mechanistic modeling is in many ways an art, and it is important to start the process by crafting equations that are based on plausible immunological mechanisms. Indeed, one may think of mechanistic modeling as “the art of the possible”: if one includes well-vetted mechanisms and/or agreed-upon hypotheses, does the system as a whole behave as everyone thinks it should (i.e., is the behavior “possible” or “impossible”)? If so, then the model suggests (but does not prove) that the underlying hypotheses are correct to some level of precision. If not, then either the underlying hypotheses are incorrect, or there is something incorrect or missing in the model. Either way, knowledge is gained in a rational fashion. In order to practice this, there is a need for closer collaborations between modelers and experimentalists, as well as for better training of modelers in immunology and of experimental immunologists in modeling, as described further below.

More success in predictive analysis will benefit from additional data and the release of more experimental and clinical trials data to the public. The NIAID-supported Immunology Database and Analysis Portal (ImmPort) system [75] is a repository for these types of data. More than 200 data sets are now available at ImmPort (with the number rapidly growing), and many of these reflect the raw data released upon the completion of an interventional clinical study. Such raw data can be re-analyzed to defend the reproducibility of statistical testing from the original publication, and the aggregation of multiple studies through meta-analysis can be used to increase power to detect subtle signals. They could also be useful for new scientific discoveries, such as finding patient subsets that best respond to an intervention [76], or predicting why drugs might be succeeding or failing in clinical trials.

The NIAID meeting participants noted that interdisciplinary collaborations are key to realizing the iterative cycle of modeling➔data➔modeling. Many obstacles can derail interdisciplinary collaboration, and so it is important to consider communication and cultural roadblocks between immunology experimentalists and computational modelers, and how to overcome them.

Recommendations on Establishing Integrative Collaborations

The first obstacle to overcome is the identification of appropriate and suitable collaborators. The panel’s recommendations focus on collaborations in which the biological questions determine the computational and mathematical tools utilized. From the immunologist’s point of view, it is crucial first to identify the key immunological questions of interest and the biological scales encompassed by the questions. Finding the “right” fit within the multivariate space of experimentalists, modelers, and biological questions will undoubtedly require multiple conversations, and the entire search process may take several iterative cycles.

When beginning the conversation, both experimentalists and modelers should be prepared for a “culture shock” of sorts, as each attempts to describe the aspects of one’s field relevant to the question to be studied. Even seemingly innocuous vocabulary can become a stumbling block, perhaps best exemplified by terms such as “model”: one party may be thinking of a mouse model while the other is thinking in terms of mathematical equations or a set of rules. In a similar vein, the limitations of each collaborator’s field should be freely discussed, to avoid over-estimating what either experiments or modeling can achieve.

Both experimentalists and modelers need to keep in mind that their collaborative process is necessarily a feed-forward, feed-back endeavor that originates with, and repeatedly returns to, addressing important immunological questions and leveraging critical experimental datasets as well as novel computational technologies. These data can then be fed into the development of mathematical models that represent the known biological processes and interactions of various biological entities or into the implementation of computational methods. These computational tools can then feedback into the biological side by raising novel hypotheses and suggesting additional data to collect or to generate testable hypotheses to guide further experimental work. Additional experimental findings can then feed-forward again to refine further and calibrate mechanistic models.

Concluding Remarks

At its core, the integration of modeling in mechanistic, preclinical, translation, and clinical immunology is centered on rigor and a foundational “back-to-basics” approach. The lack of rigor and reproducibility of experimental studies is an area of widespread concern in both preclinical and clinical research [77, 78]. When quantitatively predictive modeling is built on data, the integration of modeling into the research pipeline provides an additional quality control mechanism that improves the rigor and reproducibility of immune studies. Furthermore, mechanistic modeling might be crucial when attempting to circumvent the difficulty in extrapolating from reductionist mechanisms to system-level outcomes in individuals and populations suffering from immune-mediated diseases [79].

The remarkable advances in computational modeling described above have occurred in an environment of relatively stable NIH funding opportunities for systems biology and “omics” research, although most of the rapid progress has related to the adoption of bioinformatics techniques by the immunology research community. While 21% (38 of 178) NIH “omics” and “systems biology” Funding Opportunity Announcements (FOA) identified at the time of this manuscript are standing requests that are open over multiple years, the rare mechanistic immune modeling FOAs have been overwhelmingly onetime opportunities. If the broader immunology research enterprise is to reap the synergies of modeling, key changes are required in order to achieve a cohesive, growing and efficient interdisciplinary effort. Mechanisms to encourage the further development of software platforms and interchange standards that improve model reuse and hypothesis testing, especially by researchers with limited mathematical/computational training, will assist the beneficial integration of modeling into immunology research. Improved understanding of the value and limitations of modeling by the experimental immunology research community is key; experiential learning could be encouraged by student and fellowship training, workshops and visiting scientist programs. Finally, stable large-scale (P01, U19, U24, BAA) and smaller (R01, R21, SBIR/STTR) funding mechanisms are needed to encourage the integration of simulation and experimental immunology, ultimately leading to the improved therapeutic development and clinical outcomes. Changing the culture, language, tools and research enterprise to improve the synergy of data mining, mechanistic modeling, and data-generating immunology research techniques should accelerate the translation into improved diagnosis and treatment of infectious, inflammatory and immune-mediated diseases.

Outstanding Questions Box.

• How should the various approaches to modeling be standardized to improve model sharing and integration?

• Can model formatting and annotation be standardized without restricting the applicability of these approaches to divergent goals and questions?

• How can model simulation platforms be refined to facilitate their use by immunology researchers not trained in modeling without compromising scientific rigor?

• How can data-driven analysis approaches and hypothesis-based mechanistic modeling be best integrated?

TRENDS BOX.

• Unbiased high-throughput data driven analysis approaches are identifying molecular processes associated with immunological function and immune-related diseases, as well as candidate immune disease-modulating gene elements.

• Hypothesis-based mechanistic modeling tests whether our understanding of how a system works provides a possible explanation for the existing immunological data, and helps focus subsequent experiment.

• A variety of immunology-friendly computational modeling tools have been developed.

• Mechanistic modeling and simulations are serving increasingly important roles in drug development and clinical trials.