Meta-analysis of time-to-event outcomes from randomized trials using restricted mean survival time: application to individual participant data

Abstract

Meta-analysis of time-to-event outcomes using the hazard ratio as a treatment effect measure has an underlying assumption that hazards are proportional. The between-arm difference in the restricted mean survival time is a measure that avoids this assumption and allows the treatment effect to vary with time. We describe and evaluate meta-analysis based on the restricted mean survival time for dealing with non-proportional hazards and present a diagnostic method for the overall proportional hazards assumption. The methods are illustrated with the application to two individual participant meta-analyses in cancer. The examples were chosen because they differ in disease severity and the patterns of follow-up, in order to understand the potential impacts on the hazards and the overall effect estimates. We further investigate the estimation methods for restricted mean survival time by a simulation study.

1. Introduction

In meta-analysis of time-to-event outcomes, we often use the hazard ratio as a measure to evaluate the effect of a treatment across randomized controlled trials. Methodological developments on extracting the hazard ratios from published survival curves [1–3] and comparing two-stage and one-stage meta-analysis of hazard ratios estimated from the widely used Cox model [4–6] have improved how we include all the available evidence from trials with time-to-event data. However, concerns have been raised regarding non-proportional hazards in individual trials [7, 8]. While the trials included in a meta-analysis can be used to address similar research questions, they can differ in the length of follow-up, censoring pattern and design aspects. Therefore, the assumption of proportional hazards (PH) for multiple included trials may be unrealistic [9–12].

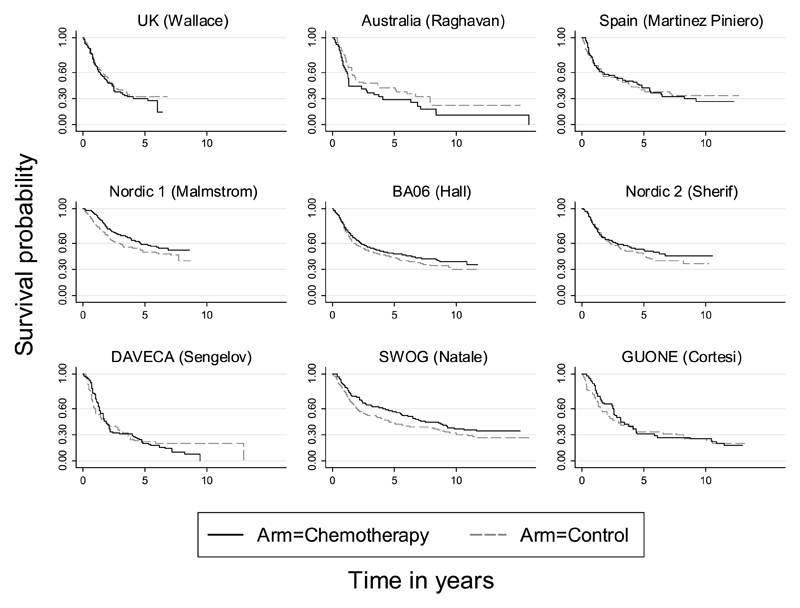
A graphical display of crossing survival curves may provide incontrovertible evidence of departures from the PH assumption. The Kaplan–Meier survival curves for each trial in an individual participant data (IPD) meta-analysis in bladder cancer [13, 14] are shown in Figure 1 and will be discussed later in this paper. It can be seen for the GUONE trial that the curves cross at about 4 and 8 years. In contrast, the curves for trial BA06 seem to be nearly parallel in the right panel. This indicates that hazards may not be proportional in some trials.

Figure 1.

Trials included in the advanced bladder cancer (ABC) meta-analysis. Kaplan–Meier survival curves.

In the presence of non-proportional hazards, time-dependent hazard ratios [11] and a piecewise-constant hazards model [10] can help one to assess how treatment effects may change with time. Recently proposed by Siannis et al. [12] and Barrett et al. [9], the ratio of a single or a set of percentiles of survival distributions between the treatment and control groups is an alternative measure to time-dependent hazard ratios. The percentile ratio was estimated from accelerated failure time models or proportional hazards models, and the choice between the two depended on the validity of the PH assumption. Combining flexible summary measures of this kind is appealing in a meta-analysis, but the summary statistics are not usually available. The analysis based on flexible modelling requires IPD, which are considered as the gold standard approach in meta-analysis [15]. However, raw time-to-event data, if unavailable, can be reconstructed from published survival curves [16] along with number of participants at risk in observed intervals. Thus, flexible modelling of time-to-event outcomes need not be restricted to IPD and it is, in principle, possible for aggregated survival data.

The main aim of this paper is to describe and evaluate the use of the restricted mean survival time (RMST) in meta-analysis of time-to-event outcomes, through an empirical study with applications to two IPD meta-analyses. The RMST [8] incorporates a number of desirable properties. It is free of the PH assumption and can provide insights into how treatment effects may change with follow-up time. Also, it is a measure of treatment effect on the scale of the time to event, and its interpretation is arguably more intuitive than measures on the scale of the relative hazard. The RMST is valid under any distribution of the survival time in the treatment groups [17]. Here, we focus on two-stage meta-analyses. Comparisons of one and two-stage methods [4, 5, 18] suggested that, if the aim was to estimate the main effects, the one-stage and two-stage approaches produce similar parameter estimates, in terms of estimation bias and coverage probability. Thus, the more complicated one-stage method does not seem to outperform the simpler and practically more popular [19] two-stage method.

In the following section, we define the RMST and review the estimation methods. We then review and describe the calculation of the effect size and its variance for use in meta-analyses. In Section 3, we propose the use of combined p-values to help diagnose the presence of non-proportional hazards in the overall treatment effects. In Section 4, we re-analyse two example data sets to illustrate methods described in Sections 2 and 3. In Section 5, we perform a simulation study to evaluate three approaches to estimating the RMST. Section 6 is a discussion.

2. Restricted mean survival time

2.1. Definition of restricted mean survival time

Suppose we are interested in the mean, μ say, of a random variable T, which denotes the time to an event. Then, the mean (expectation) of the survival time can be shown to be

$$\mu ={\displaystyle {\int }_0^{\infty }S(t)dt}$$

where S(t) is the survival function for T. The integral is not in general evaluable due to the almost universal right-censoring of the time to event. However, the mean survival time up to a specific time point, t* say, can be obtained as

$${\mu }^{*}={\displaystyle {\int }_0^{t^{*}}S(t)dt}$$ (1)

where μ* is the restricted mean survival time [8, 20] at time t*. When the survival time is years to death, we may interpret μ* as t* year life expectancy. The measure μ* increases monotonically with the t* [8] because Equation (1) gives a non-negative, increasing function of t*.

2.2. Estimations of restricted mean survival time

2.2.1. Method 1: Pseudo-values

The RMST for individual participants can be estimated by a non-parametric jack-knife method using pseudo-values [20]. Suppose we are interested in a parameter, θ. We first estimate θ based on the whole sample with observations for each individual i (i = 1, 2, … , n). We then estimate θ again but at this time based on a subsample omitting an observation, i say. The pseudo-value θ̂_i for observation i is the difference between the two estimates of θ, and is formally defined as

$${\widehat{\theta }}_i=n\widehat{\theta }-(n-1){\widehat{\theta }}_{-i}$$ (2)

where θ̂ is the estimate based on the whole sample and θ̂_−i is the estimate based on the sample without the observation i. The pseudo-values estimator for parameter θ is given by

$${\widehat{\theta }}_{pseudo}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{\theta }}_i},$$ (3)

the average of pseudo-values across all observations. From this equation, we have

$$E({\widehat{\theta }}_{pseudo})=E({\widehat{\theta }}_i),$$

indicating E (θ̂_pseudo) = θ, if E(θ̂_i) = θ. Further, according to the definition of an individual’s pseudo-value in (2), we have E(θ̂_i) = θ if E(θ̂) = θ. Thus, the use of the unbiased estimator θ̂ is crucial for θ̂_pseudo to be unbiased for θ.

The pseudo-values for the RMST [8, 20] are given by

$$\begin{array}{l}{\widehat{\mu }}_i^{*}={\displaystyle {\int }_0^{t\ast }{\widehat{S}}_i}\left(t\right)dt\\ =\text{n}{\displaystyle {\int }_0^{t*}\widehat{S}\left(t\right)dt-\left(n-1\right)}{\displaystyle {\int }_0^{t\ast }{\widehat{S}}_{-i}\left(t\right)dt}\end{array}$$

where the survival function Ŝ (t) can be substituted by a Kaplan–Meier estimate

$$\widehat{S}\left(t\right)={\displaystyle \prod _{u\le t}\left(1-\frac{d_u}{n_u}\right)}$$ (4)

with d_u denoting the total number of failures from time origin to time u and n_u denotes the total number of individuals still at risk just prior to time u.

The pseudo-values estimator for the RMST is then given as

$${\widehat{\mu }}_{pseudo}^{*}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{\mu }}_i^{*}.}$$

As just discussed, ${\widehat{\mu }}_{pseudo}^{*}$ is an unbiased estimator for the RMST when the Kaplan–Meier estimate (4) is an unbiased estimator of the survival function. This is the case when the censored survival time is, independent of participants’ covariates, within treatment arms. In a simulation study, Anderson and Perme [20] have shown that, if censoring depends on a categorical covariate on participants’ characteristics, a mixture estimator combining the Kaplan–Meier estimates from each category produces less bias results, compared with the conventional Kaplan–Meier estimates. However, developing techniques for dealing with dependent censoring is beyond the scope of this paper.

Both pseudo-values and Kaplan–Meier estimates are non-parametric. The combination of the two provides a non-parametric estimate of the restricted mean survival time. In the following section, we describe a parametric method to calculate the RMST.

2.2.2. Method 2: Flexible parametric survival model

In the hazards scaled class of flexible parametric survival models, Royston and Parmar [7] proposed to approximate the baseline log cumulative hazard function using restricted cubic spline functions. More specifically, they proposed to approximate the log of the cumulative baseline hazard H₀(t) using a function of the log of time

$$\text{ln}{H}_0(t)={\gamma }_0+{\gamma }_1\text{ln}t+{\gamma }_2{\nu }_1(\text{ln}t)+\dots +{\gamma }_{K_0+1}{\nu }_{K_0}(\text{ln}t)$$ (5)

where γ_i(i = 0, 1, … , K+1) are regression parameters and ν_i(i = 1, 2., , ,K₀) is the ith spline basis function defined in [7]. Here, K₀ denotes the number of distinct internal knot, which is the joint-point in log time of a pair of adjacent cubic polynomial segments. Their model is sufficiently flexible to incorporate a wide range of continuous baseline distributions and it simplifies to a Weibull model when K₀ = 0. The RMST in (1) can be rewritten as

$${\mu }^{\ast }={\displaystyle {\int }_0^{t\ast }S(t)dt={\int }_0^{t\ast }\text{exp}(-H(t))dt.}$$

Setting ln H₀(t) = s(ln t|γ, K₀), the log cumulative hazard function can be written as

$$\text{ln}H(t)=s(\text{ln}t|\mathit{\text{γ}},{\text{K}}_0)+s(\text{ln}t|\mathit{\text{δ}},{\text{K}}_1)x+\beta x.$$

where x presents the treatment arm indicator. The interaction term s(ln t|δ, K₁)x is added to account for the non-proportional hazards. The parameters γ = (γ₀, γ₁, … , γ_{K0 +1}) are the regression coefficients in the baseline spline function s(ln t|γ, K₀), which has K₀ knots; and δ = (δ₁, … , δ_K1) are the regression coefficients in the interaction spline function s(ln t|δ, K₁) , which has K₁ knots. Because the model is fully parametric, the model parameters can be estimated by the maximum likelihood approach.

If the number of knots is increased, the model complexity is also increased. It is found that the estimates of RMST are similar when the degrees of freedom (d.f.) for the baseline distribution is 3 (2 knots, i.e. K₀ = 2) or higher. Throughout this paper, we set 3 d.f. for the baseline distribution and 1 d.f. for the time-dependent effect.

2.2.3. Method 3: Integrated difference of survival functions

An alternative method to estimate the RMST is to directly integrate the Kaplan–Meier estimate of the survival function from time 0 to t* [20]. The integral is calculated by the summation

$${\displaystyle \sum _{j=1,0<t_j\le t*}^k\widehat{S}(t_j)(t_{j+1}-t_j)+1\cdot (t_1-0)}$$

where Ŝ(t_j) is the Kaplan–Meier estimate at time t_j(0 ≤ t_j ≤ t*) and t_j is the time where an event occurs.

2.3. Calculations of the difference in restricted mean survival time and its variance

2.3.1. Effect measure 1: Difference in restricted mean survival time

From here forward, to distinguish between treatment arms, we add subscripts to let ${\mu }_1^{*}$ and ${\mu }_0^{*}$ denote the RMST at t* for the research and control arms, respectively. We measure the treatment effect by the difference between the RMSTs between the two arms of a trial

$${\Delta }^{*}={\mu }_1^{*}-{\mu }_0^{*}.$$ (6)

The quantity Δ* measures the amount by which the research treatment changes the survival time on average up to time t* compared with the control. We refer to this measure as the restricted mean difference (rmstD).

The interpretation of Δ* is straightforward. If the time-scale is in years, the difference in RMST can be interpreted as patients in research arm having Δ* more years gain/loss in life expectancy from the time origin to t* years, compared with patients on conventional treatment.

2.3.2. Effect measure 2: Relative difference in restricted mean survival time

The relative difference in RMST is given as the rmstD divided by t* [8]

$${\overline{\Delta }}^{\ast }=\frac{1}{t*}({\mu }_1^{*}-{\mu }_0^{\ast }),$$

which is also proposed in Zhao et al. [21] as an alternative measure to the hazard ratio. This measure allows us to quantify how the difference in RMST changes with t*. Because it is the difference in the integrated survival functions between treatment and control arms, it measures the mean difference in survival probabilities between the two arms. It expresses the size of treatment effect relative to the chosen time t*, reflecting the amount by which the research treatment changes the average survival probability up to time t* compared with control. In short, we refer to this measure as rmstRD. This measure can be interpreted as a percentage. It lies in the interval (0, 1).

In the following, we describe the approaches to calculating the variance of rmstD. Because the mean survival probability difference only differs by a constant term 1/t*, its variance requires multiplying var(rmstD) by 1/(t*)².

2.3.3. Variance for difference in restricted mean survival time: flexible parametric model. Delta method for variance

We drop the superscript * from this point forward for simplicity. For each trial, due to the randomisation, the estimates of the RMST in each arm are independent so the variance of Δ̂ can be calculated by

$$\text{var}(\widehat{\Delta })=\text{var}({\widehat{\mu }}_1^{*}-{\widehat{\mu }}_0^{*})=\text{var}({\widehat{\mu }}_1^{*})+\text{var}({\widehat{\mu }}_0^{*}).$$

or

$$\text{var}(\widehat{\Delta })={\widehat{\sigma }}_0^2+{\widehat{\sigma }}_1^2,$$ (7)

where ${\widehat{\sigma }}_0^2$ and ${\widehat{\sigma }}_1^2$ are respective variances of the RMST for research and control arms, both can be estimated from the flexible parametric survival model using the delta method [17]. The delta method is a rapid approach to calculating the variance. As it is based on a first-order Taylor series expansion, it may be susceptible to approximation errors. In Sections 4 and 5, we compare the flexible model to methods by Andersen and Perme [20] and Zhao et al. [21].

Bootstrap variance estimation. Var(rmstD) can be estimated by a non-parametric bootstrap method. We first resample the original data with replacement. This step typically results in a sample that has the same number of observations with potential multiple occurrences of observations. We repeat the resampling procedure for a sufficient large number, M say, and calculate the difference in RMST for each sample. We then obtain the bootstrap estimation as the variance of the difference in RMST over M samples. The number of replicates M is said to be sufficiently large for bootstrapping if a larger number of replicates result in similar estimates; and the change of the random seed does not introduce discrepancies between the estimates. We use 1000 replicates in the application in Section 4.

2.3.4. Variance of difference in restricted mean survival time: pseudo-values method

When using the pseudo-values method, we first estimate the pseudo-values of RMST for each individual (Equation 2). To estimate the between-arm difference in RMST using the pseudo-values method, we then fit a generalized linear model (GLM) with individuals’ pseudo-values as the response and treatment arms as a predictor [20]. According to Andersen and Perme [20], the link function in GLM is an identity or a log-link function, and regression coefficients are estimated by solving a generalized estimating equation. The variance of the coefficients is estimated by a sandwich estimator. It is also known as a robust estimator [22], which has two appealing properties, which are as follows: first, it makes no distributional assumptions about the response and second, it is robust to the misspecification of link functions. As an alternative option to estimate the variance, the bootstrap method is computationally intensive. It takes a longer time to complete the estimation procedure, which switches between re-sampling of pseudo-values and variance estimation. For efficiency, with the pseudo-values method, we used only the sandwich estimator of var(rmstD).

2.3.5. Variance of difference in restricted mean survivial time: integrated difference in survival functions

Zhao et al. [20] used a perturbation-resampling method to calculate the variance of the relative difference in restricted mean survival time (rmstRD). A large number, M, of random samples are drawn according to Equation (3) in [21]. Based on the M samples, we can compute the variance of the rmstRD. Multiplying var(rmstRD) by (t*)² gives the variance of rmstD.

2.4. Implementation

Flexible parametric survival models and pseudo-values method are both available in Stata (Stata Corp, College Station, TX, USA). For the flexible model, we use stpm2 [23,24] with treatment arm as a covariate; we then use the post-estimation command predict rmst to estimate the RMST at a given t* and its variance for each treatment arm. For the pseudo-values method, we use stpmean [25] to estimate the RMST and the treatment arm as a predictor, with robust estimation for the variance. The integrated survival function difference is implemented in R (R Foundation for Statistical Computing, Vienna, Austria) as the function FUN.IRD [20]. We use the inverse variance weighting method to combine the effect measures from individual studies. Note that the stpm2, stpmean and FUN.IRD are tools to analyse individual trials.

3. Testing the proportional hazards assumption across multiple trials

3.1. Testing the proportional hazards assumption for individual trials

Departure from the proportional hazards assumption may be assessed informally by inspecting the Kaplan–Meier curves. In some cases, crossing curves may be the evidence for non-proportional hazards. However, in some other cases, the survival curves may not necessarily cross each other when hazards are not proportional. In fact, the log of cumulative hazard functions (equivalent to log of minus log survival probability) of two arms rather than the survival curves (survival probability) are parallel if the hazard ratio is constant. In addition, two curves crossing late in follow-up, where the data are sparse, may provide misleading evidence of non-proportional hazards. We consider statistical tests of the PH assumption at the trial level.

Grambsch and Therneau’s (G-T) approach to diagnosing non-proportionality [26] is based on testing whether or not the scaled-Schoenfeld residuals [27] for the regression coefficient of the predictor are independent of time. If the residuals are time-dependent, this provides evidence of non-proportional hazards. Recently, Royston and Parmar [8] used a likelihood ratio test to compare survival models with and without a time-dependent covariate. If the likelihood ratio test result suggests that a model with a time-dependent treatment effect fits the data better than the model with a constant treatment effect, it suggests that hazards are not proportional. The two approaches are comparable in that both are based on testing the statistical significance of possibly time-dependent effects.

3.2. Testing the proportional hazards assumption in multiple trials

When testing non-proportional hazards in individual trials, we might obtain heterogeneous results, with evidence of non-proportional hazards in some and not others. However, these tests tend to have low power and thus, it is not immediately obvious whether an overall proportional hazards assumption is appropriate. When the hazard ratio is used as the overall effect measure, the implicit assumption is that the hazards are proportional in each trial. The overall effect measures require the assumption of proportional hazards to be imposed on all trials. This makes an overall non-proportional hazards test compelling. For this purpose, we combine p-values from individual trials using Fisher’s method [28]. The test statistic is given by

$${\chi }^2=-2{\displaystyle \sum _{i=1}^n\text{log}(p_i),i=1,2,\mathrm{\dots },n,}$$

with n denoting the total number of trials and p_i the p-value from the non-proportionality test for trial i. The statistic χ² follows a Chi-squared distribution with 2n d.f. under the global null hypothesis that the hazards are proportional on all trials, with a one-sided alternative that in at least one study the hazards are not proportional. At a 5% significant level, the critical value is ${\chi }_{0.95,2n}^2,$ taken from the upper tail of a Chi-square distribution. A test result, if statistically significant, suggests that the hazards are not proportional on all trials.

4. Examples

In this section, we apply the methods described in Sections 2 and 3 to two IPD meta-analyses originally performed by the Medical Research Council Clinical Trials Unit on behalf of collaborative groups. The examples were chosen because they present different levels of disease severity and different patterns of follow-up between and within meta-analyses, in order to understand the potential impacts of non-proportional hazards in the analyses.

4.1. Example 1. Locally advanced bladder cancer data

The advanced bladder cancer (ABC) meta-analysis [13] examined the effects of neo-adjuvant chemotherapy on patients with locally advanced bladder cancer. Patients in the treatment group were treated with chemotherapy prior to local treatment, while patients in the control group were treated with local therapy only. Data on 2603 patients from nine trials are available for this analysis. The primary endpoint was overall survival. We were unable to use the data from one trial [29], therefore we performed the analysis on the remaining nine trials, which produced similar results. Using the hazard ratio and log-rank test approaches, there was evidence of a difference in treatment effect with combination chemotherapy (HR: 0.89 with 95% CI: 0.81, 0.99), which translated into a 4.3% (with 95% CI: 3.5%–8.2%) improvement in 5-year survival. There was no clear evidence of an effect of single agent chemotherapy (HR: 1.15 with 95%CI: 0.90–1.47) [13, 14].

According to the G-T test [26], there is no evidence of non-PH in the treatment effect for six trials, while there is evidence in three trials (Nordic 1, GUONE and DEVECA) from the combination chemotherapy subgroup. By performing a likelihood ratio test to compare the flexible parametric models with and without time-dependent coefficients for treatment arms, we obtained results similar to those from the non-PH tests. The combined p-values in Table I suggest that the PH assumption is appropriate in the single agent subgroup (p = 0.59 from G-T test and p = 0.56 from a likelihood ratio test based on the flexible parametric survival model) but not appropriate in the combination chemotherapy subgroup (p = 0.001 from the G-T test and p = 0.001 from the likelihood test). This results in a combined p-value of 0.006 or 0.004 (G-T test or likelihood ratio test) across all trials.

Table I.

Advanced bladder cancer meta-analysis. Results of non-proportional hazards (PH) test (Grambsch-Therneau (G-T) test and likelihood ratio test from flexible parametric survival models) as well as fixed effect meta-analysis of the hazard ratio from Cox model. In addition, difference in restricted mean survival times computed from flexible parametric survival model [8], pseudo-values [20] and integrated survival function difference method [21].

						Difference in restricted mean survival time (5 years)
	Cox Model			Test of non-PH p-values		Flexible parametric model Model				Pseudo-values method Method		IDS estimator Estimator
Trials	HR	95% CI	p-values	G-T*	Flex.	Diff.	95% CI1	p-values	95% CI2	Diff.	95% CI3	Diff.	95% CI4
Single-agent chemotherapy
UK (Wallace [30], n=159)	1.11	(0.76, 1.61)	0.60	0.74	0.71	−0.14	(−0.72, 0.44)	0.64	(−0.73, 0.45)	−0.11	(−0.69, 0.48)	−0.11	(−0.69, 0.47)
Australia (Raghavan [30], n=96)	1.41	(0.88, 2.26)	0.15	0.63	0.96	−0.58	(−1.32, 0.16)	0.13	(−1.29, 0.14)	−0.51	(−1.28, 0.27)	−0.51	(−1.27, 0.26)
Spain (Martinez-Piniero [31], n=121)	1.02	(0.66, 1.57)	0.94	0.21	0.13	0.14	(−0.56, 0.85)	0.69	(−0.55, 0.83)	0.14	(−0.59, 0.86)	0.14	(−0.58, 0.85)
Subtotal	1.15	(0.90, 1.47)	0.26	0.59	0.56	−0.17	(−0.56, 0.21)	0.38	(−0.56, 0.20)	−0.14	(−0.53, 0.26)	−0.14	(−0.53, 0.25)
Combination-agent chemotherapy
Nordic 1 (Malmstrom [32], n=311)	0.77	(0.56, 1.06)	0.11	0.02	0.02	0.48	(0.10, 0.87)	0.01	(0.12, 0.85)	0.46	(0.08, 0.85)	0.46	(0.08, 0.85)
BA06 (MRC/EORTC [33], n=976)	0.85	(0.72, 1.00)	0.05	0.72	0.54	0.20	(−0.04, 0.44)	0.11	(−0.04, 0.44)	0.19	(−0.06, 0.43)	0.19	(−0.06, 0.43)
Nordic 2 (Sherif [34], n=317)	0.86	(0.64, 1.16)	0.33	0.14	0.2	0.12	(−0.29, 0.53)	0.58	(−0.28, 0.52)	0.10	(−0.32, 0.53)	0.10	(−0.32, 0.52)
DAVECA (Sengelov [35], n=153)	1.06	(0.75, 1.50)	0.75	0.01	0.01	0.10	(−0.46, 0.65)	0.73	(−0.45, 0.65)	0.10	(−0.47, 0.67)	0.10	(−0.46, 0.66)
SWOG (Grossman [36], n=317)	0.77	(0.58, 1.00)	0.06	0.10	0.07	0.51	(0.11, 0.92)	0.01	(0.11, 0.92)	0.52	(0.11, 0.92)	0.51	(0.10, 0.93)
GUONE (Cortes[unpublished], n=153)	0.92	(0.60, 1.40)	0.68	0.06	0.05	0.42	(−0.26, 1.10)	0.16	(−0.28, 1.11)	0.33	(−0.37, 1.02)	0.33	(−0.34, 1.00)
Subtotal	0.85	(0.76, 0.95)	0.00	0.001	0.001	0.28	(0.13, 0.44)	0.000	(0.13, 0.44)	0.27	(0.11, 0.43)	0.27	(0.11, 0.43)
Overall	0.89	(0.81, 0.99)	0.02	0.006	0.004	0.22	(0.08, 0.36)	0.002	(0.08, 0.36)	0.21	(0.07, 0.36)	0.21	(0.07, 0.36)

¹Standard errors were calculated using the formula in [7].

²Standard errors from bootstrapping based on 1000 replications.

³Standard errors from sandwich estimator.

⁴Standard errors from resampling method with 10 000 replications.

^*Grambsch-Thernau’s non-proportional hazards test.

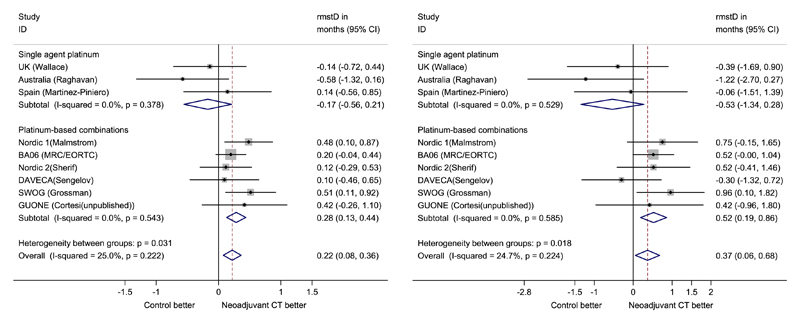
For the RMST analysis, we selected t* = 5 years. Firstly, all trials have follow-up longer than 5 years, but beyond this time point, there are limited numbers of participants at risk and therefore analysis may not be reliable. Secondly, the original meta-analysis reported an improvement in survival at 5 years, a time point of clinical interest. Table I shows the fixed-effect meta-analysis results for the difference in RMST. Following the recommendations in [8], in the flexible parametric model, we used 3 d.f. for the baseline distribution and 1 d.f. for a time-dependent coefficient to account for the possible non-PH. For the trials of single-agent platinum chemotherapy, the RMST is estimated as 2.62 years (95% CI: 2.35 to 2.88) with neo-adjuvant chemotherapy and 2.79 years (95% CI: 2.52 to 3.06) for control groups. For the trials using combination chemotherapy, the 5-year RMST is estimated as 3.34 (95% CI: 3.23 to 3.45) years and 3.05 (95% CI: 2.94 to 3.16) years for treatment and control groups, respectively. Based on the flexible parametric model and formula (7) for standard errors, the combined difference in RMST are estimated as −0.17 (95% CI: −0.56 to 0.21) years and 0.28 (95% CI: 0.13 to 0.44) years for the two subgroups, respectively. There is no evidence that the single-agent based chemotherapy can extend the RMST at 5 years compared with a local treatment alone. In contrast, for trials using combination chemotherapy, the statistical significance in the difference in RMST at 5 years suggests a prolongation of 3 month in life expectancy during the first 5 years for patients with combination chemotherapy compared with patients with local treatment only.

We perform a sensitivity analysis with t* = 10 years, to assess the effect of this choice on effect estimates and whether the conclusion based on 5-year RMST analysis is robust. Figure 2 provides the forest plots for the difference in the RMST for 5 and 10 years separately. The combined difference in 10-year RMST is −0.53 (95% CI: 1.29–0.24) years for the single-agent group of trials and 0.52 (95% CI: 0.19–0.85) years for the combination-agent group of trials. The magnitude of difference in RMST in both groups is bigger than that in 5-year RMST. For trials with follow-up of less than 10 years, the flexible parametric model extrapolates the survival function where t* exceeds the maximum follow-up. However, the pseudo-values method cannot extrapolate beyond the end of follow-up. If we exclude these trials (UK Wallace, Noridic 1 Malmstrom and Nordic 2 Sengelov) for a sensitivity check, the combined difference in RMST at 10 years is −0.63 (95% CI: −1.66–0.40) years and 0.59 (95% CI: 0.22–0.97) years for the single-agent and combination-agent subgroups of trials, respectively. This is in good agreement with analysis based on all trials, whereas the confidence intervals become wider due to fewer trials being included. The RMST analysis results are similar between the pseudo-values method and the flexible parametric model.

Figure 2.

Advanced bladder cancer (ABC) meta-analysis. Forest plots for differences in restricted mean survival times at 5 year (left panel) and 10 year (right panel), with overall effect estimated from fixed-effect meta-analysis.

4.2. Example 1: Change of overall treatment effect over time (locally advanced bladder cancer data)

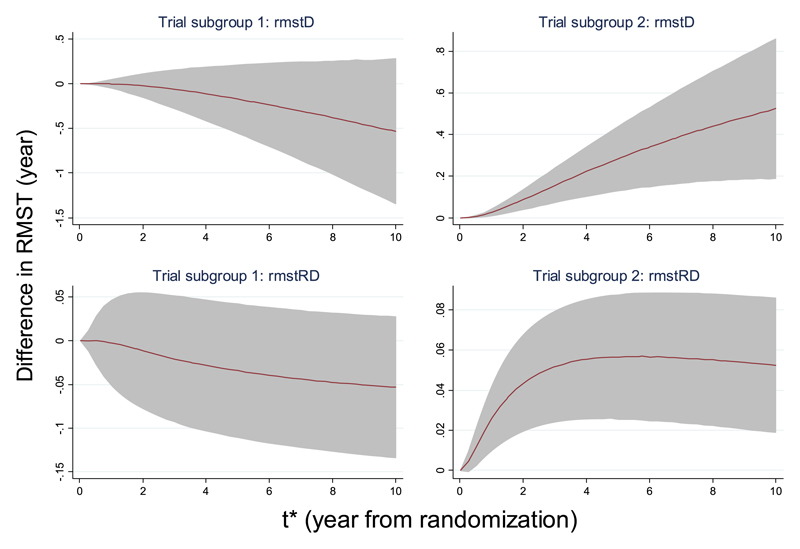
We now study the change of treatment effects over time by analysing the quantities rmstD and rmstRD. For the ABC data, both the pooled rmstD and rmstRD change with t* (Figure 3). For trials with single agent chemotherapy, the rmstD decreases monotonically as the t* increases. This again contrasts with the other trials, with the magnitude of rmstD increases over time. As expected, the precision of the rmstD decreases as t* increases, due to fewer trials having long follow-up and within-trial attrition over time. There is a turning point in the bottom right of Figure 3, where it shows that the rmstRD is around 2% at the first year, then increases to near 6% at 4 years, after which it reduces slightly. In the right panel plots, the 95% CI from time origin to 10 years excludes the non-effect zero-line, confirming the benefits of using local treatment plus combination chemotherapy compared with local treatment alone. In contrast, the 95% CI in the left panel plots include the non-effect zero-line, suggesting that there is no evidence to support the benefits of local treatment plus single-agent chemotherapy compared with local treatment alone.

Figure 3.

Advanced bladder cancer meta-analysis. Effects of varying t* on the overall effects in the difference of restricted mean survival time (RMST) by subgroups of trials^‡, using the fixed-effect meta-analysis model. Left: Single agent platinum chemotherapy in research arm; right: Platinum-based combination chemotherapy in research arm. Estimation of RMST for individual trial was obtained from a flexible parametric survival model with 3 degrees of freedom (d.f.)/1 d.f. (3 d.f. for the baseline distribution and 1 d.f. for the time-dependent treatment effect) and standard errors estimated by formula (7).

4.3. Example 2: Non-small cell lung cancer data

The trials in the non-small cell lung cancer (NSCLC) IPD meta-analysis [37] compared chemotherapy given after surgery and with surgery alone for treating patients with operable NSCLC. Data on a subset of 2416 patients from 13 trial comparisons of chemotherapy in non-Asian patients were available for this analysis. We are unable to obtain data for four trial comparisons [38–40], thus we analyse the data based on the 13 trial comparisons. The data are taken from three subgroups, which are as follows: (1) platinum in combination with vinca alkaloid/etoposide; (2) platinum in combination with vinorelbine; and (3) other platinum regimens. Previous analyses showed that there was no treatment by covariates interaction, and the conclusions in [37] were based on the overall effects across these subgroups. In the following, we will mainly present the overall results.

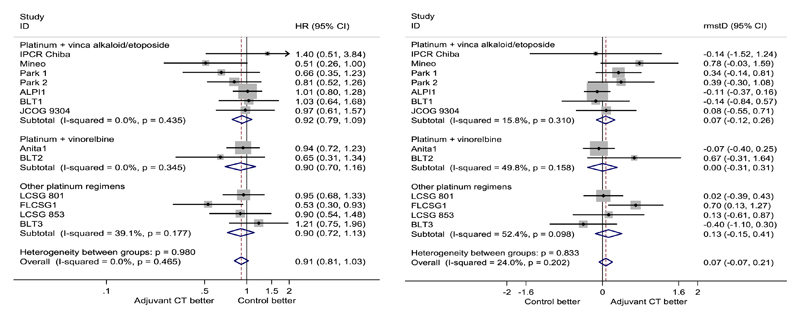
Based on the available data, Table II shows the pooled hazard ratios are 0.91 (95% CI: 0.81, 1.03) with no evidence of improvement by using chemotherapy. One trial (IPCR Chinba, ANITA1, BLT3) from each subgroup shows statistical significance in the G-T test, while the test is statistically significant for only one trial (ANITA1) using the likelihood ratio test. The global test suggests non-proportional hazards are evident only in one subgroup of trials (platinum in combination with vinorelbine), which include the trial ANITA1. The combined p-value across all trials is 0.03 or 0.04 (G-T test or likelihood ratio test), suggesting there is some degrees of departure from proportional hazards across the trials.

Table II.

Non-small cell lung cancer meta-analysis. Results of tests of non-proportional hazards (PH) (Grambsch-Therneau (G-T) test and likelihood ratio test from flexible parametric survival models) as well as fixed effect meta-analysis of the hazard ratio from Cox model. In addition, difference in restricted mean survival times (rmstD) computed from flexible parametric survival model [8], pseudo-values [20] and integrated difference in survival function [21].

						Difference in restricted mean survival time (5 years)
	Cox model			Test of non-PH p-values		Flexible parametric model Model				Pseudo-values method Method		IDS estimator Estimator
Trials	HR	95% CI	p-values	G-T*	Flex.	Diff.	95% CI1	p-values	95% CI2	Diff.	95% CI3	Diff.	95% CI4
Platinum in combination with vinca alkaloid/etoposide
IPCR Chiba [41] (n=29)	1.40	(0.51, 3.84)	0.51	0.02	0.06	−0.14	(−1.52, 1.24)	0.83	(−1.65, 1.38)	−0.38	(−1.86,1.09)	−0.35	(−1.67, 0.98)
Mineo [42] (n=66)	0.51	(0.26, 1.00)	0.05	1.00	0.86	0.78	(−0.03, 1.59)	0.06	(−0.08, 1.64)	0.79	(−0.04,1.62)	0.79	(−0.01, 1.59)
Park 1 [43] (n=118)	0.66	(0.35, 1.23)	0.19	0.62	0.52	0.34	(−0.14, 0.81)	0.16	(−0.14, 0.81)	0.37	(−0.11,0.85)	0.37	(−0.10, 0.84)
Park 2 [44] (n=108)	0.81	(0.52, 1.26)	0.36	0.49	0.61	0.39	(−0.30, 1.08)	0.27	(−0.31, 1.10)	0.34	(−0.38,1.05)	0.34	(−0.36, 1.03)
ALPI1 [45] (n=618)	1.01	(0.80, 1.28)	0.92	0.09	0.09	−0.11	(−0.37, 0.16)	0.43	(−0.37, 0.15)	−0.12	(−0.39,0.16)	−0.12	(−0.39, 0.15)
BLT1 [46] (n=136)	1.03	(0.64, 1.68)	0.90	0.29	0.14	−0.14	(−0.84, 0.57)	0.67	(−0.86, 0.58)	−0.15	(−0.87,0.57)	−0.16	(−0.87, 0.55)
JCOG 9304 [47] (n=119)	0.98	(0.61, 1.57)	0.92	0.31	0.45	0.08	(−0.55, 0.71)	0.79	(−0.55, 0.71)	0.05	(−0.59,0.69)	0.05	(−0.57, 0.68)
Subtotal	0.92	(0.79, 1.09)	0.34	0.02	0.06	0.07	(−0.12, 0.26)	0.52	(−0.13, 0.25)	−0.38	(−1.86,1.09)	0.06	(−0.13, 0.25)
Platinum in combination with vinorelbine
ANITA1 [48] (n=463)	0.94	(0.72, 1.23)	0.65	0.01	0.01	−0.07	(−0.40, 0.25)	0.67	(−0.42, 0.28)	−0.05	(−0.37,0.29)	−0.05	(−0.37, 0.28)
BLT2 [46] (n=65)	0.65	(0.31, 1.34)	0.24	0.24	0.23	0.67	(−0.12, 1.46)	0.80	(−0.33, 1.66)	NA	NA	0.43	(−0.54, 1.39)
Subtotal	0.90	(0.70, 1.16)	0.41	0.02	0.02	0.00	(−0.31, 0.31)	0.82	(−0.32, 0.34)	−0.05	(−0.37,0.29)	0.00	(−0.31, 0.32)
Other platinum regimens
LCSG801 [49] (n=283)	0.95	(0.68, 1.33)	0.76	0.58	0.58	0.02	(−0.39, 0.43)	0.91	(−0.39, 0.44)	0.08	(−0.34,0.49)	0.08	(−0.34, 0.49)
FLCSG1 [50] (n=110)	0.53	(0.30, 0.94)	0.03	0.37	0.33	0.70	(0.13, 1.27)	0.01	(0.14, 1.26)	0.63	(0.04,1.22)	0.63	(0.05, 1.21)
LCSG853 [51] (n=188)	0.90	(0.54, 1.48)	0.07	0.89	0.88	0.13	(−0.61, 0.87)	0.60	(−0.57, 0.83)	NA	NA	0.32	(−0.41, 1.05)
BLT3 [46] (n=118)	1.21	(0.75, 1.96)	0.43	0.04	0.06	−0.40	(−1.10, 0.30)	0.24	(−1.11, 0.31)	−0.37	(−1.09,0.34)	−0.38	(−1.08, 0.33)
Subtotal	0.91	(0.73, 1.13)	0.38	0.28	0.33	0.13	(−0.15, 0.41)	0.34	(−0.14, 0.42)	0.14	(−0.16,0.45)	0.17	(−0.11, 0.45)
Overall	0.91	(0.81, 1.03)	0.13	0.03	0.04	0.07	(−0.07, 0.21)	0.28	(−0.07, 0.21)	0.06	(−0.09,0.20)	0.08	(−0.07, 0.22)

¹Standard errors were calculated using the formula in [7].

²Standard errors from bootstrapping based on 1000 replications.

³Standard errors from sandwich estimator.

⁴Standard errors from resampling method with 10 000 replications.

^*Grambsch-Thernau’s non-proportional hazards test.

The NSCLC trials have variable lengths of follow-up, from less than 5 years (two comparisons) to longer than 10 years (three comparisons), making the selection of cut-point not straightforward. We advocate that the analysis be dominated by the observed data rather than estimates based on extrapolation, although technically extrapolation can be achieved by using the flexible parametric survival model. Also, an absolute difference in survival probability was reported at 5 years in the original meta-analysis, from which our analysis follows. Thus, we consider 5 years as a reasonable t* in the RMST analysis. Using the flexible model, we estimated the RMST for treatment and control groups as 3.62 (95% CI: 3.5–3.72) years and 3.51 (95% CI: 3.41–3.61) years, respectively. As shown in Figure 4, we obtained the overall rmstD as 0.07 (95% CI: −0.07, 0.21) year. The gain in RMST is less than 1 month, and the effect is not statistically significant, suggesting there is no evidence to support a benefit of adding chemotherapy after surgery. Using the pseudo-values method, we were unable to include trials with follow-up less than 5 years for an RMST analysis with t* ⩾ 5 years. Nevertheless, where available, the estimated rmstD for individual trials is similar across the estimation methods.

Figure 4.

Non-small cell lung cancer meta-analysis. Forest plots for hazard ratios estimated from the Cox model (left panel) and differences in restricted mean survival times at 5 years (right panel), with overall effect estimated from fixed-effect meta-analysis.

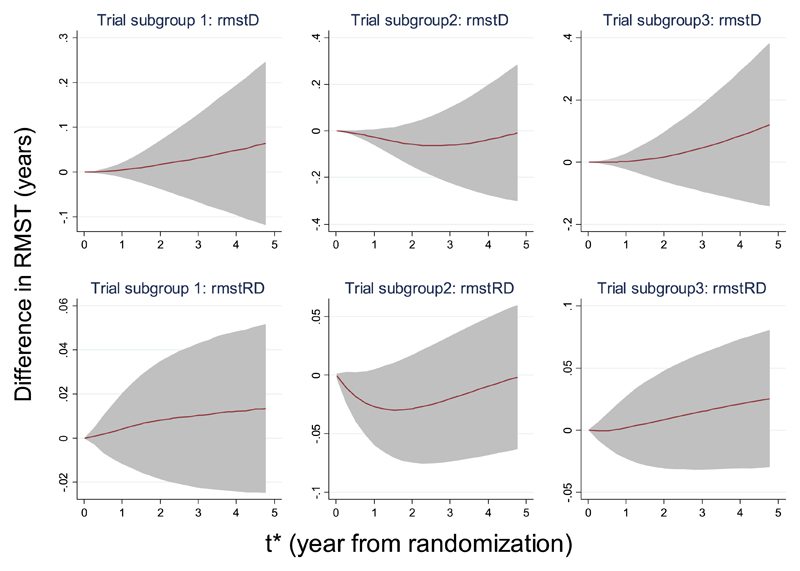
Figure 5 shows how the difference in RMST changes over time for each subgroup of trials. In two subgroups (left and right panels in Figure 5), we observed a monotonically increasing trend in both the pooled difference in RMST and pooled mean difference in survival probabilities; in contrast, for the remaining subgroup, the difference decreases below zero in the earlier follow-up and increases above zero in the later follow-up. However, the 95% confidence regions always cover the non-effect line, indicating that throughout the 5 years follow-up, there is no evidence to support the benefits of surgery with chemotherapy compared with surgery alone.

Figure 5.

Non-snall cell lung cancer meta-analysis. Effects of varying t* on the overall effects in the difference of restricted mean survival time (RMST) by subgroups^§, using fixed-effect meta-analysis model. Estimation of RMST for individual trial was obtained from a flexible parametric survival model with 3 degrees of freedom (d.f.)/1 d.f. (3 d.f. for the baseline distribution and 1 d.f. for the time-dependent treatment effect) and standard errors estimated by formula (7).

5. A simulation study

5.1. Design

To further the comparison of the estimation methods for RMST, we conducted a simulation study. Previous work has compared the flexible parametric survival model and the pseudo-values method for estimating the RMST based on several real data sets [7]. In addition, Zhao et al. [21] have evaluated the statistical properties of their method (Integrated Difference of Survival Functions) using survival data simulated from a two-parameter Weibull model. Within each arm, we simulate time to the event of interest and time to censoring, both from Weibull distributions [52], with parameters specified in the web appendix. We then generate the event indicator for each participant. The event indicator is set to be 1 if the event of interest occurs earlier than censoring; otherwise, it is set to be 0. For each participant, the survival time is recorded as the smaller value of the time to event and time to censoring. The comparison of the three estimation methods has not been studied before. Here, we conduct a simulation study to compare three methods in terms of the bias, mean square error and coverage probability of the 95% confidence interval.

In the simulation study, we include several scenarios by varying the parameters in the Weibull survival distribution (Scenarios 1–4, Web Supporting Information). We consider the possible impact of censoring on the estimation by including higher level of censoring in Scenarios 5–8 (Web Supporting Information). The influence of sample size is examined by including two sizes (250 and 500 observations) within each scenario. We simulate 1000 survival data for each scenario and carry out the estimation for each simulated data. We also compare the methods for variable t* by reporting the results at 3, 5 and 10 years of follow-up. As the effect measure rmstRD only differs with rmstD by a constant factor of t*, the statistical properties of the two are the same. We therefore present simulation results for one effect measure, rmstRD. Within each scenario, we report average bias, mean square error and coverage probability of rmstD over 1000 simulated data sets.

5.2. Results

Summary statistics from the simulation are given in Tables A.1-8 (Web Supporting Information). The two non-parametric methods (pseudo-values and integrated difference of survival functions) produce nearly identical results in terms of bias and mean square errors. This may be because both methods use a Kaplan–Meier estimate for the survival function, although the resampling techniques are different. This leads to similar but not identical coverage probabilities. Among the three methods, the coverage probabilities are close to their nominal values. There is no clear indication of whether one method is better than the other in terms of the coverage. However, in the flexible parametric survival model, mean square errors are smaller than the other two methods. This may be because the flexible parametric model is able to correctly specify the survival function when the survival time follows a Weibull distribution. The non-parametric methods do not assume any parametric distribution, so the mean square errors are inflated. We acknowledge that the survival time does not always follow a Weibull distribution and that the mean square errors of the rmstD from the flexible parametric method are not always smaller compared with that from the non-parametric methods. In scenarios 6 and 8 (see Table A.6 and Table A.8 of our Web Supporting Information), some simulated data sets have maximum follow-up of less than 10 years, due to a higher level of censoring and higher event probability in these two scenarios. Both the flexible parametric survival model and the integrated difference of survival functions (IDS) method can extrapolate the RMST to 10 years, while the pseudo-values method do not provide estimates in such situations. The difference in the summary statistics for 10 years rmstD is apparent in Scenarios 6 and 8. First, the bias and the mean square errors are no longer identical between the two non-parametric methods. This is because results of the flexible model and IDS are based on all simulated data sets while the results from the pseudo-values method is based on a subset where the maximum follow-up is longer than 10 years. Second, extrapolation appears to have little influence, as across the three methods the coverage probabilities are still quite close to the nominal value. Again, the flexible parametric survival model shows a small reduction in the mean square error although some of the results are based on extrapolation in these two scenarios.

6. Discussion

Meta-analysis of time-to-event outcomes often use the hazard ratio as the treatment effect measure. However, the PH assumption may not hold for all the included trials. A combined p-value from the non-PH tests for the treatment effects from each individual trial can be used to test the PH assumption for the overall effect in a meta-analysis. The RMST is an appealing effect measure in meta-analysis, because it does not require the PH assumption.

We have described and extended the use of RMST to meta-analysis. The difference from the other measures in previous studies [9–12] is that we allow the evaluation of treatment effects to rely on the difference in time to event, for ease of interpretation and to ensure that the implementation is straightforward using both parametric and non-parametric methods. The IPD have enabled us to illustrate the use of RMST in meta-analysis with a comparison with the conventional hazard ratio approach.

From the two example analyses, the conclusions from RMST analysis are similar to meta-analysis of hazard ratios. This is similar to other work where alternative measures were used to cope with non-proportional hazards [9, 12]. Although the p-values for treatment effect estimates are similar between analyses using hazard ratio and difference in RMST, as a time-dependent outcome measure, the difference in RMST can provide graphical displays to illustrate how the effect may change over time. Further, we find the interpretation of the difference in RMST easier because it is directly related to survival time instead of (relative) hazards. In addition, meta-analyses of RCTs are often used in cost effectiveness studies (e.g. NICE), where it often requires the possibility to extrapolate survival curves beyond the observed time and the calculation of a mean survival time for economic evaluations. The flexible parametric model with the use of RMST as the outcome measure will provide both calculations.

Most of the trials in the two example data sets provide no evidence of non-proportional hazards, and the degrees of departures from non-proportional hazards do not seem to be very large, suggested in part by the combined p-values (0.02 for ABC meta-analysis and 0.03 for NSCLC meta-analysis). Furthermore, the trials with non-proportional hazards contribute only 26% (trials Nordic 1, DEVACA and GUONE) and 17% (trial Anita1) of the weight in the ABC and NSCLC meta-analyses, respectively. Thus, the analysis results are dominated by trials in which the PH assumption is not violated. However, in a contrasting situation where the meta-analysis is dominated by trials with greater degrees of non-PH or trials with greater weight in the analysis have non-PH, we are uncertain about how reliable and informative a meta-analysis based on the hazard ratio would be. This may be more of concern in the future, especially as extreme non-proportional hazards have been observed in some large trials (ICON7 [53], IPASS [54]). Thus, we consider the difference in RMST as a safer measure because it is free of the PH assumption. Otherwise, a meta-analysis with time-to-event outcomes should be accompanied with a sensitivity analysis using RMST analysis, where possible.

We have fitted the 3 d.f./1 d.f. flexible parametric survival model to both arms of the trial data simultaneously. An alternative would be to fit the 3 d.f. flexible model to each arm separately and obtain a separate estimate of the RMST. Results from separate analyses were given in Figures A.1-A.4 of the Web Supporting Information. The estimated differences in RMST were similar between the separate and simultaneous analyses, using the flexible parametric model. This is expected because the two arms in a randomized trial can be assumed independent.

A further advantage of estimating the RMST by a flexible parametric survival model is that we can predict the RMST beyond the actual follow-up time, which allows us to include all the trial data in a meta-analysis even when some trials actually have follow-up less than t*. This is appealing in meta-analysis context because trials typically have different lengths of follow-up. The pseudo-values method does not have such a property, with its estimation of the RMST necessarily constrained within the observed time period. In the NSCLC dataset, the trials BLT2 and LCSG853 have follow-up less than 5 years, and we were not able to include them in the 5-year RMST meta-analysis with the pseudo-values method. The flexible parametric survival model can produce reasonable extrapolation (see pp.153-156 in [23]) for the survival function, which is essential for predicting the restricted mean survival time, the integral of the survival function (Equation 1). Royston and Lambert (2011) compared the survival function estimated from observed data and from the predicted data and showed that the flexible parametric survival model can extrapolate the survival function, and the extrapolated survival functions are reasonably close to the observed survival function. They also showed that the extrapolation based on the 3 d.f. model is more precise than the 1 d.f. model (Weibull, loglogistic and lognormal). We have used 3 d.f. for the baseline distribution throughout the paper. In addition, in Scenarios 6 and 8 of our simulation study, extrapolation took place at a 10-year follow-up for a number of the simulated data sets as their follow-up are less than 10 years. The results from these two scenarios (see Table A.6 and Table A.8 of the Web Supporting Information) suggest that the extrapolation from both the flexible model and the non-parametric method [21] seems to be reasonable. In addition, the flexible parametric survival model gives a small reduction in the mean square errors when the survival time follows a Weibull distribution. The extrapolation using the flexible parametric model is useful when a small number of trials within a meta-analysis have followup shorter than t* while the majority of the trials have follow-up longer than t*. It allows us to combine results across trials with a unified t* as well as keep the analysis dominated by the observed data.

However, it is worth noting that the RMST is dependent on t* [8]. The considerable follow-up in the ABC meta-analysis enables the RMST analysis to be performed at 10 years. This does not necessarily mean the 10-year RMST analysis should typically form a primary analysis. In fact, there was a relatively small sample of trials with 10-year follow-up and we expect that the RMST at 10 years will be imprecisely estimated. This is confirmed in Figure 3, where the precision is highest at the time of randomisation and gets poorer over time. Our simulation study also shows that the mean square errors become larger as the t* increases and the coverage probabilities can be slightly further away from their nominal values. It is therefore important that the t* is chosen with due caution. A choice of t* too near to the time of randomisation may be insufficient to evaluate the alternative treatments. In contrast, a choice of t* too close to the time when most at-risk patients have been censored can produce estimates with very wide 95% CI. This can potentially make the meta-analysis inconclusive. Thus, a compromise between the two is perhaps necessary. The choice of t* is disease and problem specific and likely to further depend on the disease type, clinical interests and the available length of follow-up. Where an RMST analysis is planned, it is desirable for t* to be prespecified in the trial protocol [8] and in meta-analysis or systematic review protocols, perhaps based on the clinical questions or motivations, disease severity and the planned follow-up time. The choice of t* is an issue in meta-analyses with variable follow-up times. A chosen time point t* may be greater than the maximum follow-up in some trials so extrapolation is needed; in contrast, the chosen t* may be smaller than the maximum follow-up time in other trials so data beyond t* are not included in the meta-analysis. From a statistical perspective, a reasonable choice of t* will be that allows using as much data as possible and minimizes the need of extrapolation. The optimal choice of t*, which satisfy this conditions, is a future research question. In the absence of such choice, plotting the difference in RMST against t* (Figures 3 and 5) would be helpful to gain insights into how treatment effect estimates may vary across the follow-up time and if the conclusions are sensitive to the choice of t*.

We have demonstrated the RMST meta-analysis with a two-stage approach. As well as its popularity in practice [19], the two-stage approach is flexible to determine a parsimonious model for all the trials in the first stage. This is beneficial because the flexible parametric survival model requires the specification of the number of d.f. for the baseline distribution function and the time-dependent coefficient, although a general choice of 3 d.f./1 d.f. is recommended [8]. In addition, the two-stage approach also allows us to investigate the estimated RMST for each trial and to study how much weight is assigned to the trials with non-PH. The RMST meta-analysis can be adapted to incorporate the participant-level covariates and their interactions with treatment effects, in order to detect whether treatments are more likely to benefit patients with specific characteristics. A further extension is to jointly synthesize the 5-year and 10-year differences in RMST using a multivariate meta-analysis model, which may improve precisions due to taking into account correlations of effect sizes estimated at multiple time points [55].

In summary, we have demonstrated the use of RMST in meta-analysis of time-to-event outcomes based on IPD. The difference in RMST is a useful effect measure in a meta-analysis because it avoids the proportional hazards assumption. The measure is interpretable and helpful in situation when treatment effects may change with time. Recent development in data reconstruction techniques enables the extension of RMST meta-analysis for aggregate data, and we are currently investigating the methodology in this domain.

Supporting information

Additional supporting information may be found in the online version of this article at the publisher’s web site.