Using Large-Scale Granger Causality to Study Changes in Brain Network Properties in the Clinically Isolated Syndrome (CIS) Stage of Multiple Sclerosis

Abstract

Clinically Isolated Syndrome (CIS) is often considered to be the first neurological episode associated with Multiple sclerosis (MS). At an early stage the inflammatory demyelination occurring in the CNS can manifest as a change in neuronal metabolism, with multiple asymptomatic white matter lesions detected in clinical MRI. Such damage may induce topological changes of brain networks, which can be captured by advanced functional MRI (fMRI) analysis techniques. We test this hypothesis by capturing the effective relationships of 90 brain regions, defined in the Automated Anatomic Labeling (AAL) atlas, using a large-scale Granger Causality (lsGC) framework. The resulting networks are then characterized using graph-theoretic measures that quantify various network topology properties at a global as well as at a local level. We study for differences in these properties in network graphs obtained for 18 subjects (10 male and 8 female, 9 with CIS and 9 healthy controls). Global network properties captured trending differences with modularity and clustering coefficient (p<0.1). Additionally, local network properties, such as local efficiency and the strength of connections, captured statistically significant (p<0.01) differences in some regions of the inferior frontal and parietal lobe. We conclude that multivariate analysis of fMRI time-series can reveal interesting information about changes occurring in the brain in early stages of MS.

1. INTRODUCTION

Clinically Isolated Syndrome (CIS) is considered as the first clinical episode of Multiple Sclerosis (MS) in about 85% of the patients. Although MRI scanning of such subjects often shows multiple asymptomatic lesions, quantitative criteria such as those derived from diffusion tensor imaging, magnetic transfer ratio and measures of atrophy have been shown to be more sensitive for predicting the progression to MS. Cognitive decline is an established symptom of MS, however relatively little is known about prevalence of abnormalities at the CIS stage of the disease. It has been shown in a recent study that specific deficits manifesting during CIS can provide prognostic insights regarding the progression of the symptoms to MS. However, further research is needed to develop accurate models for predicting long-term effects after an episode of CIS [13].

In recent years various studies [1,2,3] have shown changes occurring in synchronization within the brain at different stages of MS using functional MRI (fMRI). These have been shown to correlate well with structural changes observed in the brain of subjects suffering from MS. Hence fMRI has proven to be a valuable tool for improving our understanding of the pathophysiology of this disease. Most current literature analyzing fMRI in subjects with MS commonly use correlation-based approaches for quantifying connectivity between different regions, which ignores directional and multivariate information prevalent in brain networks.

We have previously demonstrated the use of large-scale Granger Causality (lsGC) [4], which is a purely data-driven and multivariate approach to investigate causal influence at a voxel resolution scale in resting-state fMRI. In this study we illustrate how such information can be used to extract clinically relevant information for studying the pathophysiology of neurological disorders such as MS. We hypothesize that this approach may be better suited to capturing changes in connectivity patterns than conventionally used linear cross-correlation methods, because it permits multivariate analysis that also avoids a priori assumptions on the underlying connection patterns frequently implied by model-based approaches, such as Dynamic Causal Modeling (DCM) [5] or Structural Equation Modeling (SEM) [6]. Using our approach, we can represent the human brain as a directed network graph with brain regions representing nodes and the influence score (lsGC index) being the edge weights.

A large body of literature in neuroscience has analyzed brain networks from the perspective of graph theory, where network graphs can be quantified with a wide range of simple yet ‘neuro-biologically’ meaningful measures [7]. These measure are able to provide quantifiable insights into the specific properties of brain networks specifically with regards to their topological organization. In this study, we have focused on a few metrics characterizing global graph properties, as well as measures that can provide local/regional information from the graphs. We study these measures with regards to their ability to identify differences between the two subject groups, with the aim of better quantifying early neurological damage in subjects at the CIS stage of MS. This work is embedded in our group’s endeavor to expedite ‘big data’ analysis in biomedical imaging by means of advanced machine learning and pattern recognition methods for computational radiology and radiomics, e.g. [14–45].

2. DATA

Functional MRI scans from a cohort of 18 subjects (9 with CIS, 9 healthy controls, 21–53 yrs, 10 male, 8 female) underwent resting-state fMRI scanning (TR = 3000ms, FA = 90°, slice spacing = 1 mm, voxel size = 3.3×3.3×3.3 mm³, 25 slices, 150 acquisitions) were obtained using a 1.5T (SignaHDxt scanner, GE Medical Systems) with a 8-channel transmit/receive head coil. High-resolution anatomical scans were acquired with the following parameters: 3D T1-weighted FSPGR (TR = 11.6 ms TE = 5.048 ms TI = 500 ms; FA = 8°, voxel size = 1×1×1 mm³). The latter was used for registration of the functional MRI data to the standard MNI152 template [10].

3. METHODS

The analysis performed on the dataset is summarized the flow chart (Figure 1).

Figure 1.

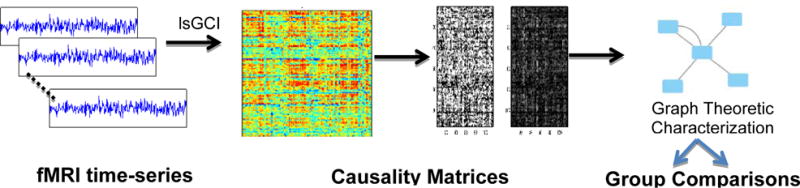
Flow chart for sample fMRI time series data for computing graph measures. A brain registered to the standard MNI Atlas is segmented based on AAL template into 90 regions. Time series from each of these regions are analyzed using large-scale Granger Causality (lsGC). The matrix obtained is converted to an undirected graph using thresholding and a directed graph using sparsing and graph measure described in Aim 2 are computed

3.1 Preprocessing and Parcellation

All data was preprocessed using the Configurable Pipeline for the Analysis of Connectomes (C-PAC) [8]. Standard preprocessing steps were applied to the data. The first 5 volumes were deleted to remove initial saturation effects. The volumes were then motion-corrected and the brain was extracted. High-pass filtering (0.01 Hz) was performed to remove the effects of signal drifts. Subsequently, the slices were registered to the standard MNI152 template. Nuisance regression was performed to remove the effects of the global signal, ventricular signal averaged from CSF and also the white matter signal. Also, the time series were normalized to zero mean and unit standard deviation to focus on signal dynamics rather than amplitude [9]. For each dataset, 90 regional time-series were computed based on the average time-series of each of these 90 regions, excluding regions located in the cerebellum and the brain stem according to the Automated Anatomic Labeling (AAL) template [11].

3.2 Large-Scale Granger Causality Analysis

We use large-scale Granger Causality [4] to obtain a casual influence score between every pair of voxel time series in the resting state human brain. Large-scale Granger Causality works on the principle of Granger Causality, which obtains the casual influence of time series x_r on time series x_s by quantifying the improvement in prediction of x_s in the presence of x_r. Large-scale Granger Causality obtains an influence score between every pair of voxels in a multivariate sense. The limitation with using a multivariate approach to Granger Causality, without incorporating dimensionality reduction, on large systems like the brain, is that the prediction model cannot estimate model parameters as the system is undetermined. We show how using lsGC approach, this problem can be overcome.

Consider the ensemble of time series X ∈ ℝ^N×T, where N is the number of time series and T the number of temporal samples. Let X = (x₁, x₂, x₃, …, x_N)^T be the whole multidimensional system, x_n ∈ ℝ^1×T a single time series with n ∈ {1,2, …, N}, where x_n = (x_n(1), x_n(2), …, x_n(T)). lsGC obtains a multivariate GC score by first decomposing X into its first p high-variance principal components Z ∈ ℝ^p×T using Principal Component Analysis (PCA), i.e.,

$$Z=WX.$$

Following this, we model Z using Vector Auto-Regressive (VAR) modeling of order m and compute the estimate $\widehat{Z}$ by using the m auto-regression ℝ^p×p parameter matrices obtained from VAR modelling of Z. To obtain the influence of time series x_r on all other time series, we remove the information of x_r from the transformation matrix W, obtain $Z_{\backslash \left\{x_r\right\}}$ and model ${\widehat{Z}}_{\backslash \left\{x_r\right\}}$ as its VAR estimate. In this manner, lsGC obtains a causality score between every pair of time series in a multivariate sense.

The errors of the two estimates are projected into the original high-dimensional space using the respective inverse PCA transformation. After the errors are obtained, we quantify the prediction quality by comparing the variance of the prediction errors obtained with and without consideration of x_r. If the variance of the prediction error of a given time series, say x_s, decreases with using x_r, then we say that x_r Granger-causes x_s [4].

$$f_{x_r\to x_s}=\ln \frac{\mathrm{var}\left(e_{s,\backslash \left\{x_r\right\}}\right)}{\mathrm{var}\left(e_s\right)}$$

$f_{x_r\to x_s}$ is the GC index for the influence of x_r on x_s, which is stored in the affinity matrix A at position (A)_sr. $e_{s,\backslash \left\{x_r\right\}}$ is the error in predicting x_s, when x_r was not considered, and e_s is the error when x_r was used. ∈ R^N×T

3.3 Graph Theoretic Measures

A directed binary graph a, was obtained from the network matrix A, of each fMRI data set by thresholding. The appropriate choice of the threshold for binarization of network graphs obtained from fMRI data analysis is subject to ongoing discussions in the pertinent literature [7]. Based on earlier studies [12], we chose a threshold value that retained 45% of the connections. At such a threshold, the networks are not fragmented, and they still preserve their ‘small-world’ topology [10]. Measures [7] to characterize local and global network properties (summarized in Table 1) were computed for the thresholded graphs obtained for each subject.

Table 1.

List of the graph-theoretic measures used in this study. For a detailed description, please refer to [7].

Global Measures	Variance of degree distribution (incoming and outgoing), Efficiency, Clustering Coefficient, Assortativity, Modularity
Local Measures	Causal Strength, Degree, Local Efficiency, Nodal Clustering Coefficient

All procedures, excluding the preprocessing steps discussed in section 3.1, were implemented using MATLAB (MathWorks Inc., Natick, MA, 2013). The network measures definitions were taken from [7]. Significance testing was performed using a permutation-based testing with False Discovery Rate (FDR) correction.

4. RESULTS

The results obtained using global graph measures are represented in Figure 2. Certain differences are seen in the properties between the subject groups. A trending increase in modularity and clustering co-efficient is observed in the CIS subjects. No changes were observed in the remainder of the global properties studied.

Figure 2.

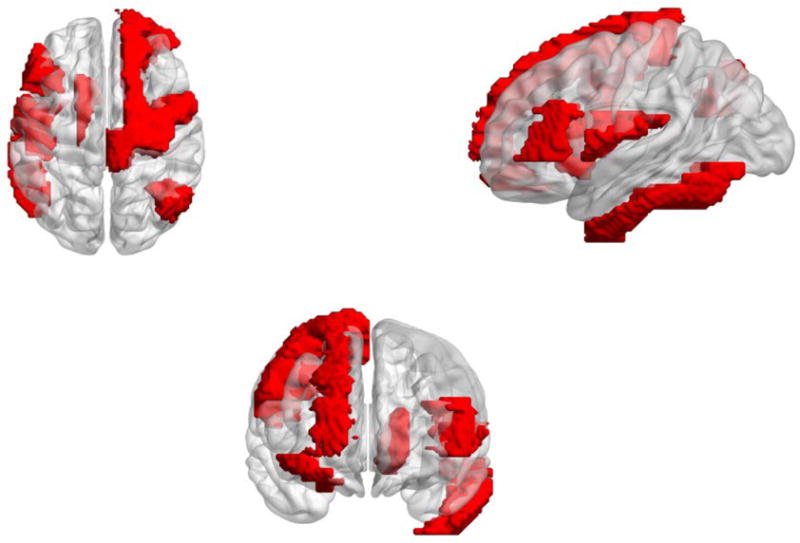
A simplified view of the brain representing the regions highlighting differences (seen in red) in local graph properties. Some of the affected regions have been shown in other pertinent literature [1,3]. The regions shown here represent the differences using all the features and are mapped over the standard atlas. Regions are specifically detailed in the text.

To investigate further, we studied the possibility of changes occurring within the brain network at a more regional level. Graph theory allows for characterization of properties of individual nodes also (as noted in Table 1). Multiple properties of the frontal superior region (portions of the precentral gyrus) are significantly (p<0.01) perturbed in the CIS subjects. Other affected regions, based on the analysis, involved parts of the frontal gyrus and also the parietal lobe. These regions are highlighted in Figure 3.

Figure 3.

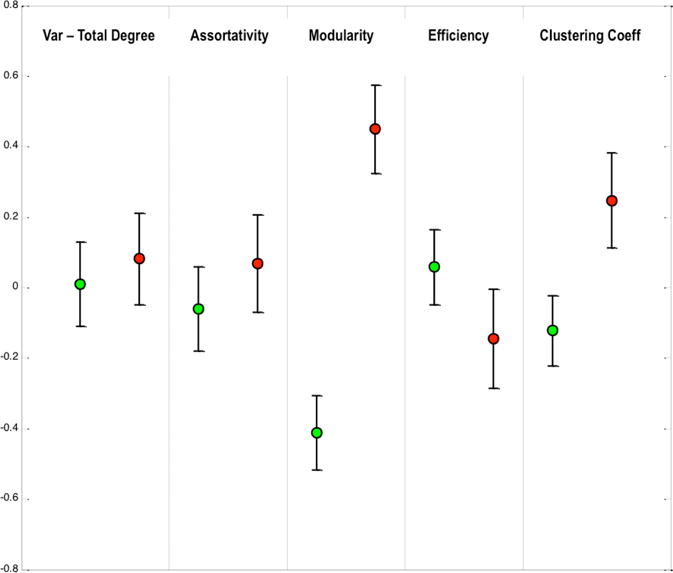
The distribution of global graph measures for the two subject groups (Red: Diseased, Green: Healthy). Error bars represent the standard error of mean. Trending differences are seen for Modularity and Clustering Coefficient (p<0.1).

5. DISCUSSION

MS is a complex disease with a diverse presentation that can eventually lead to disability along associated with considerable socio-economic impacts. The exact mechanism of progression from CIS to MS is not very well understood. Imaging techniques, specifically MRI has served as essential supplementary tools for assessment of MS. Due to high variability in outcomes associated with progression from CIS, methods that can accurately predict the long-term disability are needed to appropriately implement treatment paradigms better patient management. Newer methods will also aid in developing a better understanding of the pathophysiology of MS.

We present a clinical application of our large-scale Granger Causality (lsGC) framework for multivariate analysis of resting-state fMRI data. Based on the evaluation of causality between regional time-series, we construct connectivity profiles from a parcellated human brain. Subsequently, we carry out quantitative analysis of the resulting profiles using graph-theoretic approaches to identify specific differences in connectivity patterns between the network profiles of healthy and subjects with a CIS episode.

We have detected some differences in these profiles at a global as well as a regional level. The increase of clustering and modularity at a global level could indicate the increased synchronization within specific networks as a compensatory response of the brain to initial damage occurring in early stages of MS [1]. Although significant differences are not seen, our findings may suggest a subtle reorganization occurring within the brain in an early stage MS, which is in line with other studies [2].

When specific regions are analyzed, we detect changes in properties specifically in the precentral as well as frontal gyrus and some portion of the parietal lobe. Similar regions have been found to be associated with disease progression in other studies using graph-theoretic properties at a regional level [1]. Although the results in this study are consistent with other literature on MS [2,3], some differences can be seen, which may be attributed to the fact that we have applied a multivariate approach to constructing the network graphs. Additionally, for this study we have restricted the analysis to subjects with CIS i.e. subjects that may be suffering with a mild and initial form of MS.

This approach, we conclude, can capture additional information when compared to conventionally used correlation-based analyses. We aim to explore this aspect further in future studies, as we pursue to utilize our approach to potentially develop image-derived biomarkers for MS and other neurological diseases.

6. CONCLUSION

In conclusion, the results presented in this work indicate that the multivariate large-scale Granger Causality (lsGC) approach, in combination with graph-theoretic network characterization, can be applied to detect changes in brain network connectivity patterns observed in patients with CIS. While avoiding certain inherent limitations of traditional approaches, the lsGC technique can hence serve as an alternate method for fMRI-based connectivity analysis in the human brain. The preliminary results here suggest that such an analysis protocol can be used to study neuro-degeneration in early stage MS, however further in depth analyses are needed.