Increasing the field of view of adaptive optics scanning laser ophthalmoscopy

Abstract

An adaptive optics scanning laser ophthalmoscope (AO-SLO) set-up with two deformable mirrors (DM) is presented. It allows high resolution imaging of the retina on a 4°×4° field of view (FoV), considering a 7 mm pupil diameter at the entrance of the eye. Imaging on such a FoV, which is larger compared to classical AO-SLO instruments, is allowed by the use of the two DMs. The first DM is located in a plane that is conjugated to the pupil of the eye and corrects for aberrations that are constant in the FoV. The second DM is conjugated to a plane that is located ∼0.7 mm anterior to the retina. This DM corrects for anisoplanatism effects within the FoV. The control of the DMs is performed by combining the classical AO technique, using a Shack-Hartmann wave-front sensor, and sensorless AO, which uses a criterion characterizing the image quality. The retinas of four healthy volunteers were imaged in-vivo with the developed instrument. In order to assess the performance of the set-up and to demonstrate the benefits of the 2 DM configuration, the acquired images were compared with images taken in conventional conditions, on a smaller FoV and with only one DM. Moreover, an image of a larger patch of the retina was obtained by stitching of 9 images acquired with a 4°×4° FoV, resulting in a total FoV of 10°×10°. Finally, different retinal layers were imaged by shifting the focal plane.

1. Introduction

Imaging of the retina is limited by the eye itself. High transverse resolution is prevented by imperfections of the ocular media that are changing both temporally and spatially [1–4]. The introduction of adaptive optics (AO) to ophthalmic imaging has allowed compensation of these aberrations. AO relies on a correcting device (usually a deformable mirror (DM)) in the optical train that corrects for the wave-front error (WFE), and thus provides diffraction limited performance over the corrected field of view (FoV) [5–7]. Over the past decades, most of the ophthalmic techniques have been combined with AO: flood illumination fundus imaging [8], scanning laser ophthalmoscopy (SLO) [9] and optical coherence tomography (OCT) [10]. More details on the individual techniques can be found in recent review articles [11–14]. With such techniques, microscopic structures of the eye, that were previously only visible ex-vivo with histology [15], can now be revealed in vivo, and in a non invasive way.

Although AO is used successfully in ophthalmology [16, 17], it presents some significant limitations, which prevent a wide clinical use. One of them is the small area that can be imaged with high resolution. Typical AO systems support patches on the retina between 1°×1° and 2°×2° [18]. This limit is due to anisoplanatism, which is a well known problem in AO systems. Aberrations are varying within the FoV, and as the DM is localized in the pupil plane, it can only compensate for aberrations that are constant in the FoV [19]. For the examination of the eye, the variation of the WFE with the FoV is due to the imaging instrument aberrations and to the size of the isoplanatic patch of the eye. Indeed, the imaging systems are typically designed for good on-axis performance and present more aberrations off axis, which limits the performance of the AO correction on larger scanning angles. Furthermore, the eye itself is an anisoplanatic optical instrument. Different studies have shown that the WFE of the eye can be considered constant only on patches smaller than 2.5°×2.5° for pupil diameters between 4 mm and 6 mm [20, 21]. The size of this so-called isoplanatic patch determines the FoV on which AO correction performs efficiently [18,22]. In order to increase the FoV, a smaller pupil diameter can be used at the cost of transverse resolution. This concept has been applied for a commercial AO fundus camera (Imagine Eye rtx1). Extending the FoV while maintaining the high resolution is more challenging.

A technique to increase the FoV of AO instruments, known as multi-conjugate AO (MCAO), was developed in astronomy [23–25]. Different DMs are placed at locations that are conjugated to different layers of the atmosphere in order to correct aberrations separately for the individual layers and thus to extend the FoV. The DM control is an important aspect of any AO system [26,27]. In conventional AO systems, the single DM is generally driven by the measurement of a Shack-Hartmann wave-front sensor (SH), which is located in a plane conjugated to the DM [28]. Similarly, several SHs can be used to drive several DMs. In order to have WFE measurement within the entire FoV, each SH observes a different guide star [29]. A variation of this concept consists of using a single SH but the fields are spatially dissociated before arriving on the SH, resulting in separated SH spots for the different fields [30]. Finally another technique, sensorless AO, can be used. It uses metrics on the image quality to drive the DM [31,32].

MCAO can be applied to ophthalmic imaging [33]. An AO flood illumination fundus camera with 2 DMS was developed, providing images of the retina on a 7°×7° FoV, for a 6 mm pupil diameter [34,35]. This instrument uses five guide stars to perform a uniform correction over the entire FoV. The WFE is indeed measured on five points in the FoV by analyzing the SH spots of these five reference sources on a single detector.

In this paper, we extend the concept of dual-conjugated AO to SLO. We present a relatively simple system with two DMs, one single SH and no guide stars. The instrument provides high resolution imaging of the retina over a 4°×4° FoV, for a 7 mm pupil at the eye. The 2 DM configuration minimizes isoplanatism issues of both the eye and the set-up. The AO correction is performed by using a combination of classical AO and sensorless AO.

The concept and the design of the instrument is described and the imaging performances are validated with measurements on a model eye and in 4 healthy in-vivo eyes. Images recorded with our 2 DM set up are compared with images obtained using only a single DM and with images that were recorded on a small FoV (typical AO mode). We also imaged a 10°×10° FoV by stitching 9 acquired retinal images.

2. Method

2.1. Adaptive optics scanning laser ophthalmoscope set-up

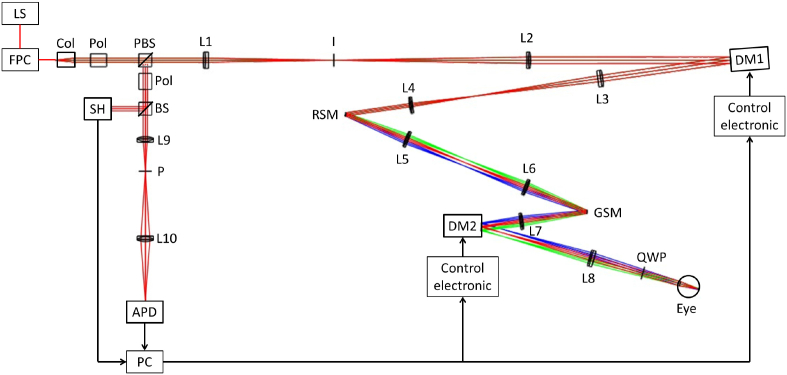
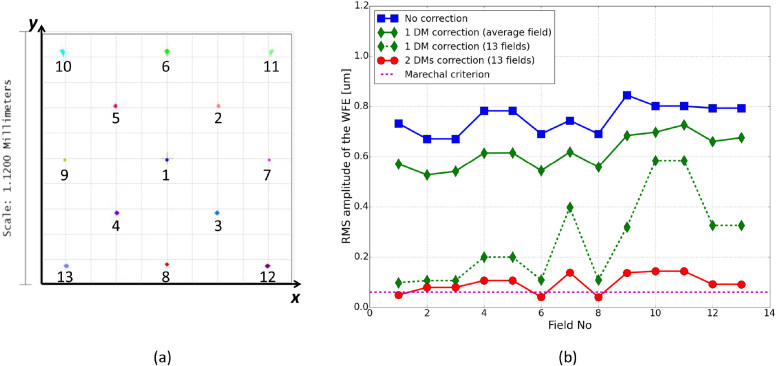
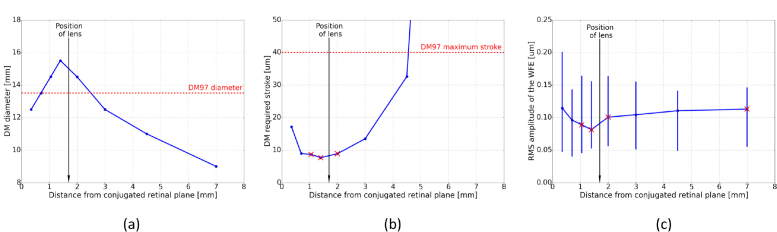
Our AO-SLO set-up originates from a lens-based principle that allows visualization of foveal cones and rods, developed by Felberer et al. [36]. A schematic of the system is shown in Fig. 1 . Typically, AO-SLO instruments have one DM located in a pupil plane [9, 36, 37]. Here, we add a second DM in order to compensate for the aberrations varying within the FoV. Magnetic DMs, from the company Alpao, are used. The DM in the pupil plane is the DM69, with 69 actuators and a diameter of 10.5 mm. The second DM is the DM97, with 97 actuators and a diameter of 13.5 mm. It is located in a convergent beam, and conjugated to a plane in the eye that lies 0.7 mm anterior to the retina. Several positions for this second DM were analyzed with an optical ray-tracing software (Zemax OpticStudio). A model of the set-up was created and the Liou & Brennan eye model [38] was used in the simulation. The optical properties of the eye model impact the outcomes of this study. The Liou & Brennan model was chosen because it is anatomically accurate and the resulting aberrations match normative data of the population. Both DMs were modeled by Zernike surfaces. In order to take into account the number of actuators, Zernike modes up to the 6^th order could be generated with DM69 and up to the 8^th order for DM97 (except piston, tip and tilt in both cases). Thirteen points in the scanned field were considered, by defining different tip and tilt configurations for the scanning mirrors (see Fig. 3(a)). The AO loop was simply simulated by optimizing the Zernike coefficients of the DMs, with the minimization of the root mean square (RMS) amplitude of the WFE as an objective. The choice of the second DM location was based on simulations that are presented in Fig. 2 . This figure shows the evolution of some system characteristics in dependence on the location of the DM in respect to a plane that is conjugated to the retina. Different positions of the DM between the galvanometer scanning mirror (pupil plane) and the focal plane after the next lens L7 (retina plane) were examined. The first constraint is the diameter of our DM97 (13.5 mm). In Fig. 2(a), we can see that for three possible DM locations that lie close to the lens the diameter of our DM is too small which would result in a vignetting of the imaged area. Thus, these locations have to be discarded. The second constraint is the maximum stroke provided by the DM (∼40 μm). Figure 2(b) shows the required stroke to correct for the varying aberrations in the FoV for the different DM positions. A minimum of the required stroke can be found around the position of the lens. A small stroke allocated for the correction is preferable, so that the DM can handle additional WFE in operation. Finally, the correction efficiency is investigated for the different DM locations in order to determine the optimum DM position for our setup. Figure 2(c) shows the RMS amplitude of the corrected WFE over the entire FoV. The best performance (within the available position range) is obtained for a DM that is located in a plane conjugated to a position of 0.7 mm in front of the retina. It is also important to note that the focal length of the different lenses of our instrument were chosen to be long enough to minimize off-axis aberrations, while still providing a reasonable optical path length.

Fig. 1.

Optical design of the MCAO-SLO set up. The different colors show the beam path for different scanning positions. LS: Light Source; FPC: fiber polarization controller; Col: collimator; Pol: polarizer; PBS: polarizing beam splitter; L1: 200 mm focal length lens; I: variable aperture iris; L2: 300 mm focal length lens; DM1: deformable mirror (DM69); L3: 200 mm focal length lens; L4: 100 mm focal length lens; RSM: resonant scanning mirror; L5&L6: 100 mm focal length lenses; GSM: galvanometer scanning mirror; L7: 100 mm focal length lens; DM2: deformable mirror (DM97); L8: 140 mm focal length lens; QWP: quarter wave plate; BS: cube beam splitter; L9: 50 mm focal length lens; P:Pinhole; L10: 50 mm focal length lens; APD: avalanche photo-diode; SH: Shack Hartmann wave-front sensor.

Fig. 3.

(a) Spot diagrams on the image plane for the 13 considered points in the field, obtained with the 2 DMs correction. (b) WFE for these fields, in the 3 correction cases.

Fig. 2.

Simulations for finding the optimum position of the second DM within the set-up. (a) Diameter of the illuminated area during scanning. (b) Evolution of the required stroke. (c) Evolution of correction performance (bars represent the range of RMS within the entire FoV). The red crosses indicate locations that cannot be used because the diameter of the illuminated area is too large for the DM or the required stroke exceeds the maximum stroke provided by DM97.

The entire set-up is illuminated with a superluminescent diode at 840 nm with a 50 nm bandwidth (Superlum BLM-S-840). The light exits a fiber and is collimated before traversing a Glan-Thompson polarizer and a polarizing cube beam-splitter, resulting in linear polarized light. The light then passes through a first telescope, composed of two achromatic lenses, and is reflected by DM69, which is located in a plane conjugated to the pupil of the eye. After traversing a second telescope, the light is reflected by a resonant scanner (GSI Lumonics, resonant frequency of 4 kHz) and sent to a third telescope before being reflected by a galvanometer scanner (Thorlabs GVS011). The light is then incident upon an achromatic lens and is reflected by DM97 before being collimated by another achromatic lens. A quarter wave plate oriented at 45° to the input linear polarization state then results in a circularly polarized light beam entering the eye. The diameter of the beam at the pupil of the eye is 7 mm. The size of the diffraction limited spot on the retina can be calculated considering a Gaussian beam and a 16 mm focal length for the eye. It corresponds to the Airy radius: 1.22λf/D = 2.3μm. The power entering the eye is 650 μW, which is far below the permissible limits for safe illumination of the eye given in the European Laser Safety Standard for a scanning beam at 840 nm [39]. The light is back-scattered from the retina and traverses back through the system. Due to the second passage through the quarter wave plate, the polarization state is perpendicular to the initial state, so the light is reflected by the polarizing beam-splitter. It passes then through a second Glan-Thompson polarizer which blocks back-reflections from lenses. In addition, the variable aperture iris located in the focal plane between the two lenses of the first telescope minimizes reflections from the cornea. The light is then separated into two paths by a 50/50 cube beam splitter. The reflected light is directed to a custom built Shack-Hartmann wave-front sensor (SH), which is located in a plane conjugated to the DM69 and the pupil of the eye. The SH is composed of a lenslet array with 22×22 micro-lenses (Adaptive Optics Associate, 300 μm pitch and 16 mm focal length) in front of a CMOS camera (Pixelink PL-A741, 1280×1024 pixels with a pixel size of 6.7 μm). The transmitted light is focused by an achromatic lens to a 15 μm pinhole. The light exiting the pinhole is focused by a last lens onto an avalanche photo-diode (APD C10508, Hamamatsu). The signal of the APD is recorded at a 10 MHz sampling rate, using a data acquisition board (Gage Digitizers CS14200, Dynamics Signal).

2.2. Control of the deformable mirrors

The two DM system is controlled by using a combination of classical AO (to compensate for pupil aberrations with DM69) and sensorless AO (to compensate for field aberrations with DM97).

The DM69 is controlled using the measurement of the SH. The measured WFE is decomposed onto the DM influence functions basis in order to determine the correction commands [40]. The control loop is operated using the software Alpao Core Engine (ACE). For calibration we performed a procedure that is described in detail in our previous paper [41]. In brief, the influence functions of the DM are recorded, with the scanning mirrors off and a flat mirror instead of the eye pupil. Then the control matrix is computed, with the filtering of the highest 14 eigenmodes (i.e. the inverse of the 14 largest eigenvalues is set to 0 for the inversion of the interaction matrix) in order to increase the stability of the AO-loop. The commands can then be calculated during in-vivo measurement by simply multiplying the measured WFE with the control matrix. The exposure time of the SH is set to 25 ms and 10 WFE measurements are averaged before calculating and applying the DM commands. This way the SH averages twice the WFE over the entire scanned field for each correction iteration. With these conditions, the correction frequency is 4 Hz, as the frame rate of the AO-SLO was set to 8Hz. Finally, the AO loop is closed with a gain of 0.5, allowing a fast convergence of the correction.

The DM97 provides a static correction. However, it compensates for both the field aberrations of the set-up and the anisoplanatism of the eye. The aberrations of the set-up are corrected in a calibration step. Thereby, a flat mirror is placed at the position of the eye pupil and the WFE is measured at different points of the field. The influence functions of this DM are also measured for the different fields, in order to create an interaction matrix including the different points of the FoV. This determines the shape of the DM that is required to compensate for the system aberrations. This shape is then applied prior to an in-vivo measurement. To account for the anisoplanetism if the eye, a sensorless approach is adopted to further optimize the shape of the DM and to minimize aberrations within the FoV. This step is performed after the subject has been aligned and the AO-loop has been closed (with the DM69 in the pupil). Thereby, the AO-SLO image that is displayed in real time is used to determine an image quality criterion which is optimized by applying additional commands to DM97. The criterion assesses the overall image quality and the uniformity of the image. For this purpose, the frame is divided into four quadrants and the standard deviation of the APD signal σ_i is calculated for each quadrant i. The criterion c, defined in Eq. 1, allows the maximization of the sum of these four standard deviations, while minimizing the differences between quadrants. The standard deviation was chosen as a metric as it reliably characterizes both contrast and level of signal.

$$c=\sum _{i=1}^4{\sigma }_i-\sum _{i=1}^3\sum _{j=i+1}^4|{\sigma }_i-{\sigma }_j|.$$ (1)

In order to maximize the criterion, the first five Zernike modes (focus, astigmatisms and comas) are adjusted by the operator of the instrument. The determination of the values of these 5 modes is performed sequentially. First, the focus mode of the DM is changed by the operator until the image criterion reaches a maximum, then the astigmatism is changed the same way, and so on. With this method, adjusting the shape of the DM97 takes a couple of minutes and is performed at the beginning of each imaging session and prior to image recording. In principle this procedure can be automated in order to reduce the amount of time that is needed for this step.

2.3. Measurements

The evaluation of the system performance was done first with a model eye, composed of an achromatic lens (30 mm focal length) and a piece of paper located at its focal plane. Then the right eyes of four healthy volunteers were measured (three males, one female, average age of 30). The refraction error of three volunteers (V1, V2 and V4) is below 0.25 diopters and it is of −1 diopter for volunteer V3. The subject interface of the instrument was a standard head rest. Prior to imaging, the nature and possible risks of the measurement were explained and informed consent was obtained. The evaluation was performed under a protocol approved by the local ethics committee (Medical University of Vienna), which adheres to the tenets of the Declaration of Helsinki. The pupils of the subjects were artificially dilated with one drop of Tropicamide in order to fit the 7 mm diameter but accommodation was not blocked.

One measurement takes ∼6 seconds. In this time 50 frames are recorded. One AO-SLO frame consists of 1000 lines (y-direction) of 1250 pixels (x-direction). During imaging, the AO correction loop is closed with DM69, while the previously optimized DM97 holds its shape (see Sec. 2.2). In post-processing, the recorded frames are motion corrected and averaged to improve the SNR. For this purpose, we apply the method detailed by Akihito et al. [42]. The AO-SLO frames are registered with the ImageJ plug-in bUnwarpJ, which is an elastic registration method using B-splines model [43].

For each subject AO-SLO images were recorded at different locations of the retina and different imaging conditions were compared. Imaging on a 4°×4° FoV was performed either using only the DM69 in the pupil for the AO correction (the second DM was kept flat) or using both DMs. Furthermore, AO-SLO images were also recorded on a small FoV (1°×1°) for a comparison of resolution and image quality. In addition, a larger FoV (10°×10°) image was obtained for one volunteer. It was created by stitching 9 averaged SLO frames, with 4°×4° FoV. The stitching was performed using the MosaicJ plugin from ImageJ [44]. Finally, imaging of vessels and the retinal nerve fiber layer was done in one volunteer, also with 4°×4° FoV.

3. Results

3.1. Simulation of correction performance

As explained in Sec. 2.1, a Zemax model of the system, including the Liou & Brennan model eye [38], was created in order to optimize the design and to predict the correction performance. Figure 3(b) presents the WFE for the different points in the FoV in four cases: no correction (flat DMs), correction with the DM in the pupil using 13 guide stars, correction with the DM in the pupil using one SH which measures an averaged WFE over the FoV and correction with both DMs using 13 guide stars. The RMS amplitude of the WFE is compared to the system diffraction limit, defined as λ/14 = 0.060μm RMS, according to the Marechal criterion [45].

The dotted green line shows the results of the correction made with the first DM (located in a pupil plane) using the measurements of the 13 points in the FoV (i.e. 13 guide stars). We can see that the WFE is significantly improved by this correction but it stays well above diffraction limit especially for larger scanning angles. However, this correction scheme is not very feasible and is not representative of our experimental conditions. Indeed, our DM69 is driven by a single SH measuring an average of the WFE in the scanned field. The solid green line shows the simulation of such a case. The resulting correction is uniform within the FoV but not efficient as the WFE is only decreased by ∼0.2 μm compared to the non-corrected case. Finally, the red line presents the results of the 2 DM correction, using the 13 points in the FoV. It should be noted that this simulation is an approximation to the experimental condition presented in this paper as we use image metrics retrieved from the entire FoV in order to drive the second DM and not the information of 13 guide stars. As can be seen in Fig. 3(b), the correction is both efficient and uniform. With the RMS amplitude varying between 0.025 and 0.132 μm, the WFE over the entire FoV is close to diffraction limit.

3.2. Model eye measurement

In order to test the predictions of the simulation, we performed measurements in the model eye. The recorded AO-SLO images are presented in Fig. 4 , again for the 3 correction cases: no correction (both DMs are flat), DM69 correction and 2 DMs correction. A similar evolution as predicted by the Zemax model can be observed. Due to system’s aberrations, the image quality without correction is poor. It is improved by AO-correction using the DM69 in the pupil but this improvement is only visible on a ring of the image, illustrating the impossibility to handle the aberrations varying within the FoV. Finally, the image recorded with the two DMs correction presents a significantly better image quality, and this on the entire image.

Fig. 4.

AO-SLO images of the model eye. (a) Image obtained without correction. (b) Image obtained by correcting only with DM69. (c) Image obtained with 2 DMs correction. The same grey scale is used for each image.

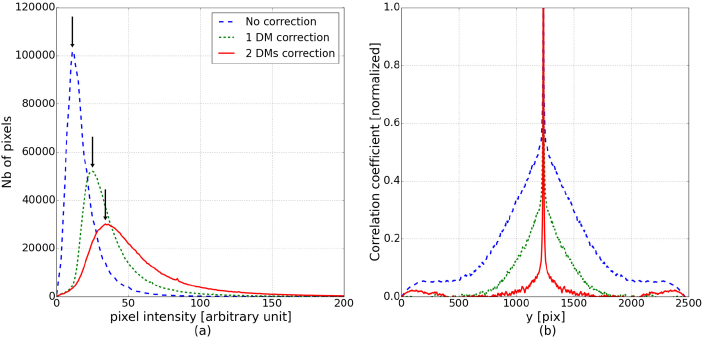
We quantified the improvement of image quality with three characteristics which are summarized in Table 1 . First, the image criterion c, defined in Eq. 1, is computed and we can verify that it is increasing with the number of DMs used for the correction. Second, the distribution of the pixel intensity can be analyzed to assess the overall image quality [9]. Figure 5(a) shows the histograms of the pixel values in the three studied imaging cases and we can see that the maximum value of the distribution is increasing with the number of DMs, illustrating the improvement of the image quality. Finally, the resolution can be assessed by studying the auto-correlation function of each image (see Fig. 5(b)). The full width at half maximum (FWHM) of the auto-correlation peak corresponds to roughly twice the system resolution. The conversion from pixel to μm is done considering the back focal length of the lens of the model eye and the number of pixels covering the entire FoV. In our case one pixel corresponds to 1.4 μm. The FWHM of the auto-correlation function is decreasing while the number of DMs is increasing, demonstrating the improvement of the resolution. With the 2 DMs correction, the measured resolution is ∼5.5 μm, which is close to the theoretical diffraction limit of the system (1.22λ f/D = 4.4μm, for the 30 mm focal length of the model eye).

Table 1.

Comparison of image quality characteristics of the 3 images shown in Fig. 4.

	Image criteria [arbitraty unit]	Max histogram [arbitraty unit]	FWHM auto-cor [μm]
No correction	4556	11	112
1 DM correction	6589	25	20
2 DMs correction	16030	34	11

Fig. 5.

Characterization of the image quality of the three images from Fig. 4. (a) Histogram of the pixel values. The arrows indicate the maximum of the distributions. (b) Vertical section of the auto-correlation function.

3.3. In-vivo measurements, with one DM and two DMs

The same comparison was performed in-vivo. Four eyes of four healthy volunteers were imaged with a 4°×4° FoV in the fovea. First, only the DM in the pupil (DM69) was controlled in a closed loop mode and images were recorded. Then, the shape of the second DM (DM97) was adjusted in order to optimize the imaging performance over the entire FoV. Table 2 presents the value of the image criterion c computed on the different recorded images. A significant improvement of image quality was observed in each case when the field correction was applied using the second DM. As an example, Fig. 6 presents the images obtained for volunteer V1 (see Visualization 1 ^{(9.2MB, tif)} and Visualization 2 ^{(9.2MB, tif)} for the full resolution images).

Table 2.

Image criterion c for the different correction conditions for the right eye of each volunteer (arbitrary unit).

	V1	V2	V3	V4
1 DM correction	22608	21857	18781	12829
2 DMs correction	26350	29347	21702	16153

Fig. 6.

Comparison of the AO-SLO image quality between a 1 DM and 2 DM configuration, for healthy volunteer V1. (a1) Image obtained by correcting only with DM69 (full resolution image available in Visualization 1 ^{(9.2MB, tif)} ). (a2) Image obtained with 2 DMs correction (full resolution image available in Visualization 2 ^{(9.2MB, tif)} ). (b1) Zoom from (a1): 1°×1° at the fovea. (b2) Zoom from (a2): 1°×1° at the fovea. (c1) Zoom from (a1): 1°×1° at 2.2° eccentricity. (c2) Zoom from (a2): 1°×1° at 2.2° eccentricity. The same grey scale is used for each image.

Figure 6 demonstrates the benefit of the 2 DMs correction. We can observe that contrast and resolution are improved. Especially, the region of the fovea seems to be out of focus in the case of one DM correction (Fig. 6(b1)). The same region appears with more contrast on the image recorded with 2 DMs correction and cones can be resolved closer to the fovea (Fig. 6(b2)). Furthermore, at larger eccentricities (for instance the upper right corner), significant distortions can be observed on the image obtained with one DM correction: the cones appear elliptical, indicating astigmatism (Fig. 6(c1)). These distortions are suppressed with the 2 DMs correction (Fig. 6(c2)).

3.4. Comparison of performance between large and small field of view imaging

As the isoplanatic patch of the eye is typically around 1° [18], we regarded the quality of AO-SLO images recorded with a 1°×1° FoV as the reference image quality of our system. Thus, to assess the imaging performance of our large FoV imaging mode (4°×4°), details of the obtained images are compared to the corresponding images recorded with a small FoV (1°×1°). The small FoV images were recorded using only the DM69 in the pupil for the AO correction, corresponding to a classical AO-SLO set-up operation.

Figure 7 presents this comparison for volunteer V2. Figure 7(a) shows the large FoV image obtained with 2 DMs correction. Two small areas of this image are studied in detail: the central area at the fovea (see the zoom displayed in Figure 7(b1)) and one area at an eccentricity of ∼2.1° from the fovea (see the zoom in Figure 7(c1)). Both locations were imaged several minutes before with the small FoV mode and the resulting images are presented in Figure 7(b2)&(c2).

Fig. 7.

Comparison of the AO-SLO image quality between a large FoV and small FoV configuration, for healthy volunteer V2. (a) Image obtained on a 4°×4° FoV at the fovea. (b1) 1°×1° zoom from (a), at the fovea. (b2) Same area recorded with a 1°×1° FoV. (c1) 1°×1° zoom from (a), at 2.1° eccentricity from the fovea. (c2) Same area recorded with a 1°×1° FoV. The same grey scale is used for each image.

Overall, we can observe a better image quality for the small FoV. The resolution is slightly decreased in the case of the large FoV imaging. This is mainly impacting the imaging of the foveal cones: they can be resolved closer from the fovea with the small FoV than with the large one. In the case of the small FoV, the residual WFE, measured by the SH after AO correction, is rather low (RMS amplitude of 0.015 μm, simulations of the AO correction within the small FoV yielded 0.007 μm). This measured residual WFE is larger for the large FoV, which explains part of the resolution loss. Indeed, the SH measures a RMS amplitude of ∼ 0.16 μm, which corresponds to an average of the WFE over the entire FoV. From the simulations, an average WFE of 0.096 μm RMS was expected. The discrepancy between simulations and measurements mainly comes from the difference between the Liou & Brennan model eye and the characteristics of the measured eye. Moreover, noise, misalignments and real DMs’ influence functions were not modeled. However, the order of magnitude of the amplitude of simulated and measured WFE is in accordance and is explained by the fact that we are performing a uniform correction over a large FoV (see Sec. 3.1). Also, both images (small and large FoV) have the same number of pixels, so there is a factor of 4 between their sampling. The lower sampling density of the large FoV also limits the resolution. Finally, the contrast appears better for the small FoV imaging. This is simply due to the fact that less light is available from the same area for the large FoV scan. Despite this contrast difference, the same structure can be observed in both images (except for the foveal cones).

3.5. 10°×10° FoV obtained by image stitching

In order to provide an image of a 10°×10° FoV at the fovea, nine images were acquired at different locations of the retina, for volunteer V3. After averaging, the acquired images were stitched together and the result is presented in Fig. 8 . The measurement time to obtain such an image (including subject alignment and FoV correction) is about 10 minutes. For comparison, if we consider an AO-SLO instrument with a FoV of 1.5°×1.5°, obtaining an image of the same area requires the stitching of ∼100 images. The measurement and processing time would then be at least multiplied by a factor 10. Moreover, the larger FoV allows the reduction of the number of overlapping areas which increases the overall quality of the image.

Fig. 8.

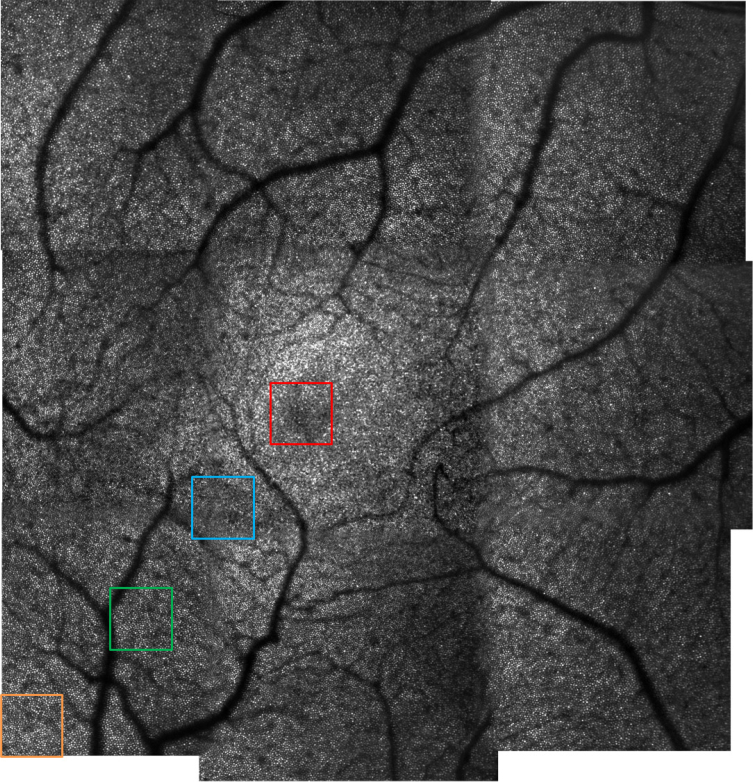
AO-SLO image of healthy volunteer V3, on a 10°×10° FoV (full resolution image available in Visualization 3 ^{(18MB, tif)} ). Nine 4°×4° FoV were stitched together for the final image.

We can observe that the resolution is high and uniform over the entire image. However, due to the size and limited sampling density of the figure, the visibility of small details cannot be fully appreciated. For this purpose, Visualization 3 ^{(18MB, tif)} provides the full resolution image. In addition, Fig. 9 presents 0.7°×0.7° details of the image, for different eccentricities from the fovea, together with the corresponding Fourier transformation. Yellot rings can be observed in each case and the evolution of the ring’s radius with the eccentricity indicates the variation of the cones density [46]. Finally, the shadows of vasculature of the retina can clearly be seen on the large FoV image.

Fig. 9.

(a1),(b1),(c1),(d1) Regions of interest of 0.7°×0.7° obtained from the full resolution image displayed in Fig. 8. The different regions are color coded in accordance with Fig. 8. (a2),(b2),(c2),(d2) FFT of these 4 regions. The arrows point to Yellot rings.

3.6. Imaging of different retinal layers

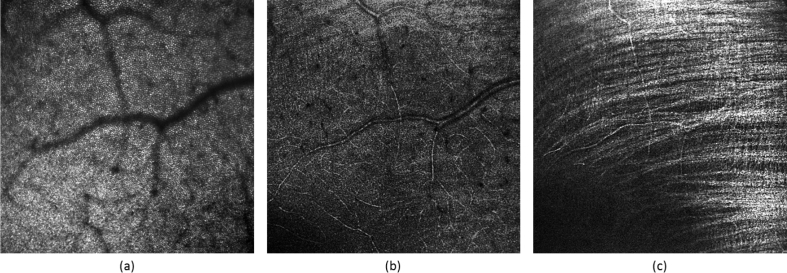
By changing the focus on the DM69 in the pupil plane, the focal plane of the system is changed and different layers of the retina can be imaged. Figure 10 presents images of the photoreceptor layer, a vasculature layer and the retinal nerve fiber layer (RNFL), acquired at 2.5° eccentricity from the fovea, in volunteer V4.

Fig. 10.

AO-SLO images obtained on a 4°×4° FoV at a 2.5° eccentricity from the fovea of healthy volunteer V4, for three different retinal layers. (a) Focus set to photoreceptor layer. (b) Focus set to anterior vasculature layer. (c) Focus set to retinal nerve fiber layer.

As presented in the previous sections, the cone photoreceptor mosaic can clearly be identified in Fig. 10(a). Moreover, small capillaries of the retina can be visualized in Fig. 10(b). Finally, the orientation of the individual nerve fiber bundles can be observed in Fig. 10(c).

4. Discussion

We have presented an AO-SLO system providing high resolution images of the retina on a 4°×4° FoV. It uses two DMs and one SH. With such a system, imaging of a relatively large area of the retina (patch of ∼1.2 mm × 1.2 mm) is possible in reasonable time (less than 5 minutes from subject alignment to acquisition of multiple SLO frames). Compared to conventional AO systems, the instrument design stays relatively simple. Apart from the second DM, there are no guide stars or additional wave-front sensors needed.

The variability of the image criterion c is an interesting indicator of the stability and robustness of the AO loop. In order to test the reproducibility of the imaging performance of our set-up we evaluated this image quality metric within one imaging session and at different measurement days. In one imaging session (4°×4° FoV) 150 AO-SLO frames are recorded over a period of ∼5 minutes (3 data-sets of 50 frames recorded in 6 seconds). For the four healthy volunteers, we found a variability of the criterion of ∼8% when a single DM is used for the correction. Using the 2 DM configuration, this variability is reduced to ∼4%. Both cases illustrate a good reproducibility of the imaging performance. In addition, the evaluation shows that the 2 DM configuration provides better correction stability over time. In order to test the long term reproducibility, healthy volunteer V3 was measured on five different days that were distributed over a period of 5 months. For the analysis image data from an imaging session were averaged and the criterion was calculated for the final averaged frame. The variability of the criterion between the AO-SLO images recorded at the different time points was varying less than 0.1%.

Although the obtained image quality is already satisfactory, it could be further improved with a better control of the DMs. Temporal fluctuations of ocular aberrations occur at high frequency, around 30 Hz [4,47], and it was shown that it is beneficial for the correcting loop to operate at higher frequency, around 90 Hz [48]. In addition, a fast system is less sensitive to eye motion, which facilitates image registration and improves imaging performance. With this in mind, the correction frequency of our AO loop is low, as we have to wait until the entire scanned field has been measured by the SH to control the DM69 in the pupil, which is essential to ensure a stable AO loop. The correction frequency can be increased by a faster AO-SLO frame acquisition speed through the implementation of a faster resonant scanner. Alternatively, the WFE measurement can be performed using a guide star that is not scanned over the entire FoV. This decouples the WFE measurement from the AO-SLO frame rate and could be an option for high speed AO correction. In this case, the wave-front sensing would be the limiting factor for the correction speed. If this solution is chosen, the ratio between number of actuators of the DM in the pupil and number of lenslets of the SH would need to be minimized, in order to reduce the exposure time on the SH and the computation time [41].

In our experiment we used part of the imaging light for wave-front sensing. Thus, it is interesting to discuss the use of a guide star (or several guide stars) and to analyze the implications on the imaging performance. The introduction of a single guide star will only improve the WFE in a small FoV. For instance, a guide star that is located in the center of the FoV enables a good correction only on the central part of the image. Compared to the case using the averaged WFE, we expect a better correction (and associated image quality) centrally but poorer performance in the rest of the FoV. Thus, both configurations will yield limited image quality when only 1 DM is used. In the 2 DM configuration, WFE variations within the FoV will be corrected which will most likely result in comparable image quality of both wave-front sensing methods as the averaged WFE will be very similar to the WFE in the central part of the FoV. However, adding more guide stars may provide a better performance even in the case of using 1 DM. In the simulations presented in Fig. 3(b), we can see that using the information of 13 guide stars yields a much lower WFE than using a WFE averaged within the FoV. Nevertheless, the correction performance is still poorer than in the case of 2 DMs. This is quite pronounced for fields that are more off-axis. So, we can say that the number and position of guide star(s) significantly impact the correction performance of the system. However, adding guide stars certainly increases system complexity and operation. In addition, the calibration of non-common path errors can be challenging.

Another aspect that we want to emphasize here is that the contrast of the acquired images could be improved by increasing the power of the light entering the eye. Indeed, as we perform a fast scan of a large area of the retina, the safety limit is higher than in conventional small FoV AO retinal imaging.

Finally, the sensorless approach to control the second DM97 is not optimal: the criterion on the image is not evolving only due to the change of shape of the DM but also because of eye motions. A pupil tracker would limit the impact of these eye motions and would help to better control this DM. Also, instead of using the DM97 in a static mode, it could be controlled in closed loop during the measurement. As the sensorless AO technique is rather slow, the actuation frequency would be limited and the benefits of this approach might be minimal. If a real-time correction of the anisoplanatic effects is required, an approach with several guide stars and wave-front sensors could be more adequate [34]. Another limitation of sensorless AO will occur when imaging of pathological eyes is performed. Indeed, some retinal pathologies will impact the image metric and complicate the optimization of the shape of the DM97. To make the system more robust, the sensorless AO step at the beginning of the imaging session could be suppressed. Instead, the WFE of the eye could be measured beforehand at different incident angles. Thus, the shape of the DM correcting for these errors could be deduced and set before the measurement.

Theoretically, the FoV of the instrument could be further increased, still using the same concept. Currently, the size of the second DM is a limitation as it has to accommodate the entire scanned field. Thus, a larger DM diameter would be required to support a larger FoV. Another possibility is to move the DM closer to the pupil plane (cf. Fig. 2). However, this would require a DM with more stroke and lead to slightly degraded correction performance. An additional limitation to the FoV size is the sampling density, which is already at the lowest acceptable value for the current FoV. A larger FoV would require more measurement points, which would take a longer time to acquire (with our current scanning frequency). Under this condition, eye blinks and motion artifacts would have a more significant impact on the image processing and quality. From Zemax modeling, we can conclude that satisfactory wave-front correction can be obtained for FoV up to 7°×7°, with the 2 DM concept. For larger FoV, the residual WFE is too high to allow satisfactory image quality. A third DM would be needed to reach optimal performance [33]. These simulation results are in agreement with previous studies by Thaung et al. and Popovic et al. [34,35]. The fundus camera developed by this group allows imaging of a larger FoV than our AO-SLO (7°×7°). However, a different imaging technique is used and the system is operated in the visible range (575 nm) with a smaller pupil diameter (6 mm).

There are many design parameters impacting the performance of an AO-SLO set-up. For instance, we have used refractive telescopes, while many set-ups prefer reflective telescopes. In principle, the concept of 2 DMs can be translated to reflective telescopes. However, simulations need to be performed for a specific instrument. The magnification of the different telescopes also impacts the aberrations of the set-up, so are the focal lengths of the optical elements. One benefit of having a second DM for the conception of an instrument is a large flexibility in order to minimize off-axis aberrations, even for a relatively simple optical design. Moreover, it offers some advantages in terms of system integration, as it is able to compensate for possible misalignments.

Due to its location, the DM applying the field correction is also inducing some field distortions. With the Zemax model, distortion grids were computed with and without the second DM and we found that the induced distortions were negligible.

Although the concept was demonstrated for our lens based AO-SLO, it can be easily translated into state of the art AO systems, including AO-OCT. It only requires one additional DM, which should be placed between two telescope lenses.

5. Conclusion

The developed AO-SLO system is a step forward towards high resolution imaging of larger areas of the retina. The concept of multi-conjugate adaptive optics was adapted to provide close to diffraction limit performance of an AO-SLO instrument using a 7 mm pupil diameter on a 4°×4° field of view. Two deformable mirrors allow compensation of not only pupil aberrations, but also isoplanatic effects of the eye and the set-up. The DM69 in the pupil is operated in closed loop and the measurement from a Shack-Hartmann wave-front sensor is used to drive its shape. The DM97 is used to compensate for the field effect, it is controlled using a sensorless adaptive optics approach. Its shape is adjusted by maximizing a criterion characterizing both image quality and uniformity.

Four healthy volunteers were successfully imaged on this set-up, demonstrating the imaging performance of the developed concept.

Funding

The authors acknowledge the following sources of fundings: the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 701859; the Austrian Science Fund under the FWF project P22329-N20; the macula vision research foundation.

Disclosures

MP and MS: Imagine Eyes (F).