Abstract
Vision begins when light isomerizes the photopigments within photoreceptors. Noninvasive cellular-scale observation of the structure of the human photoreceptor mosaic is made possible through the use of adaptive optics (AO) enhanced ophthalmoscopes, but establishing noninvasive objective measures of photoreceptor function on a similar scale has been more difficult. AO ophthalmoscope images acquired with near-infrared light show that individual cone photoreceptor reflectance can change in response to a visible stimulus. Here we show that the intrinsic response depends on stimulus wavelength and intensity, and that its action spectrum is well-matched to the spectral sensitivity of cone-mediated vision. Our results demonstrate that the cone reflectance response is mediated by photoisomerization, thus making it a direct measure of photoreceptor function.
OCIS codes: (330.5310) Vision - photoreceptors, (330.4270) Vision system neurophysiology, (330.4300) Vision system - noninvasive assessment, (330.4460) Ophthalmic optics and devices
1. Introduction
To probe the functional state of photoreceptors in vivo, researchers and clinicians alike have traditionally relied on electroretinograms or microperimetry. While these techniques are sensitive to substantial photoreceptor loss, they have insufficient resolution to discern functional changes on the scale of individual cones. AO-enhanced ophthalmoscopes have the resolution necessary to observe the human photoreceptor mosaic at a cellular scale [1–4], but are currently used primarily to analyze the structural arrangement of photoreceptors. While quantifying a cone mosaic's structure is one approach to evaluating photoreceptor integrity, functional correlates are difficult to establish with conventional tests of visual function [5–8]. Thus, a concomitant cellular-scale measurement of visual function is needed.
Recently, near-infrared AO ophthalmoscope images obtained from the human eye have shown that cone photoreceptor reflectance [9–11] and optical path length [12] change in response to a visible stimulus [9–12]. The origin of this stimulus-evoked change in cellular reflectance is not known; one hypothesis is that the intrinsic response arises from subtle morphological/biophysical changes in cones induced by isomerization of cone photopigment [9] (see also [13]). Alternatively, the intrinsic response could be an energy dependent response unrelated to phototransduction. It is known, for example, that retinal pigment epithelium cells exhibit reduced autofluorescence after exposure to high photic energies [14] and a priori it seems possible that energy-induced changes could also occur within cone cells.
If the intrinsic reflectance response is initiated by phototransduction, we would expect that it would be governed by known properties of vision. Specifically, we know that phototransduction begins when a photon isomerizes photopigment molecules. A characteristic signature of photopigments is their action spectrum - the relative efficiency with which incoming photons of different wavelengths cause isomerization. In the human retina, there are three spectral classes of cones, categorized by their long (L), middle (M), or short (S) wavelength sensitivities. The L and M cones predominate, comprising approximately 93% of cones in the human cone mosaic [15], with L cones outnumbering M cones by a factor of about 2:1 on average [16–18]. If we neglect the relatively small number of S cones and account for pre-retinal absorption as well as photopigment self-screening, we can characterize the visual system’s overall spectral sensitivity for daylight light levels as a weighted average of the L and M cone sensitivities, where the weights are determined by the L:M ratio in the cone mosaic. This weighted average, for a typical eye, is called the phototopic luminosity function [19]. If the intrinsic reflectance response is governed by phototransduction, the action spectrum of the aggregate reflectance response should, to first order, follow the luminosity function. To test this prediction, we developed a method to extract clear, reliable, and quantifiable intrinsic responses, and used it to determine if stimulus-evoked changes in cone reflectance are mediated by phototransduction.
2. Methods
2.1 Human subjects
This research was approved by the Institutional Research Board at the University of Pennsylvania, and was conducted in accordance with the tenets of the Declaration of Helsinki. Five subjects with normal vision were recruited for this study (age range: 25-56). Subjects provided informed consent after the nature and possible risks of the study were explained. Each subjects’ pupil was dilated and accommodation arrested using one drop of tropicamide (1%) and, if necessary, phenylephrine (2.5%).
2.2 Imaging the photoreceptor mosaic
The photoreceptor mosaic was imaged using a previously described adaptive optics scanning light ophthalmoscope (AOSLO) [3], with a ~2 µm Rayleigh resolution. Image sequences were acquired from a photomultiplier tube using a 795 nm super-luminescent diode with a full-width at half-maximum bandwidth (FWHM) of 15.3 nm. We estimated the coherence length of the 795 nm imaging source to be 13.6 μm, assuming a cone outer segment with a refractive index of 1.43 [20]. This is roughly half of the typical outer segment length (~35 μm) of cones in the retinal region that we studied [21]. Cones were stimulated using a super-luminescent diode at 675 nm (Superlum Ireland; Carrigtwohill, County Cork, Ireland), and a SuperK EXTREME super-continuum laser (NKT Photonics; Birkerød, Denmark). Image sequences were obtained 0.71° from the center of fixation (0.5° temporal and 0.5° superior for four subjects, 0.5° nasal and 0.5° superior for one subject) at a rate of 16.6 frames per second, using a 1x1° field of view.
Each imaging trial consisted of two minutes of dark adaptation, four seconds of pre-stimulus recording, a two-second stimulus delivered to half of the imaging field (1° wide by 0.5° high), and nine seconds of post-stimulus recording, resulting in 249 images per sequence. Across trials, the stimulus was varied in both wavelength and intensity. Four of the stimulus wavelengths (480, 510, 550, 590 nm) were delivered using the super-continuum laser, with a 10 nm FWHM for 510, 550, and 590 nm wavelengths, but a 30 nm FWHM at 480 nm. The 675 nm (8.5 nm FWHM) stimulus was delivered using the super-luminescent diode. For each wavelength, we used up to four different stimulus intensities tailored to produce a range of intrinsic reflectance responses. The highest stimulus intensity at 480 nm required use of a 30 nm rather than a 10 nm FWHM, and was the maximum irradiance obtainable at that wavelength. We gated stimulus delivery using an acousto-optic modulator (AOM; Brimrose Corporation, Sparks, MD, USA). We repeated each combination of stimulus wavelength and intensity (hereafter referred to as a “stimulus condition”) for six trials. Even when the AOM was gated “closed”, a small quantity of stimulus “leak” still passed through the system (~0.01% of the input irradiance), so that the leaked light for the nominally unstimulated condition varied with stimulus wavelength and irradiance. Thus we acquired two unstimulated (control) image sequences per wavelength and irradiance condition. For each control trial, the cones were illuminated with 90 µW of 795 nm imaging light combined with 8 µW of 848 nm (FWHM 26 nm) light for wavefront sensing and the leaked light for that condition.
2.3 Processing the image sequences
To correct for static intra-frame distortion from the sinusoidal motion of the resonant optical scanner, we estimated the static spatial distortion after each imaging session from images of a stationary Ronchi ruling and resampled each frame over a grid of equally spaced pixels. Next,a minimally distorted frame was selected from within each of the “desinusoided” 795 nm image sequences and used as the reference frame for strip-based registration [23]. If fewer than 60% of the images within the sequence aligned (had a positive normalized cross correlation) to any reference frame, then the image sequence was removed from further consideration. 18% of the image sequences were removed in this manner, leading to an average of 4.9 trials being used for further analysis at each stimulus condition (range: 2-6). Following strip registration, a frame-wide affine registration was performed to remove residual torsion. The fully registered image sequences were cropped to a common area, and cone locations were identified [24] within an image generated from the average of all cropped frames (Fig. 1(A)).
Fig. 1.
The steps taken to determine which cones were included for reflectance analysis. A) The average image (cropped to 113x113 µm [~0.4x0.4°] for visualization) from the top half of a stimulus trial’s image sequence, with overlaid cone locations. For each image sequence, we created a map of the extent of the stimulus delivered to the photoreceptors (B), color coded to indicate the percentage of the total stimulus that was delivered to each retinal region. Warmer colors correspond to a delivery of a greater percentage of the stimulus. Cones that received greater than 90% of the stimulus were categorized as ‘stimulated’ cones; cones that received less than 90% of the stimulus (dashed line) were excluded from analysis. (C) A map of the categorized cone locations. Red points label stimulated cones and orange points label excluded cones. After the cells were categorized, a motion contrast image (D) was generated using Tam et al.’s algorithm [22]. The motion contrast image was thresholded to create a mask (E) of the capillaries present in the image. (F) This mask was used to further exclude cones (additional orange points) underlying capillaries. The remaining stimulated cones (red points in (F) were used in subsequent analyses. Scale bar is 30 µm.
Because the eye is constantly in motion, even for fixating subjects, cones along the border of the imaging field might not receive the full two-second stimulus. For each stimulus image sequence, we classified which cones were stimulated by determining whether the cone was within the stimulated portion of the 795 nm image sequence for at least 90% of the registered frames (Fig. 1(B)). Cones that did not receive at least 90% of the stimulation as determined by this method were excluded from further analysis (Fig. 1(C)). For both stimulus and control image sequences, we excluded cones underlying retinal capillaries by highlighting the vasculature present within each image sequence using a modified version of apreviously described algorithm (Fig. 1(D)) [22]. A binary mask was created from this “motion contrast” image by thresholding at a criterion defined as two standard deviations greater than the sequence’s mean (Fig. 1(E)). Cones falling within the mask were also excluded from the analysis (Fig. 1(F)). On average, 665 (range: 219-1,837) cone signals were analyzed per trial.
2.4 Extracting the reflectance signal
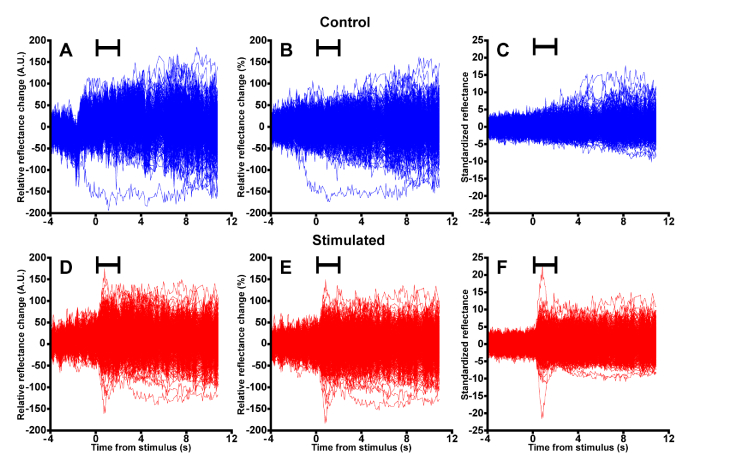
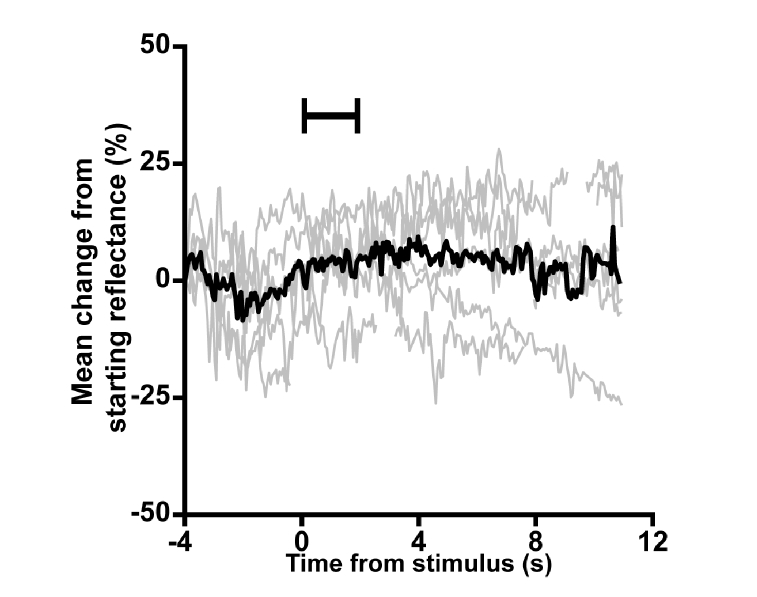
A 2-dimensional reflectance signal (reflectance vs time) for each cone was created by first projecting a 3x3 pixel column through the aligned image sequence at each included cone location and then averaging the 9 (3x3) pixels in each frame. In a preliminary analysis (Appendix Fig. 9), we found that the mean of the aggregate cone signals did not exhibit a stimulus-evoked change. Rather, the effect of stimulation was to increase the variability of the reflectance. To quantify the stimulus-evoked component of the variability observed in the image sequences, we adopted the process described below.
First, to correct for frame-wide changes in image intensity (due to tear film disruption, microsaccades, and changes in AO correction quality), each cone’s reflectance for each frame (Fig. 2(A), 2(D)) was divided by the mean reflectance of the same frame of all analyzed cones
| (1) |
where is the scaled reflectance of a cone as a function of time , and is the mean reflectance for the same frame of all analyzed cones (Fig. 2(B), 2(E)). Second, it is a well-known feature of cone reflectance images that there is cone-to-cone variation in reflectance of unknown origin [25, 26]. To remove this stimulus-independent source of variation from our signals, each cone signal was standardized with respect to its own pre-stimulus mean and standard deviation
| (2) |
where is the scaled, standardized reflectance signal from cone as a function of time , is the pre-stimulus reflectance mean for cone , and is the standard deviation of the pre-stimulus reflectance of cone (Fig. 2(C), 2(F)).
Fig. 2.
The pre-processing steps used to standardize each cone’s reflectance. Raw cone reflectance signals were extracted from each included cone for the control (A, 569 cones) and stimulated (D, 675 cones) image sequences. For visualization here, we display each cone’s reflectance signal relative to its starting value. To remove the effect of frame-to-frame changes in image intensity, each cone’s reflectance was scaled by the mean cone reflectance at each time point for the control (B) and stimulated image sequences (E). As in (A) and (D), each cone’s reflectance signal is relative to its starting value for visualization only. (C, F) Finally, individual cone reflectance signals were standardized to their pre-stimulus behavior by subtracting each cone’s pre-stimulus mean from itself, then dividing by its pre-stimulus standard deviation. Stimulus duration indicated by the black bars.
2.5 Analyzing the reflectance signals
Because we observed that the intrinsic response was heterogeneous within and across cones (see Results), we developed a statistical measure to capture a population response. We calculated the standard deviation across all cones’ standardized cone reflectance signals at each time point for each trial. The pooled variance of all control trials was subtracted from the pooled variance of all stimulated trials. The square root of the result was taken as the measured intrinsic reflectance response, which we denote as .
For the purpose of quantifying the intrinsic reflectance response, a piecewise parametric function consisting of a gamma probability density function and an exponential decay function was fit to
| (3) |
where the fit was defined by a gamma probability density function for times less than the fit maximum at time , and an exponential decay function for times greater than or equal to . was determined such that the upper (gamma) and lower (exponential) parts of the piecewise function maintained the same maximum value at time . To fit the signal peak, the gamma fit parameters (amplitude), (scale), (shape), and (delay) were allowed to vary. The value of was the prestimulus mean of the signal. To fit the signal falloff, exponential fit parameters (amplitude) and (decay constant) were allowed to vary. Peak amplitude was then extracted from each fit, defined as the difference between the fit maximum () and the prestimulus mean.
To obtain a reasonable estimate of measurement variability, we bootstrapped the above process for each subject and condition. To create a single bootstrapped signal, we first randomly sampled with replacement the response at each time point over all trials of a given condition times (where is the number of trials containing data at time ) for both stimulated and control image sequences. The bootstrapped samples were then combined using pooled standard deviation, and the pooled standard deviation of the control data was subtracted from the stimulated data. This bootstrapped reflectance response was fit with a piecewise function and the amplitude was extracted as described above. This process was repeated 1,000 times, creating a distribution of bootstrapped amplitudes for each subject and condition. The measurement variability was estimated from the 5th and 95th percentiles of each distribution.
2.6 Determining the action spectrum of the reflectance response
We determined the action spectrum for each subject by fitting the amplitude-irradiance functions from each wavelength with a sigmoid function
| (4) |
where is the sigmoid fit of the amplitude as a function of the log-irradiance , is the saturating amplitude, is the slope, and is the irradiance shift (on the log scale) for a given wavelength . For each subject, five sigmoidal functions were fit simultaneously to the amplitude-irradiance functions for the five wavelengths. During fitting, a single , a single and five wavelength shifts (one per wavelength) were varied to obtain the best fit to the whole data set (all five measured amplitude-irradiance functions). This created a set of fit amplitude-irradiance functions for each subject with the same shape (on a log irradiance axis) across wavelengths. To obtain the action spectrum, we then calculated from the fitted amplitude-irradiance functions the irradiance shift for each wavelength relative to the 550 nm irradiance shift. To account for variability in 550 nm data, we performed a vertical shift of each subject’s action spectrum on a log sensitivity axis, minimizing the root mean square error between our observed data and the human log-luminosity function.
To obtain an estimate of the variability in each action spectrum, we bootstrapped our analysis. Drawing from the distribution of amplitudes created for each subject and condition obtained through the bootstrapping amplitude analysis, we randomly selected a bootstrapped amplitude for each stimulus intensity and wavelength. We then repeated the process described above 1,000 times and extracted the 5th and 95th percentiles to obtain an estimate of the variability associated with each subject’s action spectrum.
3. Results
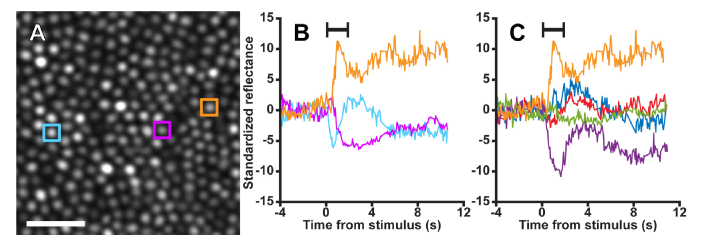
We found that the reflectance of cones changed following visible light stimulation (Fig. 3). After extracting the standardized intrinsic reflectance response of cone photoreceptors (Eq. (2), we observed that the intrinsic cone reflectance signals were highly heterogeneous: some cones increased their reflectance (Fig. 3(B); orange profile), others decreased their reflectance (Fig. 3(B); purple profile), and others oscillated (Fig. 3(B); cyan profile). Moreover, the form of the response from an individual cone could differ across trials, and not all cones showed a clear response on all trials (Fig. 3(C)).
Fig. 3.
Individual infrared cone reflectance responds idiosyncratically to visible light stimulation (See also Visualization 1 (5.5MB, mp4) ). A) A 58x58 µm cropped section of an image of the cone mosaic exposed to a two-second, 390 nW/degree2 (2.2·104 cd/m2) 550 nm stimulus in subject 11015. B) Cones’ reflectance signals responded to the stimulus in a highly variable manner. Some cones increased their reflectance (orange profile) in response to the stimulus, others decreased their reflectance (purple profile), and some oscillated (cyan profile). C) The reflectance response of a single cone was also heterogeneous across trials. While the reflectance in the first trial increased (orange profile), following trials decreased (purple profile), increased (red, blue profiles), and showed minimal to no change (green profile). Stimulus duration indicated by the black bar. Scale bar is 15µm.
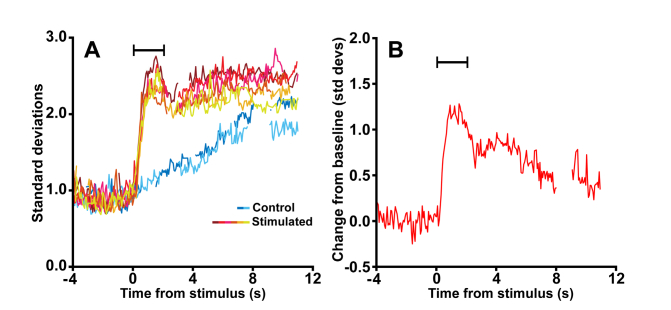
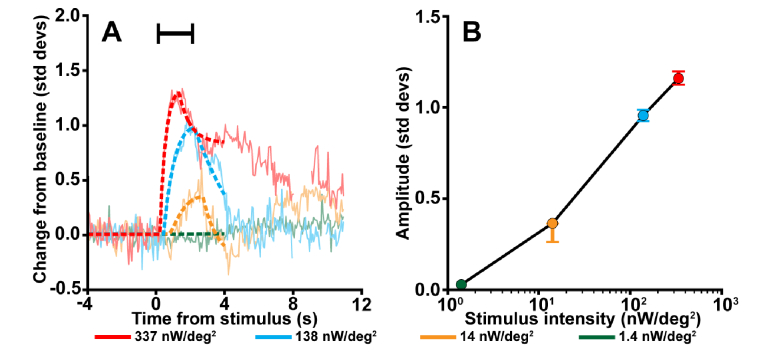
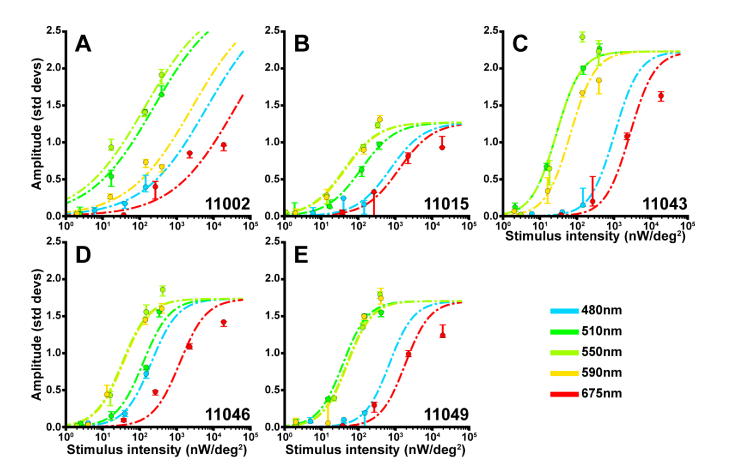
Despite this heterogeneity, all cone populations showed a measurable aggregate intrinsic reflectance response (Fig. 4) when it was quantified using our approach. This response was clear and reliable across trials for both stimulated and control conditions, allowing us to pool the results from multiple trials to obtain a final intrinsic reflectance response for each condition (Fig. 4(B)). The intrinsic reflectance response systematically increased with stimulus intensity (Fig. 5(A)). Extracting the amplitude from the piecewise parametric fit showed an increase in response amplitude with stimulus irradiance (Fig. 5(B)). This relationship held for most wavelengths for all subjects tested (Table 1).
Fig. 4.
The aggregated cone reflectance response. The figure shows the cone intrinsic reflectance response measured from the stimulated and control trials using all data from the condition illustrated by Fig. 3. (A) Repeat control and stimulated trials show a clear, measureable and reliable intrinsic reflectance response. The baseline is centered at 1 because Eq. (2) standardizes the response to the mean and standard deviation of the stimulus behavior. The warmer colors correspond to stimulated trials and the cooler colors correspond to control trials. (B) All trials for a given condition were then combined using pooled standard deviation, and the stimulus-evoked intrinsic reflectance response was taken as the difference between the stimulated and control pooled standard deviations. Signal gaps correspond to frames within each image sequence where the cone reflectance could not be measured due to failed registration (e.g. resulting from blinks or excessive eye motion). Stimulus duration indicated by the black bar. Data shown are from subject 11015 using a 550 nm, 337 nW/deg2 stimuli.
Fig. 5.
The cone reflectance response increases with stimulus irradiance. A) The reflectance response as a function of time for four stimulus intensities, overlaid with piecewise function fits (dotted lines; Formula 3). The reflectance response amplitude was extracted from each function by subtracting the mean prestimulus value from the peak fit value. As the intensity of the stimulus increased, the amplitude of the response also increased. Moreover, a more intense stimulus appeared to cause the peak of the intrinsic response to occur earlier in time with a steeper response slope. Stimulus duration indicated by the black bar. (B) The reflectance response amplitudes from (A) as a function of stimulus intensity. Data shown are from subject 11015 using 550 nm stimuli. Error bars delineate the 5th through the 95th percentile of the bootstrapped values.
Table 1. Reflectance response amplitudes averaged over all trials of a stimulus condition for each subject.
| 480 nm | 510 nm | 550 nm | 590 nm | 675 nm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sex | Age | Irradiance (nW/deg2) | Amplitude | Irradiance (nW/deg2) | Amplitude | Irradiance (nW/deg2) | Amplitude | Irradiance (nW/deg2) | Amplitude | Irradiance (nW/deg2) | Amplitude | |
| 11002 | F | 36 | 6 | 0.07 | 2.4 | 0.03 | 2.2 | 0.02 | 2 | 0.03 | 37 | 0.02 |
| 40 | 0.17 | 17 | 0.54 | 17 | 0.93 | 16 | 0.26 | 266 | 0.40 | |||
| 145 | 0.40 | 140 | 1.41 | 138 | 1.41 | 147 | 0.73 | 2,260 | 0.85 | |||
| 390 | 1.65 | 390 | 1.91 | 398 | 0.67 | 18,900 | 0.97 | |||||
| 11015 | F | 26 | 6 | 0.04 | 1.9 | 0.06 | 1.4 | 0.06 | 2.1 | 0.04 | 37 | 0.05 |
| 40 | 0.24 | 17 | 0.13 | 14 | 0.28 | 14 | 0.26 | 266 | 0.33 | |||
| 145 | 0.16 | 124 | 0.63 | 138 | 0.94 | 141 | 0.90 | 2,260 | 0.81 | |||
| 370 | 0.98 | 337 | 1.23 | 384 | 1.31 | 18,900 | 0.92 | |||||
| 11043 | M | 34 | 6 | 0.03 | 2.1 | 0.12 | 2.5 | 0.02 | 2.1 | 0.06 | 37 | 0.00 |
| 40 | 0.06 | 15 | 0.67 | 18 | 0.64 | 16 | 0.34 | 266 | 0.20 | |||
| 145 | 0.15 | 148 | 2.00 | 140 | 2.42 | 140 | 1.67 | 2,260 | 1.08 | |||
| 409 | 2.27 | 389 | 2.23 | 395 | 1.84 | 18,900 | 1.63 | |||||
| 11046 | M | 57 | 4 | 0.05 | 2.5 | 0.04 | 1.5 | 0.01 | 4 | 0.02 | 37 | 0.09 |
| 42 | 0.18 | 17 | 0.15 | 16 | 0.43 | 13 | 0.43 | 266 | 0.47 | |||
| 150 | 0.72 | 150 | 0.81 | 150 | 1.56 | 142 | 1.45 | 2,260 | 1.08 | |||
| 340 | 1.56 | 420 | 1.86 | 398 | 1.60 | 18,900 | 1.42 | |||||
| 11049 | M | 30 | 5 | 0.08 | 2.1 | 0.05 | 2.2 | 0.00 | 2 | 0.06 | 37 | 0.00 |
| 40 | 0.10 | 15 | 0.48 | 22 | 0.39 | 15 | 0.08 | 266 | 0.30 | |||
| 147 | 0.19 | 148 | 1.51 | 130 | 1.35 | 142 | 1.50 | 2,260 | 0.99 | |||
| 409 | 1.55 | 382 | 1.79 | 404 | 1.74 | 18,900 | 1.24 | |||||
| Average | 36.6 | 5.4 | 0.04 | 2.2 | 0.06 | 1.96 | 0.03 | 2.44 | 0.07 | 37 | 0.02 | |
| 40 | 0.11 | 16.2 | 0.36 | 17.4 | 0.56 | 14.8 | 0.35 | 266 | 0.36 | |||
| 146.4 | 0.35 | 142 | 1.26 | 139.2 | 1.57 | 142.4 | 1.25 | 2,260 | 0.95 | |||
| 383.6 | 1.64 | 383.6 | 1.78 | 395.8 | 1.42 | 18,900 | 1.14 | |||||
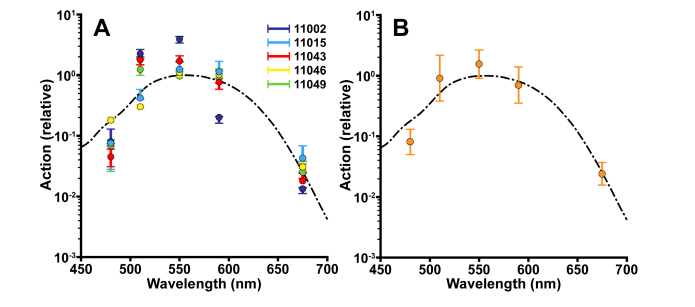
In addition to stimulus intensity, the intrinsic reflectance response depended on stimulus wavelength. The dependence is shown in Fig. 6, where we plot each subject’s peak amplitude from the fit for all stimulus wavelength/irradiance combinations on a common irradiance axis. From the data, we then found the action spectrum for each subject (determined from the horizontal shift between the sigmoid fit at each stimulus wavelength and the sigmoid fit for the 550 nm stimuli, see Methods) was well-matched to the human photopic luminosity function (Fig. 7).
Fig. 6.
Intrinsic reflectance response action spectrum for each subject. To determine the action spectrum for each subject, we fit the amplitude-irradiance functions across all wavelengths using a sigmoid with a common amplitude and slope, but unique shifts along the abscissa for each wavelength. The fit derived for each subject and each wavelength (dashed lines) is overlaid on each subjects’ amplitude response. Displayed data points were obtained from each condition’s pooled reflectance response. Error bars delineate the 5th through the 95th percentile of the bootstrapped amplitude distribution.
Fig. 7.
The wavelength dependence of the reflectance response links it to phototransduction. (A) For each subject, the horizontal shifts of the sigmoid fits for each wavelength relative to the 550 nm fit were taken as the relative action. To assess the variability of the amplitude responses and the sigmoidal fits, we bootstrapped each reflectance response, extracted the reflectance response amplitudes and repeated the fitting process 1,000 times. Error bars delineate the 5th through the 95th percentile of the bootstrapped values. In cases where error bars are not visible, they are smaller than the plotted points. (B) The average (across subjects) action spectrum of the intrinsic reflectance response (gold) overlaid on the human luminosity function (black dashed line). Overall, the action spectrum of the intrinsic reflectance response is well-matched to the photopic luminosity function. Error bars are ± 2 standard deviations.
4. Discussion
We have successfully developed a method that enables extraction of a reliable, quantifiable intrinsic signal from cones imaged using an AOSLO. It is well-known that the number of photoisomerizations in a functioning cone outer segment, as well as the magnitude of the resulting photocurrent via phototransduction, increases with stimulus intensity [27]. Thus, if the cone intrinsic reflectance response is related to the physiologic function of the cones, we would expect: 1) its magnitude to be intensity dependent and 2) its action spectrum to match the spectral sensitivity of cone-mediated vision. Indeed, we found that the peak response increased systematically with stimulus intensity for all wavelengths (Fig. 6, Table 1) across all subjects and the action spectrum of the cone intrinsic reflectance response from each subject matched the photopic luminosity function to first order (Fig. 7). These results strongly indicate that the absorption of light by cone photopigment initiates a reflectance response, thereby making the intrinsic reflectance response a direct non-invasive measure of photoreceptor function.
The precise origin of the reflectance changes we measure remains elusive. Previous work has suggested that changes in cone outer segment scattering, refractive index, or structure cause reflectance fluctuations [9]. If the changes in reflectance are due to metabolic changes within each cone, it is uncertain which aspect of phototransduction leads to those changes. The slow time course of the responses suggests a transduction stage downstream from the initial isomerization of photopigment [28–30], or a cellular change that is a consequence of the transduction process, such as swelling or shrinking of the photoreceptor cells [13, 28, 31, 32].
Regardless of the source of the reflectance changes, it is clear that both cone-to-cone and trial-to-trial intrinsic reflectance responses are highly heterogeneous (Fig. 3(C)). A potential source of this heterogeneity is the stochastic initial state of each cone outer segment. The cone reflectance, or total backscattered light, observed in AOSLO retinal images is thought to arise from a combination of scattered light from each end of the cone outer segment as well as scattering from the discs [33]. The contributions from each of these components may differ across cones at the time of stimulus delivery [34], in which case it is conceivable that a stimulus could evoke a change that either increases or decreases backscattering within a cone, depending on that cone’s initial state. Similarly, interference that arises between imaging light reflected from multiple surfaces will depend upon the initial optical path length between the surfaces and the coherence length of the imaging source. If a stimulus leads to a change in the optical path length between the two (or more) reflective surfaces within a cone, then the amount of constructive and destructive interference in that cone can change [9]. Cone-to-cone variations in the initial optical path length would cause the effect of interference (constructive or destructive) to vary across cones in both sign and magnitude. More work is needed to determine the mechanisms that lead to the stimulus-evoked reflectance response and understand the heterogeneity of the response in terms of these mechanisms.
Grieve et al. [10] reported a slight stimulus-evoked increase in mean cone reflectance, but one that was quite variable. In our preliminary analysis, we did not observe a change in mean reflectance (Appendix Fig. 9), and chose to focus our attention on the change in reflectance variation. The reason for the difference between our results with respect to mean reflectance and those of Grieve et al. [10] is not immediately clear.
Jonnal et al. [9] also reported that a visible stimulus could increase the variability of cone reflectance measured in the infrared. They used a different set of stimulus parameters and analysis method from ours, and did not find an increased response with increased stimulus energy. Specifically, they varied stimulus energy by varying stimulus duration, rather than stimulus irradiance as we did. If we ignore the differences in stimulus duration, however, and convert our stimulus irradiances to Td·s, the dimmest stimulus used by Jonnal at their stimulating wavelength of 670 nm (4.2 x 104 Td·s) is roughly comparable to our highest-energy stimulus at a similar wavelength (675 nm, 5.1 x 104 Td·s). Given that three of our subjects (11002, 11015, 11049) show signs of response saturation at our highest stimulus irradiance, it is possible that Jonnal et al. did not detect a significant response difference across stimulus levels because their responses were approaching saturation. Differences in analysis method or the fact that the coherence length of their imaging source was longer than ours may also contribute to differences in the intensity dependence of the response across the two studies.
The across-wavelength amplitude-irradiance function fits are not perfect (Fig. 6), indicating that the reflectance response satisfies the principle of univariance only in approximation [35]. This is not unexpected, as our measurement combines signals from individual cones of different spectral types in a non-linear manner (both because we use the standard deviation as our aggregation method and because the shape of the individual-cone amplitude-irradiance function is not linear). If it is possible to improve the resolution at which we can measure a reflectance response to the order of a single cone, we predict that each cone’s reflectance response will be more closely univariant. Measuring the action spectrum of individual cones may also allow resolution of some of the subject-to-subject differences in the action spectrum calculated from the aggregate signal (Fig. 7(A)) which in turn may arise from individual variations in L to M cone ratio, lens density and macular pigment density [18, 35, 36]. Studying individual cones would also allow us to separate out the contribution of S cones from those of L and M cones.
The agreement between our measured action spectra and the photopic luminosity function differs across subjects. For one subject (11046) it is excellent, while for others there are deviations larger than our estimates of measurement precision. Because the estimates of precision are bootstrapped from a small number of trials, they may themselves be too small. Other factors that might affect the agreement include those discussed in the previous paragraph. We also note that we were limited by our apparatus in the maximum stimulus irradiance available at 480 nm, and that as a result the fit to each subject’s 480 nm amplitude-irradiance function was not as well-constrained by the data as for other wavelengths.
For this work, calculation of action spectra was based on the assumption that the stimuli were purely monochromatic, while the actual stimuli had finite bandwidth. For the stimulus with the widest bandwidth (480 nm, 30 nm FWHM), we compared the luminance for the actual spectral power distribution (taken to be a Gaussian function of wavelength centered at 480 nm and with a 30 nm FWHM) with that for a purely monochromatic stimulus at 480 nm with the same total irradiance. These differ by less than 0.04 log10 units, which we regard as too small relative to measurement variability to justify the added complexity of injecting a correction into the analysis.
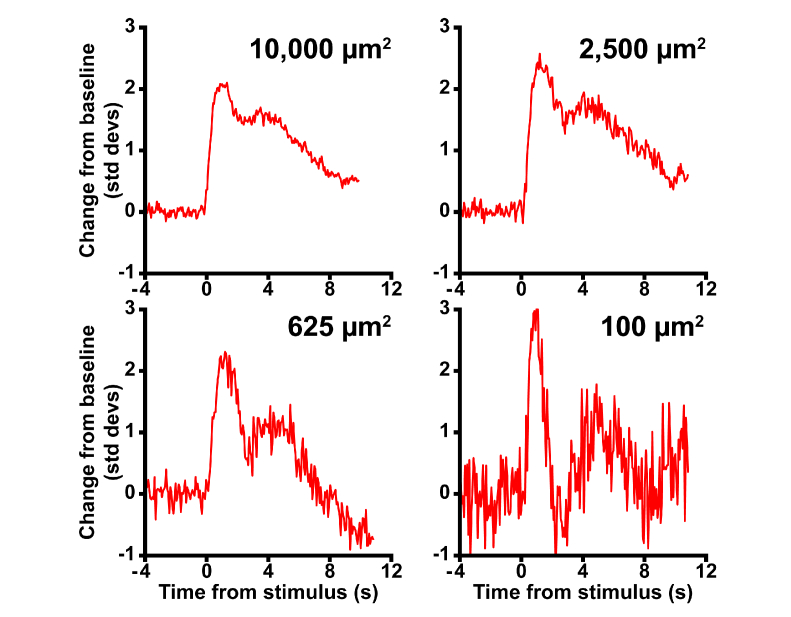
There are aspects of both the measurement and analysis techniques that may benefit from further refinement. While we have chosen to focus on the most intuitive aspect of the reflectance response, amplitude, to assess its action spectrum there are other features of the data that could be of interest for future work. For example, extracting other aspects of the reflectance response such as response latency or time-to-peak (Fig. 5(A)) may provide further insight as to the origins of these signals. Moreover, varying the coherence length of our imaging light may enhance the signal [9], as should apparatus modifications to eliminate light leakage from the visible stimulus. However, even if we are unable to enhance the signal further, we have already found that we can reliably extract a stimulus-evoked response in an area as small as 100 µm2 (Fig. 8, corresponding to about five cones at ~0.71° from the fovea), and believe it will be possible to reduce the area further. A 100 µm2 analysis window (Fig. 8, bottom right), encompasses area several times smaller than the smallest stimuliused in clinical perimetry (Goldmann I ≈830 µm2) and multifocal electroretinography (0.8° diameter hexagons ≈45,000 µm2, see also [37]). Thus, even with our current methods we have a functional measurement whose resolution far exceeds that of tools currently available to the clinician.
Fig. 8.
The cone photoreceptor intrinsic reflectance response as a function of analysis area. To examine the signal-to-noise characteristics of the response, we selected concentric 10,000, 2,500, 625, and 100 µm2 areas for analysis. As region area decreased, the signal to noise ratio of the reflectance response decreased. Despite this, a clear response was observed even from the smallest analysis area. Data was obtained from an irradiance of 337 nW/deg2 at 550 nm, from subject 11015.
Crucially, the intrinsic reflectance response is an exciting candidate to provide essential non-invasive functional measurements in diseased eyes. Progressive degeneration of photoreceptors is a major cause of blinding disease [38–40], and experimental therapies (such as gene or small molecule therapy, stem cell transplantation, optogenetic approaches) are being actively developed to prevent and reverse disease progression [41–45]. Each of these therapies operates at the level of individual cells, and evaluation of their effectiveness requires an understanding of both disease etiology and the efficacy of treatment at a similar scale. The intrinsic reflectance response could provide a biomarker capable of assessing the restoration of cone function following an experimental intervention.
Acknowledgements
The authors would like to thank Min Chen, Joseph Carroll and two anonymous reviewers for their comments, Grace Han for imaging assistance, Zach Harvey, Yusufu Sulai, and Miguel Hernandez for technical assistance, and K. Matthew McKay for preliminary measurements.
Appendix
Fig. 9.
An analysis of the mean reflectance signal content. To ensure that a mean-based intrinsic signal was not lost due our normalization approach, we examined the change in mean cone reflectance across all trials of a 550 nm, 382 nW/deg2 stimulus condition for subject 11049. Individual trials (gray lines) did not show a clear, repeatable change in mean reflectance during or following the stimulus. Averaging across trials (black line) also did not produce a change in the mean.
Funding
This research was supported by a Research to Prevent Blindness Stein Innovation Award, National Institutes of Health (NIH) U01EY025477 and R01EY025231, Foundation Fighting Blindness, the F. M. Kirby Foundation, the Paul and Evanina Mackall Foundation Trust, and the Glaucoma Research Foundation Catalyst for a Cure Initiative.
Disclosures
J.I.W.M. and A.D: (P) US Patent 8226236. R.F.C., W.S.T, and D.H.B. have no conflicts of interest related to this article.
References and links
- 1.Liang J., Williams D. R., Miller D. T., “Supernormal vision and high-resolution retinal imaging through adaptive optics,” J. Opt. Soc. Am. A 14(11), 2884–2892 (1997). [DOI] [PubMed] [Google Scholar]
- 2.Roorda A., Romero-Borja F., Donnelly Iii W., Queener H., Hebert T., Campbell M., “Adaptive optics scanning laser ophthalmoscopy,” Opt. Express 10(9), 405–412 (2002). [DOI] [PubMed] [Google Scholar]
- 3.Dubra A., Sulai Y., “Reflective afocal broadband adaptive optics scanning ophthalmoscope,” Biomed. Opt. Express 2(6), 1757–1768 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Drexler W., “Ultrahigh-resolution optical coherence tomography,” J. Biomed. Opt. 9(1), 47–74 (2004). [DOI] [PubMed] [Google Scholar]
- 5.Makous W., Carroll J., Wolfing J. I., Lin J., Christie N., Williams D. R., “Retinal microscotomas revealed with adaptive-optics microflashes,” Invest. Ophthalmol. Vis. Sci. 47(9), 4160–4167 (2006). [DOI] [PubMed] [Google Scholar]
- 6.Talcott K. E., Ratnam K., Sundquist S. M., Lucero A. S., Lujan B. J., Tao W., Porco T. C., Roorda A., Duncan J. L., “Longitudinal study of cone photoreceptors during retinal degeneration and in response to ciliary neurotrophic factor treatment,” Invest. Ophthalmol. Vis. Sci. 52(5), 2219–2226 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cideciyan A. V., Hufnagel R. B., Carroll J., Sumaroka A., Luo X., Schwartz S. B., Dubra A., Land M., Michaelides M., Gardner J. C., Hardcastle A. J., Moore A. T., Sisk R. A., Ahmed Z. M., Kohl S., Wissinger B., Jacobson S. G., “Human cone visual pigment deletions spare sufficient photoreceptors to warrant gene therapy,” Hum. Gene Ther. 24(12), 993–1006 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ratnam K., Carroll J., Porco T. C., Duncan J. L., Roorda A., “Relationship between foveal cone structure and clinical measures of visual function in patients with inherited retinal degenerations,” Invest. Ophthalmol. Vis. Sci. 54(8), 5836–5847 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jonnal R. S., Rha J., Zhang Y., Cense B., Gao W., Miller D. T., “In vivo functional imaging of human cone photoreceptors,” Opt. Express 14, 16141–16160 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grieve K., Roorda A., “Intrinsic signals from human cone photoreceptors,” Invest. Ophthalmol. Vis. Sci. 49(2), 713–719 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Rha J., Schroeder B., Godara P., Carroll J., “Variable optical activation of human cone photoreceptors visualized using a short coherence light source,” Opt. Lett. 34(24), 3782–3784 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hillmann D., Spahr H., Pfäffle C., Sudkamp H., Franke G., Hüttmann G., “In vivo optical imaging of physiological responses to photostimulation in human photoreceptors,” Proc. Natl. Acad. Sci. U.S.A. 113(46), 13138–13143 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhang P., Zawadzki R. J., Goswami M., Nguyen P. T., Yarov-Yarovoy V., Burns M. E., Pugh E. N., Jr., “In vivo optophysiology reveals that G-protein activation triggers osmotic swelling and increased light scattering of rod photoreceptors,” Proc. Natl. Acad. Sci. U.S.A. 114(14), E2937–E2946 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morgan J. I. W., Hunter J. J., Masella B., Wolfe R., Gray D. C., Merigan W. H., Delori F. C., Williams D. R., “Light-induced retinal changes observed with high-resolution autofluorescence imaging of the retinal pigment epithelium,” Invest. Ophthalmol. Vis. Sci. 49(8), 3715–3729 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ahnelt P. K., Kolb H., Pflug R., “Identification of a subtype of cone photoreceptor, likely to be blue sensitive, in the human retina,” J. Comp. Neurol. 255(1), 18–34 (1987). [DOI] [PubMed] [Google Scholar]
- 16.Roorda A., Williams D. R., “The arrangement of the three cone classes in the living human eye,” Nature 397(6719), 520–522 (1999). [DOI] [PubMed] [Google Scholar]
- 17.Carroll J., Neitz J., Neitz M., “Estimates of L:M cone ratio from ERG flicker photometry and genetics,” J. Vis. 2(8), 531–542 (2002) doi:. 10.1167/2.8.1 [DOI] [PubMed] [Google Scholar]
- 18.Hofer H., Carroll J., Neitz J., Neitz M., Williams D. R., “Organization of the human trichromatic cone mosaic,” J. Neurosci. 25(42), 9669–9679 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sharpe L. T., Stockman A., Jagla W., Jägle H., “A luminous efficiency function, V*(λ), for daylight adaptation,” J. Vis. 5(11), 948–968 (2005) doi:. 10.1167/5.11.3 [DOI] [PubMed] [Google Scholar]
- 20.Jonnal R. S., Besecker J. R., Derby J. C., Kocaoglu O. P., Cense B., Gao W., Wang Q., Miller D. T., “Imaging outer segment renewal in living human cone photoreceptors,” Opt. Express 18(5), 5257–5270 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Polyak S. L., The Retina (The University of Chicago Press, 1941). [Google Scholar]
- 22.Tam J., Martin J. A., Roorda A., “Noninvasive visualization and analysis of parafoveal capillaries in humans,” Invest. Ophthalmol. Vis. Sci. 51(3), 1691–1698 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dubra A., Harvey Z., “Registration of 2D images from fast scanning ophthalmic instruments,” in Biomedical Image Registration, Fischer B., Dawant B., Lorenz C., eds. (Springer-Verlag, 2010), pp. 60–71. [Google Scholar]
- 24.Garrioch R., Langlo C., Dubis A. M., Cooper R. F., Dubra A., Carroll J., “Repeatability of in vivo parafoveal cone density and spacing measurements,” Optom. Vis. Sci. 89(5), 632–643 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pallikaris A., Williams D. R., Hofer H., “The reflectance of single cones in the living human eye,” Invest. Ophthalmol. Vis. Sci. 44(10), 4580–4592 (2003). [DOI] [PubMed] [Google Scholar]
- 26.Cooper R. F., Dubis A. M., Pavaskar A., Rha J., Dubra A., Carroll J., “Spatial and temporal variation of rod photoreceptor reflectance in the human retina,” Biomed. Opt. Express 2(9), 2577–2589 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schnapf J. L., Nunn B. J., Meister M., Baylor D. A., “Visual transduction in cones of the monkey Macaca fascicularis,” J. Physiol. 427, 681–713 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hofmann K. P., Uhl R., Hoffmann W., Kreutz W., “Measurements on fast light-induced light-scattering and -absorption changes in outer segments of vertebrate light sensitive rod cells,” Biophys. Struct. Mech. 2(1), 61–77 (1976). [DOI] [PubMed] [Google Scholar]
- 29.Kühn H., Bennett N., Michel-Villaz M., Chabre M., “Interactions between photoexcited rhodopsin and GTP-binding protein: kinetic and stoichiometric analyses from light-scattering changes,” Proc. Natl. Acad. Sci. U.S.A. 78(11), 6873–6877 (1981). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Arshavsky V. Y., Lamb T. D., Pugh E. N., Jr., “G proteins and phototransduction,” Annu. Rev. Physiol. 64, 153–187 (2002). [DOI] [PubMed] [Google Scholar]
- 31.Hofmann K. P., Schleicher A., Emeis D., Reichert J., “Light-induced axial and radial shrinkage effects and changes of the refractive index in isolated bovine rod outer segments and disc vesicles: physical analysis of near-infrared scattering changes,” Biophys. Struct. Mech. 8(1-2), 67–93 (1981). [DOI] [PubMed] [Google Scholar]
- 32.Zhao Y. B., Yao X. C., “Intrinsic optical imaging of stimulus-modulated physiological responses in amphibian retina,” Opt. Lett. 33(4), 342–344 (2008). [DOI] [PubMed] [Google Scholar]
- 33.van de Kraats J., Berendschot T. T., van Norren D., “The pathways of light measured in fundus reflectometry,” Vision Res. 36(15), 2229–2247 (1996). [DOI] [PubMed] [Google Scholar]
- 34.Pircher M., Kroisamer J. S., Felberer F., Sattmann H., Götzinger E., Hitzenberger C. K., “Temporal changes of human cone photoreceptors observed in vivo with SLO/OCT,” Biomed. Opt. Express 2(1), 100–112 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Brainard D. H., Stockman A., Colorimetry (McGraw-Hill, 2010). [Google Scholar]
- 36.Wyszecki G., Stiles W. S., Color Science: Concepts and Methods, Quantitative Data and Formulae (John Wiley & Sons, Inc., 1982). [Google Scholar]
- 37.Poloschek C. M., Sutter E. E., “The fine structure of multifocal ERG topographies,” J. Vis. 2(8), 577–587 (2002) doi:. 10.1167/2.8.5 [DOI] [PubMed] [Google Scholar]
- 38.Duncan J. L., Zhang Y., Gandhi J., Nakanishi C., Othman M., Branham K. E. H., Swaroop A., Roorda A., “High-resolution imaging with adaptive optics in patients with inherited retinal degeneration,” Invest. Ophthalmol. Vis. Sci. 48(7), 3283–3291 (2007). [DOI] [PubMed] [Google Scholar]
- 39.Zayit-Soudry S., Duncan J. L., Syed R., Menghini M., Roorda A. J., “Cone structure imaged with adaptive optics scanning laser ophthalmoscopy in eyes with nonneovascular age-related macular degeneration,” Invest. Ophthalmol. Vis. Sci. 54(12), 7498–7509 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Morgan J. I., Han G., Klinman E., Maguire W. M., Chung D. C., Maguire A. M., Bennett J., “High-resolution adaptive optics retinal imaging of cellular structure in choroideremia,” Invest. Ophthalmol. Vis. Sci. 55(10), 6381–6397 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Maguire A. M., High K. A., Auricchio A., Wright J. F., Pierce E. A., Testa F., Mingozzi F., Bennicelli J. L., Ying G. S., Rossi S., Fulton A., Marshall K. A., Banfi S., Chung D. C., Morgan J. I., Hauck B., Zelenaia O., Zhu X., Raffini L., Coppieters F., De Baere E., Shindler K. S., Volpe N. J., Surace E. M., Acerra C., Lyubarsky A., Redmond T. M., Stone E., Sun J., McDonnell J. W., Leroy B. P., Simonelli F., Bennett J., “Age-dependent effects of RPE65 gene therapy for Leber’s congenital amaurosis: A phase 1 dose-escalation trial,” Lancet 374(9701), 1597–1605 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhang K., Hopkins J. J., Heier J. S., Birch D. G., Halperin L. S., Albini T. A., Brown D. M., Jaffe G. J., Tao W., Williams G. A., “Ciliary neurotrophic factor delivered by encapsulated cell intraocular implants for treatment of geographic atrophy in age-related macular degeneration,” Proc. Natl. Acad. Sci. U.S.A. 108(15), 6241–6245 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dalkara D., Sahel J. A., “Gene therapy for inherited retinal degenerations,” C. R. Biol. 337(3), 185–192 (2014). [DOI] [PubMed] [Google Scholar]
- 44.Yizhar O., Fenno L. E., Davidson T. J., Mogri M., Deisseroth K., “Optogenetics in neural systems,” Neuron 71(1), 9–34 (2011). [DOI] [PubMed] [Google Scholar]
- 45.Giacalone J. C., Wiley L. A., Burnight E. R., Songstad A. E., Mullins R. F., Stone E. M., Tucker B. A., “Concise review: patient-specific stem cells to interrogate inherited eye disease,” Stem Cells Transl. Med. 5(2), 132–140 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]