Time domain diffuse correlation spectroscopy with a high coherence pulsed source: in vivo and phantom results

Abstract

Diffuse correlation spectroscopy (DCS), combined with time-resolved reflectance spectroscopy (TRS) or frequency domain spectroscopy, aims at path length (i.e. depth) resolved, non-invasive and simultaneous assessment of tissue composition and blood flow. However, while TRS provides a path length resolved data, the standard DCS does not. Recently, a time domain DCS experiment showed path length resolved measurements for improved quantification with respect to classical DCS, but was limited to phantoms and small animal studies. Here, we demonstrate time domain DCS for in vivo studies on the adult forehead and the arm. We achieve path length resolved DCS by means of an actively mode-locked Ti:Sapphire laser that allows high coherence pulses, thus enabling adequate signal-to-noise ratio in relatively fast (~1 s) temporal resolution. This work paves the way to the translation of this approach to practical in vivo use.

1. Introduction

Time domain near infrared spectroscopy, also known as time-resolved reflectance spectroscopy (TRS), measures the distribution of photon path lengths (or photon time-of-flights) in tissue to characterize the probed volume in terms of its wavelength dependent reduced scattering (${\mu }_s\text{'}$) and absorption (${\mu }_a$) coefficients [1,2]. By collecting this information at various wavelengths, one can estimate the concentration of chromophores like water, oxy- and deoxy-hemoglobin, lipids and collagen, and give information about tissue structure at the cellular level [2]. Furthermore, TRS allows the separation of early and late photons. Since the probability distribution for the maximum penetration depth moves towards deeper layers when photon time-of-flight increases [3], the contributions from deeper tissue volumes can be better separated from superficial ones if the longer path length (longer time-of-flight) photons are analysed. This ability to path length-resolve is crucial for the clinical success of this technique for many scenarios such as neuro-monitoring and neuro-imaging due to overlaying extracerebral tissue contamination of the signals.

Another emerging near-infrared technique is diffuse correlation spectroscopy (DCS). DCS has been proven to be a reliable tool for the assessment of blood flow in the microvasculature in a non-invasive way [4–6]. DCS exploits the speckle fluctuations of coherent light that underwent multiple scattering and quantifies its statistics by the measurement of the intensity auto-correlation function. This can then be used to estimate the electric field auto-correlation function [4–6]. In a diffusive medium, the correlation diffusion equation describes the propagation of the electric field temporal auto-correlation function through tissues and allows us to quantitatively relate its temporal decay to the motion of red blood cells and, therefore, to the blood flow. Traditional DCS uses continuous wave (CW) lasers and it does not readily contain a way to separate or gate short and long path lengths in a similar manner as TRS.

The extension of DCS to path length-resolved DCS (i.e. time domain DCS) is non-trivial. This is mainly due to the physics of pulsed light, which implies a limited coherence length for a short (about 100 ps) pulse. In other words, when the coherence time is much shorter than the distribution of photon time-of-flight in tissue, the bulk of the speckles decorrelate due to this long path length and random scattering, which washes out the contributions due to the motion of the scatterers.

Early on, Yodh et al. [7] demonstrated that by splitting the input pulse and using one path as a reference with a controlled delay, it is possible to carry out time- or path length-resolved DCS (or diffuse wave spectroscopy, as it is known in other fields). The crucial difference of this method in comparison to other path length-resolved laser speckle methods is that it is applicable for the highly multiple scattering regime. Their approach used non-linear effects and, therefore, it is unsuitable for in vivo measurements due to the need for a large amount of detected light.

Recently, Sutin et al. [8] were able to extend the concept to a relevant domain. They achieved this by using a pulsed light on a tissue phantom and, during the analysis, by considering only the photons that have travelled paths of similar length. This allowed them to relax the requirement for high coherence length in comparison to the case in which all the photon paths are considered. They have demonstrated that they are able to separate the contribution of photons coming from shallow and deep layers, that is, those arriving at early or late time gates. These experiments were carried out on phantoms and on small animals. One drawback of this approach is that the use of narrow time gates to calculate the auto-correlation limits the signal-to-noise ratio due to the scarcity of photons within a certain gate; this in turn limits its applicability to in vivo experiments on humans.

In this work, we show that a high temporal coherence pulsed source can be utilized to allow the use of broader (between hundreds of ps and few ns) time gates and break the signal-to-noise barrier. Thus, we are capable of in vivo measurements from the adult head and the arm in a continuous manner. We envisage three main advantages of the time-domain DCS approach as compared to standard CW DCS, which motivated us in this study. First, the time domain approach will add one further variable – time – which can be exploited to select photons with increasing depth sensitivities [3,9]. Therefore, a single SD pair can be used to separate contamination from superficial layers, and as opposed to a CW multiple-distance approach the depth resolution is achieved in a way that is less sensitive to the confounding heterogeneity of the probed tissue at a microscopic level [10,11]. the time domain approach conceptually decouples lateral and depth resolution: the first is encoded in the detector position while the second is attained by knowing the time of flight of the detected photons [11]. The use of multiple source-detector separations is complementary to this and can still be used with the time resolved approaches to provide a full tomographic reconstruction [12]. Besides, time-domain DCS also offers an elegant physical model that separates the distribution of time of flight of the photons in tissue and the phase shifts due to multiple scattering from those due to moving scatterers, for better quantitation of blood flow. Finally, this approach allows for a simultaneous measurement of the time-domain NIRS data types and DCS, thus providing a complete picture of blood hemodynamics. We demonstrate the technique in a two-layer phantom, on the adult brain while differentially changing the superficial blood flow and by following the changes due to an arterial arm cuff occlusion. A temporal resolution of about one second with a good signal-to-noise-ratio was achieved in dynamic in vivo measurements paving the way to the translation of this approach to practical use.

2. Materials and methods

2.1 Time domain DCS system

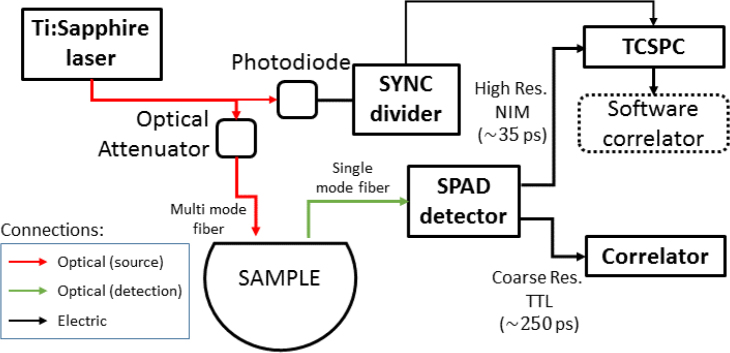
Figure 1 shows the experimental setup. The source was a custom made Ti:Sapphire laser operated in active mode-locked regime by means of an acousto-optic modulator which permits to achieve phase locking of longitudinal modes. This leads to a high temporal coherence within the laser pulse [13,14]. It is pumped by a 5 W frequency doubled continuous wave Nd:YAG laser, has a pulse repetition rate of 100 MHz, and is tuneable in the 680-1090 nm range. We have operated the laser at a wavelength ($\lambda$) of 785 nm. We have used a stack of three metallic variable attenuators (Thorlabs, Germany) to ensure that the illumination is below the maximum-permissible skin exposure limits. We have achieved the synchronization of the photon detection with the laser source pulses by splitting off a small fraction (<5%) of its light to be sent to a photodiode (Becker & Hickl, Germany). The remaining laser light was then launched into a 200 μm core step index fiber that delivered light perpendicularly to the sample. At a variable distance, depending on the experiment, a 5 μm core single mode fiber collected the diffuse light and delivered it to a single-photon avalanche diode (SPAD) detector (PDM, Micro Photon Devices, Italy) with a photon detection efficiency of about 20% at the wavelength of interest. This detector has two outputs. A high temporal resolution nuclear instrumentation module (NIM) output (nominally, with about 35 ps precision) was connected to a standard time correlated single photon counting (TCSPC) module (Pico Harp 300, PicoQuant, Berlin, Germany). The TCSPC module records the time stamps (time of arrival) and the delay with respect to the pulse emission (pulse time), with an 8 ps resolution, of each detected photon in a file. The coarser temporal resolution transistor-transistor logic (TTL) output (with few hundred ps precision) of the SPAD detector was connected to a standard hardware correlator (Correlator.com Flex-05, 8 channels, USA). The hardware correlator evaluates the intensity auto-correlation function assuming that the light is continuous wave and was used in a subset of experiments (see below).

Fig. 1.

The sketch of the experimental setup for the time domain DCS system.

We note that the TCSPC board can accept synchronization signals up to a maximum 84 MHz but our laser repetition rate was higher. To deal with this, we have developed an in-house fast circuit (SYNC divider) that reduces the number of synchronization pulses by accepting just one in three, thus recording three distribution of times of flight (DTOF) curves in the same window. To avoid any loss of photon counts, these curves are combined in data analysis. Furthermore, in some experiments, by switching the pulsed source to a continuous wave high coherence diode laser (Crystal Laser, Reno, NV, US), we have tested the scatterers dynamics of the phantoms in an equivalent manner to a standard DCS setup.

The instrument response function (IRF) was acquired by facing the source and the detector fibers directly in front of each other and by introducing a sub-millimeter thick polytetrafluoroethylene sheet in between. The full width at half maximum (FWHM) of the IRF was about 100 ps.

The FoCuS-point software correlator [15], that is available on Github [16], was used for the post-processing of the data. It relies on the algorithm for fast photon auto-correlation from Wahl et al. [17]. We have adapted it to correlate the time stamps of the detected photons that were recorded by the TCSPC within a time window or a gate. This allowed us to gather the photons that arrive in an adjustable time gate and calculate the gated auto-correlation function by using time stamps of just a portion –gate– of the DTOF at a certain delay with respect to the laser emission, offline, in a similar fashion to the work of Sutin et al. [8].

2.2 Data analysis

The Siegert relation, $g_2\left(\tau \right)=1+\beta {|g_1\left(\tau \right)|}^2$, when the assumptions behind it are fulfilled [18], can be applied in order to relate the measured normalized intensity auto-correlation function ($g_2(\tau )$) to the normalized electric field auto-correlation function ($g_1(\tau )$), in order to quantify the motion of scatterers. Here $\tau$ is the correlation delay time and $\beta$ is a constant, determined by the collection optics. $\beta$ is equal to 1 for ideal experimental conditions but decays with an approximately inverse proportionality to the number of modes detected at the same time. It also decreases by decreasing the source coherence length. As first proposed by Pine et al. [18] for diffusing wave spectroscopy, the theoretical model for $g_1(\tau )$ can be computed by evaluating the integral

$$g_1\left(k,\tau \right)=\underset{s_0}{\overset{s_1}{{\displaystyle \int }}}P\left(s\right)g_1^{single}\left(k,\tau ,s\right)ds$$ (1)

where $P\left(s\right)$ is the probability distribution of the photon path lengths ($s$) in tissue and $k$ is a quantity that describes the decay rate of the auto-correlation function. The integration over the path lengths is infinite for an ungated experiment, but, in gated experiments, just the path lengths between two extremes of the gate, $s_0$ and $s_1$, are used. The other term in the integrand,

$$g_1^{single}(k,\tau ,s)=e^{-k\tau s}$$ (2)

is the contribution to the correlation decay from a single path (of a multiply scattered photon) of length $s$. The decay rate is given by the formula

$$k=2{\mu }_s^{\text{'}}{k}_0^2\alpha D_B$$ (3)

where $k_0^2$ is the square of the wavenumber of the light in the medium and $\alpha$ is the fraction of moving to static scatterers [4]. The decay rate, therefore, represents the rate of loss of correlation per unit path length in the medium and is proportional to the scatterer Brownian diffusion coefficient ($D_B$) of the sample. By applying the above-mentioned Siegert relation we are left with two parameters to be estimated, namely the optical parameter $\beta$ and either $D_B$ (in phantoms, $\alpha =1$) or the blood flow index (BFI = $\alpha D_B$). The BFI is assumed to be related to the shear-induced Brownian motion of red blood cells [20] in case of in vivo measurements, and was shown to be proportional to both absolute and relative microvascular blood flow [4–6,21].

Equation (1) tells us that, if the gate is sufficiently narrow compared to the decay of $P(s)$, then $P(s)$ could be treated as a constant and simplified. Afterwards, the average ${\text{D}}_{\mathrm{B}}$ or the BFI of a collection of narrow adjacent gates can be recovered from the slope of the decay of the auto-correlation function at different gate positions or path lengths ($\text{s}$) [7,8]. However, for broader gates, this approximation is not anymore valid and further steps need to be taken. In particular, in order to solve Eq. (1) numerically, $P(s)$ must be estimated. As we assume an uniform refractive index in the sample, the path length is the time-of-flight of the photons times the speed of light in the sample and $P(s)$ can be rewritten, in the limits of validity of the photon diffusion approximation, as the time-resolved reflectance [22,23] for the relevant boundary conditions. For all our experiments, we have assumed a semi-infinite medium. In order to correctly recover the path lengths ($s$) from the photon time-of-flight, we have set the zero time as the time at which the IRF has a peak. In principle, the reflectance could also be estimated from the measured DTOFs and IRF by the deconvolution of the latter from the former [21] and by using a proper regularization to reduce the deconvolution noise. In our case, we have chosen to compute $P(s)$ from theory using the absorption and reduced scattering coefficients that have been measured by knowing the DTOF and IRF using a semi-infinite medium model with extrapolated boundary by convolving the theoretical model with the IRF [22].

Here, we have tested both the narrow (160 ps) and broad gate approaches on tissue simulating phantoms. The broad gates are used for fast, light-starved in vivo measurements of blood flow in humans. We chose the width of the broad gates depending on the shape of the DTOF. We have considered the photons with times of flight up to a certain fraction of the DTOF in an early gate and the rest in a late gate, for a total of two broad gates. The width of the narrow gates was chosen as a compromise between the detected photon counts within the gates and $\text{β}$ value. For the broad gates, the early gate extended from the time at which the IRF peaked (${\text{t}}_0$) to the time at which the measured DTOF dropped to 90% on the falling edge of the curve, with respect to its maximum, for a total width of about 800 ps. The late gate extends from this point to the time at which the DTOF is no longer distinguishable from the noise floor which results in a width of between 2 and 3 ns. Then, we numerically solve the full expression in Eq. (1) to model the auto-correlation.

2.3 Phantom experiments

A custom two layer phantom holder (Fig. 2) that consists of two compartments separated by a 50 μm thick Mylar sheet was used [25]. Another Mylar sheet enclosed the phantom and separated the fibers from the liquid. The first compartment, closest to the fibers, is termed shallow (S), and the other, deep (D). Superficial (S) compartment thickness, δ, could be varied to simulate different superficial tissue thicknesses. Source and detector fibers were then inserted in a black plastic holder, in which they were kept at a 15 mm separation from each other and perpendicular to the liquid/Mylar interface.

Fig. 2.

Sketch of the two-layer liquid phantom holder. δ is the thickness of the superficial layer (S).

Two liquid phantoms were made by mixing water and Lipofundin (B. Braun Melsungen AG, Germany) by the proportion of 6.5% (mass Lipofundin / mass water). In order to create a contrast in ${\text{D}}_{\mathrm{B}}$, we have added 30% in weight of glycerol (Sigma Aldrich) to one of them. To compensate for reduced scattering due the glycerol refractive index, we have then raised the concentration of Lipofundin to 13.5% by adding an index-matched solution of Lipofundin, water and glycerol. Glycerol reduces $D_B$ by increasing the solvent’s viscosity. We have then accurately titrated the concentration of Lipofundin in this second phantom to match the reduced scattering coefficient of the first [26]. In both phantoms, the scatterers show Brownian diffusion coefficients that are similar to typical in vivo values. The expected contrast between the two, in terms of $D_B$, is about 40%, and ultimately we have used the two phantoms to fill the two layer phantom holder.

The deeper (D) compartment was always filled with the phantom without glycerol, while the shallow (S) layer was filled either with the same (dynamically homogeneous configuration) or with the slower diffusing (30% glycerol added) phantom (dynamically heterogeneous configuration). We have changed the thickness of the S layer to 10 and 5 mm in dynamically homogeneous and to 5, 10 and 15 mm for the dynamically altered configurations. Five measurements in the two configurations (two homogeneous and three heterogeneous) were carried out with a count rate of approximately $2\cdot {10}^5$ counts per second, which needed a duration of about $2\cdot {10}^3$ seconds to reach the target of a total of about $4\cdot {10}^8$ photons per measurement.

We have recovered the optical properties (${\mu }_s\text{'}$ and ${\mu }_a$) of the liquid phantoms by fitting the convolution of the IRF and the solution of the radiative transport equation in the diffusion approximation with the corresponding DTOF. The DTOF was acquired for each phantom separately in a homogeneous one-litre container.

As discussed in section 2.2, we have first computed the electric field auto-correlation of narrow, 160 ps wide gates, overlapping for 80 ps from one to the next. The normalized intensity auto-correlation function for each gate was then fitted against the delay time $\tau$ with the single path length exponential decaying correlation (Eq. (2) to obtain $k\cdot s$. For each gate, $s$ is the average path length. We have plotted the fitted $k\cdot s$ against $s$ and calculated the slope, which is $k$, in two regions, separately: early, between 80% of maximum counts on the rising edge of the DTOF and 90% on the falling edge, and late, between 60% and 10% on the falling edge of the DTOF.

2.4 In vivo experiments

For all the in vivo studies, the laser power was limited by using an optical attenuator to meet the maximum permissible exposure limit for human skin. The protocol was approved by the Ethical Committee of Politecnico di Milano and it was conducted in agreement with the Declaration of Helsinki. All subjects gave written consent before their participation.

First, we have taken measurements on the forehead of a healthy subject (male, 30 years old). He was instructed to lay down supine on a bed and remain alert for the duration of the experiment. The probe was a black plastic fiber holder (5 cm by 5 cm by 1 cm) with the fibers inserted 1 cm apart and pointing perpendicularly to the skin. A cotton mesh wrap encircling the head was used to secure the probe to the right side of the forehead far from the midline. We have repeated the experiment two times. The second time we have manually applied a constant increased pressure (the maximum the subject was comfortable with for all the duration of the data acquisition). We have acquired, for each pressure scenario (no pressure, pressure), $2.7\cdot {10}^7$photons over 300 s, and we have used the broad gate approach for the analysis.

Second, we have used the same source-detector separation (1cm) for measuring the BFI in the arm of another healthy subject (male, 30 years old) before, during and after an arterial cuff occlusion. The black plastic fiber holder was applied, with the fibers perpendicular to the skin, above the brachioradialis muscle in the right arm and was secured with a loose bandage. The tourniquet for compressing the affluent arteries was applied around the arm right below the shoulder joint. The cuff occlusion started at 245 s and lasted for 180 s. During the cuff occlusion the tourniquet pressure was raised to about 180 mmHg which is well above the arterial blood pressure of the subject. In order to gain temporal resolution, we have divided the 600 s measurement period in 1 s epochs and analysed them separately. The BFI was then estimated by using the numerical integration method in the early and late gates separately for each epoch. At the same time, we have acquired correlation curves independently on the time of arrival of the photons with 1 s time resolution by using the hardware correlator. These were analysed with the standard continuous wave DCS theory and the results were compared with the gated analysis.

3. Results

The first step was to fit the measured DTOF (Fig. 3, top) from both liquid mixtures (see section 2.1) to determine the optical properties. The reduced scattering coefficients were 10.6 cm⁻¹ for the phantom with 30% glycerol and 10.5 cm⁻¹ for the phantom without glycerol. Absorption coefficients were 0.026 cm⁻¹ and 0.025 cm⁻¹, respectively. This confirms that the contrast between the two compartments would be due to the differences in viscosity and not due to differences in the reduced scattering coefficient, which is tightly coupled to $D_B$ in the correlation diffusion model.

Fig. 3.

(Top) DTOF curves of the two homogeneous liquid mixtures, with (30% gly) and without (0% gly) glycerol. (Bottom) Gated auto-correlation decay rates ($k\cdot s$) for the dynamically homogeneous (DH, triangles) and dynamically heterogeneous (DA, circles) two-layer phantom configurations. Here, δ represents the thicknessof the superficial (S) layer of the phantom (see Fig. 2). The path length s is computed from the time-of-flight as $s=v\cdot t$, where $v$ is the speed of light in the medium. Figure 6 in the Appendix shows the corresponding measured auto-correlation curves for different gate positions.

Figure 3, bottom, shows the results for the dynamically heterogeneous and dynamically homogeneous two-layer phantom. As expected, both regions (early and late) reveal the same decay constant, k, and varying the thickness $\delta$ of the superficial layer (S) does not change k in the dynamically homogeneous case (DH, triangles). All the measured auto-correlation curves are reported, for completeness, in Fig. 6 in the Appendix, for the DH, δ = 5 mm case. As expected (Section 2.2), by increasing the average gate path length, the decay constant, k∙s, of the auto-correlation curves increases. The small distortions of the early gates with respect to the late in the DH case are due to the contributions of instrument response function, the contributions of the photons that underwent a small number of scattering events and the finite gate width. The effects of these contributions are different depending on the position of the center of the gate with respect to the DTOF curve, which is a topic for future study. The value of $k$ becomes significantly different between the early and late regions when we have filled the superficial (S) layer with the reduced $D_B$ phantom with 30% glycerol (DA, circles). Notably, in this case the retrieved $D_B$ is lower (see Table 1) in the early compared to the late region, and decays faster when the thickness of layer S is increased (52%, 36% and 28% of the dynamically homogeneous case in early region; 100%, 71% and 50% in late region).

Table 1. Relative $D_B$ when S layer is filled by 30% glycerol added phantom (dynamically heterogeneous case), for changing S layer thickness δ, compared to the late gate or region, δ = 5 mm, value (100%).

		k·s fitting		Numerical integration
Thickness of layer	S	EARLY	LATE	EARLY	LATE
δ = 5 mm		52%	100%	47%	100%
δ = 10 mm		36%	71%	34%	84%
δ = 15 mm		28%	50%	28%	61%

We have then proceeded to fit the auto-correlation of the two broad gates with the numerical integration method (Section 2.2). We have computed the normalized intensity auto-correlation for each one of the two gates and fitted them separately. As shown in Table 1, just limited to the dynamically heterogeneous case, we see that the measured $D_B$ is dropping much faster in the early with respect to the late gate or region. All values are reported as relative to the smallest S layer thickness (δ = 5 mm), late gate or region (here marked as 100%). As we increase the superficial layer thickness δ, the estimated relative decrease of is $D_B$ practically independent on the evaluation methods (numeric integration or k·s-fitting).

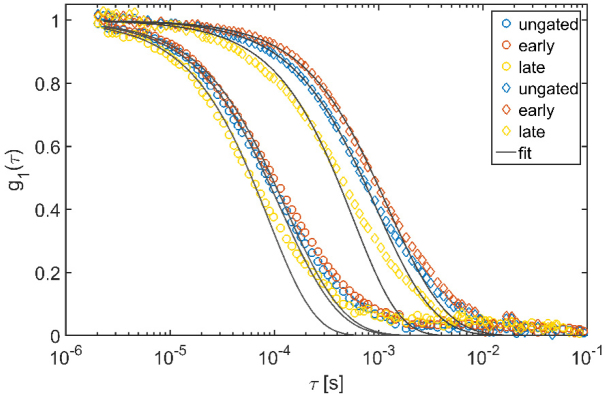
The results from the adult-human head are shown in Fig. 4. In Fig. 4(a), we report the measured intensity auto-correlation $g_2\left(\tau \right)$ functions for the early and late broad gates and for the ungated case. It is evident how, even in the pulsed case, we have achieved a good signal-to-noise ratio for the estimated correlation curves, with $\beta$ = 0.41 and 0.25, respectively for the early and late gates, and $\beta$ = 0.29 for the ungated case. We note that the values of $\beta$ observed in these experiments are higher compared with the ones reported in Sutin et al. [8], as a result of the tunable active pulse locking that our particular laser allowed.

Fig. 4.

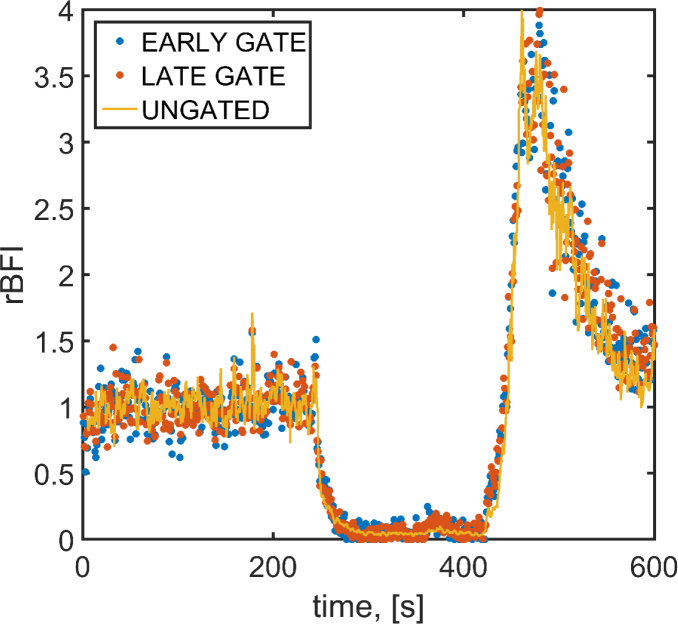
(a) Intensity auto-correlations for the early and late gates, and the ungated auto-correlation when no pressure is applied. (b) Electric field auto-correlation for the early gate when pressure is applied on the probe as compared to when no pressure applied. The distortions from the model at late lag times is a common feature of in vivo DCS data as illustrated in ref [6] (Fig. 8). Figure 7, in the Appendix, shows the full set of curves. (c) Relative BFI (rBFI) for two different gates (early and late) and two pressure conditions (no pressure, with pressure) is shown.

Figure 4(b) shows the measured electric field auto-correlation function $g_1(\tau )$ at early gates for the baseline (control) and pressure scenarios, demonstrating that the probe pressure causes a significant change in the measurements from the early gate. The numeric fit was carried out considering the experimental points up to ${\text{g}}_1~0.3$. We report the auto-correlations of the other gates in Fig. 7, in the Appendix. Figure 4(c) shows the measured BFI normalized relative to the ungated value, which reflects a mixed contribution of superficial and deep photons, of the baseline (no pressure) condition. As expected [27], when pressure was applied, the ungated analysis showed a decrease of 61% of BFI. Since the blood flow in the scalp is reduced, the contrast between the early and late gates increases when pressure is applied to the probe.

The results of the cuff occlusion experiment are summarized in Fig. 5. The measured average $\beta$ was 0.36 and 0.32 for the early and late broad gates, respectively. This set-up is able to achieve a good signal-to-noise ratio (count-rate and total number of photons) in a 1 s window, and we are able to discern the appropriate decay during the cuff occlusion, followed by the rapid and strong hyperemia. The features of the three time-traces are very similar. Trends in the estimated relative BFI (rBFI) with the broad gates analysis are in good agreement with the ungated estimation carried out with the standard hardware correlator.

Fig. 5.

Relative BFI (normalized to the first 100 s) during a cuff occlusion experiment. Dots represent the broad gates analysis and havea 1 s resolution. The continuous line is the rBFI estimation from ungated analysis carried out with the hardware correlator (1 second resolution).

4. Discussion and conclusion

We have demonstrated the feasibility of separating the Brownian diffusion coefficients of scatterers in deep and shallow layers by using a mode-locked pulsed laser source. To do so, we have used a two-layer phantom in which the two layers have a different Brownian diffusion coefficient, but same reduced scattering and absorption coefficients. When the Brownian coefficient of the superficial layer decreases, we have observed a selective drop in the typical decorrelation time corresponding to the photons arriving early to the detector. We have shown a contrast in the relative dynamics of the two layers with respect to the ungated case in both phantoms and in vivo. Even though we do not report all possible combinations of changes of dynamics and optical properties in a two layer media, this work paves the way to works of that nature by establishing the proper experimental and theoretical framework.

We have also demonstrated the feasibility of applying this technology directly in vivo on humans. This can be used to discern the blood flow of a superficial layer (e.g. scalp and skull) with respect to deeper one (e.g. the brain), in order to reduce partial volume artefacts that affect standard DCS measurements. Here, we have focused on two broad gates. However, this method can be extended to the use of an analysis that uses multiple gates and/or a full set of autocorrelation curves at different time bins. For example, Spinelli et al. [28] utilized a similar method for TRS. This could be a future extension beyond this work where the relevant physical and algorithmic aspects could be studied.

On the head of a healthy subject we have observed a reduction in the BFI corresponding to shallow tissue as we apply additional pressure. The additional pressure we have applied does not affect the deeper brain tissue, which is protected by the hard skull bone, but it causes a decrease of the blood flow in the shallow skin and scalp layers. This is in agreement also with previous studies that demonstrated that an externally applied pressure modulates the contribution of the extra cerebral layer on the BFI assessment by DCS [27,29]. In these studies, different source-detector separations were utilized to gain a pseudo-depth resolution, but here we do take advantage of the multiple gate strategy to achieve depth resolution with a single-shot measurement. We note that we have used a relatively short source detector separation (1 cm). The depth resolution is in fact achieved by the time gate only, in a way similar to the null source detector separation TRS [30]. In a similar approach, a gated detector can be used here to systematically discard the very early photons that would blind the detection electronics at very small source detector separation. This concept can be used in a multi-source, multi-detector system to increase the resolution of diffuse correlation tomography.

In the arm cuff experiment we show that the broad time gates analysis is able to achieve a good signal-to-noise ratio with 1 s resolution, and therefore it is suitable to follow fast changes of the BFI. Surprisingly, we see that the early and late gates do not differ in terms of the BFI values, and there is no statistically significant difference between the two gates, or between the ungated and gated results, during all three phases considered separately. Although we have expected a higher hyperemic peak during reperfusion in the late (deep) gate [31], due to higher oxygen consumption in the muscle, with respect to the shallower skin and fat layers, we were not able to detect it. We believe that this is due to the very thin superficial tissue (skin and fat) thickness of 2.5 mm, measured by a skin caliper, of this particular subject. Nevertheless, we were able to prove that even fast BFI-changes due to challenges like the cuff occlusion can be monitored by time domain DCS. The results are in agreement with the ones obtained with a standard hardware correlator for ungated measurements and the same pulsed light source.

In all the experiments we have used a single wavelength but, by tuning the laser wavelength sufficiently fast (i.e. every 500ms), we can gain specific sensitivity to the deoxygenated or oxygenated hemoglobin or even further, to characterize the sample multi-spectrally while also measuring the blood flow. We note also that multiple source-detector pairs can readily be utilized by this method by multiplexing.

In this work, we have assumed homogeneous optical properties and we have focused on demonstrating the ability to separate the dynamic properties of the superficial and deeper layers. However, in vivo measurements contain heterogeneities in both optical and dynamic properties. It is well known that the inaccuracies in the recovery of the optical properties are reflected in the recovery of dynamic properties [32]. However, since time domain DCS measurements contain the TRS information, we believe that the quality of the results will be similar as the quality of the TRS results [33] and this is a topic for future work.

While, as other works suggest [18,34], the Siegert relation may not be valid when the coherence length of the source is in the order of the distribution of photon path lengths in tissue, or even shorter, here we demonstrate that this relation still allows us to extract meaningful values of BFI from in vivo experiments. Sutin et al. [8] have justified the application of the Siegert relation to the use of very narrow gates, and we believe that the greater coherence length of our system allows us to avoid most distortions when working with broader (up to 1 ns) gates. Moreover, no evidence of distortion that may be caused by the non-validity of the Siegert relation, such as the intensity auto-correlation curves not decaying to one at infinite time, were observed.

The longer coherence length of the pulsed laser source that we have used here, which is manifest in the relatively high values of $\beta$ observed, allows for a time resolution that is high enough to monitor even fast hemodynamic changes like those due to the cuff occlusion in the arm. However, a dedicated setup like the one presented in this work offers several disadvantages. First, the need for a long cavity and a powerful pump laser makes the device bulky and hard to use at the bedside. Second, the fact that this is a unique system – it is a modified system adapted to operate in active mode-locking – does not allow one to easily fabricate multiple systems. The present system is a powerful laboratory workstation, suitable for exploration of basic physics of time-domain DCS and of its potential. However, the use of similar laser sources has been common in the past for human in vivo investigation [35,36] which encourages us, in order to move towards the clinics, to work on making the instrumentation more compact, by substituting the custom Ti:Sapphire laser with a modification of a commercially available laser that will provide a suitable pulse coherence and power.

Appendix

Here we report additional results for completeness. Fig. 6

Fig. 6.

(a) Electric field auto-correlation functions (g1) with respect to the lag time as calculated for narrow 160 ps gates with an increasing starting time corresponding to the gate positions shown in panel (b). (b) Colored markers represent where the gates have been selected, corresponding to the DTOF. (c) The variation of the intensity auto-correlation intercept β with respect to the sequential gate number. All curves/makers in all panels are color coded to match the position on the DTOF curve in panel (b).

shows additional narrow gate results and Fig. 7

Fig. 7.

Measured and fitted electric field auto-correlation functions for in vivo head experiments. Here we show two gated (early, late) and ungated calculations for different applied pressure conditions: no pressure (circles) and with pressure (diamonds). The solutions to the correlation diffusion equation was used to fit the ungated and the numeric integration was used to fit the gated results (solid lines).

shows additional results from the in vivo head measurements. Specifically, Fig. 6(a) shows the full set of auto-correlation curves from the narrow gate approach for a dynamically homogeneous two layer phantom (DH, δ=5mm, see Fig. 3). In accordance to what has been previously reported in [8], we see a variation in the signal to noise ratio as the gate (width 160 ps) position increases, in 80 ps steps. At later gates the photon counts are reduced due to decay of the DTOF (Fig. 6(a), 6(b)) resulting in a noisier autocorrelation curve. We report a monotonic decrease of β as the gate time increases (Fig. 6(c)).

For the broad gate approach applied in vivo in the head (see Fig. 4) we report the early and late gate estimated auto-correlation curves (Fig. 7). This way we intend to highlight the full picture of observed changes when pressure is applied, for both gates.

Funding

The study was funded by Fundació CELLEX Barcelona, Ministerio de Economía y Competitividad/ FEDER (PHOTODEMENTIA, DPI2015-64358-C2-1-R), Instituto de Salud Carlos III / FEDER (MEDPHOTAGE, DTS16/00087),the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2015-0522), the Obra social “la Caixa” Foundation (LlumMedBcn), AGAUR-Generalitat (2014SGR-1555), and LASERLAB-EUROPE IV. The research leading to these results has partially received funding from the European Union’s Horizon 2020 research and innovation program under LUCA (688303H2020-ICT-2015), the EU Marie Curie Initial Training Network “OILTEBIA” (317526), and BabyLux (620996 CIP-ICT-PSP-2013-7). The LUCA project is an initiative of the Photonics Public Private Partnership.

Disclosures

Turgut Durduran is an inventor on a relevant patent (Patent US8082015B2, “Optical measurement of tissue blood flow, hemodynamics and oxygenation”). ICFO has equity ownership in the spin-off company HemoPhotonics S.L. Potential financial conflicts of interest and objectivity of research have been monitored by ICFO’s Knowledge & Technology Transfer Department. Rainer Erdmann is CEO of Picoquant GmbH. The authors declare that there are no conflicts of interest related to this article.