Dynamics of the human brain network revealed by time-frequency effective connectivity in fNIRS

Abstract

Functional near infrared spectroscopy (fNIRS) is a promising neuroimaging method for investigating networks of cortical regions over time. We propose a directed effective connectivity method (TPDC) allowing the capture of both time and frequency evolution of the brain’s networks using fNIRS data acquired from healthy subjects performing a continuous finger-tapping task. Using this method we show the directed connectivity patterns among cortical motor regions involved in the task and their significant variations in the strength of information flow exchanges. Intra and inter-hemispheric connections during the motor task with their temporal evolution are also provided. Characterisation of the fluctuations in brain connectivity opens up a new way to assess the organisation of the brain to adapt to changing task constraints, or under pathological conditions.

1. Introduction

Functional near-infrared spectroscopy (fNIRS) is a non-invasive imaging technique that has become increasingly popular for brain function research in recent years [1,2]. Based on the exploration of hemodynamic signals, in the same way as functional magnetic resonance imaging (fMRI), and its blood oxygen level dependent signal, fNIRS provides information on the functionally evoked changes in cortical oxyhemoglobin (HbO) and deoxyhemoglobin (HHb) concentrations with relatively low spatial resolution. However, due to several technical advantages (high temporal sampling rate, portability and ability to perform long data acquisitions), fNIRS has been extensively used to measure the magnitude of brain activation during motor or cognitive tasks, in both healthy and diseased populations [3–5]. Nevertheless, as highlighted by some authors, the brain is a complex system par excellence characterised by the co-existence of functional segregated parts of the brain, and functional integration among these parts [6,7]. Functional specialisation, or segregation, implies that elements of the brain network tend to organise into separate, statistically independent areas. It refers to the idea that parts of the brain may, for example, specifically cope with the cognitive [8], perceptual [9] or motor [10,11] components of a certain task. Functional integration, on the other hand, refers to the way these different components are connected to become statistically interdependent to some degree [12]. For example, an fNIRS study [13] in healthy subjects showed different changes in the link between motor cortex (M1), premotor cortex (PMC) and supplementary motor area (SMA) between various finger movement task conditions. By using fMRI, Grefkes and Fink (2011) [14] showed relevant changes in intra- and inter-hemispheric brain links within the motor network after stroke. Therefore, a key challenge in neuroscience, in particular for portable and promising neuroimaging techniques such as fNIRS, is to move beyond identification of regional cortical activations toward the characterisation of interactions between brain areas [15].

Connectivity analyses of the brain have been the object of a growing interest in neuroimaging studies in recent years, and applied to both electrophysiology-based (electroencephalography [16]; magnetoencephalography [17,18]) and hemodynamics-based (fMRI [19,20]; fNIRS [21,22]) modalities. In this line, authors have often used bivariate Pearson correlation analysis in the time domain, or its counterpart, namely coherence in the frequency domain. While these analyses have shown their ability to distinguish between healthy and diseased populations [23,24], they present limitations in two notable respects: first, they do not take into account the directionality of the link between two regions of interest. Furthermore, the time-series analysis of brain activity is typically limited to only two signals (bivariate analysis). That is, these types of analyses are known to not provide a comprehensive assessment of inter-channel interactions, as they ignore influences from other sources [25]. In contrast to undirected functional connectivity, directed effective connectivity (EC) describes the influence that one region of the brain exerts on another. The two most commonly employed methods to analyse the directed influences within the whole brain network are Dynamic Causal Modelling (DCM) [26] and Granger-Causality Modelling (GCM) [15, 27]. DCM is based on a statistical technique to highlight how well a model fits the data. In similar approach, structural equation modeling (SEM) [28] comports a model where parameters are connection strengths or path coefficients between different regions of interest. DCM and SEM were shown to provide similar results [29]. Because these two fixed models imply that regions of interest need to be predefined, the possibly unexpected involvement of brain areas or connections between areas will not be taken into account in uncovering the pattern of connections. While DCM and SEM are model driven methods based on assumptions between intrinsic and extrinsic linked areas, the advantage of GCM is that it does not require any a priori information, as it completely relies on the multivariate auto-regressive (MVAR) modelling of the recorded brain signals [30]. Due to their assumption-free nature, GCM based methods are complementary to DCM [31]. The first studies addressing directed connectivity have adapted Granger’s formalism [32,33], considering that some form of causality from a time series x(n) onto another time series y(n) may be at play, if knowledge of x(n)’s past behaviour proves helpful in predicting y(n). The two time-domain methods derived from Granger causality, the conditional Granger causality (CGC) and partial Granger causality (PGC) [34], are particularly suitable for signals with very low signal to noise ratio. However, in biological time series, and notably in brain analysis, need is to deal with unmeasured latent variables and environmental (exogenous) inputs. For some signals, like local field potential signals, PGC has been proven more successful than CGC, notably in controlling for a third time series that could falsely cause connection between two series of interest [35]. However, CGC and PGC provide causality information only in the time domain [36].

Aside from time domain causality methods, frequency-domain causality methods are able to look at causality at a particular frequency. Frequency-domain causality measures are also tolerant of wide ranges of noise. The directed transfer function (DTF) can quantify causality between different time series, but is unable to differentiate between direct and indirect connections [37] (where the connection x to y could be mediated by z). Therefore, two new developments of DTF methods were proposed, namely the directed DTF [38] and, recently, the non-normalized DTF, which overcomes the drawbacks of DTF and allows discrimination between the direct and indirect connections [39]. Similar to DTF, partial directed coherence (PDC) is based on the Fourier transformation of the MVAR coefficient. Unlike DTF, PDC can differentiate between direct and indirect connections and is currently the most widely used method in biomedical signals. Its major shortcoming, however, is that any additional source affects the strength of already present sources, due to the fact that normalisation in the equation of PDC is done with respect to the sources [40]. Yet, the generalised partial directed coherence can accommodate differences in the individual variances of the subjected time signals [41]. The re-normalised partial directed coherence allows overcoming the limitation related to the addition of the source without requiring any frequency dependent significance level [42].

Directional information provided by the aforementioned methods offers the potential for mapping directed influences between regions of the brain. However, different studies applying such analyses to fNIRS data [43–45] have implicitly considered that patterns of connectivity were stationary within the scanning period: indeed, analysing the global (average) connectivity pattern over a relatively long time session conceals its temporal evolution during the task. Though intermittence between functional integration and segregation in the brain leads to the idea that information flows between two brain areas are highly dynamic. Recent studies have shown that brain connectivity also evolves over time in a resting state, as it may do in continuous tasks [46,47]. Such dynamic brain organisation is actually a key property of any complex system that shows high adaptive capacities [48], and time-frequency analyses can provide insight into it.

Here, we proposed to perform EC analyses based on a novel method applied in fNIRS, namely time-resolved partial directed coherence (TPDC) [20, 22]. TPDC has been developed and applied to EEG, MEG or fMRI signals [49]. This method is based on directed effective connectivity to compute a time-frequency analysis established on an MVAR model. Allowing the application over time of multiple PDC [50], TPDC makes it possible to account for the evolutions over time and frequency bands of the information transfer directed between multiple time series, i.e. between regions of interest, for probing diseased [51, 52] or healthy brain [18, 49].

To fully understand the functioning of the brain and its adaptive capacities, we have to take into account its dynamic organisation through the time-frequency evolution of connectivity patterns. The purpose of this study was therefore (i) to expose the TPDC method on fNIRS signals and (ii) to reveal the ability of the proposed method in assessing the time-dynamics of brain connectivity during a simple motor task performed by healthy subjects. To this end, we first present experimental fNIRS data collection. Second, we develop the TPDC computation steps. Third, we show results of this example application of the TPDC effective connectivity approach to experimental fNIRS data.

2. Materials and methods

2.1 Participants

Six healthy volunteers took part in this study (aged 28.6 ± 3.8 years). All participants gave written informed consent before participating in the study. All participants were right handed according to the Edinburgh Handedness Inventory [53] and reported normal hearing and normal or corrected vision. None had any sign of neurological disease, nor reported extensive practice in music. All procedures were approved by the local ethics committee and complied with the Declaration of Helsinki for human experimentation.

2.2 Experimental design

The experiment was conducted in a quiet and dimly-lit room. Participants were seated comfortably on an adjustable chair. They were instructed to remain relaxed and to refrain from extensive head motion. After positioning fNIRS probes over the head, fNIRS data recording was initiated, with a one-minute resting state (quiet baseline) while the subjects’ eyes were open. It provides the best possible baseline condition before the experimental task. Then, participants were asked to perform a continuous (6 minutes and 40 seconds) tapping task, according to a conventional synchronisation-continuation paradigm [54]. During the initial synchronisation phase (around 15 seconds), the tapping tempo was prescribed by a PC-driven auditory metronome delivering 20 signals at a frequency of 1.5 Hz. Once the metronome stopped, participants were requested to continue tapping by maintaining the prescribed tempo as accurately and regularly as possible for the whole trial duration. Data from the last 6 minutes of each trial was submitted for analysis.

2.3 Data collection

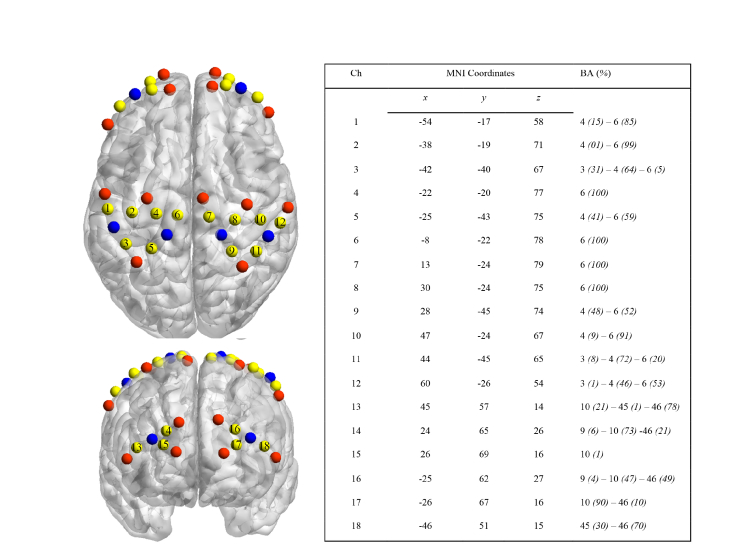
Changes in HbO and HHb were assessed using two continuous wave multi-channel near infrared spectroscopy systems (Oxymon MkIII and Octamon, Artinis Medical Systems, The Netherlands) at two wavelengths (Oxymon = 763 and 855nm, Octamon = 742 and 848nm). The sampling rate was set at 10 Hz. In the present study, we used 10 transmitters (pulsed laser) and 4 receivers (avalanche photodiode), which were coupled through fiber optic cables mounted onto a customised head cap. The 16-channel array with a transmitter-receiver spacing of 30 mm extended on three regions of interest: PMC, M1 and SMA in both hemispheres. In addition, the 2^nd 8-channels system (Octamon, inter-probe distance of 35 mm) covered the dorsolateral (DLPFC) and orbitofrontal (OFC) cortices in both hemispheres. After positioning the head cap on the vertex location (Cz), a 3D-digitiser (Fastrack, Polhemus, United States) allowed the collection of the 24 probe positions (x,y,z space). Our channels have been marked at the start of the task and thus provide time synchronization between our signals. In the present study, based on the selected 5 regions of interest (M1, PMC, SMA, OFC and DLPFC), 18 channels were retained for analysis. NFRI function [55] was used to extract the Montreal Neurological Institute coordinates (MNI). Localisation, MNI coordinates and Brodmann area (Chris rorden’s MRIcro) correspondences are reported in Fig. 1.

Fig. 1.

On the left, fNIRS probes location using BrainNet Viewer [56] with transmitters (in red), receivers (in blue) and channels (Ch, in yellow). On the right, mean MNI coordinates and Brodmann area (BA) correspondence for each channel, to check to what extent fNIRS signals reflect the effect of several cerebral areas (represented in %) due to the spatial resolution of the system.

2.4 fNIRS preprocessing

First, we extracted raw data (light intensity) from the ARTINIS software (Oxysoft v3.0.95). Data was then uploaded using a MATLAB (The MathWorks) in-house script, and converted to optical density (OD) [57] defined by:

$$\Delta O{D^{\lambda }}_{ij(t)}=Ln\left[\frac{{\Phi }^{\lambda }ij(0)}{{\Phi }^{\lambda }ij(t)}\right]$$ (1)

where Φ is the intensity, i is a source position, $j$ is a detector position, and λ the wavelength of light. Next, we applied the moving standard deviation and spline interpolation methods [58] (SDThresh = 20, AMPThresh = 0.5, tMotion = 0.5s, tMask = 2s and p = 0.99), and then wavelet artefact correction [59] (with probability threshold α = 0.1) as recommended [60], to remove possible motion artefacts. To access HbO and HHb relative concentration changes (Conc) (expressed in µM) we applied the modified Beer-Lambert Law [61] to the OD data that included an age-dependent constant differential path length factor (4.99 + 0.067*Age^0.814) [62].

White noise signal is one of the most harmful effects in connectivity analysis and can create spurious links, whether false positives or false negatives. As a consequence, we used a simple pre-processing step computing the power spectra to ensure the discrimination of noisy signals. For that purpose, we obtained the power spectra of each HbO time series (more sensitive to physiological noise than HHb) for each channel: detection of a peak value around 1Hz in the time series reflecting the presence of the heartbeat in the fNIRS signal [63], was considered to indicate a good contact between the optode and the scalp. By running this pre-processing, 2 channels were removed in our 6 subjects, leaving 106 channels (18 channels per subject, minus 2 bad channels) to be used for the subsequent TPDC’s analysis. Subsequently, a linear detrending was used to remove slow drifts of Conc data, and time series were centered to zero mean to satisfy the criteria of second order stationary. Importantly, we did not use any filtering on our Conc data before further analysis, as it has been shown that filtering could lead to spurious connections [64].

2.5 Time-resolved partial directed coherence

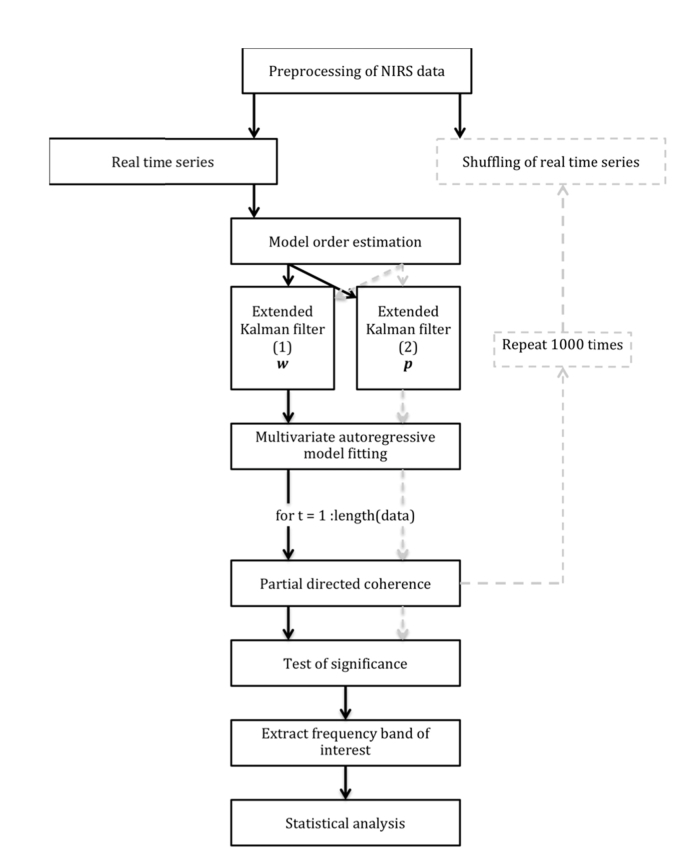
Using time-frequency causality allows for analysis of the temporal dynamics of the causality at any particular frequency in focus. The TPDC (Fig. 2) is based on dual-extended Kalman filtering [65], and allows time-dependent auto regressive (AR) coefficients to be estimated. In general, the signals are analysed with static AR coefficients, meaning that the fitted model and the AR coefficients remain the same for the complete length of the signal. For non-linear signals like fNIRS, the model should be time varying and the coefficients need to be estimated regularly over the course of the time-period. Regularly estimating the coefficients is termed as adaptive auto-regressive process.

Fig. 2.

Flow chart of the various steps used for the TPDC analysis. The black arrows and rectangles (left side) present the overall process using real fNIRS data. The dotted gray arrows and rectangles (right side) display the bootstrapping process undertaken.

The expression for an adaptive auto-regressive process can be given as follows:

$$x(t)={\displaystyle \sum _{r=1}^{r=p}{a}_r(t)x(t-r)+\eta (t)}$$ (2)

where a_r(t) are the time-varying MVAR coefficients, p is the model order of time series x(t) and η(t) is the zero-mean Gaussian noise process. To sum up, the extended Kalman filter used in the TPDC analysis is a predictor-corrector algorithm that estimates states of a process. We can model an fNIRS time series using a general non-linear state-space model:

$$x(k)=F\left[x(k-1),w\right]+B\upsilon (k)$$ (3)

$$y(k)=Cx(k)+n(k)$$ (4)

where y(k) is the target time series and the aim is to estimate x(k). Since the present purpose is to estimate the model parameters related to the non-linear function F, only the process Eq. (2) is considered. Both noise processes υ(k) and n(k) are white, zero mean and Gaussian. At each time point, previous state estimates and weight estimates are fed to both of the Kalman filters. Both predictors are then corrected on the basis of observed data y(k), such that they yield current state and weight estimates. By using two Kalman filters working in parallel with one another, we can estimate both state and model parameters of the system at each point in the time series. After estimating the time-dependent MVAR coefficients, the next step is to use those coefficients for the calculation of causality within the time series. By calculating the time-dependent MVAR coefficients at each time point, PDC, based on the principle of Granger causality can be computed. Then, the Fourier transform of these coefficients and PDC can be calculated using the formula:

$$\left|{\pi }_{i\leftarrow j}(\lambda )\right|=\frac{\left|A_{ij}(\lambda )\right|}{\sqrt{{\displaystyle \sum k{\left|A_{kj}(\lambda )\right|}^2}}}$$ (5)

where A_ij(λ) is the i,j – th element of A(λ) . Then the PDC values follow normalisation properties such as:

$$0\le {\left|{\pi }_{ij}(\lambda )\right|}^2|\le 1$$ (6)

By calculating PDC at each time point, multiple matrices corresponding to the time-frequency causality from two time series are obtained. All possible connections between channels (n = 18) were analysed and resulted in 306 connections for each subject. In fNIRS time series, the frequency band of interest is [0.009-0.08] because it reflects the neurovascular coupling frequency band [1,2]. We thus extracted this mean frequency band of interest for each connection.

2.6 Statistical analysis

The stationarity of the time series was tested using an augmented Dickey-Fuller test in which it is defined if the absolute solution of the so-called characteristic equation is greater than unity [66]. Since the PDC’s measures have a non-linear relation to the time series data from which they are derived, testing for significance can be difficult to perform. To deal with this issue, after the TPDC values had been estimated, the significance level was calculated from the applied data using a bootstrapping method [37]. In short, the original time series of length (n) is divided into (k) smaller non-overlapping windows of length υ (n = kυ) (we used parameters k = 12, v = 30 seconds). The order of these windows is randomly shuffled to form a bootstrap sample of the original time series. Then, the MVAR model is fitted to the shuffled time series, and the TPDC value can be estimated. The process is repeated 1,000 times. The TPDC value for each of these 1,000 random permutations is estimated and the 95^th percentile TPDC value is taken as the significance level. This process is performed separately for each subject. The resulting value is retained as the significance threshold value for all connections. The significance of the causal measures evaluated from the actual data can be assessed on this basis. In this study the open source Matlab package autoregressive fit (ARFIT) [67], which allows for modelling and analysing multivariate time series, was used for estimating the AR coefficients from the spatially filtered source signals.

We extracted the mean and standard deviation (std) of TPDC values during the finger-tapping task (6 minutes) to compare the connectivity strength and variability for each connections. Then we calculated the Shannon entropy (E) of the TPDC time series (wentropy Matlab function), to assess the diversity, or uncertainty of each connection’s strengths.

For all variables (mean, std and E) we checked the normality of the data using the Shapiro-Wilk test. A one-way ANOVA was then performed (Statistica 7.1) to compare among connections (n = 14 after Bootstrapping) (p = 0.05). In case of a significant difference, we performed post-hoc Bonferroni correction.

3. Results

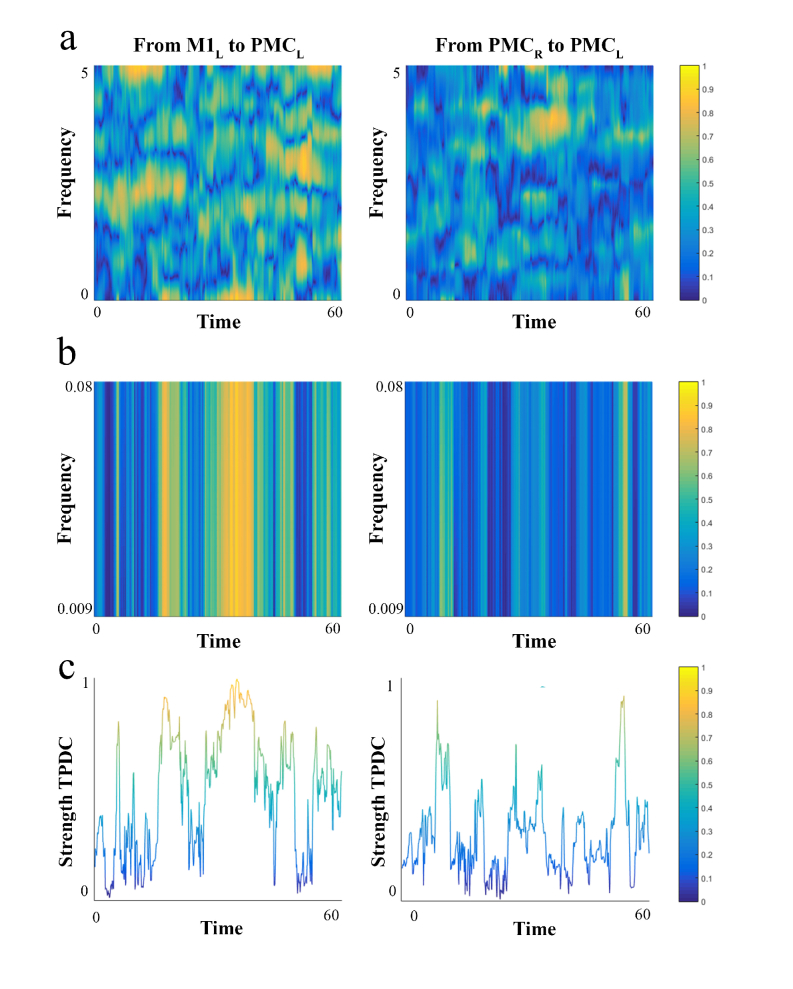
The result of the TPDC analysis is a time-frequency matrix for each connection reflecting the strength of the information exchange. We extracted our frequency band of interest and averaged the matrix in the frequency space to obtain a single time series reflecting the time evolution for each connection (Fig. 3).

Fig. 3.

Example of time-frequency plots generated by TPDC analysis during 60 seconds of the finger-tapping task for 2 connections (From M1_L to PMC_L and PMC_R to PMC_L. a) Time frequency plot for the whole frequency band (5 Hertz). X-axis represents time in seconds. Y-axis the frequency in Hertz. Color bars represent the normalised (0 to 1) coherence of the connectivity extracted from TPDC results (blue close to zero connection and yellow close to 1 representing strong connection). b) Time frequency plot for the frequency band of interest [0.009 to 0.08 Hz]. c) Mean of the frequency band of interest. Y-axis represents strength of connection. This example shows higher connectivity strength from M1_L to PMC_L compared to PMC_R to PMC_L.

All the time series were deemed stationary, as we did not detect any unit root. A total of 14 connections (at the whole group level) out of 306 survived the data-driven surrogate (p < 0.05). The whole surviving network with the directed connections is shown in Fig. 4. 12 of 14 connections were normally distributed for the mean and 13 of 14 for std and E. Of the significant connections, four were unidirectional connections and five were bi-directional. The unidirectional connections, namely M1_L to PMC_L, PMC_L to DLPFC_L, PMC_L to PFC_L and SMA_L to M1_L, were intra-hemispheric and located on the contralateral side to the tapping finger (right hand). The bi-directional connections were all inter-hemispheric between DLPFC_L - DLPFC_R, OFC_L - OFC_R, PMC_L - PMC_R, SMA_L - SMA_R and M1_L - M1_R.

Fig. 4.

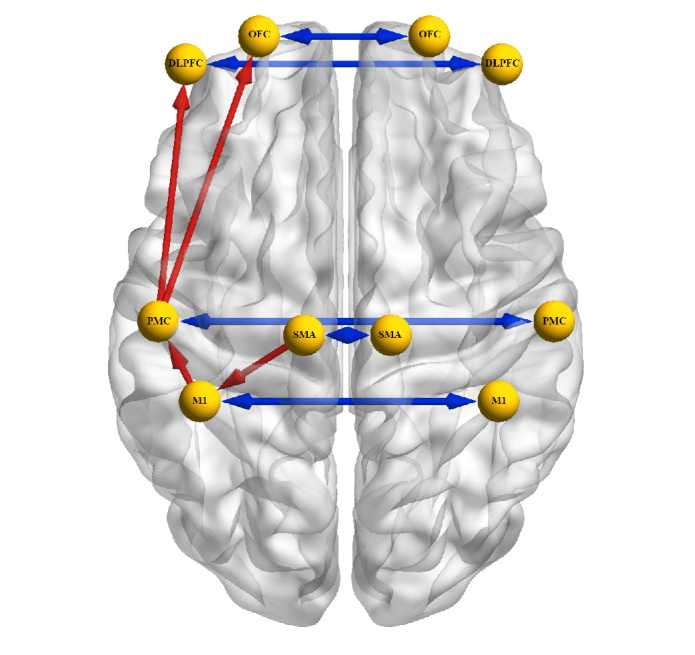
Whole surviving connections after bootstrapping analysis (n = 14). In blue, bi-directional connections (inter-hemispheric) and in red uni-directional connections located only in the contralateral hemisphere.

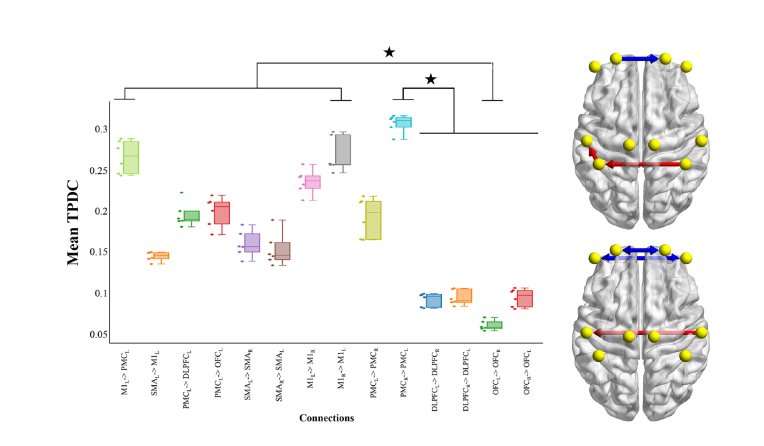
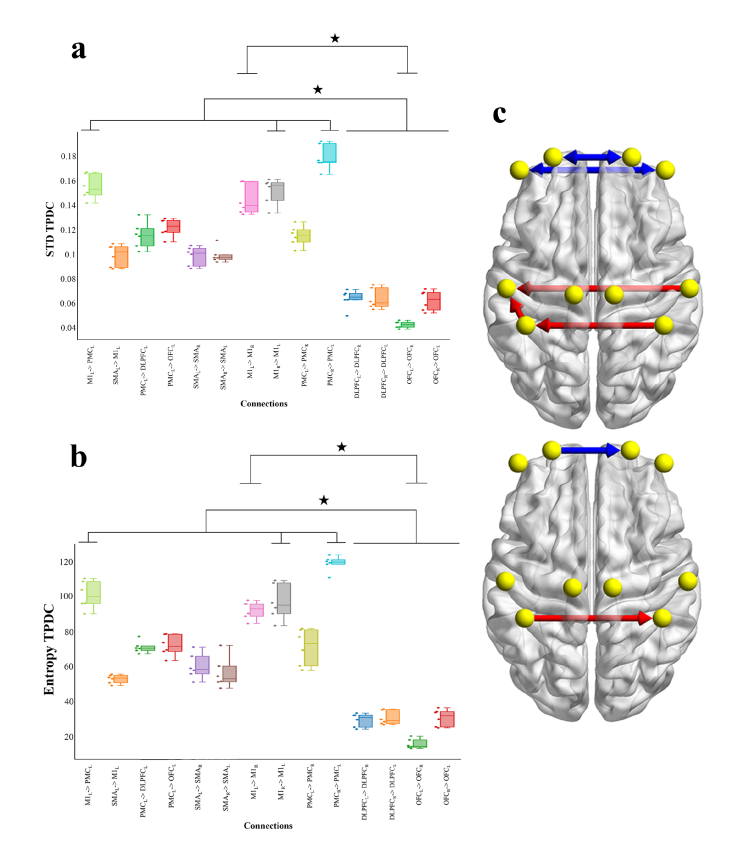
The ANOVA revealed significant differences in mean TPDC values between connections M1_L to PMC_L and PMC_R to PMC_L, compared to OFC_L to OFC_R, and PMC_R to PMC_L compared to bi-directional OFC and PFC connections (Fig. 5).

Fig. 5.

Average of the TPDC results with Box-plot, individual values and brain representation. Box-plot reflects median, quartile and dots of individuals values for each subject. X-axis represents connections. Y-axis is the mean TPDC value. Stars indicate Anova statistical significance at p = 0.05. On the right, representation of statistical significance on brain surfaces (differences are represented between red and blue connections).

For the std and the Entropy of TPDC values, the analysis showed a statistical difference between PMC_R to PMC_L, M1_R to M1_L and M1_L to PMC_L compared to bi-directional OFC and PFC connections and between M1_L to M1_R compare to OFC_L to OFC_R (Fig. 6(a)-6(c)).

Fig. 6.

Standard deviation and entropy of the TPDC results with Box-plot, individual values and brain representation. Box-plots in a) and b) reflect median, quartile and dots of individuals values for each subject. X-axis represents connections. Stars indicate Anova statistical significance at p = 0.05. a) STD TPDC. b) Entropy TPDC. c) Representation for both STD and Entropy of statistical significance on brain surfaces (differences are represented between red and blue connections).

4. Discussion

In the present study we focused on the mathematical approach to a time-frequency effective connectivity analysis applied to experimental fNIRS signals. In contrast to other methods currently used in the neuroimaging literature to assess brain network connectivity, the proposed TPDC method provides important insight into the dynamics of connectivity in both the time and frequency domains. Based on an MVAR coefficient assessed by a dual-extended Kalman filtering, this analysis can be used in a number of biological time series (e.g. EEG, MEG, fMRI and fNIRS) to assess the dynamic evolution at rest, for experimental block design as well as during prolonged cognitive and/or motor task performance. Here, we applied this method on real fNIRS data from bi-hemispheric DLPFC, OFC, PMC, SMA and M1 areas (18 channels) during a simple continuous finger-tapping task.

After correcting or disregarding noisy fNIRS signals, we applied TPDC analysis onto the time series of HbO concentration signals and extracted the dynamic effective connectivity and its temporal evolution on our frequency band of interest (i.e., neurovascular coupling [0.009 to 0.08 Hz] [1,2]). The significance testing of our possible 306 connections was performed at the end of the processing using a bootstrapping method: 14 connections survived after running the dedicated analyses. The advantage of the TPDC compared to other connectivity methods proposed in the literature is its ability to assess not only the mean connectivity during the whole time series but also its dynamics, which is of major interest for a better understanding of the brain’s dynamic functional (re)organisation.

The lagged-correlation based effective connectivity methods (e.g. GCM) have been extensively used in neuroscience to shed light on directional functional connectivity of the brain. Being complementary to DCM, GCM methods are not based on pre-assumption about the brain, hence increasing their potential applications in many fields. Studies addressing the problem of viability for using GCM on fMRI data claim that this technique is appropriate and a robust measure for fMRI [68]. This can also be relevant to fNIRS since this neuroimaging technique also reflects hemodynamic changes and relies on the neurovascular coupling in the brain [69].

Results from the present example application highlight the fluctuations of connectivity patterns between distant cortical areas, reflected by high std and Entropy results for some specific connections (Fig. 6(a), 6(c) and 6(b)). First, TPDC shows that there was higher connection’s strength over the sensorimotor areas than PFC regions. Then we show high dynamics in all connections during the motor task revealed by std and E results with higher fluctuations in M1_L to PMC_L, PMC_R to PMC_L, M1_L to M1_R compared to the four connections over the PFC. We also show a higher entropy of TPDC values in M1_L to M1_R compared to OFC_L to OFC_R. Within the context of the present study, our results (std and E) suggest that the effective connectivity evolves dynamically in time.

The network of effective connectivity between cortical regions of interest (ROIs), namely sensorimotor cortex (SMC), PMC, DLPFC, during a finger tapping task in healthy subjects has been presented in earlier studies using MEG or EEG source analysis [18,70]. The GCM analysis has also been applied to fNIRS data to determine the effective connectivity between cortical ROIs in animal and human [13,71,72] experiments. In the above-mentioned studies, simultaneous use of one or two neuroimaging modalities has shown bi-directional or uni-directional information flow patterns between the SMC, PMC and DLPFC ROIs. Recently, by combining fNIRS, EEG and fMRI neuroimaging methods, the effective connectivity of the same cortico-cortical sensorimotor networks (SMC, PMC, and DLPFC) during different finger movement tasks has been revealed [49]. However, none of the above studies has looked into the dynamics of the significant connections during the task, between the three ROIs.

Additionally, in the present study we have also included two more important regions involved in motor tasks, the SMA and OFC, assessed in the literature both in activation and connectivity studies [4,14]. We were also able to look at the dynamic inter-hemispheric connections during a unilateral hand movement task, whose importance has been previously shown in such tasks using EEG [73]. Our study highlights a low variability (std and entropy) of bi-directional connectivity in the frontal cortex during a simple prolonged motor task. The PFC being defined as one key anatomical region involved in cognitive processes [74] leads us to conclude that our present task does not seem to require a high implication at the cognitive level (low TPDC strength in OFC and DLPFC areas (cf. Fig. 5)). At the sensorimotor level, observing high bi-directional connectivity strengths (Fig. 5) between both hemispheres seems consistent with the literature: First, it is well known that there are high bi-hemispheric functional connections for multiple sensorimotor areas at rest and during a motor task [75,76]. Second, our subjects performed a uni-manual motor task, of which the contralateral motor network is known to be primarily involved [13].

The functional network of cortical ROIs involved in rhythmic and sequential finger movements in healthy subjects has been analysed using EEG [77], MEG [70], fMRI [78] and fNIRS [79] separately, and the SMC, PMC and DLPFC have been found to be the three core regions of the cortical sensorimotor network for movement control [80]. Using TPDC method, our present findings allow extending a previous fNIRS study that showed only bi-directional effective connectivity in the contralateral hemisphere between SMC and PMC during performance of a hand motor task [13]. The directions of information flow for rhythmic movements in the aforementioned studies have shown that the SMC plays a major role in directing voluntary motor tasks [22]. Nevertheless in this previous study, authors analysed only the mean of connectivity strength and didn’t take into account the dynamic of the network during the task. Since one of the key properties of the brain is the continuous juggling between functional integration and segregation, our results emphasise dynamic changes over short time windows (Fig. 3(c)) in the configuration of brain connections.

5. Methodological considerations and limitations

5.1 Pre-processing of fNIRS data

Movement artefact is known to be one of the biggest causes of spurious connectivity analysis. In this study we used a combined artefact deletion technique (spline interpolation and wavelet). While we used this combined pre-processing approach with parameters proposed in the literature [58–60], the potential effect of a few undetected artefacts, or the effect of some signal transformation due to the correction on causality analysis, remain however to be clarified. More generally, discriminating between a ‘good’ and a ‘bad’ channel in the analysis of fNIRS time series is still an unsolved methodological issue. While it seems quite easy to discriminate between very noisy or not noisy signals, several other characteristics of the signal need to be carefully taken into account to determine which fNIRS signals are suitable for subsequent analyses. A comprehensive investigation of the different fNIRS pre-processing methods, including use of simulated data with multiple levels of noise and real fNIRS data from different experiments, probe positions and systems of data collection, would be very valuable in the aim of developing a unified procedure to select physiologically relevant fNIRS signals.

5.2 Time partial directed coherence

Despite the advantages of using TPDC over conventional causality methods, one drawback is that the TPDC method is time-consuming, owing to the estimation of MVAR coefficients at each time point. This limits its usage depending on the available computational resources and is not appropriated for fast diagnosis. It is important to point out the fact that the Granger Causality approach was used in this study to measure the brain dynamics inherent to a finger-tapping task, the interplay between segregation and integration, and we did not study the underlying mechanism involved in this particular motor task. Our connectivity results are dependant on the targeted cortical areas and need to be considered within the limitation of the spatial resolution of fNIRS.

Due to its poor spatial resolution but relatively high sampling frequency, fNIRS is a promising tool to investigate the dynamic connectivity of the cortex, but appears a limited tool to realise a mapping of connectivity for the whole brain. Nevertheless, some recent studies highlight the importance of these dynamics or fluctuations in the brain more than the localisation of the static connectivity between brain areas (mapping). One of the important developments needed to improve the TPDC method is to investigate the functional properties of these multiple networks with more appropriate tools. Furthermore, we analysed the mean of the dynamics during the entire motor task and did not take into account the global network properties. A graph analysis approach could be one way to extract the functional properties of TPDC results combining each connection in the same time. In addition, to specify which parts of the brain are connected to others, graph analysis could help our understanding of the functional organisation such as integration, segregation or small world network organisation. Nevertheless, few fNIRS studies have investigated this kind of analysis up until now and refer to another level of abstraction for the comprehension of the data [81].

6. Conclusion

This study proposed TPDC as a new time frequency effective connectivity analysis to be applied to fNIRS signals over multiple bi-hemispheric brain areas (M1, PMC, SMA, OFC and DLPFC) to investigate the time dynamics of the brain network during a continuous finger-tapping task. The present contribution allows us to specify the direction of the link between two regions of interest: indeed, four connections (SMA_L to M1_L, M1_L to PMC_L, PMC_L to DLPFC_L and PMC_L to OFC_L) have been shown to be unidirectional and five are bi-directional connections, information that would typically be concealed using common functional undirected connectivity methods like correlation or coherence. Due to its ability to explore the temporal dynamics of connectivity, the present application example of TPDC highlights that this methods allows going beyond previous analysis in the literature, showing for example high Entropy during the task in the sensorimotor network. Such fluctuations constitute one of the key properties of a healthy adaptive brain that needs to respond to any upcoming internal or external constraints at multiple time scales. Thus, as a first step, it seems essential to better understand the basic dynamic organisation of the brain during a given task performance, with a view to further relating such fluctuations to the capability to adapt when facing constraints.

Funding

The PHC PROCOPE 2017 (DAAD and Campus France, Project n° 37815RK) supported this work. Doctoral School (ED 463) in Human Movement Science also made this collaborative project possible.

Disclosures

The authors declare no conflicts of interest, financial or otherwise.