A joint logistic regression and covariate-adjusted continuous-time Markov chain model

Summary

The use of longitudinal measurements to predict a categorical outcome is an increasingly common goal in research studies. Joint models are commonly used to describe two or more models simultaneously by considering the correlated nature of their outcomes and the random error present in the longitudinal measurements. However, there is limited research on joint models with longitudinal predictors and categorical cross-sectional outcomes. Perhaps the most challenging task is how to model the longitudinal predictor process such that it represents the true biological mechanism that dictates the association with the categorical response. We propose a joint logistic regression and Markov chain model to describe a binary cross-sectional response, where the unobserved transition rates of a two-state continuous-time Markov chain are included as covariates. We use the method of maximum likelihood to estimate the parameters of our model. In a simulation study, coverage probabilities of about 95%, standard deviations close to standard errors, and low biases for the parameter values show that our estimation method is adequate. We apply the proposed joint model to a dataset of patients with traumatic brain injury to describe and predict a 6-month outcome based on physiological data collected post-injury and admission characteristics. Our analysis indicates that the information provided by physiological changes over time may help improve prediction of long-term functional status of these severely ill subjects.

1. Background

In medical research, it is often of interest to investigate the association between patient specific longitudinal information collected over some period and a primary outcome. For instance, studies on patients with AIDs have assessed the relationship of CD4 counts as a longitudinal covariate marker and survival [1], and traumatic brain injury (TBI) studies have looked at the relationship between intracranial pressure and ICU length of stay [2]. A classical model to describe this type of associations is a survival model with time-dependent covariates. However, in the past few years, joint models for longitudinal and time-to-event data [3, 4] have gained popularity because the joint modeling strategy can account for measurement error on endogenous time-dependent covariates such as longitudinal biomarkers. For outcomes measured repeatedly over time, longitudinal generalized linear models with time-dependent covariates have been applied in many settings.

A stochastic process approach based on Markov chains has also been used to study associations between longitudinal outcomes and longitudinal predictors. A Markov chain is a collection of random variables or events where the probability of occurrence of future events depends only on the present state of the system and not on the path that led to the present state. Markov chains have been generally used as response or dependent variables, for example, the progression of several neurological diseases, but they have seldom been used as predictors in scientific research. In 2009, Hubbard et al. developed a joint model to study the relationship between self-rated health and changes in physical function in adults 65 years of age or older. In their model, a binary outcome measured longitudinally was related to a non-homogenous Markov process model through a logit function [5].

Although statistical methods have been proposed for longitudinal covariates and outcomes measured over time, there are few research studies on longitudinal covariates and cross-sectional responses, particularly categorical. Wang et al. proposed a joint longitudinal/generalized linear model for a cross-sectional endpoint, where one or two features of longitudinal curves from a linear random effects model are used as covariates in their primary model [6]. Extensions of this model relaxed the normal distribution assumption of the random effects [7-9], the independence assumption of the within-subject measurement errors [10], or modeled non-linear longitudinal covariate effects [11, 12]. In these models, the features included in the primary model may not be representative of the overall behavior of the individual curves. For instance, Wang et al. in a childhood growth study used the initial BMI value at age 3 (random intercept) and the rate of change of BMI (random slope) to predict the risk of hypertension later in life [6], while in a pregnant women data example, De la Cruz et al. studied the effects of β-HCG longitudinal process on normal versus abnormal pregnancy using in their primary model random effects that represented the curve levels and inflection point of the curves [11].

Functional discriminant methods such as the generalized functional linear model with a scalar response and a functional predictor [13, 14] have also been applied to model a cross-sectional outcome as a function of longitudinal covariates [15, 16]. Other functional data analysis (FDA) techniques based on dimension reduction such as functional principal component analysis and filtering methods have been applied to select features or “covariates” for posterior analysis [14]. Even though models based on FDA techniques have proven to be useful to describe associations and for prediction purposes, the application of these models poses challenges principally related to the selection of adequate parameters to represent complex processes (e.g. choosing basis functions, number of eigenfunctions, smoothing penalties, and number and location of knots) and to computational costs.

Another approach for classification problems with binary outcomes and subject features measured repeatedly over time was proposed by Tomasko et al.[17]. They introduced the longitudinal discriminant analysis classifier where estimated means and covariance matrices from mixed models are embedded in linear discriminant functions. Studies that applied this method showed good discrimination power [18, 19] but were based on saturated models for the mean response with high variance associated with its parameters. In addition, the mixed model assumptions of normal responses and linearity on the model parameters may be too restrictive to represent complex longitudinal data.

In most models that have been developed in the past for longitudinal predictors the outcome is measured multiple times or is a death process. Models proposed for responses measured at a single time point have been based on mixed models or functional predictors, characterizing continuous curves with random effects or functional parameters that may not represent the overall behavior of the individual profiles.

In an unpublished dissertation in 2011 titled ‘Logistic regression with Markov chains as covariates’, Ho used discrete-time Markov chains (DTMCs) in a logistic regression model to predict a binary outcome. In his model, the transition probabilities that characterize the discrete process were included as covariates. This method was applied to a lung cancer case-control study to assess the effects of DNA damage/non-damage processes after carcinogenic exposure on lung cancer incidence. Unlike DTMCs where a system evolves through discrete time steps, in continuous-time Markov chains (CTMCs) changes to the system can happen at any time on a continuous interval.

In this study, we propose a novel approach based on Markov chains to model a cross- sectional binary response as a function of a longitudinal covariate process. The model proposed here is a joint logistic regression and Markov chain model based on CTMCs. The applicability of this model is particularly appealing to longitudinal data where changes can occur rapidly and unexpectedly at any time, such as physiological dynamics in the ICU. The joint model developed in this manuscript is applied to a cohort of patients with traumatic brain injury, where physiological data collected after injury and other baseline data are used as predictors of a 6-month binary outcome. We expect that this model makes an important contribution in the clinical setting as a guide for clinical management of patients, and in research studies, in the design of adaptive clinical trials, where cumulative longitudinal data would allow to update model-based risk scores in interim analyses.

The organization of this manuscript is as follows. Section 2 describes the joint proposed model, likelihood function, estimation and determination of initial values. In section 3 we perform simulations to validate the estimation procedure, giving some explanation on how the data were simulated. The TBI dataset where the joint model is applied (section 4) is used to determine the simulation parameters in section 3. This paper concludes with a discussion of our findings in the last section.

2. Methods

2.1 The joint logistic regression and two-state CTMC model with covariates

The joint logistic regression and two-state CTMC model with covariates is a model where a longitudinal covariate process that depends on non-dynamic variables and is bounded by two possible values is jointly modeled with other non-dynamic covariates in a logistic regression model.

Let Y be a binary outcome (Y = 0,1) and Z(t) a homogeneous CTMC with a state space S = {1,2} characterized by the transition intensities q₂₁ and q₁₂, where q_Urepresents the transition rate from state i to state j, with i, j = 1,2. The theory of CTMC can be found elsewhere [20-22]. Assume that, x^T = (x₁, x₂, …, x_(p–1)) is a vector of p–1 covariates directly related to Y; v^T = (v₁, v₂, …, v_(r–1)) are r–1 covariates related to Y through the transition rate q₂₁; w^T = (w₁, w₂, …, w_(s–1)) are s–1 covariates related to Y through q₁₂; and π(x, q₁₂, q₂₁) is the probability of Y = 1 given the covariates x and the transition rates q₁₂ and q₂₁.

The joint logistic regression and two-state CTMC model with covariates can be written as

$$log\left(\frac{\pi (\mathbf{x},q_{12},q_{21})}{1-\pi (\mathbf{x},q_{12},q_{21})}\right)=\mathbf{x}{\ast }^T\mathbf{\beta }+{\alpha }_1{q}_{21}+{\alpha }_2{q}_{12}=\mathbf{x}{\ast }^T\mathbf{\beta }+{\alpha }_1{e}^{\mathbf{v}{\ast }^T{\mathbf{\delta }}_1}+{\alpha }_2{e}^{\mathbf{w}{\ast }^T{\mathbf{\delta }}_2}$$ (1)

where β = (β₀, β₁, …, β_p)^T is the effect of x* = (1,x^T)^T on the outcome; α₁ and α₂ are the overall effects of the transition intensities q₂₁ and q₁₂, respectively, on the outcome; δ₁ = (δ₁₀, δ₁₁, …, δ_1(r–1))^T is the effect of v* = (1,v^T)^T on the transition from state 2 to state 1; and δ₂ = (δ₂₀, δ₂₁, …, δ_2(s–1))^T is the effect of w* = (1,w^T)^T on the transition from state 1 to state 2. Because we assume a stationary process, the probability of moving from one state to another in t units of time is the same at any time point. Therefore, α₁ and α₂ are constant effects of the transition rates at any time point. The vectors v, w, and x could consist of the same covariates or at least one covariate could be different.

This model can be thought as a two-component model where the Markov chain submodel given by q₂₁ = e^v*Tδ1and q₁₂ = e^w*Tδ2 is embedded in the main outcome model that contains x, q₁₂, and q₂₁ as covariates.

Interpretation of the parameters α₁ and α₂ in the main outcome model

The association of the covariates q₂₁ and q₁₂ with the outcome Y can be interpreted as follows: for each unit increment in the hazard rate of leaving state 2, the odds of Y = is expected to change by a multiplicity of e^α1, and for each unit increment in the hazard rate of leaving state 1 the odds of Y = 1 is expected to change by a multiplicity of e^α2, holding other covariates x constant. This means that a higher hazard rate of moving from state 2 to state 1 will increase the probability of Y = 1 for a positive value of α₁, and similarly, the probability of Y = 1 will increase with a higher rate of change from state 1 to state 2 for a positive value of α₂.

2.2 The Likelihood function

The likelihood function for a regular logistic regression model [23, 24] and the likelihood function for a two-state homogeneous CTMC, where the transition probabilities can be stated explicitly by solving a system of differential equations [22], can be considered simultaneously in a single equation to build the likelihood function for the joint proposed model.

For a total of N subjects with T_n observations for subject n, the joint likelihood function can be written as,

$$L=\prod _{n=1}^N\{{\left(\frac{e^{{\mathbf{x}}_n^{\ast T}\mathbf{\beta }+{\alpha }_1{q}_{21,n}+{\alpha }_2{q}_{12,n}}}{1+e^{{\mathbf{x}}_n^{\ast T}\mathbf{\beta }+{\alpha }_1{q}_{21,n}+{\alpha }_2{q}_{12,n}}}\right)}^{y_n}{\left(\frac{1}{1+e^{{\mathbf{x}}_n^{\ast T}\mathbf{\beta }+{\alpha }_1{q}_{21,n}+{\alpha }_2{q}_{12,n}}}\right)}^{1-y_n}\left(\prod _{k=2}^{T_n}\prod _{i=1}^2\prod _{j=1}^2{[P_{Z_n\left(t_{n,k-1}\right)=i,Z_n\left(t_{n,k}\right)}=j(t_{n,k}-t_{n,k-1}\left)\right]}^{I_i\left[Z_n\right(t_{n,k-1}\left)\right]I_j\left[Z_n\right(t_{n,k}\left)\right]}\right)(\prod _{i=1}^{2}P{\left[Z_n\right(0)=i]}^{I_i\left[Z_n\right(0\left)\right]}\left)\right\}=\prod _{n=1}^N\left\{{\left(\frac{e^{{\mathbf{x}}_n^{\ast T}\mathbf{\beta }+{\alpha }_1{q}_{21,n}+{\alpha }_2{q}_{12,n}}}{1+e^{\mathbf{x}{\ast }_n^T\mathbf{\beta }+{\alpha }_1{q}_{21,n}+{\alpha }_2{q}_{12,n}}}\right)}^{y_n}{\left(\frac{1}{1+e^{{\mathbf{x}}_n^{\ast T}\mathbf{\beta }+{\alpha }_1{q}_{21,n}+{\alpha }_2{q}_{12,n}}}\right)}^{1-y_n}({\prod _{k=2}^{T_n}\left[\frac{q_{21,n}}{q_{12,n}+q_{21,n}}+\frac{q_{12,n}}{q_{12,n}+q_{21,n}}{e}^{-\left(q_{12,n}+q_{21,n}\right)\left(t_{n,k}-t_{n,k-1}\right)}\right]}^{I_1\left[Z_n\left(t_{n,k-1}\right)\right]I_1\left[Z_n\left(t_{n,k}\right)\right]}{\left[\frac{q_{12,n}}{q_{12,n}+q_{21,n}}-\frac{q_{12,n}}{q_{12,n}+q_{21,n}}{e}^{-\left(q_{12,n}+q_{21,n}\right)\left(t_{n,k}-t_{n,k-1}\right)}\right]}^{I_1\left[Z_n\left(t_{n,k-1}\right)\right]I_2\left[Z_n\left(t_{n,k}\right)\right]}{\left[\frac{q_{21,n}}{q_{12,n}+q_{21,n}}-\frac{q_{21,n}}{q_{12,n}+q_{21,n}}{e}^{-(q_{12,n}+q_{21,n})(t_{n,k}-t_{n,k-1})}\right]}^{I_2\left[Z_n\left(t_{n,k-1}\right)\right]I_1\left[Z_n\left(t_{n,k}\right)\right]}{[\frac{q_{12,n}}{q_{12,n}+q_{21,n}}+\frac{q_{21,n}}{q_{12,n}+q_{21,n}}{e}^{-(q_{12,n}+q_{21,n})(t_{n,k}-t_{n,k-1})}]}^{I_2\left[Z_n\right(t_{n,k-1}\left)\right]I_2\left[Z_n\right(t_{n,k}\left)\right]}\right)\left(P{\left[Z_n\right(0)=1]}^{I_1\left[Z_n\right(0\left)\right]}P{\left[Z_n\right(0)=2]}^{I_2\left[Z_n\right(0\left)\right]}\right)\}$$

where Z_n(t_n,k) is the observed value of the Markov chain Z(t) for subject n at its k^th observation time t_n,k, characterized by the transition rates $q_{21,n}=e^{\mathbf{v}{\ast }_n^T{\mathbf{\delta }}_1}$ and $q_{21,n}=e^{\mathbf{v}{\ast }_n^T{\mathbf{\delta }}_2}$; P_{Zn(tn,k–1)=i,Zn(tn,k)=j}(t_n,k–t_n,k–1) is the probability of changing from state “i” at time t_n,k–1 to state “j” at time t_n,k for subject n, where i, j = 1,2 and k = 2, …, T_n; P[Z_n(0) = i] is the probability that the initial state of the chain is equal to i; and for i = 1,2, I_i[Z_n(t_n,k)] is an indicator function of whether Z_n(t_n,k) is equal to i.

In the proposed joint model, problems of identifiability and estimability of parameters may occur due to the presence of a CTMC. As noted in Benoit et al. [25], a CTMC model may be non-identifiable (i.e., two or more set of parameters could result in a very close likelihood) when outcomes are recorded at pre-specified times. This is because the sojourn time and state of change for a subject are not fully recorded, that is, their Markov chain observations do not record the exact duration of the sojourn time. In general, if the mean sojourn time is much longer than the inter-observation interval the identifiability problem will be almost negligible because the total observation time where a state does not change will be very close to the sojourn time. However, in this case, unless the prespecified duration of observation is long, an estimability problem may occur because we may not observe a sufficient number of state changes. On the other hand, when the mean sojourn time interval (1/q_ii) is much shorter than the inter-observational time interval, several state changes between two observational time points could be missed and an observed transition could be reached by at least two different paths. In this situation, non-identifiability of parameters may occur.

In our model, the information contained in the covariates of the joint model may help reduce or avoid problems of identifiability. If changes of state for a subject occur much more often than what is observed, other subjects that have similar characteristics and observed transition times close to exact times of transition will dominate in the estimation process and hence reduce non-identifiability of parameters. At the same time, the covariates as well as the sequence of states observed for all subjects make the model estimable. First, the Markov chain of a subject that consists of the same state in their entire observational period is pooled with that of subjects who change their state many times, which makes possible the estimation of the Markov chain submodel. Simultaneously, the variability introduced by the covariates of the Markov chain submodel allows the estimation of the parameters associated with the transition rates and with the rest of covariates of the main outcome model.

2.3 Estimation and initial values

The method of maximum likelihood can be used to maximize (2) with respect to the parameters β, α₁, α₂, and δ in a one-stage procedure. This is a nonlinear optimization problem where there is no closed-form solution for the parameter estimators. The Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm is a quasi-Newton method that uses function values and gradients to build up a picture of the objective to be optimized [26]. In this study, we use the BFGS numerical method to find the maximum likelihood estimators (more details in the Appendix). To conduct inference, variance estimates are obtained from the final value of the inverse of the Hessian matrix in the BFGS algorithm (A.1).

The initial values for the BFGS algorithm of the estimation procedure can be determined in a two-stage procedure as described below.1- A usual two-state continuous-time Markov chain model with covariates v and w is fitted to find parameter values δ₁ and δ₂. At this stage, the covariates x and the outcome Y are ignored. The initial values for this model can be chosen based on the method proposed by Mhoon et al. [27].2- The transition rates q₁₂ and q₂₁ are computed for each subject based on the estimates δ̂₁ and δ̂₂ obtained in the first stage and a regular logistic regression model is fitted to the data x, q̂₂₁, q̂₁₂, and the outcome Y to obtain initial values for the parameters α₁, α₂, and β.

3. Validation of the estimation procedure

3.1 Description of the simulation study

We conducted simulations in order to validate the estimation procedure of the joint model (1). The “true” parameters in this simulation study were obtained from an application of the proposed model to a database of patients with TBI [28].

The data simulation procedure can be thought as a two-stage process, where covariates of the exponential functions in model (1) are simulated first to be able to obtain transition rates for each subject that will act as covariates in the main outcome model. The motivation behind this simulation process is that a two-stage procedure of this type needs to be applied when the joint models are used to make predictions. A complete description of the simulation mechanism is presented below.

3.1.1 Simulation of covariates

Because we are particularly interested in applying this model to a dataset of TBI patients, the type of covariates and distributions chosen for this simulation mimicked this type of data. However, covariates and their distributions could be chosen differently without loss of generality.1- Two covariates, one continuous (v₁) and one binary (v₂), were simulated as predictors directly associated with the transition rate q₂₁, where v₁ followed a truncated standard normal distribution and v₂ a Bernoulli distribution. Similarly, a continuous variable w₁ and a binary variable w₂ were predictors associated with q₁₂ and were simulated using the same distributions as in the transition rate q₂₁. For the binary predictors, v₂ and w₂, the parameters p that characterize the Bernoulli distributions were chosen differently.2- The “true” parameters δ₁₁, δ₁₂, δ₂₁, and δ₂₂, associated with the covariates v₁, v₂, w₁, and w₂, respectively, together with the covariates values and the “true” intercepts δ₁₀ and δ₂₀ were used to calculate transition rates q₁₂ and q₂₁ for each subject.3- An additional pair of covariates, x₁ and x₂ were simulated as predictors directly associated with the outcome Y, where x₁ followed a Bernoulli distribution and represented the initial state of the chain, and x₂/10 followed a beta distribution. The parameters used in the Bernoulli and beta distributions simulations were empirically chosen from selected covariates in the TBI dataset. For the beta distribution, the parameters that characterize the distribution were determined using the method of moments estimator.

3.1.2 Simulation of the Markov chain

We used the transition rates q₁₂ and q₂₁ simulated for each subject as parameters of exponential distributions to simulate individual Markov chains. The length of the chains was set to 120 time points per subject and the initial states of the chains were chosen as described above.

3.1.3 Simulation of the outcome Y

The logit of the probability of Y = 1 given the covariates (x, q₂₁, and q₁₂) was computed based on the “true” parameters β₀, β₁, and β₂ associated with the intercept and covariates directly related to the outcome (x₁ and x₂), and based on the “true” parameters α₁ and α₂ of the transition rates q₂₁ and q₁₂. Then, the inverse function of the logit was used to calculate the probability of Y = 1 given the covariates for each subject (π̂_n), and a Bernoulli distribution with parameter π̂_n was used to simulate the outcomes.

3.2 Implementation

We generated R=1,000 datasets with N=178 subjects under two scenarios: (i) assuming that the transition rates are associated with the outcome (the joint proposed model, where β ≠ 0, α₁ ≠ 0, α₂ ≠ 0, δ₁ ≠ 0, δ₂ ≠ 0); (ii) assuming that the effect of the transition rates on the outcome is null (β ≠ 0, α₁ = 0, α₂ = 0, δ₁ ≠ 0, δ₂ ≠ 0). The joint proposed model was then fitted to the simulated datasets of both scenarios to assess its performance in each case. Table 1 contains summarized information of the 1,000 simulations under scenario (i). All estimated coefficients are very close to their true values and the coverage probability for each coefficient is about 95%. At the same time the standard deviations (SDs) of the point estimates across the simulation runs are very close to the squared root of the average of the estimated variance for each run (standard errors, SEs), which indicates that our number of runs is adequate.

Table 1. Simulation results of the proposed model (N=178 subjects; R=1,000 runs).

Covariate in the joint model	Parameter and true value	Estimate	Bias	SDa	SEb	Coverage probability
Intercept	β0 = -5.33	-5.63	-0.30	2.22	2.23	0.96
x1 (continuous)	β1 = 0.54	0.57	0.03	0.10	0.10	0.96
x2 (binary, initial state)	β2 = -0.56	-0.58	-0.02	0.43	0.43	0.96
q12	α2 = 4.08	4.32	0.24	2.01	2.02	0.96
w0	δ20= -0.02	-0.02	0.00	0.03	0.03	0.94
w1 (binary)	δ21= 0.21	0.21	0.00	0.04	0.04	0.95
w2 (continuous)	δ22= 0.06	0.06	0.00	0.02	0.02	0.94
q21	α1= -0.05	-0.06	-0.01	0.09	0.09	0.95
v0	δ10= 1.87	1.87	0.00	0.04	0.04	0.95
v1 (binary)	δ11= -1.11	-1.11	0.00	0.04	0.04	0.95
v2 (continuous)	δ12= -0.08	-0.08	0.00	0.03	0.03	0.95

^aStandard deviation of the point estimates.

^bStandard error, obtained from the squared root of the average of the estimated variance for each run.

To assess the performance of our method in a situation where the transition rates do not affect the response (scenario (ii)), we set the parameters α₂ = α₁ = 0 and the true values for β₀, β₁, and β₂ were chosen as the estimates obtained by fitting a regular logistic regression model to the TBI study data; we separately fit a two-state CTMC to the longitudinal data to choose true values for δ₁ and δ₂. In this case, the algorithm did not converge for 1 simulated data set, and therefore its performance was evaluated based on 999 datasets. The bias is still negligible for all the parameter estimates and the coverage probabilities range from 0.94 to 0.97 (Table 2). Therefore, if there is not really an effect of the transition rates on the outcome, the estimates of our main outcome model will approximate those of a regular logistic regression model.

Table 2.

Simulation results using the proposed model to analyze the data generated from a model with no effects of Markov chains on the outcome (N=178 subjects; R=999 runs).

Covariate in the joint model	Parameter and true value	Estimate	Bias	SDa	SEb	Coverage probability
Intercept	β0 = -1.45	-1.49	-0.04	1.88	1.90	0.97
x1 (continuous)	β1 = 0.57	0.60	0.03	0.10	0.10	0.96
x2 (binary, initial state)	β2 = -0.26	-0.27	-0.01	0.42	0.42	0.95
q12	α2 = 0.00	-0.04	-0.04	1.69	1.72	0.97
w0	δ20= -0.02	-0.02	0.00	0.03	0.03	0.95
w1 (binary)	δ21= 0.22	0.22	0.00	0.04	0.04	0.95
w2 (continuous)	δ22= 0.04	0.04	0.00	0.03	0.03	0.95
q21	α1= 0.00	0.00	0.00	0.09	0.09	0.94
v0	δ10= 1.87	1.87	0.00	0.04	0.04	0.94
v1 (binary)	δ11= -1.11	-1.11	0.00	0.04	0.04	0.96
v2 (continuous)	δ12= -0.09	-0.09	0.00	0.03	0.03	0.95

^aStandard deviation of the point estimates.

^bStandard error, obtained from the squared root of the average of the estimated variance for each run.

We also evaluated the performance of a regular logistic regression model on the simulated data from scenarios (i) and (ii). Table 3 shows a summary of the logistic regression model fitted to the simulated datasets under each scenario. If there is really a joint effect of the main outcome model with the longitudinal covariate process, a regular logistic regression model will not perform as well compared to a joint logistic regression and Markov model (bias is in general larger and coverage probabilities lower). As expected, the performance of a logistic regression model on datasets where the Markov chain submodel is independent of the main outcome model is very good.

Table 3.

Simulation results using regular logistic regression to analyze the data generated from the proposed model (top) and from a model with no effects of Markov chains on the outcome (bottom).

Covariate in the joint model	Parameter and true value	Estimate	Bias	SDa	SEb	Coverage probability
Logistic regression model fitted to the simulated data from scenario (i) (β ≠ 0, α ≠ 0, α2 ≠ 0, δ1 ≠ 0, δ2 ≠ 0)
Intercept	β0 = -1.45	-1.21	0.24	0.37	0.37	0.88
x1 (continuous)	β1 = 0.57	0.53	-0.04	0.09	0.10	0.93
x2 (binary, initial state)	β2 = -0.26	-0.54	-0.28	0.40	0.41	0.91
Logistic regression model fitted to the simulated data from scenario (ii) (β ≠ 0, α = 0, α2 = 0, δ1 ≠ 0, δ2 ≠ 0)
Intercept	β0= -1.45	-1.51	-0.06	0.37	0.38	0.96
x1 (continuous)	β1= 0.57	0.59	0.02	0.10	0.10	0.96
x2 (binary, initial state)	β2 = -0.26	-0.27	-0.01	0.41	0.42	0.96

^aStandard deviation of the point estimates.

^bStandard error, obtained from the squared root of the average of the estimated variance for each run.

4. Application

4.1 Study population and description of the joint proposed model

The EPO TBI study was a clinical trial funded by the National Institute of Neurological Disorders and Stroke (NINDS) to study the effects of erythropoietin on cerebral vascular dysfunction and anemia on neurological recovery [28]. In this trial, 200 participants with severe TBI were randomly assigned to administration of erythropoietin or placebo and to hemoglobin transfusion thresholds of 7 or 10 g/dl in a 2 × 2 factorial design. The primary endpoint was the Glasgow Outcome Scale score dichotomized as favorable (good recovery and moderate disability) or unfavorable (severe disability, vegetative, or dead) at 6 months post-injury. Baseline information including demographic characteristics and type and severity of injury was obtained on admission. When patients were admitted to the ICU, nurses collected physiological data every hour that the patient was in the ICU.

We applied the joint logistic and Markov chain model to the EPO TBI study data with the aim of assessing the added value of physiological dynamics and treatment variables in predicting unfavorable 6-month GOS. Because information on the 6-month GOS outcome was not available for some patients, our analysis was based on 178 patients of which 62% had unfavorable GOS. For the physiological data, we considered hourly information recorded during the first 120 hours after ICU admission, where missingness of data was not substantial (24%).

Markov chain submodel

For the Markov chain submodel, we dichotomized intracranial pressure (ICP) following the Brain Trauma Foundation (BTF) guidelines [29] in less than or equal to 20mmHg and greater than 20mmHg and used the transition rates that characterize the ICP process as covariates in the main outcome model. Out of a total of 20,866 ICP transitions between two consecutive hours, about 11% were from ICP ≤20 mmHg to >20 mmHg and vice versa, 63% ICP values remained ≤20 mmHg in two consecutive hours, and 15% remained >20 mmHg. Before dichotomization of ICP and to minimize informative missing ICP data, we applied an imputation procedure on the raw continuous data that is similar to the procedure applied by Yamal et al. [30]; we were left with a total of 316 ICP values missing post-imputation. After consultation with an expert clinician, the transition rates were modeled as dependent variables of the following physiological variables: PaO2, hemoglobin, MAP, PaCO2, temperature, delayed intracranial hematoma (DICH), and brain tissue hypoxia (BTH). For PaO2, hemoglobin, MAP, PaCO2, and temperature, we calculated a summary measure per patient defined as the number of times in 120 hours that the variable was outside a prespecified threshold, i.e., that had an abnormal value. For DICH and BTH we created indicator variables of whether the patient had adverse events of this type during the study time. For the transition rate from high (>20 mmHg) to normal or low ICP (≤20 mmHg), q₂₁, we also considered whether the patient had surgery for increased ICP and whether the drugs mannitol or barbiturates were given to decrease intracranial pressure.

Main outcome model

In the main outcome model we included as predictors the IMPACT prognostic score of unfavorable outcome (a score that contains information on baseline characteristics built by Steyerberg et al. [31]), that was multiplied by 10 for ease of interpretation; the Injury Severity Score (a score to assess trauma severity); the first ICP value recorded; and the transition rates q₁₂ and q₂₁ that characterize the ICP process of moving from a normal or low ICP state (≤20 mmHg, state 1) to a high ICP state (>20 mmHg, state 2).

Statistical analyses for the EPO TBI study data were carried out using R version 3.3.1 (R Foundation for Statistical Computing). The optim function from the R package stats was applied to the coded joint likelihood function to obtain the parameters estimates and variance estimates of the proposed model.

4.2 Results of the joint proposed model

For our final analysis, in order to remove correlated covariates from the joint model, we applied a backward model selection based on the AIC (Akaike Information Criteria) strategy in two steps: first, we fitted the joint model and applied the backward selection in the ICP submodel only and secondly, we fitted the joint model using the reduced ICP submodel and selected covariates from the main outcome model only. Because the effect of the transition rate q₁₂ on the 6-month GOS was quite large when using hourly ICP data, we rescaled the time variable to have 15-minutes increments. Also, we standardized the continuous physiological variables in the Markov chain submodel to avoid computational issues.

Interpretation of the transition rate effects on the outcome

Table 4 contains the results of the joint proposed model after the model selection. It can be observed that for each unit increment in the hazard rate of moving from high to normal or low ICP, the odds of unfavorable 6-month GOS is expected to change by a multiplicity of e^−0.16 = 0.85, and for each unit increment in the hazard rate of moving from normal or low to high ICP the odds of unfavorable outcome is expected to change by a multiplicity of e^1.87 = 6.49, holding the IMPACT prognostic score constant. While there is a borderline significant decrease in the probability of unfavorable outcome for a higher hazard rate of moving from high to normal or low ICP (p=0.0502), the increase in the probability of unfavorable outcome with a higher rate of change from normal or low to high ICP is not statistically significant (p=0.12) despite the large effect of the covariate q₁₂. A possible explanation for this last result is that subjects remained longer in a normal or low ICP state than in a high ICP state, and therefore the standard error associated with the transition rate q₁₂ is larger than the standard error for q₂₁. We would expect to see a statistically significant effect of q₁₂ if ICP was observed for a longer period of time. A simulation study using chains of different lengths confirmed our hypothesis.

Table 4.

Results of the joint logistic regression and Markov model applied to the EPO TBI study data.

Covariate in the joint modela	Parameter estimate	Standard error	P-valueb
Main logistic regression model for unfavorable GOS
Intercept	-2.76	1.38	0.05
IMPACT prognostic score per 10% unit increment	0.54	0.10	<0.01
q12	1.87	1.19	0.12
q21	-0.16	0.08	0.05
Submodel for transition rate from normal or low to high ICP (q12)c
Intercept	0.11	0.03	<0.01
BTH	-0.17	0.06	<0.01
PaO2	0.04	0.02	0.10
MAP	0.04	0.03	0.13
PaCO2	0.11	0.03	<0.01
hemoglobin	-0.11	0.03	<0.01
Submodel for transition rate from high to normal or low ICP (q21)
Intercept	1.98	0.05	<0.01
BTH	-0.14	0.06	0.02
DICH	-0.44	0.05	<0.01
temperature	0.12	0.02	<0.01
PaO2	0.08	0.03	<0.01
MAP	-0.05	0.03	0.10
PaCO2	-0.06	0.03	0.01
hemoglobin	-0.16	0.04	<0.01
drug	-0.96	0.05	<0.01

^aPaO2, MAP, PaCO2, temperature, and hemoglobin were defined as the number of times in 120 hours that the variable was outside a prespecified threshold, and were standardized; q₁₂ and q₂₁ are the ICP transition rates of changing states in 15-minute increments.

^bP-values rounded to 2 decimal places. For q₂₁, p=0.0502; for the intercept in the main logistic regression model, p=0.045.

^cNormal or low ICP is defined as ICP≤20 mmHg; high ICP is defined as ICP>20 mmHg.

Interpretation of the physiological covariates effects of the Markov chain submodel on the outcome

Many physiological variables were significantly associated with the 6-month GOS (Table 4). The change in the odds of unfavorable outcome is not constant throughout each hour increment that the physiological variable was outside the prespecified threshold, that is, it depends on the time when we are assessing the change. For example, for PaCO2 in the transition rate q₁₂, the odds ratio for one extra hour that PaCO2 was outside the threshold is exp[1.87 × exp(0.11 × PaCO2) × (exp(0.11)-1)]. If PaCO2 was abnormal for 1 hour in 120 hours after ICU admission, then the odds of unfavorable outcome would be 27% higher in the second hour of abnormal PaCO2.

Interpretation of the physiological covariates effects of the Markov chain submodel on the transition rates

In the ICP submodel, interpretation of the covariate effects requires some caution because the physiological variables and treatment variables are post-baseline summary measures and there could be temporality issues of whether the ICP transition occurred before or after there was a change in another vital sign or treatment variable. For example, in the q₁₂ transition rate MAP has a positive sign and we would say that an additional hour of abnormal MAP is associated with a higher hazard of moving from ICP≤20 mmHg to ICP>20 mmHg. However, for the variable drug in q₂₁ the negative sign would indicate that giving a drug to a patient to decrease their ICP is associated with lower risk of moving to a normal or low ICP level, or in other words, those patients who are given the drug remain longer in a high ICP level compared to those that are not given the drug. While we would expect that the drug would decrease ICP quickly, we are observing the opposite effect because the drug is given after the patient has had sustained increased ICP.

4.3 Results of the joint proposed model vs. a prognostic score of baseline data only

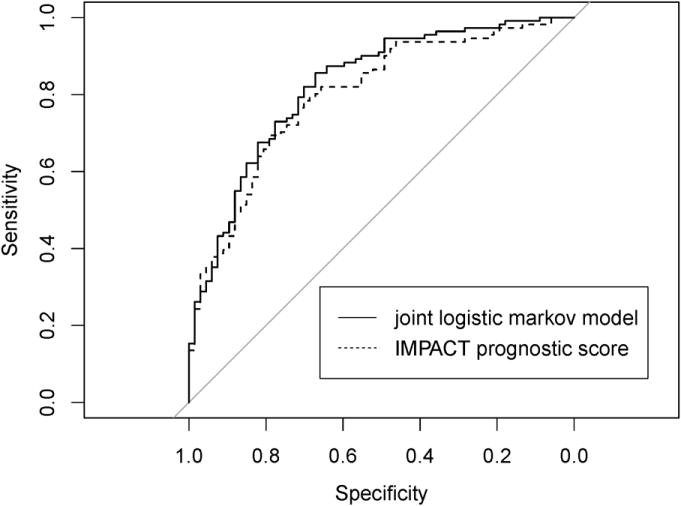
Compared to a prognostic score of unfavorable outcome that contains baseline information only (IMPACT prognostic score), the joint logistic Markov model with baseline data and longitudinal data collected in the ICU 120 hours post-injury had higher discrimination power. The area under the ROC curve was 0.824 for the joint logistic Markov model and 0.799 for the IMPACT prognostic score (p=0.052) (Figure 1).

Figure 1. ROC curves for the joint proposed model vs. the IMPACT prognostic score of unfavorable outcome.

5. Discussion

We have proposed a joint logistic regression and Markov model to assess the effect of a longitudinal covariate process on a binary outcome measured cross-sectionally. In the model, the process is represented by transition rates of a two-state CTMC, which in combination with baseline covariates are used to describe the response. Previous studies that used a similar idea based on Markov chains, either modeled a longitudinal outcome or used a discrete-time Markov chain approach. Specifically, in Hubbard et al.'s study [5], one component of a time-dependent transition probability matrix of a multistate CTMC model was used as a covariate process to describe a longitudinal binary outcome. While in Hubbard et al.'s method two processes are modeled simultaneously (the outcome and the covariate processes), we propose a method where the elements of one process (transition rates of the CTMC covariate process) are modeled as a function of a response measured at a single time point. Therefore, Hubbard et al.'s model cannot be simplified to our model with a single outcome measurement; if we attempted to do so, the covariate process would also reduce to the baseline observation. Our model also differs from Hubbard et al.'s in how the covariate process is included in the model. While they use one transition probability to represent a five-state CTMC at each time point, we use two transition rates to represent a two-state CTMC across time. That is, the process is fully identified in our model using the fundamental elements of a CTMC, as opposed to a partial representation of the process in their model given by one sequence of approximated transition probabilities. This, together with the fact that the transition rates in our model are adjusted by several key covariates, makes our model more appropriate for our targeted data example. The dissertation study by Ho used discrete time Markov chains instead of CTMC to jointly model the association between a longitudinal covariate process and a binary cross-sectional outcome using a two-stage estimation procedure. In his model, transition probabilities of the discrete process were included as predictors. Since transition probabilities of a DTMC are based only on observed changes at pre-specified time points, they do not represent the true force of transition given by transition rates of a CTMC, which are based not only on data that are observed but also on unobserved changes between time points. Hence, a CTMC approach, as was adopted in our study, may be more appropriate to describe the longitudinal covariate process.

Our simulation studies showed good performance of our method, even if the longitudinal covariate process does not influence the outcome. We showed that ignoring the longitudinal covariate effects in a regular logistic regression model when they actually exist will introduce some bias in the parameter estimates and the logistic regression model will not capture the true values as often as the joint model does.

The application of this model was in a dataset of patients with severe traumatic brain injury, where we used quarter-hour longitudinal physiological data in addition to other non-dynamic covariates to predict 6-month GOS. The rationale of using a continuous-time Markov chain approach to model the ICP data measured discretely at each hour post-injury is that ICP changes may not occur exactly during the observation time. Prognostic models for 6-month GOS in patients with TBI have been developed on admission hospital only and are currently considered useful tools in the clinical setting [31, 32]. However, the predictive value of physiological data collected during the acute phase of injury seems promising [33-35], particularly the value of elevated intracranial pressure that can lead to ischemia, cerebral herniation and death. Our joint model applied to the TBI data showed that neither the hazard of moving from ICP>20 mmHg to ICP≤20 mmHg nor the hazard of moving from ICP≤20 mmHg to ICP>20 mmHg in the first 120 hours after ICU admission significantly affects patient recovery at 6-months post-injury. However, the association between 6-month GOS and the hazard of moving from high to normal or low ICP was borderline significant. When we compared the joint model versus a prognostic score with baseline data only in terms of their classification performance, we observed that the physiological information collected post-injury helped improve predictive power. A further increase in prediction power may be achieved if automated physiological data instead of hourly data recorded by a practitioner were used to fit the joint proposed model [36].

Our proposed model is based on a two-state CTMC and requires dichotomization of the longitudinal covariate of interest if this one is measured in a continuous scale. We know that dichotomization of continuous predictors may result in some information loss. However, when recoding a continuous variable based on a particular threshold measurement error in raw and imputed data is reduced and data become more reliable. In our application study, ICP was dichotomized as normal or low (≤20 mmHg) versus high (>20 mmHg). The rationale for modeling ICP as a two-state process is that we aimed to capture the underlying normal or abnormal ICP behavior that characterizes the continuous ICP paths; we consider that two ICP values larger than 20mmHg do not provide as much information as one below and another above 20mmHg do. In addition, in this case, the population of TBI patients were managed based on a threshold of ICP. Other application areas should consider finding meaningful cutpoints for the longitudinal covariates or use thresholds based on management strategies as we did for the TBI study.

In this study, when we applied the joint proposed model to the TBI dataset, the ICP transition rates of the Markov chain submodel were modeled as a function of covariates that are summary measures of longitudinal data post-baseline. In this case, special attention should be paid to the interpretation of these covariates' effects on the transition rates due to the lack of temporality between the ICP process and the treatment and physiological variables that affect this process. Otherwise, if the Markov process was influenced by baseline covariates only, the interpretation of the covariates effects on the transition rates would be straightforward. Nevertheless, the effect of the transition rates on the main outcome, which is the focus of our study, has a direct and clear interpretation.

We have developed a model where a longitudinal process can be incorporated in a logistic regression model to predict a cross-sectional binary outcome. The transition rates that characterize this longitudinal process act as predictors of the main outcome and can be jointly modeled with other non-dynamic covariates. This model could be applied to diverse public health problems; for instance, it could incorporate longitudinal electroencephalogram data to predict episodes of epilepsy in subjects with seizures, or glucose monitoring data to predict the risk of kidney failure in patients with diabetes.

Appendix.

The Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm is an iterative method to solve unconstrained nonlinear optimization problems that approximates Newton's method. Unlike Newton's method, the BFGS does not require the calculation of second derivatives. The algorithm is briefly described below.

Let f:ℝⁿ → ℝ be a convex, twice-differentiable function to optimize. Denote the gradient of f at a current point x_k by ∇f_k, and the Hessian matrix or matrix of second partial derivatives by H_k, symmetric and positive definite. For any point x define, p = x–x_k. The second order Taylor expansion around x_k is given by

$$m_k\left(\mathbf{p}\right)=f_k+{\mathbf{p}}^T\nabla f_k+\frac{1}{2}{\mathbf{p}}^T{\mathbf{H}}_k\mathbf{p}$$

and defines a quadratic model. The gradient of m_k(p) with respect to x is ∇m_k(p) = ∇f_k + H_kp, and it is minimized at ${\mathbf{p}}_k=-{\mathbf{H}}_k^{-1}\nabla f_k.$

Let ${\mathbf{H}}_k^{-1}={\mathbf{B}}_k$. The BFGS algorithm can be described as follows:

1. Obtain a direction p_k by solving p_k = −B_k∇f_k.

2. Perform a line search in the direction of p_k to find some α ∈ (0,∞) and then update x_k#x0002B;1 = x_k + α_kp_k. The step length α_k is required to satisfy certain conditions to guarantee convergence.

3. Define s_k = x_k+1–x_k = α_kP_k and y_k = ∇f_k#+1–∇f_k.

4. Compute

   $${\mathbf{B}}_{k+1}=\left(\mathbf{I}-{\rho }_k{\mathbf{s}}_k{\mathbf{y}}_k^T\right){\mathbf{B}}_k\left(\mathbf{I}-{\rho }_k{\mathbf{y}}_k{\mathbf{s}}_k^T\right)+{\rho }_k{\mathbf{s}}_k{\mathbf{s}}_k^T\text{where}{\rho }_k=\frac{1}{{\mathbf{y}}_k^T{\mathbf{s}}_k}.$$ (A.1)

   This is the solution to the matrix minimization problem, ${\mathbf{B}}_{k+1}=\underset{\mathbf{B}}{arg\; min}{\Vert \mathbf{B}-{\mathbf{B}}_k\Vert }_{\mathbf{W}}$ subject to B = B^T, By_k = s_k, where ${\Vert \mathbf{B}-{\mathbf{B}}_k\Vert }_W={\Vert {\mathbf{W}}^{\frac{1}{2}}(\mathbf{B}-{\mathbf{B}}_k){\mathbf{W}}^{\frac{1}{2}}\Vert }_F={\Vert \mathbf{C}\Vert }_F=\sqrt{\sum _{i=0}^n\sum _{j=0}^n{c}_{ij}^2}$ and W is the inverse ${\overline{G}}_k^{-1}$ of the average Hessian, ${\overline{G}}_k=\underset{0}{\overset{1}{\int }}{\nabla }^{2}f({\mathbf{x}}_k+\tau {\alpha }_k{\mathbf{p}}_k)d\tau$.

The initial value for the inverse of the Hessian matrix, B₀, can be selected as a scalar multiple of the identity matrix or a finite difference approximation at x₀, for instance. Convergence is achieved when the norm of the gradient |∇f(x_k)|<∈, where ∈>0.