Testing for the Indirect Effect Under the Null for Genome Wide Mediation Analyses

Abstract

Mediation analysis helps researchers assess whether part or all of an exposure’s effect on an outcome is due to an intermediate variable. The indirect effect can help in designing interventions on the mediator as opposed to the exposure and better understanding the outcome’s mechanisms. Mediation analysis has seen increased use in genome-wide epidemiological studies to test for an exposure of interest being mediated through a genomic measure such as gene expression or DNA methylation. Testing for the indirect effect is challenged by the fact that the null hypothesis is composite. We examined the performance of commonly used mediation testing methods for the indirect effect in genome-wide mediation studies. When there is no association between the exposure and the mediator and no association between the mediator and the outcome, we show that these common tests are overly conservative. This is a case that will arise frequently in genome-wide mediation studies. Caution is hence needed when applying the commonly used mediation tests in genome-wide mediation studies. We evaluated the performance of these methods using simulation studies, and performed an epigenome-wide mediation association study in the Normative Aging Study, analyzing DNA methylation as a mediator of the effect of pack-years on FEV₁.

Introduction

Mediation analysis is an attractive tool to study disease causal pathways. It allows researchers to partition an exposure’s effect on an outcome into a direct effect and an indirect effect through an intermediate variable (the mediator). The natural indirect effect (NIE) provides evidence of whether the mediator is on a pathway from the exposure to the outcome and is often of primary interest [Pearl 2001; Robins and Greenland 1992]. This can have important policy/intervention consequences as it may not be possible to change an exposure, but we could intervene to disable the mechanism from the exposure to the outcome.

There has been a rise in genomic studies that have incorporated some form of mediation analysis in recent years [Fasanelli, et al. 2015; Huan, et al. 2016; Liu, et al. 2013; VanderWeele, et al. 2012]. This could be in form of a single nucleotide polymorphism (SNP) acting on gene expression which then acts on a phenotype further downstream, or that a genomic measure such as DNA methylation being a mediator for an environmental exposure’s effect on disease status. Mediation in genomic studies is an ongoing area of research that will continue to grow as more data are collected and pathways are better understood. Given this rise, the statistical problems inherent to genomic mediation studies need to be better understood.

In this paper, we examine the performance of testing the natural indirect effect in epigenome wide association studies where we test the null of no NIE for a single mediator. We examine the performance of four common methods for testing the NIE in simulation studies under various null scenarios. We examine the joint significant method (causal steps method) [MacKinnon, et al. 2002], the product method (Sobel’s method) [Baron and Kenny 1986; Sobel 1982], the bootstrap method [Fritz and MacKinnon 2007] and the difference method [Mackinnon, et al. 1995]. There are other methods not covered here but the message extends to those approaches [Baron and Kenny 1986; Bayarri and Berger 2000; Biesanz, et al. 2010; Judd and Kenny 1981; MacKinnon and Fairchild 2009; MacKinnon, et al. 2007; Yuan and MacKinnon 2009].

The empirical performance of these tests under continuous outcome and mediator has been analyzed in detail in the Nursing, Psychology, and Sociology fields [Biesanz, et al. 2010; Krause, et al. 2010; MacKinnon, et al. 2007; MacKinnon, et al. 2002]. To the best of our knowledge, it has not been brought to the attention of the public health and genetic epidemiology fields, nor has any literature illustrated the effects in the genome-wide multiple testing context. There have been some methodology developments of new approaches for high-dimensional testing in genomic studies [Huang, et al. 2015; Huang, et al. 2014; Huang and Pan 2016; Zhang, et al. 2016], but these developments did not rigorously discuss the limitations of standard testing approaches.

We first demonstrate that the null hypothesis of no NIE is a composite null that occurs under three cases. In genome-wide epigenetic studies, the genomic marker is likely not associated with both the exposure and the outcome. We show that the existing tests for the NIE are conservative in this case. It follows that then applying these commonly used tests in genome-wide epigenetic studies will result in loss of power. We also extend the discussion of the performance of these tests under the null hypothesis to different data types.

The structure of this paper is as follows, we first put forth the methods and notation that will be used in testing. We next perform a simulation analysis to assess how well each testing procedure performs under various null scenarios. We demonstrate the performance of existing methods in assessing the NIE and issues with test sizes (α) under scenarios of the null hypothesis. We then finally perform a mediation analysis in the Normative Aging Study, with DNA methylation as the mediator, pack years as the exposure, and forced expiratory volume in 1 second (FEV₁).

Methods

Base Models

We first focus on when we have a continuous outcome (Y) and mediator (M). We have a primary exposure of interest (A) and baseline covariates (X). We consider the following simple model (though this discussion is extendable so as to include interactions [VanderWeele and Vansteelandt 2009]) with zero mean residuals ( ${\epsilon }_f$, ${\epsilon }_r$, ${\epsilon }_m$) and finite variance:

$$Y={\theta }_0+{\theta }_{1}A+{\theta }_{2}M+{\mathit{\theta }}_{\mathbf{3}}^{\mathit{T}}\mathit{X}+{\epsilon }_f$$ (1)

$$Y={\varphi }_0+{\varphi }_{1}A+{\mathit{\varphi }}_{\mathbf{2}}^{\mathit{T}}\mathit{X}+{\epsilon }_r$$ (2)

$$M={\beta }_0+{\beta }_{1}A+{\mathit{\beta }}_{\mathbf{2}}^{\mathit{T}}\mathit{X}+{\epsilon }_m.$$ (3)

We assume the baseline covariates (X) suffice to control for exposure-outcome, mediator-outcome, and exposure-mediator confounding, with no mediator-outcome confounders affected by the exposure [Pearl 2001; VanderWeele 2015], assumptions which are needed for a causal interpretation. Note that the covariates in the outcome model and the mediator model do not need to coincide, but for ease of notation, we let X denote all baseline covariates, which include confounders for both M and Y models. The NIE of A on Y through M conditional on X is given by θ₂β₁ or ϕ₁-θ₁, as there is no interaction between A and M on Y. A directed acyclic graph of the various causal effects highlighting the NIE is given in Figure 1. The composite null hypothesis of no NIE (H₀: θ₂β₁ = 0) occurs when:

• Case 1: No association between A and M but association between M and Y given A and X: β₁=0; θ₂≠0.

• Case 2: Association between A and M but no association between M and Y given A and X: β₁≠ 0; θ₂=0.

• Case 3: No association between A and M and no association between M and Y given A and X: β₁=θ₂=0.

Figure 1. Directed Acyclic Graphs for the continuous mediator and outcome model.

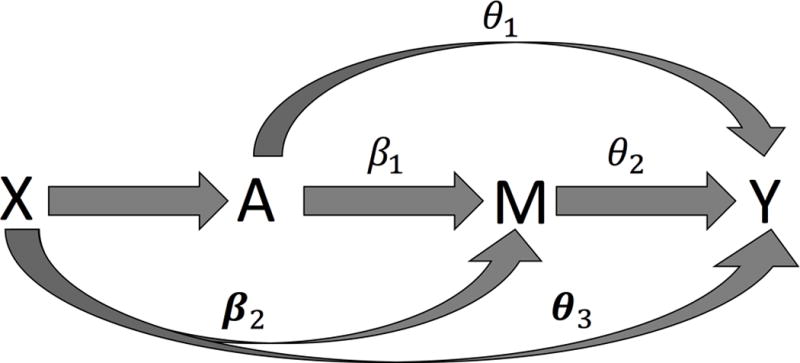
The Natural Indirect Effect (NIE) is the effect of A on Y through M conditional on confounders X, therefore ${\beta }_1{\theta }_2$. This is the path through M. The Natural Direct Effect (NDE) is the effect of A on Y not through M conditional on X, therefore ${\theta }_1$.. Finally, the Total Effect is the total effect of A on Y either through or not through M, therefore ${\theta }_1+{\beta }_1{\theta }_2$. This is equal to ${\varphi }_1$ from the reduced model without M included.

The majority of mediation applications in traditional epidemiological studies where there is no NIE likely consist of Cases 1 or 2, where researchers have a-priori information and a meaningful reason to investigate a mediator. Case 3 would then not be frequently encountered. However, with increasing genome-wide epidemiological studies, Case 3 arises much more often as researchers test hundreds of thousands of potential genomic mediators across the genome, such as gene expression or methylation.

Statistical Methods for NIE test

We examine four common approaches as mentioned in the introduction. The joint significant test (causal steps method) for NIE is based on the path specific p-values and does not provide an estimate. The p-value is the maximum of the two path specific p-values. If it is less than level α, the null is rejected. Under Case 3, it will have type I error rate equal to α². For the other two cases, it will converge to α as evidence for the non-null path increases. The product of coefficients method, focuses on the outcome model (1) and mediator model (3) and estimates the NIE by ${\hat{\theta }}_2{\hat{\beta }}_1$. In terms of estimating the variance, the most commonly used is the Sobel estimator [Sobel 1982]:

$$\mathit{\text{var}}\left({\hat{\theta }}_2{\hat{\beta }}_1\right)\approx {\beta }_1^2{\sigma }_{\theta ,2 }^2+{\theta }_2^2{\sigma }_{\beta ,1}^2,$$

where ${\sigma }_{\theta ,2 }^2=\mathit{\text{var}}\left({\hat{\theta }}_2\right)$ and ${\sigma }_{\beta ,1}^2=\mathit{\text{var}}\left({\hat{\beta }}_1\right)$. The Sobel variance estimate is based on the multivariate delta method, which requires that the gradient of the expression evaluated at the truth be non-zero. The Sobel variance is estimated by substituting the above terms with the corresponding estimators. Testing is conducted by dividing the product ${\hat{\theta }}_2{\hat{\beta }}_1$ by the square root of this estimate and compared with standard normal distribution. Under Case 3, evaluating the Sobel estimator with the true parameters yields 0 (θ₂ =β₁= 0), and the multivariate delta method does not hold, as the gradient is 0. This is because the product estimator follows a normal product distribution. The difference in coefficients method, considers the outcome model (1) and a reduced outcome model (2). The mediation effect of A on Y through M is ϕ₁-θ₁. A test for the NIE can be developed by comparing $({\hat{\varphi }}_1-{\hat{\theta }}_1)/\sqrt{ \widehat{\mathit{\text{var}}} \left({\hat{\varphi }}_1\right)+\widehat{\mathit{\text{var}}} \left({\hat{\theta }}_1\right)-2\widehat{\mathit{\text{cov}}} \left({\hat{\varphi }}_1,{\hat{\theta }}_1\right)}$with a standard normal distribution. Under Case 3, the difference method does not follow a normal distribution, but a normal product distribution as the point estimate is equal to ${\hat{\theta }}_2{\hat{\beta }}_1$ [Mackinnon, et al. 1995]. Hence the normality based difference method also fails.

Finally, the bootstrap approximates the empirical distribution of the product method and then derives an empirical p-value by the number of bootstrap sample estimates greater than the observed ${\hat{\theta }}_2{\hat{\beta }}_1$ [Fritz and MacKinnon 2007; Mackinnon, et al. 2004]. the bootstrap method attempts to account for departures from normality, as it uses the empirical distribution.

Here we note that the mediation test statistic is a product of two normals, which in itself is not normal and under Case 3 is symmetric around zero with excess kurtosis of 6 [Craig 1936; Mackinnon, et al. 2004]. Under Case 1 and Case 2 the excess kurtosis will go to 0 as more evidence of the non-null relationship. Given the non-normality of the parameter we are interested in under Case 3 ( ${\hat{\theta }}_2{\hat{\beta }}_1$) we expect that the Bootstrap will also fail [Bickel, et al. 2012; Efron 1992].

Binary Mediator or Outcome

We next briefly discuss the product method for the NIE under three other scenarios which are commonly seen in epidemiologic studies. Consider a binary outcome (such as disease status) and the following models for mediation analysis:

$$\mathit{\text{logit}}\left(P\left(Y=1\right)\right)={\theta }_0+{\theta }_{1}A+{\theta }_{2}M+{\mathit{\theta }}_{\mathbf{3}}^{\mathit{T}}\mathit{X}$$

$$M={\beta }_0+{\beta }_{1}A+{\mathit{\beta }}_{\mathbf{2}}^{\mathit{T}}\mathit{X}+{\epsilon }_m .$$

Under sufficiently rare outcome and the necessary causal assumptions [VanderWeele and Vansteelandt 2010], we can approximate the log of the NIE as:

$$\log \left(\mathit{\text{NIE}}\right)\approx {\theta }_2{\beta }_1.$$

We then obtain a NIE estimate by substituting in ${\hat{\theta }}_2$ and ${\hat{\beta }}_1$. The three cases of no NIE, will thus apply again, and similarly, under Case 3 the product method will fail due to having zero gradient. Note, for this scenario the NIE is defined on the scale of odds ratio as opposed to the mean of a continuous outcome. The null is then NIE=1 or log(NIE)=0.

Next, if the mediator is also binary, we have the following models and expression for the NIE (NIE is measured on the odds ratio) [Valeri and VanderWeele 2013]:

$$\mathit{\text{logit}}\left(P\left(Y=1\right)\right)={\theta }_0+{\theta }_{1}A+{\theta }_{2}M+{\mathit{\theta }}_{\mathbf{3}}^{\mathit{T}}\mathit{X},$$

$$\mathit{\text{logit}}\left(P\left(M=1\right)\right)={\beta }_0+{\beta }_{1}A+{\mathit{\beta }}_{\mathbf{2}}^{\mathit{T}}\mathit{X},$$

$$\mathit{\text{NIE}}\approx \frac{1+\exp \left({\beta }_0+{\beta }_1{a}^{\prime }+{\beta }_2^{T}x\right)}{1+\exp \left({\beta }_0+{\beta }_{1}a+{\beta }_2^{T}x\right)}\left(\frac{1+\exp \left({\theta }_2+{\beta }_0+{\beta }_{1}a+{\beta }_2^{T}x\right)}{1+\exp \left({\theta }_2+{\beta }_0+{\beta }_1{a}^{\prime }+{\beta }_2^{T}x\right)}\right).$$

Under Case 3, the gradient of this term evaluated at the truth will be 0. Finally, for a continuous outcome and a binary mediator, under the necessary causal assumptions [Valeri and VanderWeele 2013]:

$$Y={\theta }_0+{\theta }_{1}A+{\theta }_{2}M+{\mathit{\theta }}_{\mathbf{3}}^{\mathit{T}}\mathit{X}+{\epsilon }_f$$

$$\mathit{\text{logit}}\left(P\left(M=1\right)\right)={\beta }_0+{\beta }_{1}A+{\mathit{\beta }}_{\mathbf{2}}^{\mathit{T}}\mathit{X}$$

$$\mathit{\text{NIE}}={\theta }_2\left(\frac{\exp \left({\beta }_0+{\beta }_{1}a+{\beta }_{2}x\right)}{1+\exp \left({\beta }_0+{\beta }_{1}a+{\beta }_{2}x\right)}-\frac{\exp \left({\beta }_0+{\beta }_{1}a\prime +{\beta }_{2}x\right)}{1+\exp \left({\beta }_0+{\beta }_1{a}^{\prime }+{\beta }_{2}x\right)}\right)$$

The gradient of this term evaluated at the truth will be 0 for both Case 1 and Case 3. For these mediation studies above, Case 3 will provide invalid results for the product method.

In mediation analysis with the above mediator and outcome combinations, the primary interest may lie in estimation as opposed to testing of NIE. Regardless, we felt it would be prudent to present these data types under testing. Note that the three cases under the null of no NIE affect statistical inference for these data types as well. Confidence intervals calculated using the normality assumption, may not be at the desired level. This is primarily an issue with a binary outcome and continuous mediator, as the delta method will likely be used in a similar manner as the continuous setting. Bootstrap method used to construct the CI’s for the other scenarios may result in similar issues, due to the non-normality of the estimates under certain scenarios [Bickel, et al. 2012; Efron 1992].

Simulation Study

We performed a simulation study to assess the Type I Error (TIE). Without loss of generality, we considered scalar confounder X for both outcome and mediator models. Let θ₂, β₁ ∈ (0, 0.14, 0.39), and other parameters set as fixed θ₀=θ₁=β₀=θ₃=β₂=0.14 (Equations 1, 3). These values were taken as a subset of the values from MacKinnon et al [MacKinnon, et al. 2002]. We considered all nine combinations of the values of ${\theta }_2$ and ${\beta }_1$ to examine the sizes and powers of the four commonly used methods for testing the NIE: joint, product, difference and bootstrap methods. If only one of ${\theta }_2$and ${\beta }_1$ equals to 0, it corresponds to Case 1 or 2 under the composite null of no NIE $H_0: {\theta }_2{\beta }_1=0.$Case 3 corresponds to ${\theta }_2={\beta }_1=0.$ If both ${\theta }_2$ and ${\beta }_1$ are not equal to 0, we study the power.

We generated X and A from independent standard normal and then sequentially generated M and Y with standard normal errors. The sample size was examined at 50, 100, 500, 1,000 and 5,000. For each set, 50,000 replications were performed. The type I error and power were evaluated at α=0.05. For each setting, we applied the four methods for testing for the NIE.

When ${\beta }_1=0.14$, A explains approximately 2% of the variation in M conditional on X and when ${\beta }_1=0.39$, it is 13%. This is when all errors are standard normal. Break downs of the total variation in Y due to A conditional on X are given in Table 1. This also gives how much of the total variation in Y that is due to the indirect effect of A conditional on X and the direct effect (Supplementary Table 1). When ${\beta }_1={\theta }_2=0.14$, A explains 2.4% of the variation in Y conditional on X with .3% of that variation coming from the NIE. If ${\beta }_1={\theta }_2=0.39$, 6.9% of the variation in Y is due to A, with 3.6% of the variation is due to the NIE.

Table 1. Simulations results for Empirical Type I Error and Power.

of linear regression mediation analysis comparing different commonly used mediation analysis methods based on 50,000 runs: Joint [MacKinnon, et al. 2002], Product [Baron and Kenny 1986; Sobel 1982], Difference [Mackinnon, et al. 1995], and Bootstrap [Fritz and MacKinnon 2007]. Type I error and power were evaluated at an α of 0.05.

β1	θ2	N	Joint	Product	Difference	Bootstrap
		50	0.0024	0.0002	0.0003	0.0024
		100	0.0021	0.0001	0.0001	0.0016
0	0	500	0.0024	0.0001	0.0002	0.0016
		1000	0.0026	0.0001	0.0002	0.0015
		5000	0.0027	0.0001	0.0002	0.0014
		50	0.0074	0.0006	0.0010	0.0073
		100	0.0131	0.0011	0.0018	0.0113
0	0.14	500	0.0452	0.0138	0.0175	0.0420
		1000	0.0510	0.0280	0.0321	0.0513
		5000	0.0514	0.0466	0.0480	0.0524
		50	0.0075	0.0009	0.0013	0.0072
		100	0.0140	0.0017	0.0026	0.0125
0.14	0	500	0.0445	0.0134	0.0173	0.0418
		1000	0.0499	0.0277	0.0317	0.0511
		5000	0.0503	0.0459	0.0471	0.0516
		50	0.0338	0.0094	0.0120	0.0373
		100	0.0489	0.0212	0.0262	0.0541
0	0.39	500	0.0511	0.0457	0.0473	0.0539
		1000	0.0515	0.0492	0.0499	0.0531
		5000	0.0514	0.0511	0.0512	0.0524
		50	0.0366	0.0114	0.0145	0.0397
		100	0.0479	0.0233	0.0277	0.0541
0.39	0	500	0.0508	0.0454	0.0471	0.0535
		1000	0.0503	0.0477	0.0484	0.0525
		5000	0.0503	0.0497	0.0498	0.0516
		50	0.0232	0.0041	0.0056	0.0215
		100	0.0744	0.0158	0.0210	0.0638
0.14	0.14	500	0.7663	0.5744	0.6154	0.7483
		1000	0.9855	0.9674	0.9724	0.9842
		5000	1	1	1	1
		50	0.1103	0.0405	0.0499	0.1101
		100	0.2690	0.1659	0.1859	0.2717
0.14	0.39	500	0.8757	0.8648	0.8676	0.8736
		1000	0.9926	0.9920	0.9923	0.9920
		5000	1	1	1	1
		50	0.1133	0.0442	0.0531	0.1115
		100	0.2636	0.1642	0.1841	0.2663
0.39	0.14	500	0.8750	0.8645	0.8676	0.8744
		1000	0.9928	0.9921	0.9923	0.9924
		5000	1	1	1	1
		50	0.5356	0.3403	0.3780	0.5153
		100	0.9251	0.8594	0.8777	0.9198
0.39	0.39	500	1	1	1	1
		1000	1	1	1	1
		5000	1	1	1	1

We also considered the case when the outcome Y is binary, which is also commonly seen in epigenomic studies. We generated data according to mediator model (3) and a logit outcome model (4), with similar parameter settings as for continuous Y. In detail, we let θ₂, β₁ ∈ (0, 0.14, 0.39), and set θ₁=β₀=θ₃=β₂=0.14. We set θ₀=−5 to mimic the situation when the outcome is the incidence of a rare disease (about 1%). We examined a cohort with sample size N=5,000. For each set of parameters (θ₂, β₁), 50,000 replications were performed, joint method, product method and bootstrap method were employed to evaluate the type I error and/or power at α=0.05.

$$\mathit{\text{logit}}\left(\mathrm{Pr}\left(Y=1\right)\right)={\theta }_0+{\theta }_{1}A+{\theta }_{2}M+{\theta }_{3}X$$ (4)

Application to the Normative Aging Study

We next performed an epigenome-wide mediation analysis using DNA methylation (DNAm), the most well studied epigenetic mechanism. This biological process occurs when a methyl group has been added to a cytosine followed by a guanine (CpG site) based pair on the genome and is measured across the genome. It has been found to be associated with a variety of diseases and exposures [Ciernia and LaSalle 2016; Panni, et al. 2016; Teschendorff, et al. 2015]. We performed an epigenome-wide Mediation Study to assess mediation of smoking behavior (pack years) on FEV₁ through logit transformed DNAm probes [Du, et al. 2010]. Pack years is a measure of how much an individual has smoked over multiple years. It is defined as the number of packs of cigarettes smoked per day times the years the individual has smoked. FEV₁ measures the forced expiratory volume in 1 second of an individual. FEV₁ is affected by airway narrowing and is often used to diagnose and measure severity of cases of Chronic Obstructive Pulmonary Disease (COPD) and cystic fibrosis [Taylor-Robinson, et al. 2012; Weiss 2010]. The analysis was performed on FEV₁ in the Normative Aging Study, a cohort study in the Greater-Boston metropolitan area [Bell, et al. 1972]. We focused on the data consisting of 575 Caucasian men, with DNAm measured on the Illumina 450k array.

Briefly, DNAm was collected in whole blood in study participants between 1999 and 2007. We removed any probes on the sex chromosomes, non-CG probes and probes within 10 bp of a known SNP within the 1000 genomes population [Butcher 2013]. More information about the preprocessing and collection of the data has been published elsewhere [Panni, et al. 2016]. We adjusted for: age, log of height, visit information, cell type proportion [Houseman, et al. 2012], health history, smoking status, top ten surrogate variables (SV) [Leek and Storey 2007] and technical variables. The SV’s were calculated on a subset of the DNAm probes with an interdecile range greater than 0.1 (111,189 or approximately 25% of probes). This was to decrease computational time and to use more informative probes. SV analysis was performed to control for additional batch effects, given our design matrix of covariates X and pack-years. Testing of the NIE was done using the joint significance and the product using the Sobel variance method. We did not use the bootstrap approach due to the computational cost of performing the number of bootstrap samples for the empirical p-value to be significant at the genome-wide scale. The analysis was done on a total of 449,547 probes.

Results

Simulation Study

When either θ₂ is non-zero (Case 1) or β₁ is non-zero (Case 2), but not both, the type I error of the four methods for testing NIE is controlled under 0.05 if the sample size is large and the effects size of the non-zero β₁ or θ₂ is not small (Table 1). If the nonzero coefficient β₁ or θ₂ is small and the sample size is not sufficiently large, the four tests are conservative, especially the product estimator and the difference estimator. For β₁=θ₂= 0 (Case 3), the type I error is extremely low even for large sample sizes, indicating these commonly used tests are conservative. This is due to the fact that the tests do not follow the standard normal distribution but a normal product distribution in Case 3. Using non-Sobel variance estimators [Aroian 1947; Goodman 1960] leads to similar results (data not shown) [MacKinnon, et al. 2002].

In genome-wide epigenetic/epidemiological studies, the effect sizes associated with single CpG sites, such as β₁ and θ₂ tend to be small and a vast majority of probes are Case 3, thus the genome-wide type I error control is likely to be a problem when applying mediation tests over the CpG markers genome-wide. Further, we do not know which case (Cases 1, 2, 3) a probe belongs to, we would not be able to know what null distribution to use as a reference distribution, e.g., using a normal distribution or a product normal distribution for the product method. Among all settings the joint and bootstrap procedures have sizes closer to the null and the highest power (last nine rows of Table 1).

When the outcome is binary, deflated type I error were also observed for all methods under consideration for β₁=θ₂= 0 (Case 3), as well as for the Case 1 and Case 2 when the true effect size of the non-zero parameter (β₁ or θ₂) is small (Table 2). Thus existing methods also tend to be conservative for problems with binary outcomes. Notice here the bootstrap method may tend to have slight inflation on type I error and power in some of the cases, which is likely to be related to unbalanced data (smaller number of cases than controls), thus in practice, it may not be recommended to use bootstrap method unless the sample size is large, or special bootstrap techniques that are designed for unbalanced samples may be employed to overcome such issues.

Table 2. Simulations results for Empirical Type I Error and Power when the outcome is binary.

Simulation results for cohort study with N=5000, with disease prevalence of around 1%. Type I error and power were evaluated at an α of 0.05.

β1	θ2	Joint	Product	Bootstrap
0	0	0.0026	0.0001	0.0017
0	0.14	0.0065	0.0005	0.0043
0.14	0	0.0509	0.0463	0.0592
0	0.39	0.0351	0.0064	0.0286
0.39	0	0.0509	0.0505	0.0592
0.14	0.14	0.1310	0.1226	0.1398
0.14	0.39	0.6795	0.6652	0.6730
0.39	0.14	0.1322	0.1309	0.1397
0.39	0.39	0.6884	0.6869	0.6839

Application to the Epigenome-Wide Normative Aging Study

We examine the QQ-plots for the associations between smoking and DNA methylations and the associations between DNA methylations and FEV₁. We see little to no inflation in the distribution of p-values (Figures 2A and 2B). Under the null hypothesis of no NIE, we also expect a test to yield uniformly distributed p-values, which does not occur here (Figure 2C). The observed deflation is likely due to most probes existing in Case 3. This deflation is not likely just due to any unmeasured confounders, as the p-values from exposure to mediator and mediator to outcome given exposure appear to follow a uniform distribution (Figures 2A and 2B). Under Case 3, the joint p-value, which is the maximum of the path-specific p-values, does not follow a uniform distribution. This deflation is also seen if we used the product method with Sobel’s estimator (Figure 2D).

Figure 2. QQ-plots of individual p-values for various associations in Normative Aging genome-wide Study.

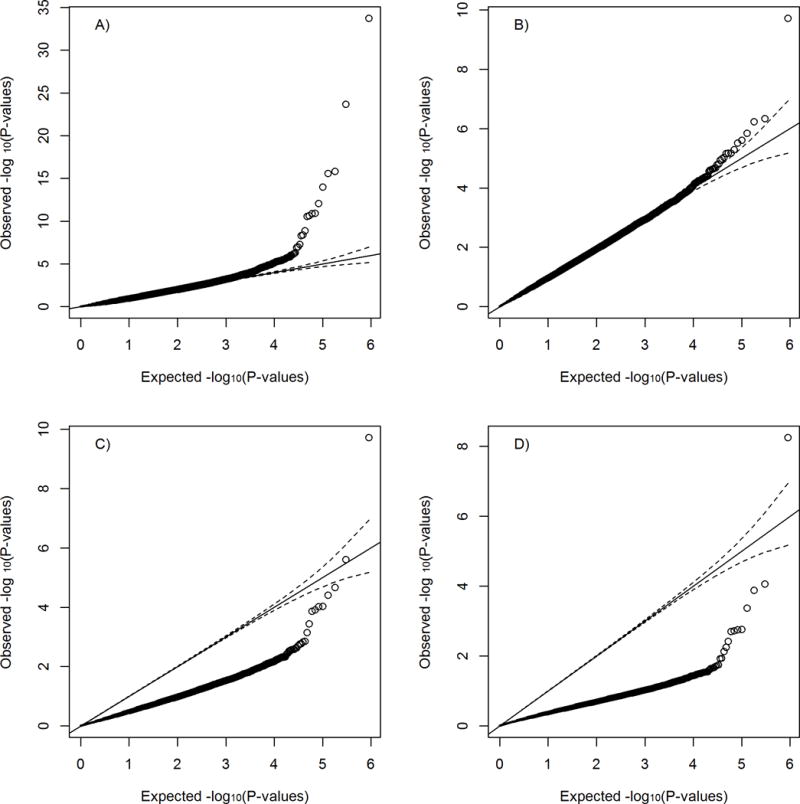
A) P-values from pack-years to DNAm B) P-values from DNAm to FEV₁ adjusting for pack-years C) Testing DNA methylation as a mediator for the association between pack years and lung function using the joint significance approach D) Testing DNA methylation as a mediator for the association between pack years and lung function using product p-value with Sobel variance estimate.

One probe was found to be genome wide significant: cg05575921, at the AHRR (Aryl-Hydrocarbon Receptor Repressor) gene (p-value 1.92 e-10, NIE estimate −0.0036, product method p-value 5.62e-09). This probe has been found to be associated with smoking in several previous studies [Fasanelli, et al. 2015; Zeilinger, et al. 2013]. It is located at chr 5:373378 on the north shore of AHRR [Fasanelli, et al. 2015]. The aryl-hydrocarbon receptor helps to regulate the effects of stressors from the outside environment, and AHRR prevents that mechanism from occurring [Fasanelli, et al. 2015]. There was evidence that this probe (with a collection of other probes) potentially mediates the effect of maternal smoking on offspring birthweight [Kupers, et al. 2015]. It has also been suggested that this probe is a risk factor for lung cancer [Baglietto, et al. 2017]. The association with smoking in DNAm at this probe is one of the more frequently reported associations in the epigenome wide field so far. This significant NIE suggests a further association of interest, with pack years’ effect on FEV₁ being mediated by DNAm.

Conclusion

In addition to the traditional considerations of whether a variable meets the criteria of a mediator, it is important to consider the statistical test for the NIE. We have demonstrated that the classical mediation analysis methods, such as Sobel’s product, are not statistically appropriate under Case 3 (Table 1). Other approaches also fail to have the proper type I error under Case 3 [Biesanz, et al. 2010; MacKinnon, et al. 2002]. We have shown that this could lead to severe problem in epigenome-wide studies for mediation, where the task is to test a large number of potential mediators and pathways for NIEs and very commonly there is a mixture of Case 1, 2 and 3, with Case 3 likely occurring most often. These studies could result in severe deflation in the p-value distribution. Case 3 needs to be further studied to derive proper testing procedures for these new challenges.

We demonstrated how Case 3 can affect real data analysis where a mediation analysis equivalent of an epigenome-wide association study was performed. The deflation we observe in the tests of no NIE is likely due to the statistical properties of the tests as we did not see deflation in the association specific p-value distribution. We also provide more evidence for the AHRR gene being an important mediator of smoking history and lung function.

We note that in practice the genomic mediators are likely correlated. This could lead to biased estimates of the natural indirect effect due to failure to account for unmeasured confounders in the form of nearby DNAm markers. Methods for testing the joint mediated effect should be further developed. There have been approaches for this multiple mediator case in the epidemiology field [Daniel, et al. 2015; VanderWeele and Vansteelandt 2014], as well as the higher dimensionality of the genomic case [Huang and Pan 2016; Zhang, et al. 2016]. However, we feel that it is important to derive proper testing size under the single mediator case which can then guide testing under the multiple mediator situation for Case 3.

In most epidemiological studies, where there is prior knowledge of being in Case 1 or 2 and sample sizes are large, the product and difference methods are likely appropriate. However, in genome-wide genomic studies, Case 3 is common and it is unknown in advance which of the three cases a probe falls in when scanning the genome. For now, if Case 3 is thought to be a reasonable possibility, we suggest that the product and difference methods be avoided as the conditions for the multivariate delta method do not hold. We suggest the joint significance or bootstrap might be considered with the understanding that these are conservative under Case 3. Future research is needed to develop tests for the NIE in genome-wide genetic/epigenetic studies by accounting for the fact that null hypothesis is a composite null.