Ionic effects on the temperature–force phase diagram of DNA

Abstract

Double-stranded DNA (dsDNA) undergoes a structural transition to single-stranded DNA (ssDNA) in many biologically important processes such as replication and transcription. This strand separation arises in response either to thermal fluctuations or to external forces. The roles of ions are twofold, shortening the range of the interstrand potential and renormalizing the DNA elastic modulus. The dsDNA-to-ssDNA transition is studied on the basis that dsDNA is regarded as a bound state while ssDNA is regarded as an unbound state. The ground state energy of DNA is obtained by mapping the statistical mechanics problem to the imaginary time quantum mechanics problem. In the temperature–force phase diagram the critical force F _c(T) increases logarithmically with the Na⁺ concentration in the range from 32 to 110 mM. Discussing this logarithmic dependence of F _c(T) within the framework of polyelectrolyte theory, it inevitably suggests a constraint on the difference between the interstrand separation and the length per unit charge during the dsDNA-to-ssDNA transition.

Introduction

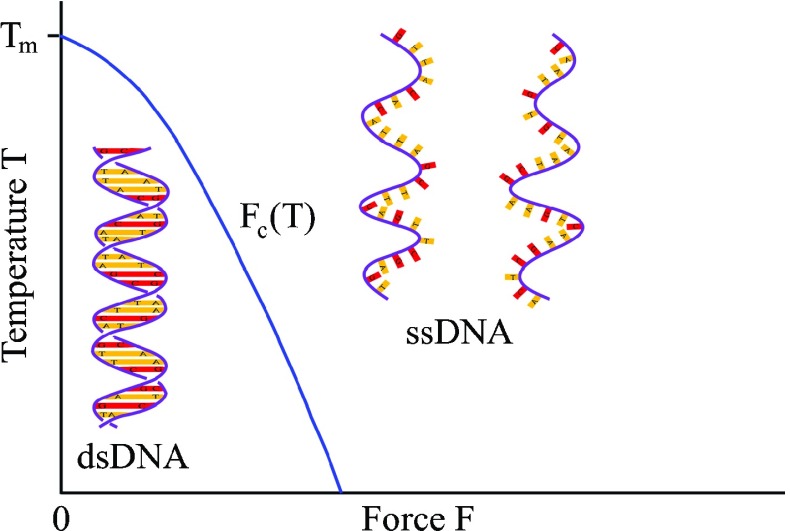
The bound base pairs, adenine-thymine (A-T) and guanine-cytosine (G-C), are unzipped in order to read and copy the encoded genetic information. This unzipping of the bound base pairs makes the double-stranded DNA (dsDNA) transition structurally to single-stranded DNA (ssDNA). Having increased the temperature, the neighboring base pairs on each strand unstack and the hydrogen bonds between complementary base pairs are thermally broken. The unstacking and the hydrogen bond breaking give individual strands more degrees of freedom, thus an increase in entropy. The fraction of the unzipped base pairs, which is inferred from measuring the UV absorption of a DNA solution, increases with temperature following a sigmoidal shape [1]. The temperature at the center of the sigmoidal shape, where the fraction of the unzipped base pairs rises abruptly to one, is identified as a melting temperature T _m typically around 90 °C [2]. The thermally induced dsDNA-to-ssDNA transition, called DNA denaturation, occurs in polymer chain reactions [3]. A rise in the temperature is fatal to the cells. Instead, the cell exploits the enzymatic force to unzip the base pairs. Thanks to optical tweezers, the force-induced dsDNA-to-ssDNA transition, called DNA unzipping, can now be studied extracellularly in well-controlled environmental conditions. To unzip the base pairs between two strands, one bead is captured and fixed in an optical trap while the other bead, attached to a piezo-electric actuator, is laterally displaced. The force, inferred from the interferometric measurement of the bead in the optical trap, shows a plateau about 15 pN, which is the critical force F _c of the dsDNA-to-ssDNA transition at room temperature [4]. The base pairs can be either unzipped thermally by increasing the temperature or unzipped mechanically by applying an external force. In the temperature–force phase diagram illustrated schematically in Fig. 1, dsDNA is the low-temperature, small-force phase and ssDNA is the high-temperature, large-force phase. The boundary between dsDNA and ssDNA phases is the temperature-dependent critical force F _c(T).

Fig. 1.

In the absence of force, an increase in temperature above the melting temperature T _m transits dsDNA to ssDNA. For temperatures T < T _m, the dsDNA-to-ssDNA transition is achieved by applying an external force F larger than the critical force F _c(T)

The negative charges on the phosphodiester backbones give rise to the intermolecular repulsion. The positively monovalent ions, such as Na⁺ from NaCl salt solutions, mediate an attraction between the negatively charged backbones [5]. In other words, the Na⁺ ions reduce the intermolecular repulsion. The positively multivalent ions, such as Mg²⁺ from Mg Cl₂ solutions, screen the intermolecular repulsion more effectively. As a result, the DNA in low concentration of 10 mM Mg²⁺ has a melting temperature T _m and the critical force F _c comparable to DNA in high concentration of 150 mM Na⁺ [6].

Model with Debye-Hückel interstrand potential

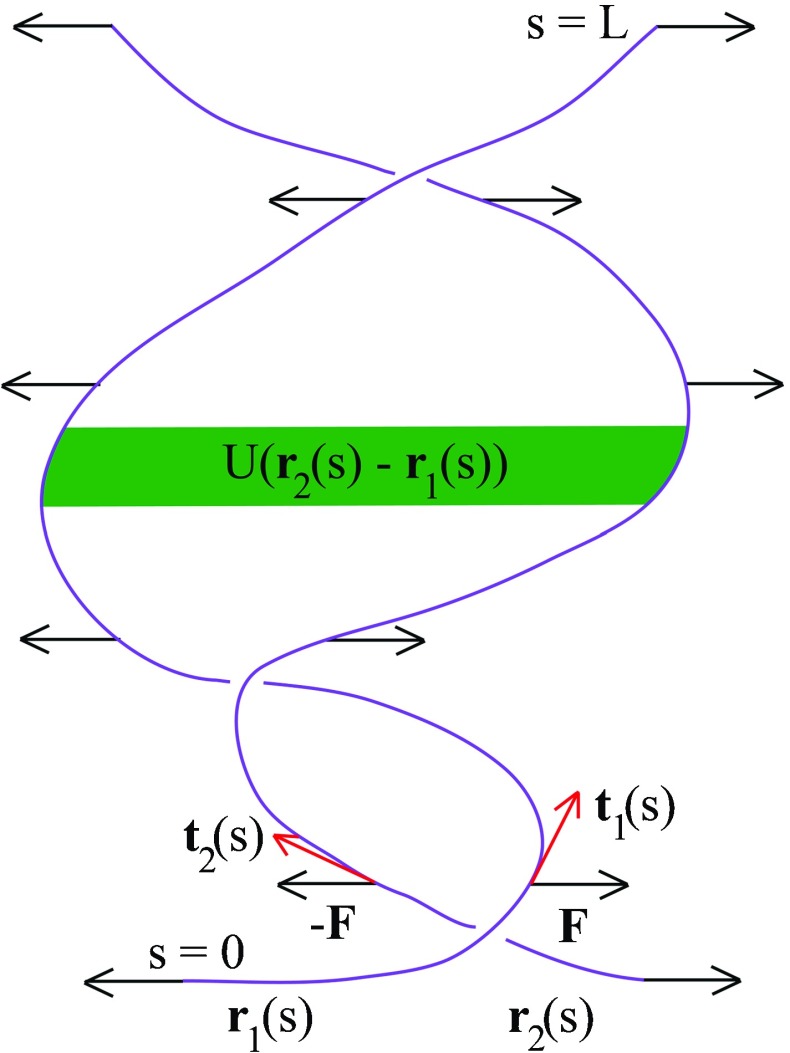
DNA has a very long length on the order of μ m compared to its 2-nm diameter, so that the DNA can be treated as a one-dimensional object. The distance between adjacent base pairs on the same strand is only 0.34 nm, much shorter than the μ m length, so it makes sense to use a continuum description. As depicted in Fig. 2, DNA is modeled as two continuous curves r ₁(s) and r ₂(s), where s denotes an arc length. Each curve has an entire length L, which could be as long as 15.1 μ m for the lambda bacteriophage virus [7]. The orientation of the length element at s is a tangent to the curve, d r ₁/ds, and similarly for the other curve. The resistance to stretching is described by a spring constant K. The deformation of the curve from the straight conformation gives the elastic energy $(K/2){\int }_0^{L}ds{(d{\mathbf{\text{r}}}_1/ds)}^2$ and similarly for the other curve. An adenine-thymine base pair is held by two hydrogen bonds and a guanine-cytosine base pair is held by three hydrogen bonds. The interaction between two strands is sequence dependent. Having coarse grained the interaction over a large number of bases, we however describe phenomenologically the interaction by a short-ranged attractive potential like the Debye-Hückel potential U(r ₂(s) −r ₁(s)) [8–10]. Alternatively, the other form of the short-ranged potential used is the Morse potential, which captures both the repulsion for small interstrand separation and the attraction for large interstrand separation [11–13]. Applying the external constant force F, the first strand displaces by d r ₁(s), the work done by F being F.d r ₁(s). The equal magnitude but opposite direction force −F, which acts on the second strand, displaces it by d r ₂(s), the work done by −F being −F.d r ₂(s). In experiments, the force is introduced at one end s = 0 by translating the glass slide with a piezo stage [14]. To make the correspondence between statistical mechanics and imaginary time quantum mechanics, we however assume that the constant force F is uniformly distributed along the entire length. This assumption would at most lead to an overestimate of the critical force F _c but does not alter the dependence of F _c on the Na⁺ concentration. Adding the elastic energy, interstrand potential, and the work done by external constant force gives the Hamiltonian

$$\begin{array}{rcl}H& =& \frac{1}{2}K{\int }_0^{L}ds\left[{\left(\frac{d{\mathbf{\text{r}}}_2}{ds}\right)}^2+{\left(\frac{d{\mathbf{\text{r}}}_1}{ds}\right)}^2\right]+{\int }_0^L\mathrm{dsU}\left({\mathbf{\text{r}}}_2\right(s)-{\mathbf{\text{r}}}_1(s\left)\right)\\ & & -\mathbf{\text{F}}\mathrm{.}{\int }_0^{L}ds\left(\frac{d{\mathbf{\text{r}}}_2}{ds}-\frac{d{\mathbf{\text{r}}}_1}{ds}\right)\mathrm{.}\end{array}$$ 1

Focusing on the interstrand separation r ₂(s) −r ₁(s) resulting from the unzipping of base pairs, we define the new coordinates, namely the “center-of-mass” coordinates r _cm ≡ (r ₂(s) + r ₁(s))/2 and the relative coordinates r ≡r ₂(s) −r ₁(s). The “center-of-mass” part of Hamiltonian is irrelevant to the strand separation, so we neglect it, leaving the relative-coordinate part of Hamiltonian

$$H=\frac{1}{4}K{\int }_0^{L}ds{\left(\frac{d\mathbf{\text{r}}}{ds}\right)}^2+{\int }_0^L\mathrm{dsU}\left(\mathbf{\text{r}}\right(s\left)\right)-\mathbf{\text{F}}\mathrm{.}{\int }_0^{L}ds\frac{d\mathbf{\text{r}}}{ds}\mathrm{.}$$ 2

The partition function Z is a path integral of the Boltzmann distribution over all configurations with two opposite ends fixed r(0) = r ₀ and r(L) = r _L

$$Z=\int D\mathbf{\text{r}}\left(s\right)exp\left(-\frac{1}{k_{B}T}H\left[\mathbf{\text{r}}\right(s\left)\right]\right)\mathrm{.}$$ 3

To evaluate the partition function, we exploit the correspondence between statistical mechanics and imaginary time quantum mechanics [15]. The present statistical mechanics problem corresponds to the quantum mechanics of a particle with mass m and charge q moving under the imaginary vector potential i A and under the potential U(r). The Hamiltonian of this quantum mechanics system reads

$$\widehat{\mathbf{\text{H}}}=-\frac{{\overline{h}}^2}{2m}{\left(\nabla -i\frac{q}{\overline{h}}\mathbf{\text{A}}\right)}^2+U\left(\mathbf{\text{r}}\right)\mathrm{.}$$ 4

The role of $\overline{h}$ is played by thermal energy k _B T, that of mass 2m played by spring constant K, and that of imaginary vector potential iq A played by force F. The Hamiltonian of this quantum mechanics problem is equivalent to the Hamiltonian of statistical mechanics problem

$$\widehat{\mathbf{\text{H}}}=-\frac{{\left(k_{B}T\right)}^2}{K}{\left(\nabla -\frac{1}{k_{B}T}\mathbf{\text{F}}\right)}^2+U\left(\mathbf{\text{r}}\right)$$ 5

whose eigenfunctions and eigenenergies are determined from $\widehat{\mathbf{\text{H}}}{\psi }_n\left(\mathbf{\text{r}}\right)=E_n{\psi }_n\left(\mathbf{\text{r}}\right)$. The potential in the quantum mechanics problem, (4), is the same Debye-Hückel potential U(r) in the statistical mechanics problem, (5). We find the eigenfunctions ψ _n and eigenenergies E _n of the Hamiltonian of statistical mechanics problem, (5), by considering instead the equivalent Hamiltonian of the quantum mechanics problem, (4). The eigenfunctions ψ _n(r) of (4) are obtained by the gauge transformation, A ^′ = A −∇Λ. The change in the eigenfunctions under gauge transformation is [15]

$${\psi }_n^{\prime }\left(\mathbf{\text{r}}\right)=exp\left(-i\frac{q\mathrm{\Lambda }}{\overline{h}}\right){\psi }_n\left(\mathbf{\text{r}}\right)\mathrm{.}$$ 6

To simplify the problem of finding the eigenfunctions, we choose the gauge Λ in such a way that A ^′ = 0 thereby Λ = A.r. We can say that ψn′(r) are the eigenfunctions in the absence of vector potential. To make the notations more physically appealing, we change the notation from ψn′(r) to ψn(A = 0)(r). In the presence of vector potential, the eigenfunctions of (4) are

$${\psi }_n\left(\mathbf{\text{r}}\right)=exp\left(i\frac{q}{\overline{h}}\mathbf{\text{A}}\mathrm{.}\mathbf{\text{r}}\right)\underset{n}{\overset{(\mathbf{\text{A}}=0)}{\psi }}\left(\mathbf{\text{r}}\right)\mathrm{.}$$ 7

These eigenfunctions ψ _n(r) of the quantum mechanics problem are then translated to those of the statistical mechanics problem by replacing $\overline{h}$ with k _B T and iq A with F

$${\psi }_n\left(\mathbf{\text{r}}\right)=exp\left(\frac{1}{k_{B}T}\mathbf{\text{F}}\mathrm{.}\mathbf{\text{r}}\right)\underset{n}{\overset{(\mathbf{\text{F}}=0)}{\psi }}\left(\mathbf{\text{r}}\right)$$ 8

which are the eigenfunctions of (5). The partition function can be written as a superposition of the eigenfunctions ψ _n and the corresponding eigenenergies E _n of the statistical mechanics problem [16]

$$Z=\sum _n{\psi }_n\left({\mathbf{\text{r}}}_0\right){\psi }_n\left({\mathbf{\text{r}}}_L\right)exp\left(-\frac{L}{k_{B}T}{E}_n\right)\mathrm{.}$$ 9

In the limit of infinitely long length L →$\infty$, the ground state n = 0 dominates over all the excited states, thereby approximating $Z\approx {\psi }_0\left({\mathbf{\text{r}}}_0\right){\psi }_0\left({\mathbf{\text{r}}}_L\right)exp(-L{E}_0/k_{B}T)$. The magnitude squared of the ground state eigenfunction |ψ ₀(r)|² describes the probability of the interstrand separation being r. In the next section, we focus primarily on finding the ground state eigenfunction ψ ₀ and the ground state eigenenergy E ₀.

Fig. 2.

DNA is smeared out to form two continuous curves r ₁(s) and r ₂(s) interacting to each other by the attractive Debye-Hückel potential U(r ₂(s) −r ₁(s)). The constant force F acts uniformly along the curves r ₁(s) and r ₂(s) with equal magnitude but opposite direction. Elastic energy is contributed from the spatially varying orientation described by the tangent vectors t ₁(s) = d r ₁/ds and t ₂(s) = d r ₂/ds

Ground state

Owing to the fact that the Debye-Hückel potential is the screened Coulomb potential, we split the Debye-Hückel potential into the Coulomb potential and the screening effect, which the latter is treated as a perturbation. Since the eigenfunctions and eigenenergies of the Schrödinger equation with Coulomb potential, which describes a hydrogen atom, are well known, we use them as the unperturbed eigenfunctions and the unperturbed eigenenergies. Subsequently, we calculate perturbatively the first-order correction to the ground state eigenenergy E ₀ due to the screening effect.

As explained in Section 2, the essential feature of the attractive interstrand potential is short ranged, so we reasonably model it as the Debye-Hückel potential

$$U\left(\mathbf{\text{r}}\right)=-\frac{k_{B}T{l}_B}{r}exp\left(-\frac{r}{{\lambda }_D}\right)$$ 10

where l _B denotes the Bjerrum length l _B = e ²/𝜖k _B T with 𝜖 being the dielectric constant of the medium, and λ _D denotes the Debye screening length [5]. Keep in mind that there exists an interstrand separation cutoff below which the interstrand potential becomes repulsive. As long as we are concerned with the dsDNA-to-ssDNA transition, the DNA elasticity is a long-wavelength property insensitive to the detail of the short-length scale physics, that is to say the sequence of base pairs. The power series expansion gives

$$U\left(\mathbf{\text{r}}\right)=-\frac{e^2}{\mathrm{𝜖r}}+\frac{e^2}{𝜖{\lambda }_D}\sum _{n=0}^{\infty }\frac{{(-1)}^n}{(n+1)!}{\left(\frac{r}{{\lambda }_D}\right)}^n\mathrm{.}$$ 11

The first term is the attractive Coulomb potential and the second term is the ion-induced screening effect whose energy scale is e ²/𝜖λ _D and the length scale is r/λ _D, a ratio of the interstrand separation r to the Debye screening length λ _D. We write the Hamiltonian, (5), as $\widehat{\mathbf{\text{H}}}={\widehat{\mathbf{\text{H}}}}_0+{\widehat{\mathbf{\text{H}}}}^{\prime }$ where the unperturbed Hamiltonian is

$${\widehat{\mathbf{\text{H}}}}_0=-\frac{{\left(k_{B}T\right)}^2}{K}{\left(\nabla -\frac{1}{k_{B}T}\mathbf{\text{F}}\right)}^2-\frac{e^2}{\mathrm{𝜖r}}$$ 12

and the perturbation, which is the second term in (11), is a screening effect

$${\widehat{\mathbf{\text{H}}}}^{\prime }=\frac{e^2}{𝜖{\lambda }_D}\sum _{n=0}^{\infty }\frac{{(-1)}^n}{(n+1)!}{\left(\frac{r}{{\lambda }_D}\right)}^n\mathrm{.}$$ 13

Precisely the electron charge e in (12) and (13) would be considered as the effective charge of DNA, because DNA is a highly charged polymer with one fundamental negative charge every 0.17 nm of its contour length [5]. In what follows, we find the ground state eigenfunction and the ground state eigenenergy of the unperturbed Hamiltonian ${\widehat{\mathbf{\text{H}}}}_0$, and then use them to calculate the ground state eigenenergy of the full Hamiltonian $\widehat{\mathbf{\text{H}}}$ by the first order perturbation theory.

In the absence of force, i.e., F = 0 or equivalently in quantum mechanics A = 0, substituting $\overline{h}$ for k _B T and 2m for K makes (12) becoming identically to the Hamiltonian of a hydrogen atom

$${\widehat{\mathbf{\text{H}}}}_0=-\frac{{\overline{h}}^2}{2m}{\nabla }^2-\frac{e^2}{\mathrm{𝜖r}}=-\frac{{\overline{h}}^2}{2m}\left(\frac{1}{r}\frac{{\partial }^2}{\partial r^2}r\right)+l(l+1)\frac{{\overline{h}}^2}{2m{r}^2}-\frac{e^2}{\mathrm{𝜖r}}$$ 14

in which we are concerned only with the radial component because the interstrand potential U(r) is spherically symmetric. Notice that 𝜖 replaces the familiar term 4π𝜖 ₀ in the conventional hydrogen-atom Hamiltonian. The normalized ground state eigenfunction, which has the principal quantum number n = 1, orbital quantum number l = 0, and magnetic quantum number m _l = 0, is

$${\psi }_0^{(\mathbf{\text{A}}=0)}\left(\mathbf{\text{r}}\right)=\frac{1}{\sqrt{\pi }{a}_0^{3/2}}exp\left(-\frac{r}{a_0}\right)$$ 15

where the Bohr radius is

$$a_0=𝜖\frac{{\overline{h}}^2}{m{e}^2}\mathrm{.}$$ 16

The normalized ground state eigenfunction of quantum mechanics problem, (15), is translated to the normalized ground state eigenfunction of the statistical mechanics problem

$${\psi }_0^{(\mathbf{\text{F}}=0)}\left(\mathbf{\text{r}}\right)=\frac{1}{\sqrt{\pi }{a}^{3/2}}exp\left(-\frac{r}{a}\right)$$ 17

where now the Bohr-like radius is

$$a=2𝜖\frac{{\left(k_{B}T\right)}^2}{K{e}^2}\mathrm{.}$$ 18

At temperature T = 293 K, spring constant K = 4 pN/nm, and dielectric constant of water 𝜖 = 80𝜖 ₀, the Bohr-like radius a is of order 0.23 nm comparable to the 0.17-nm length which contains one fundamental negative charge [5].

In the presence of force, the normalized ground state eigenfunction, obtained by substituting (17) in (8), is

$${\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\equiv {\psi }_0^{(\mathbf{\text{F}}\ne 0)}\left(\mathbf{\text{r}}\right)=N\left(F\right)exp\left[-\left(1-\frac{Fa}{k_{B}T}\right)\frac{r}{a}\right]$$ 19

in which the subscript 0 denotes the ground state and the superscript 0 written in parentheses denotes the eigenfunction of the unperturbed Hamiltonian ${\widehat{\mathbf{\text{H}}}}_0$, (12). The normalization constant is

$$N\left(F\right)=\frac{1}{\sqrt{\pi }}{\left(\frac{1-\frac{Fa}{k_{B}T}}{a}\right)}^{3/2}\mathrm{.}$$ 20

The ground state eigenenergy is $E_0^{\left(0\right)}=<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}_0\right|{\psi }_0^{\left(0\right)}>$ resulting in

$$E_0^{\left(0\right)}=-\frac{3}{4}\frac{e^2}{\mathrm{𝜖a}}+\frac{2}{K}{\left(F-\frac{1}{2}\frac{k_{B}T}{a}\right)}^2$$ 21

with the detailed calculation presented in Appendix A. Unless the force is sufficiently large the ground state eigenenergy E0(0) is negative, i.e., a bound state. Consider the second term in parentheses, apart from a prefactor 1/2, the quantity k _B T/a sets the force scale for the dsDNA-to-ssDNA transition. Remarkably, when the force F > k _B T/a the ground state eigenfunction ψ0(0)(r) becomes non-normalizable, as seen from (19) ψ0(0)(r) grows infinitely at large r, signifying the delocalized state that is the ssDNA. If the ground state eigenfunction is delocalized, all the excited state eigenfunctions are delocalized as well. Making use of the Bohr-like radius a from (18), we obtain the force scale k _B T/a = Ke ²/2𝜖k _B T ≈ 18 pN for K = 4 pN/nm, 𝜖 = 80𝜖 ₀, and T = 293 K which is of the right magnitude with the 15 pN critical force measured in experiments [4].

At this stage, we calculate the ground state eigenenergy E ₀ of the full Hamiltonian $\widehat{\mathbf{\text{H}}}$ by the first order perturbation theory

$$E_0=E_0^{\left(0\right)}+<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}>$$ 22

where the first-order correction due to the screening effect is

$$<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}>=\left(1-\frac{Fa}{k_{B}T}\right)\frac{e^2}{𝜖}\frac{4\left(1-\frac{Fa}{k_{B}T}\right){\lambda }_D+a}{{\left[2\left(1-\frac{Fa}{k_{B}T}\right){\lambda }_D+a\right]}^2}$$ 23

with the detailed calculation presented in Appendix B. Two important length scales are the Debye screening length λ _D and the Bohr-like radius a. The force F appears in the first-order correction as a combination Fa/k _B T, a ratio of the work done by the force over the Bohr-like radius a to the thermal energy k _B T. In the T = 0 limit, < ${\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}$ > is simply reduced to e ²/𝜖λ _D, the Coulomb energy associated with the interstrand separation r equal the Debye screening length λ _D. The high ion concentration shortens the range over which the Debye-Hückel potential is effective. The Debye screening length λ _D thus decreases with increasing the Na⁺ concentration, λ _D = $0.25/\sqrt{\left[{\text{Na}}^{+}\right]}$ where λ _D is in units of nm and [Na⁺] is in molar units [17]. At [Na⁺] = 0.1 M, the Debye screening length λ _D is about 0.8 nm. For the Debye-Hückel potential, the stretching modulus is renormalized from its bare value K ₀ to K = $K_0-(e^2/2𝜖b^3)exp(-b/{\lambda }_D)$ where K ₀ = 4 pN/nm and b = 1 nm taken to be the double-helix radius [18]. Because λ _D becomes shorter at high Na⁺ concentration, the rise in Na⁺ concentration leads to the larger stretching modulus K, namely electrostatic stiffening.

Ion concentration dependence of melting temperature in DNA denaturation

In the temperature–force phase diagram shown in Fig. 1, the DNA denaturation takes place on the temperature axis when temperature T is above the melting temperature T _m. Setting the force F = 0 reduces (21) to

$$E_0^{\left(0\right)}=-\frac{K}{4}{\left(\frac{e^2}{𝜖k_{B}T}\right)}^2\mathrm{.}$$ 24

Alternatively, we could arrive at the same result by recalling that the ground state energy of the hydrogen atom is $E_0^{\left(\text{hydrogen}\right)}=-(m/2){\left(e^2/{𝜖}_0\overline{h}\right)}^2$. The correspondence between statistical mechanics and imaginary time quantum mechanics suggests replacing 2m by K and $\overline{h}$ by k _B T, which translates E0(hydrogen) into E0(0) as in (24). We cast E0(0) in terms of the Bohr-like radius a, which simplifies its expression to E0(0) = −e ²/2𝜖a. Likewise, setting the F = 0 in (23) gives the first-order correction due to the screening effect

$$<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}>=\frac{e^2}{𝜖}\frac{4{\lambda }_D+a}{{\left(2{\lambda }_D+a\right)}^2}\mathrm{.}$$ 25

In the absence of force, the ground state eigenenergy $E_0=E_0^{\left(0\right)}+<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}>$ becomes

$$E_0=-\frac{1}{2}\frac{e^2}{\mathrm{𝜖a}}+\frac{e^2}{𝜖}\frac{4{\lambda }_D+a}{{\left(2{\lambda }_D+a\right)}^2}\mathrm{.}$$ 26

The bound state representing dsDNA corresponds to negative E ₀. When the ground state eigenenergy E ₀ ≥ 0, all the excited state eigenenergies are also positive. These positive eigenenergies form a continuous spectrum corresponding to the unbound state representing ssDNA, which occurs in the range of temperatures

$$T^2\ge (\sqrt{2}-1)\frac{K{\lambda }_D{e}^2}{𝜖k_B^2}\mathrm{.}$$ 27

The right-hand side of this inequality is thus identified as the square of the melting temperature

$$T_m^2=(\sqrt{2}-1)\frac{K{\lambda }_D{e}^2}{𝜖k_B^2}\mathrm{.}$$ 28

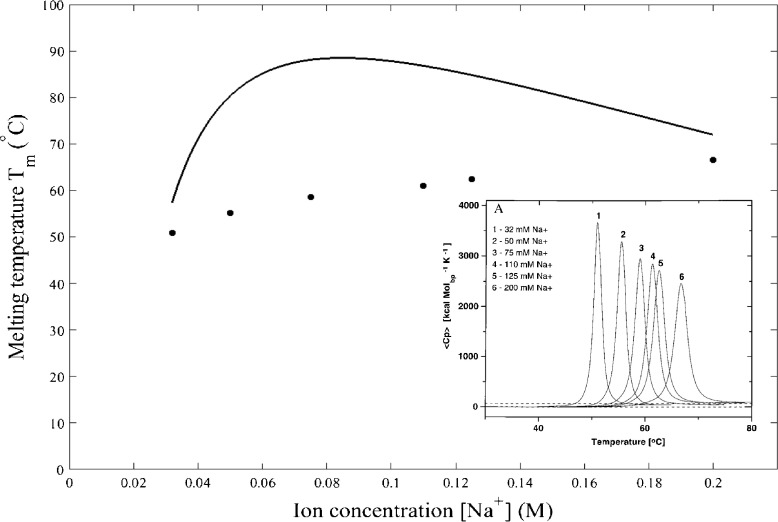
A rise in the Na⁺ concentration has two profound consequences. One is to shorten the Debye screening length, ${\lambda }_D=0.25/\sqrt{\left[{\text{Na}}^{+}\right]}$ [17], and the other is to stiffen the strands, K = K ₀ −$(e^2/2𝜖b^3)exp(-b/{\lambda }_D)$ [18]. Experimentally, the melting temperature T _m is deduced from the peak of the heat capacity of DNA, shown as an inset in Fig. 3 with varying the Na⁺ concentration from 0.032 M to 0.200 M [19]. The fit of (28) to these experimental data gives the effective charge e = 1.5 × 10⁻¹⁹ C, rather than the electron charge 1.6 × 10⁻¹⁹ C. The neutralization of negative charges due to the positive Na⁺ ions accounts for the reduction in effective charge. The overestimate of T _m, seen as a solid curve above the dots in Fig. 3, arises from the fact that the solution used in differential scanning calorimetry may contain more than one DNA molecule, hence the DNA–DNA interaction, which does not exist in our model of a single DNA molecule, is also important in the DNA thermodynamic properties. The DNA–DNA interaction, which is repulsive, destabilizes the DNA double-helix structure, thus requiring the smaller thermal energy for DNA denaturation as evidenced from the experimentally measured T _m lower than the theoretically predicted values. When increasing the Na⁺ concentration, the melting temperature T _m rises rapidly and then slightly drops when [Na⁺] is higher than 0.110 M. This small drop in T _m results from the fact that at such high Na⁺ concentration, the range of the attractive interstrand potential is so short that the small thermal energy is sufficient to separate strands, namely lowering T _m, although the small drop in T _m at high [Na⁺] appears more weak in experiments and is only seen as a tendency of the saturation of T _m.

Fig. 3.

Dependence of melting temperature T _m on the Na ⁺ concentration, calculated by Eq. (28), is compared with T _m, shown as dots, determined from the calorimetric measurements. Note that T _m obtained from Eq. (28) is in unit of Kelvin and is converted to unit of Celsius for comparison with experiments. Experimentally, the melting temperature is identified to be the temperature at which heat capacity is maximum, shown as an inset for six values of sodium ions 32, 50, 75, 110, 125, and 200 mM (Copyright 1999 National Academy of Sciences) [19]

It is well known that the melting temperature T _m is sequence dependent, with the higher T _m for the G-C-rich DNA molecule, because a G-C base pair is bound by three hydrogen bonds while an A-T base pair is bound by two hydrogen bonds [3]. As DNA undergoes denaturation, the structural order can be inferred from the X-ray diffraction patterns. The intensity of the Bragg peaks reduces in magnitude with increasing temperature. Melting temperature T _m is identified as the temperature at which the intensity of the Bragg peak decreases by one-half [20]. Upon melting, the loss of the translational order and rotational order makes the diffraction patterns less sharp.

Our results rest on the first-order perturbation theory, which is valid when $|<{\psi }_0^{\left(0\right)}|{\widehat{\mathbf{\text{H}}}}^{\prime }|{\psi }_0^{\left(0\right)}>|\ll \left|E_0^{\left(0\right)}\right|$ [15]. Using (24) and (25), the validity of the perturbation theory restricts the Na⁺ concentration in the sufficiently low range [Na⁺] ≪ [Na⁺]^∗, where the characteristic concentration ${\left[{\text{Na}}^{+}\right]}^{\ast }=0.25/{(\sqrt{2}+1)}^2{a}^2$ with the Bohr-like radius a in units of nm. At a temperature of 293 K, the Bohr-like radius a is about 0.23 nm. This places the Na⁺ concentration in the range [Na⁺] ≪ 0.8 M for the validity of the perturbation theory, justifying the Fig. 3 in which the maximum Na⁺ concentration is only 0.2 M still below the upper bound 0.8 M.

Ion concentration dependence of critical force in DNA unzipping

In experiments, the DNA molecules of the double-stranded virus lambda phage are prepared in a NaCl-containing buffer. The monovalent Na⁺ ions modify the structure and elastic properties of DNA. The persistence length is the length scale over which the directionality of strands is maintained. In monovalent ions, the persistence length varies inversely with the Na⁺ concentration [21]. The ion-induced shortening of the persistence length can be understood on the basis of the Poisson–Boltzmann theory for uniformly charged cylinders. The single dsDNA molecule, which is pulled apart by applying the constant force at a constant temperature, structurally transits to ssDNA when the force F exceeds the critical force F _c. Over the range of temperatures from 15 °C to 50 °C, which are below the melting temperature T _m, the critical force F _c decreases with increasing temperature [22]. Given that one can vary the Na⁺ concentration in a buffer, it is worth considering how F _c depends on the Na⁺ concentration.

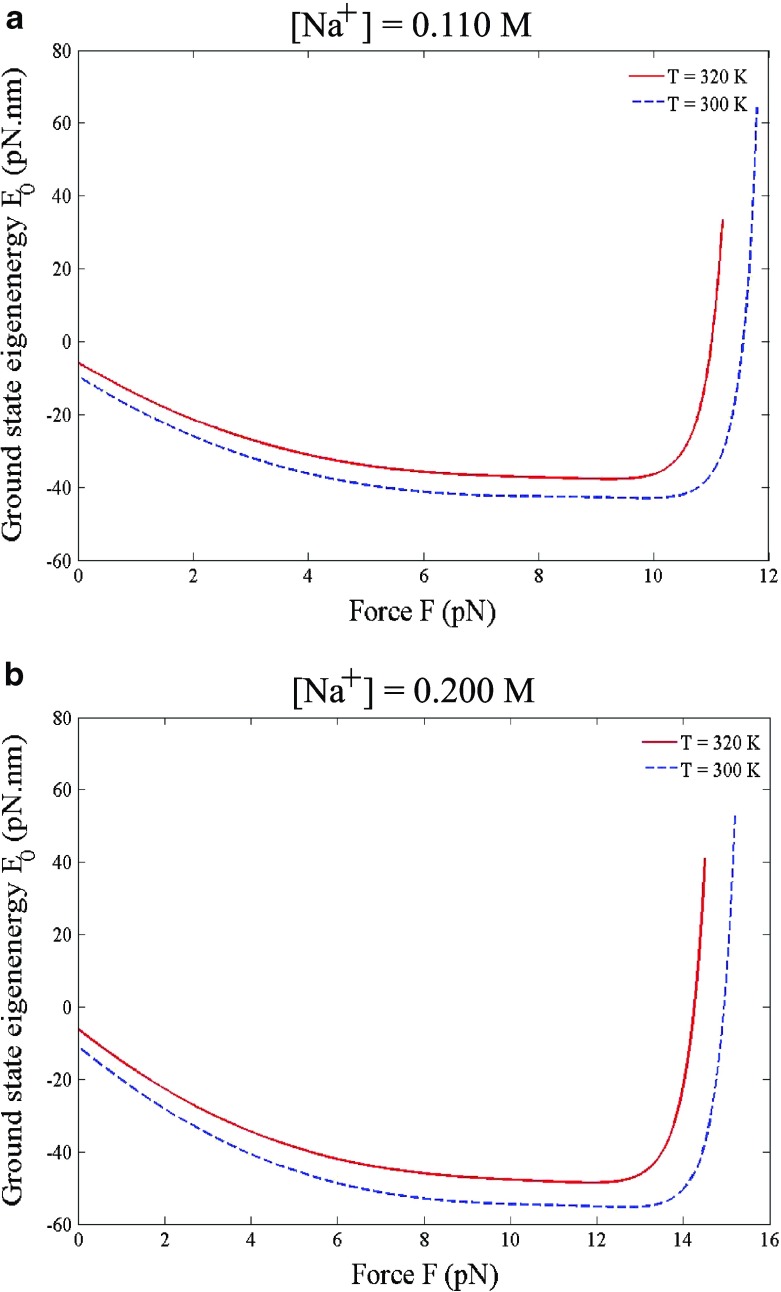
From the viewpoint of quantum mechanics, the dsDNA appears as a bound state with discrete negative eigenenergies while the ssDNA appears as an unbound state, or a scattering state, with continuous positive eigenenergies. The critical force F _c, at which the dsDNA-to-ssDNA transition occurs, is determined from the zero of the ground state eigenenergy E ₀, (22). The Na⁺ concentration enters the problem through the Debye screening length λ _D = $0.25/\sqrt{\left[{\text{Na}}^{+}\right]}$ [17], which in turn brings the Na⁺ concentration dependence to the renormalized spring constant K = K ₀ − (e ²/2𝜖b ³) $exp(-b/{\lambda }_D)$ [18]. At concentration [Na⁺] = 0.110 M, which is about the physiological condition, the ground state eigenenergy E ₀ is shown in Fig. 4a as a function of force F. The zero of E ₀ gives F _c = 11.6 pN at temperature 300 K and F _c = 11.0 pN at temperature 320 K. We can repeat the calculation to find F _c at other temperatures to construct the line of F _c(T) for [Na⁺] = 0.110 M. Next, we increase the Na⁺ concentration to [Na⁺] = 0.200 M, shown in Fig. 4b, at which the zero of E ₀ gives F _c = 15.0 pN at temperature 300 K and F _c = 14.3 pN at temperature 320 K. At the same Na⁺ concentration, the decrease in F _c with increasing temperature can be understood on a basis that thermal fluctuations bend the strands in random directions so the dsDNA at higher temperature deforms more easily. At the same temperature, the increase in F _c with increasing the Na⁺ concentration is attributed to the enhancement of the DNA stability, because the Na⁺ ions reduce the self repulsion of the negatively charged backbones.

Fig. 4.

The critical force F _c is determined from the zero of the ground state eigenenergy E ₀, (22). a At [Na⁺] = 0.110 M the critical force F _c is 11.6 pN at 300 K (27 °C) and 11.0 pN at 320 K (47 °C). b At [Na⁺] = 0.200 M the critical force F _c is 15.0 pN at 300 K (27 °C) and 14.3 pN at 320 K (47 °C)

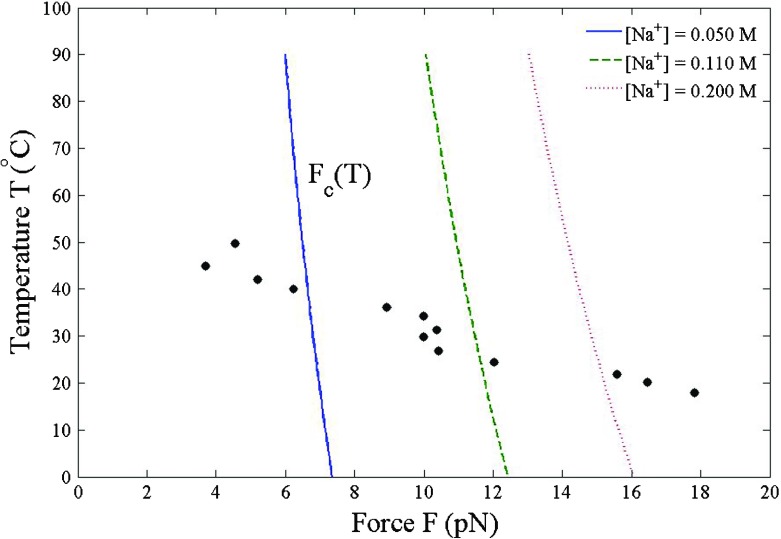
Given a Na⁺ concentration, the critical force F _c(T) appears in the temperature-force phase diagram as a boundary between dsDNA and ssDNA shown in Fig. 5. When the force F < F _c(T), dsDNA is energetically favored. Once the force F > F _c(T), all base pairs are unzipped and dsDNA is converted to ssDNA. The positive Na⁺ ions stabilize DNA. The dsDNA in the high Na⁺ solution is more resistant to the structural transition. When increasing the Na⁺ concentration, the shift of critical force F _c(T) to the higher values is particularly evident in the range of low temperatures 0 °C– 30 °C. At higher temperatures, the thermal fluctuations lessen the effect of Na⁺ ions on F _c(T). Also shown in Fig. 5 as dots are the measured critical force F _c(T) of the lambda bacteriophage virus at the 0.110 M Na⁺ concentration [22]. Our calculated critical force F _c(T) decreases more slowly with increasing temperature than that observed in experiments. If the screening effect is not taken into account, that is to say ${\widehat{\mathbf{\text{H}}}}^{\prime }$ = 0 i.e., Coulomb interstrand potential, the critical force is simply F _c = k _B T/a decreasing with increasing temperature as F _c(T) ∼ T ⁻¹. The linear fit to the calculated critical force at [Na⁺] = 0.110 M, which is the middle dash line in Fig. 5, yields the slope dF _c/dT = − 0.03 pN/ °C. According to a change in entropy ΔS = − (dF _c/dT)Δr [23], assuming a change in the interstrand separation Δr being of order the 2-nm helix diameter, this slope dF _c/dT = − 0.03 pN/ °C leads to an increase in entropy ΔS = 0.05 pN.nm/ °C. The force-induced breaking of hydrogen bonds promotes a larger number of degrees of freedom, which in turn accounts for the entropy production.

Fig. 5.

The DNA in high Na⁺ concentration requires the larger critical force F _c(T) for the dsDNA-to-ssDNA transition. For comparison, the dots are the experimentally measured critical force of the lambda bacteriophage virus at [Na⁺] = 0.110 M [22]

The criterion for the validity of the first-order perturbation theory is $|<{\psi }_0^{\left(0\right)}|{\widehat{\mathbf{\text{H}}}}^{\prime }|{\psi }_0^{\left(0\right)}>|\ll \left|E_0^{\left(0\right)}\right|$. By making use of (21) and (23), this criterion restricts the Na⁺ concentration to [Na⁺] ≪ [Na⁺]^∗, where the characteristic concentration [Na⁺]^∗ = $0.25\left[1+4(Fa/k_{B}T)+\right.$ $\left.\mathrm{O}\left({(Fa/k_{B}T)}^2\right)\right]/a^2$ for the ratio Fa/k _B T ≪ 1. Increasing the force F raises [Na⁺]^∗ higher. The range of the Na⁺ concentration for the validity of perturbation theory is broader in the presence of force, i.e., DNA unzipping, than in the absence of force, i.e., DNA denaturation.

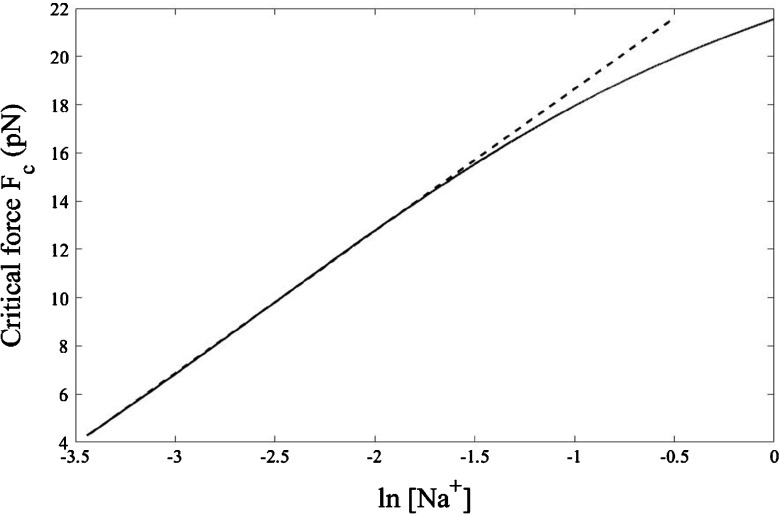
To elucidate clearly the role of Na⁺ ions, we plot the critical force F _c as a function of $ln\left[{\text{Na}}^{+}\right]$, as shown in Fig. 6 for T = 300 K. The relationship is linear up to [Na⁺] = 0.110 M, above which F _c rises slower than linearly. Incidentally, this [Na⁺] = 0.110 M is also the value at which melting temperature T _m in Fig. 3 starts to decline slightly. In the range of Na⁺ concentration lower than 0.110 M, the linear fit gives the slope 5.9 pN. Because DNA is a polyelectrolyte, its conformation is affected by the Na⁺ ions. The polyelectrolyte theory predicts the slope [24]

$$\frac{d{F}_c}{dln\left[{\text{Na}}^{+}\right]}=\frac{k_{B}T}{l_B}\nu$$ 29

where ν = (l _ssDNA − l _dsDNA)/(r _ssDNA − r _dsDNA) is the ratio of the difference in the length per unit charge of ssDNA, l _ssDNA, and dsDNA, l _dsDNA, to the difference in the interstrand separation of ssDNA, r _ssDNA, and dsDNA, r _dsDNA. At temperature T = 300 K the Bjerrum length l _B = e ²/𝜖k _B T is about 0.7 nm, yielding the prefactor k _B T/l _B = 5.9 pN. Therefore, the slope $d{F}_c/dln\left[{\text{Na}}^{+}\right]$ = 5.9 pN obtained from the linear fit suggests the value of the ratio ν = 1, resulting in r _dsDNA − l _dsDNA = r _ssDNA − l _ssDNA implying that at 300 K the difference between the interstrand separation and the length per unit charge is conserved as dsDNA structurally transits to ssDNA. The double-helix structure of dsDNA has the interstrand separation r _dsDNA ≈ 2 nm and the length per unit charge l _dsDNA ≈ 0.17 nm [5], thus r _dsDNA − l _dsDNA ≈ 1.83 nm. At 300 K, applying the force larger than 11.6 pN, which is the critical force at this temperature, results in ssDNA with a longer interstrand separation r _ssDNA and a longer length per unit charge l _ssDNA, but the difference r _ssDNA − l _ssDNA would still be 1.83 nm as in dsDNA. However, at temperatures other than 300 K, the difference between the interstrand separation and the length per unit charge generally assumes different values in dsDNA and in ssDNA.

Fig. 6.

At a temperature of 300 K (27 °C), the critical force exhibits a linear relation with $ln\left[{\text{Na}}^{+}\right]$ for the Na⁺ concentration ranging from 0.032 to 0.110 M. The dashed line, which is a linear fit to the calculated results, has a slope 5.9 pN. At too high Na⁺ concentration, the perturbative expansion from the ground state eigenenergy E0(0) for the Coulomb interstrand potential is less reliable, giving rise to a deviation from the linear fit

Discussion and conclusions

The positive ions in an aqueous medium render an attraction between the like negatively charged backbones. This induced attraction makes DNA more compact by bending the nucleotide strands considerably. The resulting curvature would be of the order the inverse of the double-helix radius, i.e., 1 nm⁻¹. The movement of two attractive strands are not independent of each other, thereby limiting the number of conformations accessible to DNA. A change in the persistence length with the Na⁺ concentration indicates that the DNA elasticity is indeed influenced by the presence of positive ions [24]. Consequently, the melting temperature T _m in DNA denaturation and the critical force F _c in DNA unzipping vary with the Na⁺ concentration. For divalent ions, such as Mg²⁺, the variation of T _m and F _c with the ion concentration would be more pronounced. The DNA ejection of the lambda bacteriophage virus into a host is inhibited by the optimal Mg²⁺ concentration [25]. The multivalent ions, such as Co(NH₃)63+, when presented at sufficiently high concentration, can even neutralize the negative charges along the phosphodiester backbones, resulting in DNA condensation to a tightly packed torus [26]. In addition to the elastic energy, the interfacial energy plays a role in such DNA condensation [27]. DNA has an extremely long μ m length compared to its small nm diameter and therefore likely knots itself with the dominance of trefoil knots [28]. The ion-mediated attraction between the negatively charged backbones accounts for the experimental observation that during random cyclization the probability of DNA knotting increases with increasing the Na⁺ concentration [29]. The large number of Na⁺ ions enhances the strength of attraction, so that two strands can get so close that they are increasingly bound to each other.

Recently, an interest in ionic effects has turned to the dynamical properties of DNA. Applying the time-dependent electric field, the frequency dependent dielectric constant 𝜖(ω) describes the response function of DNA. In low-frequency regime from 100 Hz to 100 MHz, the dielectric constant 𝜖(ω) is controlled by the surrounding ions, while in high frequency regime from MHz to GHz it is dictated by molecular hydration [30]. The impedance measurement provides information about both the real part 𝜖 ^′(ω) and imaginary part 𝜖 ^″(ω) of 𝜖(ω). Alternatively, the imaginary part 𝜖 ^″(ω) is easily measured by the light absorption and then the real part 𝜖 ^′(ω) is calculated from the known 𝜖 ^″(ω) via the Kramers–Kronig relation.

Appendix A: Ground state eigenenergy of unperturbed Hamiltonian

We derive the expression of the ground state eigenenergy E0(0), (21), of the unperturbed Hamiltonian ${\widehat{\mathbf{\text{H}}}}_0$. The ground state eigenenergy $E_0^{\left(0\right)}=<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}_0\right|{\psi }_0^{\left(0\right)}>$ gives

$$\begin{array}{rcl}{E}_0^{\left(0\right)}& =& \int d^{3}r{\left({\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\right)}^{\ast }\left[-\frac{{\left(k_{B}T\right)}^2}{K}{\left(\nabla -\frac{1}{k_{B}T}\mathbf{\text{F}}\right)}^2-\frac{e^2}{\mathrm{𝜖r}}\right]{\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\\ & =& E_k+E_p\end{array}$$ 30

where we define the kinetic-like energy as

$$E_k\equiv \int d^{3}r{\left({\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\right)}^{\ast }\left(-\frac{{\left(k_{B}T\right)}^2}{K}\right){\left(\nabla -\frac{1}{k_{B}T}\mathbf{\text{F}}\right)}^2{\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)$$ 31

and we define the potential energy, due to the attractive Coulomb potential as,

$$E_p\equiv \int d^{3}r{\left({\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\right)}^{\ast }\left(-\frac{e^2}{\mathrm{𝜖r}}\right){\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\mathrm{.}$$ 32

Without loss of generality, let the external constant force F be in the $\widehat{\mathbf{\text{r}}}$-direction, i.e., $\mathbf{\text{F}}=F\widehat{\mathbf{\text{r}}}$. The Laplacian term takes the form

$$\begin{array}{rcl}{\left(\nabla -\frac{1}{k_{B}T}\mathbf{\text{F}}\right)}^2{\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)=\frac{1}{r^2}\frac{\partial }{\mathrm{\partial r}}\left(r^2\frac{\partial {\psi }_0^{\left(0\right)}}{\mathrm{\partial r}}\right)-2\frac{F}{k_{B}T}\frac{\partial {\psi }_0^{\left(0\right)}}{\mathrm{\partial r}}+{\left(\frac{F}{k_{B}T}\right)}^2{\psi }_0^{\left(0\right)}& & \\ & =& -\frac{1}{a}\left(1-\frac{Fa}{k_{B}T}\right)\left(2-\frac{r}{a}\left(1-\frac{Fa}{k_{B}T}\right)\right)\frac{1}{r}{\psi }_0^{\left(0\right)}+\frac{2}{a}\frac{F}{k_{B}T}\left(1-\frac{Fa}{k_{B}T}\right){\psi }_0^{\left(0\right)}+{\left(\frac{F}{k_{B}T}\right)}^2{\psi }_0^{\left(0\right)}\end{array}$$ 33

in which to obtain the last line we use (19) for the unperturbed ground state eigenfunction ψ0(0)(r). Substituting (33) in (31) and use the normalization of ψ0(0)(r) gives the kinetic-like energy

$$\begin{array}{rcl}{E}_k& =& -\frac{{\left(k_{B}T\right)}^2}{K}\left[-\frac{1}{a}\left(1-\frac{Fa}{k_{B}T}\right)4\pi {\int }_0^{\infty }dr{r}^2\left(2-\frac{r}{a}\left(1-\frac{Fa}{k_{B}T}\right)\right)\frac{1}{r}\left|{\psi }_0^{\left(0\right)}\right(\mathbf{\text{r}}){|}^2\right.\\ & & \left.+\frac{2}{a}\frac{F}{k_{B}T}\left(1-\frac{Fa}{k_{B}T}\right)+{\left(\frac{F}{k_{B}T}\right)}^2\right]\\ & =& \frac{1}{K}{\left(\frac{k_{B}T}{a}\right)}^2\left[2{\left(\frac{Fa}{k_{B}T}\right)}^2-4\frac{Fa}{k_{B}T}+1\right]\mathrm{.}\end{array}$$ 34

The potential energy is

$$E_p=-\frac{e^2}{𝜖}4\pi {\int }_0^{\infty }dr{r}^2{\left({\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)\right)}^{\ast }\frac{1}{r}{\psi }_0^{\left(0\right)}\left(\mathbf{\text{r}}\right)=-\left(1-\frac{Fa}{k_{B}T}\right)\frac{e^2}{\mathrm{𝜖a}}\mathrm{.}$$ 35

Adding the kinetic-like energy E _k with the potential energy E _p yields the ground state eigenenergy of the unperturbed Hamiltonian

$$\begin{array}{rcl}{E}_0^{\left(0\right)}& =& \frac{1}{K}{\left(\frac{k_{B}T}{a}\right)}^2\left[2{\left(\frac{Fa}{k_{B}T}\right)}^2-4\frac{Fa}{k_{B}T}+1\right]-\left(1-\frac{Fa}{k_{B}T}\right)\frac{e^2}{\mathrm{𝜖a}}\\ & =& \frac{2}{K}{F}^2+\left(\frac{e^2}{𝜖k_{B}T}-4\frac{k_{B}T}{Ka}\right)F+\frac{1}{K}{\left(\frac{k_{B}T}{a}\right)}^2-\frac{e^2}{\mathrm{𝜖a}}\\ & =& \frac{2}{K}{F}^2+\left(2\frac{k_{B}T}{Ka}-4\frac{k_{B}T}{Ka}\right)F+\frac{1}{2}\frac{e^2}{\mathrm{𝜖a}}-\frac{e^2}{\mathrm{𝜖a}}\\ & =& \frac{2}{K}\left(F^2-\frac{k_{B}T}{a}F-\frac{1}{4}\frac{K{e}^2}{\mathrm{𝜖a}}\right)\\ & =& \frac{2}{K}{\left(F-\frac{1}{2}\frac{k_{B}T}{a}\right)}^2-\frac{3}{4}\frac{e^2}{\mathrm{𝜖a}}\end{array}$$ 36

which is (21) in the main text.

Appendix B: First-order correction to ground state eigenenergy of full Hamiltonian

We derive the first-order correction, (23), to the ground state eigenenergy of full Hamiltonian $\widehat{\mathbf{\text{H}}}$. Using the perturbation ${\widehat{\mathbf{\text{H}}}}^{\prime }$, (13), and the ground state eigenfunction of the unperturbed Hamiltonian ψ0(0)(r), (19), we obtain

$$\begin{array}{rcl}<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}>& =& \frac{e^2}{𝜖{\lambda }_D}\frac{1}{\pi }{\left(\frac{1-\frac{Fa}{k_{B}T}}{a}\right)}^3\sum _{n=0}^{\infty }\frac{{(-1)}^n}{(n+1)!{\lambda }_D^n}4\pi {\int }_0^{\infty }dr{r}^{n+2}exp\left[-2\left(1-\frac{Fa}{k_{B}T}\right)\frac{r}{a}\right]\\ & =& \frac{1}{2}\frac{e^2}{𝜖{\lambda }_D}\sum _{n=0}^{\infty }{(-1)}^n(n+2){\left[\frac{a}{2{\lambda }_D\left(1-\frac{Fa}{k_{B}T}\right)}\right]}^n\\ & =& \frac{1}{2}\frac{e^2}{𝜖{\lambda }_D}\left(\sum _{n=0}^{\infty }{(-1)}^{n}n{C}^n+2\sum _{n=0}^{\infty }{(-1)}^n{C}^n\right)\end{array}$$ 37

where defining C ≡ a/2λ _D(1 − (Fa/k _B T)). The second summation in parentheses $S\equiv {\sum }_{n=0}^{\infty }{(-1)}^n{C}^n$, which is a geometric series equal to 1/(C + 1). The first summation in parentheses ${\sum }_{n=0}^{\infty }{(-1)}^{n}n{C}^n=\mathrm{C\partial S}/\mathrm{\partial C}$ equals − C/(C + 1)². Hence, we can write explicitly, upon substituting the definition of C,

$$<{\psi }_0^{\left(0\right)}\left|{\widehat{\mathbf{\text{H}}}}^{\prime }\right|{\psi }_0^{\left(0\right)}>=\frac{1}{2}\frac{C+2}{{(C+1)}^2}\frac{e^2}{𝜖{\lambda }_D}=\left(1-\frac{Fa}{k_{B}T}\right)\frac{e^2}{𝜖}\frac{4\left(1-\frac{Fa}{k_{B}T}\right){\lambda }_D+a}{{\left[2\left(1-\frac{Fa}{k_{B}T}\right){\lambda }_D+a\right]}^2}$$ 38

which is (23) in the main text.

Compliance with Ethical Standards

Conflict of interest

The author declares that he has no conflicts of interest.