Abstract.
Convolutional neural networks (CNNs), the state of the art in image classification, have proven to be as effective as an ophthalmologist, when detecting referable diabetic retinopathy. Having a size of of the total image, microaneurysms are early lesions in diabetic retinopathy that are difficult to classify. A model that includes two CNNs with different input image sizes, and , was developed. These models were trained using the Kaggle and Messidor datasets and tested independently against the Kaggle dataset, showing a sensitivity , a specificity , and an area under the receiver operating characteristics curve . Furthermore, by combining these trained models, there was a reduction of false positives for complete images by about 50% and a sensitivity of 96% when tested against the DiaRetDB1 dataset. In addition, a powerful image preprocessing procedure was implemented, improving not only images for annotations, but also decreasing the number of epochs during training. Finally, a feedback method was developed increasing the accuracy of the CNN input model.
Keywords: convolutional neural networks, deep learning, retina, microaneurysms, feedback
1. Introduction
The development of a noninvasive method that detects diabetes during its early stages would improve the prognosis of patients. The prevalence of diabetes in the USA is , affecting 29.1 million people.1 The retina is targeted in the early stages of diabetes, and the prevalence of diabetic retinopathy (DR) increases with the duration of the disease. Microaneurysms are early lesions of the retina, and as the disease progresses, damage to the retina includes exudates, hemorrhages, and vessel proliferation. The detection of DR in its early stages can prevent serious complications, like retinal detachment, glaucoma, and blindness. The screening methods used to detect diabetes are invasive tests, the most popular one being measuring blood sugar levels. Fundus image analysis is a noninvasive method that allows health care providers to identify DR in its early stage; a procedure now performed in clinical settings. The massification of devices that help cell phone cameras take the fundus image would make this procedure available for all populations.2 Once the image is obtained, it can be loaded to a cloud service and analyzed to detect microaneurysms.
The clinical classification of DR reflects its severity. A consensus in 20033 proposed the diabetic retinopathy disease severity scale, which consists of five classes for DR. Class zero or the normal class has no abnormalities in the retina; class 1, or the mild class, shows only microaneurysms; class 2 or the moderate class is considered as the intermediate state between classes 1 and 3; class 3 or the severe class contains either intrarretinal hemorrhages in one of the four quadrants, venous beading in two quadrants, or intrarretinal microvascular abnormalities in one quadrant; class 4 or the proliferative class includes neovascularization, or vitreous and preretinal hemorrhages. The severity level of the disease progresses from classes 1 to 4, and special consideration is given to lesions close to the macular area.
The convolutional neural network (CNN) is the most effective method of classification for images. CNNs are state-of-the-art image classifications based on Image-net4 and COCO 2016 detection5 challenges. Since CNN’s initial design,6 not only its architecture,7–10 but also its regularization parameters, weight initialization,11,12 and neural activation function13 have evolved. Within medical image analysis, CNN has been applied in several areas like breast and lung cancer detection.14,15 Specifically in fundus retina images, CNN has proven to be the best automatized system when detecting referable diabetic retinopathy (RDR),16 moderate and severe, and surpassing other algorithms performing the same task.17
Classification of images based on small objects is difficult. Although CNN classifies moderate and severe stages of DR very well, when classifying lesions that belong to class 1 and 2, it has some flaws. The lesions in these classes contain microaneurysms with a maximum size of of the entire image. For instance, Pratt’s study18 showed a total accuracy of 75%. However, from the 372 patients in class 1, none was classified correctly. Lim’s work19 proved that when detecting microaneurysms, the proportion of false positives per image is close to 90% when they try to reach a sensitivity of 90%. The purpose of this study is to improve the accuracy of detection of microaneurysms.
2. Materials
2.1. Databases
The datasets utilized in this study are Kaggle diabetic-retinopathy-detection competition,20 Messidor database [kindly provided by the Messidor program partners (see Ref. 21)], and the diabetic retinopathy database and evaluation protocol.22
2.1.1. Datasets features
The majority of the available databases contain DR images of all classes. However, because the aim of our study is to detect microaneurysms and to differentiate images with and without lesions, we chose images that belong only to classes 0, 1, and 2.
-
i.
Kaggle dataset: Eyepacs provided the images to Kaggle, where we accessed them. This dataset implements the clinical diabetic retinopathy scale to determine the severity of DR (none, mild, moderate, severe, and proliferative) and contains 88,702 fundus images. Table 1 shows unbalanced data with prominent differences between mild and normal classes. It is also evident that most of the images belong to the testing set.
The subset for our study includes 21,203 images, in which 9441 are used for training, and 11,672 are used for testing. We selected random samples from the normal class that have at most a confidence interval of 1, a confidence level of 95%, and selected all of the cases in the mild class. The testing set was subdivided into a validation and testing set.
-
ii.
Messidor dataset: Within the public domain, 1200 eye fundus color images of all classes are provided by the Messidor dataset. The annotation includes a DR grade of (0 to 3) and a risk of macular edema grade of (0 to 2), where grades 1 and 2 were included in the training set. From those, 153 are classified as grade 1 and 246 as grade 2, where only isolated microaneurysms were selected.
-
iii.
The diabetic retinopathy database and evaluation protocol (DiaRetDB1) is a public set of 89 images. This dataset also includes ground truth annotations of the lesions from four experts, which are labeled as small red dots, hemorrhage, hard exudates, and soft exudates. This set will be used for testing purposes.
Table 1.
Kaggle raw database.
| Training | Testing | |
|---|---|---|
| All | 35,126 | 53,576 |
| Normal | 25,810 | 39,533 |
| Mild | 2443 | 3762 |
Table 2 shows the number of images per class in each database used in the study.
Table 2.
Study database.
| Kaggle | Messidor | DiaRetDB1 | ||
|---|---|---|---|---|
| Training | Testing | Training | Testing | |
| Normal | 8000 | 8000 | ||
| Class 1 | 2443 | 3762 | 153 | |
| Class 2 | 246 | |||
| All | 89 | |||
2.2. Image Annotations
The main author of this study, a medical doctor and general surgeon, was the person who located and annotated the microaneurysms in the images that belong to classes 1 and 2. Some pictures have more than one microaneurysm and each is counted as different in this study.
2.3. Machine Learning Framework
Torch23 was the framework chosen for this study and the multi-graphics processing unit (GPU) Lua scripts24 were adapted to run the experiments. Other frameworks used in this study include OpenCV for imaging processing, R-Cran for statistical analysis and plotting, and Gnuplot for graphing. The training of the CNNs was performed on a 16.04 Ubuntu Server with four Nvidia M40 GPU’s using Cuda 8.0 and Cudnn 8.0.
3. Methods
An improved image was created for the annotations by applying an original preprocessing approach. Once the author selected the coordinates of the lesions, the cropping of the images with the lesions and the cropping of normal fundus images were executed. Two datasets with cropped sizes of and were obtained and trained using modified CNNs. One of our modifications included a feedback mechanism for training. We also evaluated the increase in the size of the dataset by using either augmentation or adding new images. Receiver operating characteristics (ROC)25 were used to get the cutoff of the predicted values in order to obtain a more accurate sensitivity and specificity of the models. Finally, an analysis on the more precise model with the DiaRetDB1 was performed to find its overall sensitivity in the complete image.
3.1. Processing Images
Batch transformations on the lightness and color of the images were used to produce higher quality images for annotations, and a comparative analysis of using CNNs with inputs of images with and without preprocessing was performed.
Descriptive statistics were calculated, and -means analysis was used to divide the images into three groups (dark, normal, and bright). A function based on the statistics was performed to transform the lightness of the images using LAB color space. After collecting the and intensity values in the LAB color space from vessels, microaneurysms, hemorrhages, and a normal background, a support vector machine was used to separate microaneurysms and hemorrhages from the background.
3.1.1. Getting images statistics
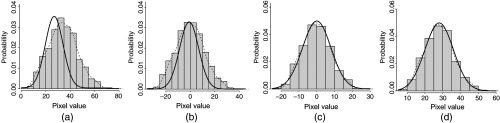
LAB color space was chosen due to its property of separating luminescence from color. Table 3 shows the descriptive statistics of all of the images in the training sets and Fig. 1 shows each image with the mean represented by the -axis and the standard deviation represented by the -axis. The range values in Table 3 and the box plots in Fig. 1 show some variety within the training set images. For the purpose of this study, we used the mean and standard deviation of the images to normalize, cluster, and develop a method for lightness adjustment.
Table 3.
Train images statistics.
| Mean | Std | Min | Max | Range | ||
|---|---|---|---|---|---|---|
| Mean per picture | 33.93 | 11.83 | 0.70 | 80.22 | 79.52 | |
| 11.07 | 7.35 | 47.63 | 56.63 | |||
| 18.23 | 8.63 | 59.82 | 61.93 | |||
| Std per picture | 18.09 | 4.83 | 0.42 | 37.38 | 36.95 | |
| 8.32 | 3.24 | 0.21 | 21.67 | 21.45 | ||
| 10.97 | 3.76 | 0.42 | 24.54 | 24.12 | ||
Fig. 1.
, , channels distribution.
3.1.2. Normalization
Normalization was done to each pixel in respect to its own image, to all of the images, and to each one of their channels , and the result was displayed using a standard software package, which in our case was OpenCV. Our image normalization equation was
| (1) |
where pv is the pixel value, npv is the new pixel value, mp is the mean value of the images, map is the mean value of all the images, constant 1, constant 2, stdp is the standard deviation value of the images, and stdap is the standard deviation value of all the images. The first part of the equation normalizes the pixel value based on the mean of the images and adjusts its value according to the proportion of the standard deviation of all the images and the images that owns the pixel value. The second part of the equation repositions the pixel value based on the mean of all the images. Figure 2 shows the steps for normalization, where the continuous line represents the density probability of all the images, the discontinuous line represents the density probability of one image, and the histogram represents the distribution of the pixels values in one image.
Fig. 2.
Pixel normalization: (a) initial state, (b) zero centering, (c) spreading data, and (d) return to initial state.
3.1.3. Adjust luminance intensity for a batch
A method used to modify the brightness of all the images in a batch is described next. Lab color space represents color-opponent dimensions as shown in Fig. 3.27
Fig. 3.
CIE , , color space.26
Once the images were normalized, an analysis of the distribution of the mean and standard deviation of the lightness of each image in the training sets was done. The elbow method was used28 to obtain the optimal number of clusters from this data. Figure 4(a) (top) shows five as the optimal number of clusters, and the mean and standard deviation values of those centroids are displayed in Table 4. Figure 4(a) (bottom) also shows the cluster data.
Fig. 4.
channel distribution: (a) top: elbow test, bottom: distribution of images on clusters and (b) distribution channel on clusters 1 and 5.
Table 4.
Centroids channel.
| Centroid | Mean | Std |
|---|---|---|
| 1 | 14.67 | 10.26 |
| 2 | 24.40 | 14.66 |
| 3 | 33.20 | 18.21 |
| 4 | 41.81 | 21.14 |
| 5 | 54.17 | 24.86 |
Figure 4(a) (bottom) reveals that most of the cases are between clusters 2 and 4 and Fig. 4(b) shows that clusters 1 and 5 represent the darkest and brightest images, respectively. The mean pixel value of the 25th percentile of the first clusters is 10, which was set as the lower limit for the transformation. We visually inspected the images with a mean value of the channel lower than 10 and found that the images were too dark to be readable. Notice that there are not any images with values in the -axis above 80, making this value our superior limit for the transformation. A sample of some of the images from other clusters was evaluated and we noticed that high-quality images belong to the third cluster. With the collected information, the goal was to transform the data in such a way that extreme data representing the darkest and brightest images would move to the center. The polynomial function we developed was
| (2) |
where is the new value and is the original value. The results can be visualized in Fig. 5, where the blue dots denote the transformed data values from the original image, which is represented by the red dots.
Fig. 5.
Distribution channel on clusters 1 and 5 before and after transformation.
3.1.4. Reducing color variance
Just like any blood extravasation, the microaneurysm color goes through a sequence of changes, the most common sequence going from a bright red, to a brownish, to a yellowish color. Because our purpose was to enhance microaneurysms, we limited the scene in order to separate blood tissues from other structures using an original approach.
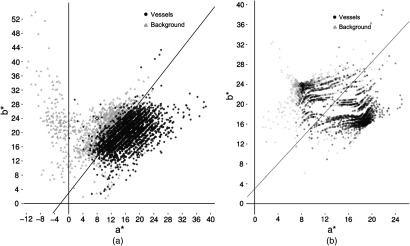
After the normalization and the adjustment of the values, we built a dataset with pixel values from vessels including microaneurysms and other structures like the optical disc, macula, exudates, normal retina, among others. In Fig. 6(a), each point represents the and pixels’ values of the vessels and background pixels. The diamond points are the centroids of the next transformation and represent a pixel value in the Lab color space. The euclidean distance of each pixel value over each centroid is calculated. Then, a division of these two values tells us which centroid is closest to this pixel value. Finally, the new pixel value was obtained after applying the following equation:
| (3) |
where pv is the pixel value of and , bed is the Euclidean distance between the pixel value and the background centroid, ved is the Euclidean distance between the pixel value and the vessel centroid, rel is the division of , and npv is the new pixel value. The new pixel values are displayed in Fig. 6(b).
Fig. 6.
Distribution and channels: (a) before transformation and (b) after transformation.
3.1.5. Generalization of the preprocessing method
The preprocessing methodology used in this study was oriented to improve the quality of retina fundus images, enhance microaneurysms and vessels, and can be applied to any similar datasets. Figure 7 shows three images that were chosen based on the mean of the channel and represent the extreme and middle values of the channel. In addition, the mean value for each channel in the color is displayed in each image. We can see that after the transformation, all of the values converge to the same middle values and the quality of the images not only improves but is enhanced in detail.
Fig. 7.
Raw and processed images sampling.
3.2. Slicing Images
Nowadays, it is difficult to process full size () images due to hardware limitations. Our approach is not to downsample the image size, but to crop the images with the lesions in it. After preprocessing the images, the approximate center of the lesion coordinates was located and we cropped the images into two different sizes: and . Each size represents a specific dataset. In our initial part of the experiment, the images were obtained by cropping the images with and without the lesion in the center, once. We called this set dataset A as shown in Table 5. Unbalanced data are shown with the majority of the cases in normal patients, which is an expected distribution due to the prevalence of DR. Training, tests, and validation cases for class 0 consist of cropped images of normal images that include all the areas of the retina.
Table 5.
Dataset A.
| Train | Validation | Testing | Train | Validation | Testing | |
|---|---|---|---|---|---|---|
| Normal | 10,977,063 | 453,808 | 8,240,000 | 194,276 | 8007 | 194,260 |
| Mild | 4520 | 485 | 1881 | 4522 | 485 | 1887 |
During the experiment, we increased the size of the training data as shown in Table 6, dataset B. The purpose of this set was to evaluate how increasing the number of new pictures or increasing the number of cropped images that include lesions using augmentation29 would impact the accuracy. For our final results, we joined all the training cases, including annotated and augmented cases together, as shown in Table 7, and we labeled this set dataset C. In datasets B and C, the cases in the normal class were the same as in dataset A.
Table 6.
Dataset B.
| Increasing training cases | ||
|---|---|---|
| With new pictures | With augmentation | |
| 7072 | ||
| 6990 | ||
Table 7.
Dataset C.
| Image size | ||
|---|---|---|
| Total images | 41,654 | 42,259 |
3.3. Convolutional Neural Network Architecture
Two independent types of architecture for the sets in Table 8 and the sets in Table 9 were created. The tables show the input size of each layer, the filter size, and the number of filters (kernels). For all of the models, one stride for the filters and padding was implemented. In our architecture, fractional max pooling30 was implemented; the dropout rate was 0.1, the activation function was leakReLu,31,32 the Microsoft Research approach was chosen33 for the weight initialization, and batch normalization was performed after each convolution layer.
Table 8.
Models for set.
| Input size | Model A | Model B | ||
|---|---|---|---|---|
| 60 | 64 | 64 | ||
| 64 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 45 | 128 | 128 | ||
| 128 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 30 | 256 | 256 | ||
| 256 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 23 | 512 | 512 | ||
| 512 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 15 | 1024 | 1024 | ||
| 1024 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 9 | 128 | 1536 | ||
| 1536 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 5 | 2048 | 2048 | ||
| 2048 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| Dropout | ||||
| Full connected layers | 2048 | |||
| Full connected layers | 2048 | |||
| Full connected layers | 1024 | |||
| Log soft max → negative log likelihood | ||||
Table 9.
Models for set.
| Input size | Model A | Model B | ||
|---|---|---|---|---|
| 420 | 32 | 32 | ||
| 32 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 360 | 48 | 48 | ||
| 48 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 300 | 46 | 64 | ||
| 64 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 240 | 72 | 72 | ||
| 72 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 180 | 96 | 96 | ||
| 96 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 120 | 128 | 128 | ||
| 128 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 60 | 48 | 190 | ||
| 190 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 45 | 256 | 256 | ||
| 256 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 30 | 348 | 348 | ||
| 348 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 23 | 512 | 512 | ||
| 512 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 15 | 1024 | 1024 | ||
| 1024 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 9 | 1536 | 1536 | ||
| 1536 | ||||
| FracMaxPool → BatchNorm → LeReLU | ||||
| 5 | 2048 | 2048 | ||
| |
|
|
|
2048 |
| Dropout | ||||
| Full connected layers | 2048 | |||
| Full connected layers | 2048 | |||
| Full connected layers | 1024 | |||
| Log soft max → negative log likelihood | ||||
Model A is a classic CNN model,7 whereas model B is a version of Visual Geometric Group (VGG).8 Implementing classical VGG that includes more convolutions in each layer would dramatically reduce the size of the training batch in the models, an unwanted side effect. In addition, our choice of fractional max pooling was due to the fact that the image sizes can be downsampled gradually.
3.4. Feedback
The torch script randomly chooses between a normal DR class and a mild DR class image to use as the input. After the batch was selected, the script, once again, randomly chooses a picture from the data pool of the class, making the processes completely stochastic. In addition, a feedback mechanism was created during training, in order to resend the images that were not classified correctly.
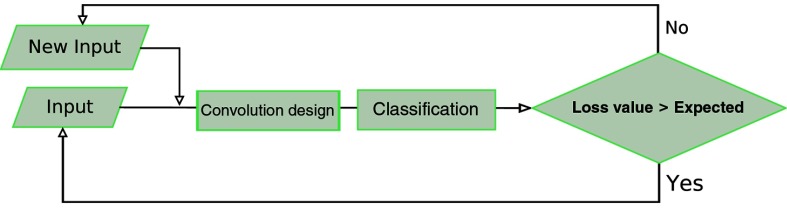
The difference of the values between the current loss function and that of the prior batch indicates that the current batch did not classify as well as the previous batch. This is the basis of our feedback function. The function created for the feedback detects the batch in which the current difference of the values of the cost function surpasses the moving average of the mean of the differences of the previous batches. The polynomial function used in our feedback is as follows:
| (4) |
where bn is the batch number and cve is the cost value expected. If the cost value of the batch during the training was greater than we expected it to be after applying Eq. (4), we present the same batch for retraining as shown in Fig. 8.
Fig. 8.
Feedback.
3.5. Monitoring
For the initial part of the experiment, the loss and accuracy of the training, the validation, and the testing sets were used to choose the most efficient model. For our final experiment, after training the more accurate CNN model, the weights of the trained CNN at regular intervals were kept. Using those weights, the probability of each image in the testing sets was obtained. Then, ROC analysis was used to get the cutoff of the probability values used to receive the maximum specificity or sensitivity of the or sets, respectively. Finally, the most accurate weights of the CNNs given by the ROC analysis were used to obtain the probabilities of the diabetic retinopathy database and evaluation protocol, which were used to compare the overall probabilities to the ground truth.
OptimalCutpoints34 from Rcran was used to obtain the optimal points of the max sensitivity and specificity and calculate the Youndex Index.
4. Experimental Design and Results
For this study, we divided the CNN into four phases. The first phase is the input phase, where input processing used to enhance features and augmentation of the dataset is performed. The second phase is the convolution design phase, where modifications to the number of convolutions and filters can be completed. Variation of the type of pooling, normalization, and neural activation function is also possible in this stage. The classification phase or the third phase includes full-connected layers with the neural activation and loss function. The dropout of nodes in a full-connected layer in this phase has been a common modification, in recent studies. The fourth phase is the training phase, where we can alter the learning parameters, learning algorithms, and perform feedback. Following pedantic rules, each phase should be evaluated separately, in order to measure the impact of changing a parameter on that phase, though changing a parameter at any point is often unpractical.
Our plan for this study was to select the modifications in the input, convolution design, classification, and training phase that would improve our sensitivity and specificity in the training, validation, and testing sets. Subsequently, dataset C was trained with all the previous modifications, in order to get the weights that performed best in the testing sets and the cut-off point values provided by ROC analysis to achieve the optimal sensitivity and specificity. Finally, the diabetic retinopathy database and evaluation protocol dataset was tested and the results were compared to their own ground truth.
4.1. Modifying Input Quality and Architecture
4.1.1. Design
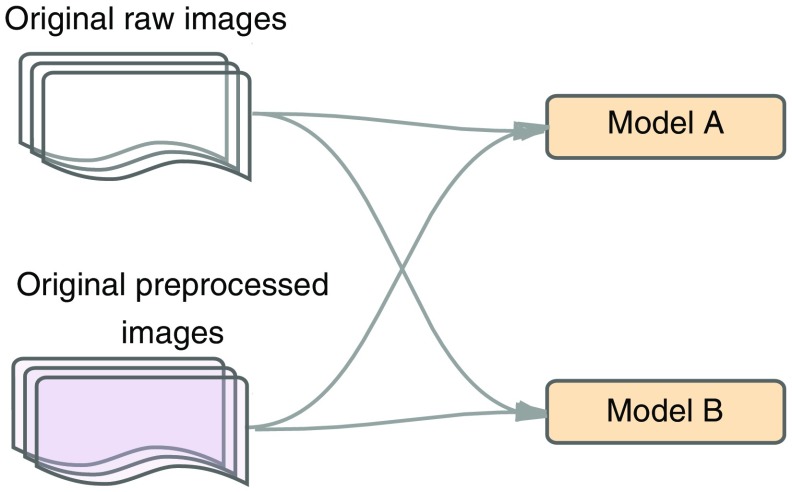
Initially, we evaluated how CNN performed in models A and B using both raw data and preprocessed images from dataset A (Table 5) as displayed in Fig. 9. Here, we evaluated the accuracy of the confusion table in the training and validation sets, by changing the quality in the input phase and the model in the architecture phase. The more accurate model and image set are used for the next stage.
Fig. 9.
Raw versus preprocessed images for models A and B.
4.1.2. Results
Table 10 and Fig. 10 display the contingency table and the accuracy plot of the images with a size of in the training set. Preprocessed images trained with model B reached a better accuracy with less epochs than the other models as shown in Table 10. It is also illustrated that processed images perform better than raw images, and that all images and models could reach a similar accuracy if the number of epochs increases. When using raw images for model A, the training was suspended, due to the slow increase in the slope. It is notable that processed images reached 90 in accuracy in the first 100 epochs and the slope was steeper in the first 50 epochs.
Table 10.
Raw versus preprocessed images for models A and B with size .
| Predictions: percentage by row | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Standard CNN | VGG CNN | ||||||||
| Raw images-250 epochs | Processed images-300 epochs | Raw images-365 epochs | Processed images-250 epochs | ||||||
| Mild | Normal | Mild | Normal | Mild | Normal | Mild | Normal | ||
| True | Mild | 84.431 | 15.569 | 98.6831 | 1.369 | 97.851 | 2.149 | 98.722 | 1.278 |
| Normal | 21.092 | 78.908 | 2.244 | 97.756 | 3.254 | 96.746 | 1.77 | 98.230 | |
Fig. 10.
Raw versus preprocessed images for models A and B with size .
Table 11 and Fig. 11 show the contingency table and the accuracy plot of the image sets in the training set. It is evident that model B performed better than model A, and that model A reaches a similar accuracy with raw pictures than the other models, but only after a long training (300 epochs). It is also noticeable that most of the accuracy was achieved in the first 50 epochs using processed images, with a steeper slope in the first 20 epochs.
Table 11.
Raw versus preprocessed images for models A and B with size .
| Predictions: percentage by row | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Standard CNN | VGG CNN | ||||||||
| Raw images-300 epochs | Processed images-180 epochs | Raw images-180 epochs | Processed images-180 epochs | ||||||
| Mild | Normal | Mild | Normal | Mild | Normal | Mild | Normal | ||
| True | Mild | 98.581 | 1.419 | 98.576 | 1.424 | 99.234 | 0.766 | 99.343 | 0.657 |
| Normal | 2.08 | 97.920 | 1.841 | 98.159 | 1.714 | 98.286 | 1.269 | 98.731 | |
Fig. 11.
Raw versus preprocessed images for models A and B with size .
Comparing the image set to the image set, the first reaches a higher accuracy in all the models with less training. In addition, it is visible that model B outperforms model A. For the next step, model B and preprocessed images were chosen.
In addition, we evaluated the impact of preprocessing images on the training time. Table 12 shows a significant reduction in the training time of the processed images compared to the training time of the raw images.
Table 12.
Processing times in raw versus processed images.
| Input size | Raw images | Processed images |
|---|---|---|
| 8 days | 4 days | |
| 24 h | 12 h |
4.2. Modifying Classification and Training
4.2.1. Design
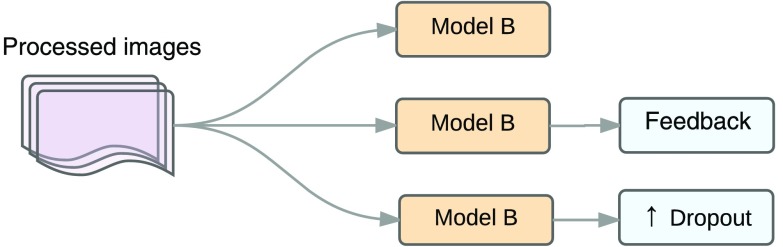
Figure 12 shows a stage that compares the effects of feedback in preprocessed images using model B against an increase in the dropout layers and dropout probability to 0.5 in the preprocessed images. Here, we looked for the effects of making changes in the classification phase versus training phase in sensitivity and specificity, using training and testing sets from dataset A.
Fig. 12.
Feedback versus dropout.
4.2.2. Results
Figure 13 shows the absence of significant differences in accuracy between the training using model B with a dropout probability of 0.1 (vanilla), the training increasing the dropout probability to 0.5 and dropout layers, and the training increasing the feedback in both the and sets. The accuracy is over 95 for all of the sets, and overfitting is presented in the validation sets. For a set, the crossing point between the training and testing lines using the validation set is reached when the accuracy is 90 for the set and 82 for the set.
Fig. 13.
Feedback versus dropout accuracy. Image size (a) and (b) .
Tables 13 and 14 show the values of the sensitivity and specificity of the training and test sets in dataset A. The sensitivity and specificity of the images were satisfactory for both sets with a small decrease in the values compared to the training set. Also, a higher sensitivity is visible in test sets when increasing the dropout. However, for the sets, the sensitivity decreased significantly, becoming more prominent when increasing the dropout layers and probability.
Table 13.
Feedback versus increasing dropout on training set.
| 180 epochs | 250 epochs | |||||
|---|---|---|---|---|---|---|
| Vanilla | Feedback | Dropout | Vanilla | Feedback | Dropout | |
| Sensitivity | 99 | 99 | 99 | 99 | 99 | 98 |
| Specificity | 99 | 99 | 98 | 97 | 97 | 99 |
Table 14.
Feedback versus increasing dropout on testing set.
| 180 epochs | 250 epochs | |||||
|---|---|---|---|---|---|---|
| Vanilla | Feedback | Dropout | Vanilla | Feedback | Dropout | |
| Sensitivity | 92 | 92 | 96 | 62 | 67 | 61 |
| Specificity | 99 | 99 | 98 | 97 | 97 | 99 |
Note that the training was not stopped as soon as overfitting was detected and that the weights used to get those values belonged to the last epoch in training.
For the next phase of the experiment, our goal was to increase the sensitivity and specificity in the set. We used the preprocessed images, model B, and feedback mechanism.
4.3. Modifying Input Quantity
4.3.1. Design
Figure 14 shows the design comparing the changes corresponding to increases in size of input by using augmentation against increases in size of input by adding new images to the dataset (dataset B), where the previous stage performed better in the set. The performance is evaluated by measuring the sensitivity and specificity of the testing set using different epochs.
Fig. 14.
Augmentation versus new images.
Of the new cases provided by the Messidor dataset, 1276 were added to the set and 1199 were added to the set. Dataset B consists of the new cases and cropped images with the lesion not centered. The augmentation set consists of images from dataset A and six cropped images with the lesion not centered assuring that the images are completely different.
4.3.2. Results
The accuracy plot of the training set in Fig. 15 shows that the input augmentation reached a higher accuracy than the new input at the beginning of the training, but at the end of the process both achieved a similar accuracy. The plot also displays overfitting on validation sets for both the input augmentation and the new input sets. In addition, Fig. 15 shows a difference in the crossing point between the training and the validation sets, by taking more epochs, when using the new input.
Fig. 15.
Augmentation versus new input accuracy .
The sensitivity increases dramatically in both sets by adding either new data or using input augmentation in the testing sets as shown in Table 15. This increase is larger in input augmentation compared to the new input.
Table 15.
Input augmentation versus new input: sensitivity and specificity .
| Augmentation | New input | ||||
|---|---|---|---|---|---|
| Sensitivity | Specificity | Sensitivity | Specificity | ||
| Epochs | 50 | 82 | 94 | 79 | 94 |
| 100 | 79 | 96 | 76 | 97 | |
| 150 | 73 | 98 | 71 | 98 | |
| 200 | 68 | 99 | 72 | 99 | |
| 250 | 74 | 99 | 72 | 99 | |
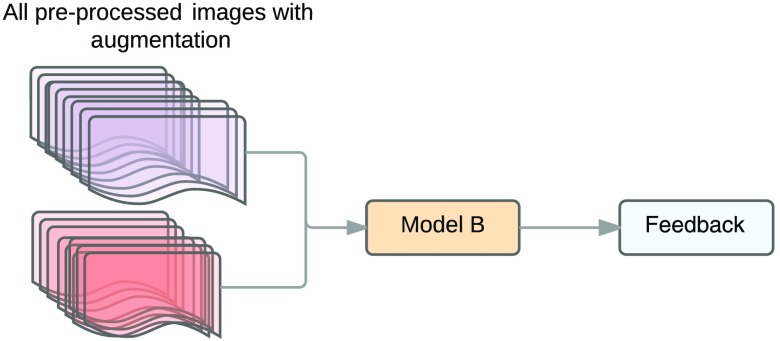
With the original and new inputs, we created a new dataset, dataset C, which contains the original images and the same images cropped by a factor of 10 with the lesion dispersed in different regions of the image as shown in Fig. 16. We trained dataset C with model B and feedback. We also kept the weights for every 50 epochs in images that have a size of and the weights for every 20 epochs in images that have a size of .
Fig. 16.
Final input.
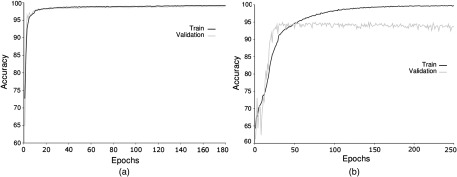
The accuracy of training dataset C with model B and feedback is shown in Fig. 17. Images that have a size of will reach a higher accuracy than images with a size of . In addition, overfitting is more prominent in the image sets.
Fig. 17.
Final input accuracy. Image size (a) and (b) .
Table 16 shows the sensitivity and specificity acquired with having the weights at different epochs in the test dataset. The highest sensitivity and specificity are reached with weights of epochs 40 and 50 in the and sets and are more accurate than those shown in Table 15. A decrease in the sensitivity of both sets occurs with a higher number of epochs as presented in Table 16. This supports the overfitting findings in the validation set depicted in Fig. 17. The weights that produce the best sensitivity for the set and the best specificity for the set are chosen in the next phase of this study.
Table 16.
Final input: sensitivity and specificity.
| Sensitivity | Specificity | Sensitivity | Specificity | ||||
|---|---|---|---|---|---|---|---|
| Epochs | 20 | 93 | 97 | Epochs | 50 | 88 | 95 |
| 40 | 93 | 98 | 100 | 79 | 98 | ||
| 60 | 91 | 98 | 150 | 75 | 99 | ||
| 80 | 92 | 98 | 200 | 76 | 99 | ||
| 100 | 91 | 98 | 250 | 71 | 99 | ||
| 120 | 90 | 98 | |||||
| 140 | 92 | 99 | |||||
| 160 | 91 | 98 | |||||
| 180 | 91 | 98 | |||||
Table 17 shows the sensitivity of the testing set for images with an input size of in different datasets. An increase in the sensitivity using the weights of the CNN results after training these images with datasets A, B, and C.
Table 17.
Sensitivity for image sizes on different datasets, epoch 50, model VGG, and processed images.
| Dataset A | Dataset B | Dataset C | ||||
|---|---|---|---|---|---|---|
| Vanilla | Feedback | Dropout | Augmentation | New input | Cutoff 0.5 | Cutoff 0.32 |
| 62 | 67 | 61 | 82 | 79 | 88 | 91 |
4.4. Receiver Operating Characteristics Analysis
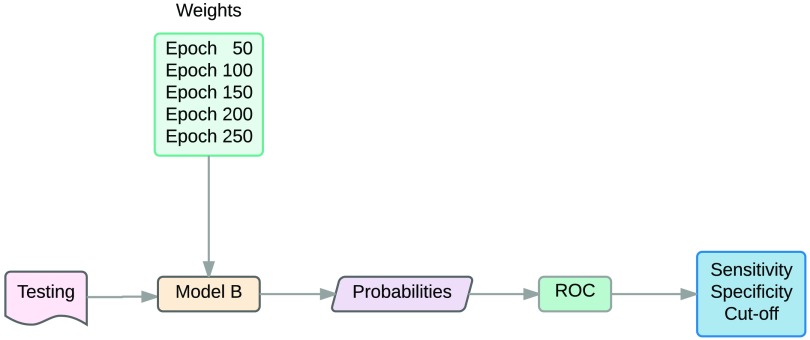
4.4.1. Design
After having run the CNN in the testing set and finding the probability of each image in each category (normal and microaneurysms), the sensitivity, specificity, and optimal cut-point values were obtained by applying ROC to the testing set as shown in Fig. 18. Later, we ran our CNN model with the weights that provided the best accuracy and sensitivity in the diabetic retinopathy database and evaluation dataset to determine how the model performed overall.
Fig. 18.
Cutoff.
4.4.2. Results
Table 18 shows that for the set, the values of the sensitivity and specificity are similar at different cut-off points, with epoch 80 providing a slightly higher specificity. For the dataset, epoch 50 displays the best accuracy and sensitivity. Those weights were used for further analysis.
Table 18.
ROC cutoff.
| Cutoff | Sensitivity | Specificity | Accuracy | Cutoff | Sensitivity | Specificity | Accuracy | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Epochs | 20 | 0.27 | 95 | 97 | 96 | Epochs | 50 | 0.32 | 91 | 93 | 91 |
| 40 | 0.18 | 95 | 97 | 96 | 100 | 0.02 | 90 | 93 | 91 | ||
| 60 | 0.09 | 95 | 97 | 96 | 150 | 0.01 | 89 | 93 | 90 | ||
| 80 | 0.13 | 95 | 98 | 96 | 200 | 0.01 | 89 | 94 | 90 | ||
| 100 | 0.06 | 95 | 97 | 96 | 250 | 0.01 | 88 | 93 | 90 | ||
| 120 | 0.06 | 95 | 97 | 95 | |||||||
| 140 | 0.11 | 95 | 97 | 95 | |||||||
| 160 | 0.05 | 95 | 97 | 95 | |||||||
| 180 | 0.04 | 95 | 97 | 95 | |||||||
Figure 19 shows a ROC analysis, with an area under the curve of 0.9828 and 0.9621 for the and datasets. Figure 19 also displays a variation in the accuracy, by having different cut-off points. For the set, an acceptable specificity was reached with a cutoff at 0.9, without sacrificing the accuracy greatly. For the dataset, we set the cut-off point to be at 0.10 and achieved a high sensitivity without sacrificing the accuracy.
Fig. 19.
(a) ROC and (b) accuracy versus cutoff.
There is a statistical significant difference () between the AUC for the input size and in the Mann–Whitney U test. Even though there is a small difference between the AUCs (0.0207), the input size performs better than the input size. When comparing the AUC of this study (0.928) with the AUC of Grinsven’s work35 (0.894) using the Mann–Whitney U test, we found that this study outperforms Grinsven’s study .
The pictures from the DiaRetDB1 were sliced into sizes of and . After getting the probabilities for each slice, we visually evaluated the lesions found by the CNN and compared them to the ground truth lesions provided by the database. The results of the 20 pictures with 51 lesions are shown in Table 19, which states that model B of the CNN in and sets detects most of the lesions but there are still a number of false positives in the set. If the CNN model is running to detect the lesions first and the model is running over those positives, the number of false positives decreases, holding the true positive cases.
Table 19.
DiaRetDB1 testing.
| 51 lesions from dataset C | ||||
|---|---|---|---|---|
| Cutoff | TP | FP | FN | |
| 0.90 | 49 | 385 | 2 | |
| 0.10 | 49 | 6 | 2 | |
| First: | 0.10 | 49 | 129 | 2 |
| Next: | 0.90 | |||
In Fig. 20, the yellow and red squares represent the predicted positive areas using two trained CNNs with sizes of and , respectively. In addition, the vertical blue and green lines on the left graph represent the cut-off point of the probability value. As depicted in Fig. 20, keeping the fixed cut-off point for the with a high probability and moving the cut-off point for the from zero to higher values of probability reduce the number of false positives.
Fig. 20.
Final results: (a) predicted lesions 24, true lesions 6, and false positives 24; (b) predicted lesions 8, true lesions 6, and false positives 2; and (c) predicted lesions 5, true lesions 6, and false positives, 0.
5. Discussion
Qualitative improvement of the image not only facilitates the detection of the lesions for annotations, but also decreases the number of epochs needed to reach a high accuracy for training and validation sets. Because the colors of microaneurysms are located between 650 and 570 nm in the light spectrum and it is not possible to find cyan colored microaneurysms, color reduction plays a significant role in medical images where its variance is limited. As an illustration, the function in Eq. (3) was successfully applied to enhance the lesions and provide contrast against their surroundings. The benefits of shortening the training time are economic, environmental, and human and can be reflected in the cost reduction.
Quantitative gain either by augmentation or with new images makes the training process more accurate. Deep learning is very dependent on the size of the data. However, sometimes the datasets are limited, so augmentation was introduced to overcome this difficulty. Although augmentation increased the accuracy of this study, adding new images had the same effect, but with a lower number of images. Using dataset C, we achieved a better accuracy compared to dataset B, but the increase in the accuracy was not as high as the one between datasets A and B. This provides evidence that augmentation has a limit in improving accuracy, but more studies are still needed.
Microaneurysms detection in DR is a complex challenge, and the difficulty of this task is determined mainly by the size of the lesions. Most of the DR studies have been focused on classifying its stages, rather than identifying the specific lesion. Indeed, R-CNN, fast R-CNN, and faster R-CNN have been used for object localization with excellent results, but this still has not solved the problem for small features. Some studies tried to overcome this obstacle by cropping the image with the lesion in the center without changing the resolution. Karphaty et al.36 introduced the idea of foveal stream for video classification by cropping the image stream into its center. Lim19 was the first author to use the CNN to classify individual lesions on DR. His work used an automatized algorithm, multiscale C-MSER segmentation, to crop the region of interest with the lesion in the center of the image. van Grinsven’s work35 developed a selective data sampling for the detection of hemorrhages, where the lesions were placed in the center of a cropped image of . Although these studies have an acceptable sensitivity and specificity, the number of false positives is considerable. The following example will explain the reason of having a high number of false positives: Having an image size of will generate 2304 images with a size of , so having a specificity of 90% will produce 231 false positive images with a size of . We claim that although the fovea in the retina has a more concentrated area with photoreceptors, it is the attention that defines the discrimination of the objects. In a similar way, we proposed that keeping the same resolution of the image, but cropping the image to the object of interest would simulate the attention. In addition, cropping the image with the lesion in different positions of the image gives the input data a higher variance. We also made sure to avoid that the CNN would learn the center position instead of the features of the lesion itself.
Using sequentially a test with high sensitivity and a test with high specificity will decrease the number of false positives. Although we used the same methodology, CNN, for both sets ( and ) they differ in the model and input size. As a result, these models could be considered different types of tests. The efforts in the study to increase the sensitivity in the set by increasing the input size and implementing feedback were well paid off by diminishing the false positives generated, when CNNs were applied to cropped images with a size of as a unique test.
In the set, applying feedback to the CNN performed better than vanilla and dropout increasing. Our approach tried to find the batch with mild and normal classes that perform poorly after back-propagation to retrain them again. One of the limitations of this approach was that we needed to know the values of the loss function per batch during all of the training in order to calculate the function. However, it is possible that a dynamic process can be created using a number of previous batches to get the threshold and update it after a certain number of batches. van Grinsven’s work35 proposed a feedback method that assigns a probability score to each pixel and is modified when “the probability scores differ the most from the initial reference level,” so the higher the weight probability the higher the chance of it being selected. One drawback of this methodology is that it is applied only to the negative sample.
Some observations that called our group’s attention were that the CNN selected some small artifacts as lesions. Also, the algorithms selected small groups of lesions, but when a bigger number of lesions were grouped in such a way that they mimic hemorrhages, they were not detected. Although we gained some progress in the detection and selection of microaneurysms and our technique’s performance surpassed all of the methods in the literature at this time, there are still a number of false positives.
6. Conclusion
This study proposed a methodology by using a CNN model that increases the performance of the identification and classification of microaneurysms representing small local features. Therefore, this study combines the sequential use of a CNN with a high sensitivity followed by a CNN with a high specificity to detect microaneurysms with few false positives. In addition, the new feedback methodology for training demonstrated that it had the ability to improve the accuracy. The preprocessing technique developed was able to decrease the training time and improve the quality of the images for annotations. Furthermore, this study reaffirms that deep learning is data dependent and obtaining new data is as important as augmentation.
Biographies
Pablo F. Ordóñez studied medicine and completed general surgery residency from the National University of Colombia. Lately, he received his master’s degree in computer science from Kennesaw State University. Currently, he is working at Kennesaw State University developing machine learning algorithms for medical data.
Carlos M. Cepeda received his bachelor’s degree in electrical engineering from the National University of Colombia and his MS degree in computer science from Kennesaw State University. He has been working on machine learning for malware detection at Kennesaw State University.
Jose Garrido received his MS degree from George Mason University, his MSc degree from the University of London, and his PhD from George Mason University. He is a professor of computer science at Kennesaw State University and his areas of interests are high-performance computing and computational models. He has authored books, more than 40 articles, and has given more than 10 guest lectureships.
Sumit Chakravarty received his MS degree from Texas A&M University, his PhD from the University of Maryland, and postdoc at SBIA, University of Pennsylvania. He is an assistant professor in the Electrical Engineering Department at Kennesaw State University. Some of his areas of interests are computer vision, machine learning, and hyperspectral images.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Yanoff M., Duker J. S., Ophthalmology, Mosby, Edinburgh: (2008). [Google Scholar]
- 2.Allyn W., iEXAMINER, 2017, https://www.welchallyn.com/en/microsites/iexaminer.html (7 November 2017).
- 3.Wilkinson C. P., et al. , “Proposed international clinical diabetic retinopathy and diabetic macular edema disease severity scales,” Ophthalmology 110, 1677–1682 (2003). 10.1016/S0161-6420(03)00475-5 [DOI] [PubMed] [Google Scholar]
- 4.ILSVRC2016, 2017, http://image-net.org/challenges/LSVRC/2016/results (7 November 2017).
- 5.MsCoCo, 2017, http://mscoco.org/dataset/#detections-leaderboard (7 November 2017).
- 6.LeCun Y., et al. , “Handwritten zip code recognition with multilayer networks,” in Proc. of the Int. Conf. on Pattern Recognition (IAPR), Vol. II, pp. 35–40, IEEE, Atlantic City: (1990). 10.1109/ICPR.1990.119325 [DOI] [Google Scholar]
- 7.Krizhevsky A., Sutskever I., Hinton G. E., “Imagenet classification with deep convolutional neural networks,” in Proc. of the 25th Int. Conf. on Neural Information Processing Systems, pp. 1097–1105, Curran Associates, Inc. (2012). [Google Scholar]
- 8.Simonyan K., Zisserman A., “Very deep convolutional networks for large-scale image recognition,” CoRR abs/1409.1556 (2014).
- 9.Zagoruyko S., Komodakis N., “Wide residual networks,” Computer Vision and Pattern Recognition abs/1412.6071 (2014).
- 10.Szegedy C., et al. , “Going deeper with convolutions,” Computer Vision and Pattern Recognition, arXiv:1409.4842 (2014).
- 11.Glorot X., Bengio Y., “Understanding the difficulty of training deep feedforward neural networks,” in Proc. of the Thirteenth Int. Conf. on Artificial Intelligence and Statistics, JMLR (2010). [Google Scholar]
- 12.Ioffe S., Szegedy C., “Batch normalization: accelerating deep network training by reducing internal covariate shift,” in Proc. of the 32nd Int. Conf. on Machine Learning, pp. 448–456 (2015). [Google Scholar]
- 13.Goodfellow I. J., et al. , “Maxout networks,” in Proc. of the 30th Int. Conf. on Machine Learning, Atlanta, Georgia, pp. III-1319–III-1327 (2013). [Google Scholar]
- 14.Su H., et al. , “Region segmentation in histopathological breast cancer images using deep convolutional neural network,” in IEEE 12th Int. Symp. on Biomedical Imaging (ISBI), pp. 55–58 (2015). 10.1109/ISBI.2015.7163815 [DOI] [Google Scholar]
- 15.Nithila E. E., Kumar S., “Automatic detection of solitary pulmonary nodules using swarm intelligence optimized neural networks on CT images,” Eng. Sci. Technol. Int. J. 20, 1192–1202 (2016). 10.1016/j.jestch.2016.12.006 [DOI] [Google Scholar]
- 16.Gulshan V., et al. , “Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs,” J. Am. Med. Assoc. 316(22), 2402–2410 (2016). 10.1001/jama.2016.17216 [DOI] [PubMed] [Google Scholar]
- 17.Sankar M., Batri K., Parvathi R., “Earliest diabetic retinopathy classification using deep convolution neural networks.pdf,” Int. J. Adv. Eng. Technol. (2016). 10.6084/M9.FIGSHARE.3407482 [DOI] [Google Scholar]
- 18.Pratt H., et al. , “Convolutional neural networks for diabetic retinopathy,” Procedia Comput. Sci. 90, 200–205 (2016). 10.1016/j.procs.2016.07.014 [DOI] [Google Scholar]
- 19.Lim G., et al. , “Transformed representations for convolutional neural networks in diabetic retinopathy screening,” in AAAI Workshop: Modern Artificial Intelligence for Health Analytics (2014). [Google Scholar]
- 20.“Diabetic retinopathy detection Kaggle,” 2017, https://www.kaggle.com/c/diabetic-retinopathy-detection (7 November 2017).
- 21.Guillaume Patry D., “ADCIS Download Third Party: Messidor Database,” 2017, http://www.adcis.net/en/DownloadThirdParty/Messidor.html (7 November 2017).
- 22.“Optimal detection and decision-support diagnosis of diabetic retinopathy (IMAGERET),” 2017, http://www.it.lut.fi/project/imageret (7 November 2017).
- 23.“Torch scientific computing for LuaJIT,” 2017, http://torch.ch/ (7 November 2017).
- 24.GitHub, https://github.com/soumith/imagenet-multiGPU.torch (7 November 2017).
- 25.Fawcett T., “An introduction to roc analysis,” Pattern Recognit. Lett. 27(8), 861–874 (2006). 10.1016/j.patrec.2005.10.010 [DOI] [Google Scholar]
- 26.Carl Zeiss Spectroscopy GmbH, https://www.zeiss.com/spectroscopy/solutions-applications/color-measurement.html.
- 27.Mahy M., Van Eycken L., Oosterlinck A., “Evaluation of uniform color spaces developed after the adoption of CIELAB and CIELUV,” Color Res. Appl. 19(2), 105–121 (1994). 10.1111/j.1520-6378.1994.tb00070.x [DOI] [Google Scholar]
- 28.Thorndike R. L., “Who belongs in the family?” Psychometrika 18(4), 267–276 (1953). 10.1007/BF02289263 [DOI] [Google Scholar]
- 29.Deep image: scaling up image recognition,” Computer Vision and Pattern Recognition, abs/1501.02876 (2015).
- 30.Graham B., “Fractional max-pooling,” Computer Vision and Pattern Recognition, arXiv:1412.6071 (2014).
- 31.Maas A. L., Hannun A. Y., Ng A. Y., “Rectifier nonlinearities improve neural network acoustic models,” in ICML Workshop on Deep Learning for Audio, Speech and Language Processing (2013). [Google Scholar]
- 32.Xu B., et al. , “Empirical evaluation of rectified activations in convolutional network,” CoRR abs/1505.00853 (2015).
- 33.He K., et al. , “Delving deep into rectifiers: surpassing human-level performance on imagenet classification,” CoRR abs/1502.01852 (2015).
- 34.CRAN-Package OptimalCutpoints, https://cran.r-project.org/web/packages/OptimalCutpoints/index.html (9 November 2017).
- 35.van Grinsven M. J. J. P., et al. , “Fast convolutional neural network training using selective data sampling: application to hemorrhage detection in color fundus images,” IEEE Trans. Med. Imaging 35, 1273–1284 (2016). 10.1109/TMI.2016.2526689 [DOI] [PubMed] [Google Scholar]
- 36.Karpathy A., et al. , “Large-scale video classification with convolutional neural networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), pp. 1725–1732, IEEE Computer Society, Washington, DC: (2014). 10.1109/CVPR.2014.223 [DOI] [Google Scholar]