Effects of Image Quality on the Fundamental Limits of Image Registration Accuracy

Abstract

For image-guided procedures, the imaging task is often tied to the registration of intraoperative and preoperative images to a common coordinate system. While the accuracy of this registration is a vital factor in system performance, there is relatively little work that relates registration accuracy to image quality factors such as dose, noise, and spatial resolution. To create a theoretical model for such a relationship, we present a Fisher information approach to analyze registration performance in explicit dependence on the underlying image quality factors of image noise, spatial resolution, and signal power spectrum. The model yields analysis of the Cramer-Rao lower bound, CRLB, in registration accuracy as a function of factors governing image quality. Experiments were performed in simulation of CT low-contrast soft tissue images and high-contrast bone (head and neck) images to compare the measured accuracy [root mean squared error (RMSE) of the estimated transformations] with the theoretical lower bound. Analysis of the CRLB reveals that registration performance is closely related to the signal-to-noise ratio of the cross-correlation space. While the lower bound is optimistic, it exhibits consistent trends with experimental findings and yields a method for comparing the performance of various registration methods and similarity metrics. Further analysis validated a method for determining optimal post-processing (image filtering) for registration. Two figures of merit (CRLB and RMSE) are presented that unify models of image quality with registration performance, providing an important guide to optimizing intraoperative imaging with respect to the task of registration.

I. Introduction

In image-guided interventions, registration performance pertains to the accuracy with which the preoperative image (denoted I₁) and intraoperative image (denoted I₂) can be co-registered in a common coordinate system. In many scenarios, the ability to accurately register I₂ to I₁ (and planning data therein) may be even more important than the ability to visualize structures in I₂ directly. For example, Uneri et al. [1] developed a registration method to evaluate surgical screw placement relative to preoperative CT, enabling quantitative evaluation of screw malplacement in 3D rather than qualitative visualization interpretation of 2D projection radiographs. In this scenario, the primary task is accurate registration to CT (and overall perceptual image quality in the radiographs is of secondary importance). In related work, Uneri et al. [2] reported that accurate registration could be achieved even when the radiograph was acquired at a dose ~1/10^th that of standard technique, indicating that the task of registration may be more robust against noise than the task of visualization; hence, imaging parameters that are optimal for visualization may not correspond to those that are optimal for registration. The development of imaging systems for interventional guidance therefore prompts consideration that the optimal I₂ imaging technique (i.e., factors governing image noise and spatial resolution) is that which provides a desired level of registration accuracy, rather than visual image quality. This consideration in turn motivates a quantitative framework to relate registration accuracy to image quality.

A considerable body of ongoing research seeks to establish reliable relationships between image quality and detection tasks [3], [4], helping to design new systems [5], [6], determine optimal imaging techniques [7], and substantiate claims of low-dose imaging performance [8], [9]. For example, in computed tomography (CT) and cone-beam CT (CBCT), the image quality characteristics are well characterized by information-theoretic descriptors such as noise-equivalent quanta (N E Q), which encompasses spatial-frequency-dependent descriptors of spatial resolution (modulation transfer function, MT F) and image noise (noise-power spectrum, N PS). Moreover, such analysis provides knowledgeable guidance of image acquisition and reconstruction techniques with respect to tasks of detection and visualization [10]–[12]. However, while CT and CBCT images are increasingly employed in image-guided interventions, there is comparatively little rigorous understanding of the relationship between these image quality factors and registration performance, leaving largely unanswered fundamental questions in determining imaging techniques that achieve a desired level of registration accuracy.

Registration performance is commonly investigated by rigorous measurement and experimental evaluation of geometric accuracy in contexts appropriate to a particular application. Such investigation often involves registration repeated for either a large data set or simulated noise realizations, where the output transformation parameters are compared to the ground truth transformation. Results from such experiments provide an important basis for quantifying performance in support of the clinical application; however, they are still often performed using the general understanding that a “higher quality” image will give better registration performance– or that a level of image quality sufficient for visualization will in turn be sufficient for registration–without rigorous guidance of an analytical model for registration. As a result, there are untested opportunities for imaging methods that are best suited for the task of registration–e.g., methods that achieve a desired level of registration accuracy with reduced radiation dose.

We seek an analytical framework that will help to unify models of image quality (e.g., spatial resolution and noise) with models for registration performance, providing a rigorous basis and guide to selection of image acquisition protocols, reconstruction methods, and post-processing techniques sufficient (or optimal) for the task of registration. We approach the question by analyzing a simple model involving 2D translation-only registration to gain initial insight into the more complicated general registration problem. Future work will consider translation+rotation, affine, and potentially deformable registration. As detailed below, we build from well-established, image quality considerations for CT/CBCT image quality [13]–[15] and realize a framework that relates these factors to the task of image registration. While this framework is general to the broader field of image registration, it is presented here specifically in the context of medical imaging, relating registration performance to concepts of image noise, spatial resolution, and information-theoretic metrology (viz., image N PS, MT F, and N E Q) that are familiar and prevalent in medical image quality assessment – particularly in x-ray CT and CBCT.

II. Background Methods

Robinson and Milanfar [16] proposed a fundamental limit on registration accuracy by deriving the Cramer-Rao lower bound (CRLB) for 2D translation between two images. Their model considered registering images of the same content in the presence of additive white Gaussian noise (AWGN) and was further extended to rigid registration (including rotation) and 3D registration [17]. To examine the effect of spatial resolution on registration performance, Zhao et al. [18] similarly considered the AWGN assumption, finding that optimal performance could be achieved by blurring the higher-resolution image to match the MT F of the lower-resolution image. In the context of image-guided interventions, the framework for such lower bounds and spatial resolution analysis requires modification to account for both non-white noise (e.g., correlated noise that is intrinsic to CT and CBCT) as well as strong differences in image quality characteristics between the preoperative and intraoperative image (i.e., the I₂ CBCT typically exhibiting higher noise than the I₁ CT image). We therefore consider the following model for registration:

$$I_1[x,y]=g(x,y)+n_1(x,y)$$ (1)

$$I_2[x,y]=g(x-u,y-u)+n_2(x,y)$$ (2)

where g is the true underlying image function, and n_i are Gaussian additive noise terms that are independent of the signal and each other. The image I₂ is formed with a translation-only displacement of g, with the transformation θ = [u, υ] representing the unknown translation between the two images. The [·] bracket notation represents the process of discretely sampling the continuous underlying image functions. By convention, we use the discrete form using [·] when referring to the image domain and the continuous form (·) for the underlying spatial domain image functions or functions in the frequency domain.

III. Derivation of the Cramer-Rao lower bound (CRLB) For image registration

The CRLB is of fundamental interest to many parameter estimation problems, as it provides a theoretical statistical limit on the expected error of the estimator. In the case that the estimator is unbiased, the CRLB matrix (C_{L B}) is simply the inverse of the Fisher Information Matrix (F I M) which is derived from the log-likelihood function, log L(I|θ), of the data conditioned on the parameter vector θ. The FIM examines the curvature of the likelihood function with respect to changes in θ, representing the intuitive concept that if the likelihood function is highly sensitive to perturbations of θ, then θ can be estimated more accurately. Note that the FIM itself is independent of the estimator and bias. By definition [19], we have:

$$\begin{gathered} {[\mathit{FIM}]}_{ij}=E\left\{\frac{\partial \text{log}(I\mid \theta )}{\partial {\theta }_i}\frac{\partial \text{log}(I\mid \theta )}{\partial {\theta }_j}\right\} \\ =-E\left\{\frac{{\partial }^{2}logL(\mathit{I}\mid \mathit{\theta })}{\partial {\theta }_i\partial {\theta }_j}\right\} \end{gathered}$$ (3)

where the second equality holds under conditions satisfying interchangeable differentiation and integration of the log-likelihood function. Taking a 2D model for simplicity of notation, I refers to the image data, and θ is the vector of transformation parameters given by [u, υ]^t for the translation-only case.

A. CRLB for Signal-Known-Exactly (SKE) With White Noise

As shown in [20], the F I M result presented in [16] applies to the simplified case of a noiseless I₁ [simplified from (1–2)] and therefore the signal-known-exactly (SKE) scenario (i.e., exactly known g [x, y] = I₁[x, y]) described by:

$$I_1[x,y]=g(x,y)$$ (4)

$$I_2[x,y]=g(x-u,y-u)+n_2(x,y)$$ (5)

in which only the shifted image is considered to be contaminated by AWGN with variance σ². As shown in [20], the subtraction of the images at the true shift leaves only the AWGN noise term; therefore, L (I|θ) is simply the product of Gaussian probability density functions, giving:

$${\mathit{FIM}}_{\mathit{SKE},\mathit{AWGN}}=C_{LB}^{-1}=\frac{1}{{\sigma }^2}\left[\begin{array}{cc}\sum _{x,y}{g}_x^2& \sum _{x,y}{g}_x{g}_y\\ \sum _{x,y}{g}_x{g}_y& \sum _{x,y}{g}_y^2\end{array}\right]$$ (6)

where g_x [x, y], g_y[x, y] are the partial derivative images with respect to x, y. Examining the F I M, we see that registration performance depends generally on two primary components: (i) the image noise (i.e., variance, which is governed largely by image acquisition technique factors such as the level of radiation dose); and (ii) the sum-of-squared image gradients (which are governed by the contrast and frequency content of the subject). While this formulation provides useful basic insight, it is limited in that it does not account for the presence of noise in both the I₁ fixed and I₂ moving images; nor does it account for correlated noise. In the following section, we address this limitation by deriving the lower bound for the scenario in which the noise terms have different magnitude and frequency content.

B. CRLB for Image Registration

A typical scenario in image-guided procedures involves the registration of a high-quality preoperative image to a lower-quality (noisy and/or blurry) intraoperative image, requiring an alternate formulation of the F I M to explicitly address the presence of noise in both images and allowing the noise in each image to carry disparate (heteroscedastic) magnitude and correlation. We assume linear systems having stationary jointly Gaussian signal and noise for the setting of (1–2), where n_i is zero-mean and independent of g and n _j≠i - a common starting point in formulation of image statistics that can be extended to ‘local’ approximation for nonlinear, nonstationary systems (discussed below and in [11] and [21]). Appendix A demonstrates a proof analogous to that derived for 1D time-delay estimation (TDE) in [22]–[24] to achieve the following key result, which for the purposes of analytical tractability is derived in the frequency domain:

$$\begin{gathered} \mathit{FIM}={(2\pi )}^{2}A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right], \\ \text{where}{\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i{f}_j\frac{G^2}{G{N}_1+G{N}_2+N_1{N}_2}d{f}_{x}d{f}_y \end{gathered}$$ (7)

where G (f_x, f_y) is the power spectrum of g (x, y), the N_i(f_x, f_y) are the N PS of images I_i, A is the image area, and f_Nyq refers to the Nyquist frequency. For notational convenience, we leave out the explicit frequency (f_x, f_y) dependence in G and N_i. Equation (7) provides the necessary framework to analyze registration performance bounds when the two images have separate noise forms that are not necessarily white. We rewrite (7) as follows to more explicitly show the dependence of Fisher information on the image signal and noise:

$$\begin{gathered} \mathit{FIM}={(2\pi )}^{2}A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right], \\ \text{where}{\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i{f}_j{\mathit{SNRdf}}_{x}d{f}_y \end{gathered}$$ (8)

$$\text{and}\mathit{SNR}(f_x,f_y)=\frac{G^2}{G{N}_1+G{N}_2+N_1{N}_2}$$ (9)

Equation (9) carries intuitive dependencies of registration performance on SNR, namely: the numerator scales with signal feature strength (i.e., contrast and gradient magnitude), and the denominator scales with image noise, including cross terms corresponding to noise in cross-correlation (examined further in section IV).

One can see that the general form in (7) reduces to that of (6) in the simplified case of noiseless I₁ (N₁ = 0) and AWGN (N₂ is “white” with magnitude σ²). From (7) this suggests:

$$\begin{gathered} {\mathit{FIM}}_{\mathit{SKE},\mathit{AWGN}}={(2\pi )}^{2}A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right], \\ \text{where}{\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i{f}_j\frac{G}{N_2}d{f}_{x}d{f}_y \\ =\frac{1}{{\sigma }^2}\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i{f}_j{\mathit{Gdf}}_{x}d{f}_y \end{gathered}$$ (10)

which is equivalent to (6) via Parseval’s Theorem and the Fourier derivative theorem.

C. Strong Signal Approximation

A simplifying approximation of the F I M is obtained when the denominator of the SN R is not a function of G, as in the simple case of (10). This form is achieved when N₁ N₂ ≪ G N₁ +G N₂ allowing approximation of the denominator in (9) as G N₁ + G N₂ and giving:

$$\begin{gathered} {\mathit{FIM}}_{\widehat{N}\ll G}={(2\pi )}^{2}A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right], \\ \text{where}{\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i{f}_j{\mathit{SNR}}_{\widehat{N}\ll G}d{f}_{x}d{f}_y \\ \text{with}{\mathit{SNR}}_{\widehat{N}\ll G}\left(f_x,f_y\right)=\frac{G}{N_1+N_2} \end{gathered}$$ (11)

The approximation can also be written as N₁ N₂/ (N₁ + N₂) = N̂ ≪ G, showing that this approximation holds when the signal is strong compared to the noise. An interesting observation is that this approximation is equivalent to treating the noise as being contained in only one image:

$$I_1[x,y]=g(x,y)$$ (12)

$$I_2[x,y]=g(x-u,y-u)+n_2(x,y)+n_1(x,y)$$ (13)

indicating that (for low noise levels) it is not important how the noise is distributed between the two images, and only the sum (N₁ + N₂) affects registration performance. For the simple AWGN case, (11) amounts to the scenario in (4–5) and the FIM becomes:

$${\mathit{FIM}}_{\widehat{N}\ll G,\mathit{AWGN}}=\frac{1}{{\sigma }_1^2+{\sigma }_2^2}\left[\begin{array}{cc}\sum _{x,y}{g}_x^2& \sum _{x,y}{g}_x{g}_y\\ \sum _{x,y}{g}_x{g}_y& \sum _{x,y}{g}_y^2\end{array}\right]$$ (14)

where we now have the sum of the variances from the two images entering the denominator of the F I M, simplifying the explicit relationship between registration performance and total image variance. In the case of equal variance (homoscedastic), this amounts to an increase in the CRLB by a factor of 2 compared to (6).

In this reduced form, the F I M_N̂≪G captures intuitive dependencies between noise and registration performance (i.e., the CRLB scales directly with total variance). However, we will see that it further yields simple relationships for N E Q and DQE (shown in Section V). The N₁ N₂/ (N₁ + N₂) = N̂ ≪ G condition corresponds to at least three relevant scenarios: (i) the signal is strong compared to the noise sum (i.e, G ≫ (N₁ + N₂) > N₁ N₂/ (N₁ + N₂), indicating that SNR_N̂≪G is large; (ii) I₁ is noiseless (N₁ ≈ 0); or (iii) I₂ is much noisier than I₁ (i.e., N₁ ≪ N₂) and the signal power is strong compared to the noise in I₁ (i.e., N₁ ≪ G). These are suitable approximations, for example, in registration of high-contrast bone anatomy (high signal power in g) from a high quality preoperative CT (low N₁) to a lower quality (high N₂) intraoperative CBCT.

IV. cross-Correlation and Optimal Filtering

An important question that an analytical registration model must also address is the impact of (optional) post-processing blur. It can be seen in (7) that blur by a simple linear filter (described by the MT F² implicit in both the G and N_i terms) will exactly cancel out for invertible filters (with non-zero MT F), exemplifying the information-theoretic data processing inequality: application of a linear blur filter does not reduce the CRLB in registration performance. However, in practice the benefits of post-processing blur are well known (and shown in section VII-C) for reducing the impact of high-frequency noise on registration performance. Therefore, to more fully examine the question of spatial resolution and optimal filtering, the registration method itself must be examined. In this section we focus on the commonly used registration method of maximizing cross-correlation:

$$\begin{gathered} r(\tau ,\phi )=\left(I_1\otimes I_2\right)(\tau ,\phi ) \\ =\sum _{x,y}{I}_1[x,y]I_2[x+\tau ,y+\phi ] \end{gathered}$$ (15)

where an interpolation over I₂ must take place to achieve the continuous cross-correlation function. By examining a local region near the peak of the cross-correlation function, we observe that an equivalent estimator of θ = [u, υ] is one that solves for θ̂ = [û, υ̂] such that $r_{\tau }\left(\widehat{u},\widehat{\upsilon }\right)=\frac{\partial r\left(\widehat{u},\widehat{\upsilon }\right)}{\partial \tau }=0$ and $r_{\phi }\left(\widehat{u},\widehat{\upsilon }\right)=\frac{\partial r\left(\widehat{u},\widehat{\upsilon }\right)}{\partial \phi }=0$. If we assume errors in the estimation to be contained within the linear region near the true solution (similar to [25] in 1D TDE), a first-order Taylor series approximation near θ yields the error estimate:

$${\left[\begin{array}{c}\left(\widehat{u}-u\right)\\ \left(\widehat{\upsilon }-\upsilon \right)\end{array}\right]}^t\approx {\left[\begin{array}{c}{r}_{\tau }(u,\upsilon )\\ r_{\phi }(u,\upsilon )\end{array}\right]}^t{\left[\begin{array}{cc}{r}_{\tau \tau }(u,\upsilon )& r_{\tau \phi }(u,\upsilon )\\ r_{\tau \phi }(u,\upsilon )& r_{\phi \phi }(u,\upsilon )\end{array}\right]}^{-1}$$ (16)

where $r_{\tau \tau }(u,\upsilon )=\frac{{\partial }^{2}r(u,\upsilon )}{\partial {\tau }^2}$, and similarly for the other 2^nd derivative terms. The root mean square error (RMSE) of the estimate is obtained by computing the magnitude of the expectation of this error. We show in Appendix B that under the same assumptions of stationarity and independence used for the F I M derivation and by assuming r_τφ (u, υ) to be small in comparison to the diagonal terms (appropriate when the image gradients are evenly distributed in orientation), the RMSE for the maximizing cross-correlation estimate is approximately:

$$\begin{gathered} \mathit{RMSE}\approx \sqrt{1/{\rho }_x+1/{\rho }_y},\text{where} \\ {\rho }_i=\frac{{(2\pi )}^{2}A{\left[\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i^2{\mathit{Gdf}}_{x}d{f}_y\right]}^2}{\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i^2(G{N}_1+G{N}_2+N_1{N}_2)d{f}_{x}d{f}_y} \end{gathered}$$ (17)

The result bears many similarities to the F I M in (7), particularly with respect to the noise term G N₁ + G N₂ + N₁ N₂. From the associative property of cross correlation, we see that I₁ ⊗ I₂ = g ⊗ g + g ⊗ n₂ + n₁ ⊗ g + n₁ ⊗ n₂, which comprises two primary terms: (i) the true cross correlation of the signal g ⊗ g; and (ii) the remaining terms associated with additive noise in the cross-correlation. The power associated with these noise terms is represented in the Fourier domain as G N₁ + G N₂ + N₁ N₂, which appears in both (7) and (17). Equation (17) is particularly interesting in that the signal and noise terms (numerator and denominator of ρ_i, respectively) are integrated separately, analogous to a non-prewhitening (NPW) model, for which an “optimal blur” can be derived - distinct from the simple data processing concept noted above. Noting that blurring the images leads to a blur of the cross-correlation [i.e., (h₁ * I₁) ⊗ (h₂ * I₂) = (h₁ ⊗ h₂) * (I₁ ⊗ I₂) = h * r], we may consider a blur kernel (h) with Fourier transform H, giving:

$$\begin{gathered} \mathit{RMSE}\approx \sqrt{1/{\rho }_x+1/{\rho }_y}\text{where}, \\ {\rho }_i=\frac{{(2\pi )}^{2}A{\left[\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i^{2}H{\mathit{Gdf}}_{x}d{f}_y\right]}^2}{\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i^2{H}^2(G{N}_1+G{N}_2+N_1{N}_2)d{f}_{x}d{f}_y} \end{gathered}$$ (18)

This result then can be minimized as a function of H. In the 1D TDE case, Knapp and Carter [25] showed that the maximum likelihood estimate is achieved by filtering according to the data-dependent Hannan and Thompson method, giving:

$$H_{HT}=\frac{G/(N_1{N}_2)}{1+G/N_1+G/N_2}$$ (19)

In practice, however, blurring of I₁ or I₂ is typically achieved using a simple kernel (e.g., symmetric Gaussian blur); thus, we consider a blurring function H_b with kernel width σ_b:

$$H_b\left(f_x,f_y\right)=e^{-4{\pi }^2\left(f_x^2+f_y^2\right){\sigma }_b^2}$$ (20)

where H_b represents blurring both images by a Gaussian kernel of width σ_b. Therefore, we can solve for the optimal blur by minimizing (18) with respect to σ_b. Depending on the registration method, additional blur can be included explicitly (such as the blur incurred with interpolation, described by H_interp), giving a combined H = H_interp H_b for the total blur appearing in (18).

V. Connection to Models of Image Quality

As derived above, the CRLB for image registration depends explicitly on the noise and resolution characteristics of the imaging system(s). Recent decades have seen the development of accurate models for the image quality characteristics of CT and CBCT imaging systems [13]–[15], including the MT F, NPS, and their dependence on each factor in the imaging chain, such as dose, system geometry, acquisition technique, and reconstruction technique. Such models consider the propagation of signal and noise through the imaging chain to describe the MT F and NPS. Simplifying from the 3D case in [13] to the 2D case considered here, a simple form for the ideal axial CT image NPS (i.e., a deterministic system featuring quantum noise without aliasing or electronic noise) can be written:

$${\mathit{NPS}}_{\mathit{ideal}}\left(f_x,f_y\right)=\frac{\pi \sqrt{f_x^2+f_y^2}}{m\overline{q}{M}^2\mathrm{\Gamma }}{\mathit{MTF}}^2\left(f_x,f_y\right)$$ (21)

(with the full form of the NPS detailed in [13]) where the dose is related to the number of projections (m) and incident x-ray fluence (q̄), M refers to system magnification, and is the system gain. Considering the SKE white noise registration model of (6) and the image quality model of (21), we reach an immediate finding: since noise-power [and thus σ², given by the integral of (21)] is inversely proportional to dose (via the mq̄ term in the denominator), and the CRLB is proportional to σ², then the lower bound on registration error scales in inverse proportion to dose. Incorporating noise terms in both images shows a more complex relationship that depends not only on the total dose, but the relative dose in each image.

We can consider such relationships further in terms of metrics of fidelity that incorporate both the NPS and MT F. The performance of an imaging system is commonly described in terms of the NEQ, representing the effective number of incident photons contributing to each spatial frequency [13]:

$$\mathit{NEQ}\left(f_x,f_y\right)=\pi \sqrt{f_x^2+f_y^2}\frac{{\mathit{MTF}}^2\left(f_x,f_y\right)}{\mathit{NPS}\left(f_x,f_y\right)}$$ (22)

Arranging terms from (22) and combining with the F IM_N̂≪G formulation of (11) yields a relationship between image quality and registration performance. For example, in a scenario where the two images are produced by the same imaging system (equivalent MT F), the F IM_N̂≪G in (11) becomes:

$${\mathit{FIM}}_{\widehat{N}\ll G}=4\pi A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right],$$

where

$${\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}\frac{f_i{f}_j}{\sqrt{f_x^2+f_y^2}}\frac{{\mathit{NEQ}}_1{\mathit{NEQ}}_2}{{\mathit{NEQ}}_1+{\mathit{NEQ}}_1}{G}_{\mathit{obj}}d{f}_{x}d{f}_y$$ (23)

where G_obj refers to the power spectrum of the object rather than the image of the object (equal to G divided by MT F²). In this form, we see that registration performance is dependent on high-frequency weighting [carried by the $f_i{f}_j/\text{sqrt}(f_x^2+f_y^2)$ term] of the object, in turn modified by the effective NEQ term.

Alternatively, the DQE describes the performance in terms of the dose, MT F, and NPS as:

$$\mathit{DQE}\left(f_x,f_y\right)=\frac{\pi \sqrt{f_x^2+f_y^2}}{m\overline{q}}\frac{{\mathit{MTF}}^2\left(f_x,f_y\right)}{\mathit{NPS}\left(f_x,f_y\right)}$$ (24)

Similarly, taking the example of two images produced by the same system (equivalent MT F), rearranging (24) allows the F IM_N̂≪G (11) to be written as a function of DQE:

$$\begin{gathered} {\mathit{FIM}}_{\widehat{N}\ll G}=4\pi A\frac{{(m\overline{q})}_1{(m\overline{q})}_2}{{(m\overline{q})}_1+{(m\overline{q})}_2}\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right], \\ \text{where}{\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}\frac{f_i{f}_j}{\sqrt{f_x^2+f_y^2}}\mathit{DQE}·G_{\mathit{obj}}d{f}_{x}d{f}_y \end{gathered}$$ (25)

Examination of (18) similarly elucidates the dependence of registration accuracy on resolution characteristics, particularly for the case of maximizing cross correlation. Reduced system MT F (via system blur and/or coarser voxel size) carries the benefit of reduced noise but also reduces the strength of image gradients via H; therefore, the lower bound on registration accuracy follows a non-monotonic dependence on spatial resolution, suggesting an ‘optimal’ resolution (alternatively, an optimal post-processing filter) that balances the tradeoffs between noise and gradient strength.

VI. Experimental Methods

A. Formation of Test Images

Experiments were conducted based on two digitally simulated axial CT images: (i) a soft-tissue model and (ii) an anthropomorphic head phantom. The soft-tissue model was based on a power-law noise distribution with frequency content following the distribution F {g} (f) ∝ f^−β, as common in statistical modeling of anatomical “clutter” [26]–[28]. A value of β = 3 has been shown to model a stochastic arrangement of self-similar, soft-tissue anatomy [27]. A realization of such power-law distribution in 3D was generated and taken as ground truth soft-tissue anatomical structure for CT simulation. For the head image, ground truth was measured from a high-quality CT scan of an anthropomorphic head phantom (The Phantom Laboratory, Greenwich, NY) with soft-tissue manually segmented [10] and set to a constant value of 40 HU.

Simulated CT images of these two models were computed over a broad range in dose by digitally forward-projecting the ground truth images, scaling the fluence in proportion to dose, and adding Poisson noise in proportion to $1/\sqrt{(1+\mathit{SPR})\times \mathit{Dose}}$, where nominal values for scatter-to-primary ratio (SPR) were chosen: SPR = 2 for the soft-tissue image and SPR = 9 for the higher attenuation head image [20], [21]. In each case, dose is specified in terms of the x-ray tube current - time product (mAs), which is proportional to absorbed dose via the fluence per unit exposure (q/X), exposure per mAs (X/mAs), and exposure-to-dose conversion (f-factor, cGy/X), all of which are constant for a fixed beam energy (in these studies, a 100 kV spectrum computed using the SPEKTR x-ray simulation toolkit [29])

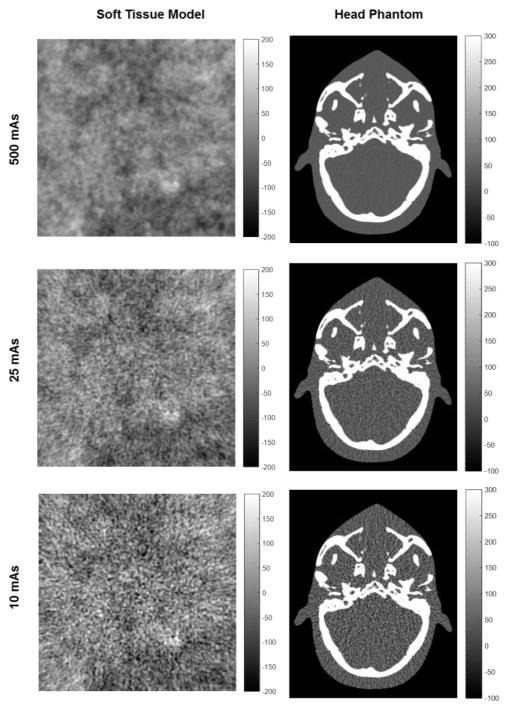
Each image was simulated from m = 720 forward projections over 360°. The fluence was scaled according to total x-ray tube output (mAs) at a beam energy of 100 kV. Images were reconstructed by filtered backprojection, and central 2D axial slices (241 × 241 pixels for the soft-tissue model and 485 × 390 for the head) at 0.5 mm × 0.5 mm voxel size were extracted. Example soft-tissue and head images at various dose levels are shown in Fig. 1. A total of 22 independent image realizations were generated for each phantom and dose level, each taken as input to the registration process, described below.

Fig. 1.

Example images of the soft-tissue model (left) and anthropomorphic head phantom (right) at various levels of dose (mAs).

B. Registration Methods and Similarity Metrics

Experiments were performed using 3 categories of registration (translation-only): (i) The first category involved intensity interpolation, which optimizes a similarity metric over θ̂ and resamples the image at each iteration under the specified interpolation model (here, cubic B-spline [30]). This was accomplished with SimpleITK [31] using 3 similarity metrics: (a) mean-square-difference (MSD), (b) Matte’s mutual information (MMI) [32] (50 bins), and (c) joint histogram mutual information (JMI) [33] (50 bins, 1.5 σ). (ii) The second category involved metric interpolation, which was computed by evaluating the maximum of a parabolic fit to the normalized cross correlation (NCC-fit) metric at the pixel-shift peak location and its surrounding 8 pixel-shift neighbors. (iii) Finally, a Fourier-based method of phase correlation (PC) [34] was evaluated. For a pair of images (generated as in Section VI-A.), registration was performed using each of these methods after introducing a known shift θ. Prior to inducing the shift, a constant intensity (equal to the mean over the image edges) was subtracted from both images to reduce the effect of zero-padding used for the image transformations.

C. Performance Evaluation

Registration performance was evaluated in terms of the root-mean-square error (RMSE) of the translation estimate θ̂. For each of the categories described above, the RMSE was compared to the two forms of lower bound derived in Section III: the CRLB (Eq. 7) and the CRLB_N̂≪G (Eq. 11). The CRLB for an unbiased estimator can be written in terms of RMSE as:

$$\mathit{RMSE}\ge \sqrt{\text{trace}(C_{LB})}=\sqrt{\text{trace}({\mathit{FIM}}^{-1})}$$ (26)

To estimate the power spectra required to calculate the CRLB, the NPS at each mAs (i.e., N_i ) was computed by averaging periodograms from a set of 20 instances of simulated noisy images with the mean image subtracted. In computing G, since we only have access to noisy images in the context of (1–2), we do not truly know g. In this work g was formed by computing the mean over 20 images simulated at 500 mAs. We then computed G using the 2D Welch periodogram method [35] using 16 windows (4 increments in each dimension) with an overlap ratio 0.5 and a Hamming window to reduce spectral leakage. While this method is suitable to image simulation, it may not be practical to acquire many instances of an image to compute g. Other methods for approximating G (not investigated in this work) include (i) computing the power spectrum from a low-noise (e.g., pre-operative) image assuming minimal noise, (ii) computing the image power spectrum and subtracting a model estimation of the NPS, or (iii) using a model estimation of the signal power spectrum (e.g., power-law model as fairly common in describing tissue parenchyma [26]–[28]). RMSE was analyzed as a function dose (proportional to mAs) and total image variance ${\sigma }_1^2+{\sigma }_2^2$ (computed by integrating N₁ + N₂).

We further evaluated each registration method in terms of the statistical registration efficiency (denoted SRE), defined as:

$$\mathit{SRE}=\frac{\text{trace}(C_{LB})}{{(\mathit{RMSE})}^2}$$ (27)

Written this way, the SRE is bounded (SRE < 1) and describes the ratio of the CRLB to the measured mean squared error performance. The SRE was evaluated as a function of dose for each category of registration and similarity metric mentioned above.

D. Registration Cases

1) Registration of Images at Equivalent Dose (Homoscedastic)

Analysis was first performed for image registration in which the noise characteristics of both images were equivalent. Each registration followed the method in section VI-B, with a known shift of θ = [1.2 pix, 1.2 pix] introduced to the moving image. 231 (i.e., 22 choose 2) registrations were performed between the 22 image realizations formed at the same dose level. 13 dose levels were considered with mAs ranging over 3 orders of magnitude (0.5 – 500 mAs).

2) Registration of a High-Dose Image to a Low-Dose Image (Heteroscedastic)

A common scenario in image-guided interventions was simulated in which a high-dose (i.e., high quality) preoperative image is registered to a low-dose (i.e., lower quality) intraoperative image. The experiment of section VI-D-1 was repeated using the MSD similarity metric, considering a fixed dose for the fixed image and varying the dose for the higher-dose moving image. Performance was evaluated in terms of RMSE as a function of the total noise magnitude in the registered images.

3) Effect of Image Blur on Registration Performance

We further examined the effect of image blur on image registration performance. Factors affecting blur [described by the image quality model leading to (21)] include the imaging system configuration (e.g., x-ray focal spot size, detector pixel size, and system geometry), reconstruction method (filter kernel), and optional post-processing and/or interpolation filters. The derivation in Section IV, leading to (18), exposed the non-trivial relationship between system blur and registration performance, suggesting an optimum tradeoff between high-frequency noise magnitude and image signal (i.e., gradient) power. To investigate the effect, the experiment of Section V-D-1 was repeated with an additional post-processing Gaussian blur kernel of width σ_b ranging from 0.5 to 7 pixels applied to both images. Results were compared to theoretical predictions for optimal Gaussian blurring using (18).

VII. Results

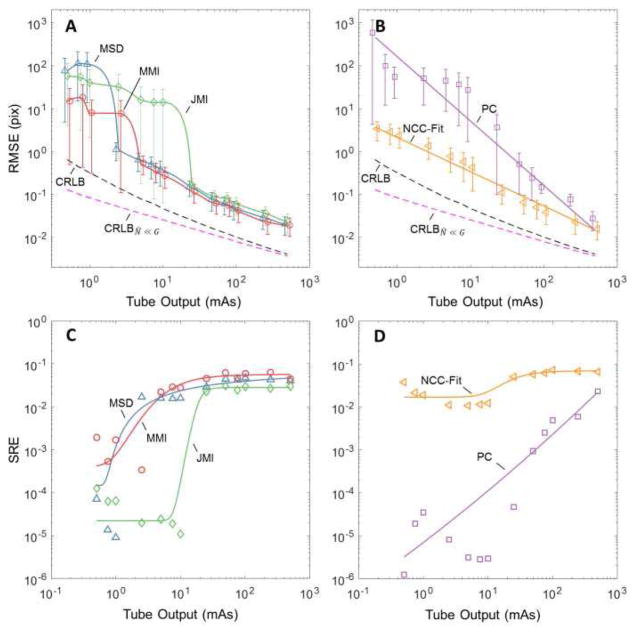
A. Registration Accuracy: Homoscedastic Images

Figure 2 shows the performance for the various categories of registration: (2A) metrics MSD, MMI, and JMI; and (2B) methods NCC-Fit and PC – each in comparison to the theoretical lower bound predicted by CRLB (Eq. 7) and CRLB_N̂≪G (Eq. 11). In Fig 2A, registration performance is seen to improve (i.e., RMSE decreases) with dose for each of the interpolation-based similarity metrics. Each metric performs equivalently at high dose, and each exhibits a low-dose threshold below which registration fails, with MSD demonstrating the strongest robustness to noise and JMI performing the worst. The threshold reflects the noise level at which point estimation errors lie outside of the main lobe of the optimization search space (causing a “failed registration”) and leading to arbitrarily large registration errors.

Fig. 2.

Effect of dose on registration performance for the “equal-dose” case (i.e., images with equivalent noise characteristics). Each case is for the soft-tissue images in Fig. 1. The dashed curves in (A) and (B) mark the lower-bound in registration accuracy predicted by the CRLB and CRLB_N̂≪G. (A) RMSE for intensity-interpolation registration using the MSD, MMI, and JMI similarity metrics. (B) RMSE for the NCC-fit and PC registration methods. (C) SRE versus dose for the MSD, MMI, and JMI metrics. (D) SRE for the NCC-fit and PC methods.

The theoretical lower bound predictions appear to be optimistic - i.e., none of the methods achieve the lower bound. However, the overall trend with dose is similar, and the estimators (MSD and MMI in particular) adhere to the trend with similar slope across the broad range of dose levels.

Figure 2B shows the same for the NCC-fit and PC registration methods. (The CRLB and CRLB_N̂≪G curves are the same as in Fig. 2A.) Interestingly, these methods do not exhibit a low-dose threshold for registration failure, instead following the general trend of the CRLB. The NCC-Fit method appears more robust against noise than PC and follows the CRLB down to the lowest dose levels investigated. This behavior is attributed in part to the brute-force sampling of NCC-Fit (thus avoiding local minima) and in part to the highly constrained search of NCC-Fit (evaluated only at pixel shifts within a fixed distance from solution), which avoids the large RMSE registration failure threshold effect. The PC registration method exhibits poorer robustness to noise (higher negative slope) and steady degradation to registration failure with reduced dose.

Figures 2C and 2D illustrate the extent to which various methods achieve the CRLB by evaluating the SRE versus dose. Figure 2C shows the SRE for the intensity-interpolation metrics (MSD, MMI, and JMI), showing that each approaches SRE ~0.04 at high dose, but efficiency falls by more than an order of magnitude at the low-dose threshold identified in Fig. 2A. Figure 2D shows that the NCC-Fit method maintains SRE over the entire range of dose investigated (again, likely attributed to the highly constrained search), whereas the PC method shows a steep degradation in SRE with reduced dose.

At high dose, each metric and method achieved SRE of only ~0.04 for the soft-tissue phantom (and ~0.11 for the anthropomorphic head, not shown for brevity). When considering this fairly low level of efficiency, it should first be noted that the CRLB is generally not guaranteed to be obtainable. Moreover, even when it is obtainable, only a selection of estimators may be able to achieve the bound, and often only asymptotically -i.e., in a manner that requires larger and larger data size to achieve the bound. Since the images used in this study were relatively small and optimal estimators were not examined [e.g., optimal filtering to minimize (18)], we do not expect the result to achieve an SRE of 1; however, we note the increased upper limit in SRE for the head phantom, as expected for a larger image.

Examining (25), we see that in the homoscedastic (equal-dose) case, registration error in the strong signal approximation is proportional to 1/sqrt(dose), which is evident in the slope of the CRLB_N̂≪G curve (Fig. 2A and 2B). For the soft-tissue image case (dominated by low-frequency signal power), the strong signal approximation appears to hold well only at high dose (i.e., low noise). For the head image (which exhibits a greater proportion of mid- and high-frequency signal power), the approximation holds within 15% of CRLB over a broader dose range – down to ~2.5 mAs. In the lower dose range, disagreement between CRLB with CRLB_N̂≪G arises due to increased influence of the N₁N₂cross-correlation noise term.

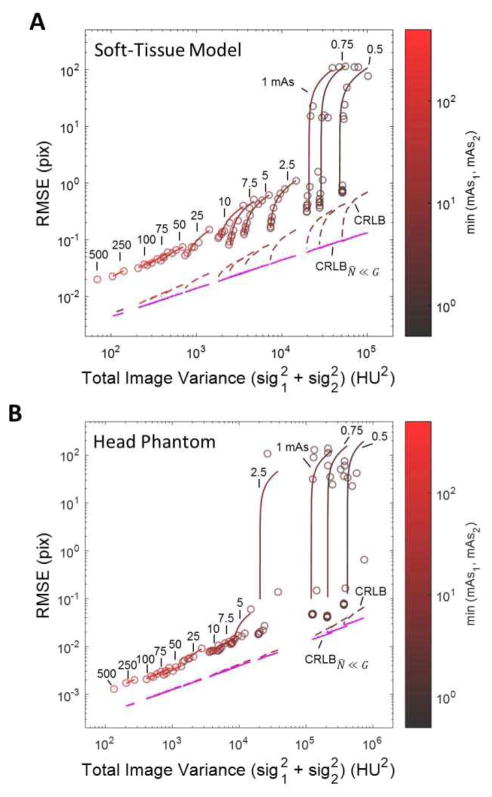
B. Registration Accuracy: Heteroscedastic Images

Figure 3 shows MSD registration performance as a function of (total) noise magnitude for the heteroscedastic case in which a low-noise (i.e., higher-dose) image is registered to a noisier (i.e., lower-dose) image. The RMSE is plotted versus total variance ( ${\sigma }_1^2+{\sigma }_2^2$) for the (A) soft-tissue and (B) head phantom images of Fig. 1. The CRLB and CRLB_N̂≪G theoretical lower limits are shown as dashed lines. The color scale on the plot symbols and curve fits refers to the mAs of the lower-dose image: for example, the lower-left of each plot shows the (red) case for which both images were formed at the maximum dose (500 mAs), whereas the upper-right of each plot shows the (black) case for which the lower-dose image was formed at just 0.5 mAs.

Fig. 3.

Registration performance (using MSD) versus total image noise for the heteroscedastic case: (A) soft tissue image and (B) head phantom image. Each circle represents the RMSE for a specific I₁,I₂ dose level combination, with connected circles of the same color indicating the same mAs for the low-dose image. The colorscale and labels denote the mAs for the lower-dose image. The CRLB (dashed) and CRLB_N̂≪G (magenta) formulations are also plotted.

Whereas Figs. 2A–B demonstrated that RMSE is proportional to 1/sqrt(dose) and thus $\text{sqrt}({\sigma }_1^2+{\sigma }_2^2)$, this simple relationship is lost in the heteroscedastic case shown in Fig. 3. In Fig. 3A, we observe a highly non-linear dependence on the total noise; however, this non-linearity is predicted very well by the CRLB. The CRLB_N̂≪G approximation, however, only describes the effect of relative dose through the (mq̄)₁ (mq̄)₂/[(mq̄)₁ + (mq̄)₂] term, appropriate only at low-noise (high-dose) conditions for the soft-tissue model.

Figure 3B shows similar trends in registration performance for the head phantom image. In this case, however, the image exhibits sufficiently large high-frequency signal power, such that N₁N₂ ≪ GN₁ + GN₂. As a result, the CRLB is roughly proportional to $\text{sqrt}({\sigma }_1^2+{\sigma }_2^2)$ and agrees with the CRLB_N̂≪G approximation over a much broader range of dose.

C. Registration Accuracy: Effect of Image Blur

Figure 4A shows the registration performance (RMSE) for the heteroscedastic soft-tissue case (as in Fig. 3A), comparing the RMSE achieved by the MSD method (which can be shown to be nearly equivalent to maximizing cross-correlation) with that predicted by (17). We immediately see that while (17) somewhat underestimates the magnitude of RMSE, it trends well with the measured dependence of registration performance on dose, yielding a correlation coefficient of R = 0.988 between the predicted and measured RMSE in the higher dose region [where the Taylor approximation in (17) is appropriate].

Fig. 4.

(A) Error in soft-tissue image registration compared to the performance predicted by Eq. (17). (B) Registration performance as a function of post-processing blur at various dose levels. The results pertain to the MSD registration method, and dose reflected in the mAs colorscale. For each curve, the magenta circle represents the predicted optimal blur level, and the blue star represents the measured optimal blur.

Figure 4B summarizes the findings of optimal post-processing blur for registration of the soft-tissue image at various dose levels. Each curve represents the RMSE (at a given dose level) as a function of blur width (σ_b). The blue star marks the measured minimum in RMSE (i.e., optimal blur), and the magenta circle marks the theoretical minimum as predicted by minimizing (18) with respect to H_b. As expected, post-processing blur is most beneficial under high-noise (low-dose) conditions (black curves). On the other hand, for low-noise (high-dose) conditions (red curves), excessive blur is seen to degrade registration performance. The measured and predicted values for optimal blur agree with this trend and match fairly well across a broad range of dose, further validating the model of (18) as a figure of merit for registration.

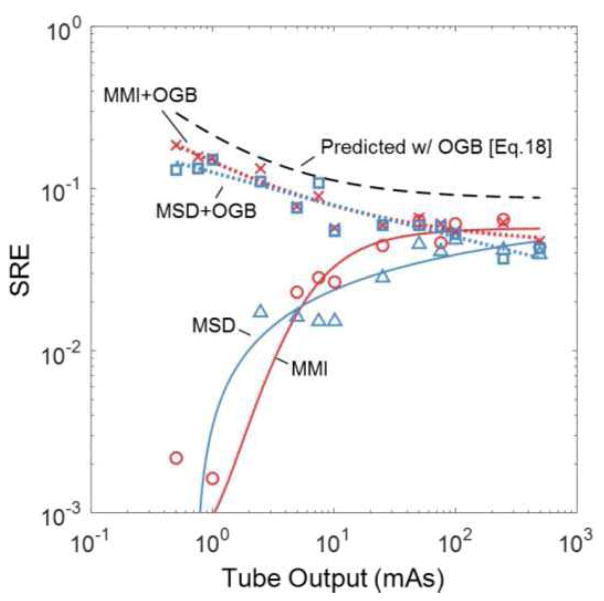
Figure 5 further investigates the predicted benefit of post-processing blur on registration performance for several similarity metrics. The data correspond to the soft-tissue image model, homoscedastic image registration, and theoretically optimal Gaussian blur (OGB) derived by minimization of (18) with respect to H_b. The SRE is plotted versus dose, and we observe that application of an optimal Gaussian blur maintains optimality (again at a level of SRE ~0.04) across the range of dose levels investigated for MMI and MSD, bearing in mind that (18) applies directly only to cross-correlation based metrics, e.g., MSD. Close inspection of Fig. 5B suggests a slight increase in SRE at the lower dose levels - a somewhat surprising result that is in agreement with the theoretical prediction. The increase in efficiency is because Gaussian blur is not a truly optimal filter as described by H_HT of (19) in minimizing (18); however, with respect to Gaussian filters, the OGB may more closely approximate H_HT under low-dose/high-noise conditions, leading to the increase in efficiency.

Fig. 5.

SRE evaluated as function of dose for MSD (blue) and MMI (red) with and without optimal Gaussian blur (OGB). The predicted SRE (with OGB) is shown as the black dashed line, demonstrating a similar dose dependence as the measurements with optimal blur.

VIII. Conclusion

To paraphrase Barrett et al. [3], an image is always acquired for a particular task, and evaluation of imaging system performance should be with respect to that task. For many scenarios in image-guided interventions, the task may relate to registration of image information more so than to visualization. The framework described above provides a means by which to evaluate an imaging system with respect to registration performance, providing a basis for assessing the performance of various registration methods and selecting optimal image acquisition and reconstruction techniques.

As a first step in establishing this framework, we presented theoretical lower bounds for registration performance and investigated several sub-pixel estimators as a function of dose and noise magnitude. Following this analysis, we examined the registration method of maximizing cross-correlation to analyze the effect of spatial resolution on registration performance, thereby deriving an RMSE figure of merit, (18). The model was shown to agree well with measurements of registration accuracy for various choices of post-processing linear filters (blur), providing understanding beyond the basic information-theoretic data processing effect (in which linear filters have no effect on SNR) and guiding selection of optimal filters that extend registration performance to lower dose levels.

In the derivation of the F IM, we assumed stationary Gaussian characteristics of the signal and noise. As discussed in [36], the Gaussian assumption is not a particularly strong requirement, since (by the Central Limit Theorem) even when the signal is not Gaussian the Fourier coefficients of the signal will tend toward a Gaussian distribution as the number of image samples increases. Nonetheless, further investigation is warranted to more fully account for nonstationary MT F and NPS characteristics in CT images [37] as well as non-Gaussian characteristics. However, in line with similar approximations for analysis of detectability index [3], we see in Section VII-B that despite the approximation the F IM proves a useful predictor of performance trends, even in the case of a high-contrast (head) image that exhibits highly non-Gaussian, non-stationary characteristics.

The current work examined the simple case of 2D translation-only registration. Extension of the formulation to 3D translation is straightforward, as shown in Appendix A. In future work, we will extend the analysis to include translation and rotation, providing a more general framework for analysis of rigid registration. Further, because image quality models (such as [21] and [11]) permit analysis of the spatially varying (i.e., nonstationary) local MT F and NPS, the analysis shown above can be similarly extended to description of local registration accuracy in regions differing in image quality. Using these local approximations to extend the analysis to deformable image registration is an exciting possibility, though beyond the current scope of investigation.

Throughout this work is the assumption that the registration method is unbiased (intrinsic to C_LB = F IM⁻¹). This assumption breaks down at least in part for the NCC-fit registration method [16] due to the parabolic fit and has yet to be rigorously investigated for the other optimization methods. While it is likely that there are small biases in the other methods as well (owing to choice of interpolation, optimizer, etc.), the assumption of unbiased estimators appears to be reasonable, as the observed RMSE was dominated by the variance term (rather than the bias), and the experiments demonstrated similar trends as the CRLB (whereas a plateau effect would likely be observed in the low-noise region for a system dominated by bias).

The F IM provides a framework that is independent of the particular registration method - whether biased or unbiased. We extended previous work in CRLB estimation in such problems by generalizing to 2D and 3D, allowing for disparate noise in the I₁ and I₂images, and including image blur as well as noise correlation, demonstrating results beyond a simple approach of AWGN (which is a poor approximation to noise in CT / CBCT). The resulting analytical framework leverages well-established models describing image quality in CT/CBCT [13]–[15] as in (23) and is consistent with the theme of task-based imaging performance. With respect to image-guided interventions, the analysis provides a new framework for understanding the performance of imaging systems with respect to the task of image registration.

Appendix A

In this appendix, we derive the CRLB for image registration. We present a derivation that extends work from 1D TDE to the scenario of 2D and 3D image registration, and thus is similar in concept to derivations presented for TDE in [22]–[24]. Here we allow the two images to exhibit disparate noise levels as well as noise correlation. Taking the 2D case, we seek to determine θ = [u, υ] for the following scenario:

$$I_1[x,y]=g(x,y)+n_1(x,y)$$ (A1)

$$I_2[x,y]=g(x-u,y-\upsilon )+n_2(x,y)$$ (A2)

where g is the true image function and the n_i are additive noise terms. Due to the presence of correlated noise terms in both images, we lose the simple form for the likelihood function presented in [20], causing the spatial domain analysis to become less tractable. A Fourier representation, however, facilitates the analysis. We take Z₁ [f_x, f_y], Z₂ [f_x, f_y] as the 2D Fourier transforms (F·}) of I₁, I₂, where for purposes of the proof we break from the convention of the (·) notation for continuous Fourier domain functions to directly represent the discrete Fourier transform of the image. We first note that for a signal bandlimited below f_Nyq (i.e., no aliasing), Z₁ comprises the sampled frequency representation of the signal and noise so that:

$$Z_1[f_x,f_y]=\mathcal{F}\{g(x,y)\}(f_x,f_y)+\mathcal{F}\{n_1(x,y)\}(f_x,f_y)$$ (A3)

and by the shift property we have:

$$Z_2[f_x,f_y]=e^{-j2\pi (f_{x}u+f_y\upsilon )}\mathcal{F}\{g(x,y)\}\left(f_x,f_y\right)+\mathcal{F}\{n_2(x,y)\}(f_x,f_y)$$ (A4)

$$\begin{gathered} K_{mn}=E\{X_{mn}{X}_{mn}^{\ast }\mathit{\theta }\}\text{where}{X}_{mn}=\left[\begin{array}{c}{Z}_1\left[f_x^{(m)},f_y^{(n)}\right]\\ Z_2\left[f_x^{(m)},f_y^{(n)}\right]\end{array}\right] \\ =\left[\begin{array}{ll}G\left[f_x^{(m)},f_y^{(n)}\right]+N_1\left[f_x^{(m)},f_y^{(n)}\right]\hfill & G\left[f_x^{(m)},f_y^{(n)}\right]e^{-j2\pi (f_x^{(m)}u+f_y^{(n)}\upsilon )}\hfill \\ G\left[f_x^{(m)},f_y^{(n)}\right]e^{j2\pi (f_x^{(m)}u+f_y^{(n)}\upsilon )}\hfill & G\left[f_x^{(m)},f_y^{(n)}\right]+N_2\left[f_x^{(m)},f_y^{(n)}\right]\hfill \end{array}\right] \end{gathered}$$ (A5)

If we examine a particular frequency $f_x^{(m)},f_y^{(n)}$ (where m, n refer to the indexed frequency samples) we see that the covariance of $Z_1\left[f_x^{(m)},f_y^{(n)}\right],Z_2\left[f_x^{(m)},f_y^{(n)}\right]$ is (A5), as shown at the bottom of this page, where G and N_i are the power spectra of g and n_i, respectively, and ^* denotes the complex conjugate transpose. With this in mind we wish to represent the entirety of the data in a single vector. Therefore we concatenate Z₁ and Z₂ into the vector X in a manner that the corresponding frequencies in Z₁ and Z₂ are adjacent to each other:

$$\mathbf{X}=[Z_1\left[f_x^{(1)},f_y^{(1)}\right],Z_2\left[f_x^{(1)},f_y^{(1)}\right],\dots Z_1\left[f_x^{(M)},f_y^{(1)}\right],Z_2\left[f_x^{(M)},f_y^{(1)}\right],Z_1\left[f_x^{(1)},f_y^{(2)}\right],Z_2\left[f_x^{(1)},f_y^{(2)}\right],\dots Z_1\left[f_x^{(M)},f_y^{(N)}\right],Z_2{\left[f_x^{(M)},f_y^{(N)}\right]]}^t$$ (A6)

where $f_x^{(i)},f_y^{(i)}$ are the indexed frequency samples ∈ [–f_Nyq, f_Nyq ]. Under the assumption of stationary signal and noise, the frequency components of Z_i are statistically independent [38], and the covariance matrix of X has a block diagonal form:

$$K=E\{{\mathit{XX}}^{\ast }\mathit{\theta }\}=\left[\begin{array}{cccccc}{K}_{11}& & & & & \\ & \ddots & & & \mathbf{0}& \\ & & K_{M1}& & & \\ & & & K_{12}& & \\ & \mathbf{0}& & & \ddots & \\ & & & & & K_{MN}\end{array}\right]$$ (A7)

where the block-diagonal components are described in (A5). By assuming both the image function and noise to be zero-mean Gaussian processes, the frequency components of the Fourier representation are also jointly Gaussian, and the likelihood function for X can be written:

$$L(\mathbf{X}\mid \mathit{\theta })=\frac{1}{det(\pi K)}exp(-{\mathbf{X}}^{\ast }{K}^{-1}\mathbf{X})$$ (A8)

As shown in [22], the F IM for this complex Gaussian likelihood function can be reduced to:

$${[\mathit{FIM}]}_{ij}=\text{Tr}\left[\left(K^{-1}\frac{\partial K}{\partial {\theta }_i}\right)\left(K^{-1}\frac{\partial K}{\partial {\theta }_j}\right)\right]$$ (A9)

$$\begin{gathered} {[\mathit{FIM}]}_{ij}=\frac{1}{2}\sum _{m,n}\text{Tr}\left[\left(K_{mn}^{-1}\frac{\partial K_{mn}}{\partial {\theta }_i}\right)\left(K_{mn}^{-1}\frac{\partial K_{mn}}{\partial {\theta }_j}\right)\right] \\ =\frac{1}{2}\sum _{m,n}\frac{2{(2\pi )}^2{f}_i^{(m)}{f}_j^{(n)}{G}^2\left[f_x^{(m)},f_y^{(n)}\right]}{G\left[f_x^{(m)},f_y^{(n)}\right]N_1\left[f_x^{(m)},f_y^{(n)}\right]+G\left[f_x^{(m)},f_y^{(n)}\right]N_2\left[f_x^{(m)},f_y^{(n)}\right]+N_2\left[f_x^{(m)},f_y^{(n)}\right]N_1\left[f_x^{(m)},f_y^{(n)}\right]} \end{gathered}$$ (A10)

$${\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}\frac{f_i{f}_j{G}^2(f_x,f_y)d{f}_{x}d{f}_y}{G(f_x,f_y)N_1(f_x,f_y)+G(f_x,f_y)N_2(f_x,f_y)+N_1(f_x,f_y)N_2(f_x,f_y)}$$ (A11)

Combining (A5), (A7), and (A9) gives the 2 × 2 F IM:

where we have denoted f₁ = f_x and f₂ = f_y in reference to $f_i^{(m)},f_j^{(n)}$ when computing [F IM]_{i j}, and the 1/2 term prior to the sum is included to compensate for symmetry in the Fourier domain (thus over-representing the information by a factor of 2). Given sufficiently high sampling density, we may approximate the summation as an integral to write (A10), shown at the top of this page as:

$$\mathit{FIM}={(2\pi )}^{2}A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right],$$

where (A11) is shown at the top of this page, where A is the image area. To simplify notation, we remove explicit (f_x, f_y) dependence:

$$\mathit{FIM}={(2\pi )}^{2}A\left[\begin{array}{cc}{\gamma }_{xx}& {\gamma }_{xy}\\ {\gamma }_{xy}& {\gamma }_{yy}\end{array}\right],$$

where

$${\gamma }_{ij}=\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}\frac{f_i{f}_j{G}^2}{G{N}_1+G{N}_2+N_1{N}_2}d{f}_{x}d{f}_y$$ (A12)

Extension to a pair of 3D images is straightforward, giving:

$$\mathit{FIM}={(2\pi )}^{2}V\left[\begin{array}{ccc}{\gamma }_{xx}& {\gamma }_{xy}& {\gamma }_{xz}\\ {\gamma }_{xy}& {\gamma }_{yy}& {\gamma }_{yz}\\ {\gamma }_{xz}& {\gamma }_{yz}& {\gamma }_{zz}\end{array}\right],$$

where

$${\gamma }_{ij}=\int \int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}\frac{f_i{f}_j{G}^2}{G{N}_1+G{N}_2+N_1{N}_2}d{f}_{x}d{f}_{y}d{f}_z$$ (A13)

where V is the image volume.

Appendix B

This appendix expands the derivation of (16) and (17) for the RMSE estimate of the cross-correlator, expanding a result for 1D TDE shown in [25]. We begin by simplifying (16) by assuming r_τφ (u, υ) to be small in comparison to the diagonal terms, giving:

$$\left(\widehat{u}-u\right)\approx r_{\tau }(u,\upsilon )/r_{\tau \tau }(u,\upsilon )$$ (B1)

$$\left(\widehat{\upsilon }-\upsilon \right)\approx r_{\phi }(u,\upsilon )/r_{\phi \phi }(u,\upsilon )$$ (B2)

By the associative property of cross correlation:

$$\begin{gathered} r(u,\upsilon )=\left(I_1\otimes I_2\right)(u,\upsilon ) \\ =\left(g\otimes g\right)(0,0)+(g\otimes n_2)(u,\upsilon )+(n_1\otimes g)(0,0)+(n_1\otimes n_2)(u,\upsilon ) \end{gathered}$$ (B3)

and without loss of generality:

$$r(u,\upsilon )=\left(g\otimes g\right)(0,0)+\left(g\otimes n_2\right)(0,0)++\left(n_1\otimes g\right)(0,0)+(n_1\otimes n_2)(0,0)$$

where the second equality carries the discretization of g and n_i in forming I_i as well as the implicit [u, υ] shift of g in I₂ so that g ⊗ g and n₁ ⊗ g are evaluated at (0, 0). Further, this equality neglects interpolation and assumes an un-aliased signal. The third equality, which does not affect the result (as the expectation is unaffected), is introduced for notational convenience. From examination of (B3), we note that the numerators of (B1) and (B2) have expected value equal to zero. Further, by definition ∂(g ⊗ g)/∂θ_i (0, 0) = 0. Therefore, near solution the numerator will be dominated by the remaining terms in the derivative of (B3). On the other hand, the expectation of the denominator is non-zero and depends only on the signal term, indicating that near solution the denominator is dominated by the signal term alone. Therefore, we have (B1) to first-order approximation:

$$\begin{gathered} \left(\widehat{u}-u\right)\approx \frac{\frac{\partial }{\partial \tau }\left(g\otimes n_2+n_1\otimes g+n_1\otimes n_2\right)(0,0)}{\frac{{\partial }^2(g\otimes g)}{\partial {\tau }^2}(0,0)} \\ =\frac{{\displaystyle \sum _{m.n}}\left(j2\pi f_x^{(m)}\right)(F_g{\overline{F}}_{n_2}+F_{n_1}{\overline{F}}_g+F_{n_1}{\overline{F}}_{n_2})}{{\displaystyle \sum _{m,n}}{\left(j2\pi f_x^{(m)}\right)}^2{F}_g{\overline{F}}_g} \end{gathered}$$ (B4)

with the second equality following from the Fourier derivative property and Parseval’s Theorem, where $F_g\left[f_x^{(m)},f_y^{(n)}\right]$ denotes the Fourier coefficients of the discretized g (similarly for F_ni) where $f_x^{(m)},f_y^{(n)}$ are the indexed frequency samples ∈ [–f_Nyq, f_Nyq ], and the hat denotes complex conjugation. Explicit notation of the frequency dependence on the F_i terms is excluded for notational convenience in (B4) and the equations below. As the expectation of the error is zero, we need only to examine the variance:

$$\text{Var}\left(\widehat{u}\right)\approx \frac{\text{Var}\left({\displaystyle \sum _{m.n}}\left(j{f}_x^{(m)}\right)(F_g{\overline{F}}_{n_2}+F_{n_1}{\overline{F}}_g+F_{n_1}{\overline{F}}_{n_2})\right)}{{(2\pi )}^2{\left[{\displaystyle \sum _{m,n}}{\left(f_x^{(m)}\right)}^2{F}_g{\overline{F}}_g\right]}^2}$$ (B5)

From the assumption of stationarity, the frequency components of the Fourier terms in the numerator are independent [38], leaving only the sum over the variance terms.

$$\text{Var}\left(\widehat{u}\right)\approx \frac{{\displaystyle \sum _{m,n}}{\left(f_x^{(m)}\right)}^{2}E\{(F_g{\overline{F}}_{n_2}+F_{n_1}{\overline{F}}_g+F_{n_1}{\overline{F}}_{n_2})({\overline{F}}_g{F}_{n_2}+{\overline{F}}_{n_1}{F}_g+{\overline{F}}_{n_1}{F}_{n_2})\}}{{(2\pi )}^2{\left[{\displaystyle \sum _{m,n}}{\left(f_x^{(m)}\right)}^2{F}_g{\overline{F}}_g\right]}^2}$$ (B6)

In expectation, only the associated power spectra terms remain non-zero giving:

$$\text{Var}\left(\widehat{u}\right)\approx \frac{{\displaystyle \sum _{m,n}}{\left(f_x^{(m)}\right)}^2(G{N}_1+G{N}_2+N_1{N}_2)}{{(2\pi )}^2{\left[{\displaystyle \sum _{m,n}}{\left(f_x^{(m)}\right)}^{2}G\right]}^2}$$ (B7)

where $G\left[f_x^{(m)},f_y^{(n)}\right]$ and $N_i\left[f_x^{(m)},f_y^{(n)}\right]$ are the signal and noise-power spectra, respectively. By analogous derivation for Var (υ̂), and approximating the sum as an integral, the RMSE is then:

$$\begin{gathered} \mathit{RMSE}\approx \sqrt{1/{\rho }_x+1/{\rho }_y},\text{where} \\ {\rho }_i=\frac{{(2\pi )}^{2}A{\left[\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i^2{\mathit{Gdf}}_{x}d{f}_y\right]}^2}{\int {\int }_{-f_{\mathit{Nyq}}}^{f_{\mathit{Nyq}}}{f}_i^2(G{N}_1+G{N}_2+N_1{N}_2)d{f}_{x}d{f}_y} \end{gathered}$$ (B8)

and A is the image area.