Large-Scale Granger Causality Analysis on Resting-State Functional MRI

Abstract

We demonstrate an approach to measure the information flow between each pair of time series in resting-state functional MRI (fMRI) data of the human brain and subsequently recover its underlying network structure. By integrating dimensionality reduction into predictive time series modeling, large-scale Granger Causality (lsGC) analysis method can reveal directed information flow suggestive of causal influence at an individual voxel level, unlike other multivariate approaches. This method quantifies the influence each voxel time series has on every other voxel time series in a multivariate sense and hence contains information about the underlying dynamics of the whole system, which can be used to reveal functionally connected networks within the brain. To identify such networks, we perform non-metric network clustering, such as accomplished by the Louvain method. We demonstrate the effectiveness of our approach to recover the motor and visual cortex from resting state human brain fMRI data and compare it with the network recovered from a visuomotor stimulation experiment, where the similarity is measured by the Dice Coefficient (DC). The best DC obtained was 0.59 implying a strong agreement between the two networks. In addition, we thoroughly study the effect of dimensionality reduction in lsGC analysis on network recovery. We conclude that our approach is capable of detecting causal influence between time series in a multivariate sense, which can be used to segment functionally connected networks in the resting-state fMRI.

1. INTRODUCTION

The development in our understanding of complex systems has directly influenced studies analyzing connectivity between different regions in the brain [1]. Of particular interest is the quantification of causal influence that different regions exert on one another. Methods such as Dynamic Causal Modelling (DCM) [2] and Structural Equation Modelling (SEM) [3] demonstrate how such interactions can be estimated. One common shortcoming of these methods is that they are unable to obtain a causality score between every pair of voxel time series in the brain, i.e., the common situation that the number of time series by far exceeds the number of temporal acquisitions. Instead, such methods are limited to the analysis of a small number of pre-selected regions. This is because the above methods encounter problems of underdetermined systems or exponential growth of models to be tested, if influence scores at a voxel level should be obtained. We demonstrate the use of large-scale Granger Causality (lsGC) [4] to investigate causal influence at a voxel resolution scale in resting-state fMRI, and we illustrate how this information can be used to extract underlying brain network structures using non-metric clustering approaches. This work is embedded in our group’s endeavor to expedite ‘big data’ analysis in biomedical imaging by means of advanced machine learning and pattern recognition methods for computational radiology and radiomics, e.g. [5–29].

Our lsGC analysis method overcomes the problem of an underdetermined system by first incorporating a dimensionality reduction step retaining high variance principal components, followed by modelling the system using Vector Auto-Regression (VAR) [31]. As Principal Component Analysis (PCA) [32] is a linear dimension reduction scheme, we can back-project the prediction errors – obtained from VAR modelling – into the original high-dimensional space of voxel time series and thus calculate Granger Causality (GC) indices at a voxel resolution scale. This measure of influence likely contains information about underlying information transfer between functionally connected times series in the brain. This influence flow is conditioned on the information present in all the time series by taking the first few high variance components and performing a multivariate analysis [33], leading to a lsGC index between every pair of voxel time series. Thus, we can represent the human brain as a directed graph with voxels being the nodes and the influence score (lsGC index) being the edge weights. We extract the underlying network structure from the indices by performing graph-theoretical approaches for community detection, such as non-metric clustering by the Louvain method [34]. The resulting network, obtained from the resting-state fMRI time series is compared with the network obtained from the task stimulation sequence using the Dice Coefficient (DC) [35]. We also investigate the effect of the number of retained principal components on the robustness of network recovery.

2. DATA

An MRI data set from a healthy male, aged 52 years, was obtained at the Rochester Center for Brain Imaging (Rochester, NY, USA). The scan was acquired using a 3.0 Tesla, Siemens Magnetom TrioTim scanner, using the fMRI scan parameters echo time (TE) = 23 milliseconds, repetition time (TR) = 1650 milliseconds, 96 × 96 acquisition matrix, flip angle of 84°. Two sequences of images were obtained: 1) Resting-state acquisition, where the subject was asked to lie down still with his eyes closed, while 250 volumes under resting state were obtained. 2) Visuomotor stimulation, where the subject had to perform a finger tapping task in the presence of an alternating visual stimulus, where 110 volumes were acquired. The task sequence was used to aid in localizing the motor and visual cortex of the subject. The study protocol also included high resolution structural imaging using a T1-weighted Magnetization-Prepared Rapid Gradient Echo (MP-RAGE) sequence (TE = 3.44 ms, TR= 2530 ms, isotropic voxel size of 1mm, flip angle = 7°). The scanned individual had given written consent as per protocol approved by the IRB.

3. METHODS

3.1 Pre-processing

The effects of initial saturation were eliminated by removing the first 10 volumes of the acquisition. The volumes were then motion-corrected and the brain was extracted. To remove effects of signal drifts, linear detrending was performed by high pass filtering (0.01 Hz). Subsequently, the slices were registered to the standard MNI152 template [36]. In addition, the ventricle mask based on the standard MNI152 template was used to eliminate time series in the corresponding regions. Finally, the time series were normalized to zero mean and unit standard deviation to focus on signal dynamics rather than amplitude [37]. The motor task sequences were further processed using the standard (FEAT) [38] boxcar design in order to test, where the BOLD signal correlated with the stimulation. The z-statistic images obtained were thresholded at z>4 with a corrected cluster significance threshold of p<0.01. This results in a map of regions corresponding to the visual and motor cortex for each individual, referred to as ‘localization aid’ in this study.

3.2 Large-scale Granger causality

We use large-scale Granger Causality [4] to obtain a casual influence score between every pair of voxel time series in the resting state human brain. Large-scale Granger Causality works on the principle of Granger Causality, which obtains the casual influence of time series x_r on time series x_s by quantifying the improvement in prediction of x_s in the presence of x_r. Large-scale Granger Causality obtains an influence score between every pair of voxels in a multivariate sense. The limitation with using a multivariate approach to Granger Causality, without incorporating dimensionality reduction, on large systems like the brain, is that the prediction model cannot estimate model parameters as the system is undetermined. We show how using lsGC approach, this problem can be overcome.

Consider the ensemble of time series X $\in {ℝ}^{N\times T}$, where N is the number of time series and T the number of temporal samples. Let X = (x₁, x₂, x₃, …, x_N)^T be the whole multidimensional system, x_n $\in {ℝ}^{1\times T}$ a single time series with n ∈ {1,2, …, N}, where x_n = (x_n(1), x_n(2), …, x_n(T)). lsGC obtains a multivariate GC score by first decomposing X into its first p high-variance principal components Z $\in {ℝ}^{p\times T}$using Principal Component Analysis (PCA), i.e.,

$$\mathbf{Z}=\mathbf{WX}$$

Following this, we model Z using Vector Auto-Regressive (VAR) modelling of order m and compute the estimate $\widehat{\mathbf{Z}}$ by using the m auto-regression ${ℝ}^{p\times p}$ parameter matrices obtained from VAR modelling of Z. To obtain the influence of time series x_r on all other time series, we remove the information of x_r from the transformation matrix W, obtain ${\mathbf{Z}}_{\backslash \left\{{\mathbf{x}}_r\right\}}$ and model ${\widehat{\mathbf{Z}}}_{\backslash \left\{{\mathbf{x}}_r\right\}}$ as its VAR estimate. In this manner, lsGC obtains a causality score between every pair of time series in a multivariate sense.

The errors of the two estimates are projected into the original high-dimensional space using the respective inverse PCA transformation. After the errors are obtained, we quantify the prediction quality by comparing the variance of the prediction errors obtained with and without consideration of x_r. If the variance of the prediction error of a given time series, say x_s, decreases with using x_r, then we say that x_r Granger-causes x_s [4].

$$f_{{\mathbf{x}}_r\to {\mathbf{x}}_s}=\text{ ln }\frac{\text{var}\left({\mathbf{e}}_{s,\backslash \left\{{\mathbf{x}}_r\right\}}\right)}{\text{var}\left({\mathbf{e}}_s\right)}$$

$f_{{\mathbf{x}}_r\to {\mathbf{x}}_s}$ is the GC index for the influence of x_r on x_s, which is stored in the affinity matrix A at position (A)_sr. ${\mathbf{e}}_{s,\backslash \left\{{\mathbf{x}}_r\right\}}$ is the error in predicting x_s, when x_r was not considered, and ${\mathbf{e}}_{s }$is the error when x_r was used.

3.3 Non-metric clustering

The affinity matrix A, whose coefficients are the large-scale Granger causality indices, can be represented as a network graph, from which the underlying network structure can be extracted using non-metric clustering approaches, such as the Louvain method [34]. Functionally connected regions within the brain can be extracted using this information. This method optimizes the modularity of a network by dividing the network into modules that have strong intra-module and weak inter-module connections.

The underlying network structure information present in the affinity matrix A, can be extracted using Louvain method which finds high modularity communities in the network. Modularity, which is a measure of the strength of the intra-module links as compared to the inter-modules links, can be used to decompose a complex network into clusters (or modules).

Modularity is given by:

$$\mathrm{Q}=\frac{1}{2m}{\sum }_{i,j}\left[{\mathbf{A}}_{\mathbf{i}\mathbf{j}}-\frac{k_i{k}_j}{2m}\right]\delta \left(C_i,C_j\right)$$ (4)

Where A_ij is the coefficient that represents the large-scale Granger causality score from nodes i to j, $k_i={\sum }_j{\mathbf{A}}_{\mathbf{i}\mathbf{j}}$ is called the strength of connections to node i, i belongs to community C_i, δ(a,b) = 1 when a = b, and 0 otherwise, and $m=\frac{1}{2}{\sum }_{ij}{\mathbf{A}}_{\mathbf{i}\mathbf{j}}$.

Optimization of modularity, Q, is carried out in an iterative process as proposed in [34]. This approach merges different nodes of the network into larger modules (communities) for a positive change in modularity. The merging terminates when further addition of nodes to communities decreases the modularity of the network. For fMRI data, the modules resulting after performing non-metric clustering correspond to different functionally connected regions in the resting human brain. The similarity between the motor and visual cortex clustering results and the localization aid obtained from the task sequence was evaluated using the Dice coefficient [35].

All preprocessing steps were carried out using the FMRI Expert Analysis Tool (FEAT) in FSL [38]. The time series analysis procedures were implemented using MATLAB (MathWorks Inc., Natick, MA, 2013). The Louvain method implementation was taken from [39].

4. RESULTS

4.1 Influence of number of principal components used on the Dice coefficient

Figure 1 shows the effect of changing the number of principal components used in obtaining the lsGC coefficients on the network recovery — quantified by the Dice Coefficient (DC). We observe that the DC increases initially with increasing number of principal components, until it reaches a maximum, and decreases subsequently. The initial rise in DC can be accounted to the fact that as the retained number of principal components increases, the amount of variability of the retained information on the data increases and hence the system is better represented with more number of principal components, where the explained variance is the measure of the retained variability of system. However, increasing the number of principal components further decreases the DC. This happens because the quality of the VAR parameter estimation is limited by the length of the time series, and hence, although the system is better represented with more principal components, we do not achieve good network recovery.

Figure 1.

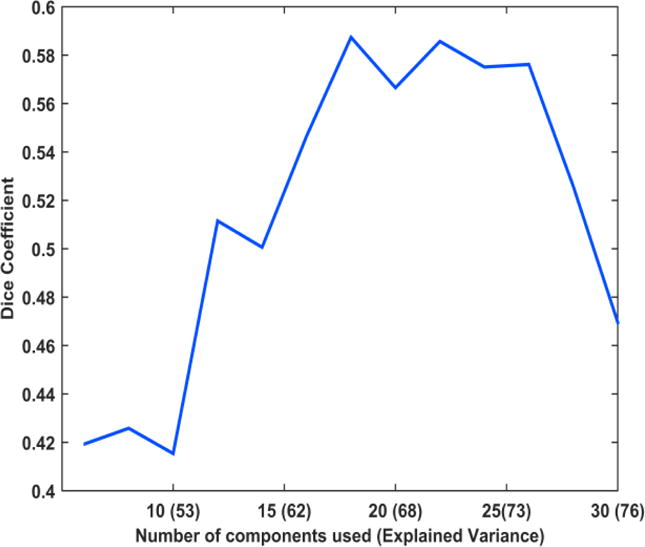
Plot showing the variation in Dice coefficient as the number of principal components (explained variance) is increased. It can be noted that the dice coefficient initially increases, reaches a peak and subsequently decreases.

4.2 Network Recovery

We compare the best network recovered using the resting-state sequence with the localization aid in Figure 2. We coarsened the resolution of the whole brain data set by averaging the signal intensity information of three adjacent voxels, where a new voxel encompasses 3×3×3 original voxels. The total number of time series in the coarsened data set was 6584. The best network recovery was achieved, when 18 principal components were retained (DC = 0.59). As clearly seen in Figure 2, there is a strong visually perceivable agreement of the two networks, i.e., the task-based localization aid and the recovered visual and motor network.

Figure 2.

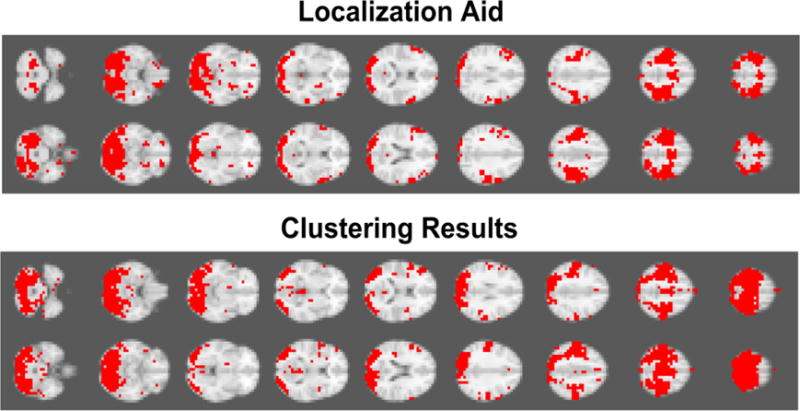
Visual Comparison between clustering results based on large-scale Granger Causality (lsGC) analysis and the localization aid for motor and visual cortices identified by a task-stimulation fMRI experiment. Dice coefficient achieved was 0.59. Recovery of the motor cortex and the visual cortex can be clearly observed.

5. NEW AND BREAKTHROUGH WORK

We demonstrate the use of large-scale Granger Causality (lsGC) to first obtain a directed multivariate Granger causality coefficient for every pair of voxel time series in the brain from resting-state fMRI data. Subsequently, we recover functionally connected networks in the brain by a community detection approach using non-metric clustering. Note that such a whole-brain multivariate connectivity analysis is not feasible using other current approaches. For example, to perform exhaustive multivariate GC analysis for every pair of voxel time series within the brain is not feasible due to the limited number of temporal fMRI acquisitions, resulting in an underdetermined problem for VAR parameter estimation. Alternatively, one would first have to pre-select a much smaller number of brain regions and obtain influence scores within such a markedly simplified network only. In contrast, the work presented here is the first approach to introduce a method to successfully evaluate multivariate effective connectivity at a voxel resolution scale for whole-brain functional MRI data.

6. CONCLUSION

We present the applicability of our approach, called large-scale Granger Causality (lsGC) analysis, to recover functionally connected networks in whole-brain human resting-state fMRI data. This analysis reveals important information about brain connectivity by quantifying the directed causal influence of every voxel time series on every other voxel time series in a multivariate sense. Using this information, we obtain functionally connected networks by performing a non-metric clustering approach, using the Louvain method. We observe a strong agreement of the visual and motor cortex networks and the localization aid provided by a task-stimulation fMRI experiment. The successful recovery of functionally connected networks demonstrates the applicability of lsGC to explore whole-brain network connectivity in human resting-state fMRI data.

This work is not being and has not been submitted for publication or presentation elsewhere.