Investigating Changes in Brain Network Properties in HIV-Associated Neurocognitive Disease (HAND) using Mutual Connectivity Analysis (MCA)

Abstract

About 50% of subjects infected with HIV present deficits in cognitive domains, which are known collectively as HIV associated neurocognitive disorder (HAND). The underlying synaptodendritic damage can be captured using resting state functional MRI, as has been demonstrated by a few earlier studies. Such damage may induce topological changes of brain connectivity networks. We test this hypothesis by capturing the functional interdependence of 90 brain network nodes using a Mutual Connectivity Analysis (MCA) framework with non-linear time series modeling based on Generalized Radial Basis function (GRBF) neural networks. The network nodes are selected based on the regions defined in the Automated Anatomic Labeling (AAL) atlas. Each node is represented by the average time series of the voxels of that region. The resulting networks are then characterized using graph-theoretic measures that quantify various network topology properties at a global as well as at a local level. We tested for differences in these properties in network graphs obtained for 10 subjects (6 male and 4 female, 5 HIV+ and 5 HIV−). Global network properties captured some differences between these subject cohorts, though significant differences were seen only with the clustering coefficient measure. Local network properties, such as local efficiency and the degree of connections, captured significant differences in regions of the frontal lobe, precentral and cingulate cortex amongst a few others. These results suggest that our method can be used to effectively capture differences occurring in brain network connectivity properties revealed by resting-state functional MRI in neurological disease states, such as HAND.

1. INTRODUCTION

The Human Immunodeficiency Virus (HIV) has been shown to invade the brain causing irreversible damage to synaptic connections, which can gradually lead to neuronal dysfunction. Such changes are reflected in the cognitive performance of HIV-infected individuals, which can be assessed using neuropsychological performance tests, however such tests are often inconclusive or cannot be administered easily. Newer methods in functional MRI (fMRI) analysis provide interesting insights into detecting global and local functional changes in the brain network performance, which may indirectly lead to a better understanding of the underlying pathophysiology of the disease. Specific brain regions belonging to extended resting state networks have been shown to exhibit altered connectivity patterns in HIV-infected subjects with cognitive impairment [1,2]. However, more work is needed to develop a better understanding of the pathophysiology of infection, to detect related early degenerative changes, and to develop imaging biomarkers for disease progression and therapy management in HIV-related cognitive impairment.

We present a global and a regional brain network analysis using our novel Mutual Connectivity Analysis (MCA) [3] framework to acquire brain network graphs. We hypothesize that this approach may be better suited to capturing changes in connectivity patterns better than conventionally used linear cross-correlation methods, because it enables a non-linear analysis that also avoids a priori assumptions on the underlying connection patterns frequently implied by model-based approaches, such as Dynamic Causal Modeling (DCM) [4] or Structural Equation Modeling (SEM) [5]. The connecitivty profiles obtained by MCA capture information regarding the interactions between the different brain network nodes. A wide range of literature in neuroscience has analyzed brain networks from the perspective of graph theory, using which such profiles can be quantitatively analyzed using a wide range of simple yet ‘neuro-biologically’ meaningful graph-theoretic measures [6,7]. This work is embedded in our group’s endeavor to expedite ‘big data’ analysis in biomedical imaging by means of advanced pattern recognition and machine learning methods for computational radiology and radiomics, e.g. [17–41].

In this study, we have considered some of these measures while focusing on a few metrics characterizing global properties, as well as measures that can provide local/regional information from the graphs. We evaluate these measures regarding their ability to identify differences between the two subject groups with the aim of better quantifying neurological damage in HIV infection.

2. DATA

Functional MRI scans from 5 healthy controls and 5 HIV+ subjects, aged 32–53 years, 4 females and 6 males, were acquired using a 3.0 Tesla Siemens Magnetom TrioTim scanner at the Rochester Center for Brain Imaging (Rochester, NY, US). A resting state sequence, where the subject stayed still with their eyes closed, was acquired. The following parameters were used — TR = 1650 ms, TE = 23 ms, 96 × 96 (2.5 mm × 2.5 mm) acquisition matrix, flip angle = 84°. Acquisition lasted 6 minutes and 40 seconds, during which 250 volumes from 25 slices, separated at 5 mm, were acquired. Additional high-resolution structural imaging was performed using a T1-weighted magnetization-prepared rapid gradient echo sequence (MPRAGE; TE = 3.44 ms, TR = 2530 ms, isotropic voxel size = 1mm, flip angle = 7°). The latter was used for registration of the functional MRI data to the standard MNI152 template [11].

3. METHODS

3.1 Preprocessing and Parcellation

Standard preprocessing steps were applied to the data. The first 10 volumes were deleted to remove initial saturation effects. The volumes were then motion-corrected and the brain was extracted. High-pass filtering (0.01 Hz) was performed to remove the effects of signal drifts. Subsequently, the slices were registered to the standard MNI152 template [11]. In addition, the ventricle mask based on the standard MNI152 template was used to eliminate time series in the corresponding regions. All these steps were carried out using the FMRI Expert Analysis Tool (FEAT) of FSL [8]. Also, the time series were normalized to zero mean and unit standard deviation to focus on signal dynamics rather than amplitude [9]. For each dataset, 90 regional time-series were computed based on the average time series of each of these 90 regions, excluding regions located in the cerebellum and the brain stem according to the Automated Anatomic Labeling (AAL) template [12].

3.2 Mutual Connectivity Analysis (MCA) Using a Generalized Radial Basis Function (GRBF) Neural Network

Our first step is to build a pair-wise affinity/similarity matrix A for all time series of the n = 90 brain regions using Mutual Connectivity Analysis (MCA) [3]. The pair-wise affinity between two regional time series X and Y (where X, Y ∈ {X_k, k = 1,…,n}) describes the degree of their dynamic coupling as a measure of their cross-prediction performance. For example, to compute matrix element (A)_X,Y, we break down time series X of length l into a set of vectors x_t, t ∈ {1,2,…,l-d+1} of dimension d, which can be interpreted as a sliding window of length d moving along X. The corresponding prediction target vectors for x_t are vectors y_t of dimension e. In this study, the parameters d and e were chosen d = 10 and e = 1. Here, x_t is mapped to future y_t, e.g. the vector x_t that comprises of the first 10 time points of X is mapped to y_t, which corresponds to the 11th time point of Y.

The set of ${\mathbf{x}}_t$ and their corresponding ${\mathbf{y}}_t$ are split into a training (Tr) and test (Te) set. The training set is then used to create a non-linear mapping f, i.e.,

$${\mathbf{y}}_t^{\mathrm{Tr}}=\mathit{f}\left({\mathbf{x}}_t^{\mathrm{Tr}}\right)$$

For defining the approximating function f, we use a GRBF neural network with three layers, i.e. the input, hidden and output layers. The activation pattern of the input layer with d neurons is represented by d-dimensional vector ${\mathbf{x}}_t$. In the training phase, this activity ( ${\mathbf{x}}_t^{\mathrm{Tr}}$) is propagated to k neurons of the hidden layer through directed connections with prototypical weight vectors ${\mathbf{w}}_j\in {ℝ}^d,j=1,2,\mathrm{\dots },k$. These weight vectors are representations of the training set ${\mathbf{x}}_t^{\mathrm{Tr}}$ and are computed using an unsupervised clustering approach. The activity $a_j$ of neurons in the hidden layer is defined as

$$a_j\left({\mathbf{x}}_t^{\mathrm{Tr}}\right)=\frac{e^{-{\left({\mathbf{x}}_t^{\mathrm{Tr}}-{\mathbf{w}}_j\right)}^2/2{\rho }^2}}{{{\displaystyle \sum }}_{i=1}^k{e}^{-{\left({\mathbf{x}}_t^{\mathrm{Tr}}-{\mathbf{w}}_i\right)}^2/2{\rho }^2}},$$

where the ρ parameter controls the width of the radial basis function kernel and defines the neighborhood of vectors that contributes to the computation of f [10]. In the final step of the training phase, the activity of the output layer ${\widehat{\mathbf{y}}}_t^{\mathrm{Tr}}$ is computed as a weighted sum of the hidden layer activations $a_j$, i.e.,

$${\widehat{\mathbf{y}}}_t^{\mathrm{Tr}}={{\displaystyle \sum }}_{j=1}^k{a}_j\left({\mathbf{x}}_t^{\mathrm{Tr}}\right)·{\mathit{s}}_j,$$

where ${\mathit{s}}_j$are the output weights obtained through minimization of the cost function $E={\Vert {\widehat{\mathbf{y}}}_t^{\mathrm{Tr}}-{\mathbf{y}}_t^{\mathrm{Tr}}\Vert }^2$. After the training phase is completed, f is subsequently used to process the test set and $\widehat{\mathbf{y}}$ is constructed from target vector estimates ${\widehat{\mathbf{y}}}_t^{\mathrm{Te}}$. Further details concerning our GRBF approach can be found in [3]. We haven chosen the value of ρ as 0.5 and used 20 hidden layer neurons based on initial experiments.

3.3 Graph Theoretic Measures

The network graph induced by the affinity matrix A was symmetrized to average out the directional influence between the nodes. An undirected binary graph a was obtained from the symmetrized matrix A by thresholding. The appropriate choice of the threshold for binarization of network graphs obtained from fMRI data analysis is subject to ongoing discussions in the pertinent literature [5]. Based on earlier studies [10], we chose a threshold value that retained 45% of the connections. At such a threshold, the networks are not fragmented, and they still preserve their ‘small-world’ topology [10]. Measures to characterize local and global network properties (summarized in Table 1) were computed for the thresholded graphs obtained for each subject.

Table 1.

List of the graph-theoretic measures used in this study. For a detailed description, please refer to [7].

Measure	Undirected definition	Description
Degree	$k_i={\displaystyle \sum }_{j\in N}{a}_{ij}$	Defined for each node i; Represents the total number of links connected to a node. It is a marker of network development and resilience.
Characteristic Path Length	$L=\frac{1}{n}{{\displaystyle \sum }}_{i\in N}{L}_i=\frac{1}{n}{\displaystyle \sum }_{i\in N}\frac{{{\displaystyle \sum }}_{j\in N,j\ne 1}{d}_{ij}}{n-1}$ where, Li is the distance between node i, and all other nodes	Characteristic Path Length is a measure of functional integration and is primarily influenced by long paths. The inverse (global efficiency) measure is considered a superior measure and is primarily influenced by short paths.
Global Efficiency	$E=\frac{1}{n}{{\displaystyle \sum }}_{i\in N}{E}_i=\frac{1}{n}{\displaystyle \sum }_{i\in N}\frac{{{\displaystyle \sum }}_{j\in N,j\ne 1}{d}_{ij}^{-1}}{n-1}$
Local Efficiency	$E_{\mathit{loc}}=\frac{1}{n}{\displaystyle \sum }_{i\in N}{E}_{\mathit{loc},i}=\frac{1}{n}\frac{{{\displaystyle \sum }}_{j,h\in N,j\ne 1}{a}_{ij}{a}_{ih}{[d_{jh}{N}_i]}^{-1}}{k_i(k_i-1)}$ where, Eloc,,i is the local efficiency of node i, and djh (Ni) is the length of the shortest path between j and h, that contains only neighbors of i.	Characterizes the efficiency of node connections at a smaller scale.
Clustering Coefficient	$C=\frac{1}{n}{{\displaystyle \sum }}_{i\in N}{C}_i=\frac{1}{n}\frac{2t_i}{k_i(k_i-1)}$ where Ci is the clustering coefficient of node i (Ci = 0 for ki < 2).	The mean clustering coefficient represents the presence of clustered connectivity around individual nodes

All procedures, excluding the pre-processing steps discussed in section 3.1, were implemented using MATLAB (MathWorks Inc., Natick, MA, 2013). The network measures definitions are taken from [7]. Significance testing was performed using a Wilcoxon signed rank test.

4. RESULTS

The results obtained using global graph measures are represented in Figure 1. We can see differences in the distribution of the various properties between the subject groups. Trending differences (p<0.1) are seen in characteristic path length, assortativity and degree variance, where as significant difference is observed for the clustering coefficient (p < 0.05). This suggests low local efficiency of the network in subjects affected with HIV, implying a loss of more local connections than connections across different regions. This has been seen in the case of other diseases such as Schizophrenia [15] and Alzheimer’s [16]. Transitivity is a variant of the clustering coefficient, it is less sensitive to the degree of the nodes that are connecting an edge. This characteristic also shows similar reduction although the differences seen are not significant.

Figure 1.

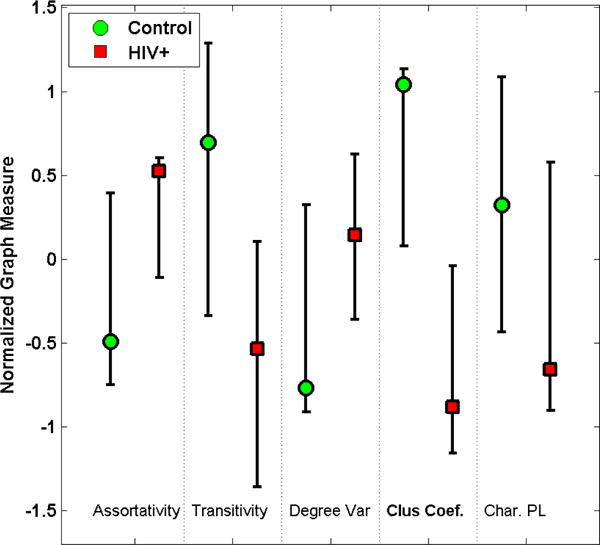
The distribution of global graph measures across the two subject groups. Certain trends are seen, though significant difference (p < 0.05) is obtained only when using the Clustering Coefficient (highlighted in boldface). Transitivity is also comparatively reduced in HIV+ subjects, though the difference was not found to be significant (p = 0.08). Note that the measures have been z-score normalized for the plot here.

We have also explored the possibility of regional characteristics being different amongst the subject groups. The different regional properties as listed in Table 1, were used for comparison across each node. There are no specific trends seen in this for example: some regions show an increase in degree whereas in other regions this is reduced, however, significant differences are noted in degree distribution are found for the frontal pole, precuneus region of the lateral occipital cortex. This indicates a loss of connections to or from these regions as a possible result of neuronal damage. Clustering coefficient of most nodes is reduced. Significant reduction is seen in the regions of of the cingulate cortex and the basal ganglia. The regions of the posterior cingulate gyrus, the basal ganglia and the lateral occipital cortex are known to be affected in HIV infection in earlier studies [1,10,11]. The regions of the brain highlighting differences using the local properties are shown in Figure 2.

Figure 2.

A simplified view of the brain representing the regions highlighting differences (seen in red) in local properties. These regions are consistent with some differences identified in other studies examining HIV-related cognitive impairment [1,10,11]. The regions shown here represent the differences using all the features and mapped over the standard atlas. Regions are specifically described in the text.

5. NEW AND BREAKTHROUGH WORK

We present a clinical application of our computational framework for non-linear Mutual Connectivity Analysis (MCA) in the human brain from resting state fMRI data. Based on the evaluation of pair-wise cross-prediction quality we construct connectivity profiles from a parcellated human brain. Subsequently, quantitative analysis of the resulting network graphs is carried out using graph theoretic approaches of characterizing network properties. We have applied this approach to identify differences in network connectivity patterns between the network profiles of healthy and diseased subjects with HIV infection. We are able to identify significant differences in these profiles at a global as well as a regional level. We show that there are certain changes in the overall topological organization of the brain in HIV infection. The results obtained here using our novel methodology are in line with earlier studies on HAND. We hypothesize that our non-linear approach has the potential to capture more accurate information on brain connectivity patterns than more traditional linear or model-based approaches. This combined with graph theoretical approach has be useful to develop biomarkers for disease progression and therapy management in patients with HIV-associated neurological disease.

6. CONCLUSION

In conclusion, the results presented in this work indicate that our non-linear time-series modelling approach (MCA) in combination with subsequent graph-theoretic network characterization can be applied to detecting changes in brain network connectivity patterns observed in patients with HAND. Hence, MCA can serve as an alternate method for fMRI-based functional connectivity analysis in the human brain, as it avoids certain inherent limitations of traditional approaches. The initial results suggest that our method may contribute to biomedical research endeavors aiming at a better understanding of underlying disease mechanisms in HAND and can potentially be useful in clinical applications to quantitatively monitor its progression.