Abstract
Aggregate data model‐based meta‐analysis is a regression approach to compare the dose–response and/or time‐course across different treatments using summary level data from the literature. Literature search and systematic review following the Cochrane approach yielded 912 sources for investigational and approved treatments for psoriasis. In addition, data for tofacitinib were obtained from an internal database. Tofacitinib is an oral Janus kinase inhibitor. Two mathematical models were developed for Psoriasis Area and Severity Index (PASI) response in moderate to severe psoriasis patients to quantify the time to maximum effect for PASI75 and to evaluate the dose–response relationship for PASI responders (PASI50, PASI75, PASI90, PASI100) at Week 12. Body weight exhibited an inverse effect on the placebo component of both models, suggesting that body weight affects the overall PASI response regardless of drug. This analysis provides a quantitative framework for efficacy comparisons across psoriasis treatments.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Treatment options for patients with moderate to severe psoriasis include oral and injectable/infusible systemic medication. However, quantitative comparison for the treatment effect across drugs remains unknown.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ Two mathematical models were developed for Psoriasis Area and Severity Index response to evaluate the magnitude of effect and the onset of the effect (time course of the treatment) for each drug. The impact of body weight (covariate) was also tested.
WHAT THIS STUDY ADDS TO OUR KNOWLEDGE
☑ This analysis furthered the understanding of psoriatic treatments by providing a framework for efficacy comparisons across systemic drugs. It also suggests that decisions to increase the dose may be particularly beneficial to heavier patients if they fail to show meaningful responses at lower doses.
HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE
☑ This model‐based meta‐analysis based on a systematic literature review provides a quantitative understanding of pharmacodynamics across drugs and may allow better dose selections.
Psoriasis is a common chronic skin disorder typically characterized by erythematous papules and plaques with a silver scale, although other clinical presentations also occur.1 Management of psoriasis may involve topical and systemic medications, phototherapy, stress reduction, climatotherapy, and various adjuncts based on individual patients' clinical situations.2
Aggregate data (study‐level) model‐based meta‐analysis is a regression approach to compare the dose–response and/or time‐course across different treatments by using data from the literature. As more drugs become available to treat patients, the compilation of clinical responses across drugs provides a better understanding of whether newer agents offer greater pharmacological benefit compared with existing ones, including faster onset of action, increased efficacy, and/or better safety profiles.
In this analysis, data from the literature on Psoriasis Area and Severity Index (PASI) response in patients with moderate to severe psoriasis were collected for both investigational and marketed drugs. Data for tofacitinib were obtained from an internal Pfizer database (all tofacitinib studies used in this analysis have been published). Tofacitinib is an oral Janus kinase (JAK) inhibitor. An oral tablet of tofacitinib dosed as 5 mg or 10 mg twice daily (b.i.d.) was demonstrated to be efficacious for the treatment of moderate to severe psoriasis in four phase III clinical studies.3, 4, 5
To evaluate the magnitude and onset of the drug effect, two mathematical models were developed: 1) a longitudinal model to quantify the time course of PASI75 (primary clinical endpoint representing the proportion of patients achieving ≥75% reduction in PASI score from baseline), and 2) a landmark model to quantify the dose–response relationship for PASI responders (PASI50, PASI75, PASI90, PASI100) at Week 12 (primary efficacy timepoint in the majority of studies; primary efficacy timepoints ranged from 10–24 weeks across all studies). The impact of body weight was tested in both models. The results from the two models were compared, and the predictive performance for PASI response was assessed. This analysis allows a quantitative understanding of treatment options for patients with psoriasis by providing a framework for efficacy comparisons across systemic agents.
RESULTS
Available data
The literature search yielded 912 abstracts, of which 151 studies were identified for potential inclusion in the analyses. Following application of additional inclusion/exclusion criteria, the final analysis included 71 studies for landmark and 57 studies for longitudinal analyses (Figure 1; Supplementary Material).
Figure 1.
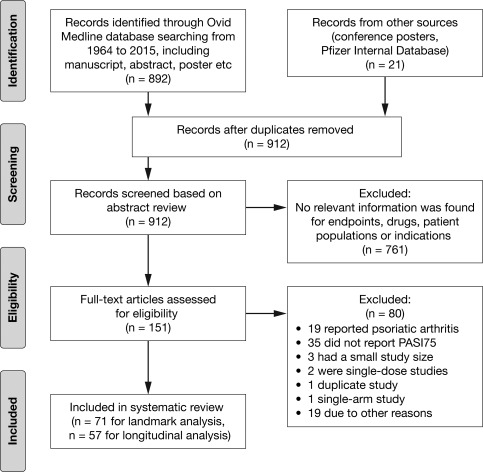
Search strategy flow diagram. Details of studies included in the final database are listed in the Supplementary Appendix. PASI75, ≥ 75% reduction from baseline Psoriasis Area and Severity Index score.
The final database included interleukin (IL)‐12/23 inhibitors (ustekinumab, briakinumab), tumor necrosis factor (TNF)‐α inhibitors (adalimumab, etanercept, certolizumab, infliximab), IL‐17 inhibitors (secukinumab, ixekizumab, brodalumab), T‐lymphocyte (CD2) antagonist (alefacept), phosphodiesterase‐4 (PDE4) inhibitor (apremilast), JAK inhibitors (tofacitinib, baricitinib), and traditional oral agents (methotrexate, cyclosporine, acitretin). All drugs were included in the landmark model; however, the longitudinal model did not include cyclosporine, acitretin, or baricitinib due to insufficient longitudinal data.
Longitudinal model
The temporal relationship between dose and PASI75 response was adequately described by the longitudinal model. PASI75 response increased toward a maximum that eventually plateaued over time for most treatments. The PASI75 time course curves for the model‐predicted PASI75 were overlaid with the observed data for each drug (Figure 2).
Figure 2.
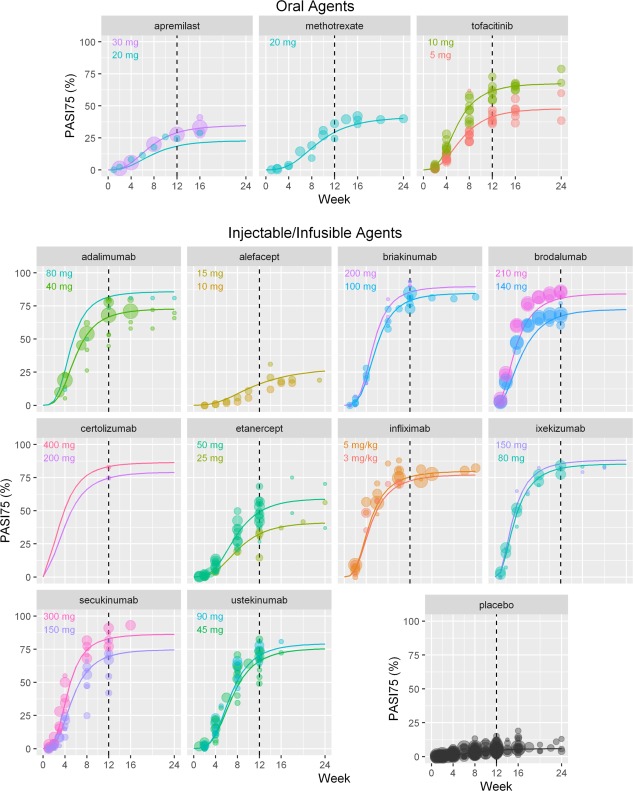
Time‐course of PASI75 response in the longitudinal model: predicted vs observed PASI75 response by drug. Placebo time course is based on results from studies including both injectable/infusible and oral agents. Lines are model prediction for average body weight 90 kg subjects. Circles represent observed data, with size proportional to the N of patients in the study arm. PASI75, ≥ 75% reduction from baseline Psoriasis Area and Severity Index score. [Color figure can be viewed at cpt-journal.com]
ET50 and ET90 (the time to reach 50% and 90% of the maximal treatment effect (Emax)) were estimated from the model (Table 1). Emax was achieved by Week 12 for the majority of drugs except alefacept (estimated ET50 for alefacept was 11.1 weeks; ET90 was not able to be estimated from available data). The mean (standard deviation (SD)) ET50 across all drugs was 6.48 (2.06) weeks, and ranged from 3.7–9.2 weeks, with the exception of alefacept (Table 1; Figure 2). The mean (SD) ET90 across all drugs, excluding alefacept, was 12.6 (2.92) weeks. A trend between ET50 and Emax was detected, such that drugs with higher Emax tended to have a shorter ET50 than those with lower Emax. For example, the IL‐17 inhibitors were predicted to achieve ET50 following ∼4 weeks of treatment. Correspondingly, the predicted PASI75 response for IL‐17 inhibitors ranged from 22–49% at 4 weeks and reached ∼80% at 12 weeks. In contrast, other systemic agents with longer ET50, such as methotrexate and alefacept, had lower PASI75 responses (less than 30% at 12 weeks).
Table 1.
Longitudinal model‐predicted percentage of PASI75 responders for systemic treatment in patients with moderate to severe psoriasis at 4 and 12 weeks
| Drug | Clinical dose | ET50 (Week) | ET90 (Week) | PASI75 (%) | |
|---|---|---|---|---|---|
| Week 4 | Week 12 | ||||
| TNF‐α inhibitor | |||||
| Adalimumab | 40 mg Q2W | 6.0 (4.6, 7.8) | 11.7 (8.5, 16.1) | 15.6 (5.15, 30.2) | 65.9 (53.6, 76.8) |
| Certolizumaba | 200 mg Q2W | 4.2 (2.8, 6.0) | 9.9 (6.5, 14.3) | 38.8 (21.7, 59.4) | 74.5 (62.2, 84.1) |
| Etanercept | 25 mg BIW | 8.2 (6.3, 10.8) | 16.4 (12.3, 20.8) | 4.64 (0.00, 10.7) | 32.0 (20.7, 44.0) |
| Etanercept | 50 mg BIW | 7.7 (6.1, 9.9) | 14.6 (11.8, 19.0) | 6.87 (1.08, 15.7) | 48.7 (34.2, 60.6) |
| Infliximab | 5 mg/kg Q8W | 4.7 (3.5, 6.2) | 10.0 (6.8, 14.2) | 32.7 (16.0, 51.5) | 75.3 (62.6, 85.8) |
| IL‐17 inhibitor | |||||
| Brodalumaba | 210 mg Q2W | 3.9 (2.8, 5.3) | 9.2 (6.1, 13.1) | 46.9 (27.1, 66.7) | 80.2 (69.0, 89.2) |
| Ixekizumab | 80 mg Q4W | 3.7 (2.6, 5.3) | 8.9 (5.7, 13.1) | 48.8 (29.4, 68.6) | 81.7 (71.7, 90.7) |
| Secukinumab | 150 mg QM | 5.5 (4.1, 7.1) | 11.0 (7.7, 15.3) | 21.5 (8.86, 37.7) | 69.2 (57.0, 79.5) |
| IL‐12/23 inhibitor | |||||
| Briakinumabb | 100 mg Q4W | 5.8 (4.7, 7.0) | 10.9 (8.8, 13.6) | 19.0 (7.13, 34.8) | 78.4 (67.2, 87.9) |
| Ustekinumab | 45 mg Q12W | 7.1 (5.8, 8.7) | 13.3 (11.1, 16.7) | 10.2 (3.01, 21.6) | 65.2 (51.9, 76.4) |
| Dihydrofolate reductase inhibitor | |||||
| Methotrexate | 18 mg QW | 9.2 (7.3, 11.5) | 18.7 (15.3, 21.6) | 3.38 (0.000, 8.61) | 28.5 (17.0, 40.0) |
| JAK inhibitor | |||||
| Tofacitiniba | 5 mg BID | 6.9 (5.0, 9.6) | 14.3 (9.4, 20.1) | 9.21 (1.85, 19.4) | 40.8 (28.2, 52.5) |
| Tofacitiniba | 10 mg BID | 6.0 (4.5, 8.1) | 12.2 (8.4, 17.5) | 16.9 (6.23, 32.8) | 60.7 (48.1, 72.5) |
| Baricitiniba | 10 mg QD | NA | NA | NA | NA |
| Vitamin A analog | |||||
| Acitretin | 30 mg QD | NA | NA | NA | NA |
| CD2 antagonist | |||||
| Alefacept | 10 mg QW | 11.1 (9.0, 13.9) | >24c (23.5, NA) | 1.99 (0.000, 6.20) | 15.6 (7.09, 24.1) |
| PDE4 inhibitor | |||||
| Apremilast | 30 mg BID | 7.4 (5.4, 10.2) | 15.1 (10.2, 20.7) | 5.66 (0.345, 12.7) | 28.5 (17.9, 39.8) |
| Calcineurin inhibitor | |||||
| Ciclosporin | 2.5–5 mg/kg/d | NA | NA | NA | NA |
Values presented are mean (90% confidence intervals) and were generated assuming a typical weight of 90 kg.
Investigational.
Discontinued. All other drugs are approved.
Alefacept data only reported up to 24 weeks; ET90 is estimated to occur sometime beyond the time period for which there were reported data.
BID, twice daily; BIW, twice weekly; CD2, T lymphocyte; ET50, time to reach 50% of the maximal treatment effect; ET90, time to reach 90% of the maximal treatment effect; IL, interleukin; JAK, Janus kinase; NA, not available; PASI75, ≥ 75% reduction from baseline Psoriasis Area and Severity Index score; PDE4, phosphodiesterase 4; QD, once daily; QM, once monthly; QW, once weekly; Q2W, once every 2 weeks; Q4W, once every 4 weeks; Q8W, once every 8 weeks; Q12W, once every 12 weeks; TNF, tumor necrosis factor.
Treatment effect was well‐characterized by an Emax model with a different Emax and potency (ED50; dose achieving 50% of maximal response) for each drug within each class. Body weight was shown to have an inverse relationship with both the placebo response (B) and the rate constant of drug effect (kdrug), in which the rate constant describes the time‐course component in the model. The median body weight effect estimates (95% confidence interval) in the final model for the maximal placebo effect and the rate constant of drug effect were –0.193 [–0.277, –0.119] and –0.867 [–1.32, –0.496], respectively (from nonparametric bootstrap; N = 1,000); both excluded 0. The final parameter estimates for the longitudinal model are presented in Supplementary Table 1.
Landmark model
Dose–response for PASI endpoints (PASI50, 75, 90, and 100) was well characterized by a sigmoidal Emax function with a different Emax for each drug class and different ED50 for every drug within each class. The final parameter estimates for the landmark model are presented in Supplementary Table 2. The dose–response relationship for the model‐predicted PASI response overlaid with the observed data for each drug is presented in Figure 3.
Figure 3.
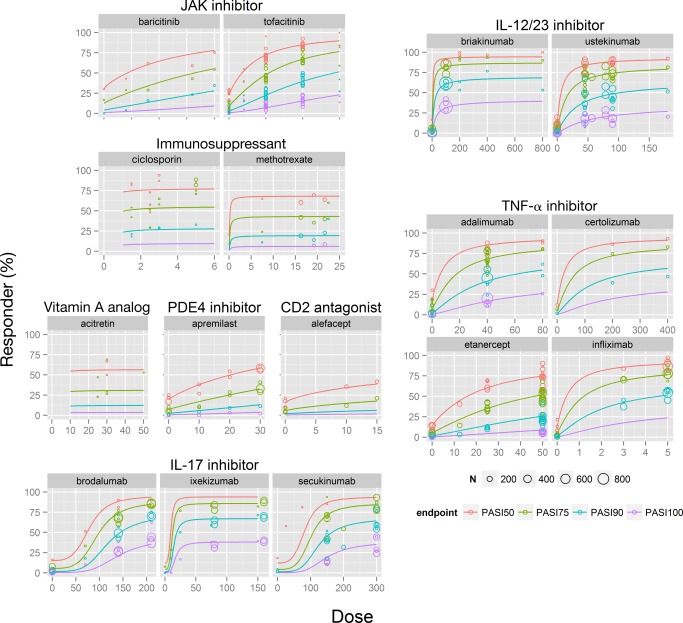
Landmark analysis of dose–response at 12 weeks in patients with moderate to severe psoriasis. Solid lines: model‐predicted PASI endpoint data at 12 weeks (not placebo‐adjusted). The PASI responses at dose = 0 represent the placebo arm in each study. Circles represent observed data, with size proportional to the N of patients in the study arm. CD2, T lymphocyte; IL, interleukin; JAK, Janus kinase; PASI50/75/90/100, ≥ 50%, ≥ 75%, ≥ 90%, or 100% reduction from baseline Psoriasis Area and Severity Index score; PDE4, phosphodiesterase 4; TNF, tumor necrosis factor. [Color figure can be viewed at cpt-journal.com]
The model‐predicted PASI responses for a typical patient for each drug are summarized in Table 2. There was close agreement between the estimates from the longitudinal model and the landmark model, although the confidence intervals were generally wider for the values generated from the longitudinal model.
Table 2.
Landmark model‐predicted percentage of PASI75 and PASI90 responders for systemic treatments in patients with moderate to severe psoriasis at 12 weeks
| Drug | Clinical dose | Landmark model‐predicted PASI responders (%) | Landmark model‐predicted difference from placebo (%) | ||
|---|---|---|---|---|---|
| PASI75 | PASI90 | PASI75 | PASI90 | ||
| TNF‐α inhibitor | |||||
| Adalimumab | 40 mg Q2W | 64.9 (59.9, 69.3) | 37.9 (32.9, 42.9) | 59.5 (54.5, 63.8) | 36.3 (31.1, 41.2) |
| Certolizumaba | 200 mg Q2W | 73.5 (55.1, 83.2) | 48.2 (28.6, 62.7) | 68.0 (49.7, 77.7) | 46.5 (26.9, 60.8) |
| Etanercept | 25 mg BIW | 37.4 (34.3, 41.1) | 16.1 (14.1, 18.2) | 31.9 (28.8, 35.7) | 14.3 (12.4, 16.6) |
| Etanercept | 50 mg BIW | 54.0 (51.3, 56.7) | 27.6 (25.4, 30.1) | 48.4 (45.8, 51.5) | 26.0 (23.7, 28.4) |
| Infliximab | 5 mg/kg Q8W | 77.0 (72.2, 80.7) | 53.0 (46.1, 58.4) | 71.6 (66.6, 75.1) | 51.3 (44.4, 56.8) |
| IL‐17 inhibitor | |||||
| Brodalumaba | 210 mg Q2W | 81.2 (77.0, 84.4) | 59.3 (52.4, 64.4) | 75.8 (71.5, 79.0) | 57.7 (50.7, 62.9) |
| Ixekizumab | 80 mg Q4W | 88.2 (86.8, 89.5) | 71.7 (69.1, 74.6) | 82.7 (81.2, 84.1) | 70.0 (67.2, 72.9) |
| Secukinumab | 150 mg QM | 75.7 (73.0, 78.4) | 51.1 (47.2, 55.2) | 70.2 (67.5, 73.1) | 49.4 (45.6, 53.4) |
| IL‐12/23 inhibitor | |||||
| Briakinumabb | 100 mg Q4W | 80.8 (78.4, 82.6) | 58.4 (54.9, 61.9) | 75.2 (72.9, 77.3) | 56.8 (53.3, 60.4) |
| Ustekinumab | 45 mg Q12W | 70.3 (67.8, 72.6) | 43.6 (40.8, 46.7) | 64.9 (62.3, 67.3) | 41.9 (39.0, 45.1) |
| Dihydrofolate reductase inhibitor | |||||
| Methotrexate | 18 mg QW | 36.4 (32.7, 40.6) | 15.5 (13.2, 18.1) | 31.0 (27.2, 35.4) | 13.8 (11.5, 16.3) |
| JAK inhibitor | |||||
| Tofacitiniba | 5 mg BID | 35.2 (30.9, 39.1) | 14.8 (12.4, 17.1) | 29.7 (25.2, 33.7) | 13.1 (10.7, 15.5) |
| Tofacitiniba | 10 mg BID | 53.8 (47.0, 58.7) | 27.5 (22.1, 31.8) | 48.2 (41.7, 53.2) | 25.8 (20.7, 30.1) |
| Baricitiniba | 10 mg QD | 33.2 (21.4, 49.0) | 13.6 (8.05, 23.7) | 27.5 (15.7, 43.9) | 11.9 (6.28, 22.1) |
| Vitamin A analog | |||||
| Acitretin | 30 mg QD | 25.0 (16.1, 36.7) | 9.57 (5.55, 15.7) | 19.6 (10.6, 31.5) | 7.92 (3.80, 14.1) |
| CD2 antagonist | |||||
| Alefacept | 10 mg QW | 22.7 (15.0, 30.3) | 8.39 (5.23, 12.3) | 17.2 (9.54, 24.9) | 6.61 (3.53, 10.5) |
| PDE4 inhibitor | |||||
| Apremilast | 30 mg BID | 26.8 (23.2, 31.8) | 10.3 (8.52, 12.8) | 21.3 (17.6, 26.1) | 8.60 (6.78, 11.1) |
| Calcineurin inhibitor | |||||
| Ciclosporin | 2.5–5 mg/kg/d | 46.7 (36.9, 56.5) | 22.1 (16.0, 29.6) | 41.2 (31.6, 50.8) | 20.4 (14.3, 27.8) |
Values presented are mean (90% confidence intervals) and were generated assuming a typical weight of 90 kg.
Investigational.
Discontinued. All other drugs are approved.
BID, twice daily; BIW, twice weekly; CD2, T lymphocyte; IL, interleukin; JAK, Janus kinase; PASI75/90, ≥ 75% or ≥ 90% reduction from baseline Psoriasis Area and Severity Index score; PDE4, phosphodiesterase 4; QD, once daily; QM, once monthly; QW, once weekly; Q2W, once every 2 weeks; Q4W, once every 4 weeks; Q8W, once every 8 weeks; Q12W, once every 12 weeks; TNF, tumor necrosis factor.
The effect of body weight on PASI response was also tested in the landmark model on placebo effect and/or drug effect terms. There was no significant improvement in the model fit when the weight effect was applied to any of the drug effect terms (Emax, ED50), while it was significant for the placebo effect term. Therefore, the presented predictions are based on a model in which body weight was retained for the placebo effect term alone. Although the effect was small, weight was shown to have a statistically significant negative effect on the placebo response (i.e., heavier patients showed a lesser response compared with lighter patients).
Among injectable/infusible agents, IL‐17 inhibitors were the most efficacious, with ixekizumab (80 mg) demonstrating the highest placebo‐adjusted response rate (88.2% [86.8, 89.5] and 71.7% [69.1, 74.6] for PASI75 and PASI90, respectively) at Week 12. Within the oral systemic treatments, tofacitinib 10 mg b.i.d. and cyclosporine 5 mg/kg/d had comparable response rates of 53.8% (47.0, 58.7) and 46.7% (36.9, 56.5) for PASI75 and 27.5% (22.1, 31.8) and 22.1% (16.0, 29.6) for PASI90, respectively. Acitretin 30 mg q.d. and apremilast 30 mg b.i.d. showed the lowest efficacy among the oral systemic agents (25.0% [16.1, 36.7] and 26.8% [23.2, 31.8] for PASI75, and 9.57% [5.55, 15.7] and 10.3% [8.52, 12.8] for PASI90, respectively).
External validation (predicting longitudinal PASI90)
The final longitudinal model, developed from the time‐course PASI75 dataset (test dataset), was used to predict the time‐course of PASI90 response (validation dataset). When scaling factors obtained from the landmark model were incorporated into the longitudinal model, predictions of PASI response were consistent with the observed data, with the majority of reported PASI90 responses falling within the 90% prediction interval (Figure 5). The central tendency of predicted PASI90 response appeared to be slightly underestimated with brodalumab; however, all other drugs were within the range of longitudinal prediction curves. Based on Figure 2 and Figure 3, both models independently showed good agreement between the observed and predicted data for these compounds, confirming that the models were reasonably describing the data.
Figure 5.
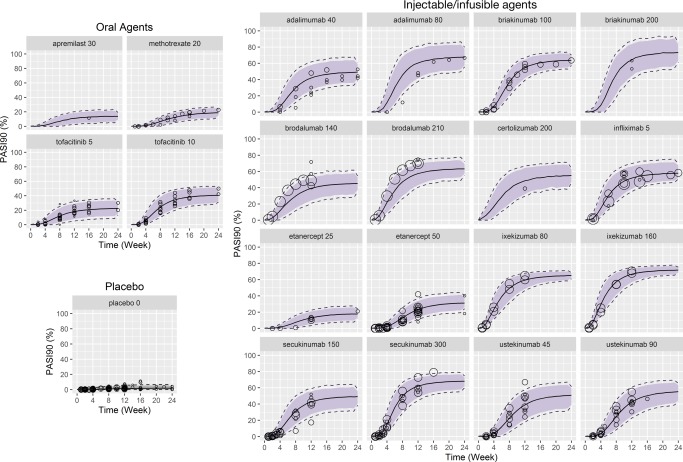
External validation of predicted PASI90 response over time. PASI90 time‐course response was predicted using the final longitudinal model (developed for PASI75) by incorporating parameter estimates (scaling factors between PASI75 and PASI90) from the landmark model on the placebo and drug term. Solid line: predicted PASI90 response; gray shaded area: 90% confidence intervals; dotted lines: 95% confidence intervals; open circles: reported PASI90 response. Doses are in mg, with the exception of infliximab (mg/kg). PASI75/90, ≥ 75% or ≥ 90% reduction from baseline Psoriasis Area and Severity Index score. [Color figure can be viewed at cpt-journal.com]
Figure 4.
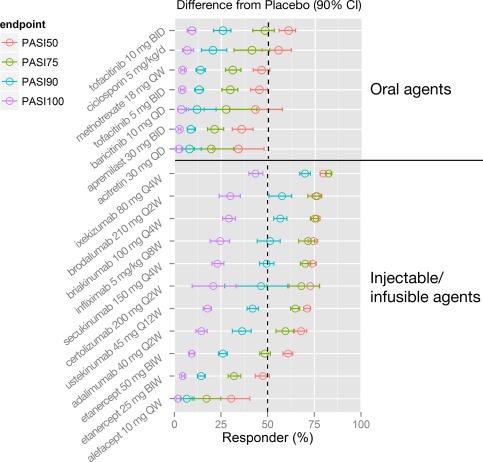
Comparison of placebo‐adjusted treatment effect (model predicted) for systemic psoriasis treatments: landmark analysis. Point estimates and 90% confidence intervals are predicted from model simulations (N = 1,000) for each drug, assuming a typical body weight of 90 kg. The recommended dosage for ustekinumab is based on body weight (45 mg ustekinumab for ≤ 100 kg or 90 mg ustekinumab for > 100 kg). Therefore, the simulation (N = 500 for each body weight strata) for ustekinumab was conducted by body weight ≤100 kg and >100 kg, in which different doses (45 mg or 90 mg) were assigned before calculating ustekinumab weighted average PASI responses. b.i.d., twice daily; b.i.w., twice weekly; CI, confidence interval; PASI50/75/90/100, ≥ 50%, ≥ 75%, ≥ 90%, or 100% reduction from baseline Psoriasis Area and Severity Index score; q.d., once daily; q.w., once weekly; q2w, once every 2 weeks; q4w, once every 4 weeks; q8w, once every 8 weeks; q12w, once every 12 weeks. [Color figure can be viewed at cpt-journal.com]
DISCUSSION
Aggregate level landmark and longitudinal models were used to evaluate the dose–response (magnitude) and time‐course (onset of drug effect) of PASI response in patients receiving systemic agents for the treatment of moderate to severe psoriasis. Both models adequately described the data, suggesting that the dose–response relationships are well‐captured using sigmoidal Emax function structures, and that the maximum drug effect is achieved within 12 weeks across most of the drugs included in this analysis. Moreover, both models suggest that drugs with the same mechanism of action demonstrate a consistent dose–response.
One of the benefits of the longitudinal model is that it enables the comparison of the rate of onset among drugs. In this analysis, ET50 was estimated from the predicted time‐course of PASI75 responses. Generally, drugs with the highest efficacy had the fastest onset of action. For example, the highest efficacy was observed with the IL‐17 inhibitors ixekizumab and brodalumab (PASI75 response ∼80%) at the primary evaluation timepoint (12 weeks), with ET50 of 3.7 and 3.9 weeks, respectively. In comparison, the lowest efficacy was observed for alefacept (PASI75 response 16%) with an ET50 of ∼11 weeks. The average ET50 across all drugs in this analysis was 6.5 weeks. Understanding differences in ET50 allows studies to be modified to provide an appropriate timeframe to compare drug efficacy. Early assessments (after 4–6 weeks of treatment) may be sufficient for drugs with shorter ET50 and highly efficacious drugs (e.g., ixekizumab and brodalumab), whereas a longer sampling duration may be required to allow patients to achieve maximum benefit for drugs with longer ET50 (e.g., etanercept, methotrexate, or apremilast).
The relationship between body weight and PASI response was of clinical interest, and an inverse relationship was detected in this meta‐analysis. In both longitudinal and landmark analyses, body weight was identified as exhibiting an inverse effect on the placebo component of the model, suggesting that body weight affects the overall PASI response regardless of drug. The body weight effect was also significant on the temporal component of drug effect (kdrug) in the longitudinal model. These data suggest that heavier patients tend to achieve lower efficacy and may also experience slower onset of effect compared with lighter patients. The significance of the weight effect on the placebo components of the models should not be interpreted in a mechanistic context, as the models were developed based on summary level, and not patient level, data. The important finding was that, despite this attribution, body weight demonstrated an effect on the absolute difference in the percentage of responders between active and control groups. Therefore, increasing drug dose may be particularly beneficial for heavier patients if they fail to show a meaningful clinical response at lower doses. Such a decision to escalate the dose in heavier patients can be achieved by evaluating the dose–response characteristics of each drug and assessing the location of the clinical dose relative to the drug's ED50.
However, caution is required in interpreting covariate effects with aggregate‐level data. In general, meta‐analyses using data from the literature report covariates (age, body weight, sex, race, etc.) as summary statistics (mean or median % of the trial dataset), which results in reduced power to detect clinically relevant interactions. In an analysis conducted by Lambert et al.,6 it was demonstrated that even moderately strong interactions may not be adequately detected in the meta‐analytic setting. Furthermore, there is also a risk that introduction of aggregate‐level covariates may result in underestimation of exposure–response effects.7 Therefore, although both meta‐analytic models reported here suggested that increasing body weight has an inverse effect on PASI response, the true magnitude of this interaction may not have been captured in this setting. Instead, the use of individual level data may provide better estimates of the magnitude of this effect and may enhance the understanding of this relationship on a mechanistic level.
As with any meta‐analysis, the utility of the results depends, in part, on the studies that provided the information for analysis. We therefore investigated heterogeneity in the aggregated pooled dataset. During study selection, only predefined inclusion and exclusion criteria were applied to control for possible heterogeneity across the pooled studies. The parameterization of the landmark model therefore incorporated a study‐specific placebo effect (E 0) for each trial. In this manner, study‐related differences were accounted for by allowing the placebo effect of the PASI response to shift across different studies. In contrast, the drug effect was assumed to be constant across studies, i.e., all of the differences in response for a given drug at a given dose were assumed to be related to differences between studies and not to the drug itself.
When predicted placebo effects (E0) from the landmark model were plotted for each study (N = 71), they were shown to be normally distributed around a single value (data not shown). However, the I 2 statistic8 of placebo effects (which describes the percentage of variance that is related to between‐study differences) was estimated to be 82%, suggesting that the parameterization for study‐specific placebo effect in the landmark model may have helped to adequately control for any potential study‐related heterogeneity in the dataset. A similar approach (estimating study‐specific placebo effects) was also attempted in the longitudinal model, but the results were inconclusive due to overparameterization. Instead, a placebo component was modeled as a population mean response with between‐study variability as a random effect. The estimated random effects in the longitudinal model were nearly normally distributed, suggesting that the parsimonious model (without estimating study‐specific placebo effects) is a reasonable alternative to describe the data.
Due to the advancement of antipsoriatic therapies, PASI90 may eventually replace PASI75 as the key indicator of efficacy in investigational trials.9 New psoriasis therapies with targeted mechanisms (e.g., secukinumab, ixekizumab, and brodalumab) have shown much higher levels of improvement in clinical studies, and therefore the emphasis from clinicians, regulators, and drug developers is shifting to higher threshold endpoints, such as PASI90. The external validation of predicted PASI90 response in the longitudinal setting shows high agreement with the scalability employed in the landmark setting, and both PASI75 and PASI90 results tended to plateau at ∼12 weeks. This suggests that a simple scaling factor can be used to link PASI75 and responses, especially in the period following attainment of Emax. It is worth noting that the external validation was performed by bridging the models, i.e., the longitudinal model for PASI75 was used to predict PASI90 by incorporating the estimated relationship between PASI75 and PASI90 from the landmark model. This represents a much higher hurdle for model validation than applying the same model on a different dataset.
The magnitude of treatment effects for systemic agents was visualized with predicted PASI responses. Consistent with previous reports,10 IL‐17 inhibitors appeared to be the most efficacious injectable/infusible psoriasis treatments, followed by other classes of drugs. Infliximab (5 mg/kg) and ixekizumab (80 mg) had the highest responses among TNF‐α inhibitors and IL‐17 inhibitors, respectively. Among the oral agents, tofacitinib 10 mg b.i.d. and cyclosporine 5 mg/kg/d appeared to have comparable efficacy, which was higher than other approved or investigational systemic oral treatments. Acitretin 30 mg q.d. and apremilast 30 mg b.i.d. showed the lowest efficacy among the oral systemic treatments.
In summary, two mathematical models were developed to describe the time‐course and dose–response from the data across all systemic treatments for patients with psoriasis. The simulation results also suggest that the model could be useful to predict the time‐course of other PASI subscales such as PASI90. These models provide a quantitative framework to understand the current treatment options and a potential use of models in drug development, either alone or bridging together, to predict the time‐course for endpoints of interest with investigational drugs.
METHODS
Database development
The data for the analysis originated from two sources: data from the literature for approved and investigational psoriasis treatments from 1998 through 2015, and summary level data for tofacitinib phase II and III clinical studies. Although the results from tofacitinib clinical studies are published, the corresponding summary data for this analysis were obtained from a Pfizer internal database to maintain numerical accuracy.
Literature search and data selection
Following the search and selection strategy proposed by the Cochrane group,11 the Ovid Medline search engine, US‐based and European regulatory documents such as Summary Basis of Approvals and European Public Assessment Reports were searched from 1964 to 2015 for reports of PASI responders in clinical trials for the pharmaceutical treatment of psoriasis. The search strategy focused on moderate to severe plaque psoriasis, randomized placebo‐ or active‐controlled trials of IL‐12/23 inhibitors, TNF‐α inhibitors, IL‐17 inhibitors, CD2 antagonists, PDE4 inhibitors, JAK inhibitors, and traditional oral agents. The primary efficacy endpoint PASI75 and other PASI scores (PASI50, PASI90, and PASI100) were captured in the database.
Abstracts of potential records were screened by qualified personnel to determine the relevance to the research objectives; the study designs, treatment regimens, and patient populations were scrutinized to ensure that all studies represented data that supported pooling. PASI response data that passed the screening process were extracted from published articles, relevant conference posters, and/or abstracts. The data from selected sources were captured or digitized, then data curation (e.g., unit standardization, normalization of different dose regimen) was performed.
Although a single database was generated to support both the longitudinal and landmark analysis, three separate datasets were created as required by the modeling objectives. In the longitudinal analysis, all repeated measures of PASI75 response (test dataset) were used for model building, and all repeated measures of PASI90 response (validation dataset) were used for the external validation. The third dataset was for the landmark analysis; PASI responses (PASI50, 75, 90, 100) at the primary efficacy measurement time (majority of studies were 12 weeks; range, 10–24 weeks) were included.
Model development
Longitudinal model
The longitudinal model structure consisted of placebo and drug effects that were exponential vs, time describing the longitudinal aspect of the effect. The response value was transformed into the logit scale to restrict the estimated probability values between 0 and 1 as shown in the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
where Pr is the probability, g is the inverse logit function to transform the treatment effect, which is the sum of placebo (f 0) and drug effect (f drug) to the probability scale. The parameter k pbo and k drug are rate constants describing onset of placebo and drug effects, respectively, with a modeled unique estimate for each drug.
The dose–response component of the model was described by a sigmoidal Emax function. The model estimated the parameters for A (intercept), B (asymptote on placebo model), E (asymptote on drug model), ED 50 (dose achieving 50% of maximal response), for each drug. The normalized dose by the regulatory approved dose regimen, or normalized dose by the most frequently reported dose regimen (for nonapproved drugs) was used to account for different doses or unique titration schemes for each drug during clinical studies. The Hill coefficient (γ) was also tested in the model. However, the parameter(s) were not estimated for rate constant or dose–response terms if there was not sufficient longitudinal or dose–response information available for a certain drug. The between‐study variability was described by η, having a normal probability distribution with mean 0 and variance ω2.
Landmark model
A joint analysis of the efficacy endpoints (PASI50, 75, 90, and 100) was performed to estimate differences in relative effect for each endpoint by treatment. The response variable was the percentage of patients achieving PASI50, 75, 90, and 100 at each trial endpoint, typically 12 weeks postfirst‐dose administration.
The structure for the joint meta‐regression model of PASI50, PASI75, PASI90, and PASI100 responses is summarized in Equations 5 through (8). The final model was structured as follows:
| (5) |
where represents the probability (%) of a patient having an event for the k th endpoint in the j th treatment arm of the i th trial and g was the inverse logit function to transform the treatment effect to the probability scale.
captures the estimated placebo response in PASI75 scores for a patient with body weight 90 kg (approximate median of the dataset) in the i th trial as defined in Equation 6. A different placebo response was estimated for every trial with a constant fixed shift between PASI levels.
| (6) |
where trial i is a baseline placebo effect for the i th trial; I 1, I 2 and I 3 are coefficients for PASI50, PASI90, or PASI100 relative to PASI75 scores.
E drug represents the drug‐response with drug‐specific model parameters, such as maximum response for each drug (em d) and an effective dose for each individual drug (ED 50,d). For the traditional oral systemic treatments (methotrexate, cyclosporine, and acitretin), the optimal PASI responses were achieved in practice by flexible dose adjustment for each patient, based on safety and efficacy. Therefore, there were insufficient data in the literature to fully describe the dose–response relationship for these drugs. As such, the maximum responses for traditional oral systemic agents were modeled as single‐step offsets (Equation 7).
For TNF‐α inhibitor, IL‐12/23 inhibitor, IL‐17 inhibitor, CD2 antagonist, PDE4 inhibitor, and JAK inhibitor, a sigmoidal E max function was used to describe the relationship between dose and PASI response for each drug (Equation 7). As with E 0, a scaling factor was applied to the estimated E max to account for differences in PASI75, PASI50, PASI90, and PASI100 scores (Equation 8).
| (7) |
| (8) |
In the above equations, em d represented the drug‐specific maximum effect; γ d was the Hill coefficient; ED 50,d was the estimated dose of half of the maximum effect and I 5, I6, and I 7 were scaling factors applied to PASI50, PASI90, and PASI100 scores, respectively. In this analysis, a single Hill coefficient was applied to all drug classes except for IL‐17 inhibitors. The dose–response curve for IL‐17 inhibitors was sufficiently different from other drugs of interest that an individual offset was required to more appropriately describe the dose–response relationship.
The random effect η i,k on overall drug response (E 0 + E drug) was defined as having a mean 0 and variance . The model included terms to account for the correlation between different PASI scores (i.e., PASI50, PASI75, PASI90, or PASI100) within the same study and to account for the correlation between PASI scores among different arms within the same study.
Covariate model
Based on previous knowledge,12, 13 body weight was an important determinant of efficacy in patients with psoriasis. Therefore, body weight was tested as a covariate in the longitudinal model and in the landmark model if body weight data were available in the literature (aggregated level, either by study arm or stratified by body weight), as described in Equations 9 and 10, respectively:
| (9) |
| (10) |
If body weight data were not reported (10–15% of studies in the literature), WEIG was set to 90 so that there was no influence on the covariate estimation. The weight effect was tested on the treatment effect of the drug (E max, ED50, or k drug), as well as on the placebo effect (E 0).
Residual error model
In both the longitudinal and landmark analyses, the predicted PASI responses represented the probability of ≥50, ≥ 75, ≥ 90, or 100% improvement in PASI scores. The residual error component (ɛ) had a normal probability distribution with mean 0 and variance σ2. Weight based on standard errors of fitted values (see Equations 11 and 12) was noted as W, and the number of subjects for each arm within each study to account for the effect on parameter estimation due to the size of each trial was noted as N. Because studies were weighted by inverse of standard errors, larger studies had more influence on estimating the parameter means.
| (11) |
| (12) |
Additionally, due to the longitudinal nature of the data and correlation within timepoint measurements of the same group of patients,14 a third level of variability (with mean 0 and variance ) was also incorporated into the longitudinal model as shown below:
| (13) |
The standard model diagnostics (e.g., goodness‐of‐fit plots, precisions of the parameter estimates) were performed for both models to assess the model adequacy and any residual error model misspecifications.
Simulations
Simulations were performed using the final model parameter estimates. The results were overlaid with observed data for both time course (longitudinal) and dose–response at 12 weeks (landmark) data by drug (and by dose) to visually compare the results and confirm the model performance. Predicted PASI75 responses generated from the longitudinal model were compared to predicted PASI75 responses from the landmark model to demonstrate consistency between the models. ET50 and ET90 (the time to reach 50% and 90% of the maximal treatment effect) were also calculated from the longitudinal model.
The final landmark model was used to simulate PASI75 or PASI90 responses at Week 12 for a typical patient with moderate to severe psoriasis for each drug at clinically recommended doses. Placebo‐adjusted treatment effect (effect size) for each drug was summarized in a forest plot.
External validation
External validation was performed for PASI90 time‐course response (using the validation dataset), in which the final model for longitudinal PASI75 was used to simulate (N = 1,000) the PASI90 time‐course by incorporating the scaling factor between PASI75 and PASI90 obtained from the landmark model, then overlaid with the observed PASI90 time‐course data.
Modeling software
Longitudinal data analyses were conducted using Nonlinear Mixed Effect Modeling software NONMEM (v. 7.3) using the first‐order conditional expectation method. A nonlinear mixed‐effects routine in S‐PLUS 8.0.4 for Windows (Insightful, Seattle, WA) was used for the landmark analysis. The input datasets and model outputs were manipulated and all graphical displays were generated using R (v. 3.0.2) and Rstudio (v. 0.99.879). Bootstrap was performed using PsN (v. 3.5.4).
Supporting information
Supplementary Table 1. Final Parameter Estimates for Longitudinal Model
Table S1.1. Drug‐Specific Parameter Estimates from NONMEM Output
Table S1.2. Common Parameter Estimates from NONMEM Output
Supplementary Table 2. Final Parameter Estimates for Landmark Model
Supplementary Appendix
References for all studies included in the model‐based meta‐analysis
Code and sample dataset for the longitudinal PASI75 model (NONMEM)
Code and sample dataset for the landmark joint PASI (PASI‐50, –75, –90, –100) model (S‐plus)
ACKNOWLEDGMENTS
The first two authors contributed equally to this work. This study was sponsored by Pfizer Inc. Editorial support, under direction from the authors, was provided by Alice MacLachlan, PhD, of Complete Medical Communications, and funded by Pfizer Inc.
CONFLICTS OF INTEREST
K.I, S.A., P.G, R.W, H.V., H.T., S.K., and A.T. are employees and shareholders of Pfizer Inc. T.C., and M.K. were employees of Pfizer Inc at the time of the analysis. J.M. has acted as a consultant for Pfizer Inc. L.P. has received consultancy/speaker's honoraria from AbbVie, Almirall, Amgen, Biogen, Boehringer, Celgene, Gebro, Janssen, Leo‐Pharma, Lilly, Merck‐Serono, MSD, Novartis, Pfizer Inc, and Sandoz. L.P. has participated in a company‐sponsored speaker's bureau for Celgene, Janssen, MSD, Novartis, and Pfizer Inc.
AUTHOR CONTRIBUTIONS
K.I., T.C., S.A., P.G., J.W.M., L.P., R.W., H.V., H.T., S.K., A.T., and M.K. wrote the article; K.I., T.C., S.A., P.G., J.W.M., R.W., H.V., H.T., S.K., A.T., and M.K. designed the research; K.I., T.C., and S.A. analyzed the data.
References
- 1. SchöN, M.P. & Boehncke, W.H. Psoriasis. N. Engl. J. Med. 352, 1899–1912 (2005). [DOI] [PubMed] [Google Scholar]
- 2. Menter, A. et al Guidelines of care for the management of psoriasis and psoriatic arthritis: Section 6. Guidelines of care for the treatment of psoriasis and psoriatic arthritis: case‐based presentations and evidence‐based conclusions. J. Am. Acad. Dermatol. 65, 137–174 (2011). [DOI] [PubMed] [Google Scholar]
- 3. Papp, K.A. et al Tofacitinib, an oral Janus kinase inhibitor, for the treatment of chronic plaque psoriasis: results from two, randomized, placebo‐controlled, phase iii trials. Br. J. Dermatol. 173, 949–961 (2015). [DOI] [PubMed] [Google Scholar]
- 4. Bachelez, H. et al Tofacitinib versus etanercept orplacebo in moderate‐to‐severe chronic plaque psoriasis: a phase 3 randomised non‐inferiority trial. Lancet 386, 552–561 (2015). [DOI] [PubMed] [Google Scholar]
- 5. Bissonnette, R. et al Tofacitinib withdrawal and retreatment in moderate‐to‐severe chronic plaque psoriasis: a randomized controlled trial. Br. J. Dermatol. 172, 1395–1406 (2015). [DOI] [PubMed] [Google Scholar]
- 6. Lambert, P.C. , Sutton, A.J. , Abrams, K.R. & Jones, D.R. A comparison of summary patient‐level covariates in meta‐regression with individual patient data meta‐analysis. J. Clin. Epidemiol. 55, 86–94 (2002). [DOI] [PubMed] [Google Scholar]
- 7. Abrahamowicz, M. et al Bias due to aggregation of individual covariates in the cox regression model. Am. J. Epidemiol. 160, 696–706 (2004). [DOI] [PubMed] [Google Scholar]
- 8. Higgins, J.P. & Thompson, S.G. Quantifying heterogeneity in a meta‐analysis. Stat. Med. 21, 1539–1558 (2002). [DOI] [PubMed] [Google Scholar]
- 9. Torres, T. & Puig, L. Treatment goals for psoriasis: should PASI 90 become the standard of care? Actas Dermosifiliogr. 106, 155–157 (2015). [DOI] [PubMed] [Google Scholar]
- 10. Puig, L. , LóPez, A. , Vilarrasa, E. & GarcíA, I. Efficacy of biologics in the treatment of moderate‐to‐severe plaque psoriasis: a systematic review and meta‐analysis of randomized controlled trials with different timepoints. J. Eur. Acad. Dermatol. Venereol. 28, 1633–1653 (2014). [DOI] [PubMed] [Google Scholar]
- 11. O'Conner, D. , Green, S. & Higgins, J.P.T. Defining the review question and developing criteria for including studies In: Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0 (eds. Higgins J.P.T. &. Green S.) (2011). [Google Scholar]
- 12. Gupta, P. et al A model‐based meta‐analysis for dose response comparison of psoriasis treatments. J. Am. Acad. Dermatol. 72, Suppl 1, (2015). [Google Scholar]
- 13. Mandema, J. et al Evaluation of the impact of body weight on the efficacy of biologic therapies for the treatment of psoriasis: a dose–response meta‐analysis. Abstract presented at the Psoriasis 2013 – 4Th International Congress On Psoriasis (2013).
- 14. Ahn, J.E. & French, J.L. Longitudinal aggregate data model‐based meta‐analysis with NONMEM: approaches to handling within treatment arm correlation. J. Pharmacokinet. Pharmacodyn. 37, 179–201 (2010). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1. Final Parameter Estimates for Longitudinal Model
Table S1.1. Drug‐Specific Parameter Estimates from NONMEM Output
Table S1.2. Common Parameter Estimates from NONMEM Output
Supplementary Table 2. Final Parameter Estimates for Landmark Model
Supplementary Appendix
References for all studies included in the model‐based meta‐analysis
Code and sample dataset for the longitudinal PASI75 model (NONMEM)
Code and sample dataset for the landmark joint PASI (PASI‐50, –75, –90, –100) model (S‐plus)


