Investigating the use of texture features for analysis of breast lesions on contrast-enhanced cone beam CT

Abstract

Cone beam computed tomography (CBCT) has found use in mammography for imaging the entire breast with sufficient spatial resolution at a radiation dose within the range of that of conventional mammography. Recently, enhancement of lesion tissue through the use of contrast agents has been proposed for cone beam CT. This study investigates whether the use of such contrast agents improves the ability of texture features to differentiate lesion texture from healthy tissue on CBCT in an automated manner. For this purpose, 9 lesions were annotated by an experienced radiologist on both regular and contrast-enhanced CBCT images using two-dimensional (2D) square ROIs. These lesions were then segmented, and each pixel within the lesion ROI was assigned a label – lesion or non-lesion, based on the segmentation mask. On both sets of CBCT images, four three-dimensional (3D) Minkowski Functionals were used to characterize the local topology at each pixel. The resulting feature vectors were then used in a machine learning task involving support vector regression with a linear kernel (SVRlin) to classify each pixel as belonging to the lesion or non-lesion region of the ROI. Classification performance was assessed using the area under the receiver-operating characteristic (ROC) curve (AUC). Minkowski Functionals derived from contrast-enhanced CBCT images were found to exhibit significantly better performance at distinguishing between lesion and non-lesion areas within the ROI when compared to those extracted from CBCT images without contrast enhancement (p < 0.05). Thus, contrast enhancement in CBCT can improve the ability of texture features to distinguish lesions from surrounding healthy tissue.

1. MOTIVATION/PURPOSE

Breast cancer is the most frequently diagnosed cancer among women and the second leading cause of cancer-related mortality among women [1]. In this research context, cone-beam CT (CBCT) has found use in mammography owing to its ability to extract three-dimensional (3D) image data, thus resulting in improved visualization of structures and while eliminating the hard compression of breasts [2]. This imaging modality also provides better coverage of the inferior, posterior, medial and lateral portions of the breast [3]. Finally, we note that the average radiation dose from cone-beam breast CT is generally within the range of that from conventional mammography [3].

This study was conducted to investigate the use of texture features in distinguishing between lesion and surrounding healthy tissue on CBCT images in the presence and absence of contrast enhancement. For this purpose, texture features derived from Minkowski Functionals were used to characterize both lesion and non-lesion areas by capturing local topological properties. Such Minkowski Functionals have been previously used for pattern recognition problems in medical imaging, such as classifying between healthy and pathological lung tissue on CT [4], estimating the bone strength through analysis of trabecular micro-architecture [5], classifying benign and malignant lesions on dynamic breast MRI [6], characterizing healthy and osteoarthritic patellar cartilage on phase contrast x-ray computed tomography [7], etc.

The goal of this work is evaluate the use of such topological descriptors in characterizing gray-level patterns corresponding to lesion and non-lesion areas in the presence and absence of contrast enhancement on CBCT. For this purpose, such features are extracted on a pixel-wise basis within regions of interest (ROI) placed on regular and contrast-enhanced CBCT images. Such features are subsequently used in a machine learning task that attempts to predict the label pixels within the ROI, as discussed in the following sections. This work is embedded in our group’s endeavor to expedite ‘big data’ analysis in biomedical imaging by means of advanced pattern recognition and machine learning methods for computational radiology, e.g. [8–25].

2. DATA

The CBCT for breast imaging system employed a horizontally oriented gantry beneath a subject support table, which incorporated an x-ray tube with a 0.3 mm focal spot at one end and a high-resolution, 40×30 cm real-time flat panel detector (FPD) (Rad-70, PaxScan 4030CB, respectively, Varian Medical Systems, Salt Lake City, Utah) at the opposite end. The gantry rotated 360° around the subject’s breast, acquiring 300 pulsed projection images at ~8 ms each. The system was designed and built in compliance with the national and international safety standards for medical equipment.

After acquisition of pre-contrast CBCT data, a bolus injection of 1ml/kg body weight of low osmolar, nonionic, 300–350 mgI/ml iodinated contrast agent was administered for acquisition of contrast-enhanced CBCT images. Specialized 3D visualization software constructed a 3D model of the breast from the acquired images taken during the rotational x-ray sequence.

In the manner described above, pre-contrast and post-contrast CBCT exams from 9 female patients were analyzed as part of this IRB-approved study. Two of the patients had benign lesions while the rest had malignant lesions; the primary lesion in each study was annotated with volumes of interest (VOI) by an experienced radiologist. Following annotation, the central slice of each lesion was chosen for further analysis. For the extraction of local volumetric features at every pixel on the central slice, the 4 slices above and below the central slice were also used. In 7 of the VOIs, this central slice consisted of an 83×83 square ROI that encapsulated the lesion; the 2 remaining cases had ROI of 103×103 pixels encapsulating the lesion. The voxel resolution of the image data analyzed was 0.27×0.27×0.27mm³.

3. METHODS

3.1 Feature analysis

Minkowski Functionals (MFs) are used to characterize morphological properties of binary images i.e. shape (geometry) and connectivity (topology) [26]. Four such features i.e. volume, surface, mean breadth and Euler characteristic can be calculated from binary volumes as follows –

$${\text{MF}}_{\text{volume}}={\mathrm{n}}_{\mathrm{c}}$$

$${\text{MF}}_{\text{surface}}=-6{\mathrm{n}}_{\mathrm{c}}+2{\mathrm{n}}_{\mathrm{f}}$$

$${\text{MF}}_{\text{breadth}}=3{\mathrm{n}}_{\mathrm{c}}-2{\mathrm{n}}_{\mathrm{f}}+{\mathrm{n}}_{\mathrm{e}}$$

$${\text{MF}}_{\text{euler}}=-{\mathrm{n}}_{\mathrm{c}}+{\mathrm{n}}_{\mathrm{f}}-{\mathrm{n}}_{\mathrm{e}}+{\mathrm{n}}_{\mathrm{v}}$$

where “n_c“ is the total number of white voxels, “n_f“ is the total number of faces, “n_e“ is the total number of edges and “n_v“ is the number of vertices. It has been shown in literature that morphological properties of objects in an image can be fully specified in terms of Minkowski Functionals [9,27]. Such features can be extracted from gray-level images by binarizing them with several thresholds and computing Minkowski Functionals on the resulting black & white images. In this work, the gray level distributions in each VOI was first quantized and then used as thresholds to calculate the 3D MF features. The results are shown in Figure 1.

Figure 1.

The central slice of an example benign and a malignant lesion; the original contrast-enhanced CBCT images are shown on the left, the binarized images are shown on the right.

In this study, such topological texture features were extracted locally through binarization of the 9×9×9 pixel³ neighborhood surrounding each pixel on the central slice of the lesion with 5 thresholds. This yields four 5-D feature vectors for each voxel, one vector per Minkowski Functional.

3.2 Classification

Once feature vectors were extracted for every pixel on the 9 lesion slices from both pre-contrast and contrast-enhanced images, the goal was then to use them in a machine learning task to predict their label as lesion or non-lesion in each case. Support vector regression [28] with a linear kernel (SVRlin) was used for the machine learning task. In order to characterize unknown VOIs, models are created based on known labeled data in the training set. The goal is to optimize classifier parameters so that they can model the best hyperplane and margins between the lesion and non-lesion classes.

In order to generalize the classification performance, the classifier was optimized using a training set of labeld VOIs and the accuracy was calculated on an independent test set. For each iteration, the feature vectors were divided into a 70% training set and a 30% test set. To ensure that feature vectors from the same patient did not serve in both training and test sets simultaneously, the 70–30 split was applied to the patients that the feature vectors were extracted from.

The training phase employed a sub-sampling cross-validation strategy where the cost parameter of the classifier was optimized using the training set. Then, during the testing phase, the trained classifier was used to evaluate the label of the feature vectors in the test set. An ROC curve was generated and used to compute the area under the curve (AUC). This process was repeated 50 times resulting in an AUC distribution for each feature (Minkowski Functional). A Wilcoxon signed rank was used to compare the AUC distributions of different features extracted from pre-contrast and contrast-enhanced images.

The SVRlin classifier was taken from LIBSVM library and implemented in MATLAB R2008b. The statistical analysis was also implemented using MATLAB R2008b (The MathWorks, Natick, MA).

4. RESULTS

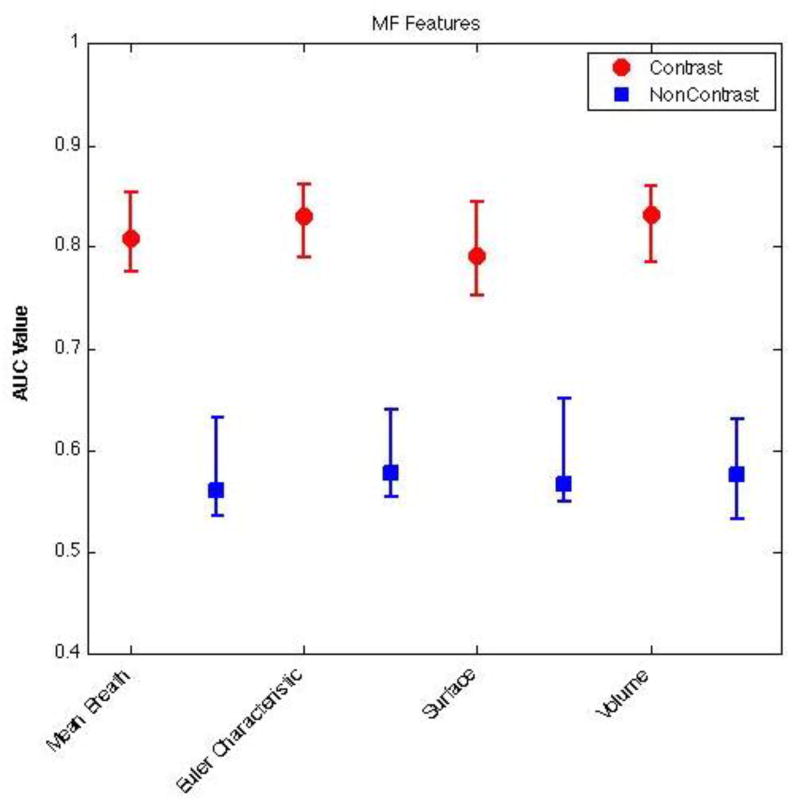
Figure 2 shows the classification performance of different Minkowski Functionals at distinguishing between lesion and non-lesion regions within ROIs annotated on pre-contrast and contrast-enhanced CBCT images. As seen, here, the best classification results were obtained by using Minkowski Functionals that were extracted from contrast-enhanced CBCT images. In fact, the classification performance with support vector regression when Minkowski Functionals were extracted from contrast-enhanced CBCT images was significantly better than when they were extracted from non-enhanced CBCT images (p < 0.05). The highest accuracy was found for the Minkowski Functional Euler characteristic for both contrast-enhanced and pre-contrast CBCT images.

Figure 2.

Classification performance of Minkowski Functionals extracted from pre-contrast (blue) and contrast-enhanced (red) CBCT images. For each distribution, the central mark corresponds with the median and the edges are the 25th and 75th percentile. As seen here, Minkowski Functionals extracted from contrast-enhanced CBCT images are significantly better at distinguishing between lesion and non-lesion regions (p < 0.05).

5. DISCUSSION

Cone beam computed tomography (CBCT) has been recently investigated for use in mammography for its ability to acquire volumetric image data of the entire breast with sufficient spatial resolution at a radiation dose comparable to that of conventional mammography. The primary goal of this study was to investigate whether contrast injection on CBCT images could increase lesion detection accuracy. To address this problem, this study investigated and quantified the ability of topological texture features derived from Minkowski Functionals to distinguish between lesion and healthy tissue on CBCT images in the presences and absence of contrast enhancement.

As observed in this work, the ability of such features to accurately identify pixels as belonging to lesion or non-lesion (healthy tissue) regions is significantly improved in the presence of contrast enhancement. This is likely due to the lesion tissue enhancement provided by such contrast, which allows imaging markers such as texture features to capture lesion characteristics and distinguish them from non-enhancing healthy tissue. Such features have significant potential to contribute to automatic lesion detection in contrast-enhanced CBCT exams. The improvement in classification performance noted with texture features in this study could also be attributed to higher contrast resolution and the reduced tissue overlap in CBCT imaging.

The results presented in this work suggest that characterizing lesion morphology on contrast enhanced CBCT breast images using topological texture features can significantly improve the performance in determining the potential lesion areas. These results have significant clinical implications in the sense that such a topological characterization of the contrast-enhanced lesion pattern can contribute to automatic lesion detection.

We acknowledge that the inclusion of only nine datasets was a limiting factor of this study. A larger collection of datasets will be required in future studies for validating the clinical applicability of our approach.

6. CONCLUSION

This study investigated the ability of topological texture features derived from Minkowski Functionals to differentiate between lesion and healthy tissue on CBCT images in the presence and absence of contrast enhancement. Our results show that such imaging markers are best able to distinguish between lesion and healthy tissue regions when contrast-enhanced CBCT images are used.