Subgroup Detection and Sample Size Calculation with Proportional Hazards Regression for Survival Data

Abstract

In this paper, we propose a testing procedure for detecting and estimating the subgroup with an enhanced treatment effect in survival data analysis. Here, we consider a new proportional hazards model which includes a nonparametric component for the covariate effect in the control group and a subgroup-treatment interaction effect defined by a change-plane. We develop a score-type test for detecting the existence of the subgroup, which is doubly robust against misspecification of the the baseline effect model or the propensity score but not both under mild assumptions for censoring. When the null hypothesis of no subgroup is rejected, the change-plane parameters that define the subgroup can be estimated based on supremum of the normalized score statistic. The asymptotic distributions of the proposed test statistic under the null and local alternative hypotheses are established. Based on established asymptotic distributions, we further propose a sample size calculation formula for detecting a given subgroup effect and derive a numerical algorithm for implementing the sample size calculation in clinical trial designs. The performance of the proposed approach is evaluated by simulation studies. An application to an AIDS clinical trial data is also given for illustration.

1. Introduction

Personalized medicine, a practice of medicine tailored to a patient’s genetic and other unique characteristic, is a rapidly emerging field of health care. The ultimate goal of personalized medicine is to optimize the benefit of treatment by prescribing the right drugs for the right patients with minimal side effects. To ensure the success of personalized medicine, it is important to identify a subgroup of patients who benefits more from the targeted treatment than others based on each patient’s characteristic. For this reason, the subgroup analysis, if properly used, can lead to more informed clinical decisions, improved efficiency of the treatment, reduced cost and side effects.

The subgroup analysis has been explored by a number of authors. For the cases of a single covariate, [1] used a moving average procedure to estimate treatment effect on the overlapping subsets of patients determined by a covariate of interest. [2] proposed a selection impact curve (SIC) for the treatment response rate given two subgroups determined by a patient’s marker value. Using the SIC function, they identified the optimal division for the treatment assignment which maximizes the overall response rate. For the cases of multiple covariates, [3] proposed a virtual twins method based on potential outcomes, and identified the subgroup with an enhanced treatment effect using machine learning approaches. [4] and [5] proposed parametric scoring systems as a function of subject specific treatment differences based on multiple baseline covariates. This function can be used for identifying a subgroup of patients whose benefits outweigh the risk and cost of the new treatment. Other approaches include [6], [7], [8] and [9].

Whatever the plan is for subgroup identification, it should be specified prior to looking at the data. However, the statistical concerns about the use of subgroup analysis are well recognized. The repeated use of subgroup identification without proper adjustment may lead to inflation of type I error, i.e, the observed significant results could arise by chance. The other issue is lack of power for clinical trials which are generally designed to test the overall treatment effect. Thus, subgroup analysis must be performed with a confirmatory testing and careful study design. Recently, [10] proposed a logistic-normal model for the response in each subgroup and the latent group membership. Under the parametric assumptions, they perform a likelihood ratio test for the existence of a subgroup with differential treatment effects, and predict the subgroup membership of each patient. [11] used a semiparametric approach in which the baseline mean function is unspecified while the interaction between treatment and the change plane indicator explicitly models a subgroup with an enhanced treatment effect. They propose a score type test statistics and develop a novel procedure to calculate the sample size based on the proposed test. This test enjoys the double robustness property, i.e, it is valid when either the baseline mean function or the propensity score is correctly specified. These studies mainly focus on uncensored data. [12] extended the method of [10] to a logistic-Cox regression for survival data. However, it requires strong parametric assumptions for covariate effects as in [10].

In this paper, we extend the testing procedure of [11] to detect the existence of a subgroup with an enhanced treatment effect for survival data. The proportional hazards model is widely used for analysis of survival data and for designing clinical trials with time-to-event endpoints. In subgroup analysis, the main interest is to study the treatment-covariates interactions. Thus, we consider a flexible proportional hazards model which includes an unspecified baseline effect model and the interaction between treatment and subgroup indicator defined by a change plane. However, as discussed later in the paper, our proposed test will have the correct type I error under the null hypothesis even when the proportional hazards assumption does not hold. On the other hand, the power and sample size calculation derived under the local alternative hinges on the assumed proportional hazards model. In particular, the considered change-plane approach for subgroup representation facilitates the derivation of sample size calculation, which is useful in clinical trail designs for subgroup detection. We propose a doubly robust score-type test using a change-plane analysis technique and derive the asymptotic distributions of the proposed test under both the null and local alternative hypotheses. The associated sample size calculation for clinical trial designs in subgroup analysis is also investigated. For censored survival data, the derivation of the doubly robust score-type test for subgroup detection is more challenging and it requires a stronger assumption for censoring times.

The rest of the paper is organized as follows. In Section 2, we introduce the new proportional hazards model for subgroup detection and the associated estimating equation for treatment-subgroup interaction. In Section 3, we construct the score-type test statistic based on the change-plane analysis technique and establish the asymptotic distributions of the test statistic under the null and local alternative hypotheses. The associated sample size calculation formula and its numerical implementation are also given. Section 4 and 5 are devoted to numerical studies including simulations and an AIDS data application. Concluding remarks are given in Section 6. All technical proofs are provided in the Appendix.

2. Data, Model, and Score Test

2.1. Data and model

Consider a study with n independent subjects. For the ith subject, we observe the p-dimensional vector of covariates X_i and treatment indicator A_i taking 0 and 1 for control and treatment, respectively. Let T_i and C_i denote the survival time of interest and censoring time, respectively. Assume that T_i and C_i are independent given covariates and treatment. Then, the observed data consists of independent and identically distributed triplets, {(X_i,A_i, T̃_i,Δ_i), i = 1, . . . , n}, where T̃_i = min(T_i, C_i) and Δ_i = I(T_i ≤ C_i). Define the counting process and at-risk process as N_i(t) = I( T̃ ≤ t, δ_i = 1) and Y_i(t) = I( T̃_i > t), respectively.

We consider the following proportional hazards model ([13]) for the failure times,

$$\lambda (t\mid A_i,X_i)=\lambda (t)e^{\varphi (X_i)+\eta A_{i}I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)}$$ (1)

where λ(t) is an unspecified baseline hazard function and ϕ(X_i) is an unspecified baseline effect model of covariates. The change plane I(γ′ X̃_i ≥ 0) defines a subgroup of patients with an enhanced treatment effect η. Here, X̃_i = (1,X_i)′ and γ = (γ₁, . . . , γ_p+1)′. For identifiability, we assume ||γ|| = 1. Our interest is to test the existence of subgroup with an enhanced treatment effect, i.e. H₀ : η = 0vs H_a : η ≠ 0. There are several challenges here. First, under the null hypothesis H₀, the parameters γ are not identifiable. Second, the baseline effect model ϕ(·) is unspecified. A testing procedure that is robust to the misspecification of ϕ(·) is desired.

2.2. Score test for η

Given the true values of γ, λ(·) and ϕ(·), a score test statistic for η can be constructed as

$$\sum _{i=1}^n{\int }_0^{\infty }I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)A_i\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i)}d\mathrm{\Lambda }(t)\}.$$ (2)

However, when ϕ(·) is misspecified, the above score test statistic is biased. It is of great interest to develop a robust test statistic that is insensitive to the misspecification of ϕ(·). For uncensored data, [11] developed a doubly robust score-type test statistic, which is consistent when either the baseline effect model or the propensity score is correctly specified. For the considered model (1), a natural extension is to consider the following test statistic

$$\sum _{i=1}^n{\int }_0^{\infty }I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i;\nu )\}\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\theta )}d\mathrm{\Lambda }(t)\},$$ (3)

where π(X_i; ν) and ϕ(X_i; θ) are the posited parametric models for the propensity score π(X_i) = P(A_i = 1|X_i) and the baseline effect model ϕ(X_i), respectively. In clinical trials, the propensity score is known by design but the baseline effect model ϕ(·) is generally unknown.

Test statistic (3) is unbiased under the null when the baseline effect model ϕ(·; θ) is correctly specified. However, it is generally biased under the null when the propensity score is correctly specified but the baseline effect model is misspecified as commonly seen in clinical trials. A main reason is that A_i and Y_i(t) are not independent given X_i under the null. To ensure the doubly robust property of test statistic (3), we make the following assumption for the censoring time: C_i is independent of A_i given X_i. In fact, this assumption only needs to hold under the null. Under this assumption, A_i and Y_i(t) are independent given X_i under the null. Then, it can be shown that (3) is unbiased when either the baseline effect model or the propensity score is correctly specified, i.e. the so-called doubly robust property. The assumed assumption for censoring is a little stronger than the usual conditional independent censoring assumption, where C_i and T_i are assumed independent given X_i and A_i. That is C_i is allowed to depend on both X_i and A_i; while in our assumption, C_i is allowed to depend on X_i but not A_i. This assumption usually holds in a well followed clinical trial. In the next section, we derive a supremum test statistic based on the doubly robust score-type test statistic (3).

3. Proposed Test and Sample Size Calculation

3.1. The proposed test

From now on, we consider a randomized clinical trial, where the propensity score π(X_i) is known. Define

$$g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )=\sum _{i=1}^n{\int }_0^{\infty }I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\widehat{\theta })}d\widehat{\mathrm{\Lambda }}(t)\},$$ (4)

where θ̂ and Λ̂(t) are estimators of θ and Λ(t) under the null, respectively. Specifically, the estimating equations for θ and Λ(t) are given by

$$\sum _{i=1}^n{\int }_0^{\infty }\frac{\partial \varphi (X_i;\theta )}{\partial \theta }\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\theta )}d\mathrm{\Lambda }(t)\}=0,$$ (5)

$$\sum _{i=1}^n\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\theta )}d\mathrm{\Lambda }(t)\}=0,$$ (6)

respectively. In our numerical studies, we always consider a linear model ϕ(X_i; θ) = θ′X_i.

Note that the score-type test statistic (4) depends on the unknown parameters γ, which are not identifiable under the null. To deal with the nonidentifiability issue, following [11], we consider a supremum of normalized squared score-type test statistic. That is

$$W_n={sup}_{\gamma \in \mathrm{\Gamma }}\frac{{\{{\sum }_{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )\}}^2}{n{S}_n(\gamma )}$$ (7)

where Γ = {γ ∈ ℝ^p+1 : ||γ|| = 1} and S_n(γ) is a consistent estimator for the variance of $n^{-1/2}{\sum }_{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )$. The derivation of S_n(γ) is given in the Appendix.

Next, we derive the asymptotic distributions of W_n under the null and local alternative hypotheses. For the local alternative hypothesis, we consider $H_a:\eta =\delta /\sqrt{n}$, where δ ≠ 0.

Theorem 1

Assume either the baseline effect model or the propensity score model is correctly specified. Under the null hypothesis and regularity conditions given in the Appendix, as n→∞, we have W_n converges in distribution to sup_γ∈ΓH²(γ), where H(γ) is a mean-zero Gaussian process with the asymptotic covariance given by

$$\mathrm{\sum }({\gamma }_1,{\gamma }_2)=\frac{E\{g(X,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };{\gamma }_1)g(X,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };{\gamma }_2)\}}{\sqrt{E\{g^2(X,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };{\gamma }_1)\}E\{g^2(X,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };{\gamma }_2)\}}}.$$

Here θ^* and Λ^*(t) are the limits of θ̂ and Λ̂(t), respectively.

Theorem 2

Assume either the baseline effect model or the propensity score model is correctly specified. Under the local alternative hypothesis and regularity conditions given in Appendix, as n → ∞, we have W_n converges in distribution to sup_γ∈ΓH²(γ; δ), where H(γ; δ) is a Gaussian process with the mean function μ(γ) and covariance function Σ(γ₁, γ₂). Here, the mean function is given by

$$\mu (\gamma )=\delta E\left[\pi (X)\{1-\pi (X)\}I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0,{\gamma }_0^{\prime }\stackrel{\sim }{X}\ge 0)e^{\varphi (X;{\theta }^{\ast })-\varphi (X)}\mathrm{\Delta }\right]/\sqrt{E\{g^2(X,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };\gamma )\}}$$

where γ₀ is the true value of γ.

To obtain the critical values of the proposed test statistic, we propose a resampling method. As shown in the Appendix, when the propensity score π(·) is known, we have

$$n^{-1/2}\sum _{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )=n^{-1/2}\sum _{i=1}^{n}g(X_i,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };\gamma )+o_p(1).$$

Therefore, the perturbed test statistic is given by

$${\stackrel{\sim }{W}}_n={sup}_{\gamma \in \mathrm{\Gamma }}\frac{{\{{\sum }_{i=1}^n{\xi }_{i}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )\}}^2}{n{S}_n(\gamma )},$$ (8)

where {ξ_i, i = 1, . . . , n} are n i.i.d. standard normal random variables. It is easy to show that the perturbed test statistics has the same limiting distribution as the original test statistic. Thus, by repeatedly generating {ξ₁, . . . , ξ_n}, we can obtain a large set of W̃_n’s. The critical value, c_α for a level-α test can be estimated by the empirical (1 − α)100th quantile of W̃_n’s. Then we reject the null when W_n > c_α. If the null is rejected, the change plane parameter is estimated by

$$\widehat{\gamma }={\text{argsup}}_{\gamma \in \mathrm{\Gamma }}\frac{{\{{\sum }_{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )\}}^2}{n{S}_n(\gamma )},$$ (9)

and the corresponding estimated subgroup is {i : γ̂′ X̃_i ≥ 0}.

In fact, it is difficult, if not impossible, to analytically obtain the supremum in (7), (8), and (9). Thus, we use the maximum as a numerical approximation of the supremum. We find the maximum of the test statistics and perturbed test statistics over a common set of finitely many γ, Γ = {γ₁, γ₂, . . . , γ_M}, where γ_j is a (p + 1) × 1 vector. To generate γ_j with the unit-norm restriction, we use a spherical coordinate transformation. The details are given in the simulation study.

3.2. Sample size calculation

In this section, we propose an algorithm for calculating the required sample size numerically based on Monte Carlo simulations. Based on the asymptotic distribution of the test statistic under the local alternative hypothesis, for a given effect size η, the sample size for a level-α test to achieve 1 − β can be obtained from the following equations

$$P({sup}_{\gamma \in \mathrm{\Gamma }}{H}^2(\gamma ;\delta )>c_{\alpha })=1-\beta ,$$ (10)

$$n={(\delta /\eta )}^2.$$ (11)

To be specific, we first find δ to satisfy equation (10) and then the sample size is determined by (11). For simplicity of computation, we assume that ϕ(X; θ^*) = ϕ(X). With some algebras, the mean and covariance function of H(γ; δ) can be written as

$$\mu (\gamma )=\frac{\delta E[\pi (X)\{1-\pi (X)\}I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0,{\gamma }_0^{\prime }\stackrel{\sim }{X}\ge 0)\mathrm{\Delta }]}{\sqrt{\pi (X)\{1-\pi (X)\}E\{I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0)\mathrm{\Delta }\}}},$$ (12)

$$\mathrm{\sum }({\gamma }_1,{\gamma }_2)=\frac{E\{I({\gamma }_1^{\prime }X\ge 0,{\gamma }_2^{\prime }X\ge 0)\mathrm{\Delta }\}}{\sqrt{E\{I({\gamma }_1^{\prime }X\ge 0)\mathrm{\Delta }\}}\sqrt{E\{I({\gamma }_2^{\prime }X\ge 0)\mathrm{\Delta }\}}}.$$ (13)

We propose to use the following algorithm to numerically find δ as the solution to (12).

• Step 1. Generate Z = (Z₁, , , Z_M) from multivariate normal distribution with mean zero and the covariance Σ(γ₁, γ₂), and compute ${max}_{1\le j\le M}{Z}_j^2$. By repeatedly generating Z = (Z₁, , , Z_M) many times, we can obtain a large sample of ${max}_{1\le j\le M}{Z}_j^2$. The critical value c_α can then be estimated by referring to the empirical (1 − α)100th quantile of the sample.

• Step 2. Given δ, generate Y = (Y₁, . . . , Y_M) from multivariate normal distribution with μ(γ) and the covariance Σ(γ₁, γ₂), and compute the maximum ${max}_{1\le j\le M}{Y}_j^2$ to approximate sup_γ∈ΓH²(γ; δ).

• Step 3. Repeat step 2 B times, where B is a large number, and estimate P(sup_γ∈ΓH²(γ; δ) > c_α) by $B^{-1}{\sum }_{i=1}^{B}I({max}_{1\le j\le M}{Y}_j^2\ge c_{\alpha })$.

• Step 4. Do a grid search for δ and find δ such that the corresponding probability $B^{-1}{\sum }_{i=1}^{B}I({max}_{1\le j\le M}{Y}_j^2\ge c_{\alpha })=1-\beta$.

4. Simulation Study

4.1. Testing and estimation

4.1.1. Type I error

We have carried out several simulation studies to evaluate the performance of the proposed test under various scenarios. Under the null hypothesis, the failure times are generated from the proportional hazards model (1) with η = 0. Two independent covariates are considered; X₁ following a uniform distribution on [−1, 1] and X₂ following a Bernoulli distribution with a success probability of 0.5. We assume the baseline hazard function λ(t) ≡ λ₀, a positive constant. The censoring times are generated from a uniform distribution on [0, c₀], where λ₀ and c₀ were chosen to yield the desired censoring level 15% and 25%.

We consider a randomized clinical trial with the propensity score π(X_i) = 0.5. For the baseline effect model, we consider the following models.

1. ϕ₁(X_i; θ) = θ₁X₁ + θ₂X₂, θ = (θ₁, θ₂) = (0.1, 0.1),

2. ${\varphi }_2(X_i;\theta )={\theta }_1{X}_1+{\theta }_2{X}_2+{\theta }_3{X}_2^2$, θ = (θ₁, θ₂, θ₃) = (0.2, 0,−1),

3. ϕ₃(X_i; θ) = θ₁ sin(θ₂X₂ + θ₃πX₂), θ = (θ₁, θ₂, θ₃) = (0.2, 1, 1).

For model (i), the posited linear baseline effect model is correctly specified, while for model (ii) and (iii), it is misspecified.

To generate Γ, we consider the spherical coordinate (ρ, ψ), where 0 ≤ ρ ≤ π and 0 ≤ ψ ≤ 2π. For each coordinate, we generate 100 grid points. Then, for γ_j, j = 1, . . . , 10000, the spherical transformation from (ρ, ψ) to (γ_j0, γ_j1, γ_j2) is given by γ_0j = cos(ρ), γ_1j = sin(ρ) cos(ψ) and γ_2j = sin(ρ) sin(ψ). In addition, the critical values of the test statistics were computed based on 1000 resampling statistics. Under each scenario, we performed 500 simulations.

For type I error analysis, we consider sample size N = 1000 for the 15% censoring rate while N = 1000 and 2000 for the 25% censoring rate. In Table 1, we report the type I errors of the proposed test for various combinations of baseline effect models and censoring rates. When the censoring rate is 15%, the type I errors are close to the nominal level under all chosen baseline effect models. When the censoring rate is 25% with N = 1000, the type I errors are lower than the nominal level, especially at level of α = 0.1. This may be due to information loss caused by the censoring. Note that the type I error calculation is based on the asymptotic distribution of the supreme statistic given in Theorem 1. When the sample size is not large enough, the asymptotic representation may not be accurate. From our numerical experiences, when the sample size is only hundreds, the type I error obtained by the resampling algorithm may be a little conservative. However, as the sample size increases to N = 2000, the type I errors are close to the nominal level under all scenarios. This implies that the proposed test has the correct size but it may require larger sample sizes to achieve the nominal level when the censoring rate increases.

Table 1.

Type I error of the proposed test

Sample size	Censoring rate	Nominal level	B1	B2	B3
N = 1000	15%	0.05	0.048	0.050	0.048
		0.10	0.098	0.098	0.100
N = 1000	25%	0.05	0.036	0.042	0.044
		0.10	0.072	0.070	0.080
N = 2000	25%	0.05	0.052	0.052	0.048
		0.10	0.104	0.103	0.099

^†B, Baseline effect model; B1 = ϕ₁(X_i; θ), B2 = ϕ₂(X_i; θ), B3 = ϕ₃(X_i; θ).

4.1.2. Power and estimation of change plane

Under the alternative hypotheses, the failure times are generated from the proportional hazards model (1) with η = ±0.2,±0.5,±0.8 and the true change plane parameter γ₀ = (−0.15, 0.3, 0.942). The empirical powers of the proposed test with sample size N = 1000 are given in Table 2. We observe that the power always increases with the increase in the treatment effect size |η|. When the censoring rate is 15%, with the smaller value of |η|, the powers of model 3 are slightly lower than those of models 1 and 2, but the differences get smaller as |η| increases. The powers under the censoring rate 25% are slightly lower than those under the censoring rate 15%. Also, we estimate the change plane parameters based on (9) and the results are given in Table 3. The results for the 15% and 25% censoring rates are comparable, thus we only report the results for the 15% censoring rate here. To evaluate the performance of the proposed test for estimation of the change plane parameter, we reported biases and standard deviations of the estimators and misspecification rates. Here, the misspecification rate is the proportion of patients whose true and the estimated subgroup do not match, and is computed by $\frac{1}{N}{\sum }_{i=1}^N\mid I({\widehat{\gamma }}^T{\stackrel{\sim }{X}}_i\ge 0)-I({\gamma }_0^T{\stackrel{\sim }{X}}_i\ge 0)\mid$. We observe that as |η| increases, the biases, standard deviations, and misspecification rates decrease. In addition, we reported the sensitivity and specificity of our proposed method for subgroup identification and the average size of identified subgroups. The results are given in the Supplementary Appendix. As the magnitude of treatment effect increases, sensitivity and specificity increase, and the estimated subgroup size becomes closer to its true value.

Table 2.

Power of the proposed test

Censoring rate	Treatment effect η	B1		B2		B3
		size 0.05	size 0.1	size 0.05	size 0.1	size 0.05	size 0.1
15%	0.2	0.230	0.344	0.226	0.332	0.194	0.304
	−0.2	0.224	0.334	0.224	0.344	0.214	0.338
	0.5	0.984	0.99	0.982	0.99	0.974	0.986
	−0.5	0.978	0.99	0.98	0.994	0.972	0.982
	0.8	1	1	1	1	1	1
	−0.8	1	1	1	1	1	1
25%	0.2	0.196	0.300	0.190	0.292	0.190	0.286
	−0.2	0.216	0.292	0.208	0.296	0.204	0.288
	0.5	0.976	0.986	0.978	0.977	0.961	0.984
	−0.5	0.956	0.984	0.96	0.982	0.952	0.970
	0.8	1	1	1	1	1	1
	−0.8	1	1	1	1	1	1

^†B, Baseline effect model; B1 = ϕ₁(X_i; θ), B2 = ϕ₂(X_i; θ), B3 = ϕ₃(X_i; θ).

Table 3.

Estimation of the change plane parameters and misspecification rates

		B1			B2			B3
Treatment effect η	Parameter	Bias	SD	MIS	Bias	SD	MIS	Bias	SD	MIS
0.2	γ0	−0.083	0.360	0.350	−0.083	0.360	0.316	−0.085	0.364	0.322
	γ1	−0.237	0.473		−0.224	0.478		−0.248	0.476
	γ2	−0.495	0.626		0.493	0.617		−0.509	0.630
−0.2	γ0	−0.089	0.382	0.325	−0.081	0.378	0.325	−0.074	0.385	0.337
	γ1	−0.227	0.463		−0.232	0.476		−0.243	0.483
	γ2	−0.502	0.620		−0.492	0.609		−0.537	0.634
0.5	γ0	0.055	0.220	0.092	0.067	0.225	0.098	0.071	0.215	0.099
	γ1	−0.072	0.300		−0.077	0.307		−0.075	0.319
	γ2	−0.051	0.134		−0.051	0.125		−0.062	0.146
−0.5	γ0	0.060	0.246	0.112	0.062	0.246	0.110	0.064	0.238	0.107
	γ1	−0.060	0.326		−0.054	0.323		−0.049	0.315
	γ2	−0.082	0.167		−0.085	0.180		−0.076	0.156
0.8	γ0	0.038	0.116	0.043	0.043	0.121	0.044	0.046	0.118	0.047
	γ1	−0.017	0.163		−0.017	0.106		−0.011	0.172
	γ2	−0.013	0.069		−0.014	0.069		−0.016	0.072
−0.8	γ0	0.051	0.161	0.060	0.053	0.162	0.060	0.053	0.156	0.057
	γ1	−0.029	0.207		−0.032	0.211		−0.019	0.197
	γ2	−0.025	0.084		−0.025	0.086		−0.024	0.083

^†B, Baseline effect model; B1 = ϕ₁(X_i; θ), B2 = ϕ₂(X_i; θ), B3 = ϕ₃(X_i; θ). Bias, bias of the estimates; SD, sample standard deviation of the estimates; MIS, misclassification rate for the subgroup.

4.1.3. Comparisons with the method of [12]

We have conducted simulations to compare with the method of [12] (denoted by EM Test). We consider simulation settings with the baseline models B1 and B2, η = 0, 0.2, and 0.5, and sample size N = 1000. Note that under the baseline model B1, the considered logistic-Cox mixture model of [12] is correctly specified while it is misspecified under B2. The simulation results are summarized in Table 4. We observe that when the baseline effect model is correctly specified under B1, the EM Test gives the correct type I errors, and the power of the EM test is slightly smaller than the proposed test. However, under B2, the EM test has inflated type I errors since the considered logistic-Cox mixture model is misspecified. Our proposed test gives the correct type I error under both baseline models B1 and B2, showing its robustness.

Table 4.

Comparisons with the test of Wu et al (2016)

	B1				B2
	EM Test		Proposed Test		EM Test		Proposed Test
η	size 0.05	size 0.1	size 0.05	size 0.1	size 0.05	size 0.1	size 0.05	size 0.1
0	0.048	0.102	0.048	0.098	0.160	0.220	0.050	0.098
0.2	0.160	0.258	0.230	0.344	0.174	0.276	0.226	0.332
0.5	0.944	0.974	0.984	0.990	0.776	0.876	0.982	0.990

4.1.4. More simulations

We have conducted additional simulations for the cases with a heavier censoring rate of 75% and with p = 4 covariates. For saving the space, the detailed descriptions and simulations results are given in the Supplementary Appendix. For the cases with 75% censoring rate, the type I errors of the proposed test are slightly lower than the nominal level with the sample sizes N = 1000 and N = 2000. However, as the sample size increases to N = 3000, the type I errors are close to the nominal level. In addition, the power increases as the sample size increases. For the cases with p = 4 covariates, the type I errors are close to the nominal level and the powers are comparable to those with two covariates. In addition, the computational time increases drastically as the number of covariates increases. However, it took less than one minute on average for one simulation with p = 4. In general, for any fixed p, the test should be valid by our asymptotic theories. However, as the number of covariates increase to a big number, say p = 20, it usually requires a large sample size and a large number of griding points for good empirical performance of the proposed supreme test statistic. Thus, the computation can be intensive.

4.2. Sample size calculation

In this section, we calculate the sample size using the proposed procedure and compute the empirical power based on the obtained sample size. We consider a single covariate which follows a uniform distribution with [−1, 1]. The failure times are generated from λ(t|A_i,X_i) = λ(t)e^{X_i+ηA_iI(X_i>γ₀)} and λ(t|A_i,X_i) = λ(t)e^{sin(πX_i)+ηA_iI(X_i>γ₀)} for setting 1 and setting 2, respectively. Other settings are chosen in the same way as for the type-I error and power simulation studies.

To estimate the mean (12) and covariance function (13), we generate the grid points γ from −1 to 1 and the true change plane parameter γ₀ is set to be −0.5, 0 or 0.5. In Table 5, we calculate the sample size that gives 90% power at the 0.05 level of significance. Based on the obtained sample size, we compute the empirical power of the proposed test.

Table 5.

Power and sample size

		Setting 1		Setting 2
η	γ0	sample size	power	sample size	power
0.2	0.5	6116	0.89	6147	0.89
	0	3015	0.89	3025	0.90
	−0.5	2035	0.89	2089	0.90
0.3	0.5	2718	0.91	2704	0.89
	0	1330	0.91	1330	0.90
	−0.5	893	0.89	921	0.88
0.4	0.5	1510	0.92	1553	0.91
	0	749	0.86	746	0.88
	−0.5	505	0.86	516	0.87
0.5	0.5	964	0.87	961	0.86
	0	479	0.88	477	0.86
	−0.5	320	0.86	329	0.87

^†Setting 1 : λ(t|X_i,A_i) = λ₀(t)e^{X_i+ηA_iI(X_i>γ₀)},

Setting 2 : λ(t|X_i,A_i) = λ₀(t)e^{sin(πX_i)+ηA_iI(X_i>γ₀)}.

Under all scenarios in Table 5, the empirical powers are close to the nominal level. The required sample size increases as the treatment effect size η and the proportion of subjects in the subgroup decrease, which means we need a larger number of subjects to detect a smaller treatment effect or a smaller subgroup.

4.3. Power and subgroup identification with smooth treatment effect

In our proposed model, the subgroup is defined by a change-plane. This implies that there is a discontinuity in the treatment effect between the treated group (A = 1) and the control group (A = 0). In practice, people may be interested in a model with smooth treatment effect among subjects. For example, we may consider the following model:

$$\lambda (t\mid X_i,A_i)=\lambda (t)e^{\varphi (X_i)+\eta A_{i}F({\gamma }^{\prime }{\stackrel{\sim }{X}}_i)},$$ (14)

where F(·) is a smooth cumulative distribution function.

Note that under the null hypothesis H₀ : η = 0, models (1) and (14) are the same. In this Section, we want to evaluate the performance of the proposed test when the true failure times were generated from model (14). The other settings are chosen the same as in the previous simulation study for type-I error and power calculation. For the baseline effect model, we chose ϕ = ϕ₁. For the smooth treatment effect function F, we consider the cumulative distribution function for the standard normal and uniform distribution. We only considered censoring rate 15% with sample size N = 1000.

Since models (1) and (14) are the same under the null, the type-I errors of the proposed test are the same here. In Table 6, we only present the powers and subgroup identification results. The results show that we can obtain comparable power as in the simulation study for the change-plane model (1). Since there is no true subgroup defined in model (14), we use the restricted mean survival time (RMST) to evaluate the treatment effect in the estimated subgroup. Specifically, based on the survival data for subjects in the estimated subgroup, we estimate the RMST of treatment groups 0 and 1, respectively. Here, the estimated RMST is computed by the R package “survRM2”. We report the mean of the estimated RMST over 500 simulation runs. For the negative value of η, patients in the estimated subgroup have larger mean RMST when given treatment 1 than given treatment 0; while for the positive value of η, patients in the estimated subgroup have smaller mean RMST when given treatment 1 than given treatment 0. We also compute the p-value of the two-sample t-test comparing the estimated RMST of A = 1 and A = 0 in the estimated subgroup using the R package “survRM2”, and report the mean and standard deviation of the p-values over 500 simulation runs. It can be seen that the p-values are all significant, and as the magnitude of η increases, the difference in the mean RMSTs between two treatment groups increases and the p-value becomes more significant. This indicates a significant treatment effect in the estimated subgroup. Finally, we also report the mean of the proportion of patients in the estimated subgroup, which increases as the magnitude of η increases. These results imply that the proposed test still performs well for finding the subgroup with an enhanced treatment effect under the smooth treatment effect model.

Table 6.

Power and subgroup identification

Function	η	Power		RMST		p-value		PROP
		size 0.05	size 0.1	A = 1	A = 0	mean	sd
F1	0.2	0.204	0.284	0.921	1.208	0.014	0.026	0.377
	0.5	0.892	0.936	0.797	1.165	0.000	0.001	0.612
	0.8	1	1	0.706	1.148	0.000	< 0.000	0.736
	−0.2	0.158	0.252	1.318	1.060	0.013	0.025	0.388
	−0.5	0.860	0.918	1.554	1.069	0.001	0.004	0.622
	−0.8	1	1	1.779	1.103	0.000	< 0.000	0.732
F2	0.2	0.214	0.296	0.918	1.198	0.012	0.020	0.389
	0.5	0.918	0.960	0.776	1.154	0.000	0.001	0.592
	0.8	1	1	0.678	1.138	0.000	< 0.000	0.689
	−0.2	0.184	0.270	1.316	1.056	0.012	0.023	0.383
	−0.5	0.884	0.928	1.571	1.062	0.001	0.003	0.597
	−0.8	1	1	1.818	1.094	0.000	< 0.000	0.687

F1 : standard normal CDF; F2 : uniform CDF; RMST, mean of the estimated RMST; p-value, mean and standard deviation (sd) of the p-value of the two-sample t-test comparing the estimated RMST of A = 1 and A = 0 in the estimated subgroup; PROP, mean of the proportion of subjects in the estimated subgroup.

Finally, we evaluate the performance of the proposed change-plane model-based sample size formula for subgroup detection when the true model has smooth treatment effects. The detailed descriptions and simulations results are given in the Supplementary Appendix. As expected, the required sample size increases as the treatment effect magnitude and the subgroup size decrease. In addition, under all scenarios, the empirical powers are close to the nominal level even when the true model is not from the change-plane model, showing certain degree of robustness of the proposed sample size formula to the misspecification of the change-plane model.

5. Data analysis

We illustrate the application of the proposed method to data from 2139 HIV-infected patients in Clinical Trials Group Protocol 173 (ACTG175), which randomized patients to four different antiretroviral treatment regimes; Zidovudine(ZDV) plus monotherapy, ZDV plus didanosine (ddI), ZDV plus zalcitabine (zal), and ddI monotherapy ([14]). Following [15], we focus on two treatment groups, one receiving zidovudine (ZDV) monotherapy denoted as A = 0and the other receiving the other three treatments denoted as A = 1. The number of patients in the treatment group and control group are 1607 and 532, respectively, so that π(X_i) = 0.75. The primary endpoint is the time to one of the following events; having a larger than 50% decline in the CD4 count, or progressing to AIDS, or death. Among n = 2139 patients, about 75% of them are censored. As in [15], we consider two covariates baseline covariates; age and homosexual activity (0=no, 1=yes).

Since our method requires the censoring time C_i is independent of A_i given X_i, we first test this assumption by fitting a proportionals hazard model for the censoring time with treatment, age and homosexual activity included as covariates. From the results in Table 7, after adjusting for age and homosexual activity, treatment effect on the censoring time is not significant. This suggests the assumed censoring assumption may be reasonable for the considered data.

Table 7.

Fitted Cox model for censoring times

	Est	Z	P-value
age	−0.007	−2.50	0.012
hsa	−0.246	−4.62	0.001
trt	−0.049	−0.81	0.419

^†hsa, homosexual activity; trt, treatment; Est, Estimators of Cox proportional hazards regression; Z, z-value of the estimator.

Next, we performed the proposed test based on W_n. The maximum is taken over {γ₁, . . . , γ_M}, where M = 10000 as in the simulation. The obtained test statistic is 38.099 and the p-value is < 0.0001 based on 1000 resamplings, which supports the existence of the subgroup with an enhanced treatment. The number of patients in the estimated subgroup is 2095, among them, 1576 and 519 patients are in the treatment and control group, respectively. The estimated change plane is γ̂ = (−0.142, 0.047,−0.989) and the subgroup estimate is I(−0.142 + 0.047age − 0.989homo > 0). For the patients with homo=1, age> 24.06, while for those with homo=0, age> 3.02. Considering the minimum age is 12, the patients with homo=0 are always included in the subgroup. Also, the estimate for the subgroup with an enhanced treatment is η̂ = −0.61, which implies treatment results in better survival than control in the estimated subgroup.

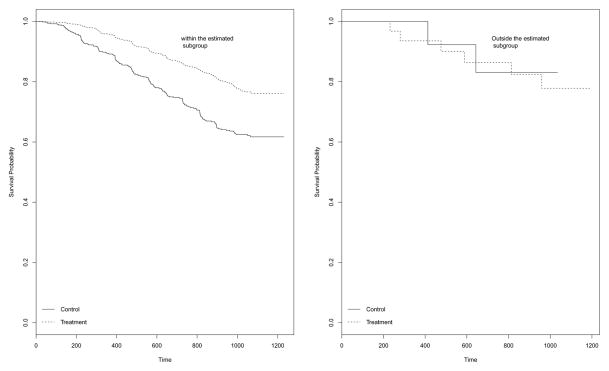
To examine the treatment effect for patients in and outside the estimated subgroup, we plot the Kaplan-Meier curves for two treatments in Figure 1. The left panel is for patients in the estimated subgroup, while the right panel is for those outside the estimated subgroup. It can be seen that for patients in the estimated subgroup, the treatment group has clearly better survival than the control group while for those outside the subgroup, theres is no difference in survival between two groups. This partly supports our finding.

Figure 1.

Kaplan Meier Plot of Survival Probability for the estimated subgroup

To obtain the sample size required for 0.9 power test at a 0.05 significance level, we generate a data set with age and homo following a normal distribution and a binomial distribution, respectively. We assume a linear function for the baseline effect model and the coefficient is set to be (0.01, 0.15). The censoring times are generated from uniform distribution (0, 0.7) to achieve 0.75 censoring rate as in the dataset and 1000 resamplings are used to obtain the critical values. We report the required sample for various treatment effect sizes in Table 8. As in the simulation study, we can observe that the required sample size increases as the effect size decreases.

Table 8.

Effect and sample size

η	Sample Size
−0.6	1003
−0.4	2094
−0.2	7225

6. Discussion

In this paper, we propose a testing procedure for detecting and estimating the subgroup with an enhanced treatment effect for survival data using a flexible proportional hazards model. The proposed test has the desired doubly robust property. The asymptotic distributions of the proposed test statistics under the null and local alternative are established, and the associated sample size calculation for clinical trial design is derived.

The proposed model does not include the main effect of treatment for convenience. One motivation for this is that in many clinical applications, treatment only has an effect for a subset of patients but has no effect for others. However, the proposed method can be extended to accommodate the main effect of treatment. Then, the null hypothesis becomes that there is not a subgroup such that the treatment effect is different from the main effect. Under such a situation, the estimation of the null model becomes more complicated. To demonstrate this, we have conducted simulations with a nonzero main effect of treatment. The results are presented in the Supplementary Appendix. They look comparable to those when the treatment main effect is not included.

Our proposed method assumes a proportional hazards model. However, our proposed test will have the correct type I error under the null hypothesis even when the proportional hazards assumption does not hold, as long as the censoring time C is assumed to be independent of A given X. On the other hand, the power and sample size calculation derived under the local alternative hinges on the assumed proportional hazards model. To demonstrate this, we have conducted simulations under the proportional odds model. In our implementation, we still fit a proportional hazards model under the null. The results are presented in the Supplementary Appendix. They are comparable to those under the proportional hazards model, however, the powers are slightly lower than those under the proportional hazards model.

The validity of the proposed test relies on the assumption that the censoring time C is independent of A given X. In many well designed and followed clinical trials, such an assumption for censoring times look reasonable. We have conducted some simulations to examine the robustness of the proposed test to the violation of this assumption. The results are presented in the Supplementary Appendix. Based on the limited results, our proposed test still gives reasonable performance. However, in general, the proposed test may not be valid when this assumption is violated. To relax this assumption, a time-dependent propensity score can be incorporated. The time-dependent propensity score can be non-parametrically estimated using a kernel method as in [16]. However, it entails a huge complexity in theoretical derivation and computation, especially for sample size calculation. This warrants future research.

Appendix

To establish the asymptotic results given in Theorems 1–2, we assume the following regularity conditions.

• (C1)
  The following limiting estimating equations have unique solutions, denoted by θ^* and Λ^*(t).

  $$\begin{gathered} E\left[{\int }_0^{\infty }\frac{\partial \varphi (X_i;\theta )}{\partial \theta }\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\theta )}d\mathrm{\Lambda }(t)\}\right]=0, \\ E\left\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\theta )}d\mathrm{\Lambda }(t)\right\}=0. \end{gathered}$$
• (C2)The probability P{Y (τ) = 1} > 0, where τ is a fixed constant; the function Λ₀(t) is continuously differentiable with Λ₀(τ ) < ∞.
• (C2)The function g(X, θ, Λ; η) is twice continuously differentiable with respect to θ. The first and second derivatives are bounded.

Proof of Theorem 1

Under the null hypothesis H₀ : η = 0, from (6), given θ̂, we obtain dΛ̂(t). Plugging it into (4) gives

$$\begin{gathered} \frac{1}{\sqrt{n}}\sum _{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma ) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\infty }I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}\left\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\widehat{\theta })}\frac{{\sum }_{j=1}^{n}d{N}_j(t)}{{\sum }_{j=1}^n{Y}_j(t)e^{\varphi (X_i;\widehat{\theta })}}\right\} \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\infty }[I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}-{\overline{X}}_1(\widehat{\theta },\gamma )]d{N}_i(t) \end{gathered}$$

where

$${\overline{X}}_1(\widehat{\theta },\gamma )=\frac{{\sum }_{j=1}^{n}I({\gamma }^{\prime }{X}_j\ge 0)\{A_j-\pi (X_i)\}{Y}_j(t)e^{\varphi (X_j;\widehat{\theta })}}{{\sum }_{j=1}^n{Y}_j(t)e^{\varphi (X_i;\widehat{\theta })}}.$$

With a simple algebra and Taylor expansion, we have

$$\begin{gathered} =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\infty }[I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}-{\overline{X}}_1(\widehat{\theta },\gamma )]\{d{N}_i(t)-Y_i(t)e^{\varphi (X;\widehat{\theta })}d\mathrm{\Lambda }(t)\} \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\infty }[I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}-{\overline{X}}_1(\widehat{\theta };\gamma )]\{d{N}_i(t)-Y_i(t)e^{\varphi (X;\widehat{\theta })}d{\mathrm{\Lambda }}^{\ast }(t)\} \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\infty }[I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}-{\mu }_1({\theta }^{\ast },\gamma )]\{d{N}_i(t)-Y_i(t)e^{\varphi (X;{\theta }^{\ast })}d{\mathrm{\Lambda }}^{\ast }(t)\} \\ +{E\left\{\frac{\partial g(X;\theta ,\mathrm{\Lambda },\gamma )}{\partial \theta }\right\}|}_{\theta ={\theta }^{\ast }}\sqrt{n}(\widehat{\theta }-{\theta }^{\ast })+o_p(1) \end{gathered}$$

where

$${\overline{X}}_1(\widehat{\theta },\gamma )\stackrel{P}{\to }{\mu }_1({\theta }^{\ast },\gamma )=\frac{E[I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0)\{A-\pi (X_i)\}Y(t)e^{\varphi (X;{\theta }^{\ast })}]}{E\{Y(t)e^{\varphi (X;{\theta }^{\ast })}\}}=0.$$

Also, it can be shown that

$$\begin{gathered} {E\left\{\frac{\partial g(X,\theta ,\mathrm{\Lambda };\gamma )}{\partial \theta }\right\}|}_{\theta ={\theta }^{\ast }}=-E\left[{\int }_0^{\infty }I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A-\pi (X_i)\}Y(t)e^{\varphi (X;{\theta }^{\ast })}\stackrel{.}{\varphi }(X;{\theta }^{\ast })d{\mathrm{\Lambda }}^{\ast }(t)\right] \\ =0 \end{gathered}$$

where $\stackrel{.}{\varphi }(X_i;{\theta }^{\ast })=\frac{\partial \varphi (X_i;\theta )}{\partial \theta }{\mid }_{\theta ={\theta }^{\ast }}$. Therefore,

$$\frac{1}{\sqrt{n}}\sum _{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )=\frac{1}{\sqrt{n}}\sum _{i=1}^{n}g(X_i,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };\gamma )+o_p(1)$$ (15)

where

$$g(X_i,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };\gamma )=I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}\{d{N}_i(t)-Y_i(t)e^{\varphi (X;{\theta }^{\ast })}d{\mathrm{\Lambda }}^{\ast }(t)\}$$

From (15), $\frac{1}{\sqrt{n}}{\sum }_{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )$ converges weakly to a zero-mean Gaussian process. The asymptotic covariance function at (γ₁, γ₂) is then E{g(X, θ^*,Λ^*; γ₁)g(X, θ^*,Λ^*; γ₂)}. Thus, for γ, the asymptotic variance of $\frac{1}{\sqrt{n}}{\sum }_{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )$ is given by $n^{-1}{\sum }_{i=1}^{n}g{(X_i,{\theta }^{\ast },{\mathrm{\Lambda }}^{\ast };\gamma )}^2$, which can be consistently estimated by $S_n(\gamma )=n^{-1}{\sum }_{i=1}^{n}g{(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma )}^2$

Proof for Theorem 2

Under the alternative hypothesis, H_a : η = n^−1/2δ, $\lambda (t\mid X_i)=\lambda (t)e^{\varphi (X_i)+\eta A_{i}I({\gamma }_0^{\prime }{\stackrel{\sim }{X}}_i\ge 0)}$. We have

$$\begin{gathered} \frac{1}{\sqrt{n}}\sum _{i=1}^{n}g(X_i,\widehat{\theta },\widehat{\mathrm{\Lambda }};\gamma ) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{\infty }[I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)\{A_i-\pi (X_i)\}-{\overline{X}}_1(\widehat{\theta },\gamma )]\{d{N}_i(t)-Y_i(t)e^{\varphi (X_i;\widehat{\theta })+\eta A_{i}I({\gamma }_0^{\prime }{\stackrel{\sim }{X}}_i\ge 0)}d{\mathrm{\Lambda }}^{\ast }(t)\} \\ +\frac{\delta }{n}\sum _{i=1}^n{\int }_0^{\infty }{A}_i\{I({\gamma }^{\prime }{\stackrel{\sim }{X}}_i\ge 0)(1-\pi (X_i))-{\overline{X}}_1(\widehat{\theta };\gamma )\}{Y}_i(t)e^{\varphi (X_i;\widehat{\theta })}I({\gamma }_0^{\prime }{X}_i\ge 0)d{\mathrm{\Lambda }}^{\ast }(t)+o_p(1) \end{gathered}$$

Since $\eta =\delta /\sqrt{n}\to 0$ as n → ∞, the first summation converges weakly to a zero-mean Gaussian process with the covariance function E{g(X, θ^*,Λ^*; γ₁)g(X, θ^*,Λ^*; γ₂)} at (γ₁, γ₂). Moreover, the second summation converges in probability to

$$\begin{gathered} \delta E\left\{{\int }_0^{\infty }AI({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0)(1-\pi )Y(t)e^{\varphi (X;{\theta }^{\ast })}I({\gamma }_0^{\prime }X\ge 0)d{\mathrm{\Lambda }}^{\ast }(t)\right\} \\ =\delta E\left[{\int }_0^{\infty }\pi (X)(1-\pi (X))I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0,{\gamma }_0^{\prime }\stackrel{\sim }{X}\ge 0)e^{\varphi (X;{\theta }^{\ast })-\varphi (X)}E\{Y(t)e^{\varphi (X)}d{\mathrm{\Lambda }}^{\ast }(t)\mid X\}\right] \\ =\delta E\left[{\int }_0^{\infty }\pi (X)(1-\pi (X))I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0,{\gamma }_0^{\prime }\stackrel{\sim }{X}\ge 0)e^{\varphi (X;{\theta }^{\ast })-\varphi (X)}E\{dN(t)\mid X\}\right] \\ =\delta E\{\pi (X)(1-\pi (X))I({\gamma }^{\prime }\stackrel{\sim }{X}\ge 0,{\gamma }_0^{\prime }\stackrel{\sim }{X}\ge 0)e^{\varphi (X;{\theta }^{\ast })-\varphi (X)}\mathrm{\Delta }\}. \end{gathered}$$

This proves Theorem 2.