Physical trade-offs shape the evolution of buoyancy control in sharks

Abstract

Buoyancy control is a fundamental aspect of aquatic life that has major implications for locomotor performance and ecological niche. Unlike terrestrial animals, the densities of aquatic animals are similar to the supporting fluid, thus even small changes in body density may have profound effects on locomotion. Here, we analysed the body composition (lipid versus lean tissue) of 32 shark species to study the evolution of buoyancy. Our comparative phylogenetic analyses indicate that although lean tissue displays minor positive allometry, liver volume exhibits pronounced positive allometry, suggesting that larger sharks evolved bulkier body compositions by adding lipid tissue to lean tissue rather than substituting lean for lipid tissue, particularly in the liver. We revealed a continuum of buoyancy control strategies that ranged from more buoyant sharks with larger livers in deeper ecosystems to relatively denser sharks with small livers in epipelagic habitats. Across this eco-morphological spectrum, our hydrodynamic modelling suggests that neutral buoyancy yields lower drag and more efficient steady swimming, whereas negative buoyancy may be more efficient during accelerated movements. The evolution of buoyancy control in sharks suggests that ecological and physiological factors mediate the selective pressures acting on these traits along two major gradients, body size and habitat depth.

1. Introduction

The evolution of marine fish from largely bottom-dwelling organisms to those capable of swimming in the water column represents one of the key evolutionary transitions that opened the largest habitable space on our planet to vertebrate life. Early fishes, such as placoderms, were heavily armoured and as a result were probably more closely associated with the seabed [1] as their highly negatively buoyant bodies would make any swimming away from the substrate very costly. Moreover, bone and muscle also have densities greater than those of water contributing to negative buoyancy [2,3]. Some of the key adaptations that have permitted animals to rise off the benthos and start exploiting the water column at a lower cost of transport include morphological alterations that counteracted this negative buoyancy, by either reducing the density of the tissues themselves, such as replacing bone with cartilage [4] or by incorporating specific air- or lipid-filled organs to provide floatation [2]. Despite its importance to locomotion, buoyancy remains an essential, yet poorly understood aspect in fish physiology and biomechanics.

Based on simple mechanics, it is intuitive that aquatic animals should evolve body densities close to neutral buoyancy, alleviating any energetic costs associated with overcoming vertical forces and maintaining position in the water column [5]. In contrast with terrestrial animals, the densities of many aquatic animal tissues are closer to the density of the supporting medium, and as a result even small changes in density will have significant consequences for locomotion [6]. Interestingly, many species have maintained negative buoyancy and indeed there is considerable variation in the body density between species [3,6–9]. It is, therefore, unclear what functional requirements drove the evolution of these apparent ‘suboptimal’ phenotypes that would lead to sinking in the absence of counteracting thrust. Alexander's hydrodynamic theory has indicated that negative buoyancy is favourable for fast-moving species, whereas neutral buoyancy becomes increasingly efficient as routine swimming speeds decline [10]. Where buoyant tissue is added, the need for the lift-producing appendages that would otherwise be necessary to maintain level swimming is reduced. But adding tissue adds body surface area, which in turn increases the parasite drag due to viscous friction and the turbulent wake. As the latter is proportional to the square of speed, neutrally buoyant species attain transport economy by swimming slower. At a given length, negatively buoyant species relying on lift production by fins or body, have less surface area (as a result of a smaller liver) and produce somewhat less parasite drag but significantly more of the induced drag generated by the lifting appendages [10,11]. Here, the costs of transport are reduced by swimming faster [6], as induced drag is inversely proportional to the square of the swimming speed.

Despite its conceptual power, Alexander's ‘low-density/slow swimming–high-density/fast swimming’ dichotomy is founded on several assumptions. First, it assumes that buoyancy is the result of adding buoyant tissue to already present lean tissue. Secondly, it assumes the drag of steady cruising swimming is an agent for selection, rather than acceleration reaction (or ‘added mass’) effects on drag [11,12], which become important in unsteady swimming manoeuvres such as burst swimming to capture prey or evade predation. Finally, the theory has not been tested in a comparative phylogenetic context, and remains a contentious issue in light of current debate regarding the adaptive benefits of negative buoyancy in aquatic animals [5,13,14].

Sharks (Selachimorpha) are a clade of cartilaginous fishes that provide an interesting model system to investigate evolutionary trade-offs associated with buoyancy control. Sharks have evolved large lipid-rich livers which provide significant upward-directed force and different species display large interspecific variation in overall buoyancy, ranging from near-neutral to substantially negative buoyancies and in some cases even positive buoyancy [3,6,7,9]. Moreover, many shark species exhibit a fusiform body shape with quasi-round cross sections and swim using caudal fin propulsion [15]. However, unlike gases found in the swim-bladder of teleost fishes, lipids are significantly greater in density and provide a comparatively inefficient solution for the production of positive buoyancy; as a result, large livers are required to provide neutral buoyancy, but at the potential expense of increased drag because of reduced streamlining. Therefore, the conflicting mechanical demands of buoyancy control and hydrodynamic efficiency in sharks provide an ideal case to investigate the evolution of body density and its relationship to locomotor performance.

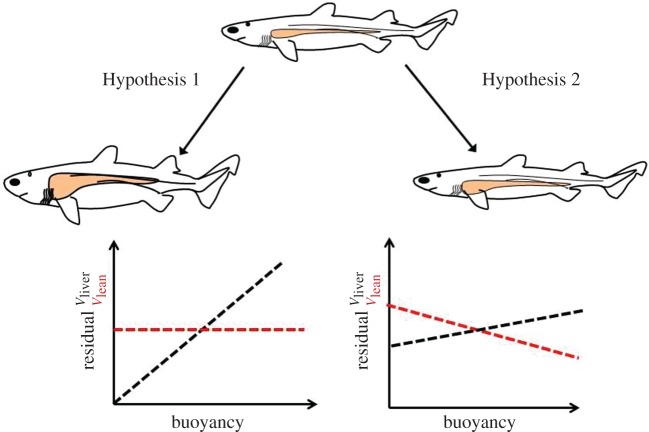
As a first approximation, two hypotheses for the evolution of buoyancy control can be considered: (i) changes in density are caused by the addition of buoyant tissue with no change in the amount of lean tissues (consistent with Alexander's theory) and (ii) changes in density are accompanied by a substitution of lean tissue for buoyant tissue (figure 1). Functionally, these two scenarios differ considerably; a substitutive evolutionary change would maintain body streamlining, but potentially at the expense of lower performance in the tissues that were substituted for floatation. The additive hypothesis, on the other hand, would result in decreased streamlining and reduce the economy of movement but with no loss of performance in other tissues. These scenarios represent two extremes that bound a wide spectrum of potential buoyancy control strategies that may be required among diverse ecological niches, especially considering that tissue density can differ substantially between species and can change over time [6,7,16,17]. Here, we provide a comparative phylogenetic analysis of body condition and buoyancy control in 32 shark species. We also explored the functional trade-offs resulting from changes in buoyancy for locomotor performance using a hydromechanical model, and then examined how these trade-offs may have influenced the vertical distribution of different shark species.

Figure 1.

Contrasting hypothetical scenarios of the evolution of buoyancy control. If locomotor capacity is an important force in influencing the buoyancy control of sharks, liver volume would be expected to have increased in animals closer to neutral buoyancy, whereas other tissues remain unchanged, supporting Alexander's theory (Additive Hypothesis 1). The alternative hypothesis asserts that the economy of movement has a more critical influence on the evolution of buoyancy control and, in order to remain slim and streamlined, any change in liver tissue would be expected to be compensated for by a decrease in other denser tissues, giving rise to density-independent residuals of whole animal volume and decreasing lean tissue volumes that represent the inverse of the increase in liver tissue (Substitutive Hypothesis 2). (Online version in colour.)

2. Material and methods

(a). Morphological data

We collated a dataset of 32 species' standard length (SL), the density and volume of the liver, and the liver-free body from published sources ([3,7,18]; see electronic supplementary material, Morphological and table S1). Our comparative approach required testing the relationships between overall animal density, liver volume and lean volume. If sharks are predicted to maintain economy of movement, changes in body density towards neutral buoyancy should accompany increases in liver volume and decreases in lean tissue volume. A constant fineness ratio (FR) (volume/length) would be maintained if loss of lean tissue would equal gain of lipid-rich tissue. This hypothesis invoked the loss of some lean tissue, such as muscle tissue (the most voluminous of all tissues in fish), which is expected to decrease the capacity for physiological function (e.g. less muscle = lower acceleration during burst swimming). The evolution of liver and lean tissue volume in relation to body density would result in increased liver volumes as density declines, but no predictable changes in lean tissue volume with changes in density, thus representing the central tenet in Alexander's theory.

Lastly, we tested the predictions of Alexander's theory; namely that the evolution of slower steady swimming speeds is expected to be correlated with decreasing submerged weight. Good depth records are available for most species and it is well established that metabolic rates and enzymatic activity decline with depth of occurrence in fish, including sharks [19,20], leading to extraordinarily low swimming speeds in the deep sea [9,20–22]. Additionally, greater depths feature colder temperatures, which have been shown to reduce swimming speeds of fish both under natural and laboratory conditions [23]. We used depth as a simple proxy for swimming speed or activity, because direct measurements remain scarce. We obtained records on the minimum and maximum occupied depths for all species in our sample from FishBase.org [24] or published sources from tagged animals and calculated the Median Depth of Occurrence [20].

(b). Comparative analysis

Different species are predicted to show differing degrees of similarity in traits according to their distances on a branching phylogeny, therefore requiring specialized statistical approaches [25–27]. We used phylogenetic generalized least squares, pGLS regression [27–29] to account for this non-independence, representing a well-established statistical procedure to deal with phylogenetic non-independence and polytomies within a phylogenetic tree. pGLS uses a variance–covariance matrix based on the resemblance and divergence of species based on phylogeny. The large range in body size of our species (43–591 cm) complicated the calculation of tissue volumes in relation to changes in buoyancy. We performed a phylogenetic size correction [30] on the log-transformed SL and liver and lean tissue volumes, by fitting a pGLS model and calculating the residuals for each species from the scaling relationship. Following size correction, we tested whether the evolution of body density is correlated with liver volume and lean volume using pGLS. We also tested whether evolutionary changes in liver volumes resulted in concomitant changes in lean tissue volume.

To inform our phylogenetic analysis, we derived the topology and branch lengths of our phylogeny from the molecular supertree presented in Naylor [31], based on variation in NADH-dehydrogenase 2 (NADH2) mitochondrial gene for 595 species of elasmobranch. We pruned the tree to only include species present in our dataset and calculated the branch lengths of the phylogeny based on those presented in [31] as the difference in the base pairs within the NADH2 gene. Our phylogeny, therefore, does not present divergence times in years, but rather the degree of difference in the molecular composition of NADH2. Naylor's analysis missed a single species (Squatina squatina) from our trait dataset, but contained a number of congeners. Based on the phylogeny of angel sharks [32], we assumed the branch length leading to S. squatina to be similar to S. aculeata, the closest relative in Naylor's dataset.

As our phylogenetic tree represents an evolutionary hypothesis and the tree's branch lengths were estimated from molecular data (a non-ultrametric phylogenetic tree), we also ran models over two arbitrarily assigned branch lengths. This is a common approach to account for uncertainty in branch lengths [28,29]. All branch lengths were set to 1, equivalent to a punctuated model of evolution, and we used the method of arbitrarily assigning branch lengths according to Grafen [33], where each branch length is represented by the difference in the number of species−1 below and above a particular node. We performed our complete analysis separately under the assumptions of our three phylogenies [28,29].

In a purely ‘Brownian motion’ (BM) model of evolution, the covariance between species is expected to be proportional to their distance on the phylogeny, whereas in a model ignoring this covariance (a ‘star’, rather than branching phylogeny), no such covariance is accounted for. Within pGLS, the covariance matrix can be modified to test the degree of phylogenetic signal denoted by Pagel's λ. If the best fit for the pGLS model is achieved by assuming phylogenetic independence, the model will return a λ = 0 and if the traits have evolved as expected under BM, the model will return λ = 1, with intermediate values representing trait evolution to a lesser degree as specified by BM. pGLS estimates optimal values of λ through maximum-likelihood. Overall, all analyses were performed with the three phylogenies and Pagel's method, including size correction. Owing to the uncertainty in our phylogeny, we compared models based on their summed Akaike weight (∑w_i, the summed relative likelihood of a subset of models divided by the summed relative likelihood of all models). Specifically, the relative likelihoods of the three models (based on the three phylogenies) including the factor of interest was divided by the sum of the relative likelihood of all models: three null models and the three models including the factor [29]. This allowed us to determine the support for the inclusion of the factor of interest, irrespective of the phylogenetic hypothesis. A major revision of phylogeny would require re-examination of these relationships.

(c). Hydrodynamic modelling

We devised a new hydrodynamic model for idealized shark morphology and behaviour to explore the functional consequences of changes in liver size and associated buoyancy and body shape, in relation to drag production during steady and accelerated swimming (table 1; electronic supplementary material, Hydrodynamics methods). Specifically, our model was based on an idealized shark body (SL = 1 m) of varying liver volume and associated buoyancy and routine swimming speeds (0.4–1.5 m s⁻¹) [35]. The model was used to explore the functional consequences of different buoyancy control strategies, including the hydrodynamics of drag during steady swimming as a proxy for the energy economy of movement, and of the drag during accelerations to predict agility performance. Net drag is calculated as the sum of parasite drag [36], induced drag [11] and the so-called acceleration reaction drag [37] (table 1; see also electronic supplementary material, eqns (S1)–(S4)). The latter is necessary as it becomes the dominant source of drag, in comparison to parasite and induced drag, during accelerations typical of predator avoidance and prey capture (electronic supplementary material, figure S3). Additionally, and most relevant here, reduction in acceleration reaction drag via morphology can only be effected via increases in body fineness (FR) (table 1 and figure 4).

Table 1.

Hydrodynamic modelling, as expressed in terms of density of seawater (ρ_w); standard length (SL); body maximal width (TM); body volume (BV); body wetted area (SA) [34]; fineness ratio (FR = SL/TM); added mass coefficient (k; ellipsoid of same FR [33]); negative buoyancy (W) (body weight, minus buoyancy); time-varying speed U(t) and acceleration a(t); cruising speed just prior to acceleration (CS); (non-dimensional) time to accelerate over one body length (n_s); and body volume BV expressed as a fraction of ellipsoid volume (φ = BV FR²/(π/6) SL³). In the total drag equation, the first, second and third terms correspond to parasite, induced and added mass drag, respectively [6,11,12]. Here, γ = 1 as explained in the text and in the electronic supplementary material, Hydrodynamic modelling.

total drag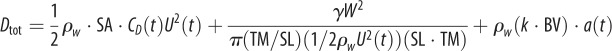
parasite drag coefficient
acceleration profile 0 < t ≤ ts ts = nsSL/1.5CS
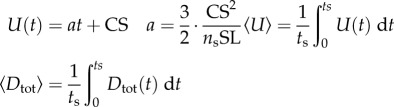time-averaged total drag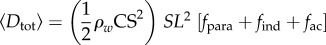
time-averaged parasite drag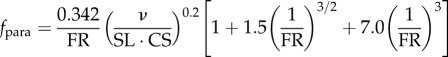
time-averaged induced drag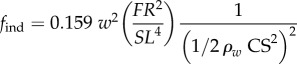
time-averaged added mass drag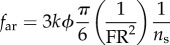

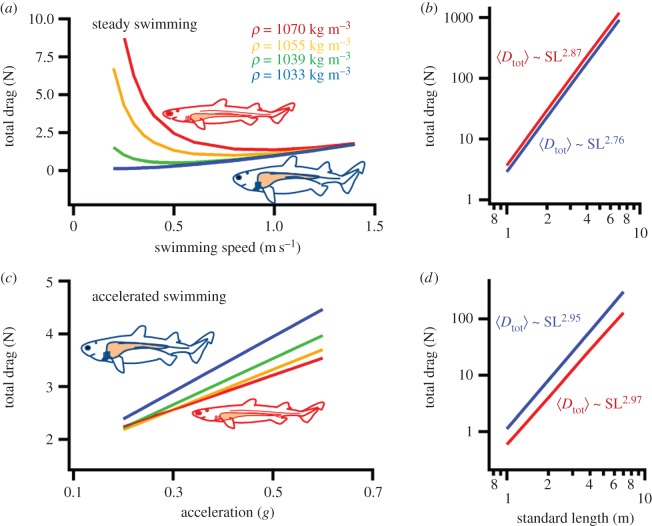
Figure 4.

Hydrodynamic simulations of the forces during steady (a,b) and unsteady swimming (c,d) for a hypothetical shark of 1 m SL with a range of liver sizes and associated body density and the two extreme cases across scale (for morphological input see electronic supplementary material, figure S2). (a) Over realistic cruising speeds (approx. 0.5–1.5 m s⁻¹), near neutral buoyancy (ρ ∼ 1033 kg m⁻³) provides the most economical morphological solution. (b) Over the two extreme cases simulated, drag during steady swimming scales with the marginally larger exponent for the more negatively buoyant scenario simulated. (c) At an arbitrarily chosen speed of 0.8 m s⁻¹ and accelerations greater than 0.2 g reveal that negative buoyancies increases the capacity for such accelerated movements, due to lower drag experienced, especially at greater accelerations (see electronic supplementary material, tables S5–S7), suggesting that increased agility and capacity produce accelerations. (d) In both extreme cases simulated, drag scales almost identically.

The first term of the drag equation in table 1 (i.e. first and second entries) models the parasite drag and has been tested experimentally, albeit in steady-speed conditions only [36]. But as further argued in the electronic supplementary material, it can be used in accelerated motions as sharks routinely swim at speeds for which the boundary layer remains turbulent over most of the body, with flow separation limited to the tail end of the body at all speeds. On the other hand, the induced drag term featured in the table (in W²) arises from the well-verified lifting line theory in the steady state [11,38] in which the lift has here been set equal to the negative buoyancy to ensure strictly horizontal trajectories in both accelerated and un-accelerated motions (as imparted by active changes of body and fin angle of attack) [39,40]. The model is corrected, via the γ-factor (γ ≥ 1), to account for the additional effects arising from accelerated motions, namely, added mass lift and wake separation [41]. In the absence of detailed calculations on shark body and fin lift properties, this factor is set to unity (γ = 1), thereby yielding a conservative, but sufficiently accurate estimate.

The last drag modelling component is the acceleration reaction term (proportional to the acceleration a in the first entry of table 1), which estimates the drag generated when accelerating the ‘entrained’ flow, or more accurately, the flow streamlines enveloping the body, boundary layer and turbulent wake. Given the extreme body streamlining of sharks and the minimal turbulent wake that they generate, we assumed that the coefficient k (table 1 or electronic supplementary material, eqn (S4)) is a constant computed from inviscid flow hydrodynamics on prolate ellipsoids [42].

As both induced and parasite drag change during accelerated motions, drag comparisons only become meaningful in the context of fitness for economy of transport after averaging over time. Because accelerated motions can be executed in many ways, we restricted our analysis to a generally representative case of sharks accelerating along a straight line to double their speed over a distance specified by the fraction (n_s) of body length (SL) travelled (distance = n_s SL). This ‘surging’ acceleration will be constant and begin at the non-zero speed U_i, characterizing an assumed steady motion prior to the surge. Specifying both initial and final speeds (= 2U_i), along with the distance travelled (via n_s), completely determines the acceleration (see third row in table 1 also electronic supplementary material, eqn (S8)). From constant-acceleration kinematics the average speeds are thus: 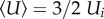, and 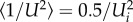, thereby yielding the averaged drag given in table 1 (fourth to seventh rows; electronic supplementary material, eqns (S12)–(S15)). We note that the averaged drag components are expressed in terms of the body FR to show its importance in determining the drag; also, the acceleration reaction drag (f_ar) increases in importance with acceleration (i.e. smaller n_s). These results are also expressed in terms of the initial speed being equal to the routine cruising speed CS, or U_i = CS. This initial speed (CS) was set as an independent parameter in the range 0.2–1.5 m s⁻¹ commonly seen with most shark species and realistic maximum accelerations of 0.2–0.6 g [43]. Where the cruising speed is expected to be correlated with body size (standard length, SL), CS is parametrized as CS = SL^0.44 + INT per Ryan et al. [35]. The detailed outputs are shown in figure 3; electronic supplementary material, S3 and tables S5–S7.

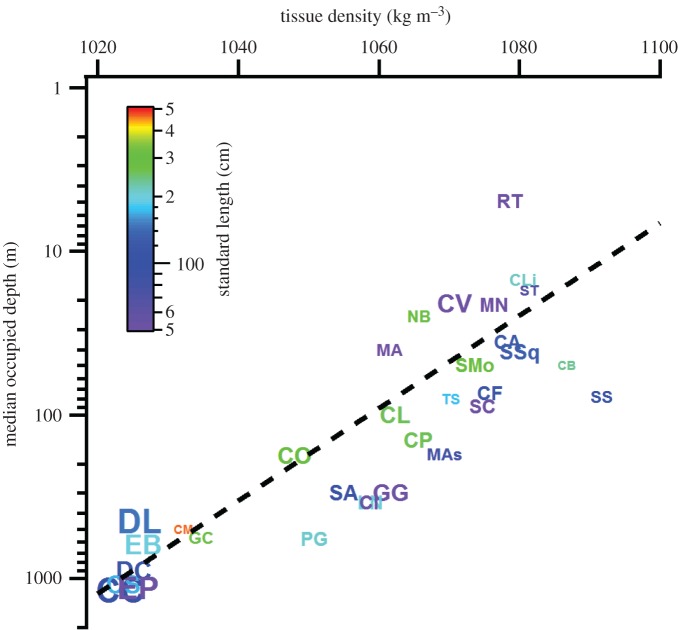
Figure 3.

Vertical distribution and body density in 32 species of shark. Median occupied depths in relation to the tissue density for 32 species of shark. Size of the individual species' symbols are colour coded according to the length of the shark, and the size of the marker is proportional to the liver volume residual calculated by our phylogenetic size correction (figure 2). For species occupying the deepest depths, buoyancy was close to neutral, whereas species primarily occupying shallower depths are increasingly characterized as having greater tissue densities leading to greater negative buoyancy (electronic supplementary material, table S3). (Online version in colour.)

3. Results

(a). Evolution of buoyancy control

(i). Scaling and calculation of residuals

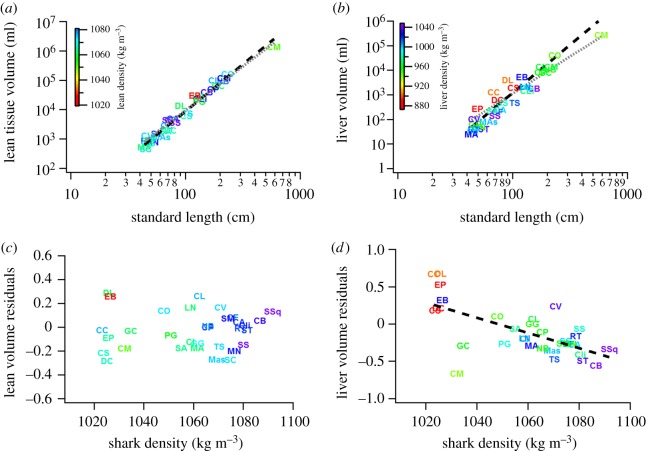
The scaling of both lean tissue and liver tissue volume was best described by Naylor's branch lengths, featuring strong phylogenetic signal (λ = 0.9 and λ = 0.8, respectively). This model showed that lean tissue volume showed no significant positive allometry (exponent = 3.07 ± 0.11, figure 2a). This scaling exponent was consistent across all models (with moderate support according to their ΔAIC < 5), suggesting that lean volume scaled isometrically or with marginal positive allometry (exponents 3.07–3.12; see electronic supplementary material, table S3), compared to liver volume which displayed strong positive allometry across all models (exponents 3.73–3.77, figure 2b). Estimates of phylogenetic signal were generally moderate to high in liver volume (λ = 0.5–0.8), whereas lean tissue volume showed a substantially larger range (λ = 0.2–0.9).

Figure 2.

Scaling of body volume for 32 species of shark (see electronic supplementary material, table S1). (a) Lean tissue volume is isometric with increase in SL (best fitting model: lean tissue volume = SL^{3.07±0.11 s.e.}, t = 28.67, p < 0.0001; electronic supplementary material, table S2, grey stippled line) with only a single model predicting significant, yet moderate positive allometry (black stippled line, electronic supplementary material, table S2), whereas (b) liver tissue volume displays considerable positive allometry in all models (best fitting model: liver tissue volume = SL^{3.904±0.193 s.e.}, t = 28.67, p < 0.0001; electronic supplementary material, table S2, black stippled line, isometry shown for comparison as a grey stippled line). (c) Size-corrected residuals from the lean tissue scaling do not correlate with density of the animals. (d) Size-corrected liver volume residual shows significant negative relationship with overall density, with increases in animal density associated with significant decrease in liver volume (table 2; electronic supplementary material, table S3). (Online version in colour.)

(ii). Correlated evolution in morphological characteristics

After size correction [30], phylogenetic regressions revealed significant negative correlation between liver volume and body density (figure 2d; electronic supplementary material, figure S1). Summed Akaike weights across models including liver volume residual as a predictor (versus the null models excluding it) showed unequivocal evidence for greater liver sizes having evolved in parallel with overall density of the animal (∑ω_i = 0.991; electronic supplementary material, table S4) and the inclusion of liver volume was highly significant irrespective of which phylogenetic tree was used in the analysis (p < 0.0005 in all three cases; electronic supplementary material, table S4). Lean tissue volumes, on the other hand, showed little evidence for the correlated evolution of lean tissue volume and overall body density (∑ω_i = 0.777; electronic supplementary material, table S4), and its inclusion as a covariate did not yield significant regressions in any of the three phylogenetic hypotheses. A number of models had equally strong support (ΔAIC_c < 2) with parameter estimates close to zero (0.00–0.99) compared to the estimates for liver volume residuals (−6.93 to −8.87), suggesting that changes in lean tissue volumes had negligible effects, in comparison to changes in liver volume, in the evolution of buoyancy. Residuals of lean and liver tissue showed evidence for correlated evolution (∑ω_i = 0.900; electronic supplementary material, table S4), with parameter estimates not significantly different from unity in all models (electronic supplementary material, table S4). Similar to the scaling analysis, liver volume residuals and density displayed significantly lower variation in phylogenetic signal (λ = 0.46–0.77) than lean volume residuals and density (λ = 0.22–0.86).

(iii). Correlated evolution of depth and density

The median depths occupied (MDO; see electronic supplementary material, table S2) by the 32 shark species showed strong negative correlated evolution with density in all three models. Negative correlations between depth and tissue density were unequivocal and showed consistent slope estimates of −52.37 to −47.79 and strong support for the models including MDO compared to the null model (∑ω_i = 0.999, figure 3; electronic supplementary material, table S4), and its inclusion yielded strong statistical significance, irrespective of the chosen phylogeny (p < 0.0005 in all three cases; electronic supplementary material, table S4). All three models including MDO were characteristic of very low phylogenetic signal (λ = −0.06–0.09).

(b). Hydrodynamic consequences of changes in buoyancy

(i). Implications of liver size for hydrodynamics

Our hydrodynamic analyses provided insight into the functional consequences of buoyancy change according to the additive and substitutive hypotheses (figure 1) that consisted of modelling four morphologies that span the range of buoyancies observed in our morphological data (electronic supplementary material, figure S2). The effects of liver volume and overall tissue density are evident in the different levels of drag predicted for steady swimming (i.e. accelerations less than 0.1 g) compared to those experienced during accelerated swimming. Our hydrodynamic model predicts the lowest steady-state drag when buoyancy is close to neutral, whereas negative buoyancy appears particularly costly at low speeds (figure 4). This is a result of induced drag dominating at slow cruising speeds compared to the increased parasite drag resulting from a decreased FR. It would also appear that neutral buoyancy would result in greater economy of movement (compared to negative buoyancy) over a large part of the range spanning realistic swimming speeds, given that, at a given swim speed, drag is reduced for neutrally buoyant fish. Beyond 1.5 m s⁻¹, induced drag becomes negligible during steady swimming, leaving parasite drag as the most important contributor. Under these conditions, sharks with larger livers generate higher drag compared to those with smaller livers. Although sharks are clearly capable of exceeding these cruising speeds, data from animal-attached speed sensors suggest these to only be sporadic in nature [23]. By contrast, simulations of accelerated swimming revealed that substantially lower drag is predicted for negative buoyancy in all but the lowest accelerations simulated. At accelerations of 0.6 g, drag is approximately 25% higher in an animal with a large liver and neutral buoyancy compared to one with a small liver and negative buoyancy (figure 4). Thus neutral buoyancy would appear to yield lower costs of transport where near-steady movements are more important for survival, whereas negative buoyancy would yield the lower costs where accelerated movement is critical. The model also revealed species with high tissue densities achieving the lowest possible drag at high speeds and species approaching neutral buoyancy at increasingly lower speeds. It has to be stressed again, however, that neutral buoyancy results in lower drag at all relevant cruising speeds (i.e. up to 1.5 m s⁻¹), yet higher drag is predicted for accelerated swimming. The latter follows from higher values of the acceleration reaction, which in this case provide a physical constraint to body design.

(ii). Hydrodynamics and scaling

In a second set of simulations, we employ the same model as described previously, to predict the effect of body size (SL) and FR on the evolution of buoyancy in sharks. We modelled the scaling in two extreme morphologies presented in the previous analysis and simply scaled the morphological input isometrically (tissue volumes ∼ SL³) using empirically determined scaling of swim speeds for sharks [35]. This scaling hypothesis resulted in similar body density and FR across scale as the two extreme cases previously simulated, namely with body densities of 1033 kg m⁻³ and 1070 kg m⁻³ and FRs of 6.3 and 7, respectively. We found that the dynamic pressure and body planar reference area factors (proportional to CS² and SL², respectively, table 1 (4th row); electronic supplementary material, eqn (S12)) were central in shaping the overall size-scaling of the total drag, with CS² SL² scaling as ∼ (SL^0.44)² SL² ∼ SL^2.88 (figure 4). Accelerated and steady-state drag were predicted to scale with very similar exponents, although with significantly different intercepts where more neutrally buoyant sharks incur greater drag during unsteady swimming. This model prediction emphasizes that sharks with greater tissue density experience lower drag in acceleration than those with lesser tissue density (electronic supplementary material, figure S3). Overall, these results suggest that swimming drag will scale with body size in a similar manner regardless of body density in unsteady conditions (figure 4). In other words, the hydrodynamic model predicts no distinct body-size dependence on the drag of steady swimming versus accelerated swimming. Finally, for steady-state conditions, a marginally greater exponent is predicted for neutrally buoyant sharks (2.87 versus 2.76, figure 4) and therefore suggests that the relative reduction in drag during steady swimming should decline with size.

4. Discussion

We present the first comparative phylogenetic investigation into the evolution of buoyancy control and its potential impact on locomotor performance in a species-rich group of marine fish. Our work highlights a morphological trade-off between low-density/low-fineness and high-density/high-fineness phenotypes in the evolution of buoyancy control, due to the addition of liver tissue. Moreover, these results suggest that ecological and physiological factors mediate the selective pressures acting on these traits along two major gradients, size of the individual and its depth of occurrence. In shallow (i.e. epipelagic) habitats, our results suggest that selection favoured enhanced agility (unsteady locomotor capacity) and high-performance steady swimming (i.e. high cruising speeds greater than 1 m s⁻¹) where predator–prey interactions may strongly influence individual fitness. In contrast, small buoyant sharks with relatively larger livers tend to occur in deeper habitats where the energy economy of slow, steady movement is favoured over either high-speed cruising or high-performance accelerations. Although our data are based on a relatively large sample size of species, these are mostly represented by a few individuals; in addition, the phylogenetic relationships of sharks and rays are still in considerable flux; drastic revisions of the phylogeny of sharks and rays coupled to substantial changes in our understanding of buoyancy and depth distributions may warrant revisiting such a dataset in the future.

(a). Economy versus burst capacity

Alexander [10] argued that the transition from a buoyancy control strategy relying on hydrodynamic lift from the body and the pectoral fins (analogous to a fixed-wing aircraft) to one that increasingly relies on hydrostatic forces (analogous to a blimp) would accompany decreasing swimming speeds, because negative buoyancy would result in substantial increases in drag at low swimming speeds compared to neutral buoyancy. The inverse correlation between depth and buoyancy in our dataset supports this hypothesis, given the evidence that metabolic activity generally decreases with depth in a range of marine animals [19,20,44], assumed to reflect a decrease in swimming activity. Swimming speeds of deep-water and arctic elasmobranchs further support this conclusion; six-gill sharks (Hexanchus griseus) and the bramble shark (Echinorhinus cookei) have shown exceptionally slow swimming speeds and densities close to neutral, albeit slightly positive [9]. Greenland sharks equally swim very slowly [45] and primarily occur in cold arctic or deep low-latitude ecosystems.

However, the hypothesis that energy economy drives the evolution of buoyancy [10] is not universally supported by our analyses because our hydrodynamic modelling indicates that, over a realistic range of swimming speeds, neutral buoyancy lowers steady drag and, by extension, cost of transport. Negative buoyancy and greater fineness, on the other hand, result in lower drag during accelerations, suggesting that this phenotype should have greater agility and burst swimming capacity. Therefore, the capacity for burst swimming appears to be selected for, even at the cost of increasing drag during steady swimming, especially in shallow environments. For highly active pelagic species such as blacktip sharks or silky sharks that forage for manoeuvrable and small prey (fish and squid), the outcome of those predator–prey interactions depends on the predator's ability to generate high accelerations. Given that available muscle power is finite [46], lower drag must lead to greater capacity for burst swimming and thus greater foraging success. The same principle also applies to smaller individuals facing predation risk, because locomotor capacity is closely linked to survival [47,48].

The prevalence of negative buoyancy is not ubiquitous; deep-sea sharks tend to feature more neutral buoyancies (figure 3). It has been suggested that shallow, well-lit habitats have driven strong selection for locomotor capacity, compared to deeper environments, due to greater incidence of visually mediated predator–prey interactions, as put forward by the visual interaction hypothesis [44]. It would therefore seem that, in shallow environments, high burst swimming capacity appears more important than economy of movement, especially in smaller taxa. However, larger taxa may face reduced predation risk, leading to the evolution of morphologies that favour efficient steady swimming, while sacrificing burst performance. Similar explanations have been put forward to explain the intraspecific scaling of morphology in tiger sharks [49]. To reduce the effects of negative buoyancy on the cost of transport, behavioural mechanisms, such as intermittent locomotion, may have evolved to reduce these disadvantages [13,50]. Although the selection for traits that increase the cost of transport, and by extension the cost of living in perpetually active ram-ventilating sharks, may seem perplexing, the observed patterns are corroborated by evolutionary theory. Traits directly related to survival are expected to be more strongly selected within natural populations [51], and predation pressure has been argued to be a strong agent for selection on traits related to locomotor capacity [52,53]. In deeper habitats, however, the selection pressures for locomotor capacity may be relaxed and replaced by an increasing necessity to manage energy judicially due to the oligotrophic nature of the deep sea [44].

(b). Scaling

Positive allometry of liver mass and body circumference has been found in a number of different species of elasmobranchs and appears relatively common with few exceptions [3,7,18,54]. However, the functional significance of this positive allometry in buoyancy and shape was largely unexplored; it is interesting to note that negative allometry of caudal fin size, aspect ratio and shape has been observed in many species [49,54,55], but not in others [56]. This has been hypothesized to reflect a relative reduction in swimming speed as sharks grow, which would explain why larger sharks tend to have lower density, a requirement for efficient low-speed travel. Similarly, Fu et al. [49] found the heads of juvenile tiger sharks to be more conical than their adult counterparts, suggesting streamlining for the sake of faster and more agile swimming to be increasingly less important during ontogeny. Moreover, increasing the length of the pectoral fins may also reduce the cost of transport in concert with the effects of increased buoyancy [57].

Our hydrodynamic scaling analysis did not reveal any substantial differences in the drag experienced across the size spectrum for either neutral (W ∼ SL⁰) or negatively buoyant (W ∼ SL³) scenarios, with the exponents for total drag being largely similar in both steady and unsteady simulations (figure 4). The only allometric scaling exponents that showed minor differences between neutral and negative buoyancy was for steady swimming. Whereas steady swimming drag for negative buoyancy is approximately 1.8× that of neutral buoyancy for an individual of 1 m SL, it is 2.1× the steady drag of neutral buoyancy for 7 m SL. This prediction suggests that selective forces on buoyancy are largely insensitive to scale, but there may be stronger selection for neutral buoyancy at larger sizes. One additional factor that may further influence the change in selective forces with body size is the scaling of muscle power available for burst swimming, which was not considered in our model, because no adequate data currently exist for sharks. Comparative and theoretical studies have pointed to the capacity to generate high accelerations to decline with size in swimming animals [58], and this would suggest that selection for higher accelerations is relaxed at larger sizes, thus further resulting in stronger selection for neutral buoyancy.

(c). The evolution of a trade-off

Our results demonstrate that liver tissue is added, rather than substituted, for lean tissue as different buoyancy control strategies evolved in the context of physical trade-offs that probably impacted locomotor performance [10]. However, this raises the question, as to why there appears to be a trade-off in the first place. We suspect that the major constraint influencing the evolution of buoyancy in sharks may relate to the fitness costs associated with losing dense tissues such as locomotor muscle. With the exception of the liver in sharks, many of the tissues that perform critical functions in vertebrates have densities greater than that of water. However, we note that the evolution of lower tissue densities (both in the liver and the remaining tissue) coincides with increases in liver size. This suggests that increasing buoyant forces are not simply due to larger livers, but also reduction in tissue densities [20]. Indeed, Treberg & Speers-Roesch [20] found that both lipid content and volume of livers increase with depth in chondrichthyans. As a result, large-scale increases in overall body volume are probably dampened, possibly to avoid severe reductions in unsteady locomotor performance. There may also be a propensity for the storage of lipids in otherwise ‘dense’ tissues; swim bladder-less Antarctic Notothenioid fish have large lipid deposits in their muscle for the sake of producing hydrostatic force [59], as does E. brucus [3]. Our analysis also suggested that some sharks with larger livers may also exhibit more non-liver tissue. This could be a result of additional lipid being stored in non-liver tissue. Equally, neutrally buoyant cephalopods readily accumulate low-density nitrogen-based compounds in their tissue, which has been shown to coincide with lower metabolic activity in those species [60,61]. Not surprisingly, negatively buoyant squids typically feature greater metabolic activity and locomotor performance [61]. In elasmobranchs, accumulation of high levels of urea and methylamines in tissues would provide a mechanism for decreasing tissue densities, in addition to an increase in lipid storage [62], assuming these solutes would take up considerable space within muscle and displace other cellular machinery. Moreover, the increasing incorporation of water into muscle may reduce its density and performance. The relationship between metabolic activity, locomotor performance and tissue density remains a significant knowledge gap that future research will help inform.

Ethics

All research was based on previously published data, and in a single case was based on a recently deceased animal donated to the laboratory.

Data accessibility

The datasets supporting this article have been uploaded as part of the electronic supplementary material.

Authors' contributions

A.C.G. conceived the paper. A.C.G. and J.P. performed the analysis. A.C.G., J.P. and J.A.G. wrote the manuscript.

Competing interests

We declare no competing interests

Funding

A.C.G. was supported by an ARC DECRA fellowship (Project number 150100321).