Specialized mutualisms may constrain the geographical distribution of flowering plants

Abstract

It is commonly assumed that the geographical distributions of plants are governed mainly by abiotic variables. However, interactions with other organisms, such as pollinators, also have the potential to influence plant distributions. To investigate this, we developed niche models for 32 plant taxa that have specialized pollination systems and which are native to a biodiversity hotspot (South Africa). We found that the distributions of these taxa are best explained by a combination of biotic (pollinators) and abiotic factors, rather than by abiotic factors alone. For approximately 66% of these plant taxa, pollinator distributions were the factor that provided the best predictor of their niches. Furthermore, co-occurrence of these plants and their pollinators was generally not explained solely by shared abiotic niches, and thus probably reflects broad-scale positive ecological interactions. These results are consistent with the proposal that pollinator distributions may constrain plant distributions and highlight the general potential for species distributions to be shaped by positive interactions with other species. This has important consequences for predicting how distributions of species might change in the face of loss of their key mutualists.

1. Introduction

Owing to accelerating anthropogenic impacts on the natural environment, there has been increased emphasis on understanding the limits to the distributions of species [1,2]. For instance, current climate-based models generally assume that the range of individual species varies according to their particular physiological tolerances [3–5]. Yet, both abiotic and biotic factors can potentially influence the geographical range of species. The role of ecological interactions in determining species distributions across broad geographical scales is an issue that is increasingly seen as being important [1,6–9]. Positive biotic interactions, such as plant pollination by animals, have been shown to be important for fecundity and abundance of organisms at local scales [10–12], and here, we explore their role in governing distributions for multiple species at larger spatial scales.

Given their importance for seed production, pollinators can reasonably be considered a component of the ecological niche of plants [13,14]. The geographical distribution of pollinator-dependent plants may therefore be shaped, not only by abiotic factors, but also by the distributions of particular mutualists, such as pollinators [7]. While generalized pollination systems are typical of plant communities in temperate regions of the Northern Hemisphere [15], plant species in biodiversity hotspots, such as South Africa and the tropics, often rely on one or a few pollinator species [16,17]. This dependence is usually asymmetric because most pollinators are generalists that do not depend on particular plant species for rewards. Examples of pairwise reciprocal dependence of plant and pollinator species are rare and mostly confined to brood-site mutualisms. We therefore focused this study on the influence of nectar and oil-collecting pollinators on plant distributions on the assumption that the distributions of these pollinators are unlikely to be shaped by the distributions of any single plant species.

To explore the role of pollinators in shaping plant distributions, we developed environmental niche models (ENMs) for a total of 32 plant taxa, representing 15 genera and five families, in the biodiversity hotspot of South Africa (electronic supplementary material, table S1). The plant species belong to eight different plant ‘pollination guilds’ [18], of which four are associated with particular bee species and four with particular long-proboscid fly species. The distributions of these eight pollinator species vary from highly restricted to widespread and therefore represent a variety of potential geographical scales of influence on plant distributions. We asked: (i) whether the extent to which the geographical distribution of pollinators influences the estimation of plant ranges, and (ii) whether shared physiological tolerances can fully account for co-occurrence of plants and pollinators, or whether there is an additional component of their co-occurrence that is probably owing to ecological interactions influencing pollination.

2. Material and methods

(a). Taxon selection

We based our selection of study plant taxa on the following criteria: (i) they are reliant primarily on a single pollinator species for reproduction, (ii) their distributions are well described, and (iii) their pollinator distributions are well described. Using these criteria, we selected a total of 32 South African angiosperms, mainly belonging to the Orchidaceae and Iridaceae (electronic supplementary material, table S1), and that represent a total of eight well-studied pollinator guilds, involving four oil-collecting bee pollinators and four long-proboscid fly pollinators. For each plant taxon, we collated presence records from the South African National Biodiversity Institute SIBIS (now POSA) database. These presence data are available in quarter degree square (QDS) resolution (25 × 27 km area) in South Africa; hence, we developed our niche models at the QDS level. We then used Quantum GIS [19] to create a binary categorical raster of the distribution of QDSs occupied by each pollinator, by mapping all of the QDSs where the pollinator species has been reported to occur, and then by considering all remaining QDSs as being where the species is absent within South Africa [20–25].

Below, we describe three approaches used to quantify whether the extent of pollinator distributions may affect the ranges of plants: (i) ENMs were used to estimate the range of each plant taxon based on abiotic variables and we tested the importance of pollinator distribution on the range of these plants by comparing models with and without pollinator distribution as a predictor variable, (ii) χ²-tests were used to test whether plants are more likely to occur within the range of their pollinator, and (iii) joint species distribution models (JSDMs) were used to test whether plant taxa and their pollinators co-occur mainly because of their shared environmental responses, or whether there are co-occurrence patterns beyond those that arise from shared environmental tolerances.

(b). Environmental niche modelling

To construct the ENMs, we used Maxent [26], a widely used machine-learning algorithm to estimate the environmental niche of taxa based on presence-only data. Maxent performs well when compared with other environmental niche modelling approaches that use presence-only data, particularly with smaller sample sizes [27]. We used the average of 50 bootstrapped replicates of each model to build a consensus model for each taxon, both with and without pollinator distribution included as an explanatory variable.

Maxent compares the distribution of environmental variables at sites occupied by focal taxa with the distribution of randomly drawn background locations. The majority of the plants investigated in this study are orchids and irises that have wind-dispersed seeds and are not considered to be dispersal limited, and hence could potentially occur over large geographical ranges within South Africa. Therefore, we assumed the background area potentially available for colonization to be the entire area of South Africa (greater than 1.2 million km²). This area consists of 2041 QDSs.

To quantify the physiological niche for each plant taxon, we selected 10 ecologically relevant abiotic variables from the BIOCLIM database [28] at the 30 arc-sec (approx. 1 km) resolution. These were: (i) altitude, (ii) annual mean precipitation, (iii) maximum temperature in the warmest month, (iv) minimum temperature in the coldest month, (v) precipitation in the driest quarter, (vi) precipitation in the wettest quarter, (vii) precipitation seasonality, (viii) mean annual precipitation, (ix) temperature annual range, and (x) temperature seasonality. We used the average of each variable for each QDS, converted to WGS84 longitude–latitude format, as an estimate of local environmental conditions. To avoid multi-collinearity in our Maxent models, we performed principal component analysis (PCA) on these environmental variables [8]. The first three axes in the PCA explained approximately 99% of the variation in these continuous abiotic variables in South Africa. The first axis is associated with a broad cline of all environmental variables, with increasing temperature seasonality. The second axis is associated with increased temperature seasonality with increasing altitude. The third axis is associated with decreased annual mean temperature with increasing altitude and annual precipitation. We used these three PCA axes as continuous predictor variables, along with the generalized geological substrate for South Africa (data from the South African Department of Agriculture, Directorate Land Use and Soil Management) as a single categorical predictor. Maxent models were developed with 25% of occurrence data used for model training and 75% of occurrence data used for model testing. The equal training specificity and sensitivity (ETSS) logistic threshold was used to identify suitable QDS where taxa could occur, but currently do not, for each model. This threshold is useful to determine which QDSs have an equal probability in predicting the presence of a taxon in a particular QDS, given the available data [29]. We examined three different threshold measures and calculated the correlation between each of them based on models that did not include pollinator distributions. ETSS was positively correlated with three other commonly used logistic thresholds—minimum training presence, ten percentile training presence, and maximum training specificity and sensitivity; hence, ETSS represents a useful objective measure to quantify suitable habitat where each taxon could potentially occur (electronic supplementary material, figure S1).

(i). Jackknife model validation

As 20 of the taxa investigated in this study had less than 25 QDS records (electronic supplementary material, table S1), we used the jackknife procedure developed by Pearson et al. [30] to test whether the predictive ability of models is negatively affected by their small sample sizes. We re-ran our ENMs for all taxa with less than 25 records using cross-validated replicate runs in Maxent to calculate the test statistic, D, which ranks possible values of success, i.e. a value of 1, where a location (QDS) was included in the predicted geographical range for each taxon, and 0 if it was not. This jackknife test is a ‘leave-one-out’, n − 1 cross-validated model, with each QDS removed once from the dataset and a model built using the remaining QDSs. This was tested against H, a completely random assignment of potential successes. To perform the jackknife tests, we used the ‘p-value compute’ software provided by Pearson et al. [30]. Using this approach, we found that the predictions of all models with sample sizes of less than 25 in our study can be considered reliable (electronic supplementary material, table S2).

(ii). Model performance and true skill statistics

To test whether model performance differs when pollinator distributions are included as an explanatory variable in our ENMs, we used the true skill statistic (TSS) proposed by Allouche et al. [31]. For each plant taxon, we used the average occurrence generated by the Maxent models and tested the average sample prediction of these models using the mean ETSS threshold (electronic supplementary material, table S3).

(iii). Generalized estimating equations

To compare whether the proportion of QDSs occupied within the estimated range of each plant taxon (range fit) differed between models that included the pollinator distribution as an explanatory variable and those that did not, we used generalized estimating equations (GEEs) [32]. For this, we calculated the proportion of QDSs that each plant taxon occupied within its estimated range and tested for differences between the two models. The GEE analysis was conducted using a binomial error distribution, an exchangeable correlation matrix and plant genus as a grouping variable to control for phylogenetic relationships using the ‘geepack’ package [33] in R.

(c). Patterns of co-occurrence of plants and pollinators

We tested whether plants in the distribution range predicted by their abiotic niche are more likely to occur in QDS cells occupied by pollinators than in cells that are not occupied by pollinators. For this, we used the distribution generated by the models that excluded pollinator distributions. For each species, we calculated the proportion of QDSs where the plant taxon is present and the pollinator is also present and compared it to the proportion of QDSs where the plant is present but the pollinator is absent. To assess the difference between these proportions for each plant taxon, we used a χ²-contingency test, as implemented in the ‘prop.test’ command in R. To calculate the significance value for all plant taxa combined, we used the formula −2Σln(P) provided by Sokal & Rohlf [34] to generate an overall χ²-value and its associated p-value.

The geographical distribution of taxa can be influenced by both environmental tolerances and interactions with other organisms. However, adding species distributions as explanatory variables directly in ENMs may result in multi-collinearity when the distribution of the predictor species is governed by a set of abiotic variables that are autocorrelated with each plant and pollinator [35]. We applied an approach that dissects species co-occurrence patterns into shared environmental responses and residual patterns of co-occurrence (i.e. co-occurrence patterns beyond those that arise from shared environmental tolerance) [36]. For each plant–pollinator pair, we constructed a binary presence–absence matrix for each QDS based on the output from the consensus bootstrapped Maxent model for each taxon excluding their pollinator distribution as an explanatory variable. We adopted the JSDM approach outlined by Pollock et al. [36] in preference to other co-occurrence indices (e.g. Schoener's and Dice's Indices) that are used to infer ecological processes, as these are not able to disentangle the influence of shared environmental responses and residual correlations on co-occurrence. The JSDM approach uses multivariate probit regression to determine the probability of taxa co-occurring within a site (in this case, a QDS). This model is parameterized indirectly using a latent variable formulation, rather than a probit link. Latent (unobserved) variables are similar to link functions in that both are used to relate a continuous linear predictor to discrete binary response data. If latent variables are independent among sites and taxa, then standard probit regression is used to model these latent variables. However, as latent variables are often correlated (i.e. non-independent), then the JSDM uses a multivariate normal distribution (a generalization of a univariate normal distribution) to model these latent variables. We ran the JSDMs according to the approach outlined by Pollock et al. [36] (see the electronic supplementary material). All JSDM models were fit with the Markov chain Monte Carlo Bayesian modelling software JAGS v. 3.4.0 run through R v. 3.1.1 via the package R2jags v. 0.03-11 [37]. From these models, we calculated the mean environmental correlation and the residual species correlation for each plant and pollinator pair.

3. Results

(a). Environmental niche modelling

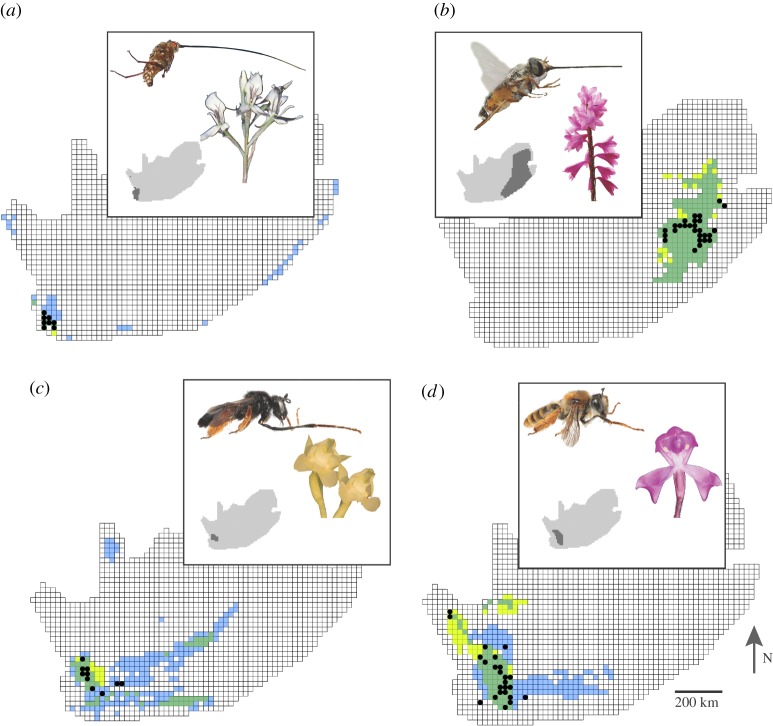
Jackknife tests of the importance of variables in Maxent revealed that pollinator distributions contributed the most useful information, based on the highest gain (a likelihood statistic that maximizes the probability of the presences in relation to the background area) when used in isolation, in models for 21 of the 32 plant species (approx. 66%, figure 1; electronic supplementary material, table S1 and figures S2–S9). We found that models containing pollinator distribution had a significantly better fit than did those lacking pollinator distribution as an explanatory variable (paired t-test: t₃₁ = 3.103; p = 0.004).

Figure 1.

Examples of how mutualists can impact the estimated niche of plants (strong effects observed in (a,c,d) and no effect in b). Estimated niches with pollinator distributions included in models are represented in yellow, while the estimated niches with pollinators excluded from the models are represented in blue. Green areas represent where models with and without the pollinator distribution overlap. Dots represent the actual plant distribution. Pollinator distributions are shown in inset. (a) Disa draconis and its pollinator Moegistorynchus longirostris, (b) Watsonia lepida and Philoliche aethiopica, (c) Pterygodium pentheranium and Rediviva longimaunus, and (d) Disperis purpurata subsp. purpurata and Rediviva macgregori. Photo credits: (a,b) Steven D Johnson; (c,d) Herbert Stärker (flowers) and Michael Kuhlmann (bees).

GEEs revealed that the inclusion of pollinator distribution as an explanatory variable in ENMs improved the predicted presence (Wald χ² = 5.38; p = 0.020), compared with models with abiotic variables alone, and hence generally creates a better fit of the observed distribution to the predicted distribution of each plant taxon. There was no difference in the proportion of QDSs occupied in bee or fly pollinators (Wald χ² = 1.86; p = 0.173), indicating that both types of pollinator had a similar constraining effect on the distribution of these plants.

(b). Patterns of co-occurrence of plants and pollinators

Based on the proportion of cells actually occupied by plants in the range predicted by their abiotic niche, they are much more likely to occur in QDSs with their pollinators than in QDSs where their pollinator is absent (overall χ² = 415.85; p < 0.001; see the electronic supplementary material, table S1 for results of each separate test).

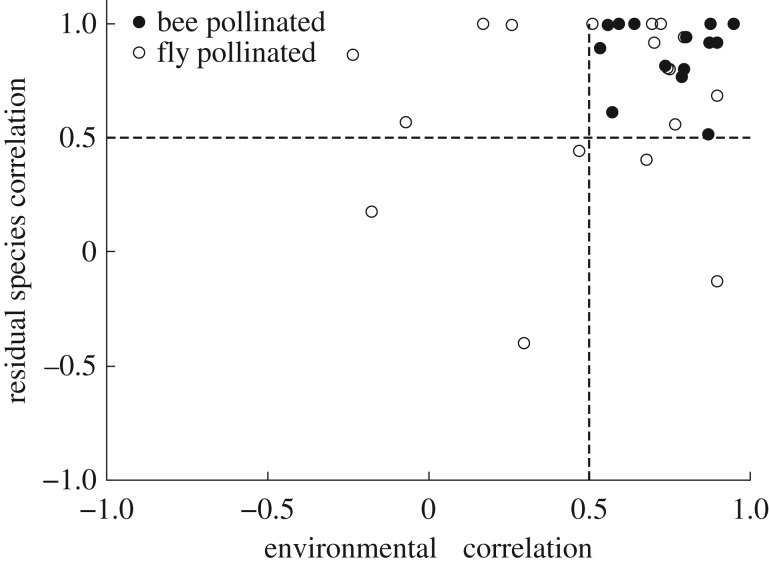
JSDMs revealed that plant and pollinator co-occurrence is often not accounted for solely by shared abiotic conditions and that, on average, the residual correlation between plants and their pollinators (i.e. co-occurrence pattern beyond that arising from shared environmental tolerance) was higher than the correlation owing to environmental variables for 24 out of 32 plant taxa investigated (10 out of 14 bee-pollinated taxa and 11 out of 16 fly-pollinated taxa; figure 2; electronic supplementary material, table S1).

Figure 2.

Bi-plot representing the mean environmental correlation and mean residual correlation from models that jointly model species distributions between each individual plant taxon and their animal pollinator. Bee-pollinated plant taxa are highlighted with filled circles, while fly-pollinated plant taxa are labelled with open circles. Environmental correlation values greater than 0.5 indicate that plants and pollinator distributions are positively correlated on account of their abiotic environmental preferences, while residual correlation values greater than 0.5 indicate that there are potentially strong ecological interactions between taxa.

4. Discussion

The results of this study support the hypothesis that pollinators can have a strong influence on the distribution of plant species with specialized pollination systems. One important implication is that niche models that include only abiotic factors may not accurately estimate the potential distribution of plants with specialized pollination systems. In this study, models based solely on abiotic variables were seldom congruent with the actual distributions of plants, whereas models that incorporated pollinator distributions more accurately defined the ranges. While these analyses were conducted on a coarse scale, these results are consistent with the idea that specialized biotic interactions may have a ‘top-down’ effect governing species distributions. These findings are also consistent with the results of translocation experiments, which have shown that some of the present study species do indeed experience strongly reduced pollination success when they are moved outside of their natural range [23,24]. We therefore argue that mutualists, such as pollinators and frugivores, that are responsible for key stages of plant reproduction, i.e. pollination and seed dispersal, should be considered to be components of the fundamental niche of specialized plant species (sensu, [38]). This is a departure from the conventional logic (based largely on a focus on competition) which decrees that biotic interactions shape only the realized niche of species [39]. Indeed, recent theoretical work has shown that plant co-existence is enhanced when they have specialized pollination systems [14,40,41]. In the light of recent concerns regarding pollinator declines and shifting plant and pollinator distributions [42,43], our results suggest that quantifying such interactions is vital for understanding how species distributions may change. For example, contraction or expansions in the distribution of a mutualist can be predicted to result in the local extinction of populations of its partner or their expansion into novel environments [44]. Without accounting for the ecological dependency of species on mutualists, ENMs would lack the information to accurately predict how species with ecologically specialized reproductive systems will respond to changing environments.

The role of biotic interactions in shaping species distributions is starting to emerge as a key research theme in ecology [7,8,45]. Recent studies that have included biotic interactions as an explanatory variable in ENMs have reached differing conclusions with respect to the effects of mutualists on range limits. For example, the presence of a specific endophytic fungal mutualist can broaden the range of a grass species, by ameliorating drought stress [8], while there is also some evidence that native plant distributions can potentially constrain the distribution of an exotic pollinator [46]. Building on experimental work which showed that pollinator distributions can have a constraining effect on plant distributions [47], our work shows that such constraints can more generally affect plants with specialized pollination systems. This result is supported by our finding of improvement in model performance and narrowing of the estimated niche when pollinator distributions are included as a component of species environmental requirements. Importantly, our evidence was obtained from a broad range of plant species covering a large geographical range in a region of high biodiversity.

Nonetheless, there are likely to be factors in addition to the variables examined in this study that would affect the estimated range of flowering plants. For instance, recent work has shown that population demographic and life-history traits (e.g. whether plants are annual or perennial, their ability to germinate from seed in a given habitat) impact on species responses to shifting habitat suitability, and not accounting for these variables may affect the estimation of plant ranges based on presence-only data [48]. In addition, while our pollinator distribution data represented the entire extent of occurrence of each pollinator taxon, further work using approaches that quantify the population abundance and demography of both plant and pollinator populations may improve our understanding of the factors underlying the limits to species distributions [49].

The plant and animal taxa investigated here belong to specialized pollination mutualisms. Species involved in more generalized pollination mutualisms are less likely to have distributions shaped by mutualists. In studies of invasive plant species, pollination system generalization and reproductive assurance through selfing have emerged as key traits that facilitate colonization and broad geographical ranges [50]. Indeed, one of the underlying assumptions behind Baker's Rule [51] is that plants will frequently be limited by pollinator availability when colonizing regions outside of their native range [52]. An evolutionary implication is that plants which disperse outside of the range of their pollinators would experience strong selection to shift to other pollinators [53,54] or to evolve selfing reproductive strategies [55]. However, other biotic interactions (e.g. soil fungi) may also influence the spread of plants outside of their native range. The plant taxa least affected by pollinator distributions in our models are the ones with pollinators that have very broad distributions (electronic supplementary material, table S1). Yet, for restricted plants with widespread pollinators, it may be the case that while their environmental correlation is low, as the pollinator can tolerate a much broader range of environmental conditions than the plant, the residual correlation between taxa is high, owing to the plant co-occurring frequently with the pollinator within its narrow range. In a very few cases, the distribution of plants extends beyond the range of the pollinator. We believe that these are exceptions that prove the rule—some South African plants with specialized pollination systems show pollinator shifts along their range margins, allowing their distributions to be broader than the range of the core pollinator, e.g. [56]. There are also some well-documented instances of plants being adapted for pollination by particular animals, yet not ecologically reliant on these pollinators on account of facultative selfing mechanisms [57].

The findings of this study should apply more broadly to any cases involving ecological facilitation among specialized species. Although we have emphasized the effect of the role of mutualists, specifically pollinators, on species distributions, we are also aware that some specialized interactions between plants and flower-visiting animals, e.g. mimicry systems [58], involve unilateral exploitation and are not true mutualisms. However, even these interactions should still conform to the general theory outlined in this paper, namely a role for pollinators in affecting the distributions of plant species with specialized pollination systems.

5. Conclusion

That pollinators can shape the distribution of these specialized plants is an insight that has broad implications for the understanding and prediction of plant geographical ranges, evolutionary pollinator shifts and plant diversification. This study provides support for the idea that pollinators are a component of the fundamental niche for some plant species and underlines the general importance of ecological interactions between plants and pollinators for the maintenance of biodiversity.

Data accessibility

Data supporting this paper are available at Dryad, doi:10.5061/dryad.b487r [59].

Author contributions

K.J.D. and S.D.J. designed the research. K.J.D. collated the data, developed the niche models and performed all analyses. K.J.D. wrote the first manuscript draft. K.J.D. and S.D.J. wrote the paper.

Competing interests

We have no competing interests.

Funding

This work was funded by a Postdoctoral Fellowship from the University of KwaZulu-Natal (K.J.D.) and a Research Chair from the National Research Foundation (S.D.J.), which we gratefully acknowledge. K.J.D. is currently funded by a Marie Sklodowska-Curie Fellowship from the European Commission (grant no. 655889 ‘MYCRONICHE’).