Physical Limits on the Precision of Mitotic Spindle Positioning by Microtubule Pushing forces

Summary

Tissues are shaped and patterned by mechanical and chemical processes. A key mechanical process is the positioning of the mitotic spindle, which determines the size and location of the daughter cells within the tissue. Recent force and fluctuation measurements indicate that pushing forces, mediated by the polymerization of astral microtubules against the cell cortex, maintain the mitotic spindle at the cell center in C. elegans embryos. The magnitude of the centering forces suggests that the physical limit on the accuracy and precision of this centering mechanism is determined by the number of pushing microtubules rather than by thermally driven fluctuations. In cells that divide asymmetrically, anti-centering, pulling forces generated by cortically located dyneins, in conjunction with microtubule depolymerization, oppose the pushing forces to drive spindle displacements away from the center. Thus, a balance of centering pushing forces and anti-centering pulling forces localize the mitotic spindles within dividing C. elegans cells.

Graphical abstract

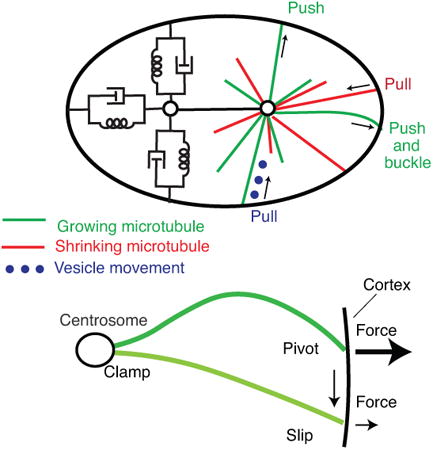
We discussmicrotubule-based mechanisms of the mitotic spindle positioning, a key mechanical process that shapes and patterns tissues. The magnitude of the centering forcesindicates that the physical limiton the accuracy and precision of centering isset by the number of contributing microtubules rather than by thermally driven fluctuations.

1. Introduction: Patterning tissues by chemical and mechanical processes

The shaping and patterning of living organisms is remarkable in its intricacy yet reproducibility^[1]. Formation of reproducible patterns in tissues requires the precise positioning of cells with appropriate identity. Two general processes, one chemical and the other mechanical, together pattern and shape tissues^[2]. Chemical patterning processes, comprising reacting and diffusing morphogens, subdivide tissues into specific regions and determine the identity of the cells within these regions^[3]. Such reaction-diffusion reactions, of the type originally investigated by Turing^[4], have been used to model a large number of patterns: the decorations on sea shells^[5]; the stripes of fish^[6]; the morphogenesis of Drosophila^[7]; the numeration of the fins of fish and the digits of mammals^[8]; and the branching of hydra^[9], feathers^[10] and neuronal dendrites^[11].

The precision of chemical patterning is limited by fluctuations in the concentrations of morphogens. For example, during the development of Drosophila, the expression of transcription factors divides the Drosophila embryo into striped domains that will become the segments in the adult fly^[12,13]. The precision of this process is exemplified in the cycle-14 embryo by the hunchback protein, whose concentration profile varies from embryo to embryo by only 1%, less than one cell diameter^[14]. It is argued that this high precision is at the very physical limit set by the diffusive movement and concentration fluctuations of the transcription factor that activates Hunchback^[15,16]. Thus, the same physical limits to discrimination of chemical gradients by microorganisms^[17] may also apply to chemical patterning of the body plan.

Mechanical processes, comprising forces acting within and between cells, influence tissue morphology and patterning by repositioning cells or by inducing anisotropic growth. For example, directed cell movements lead to stratification^[18] or elongation of tissues along a specified axis^[19]; long-range forces induce cell flow within developing epithelia^[20]; and intracellular forces position and orient the mitotic spindle to specify the plane of cell division. The orientation of the plane of cell division in turn determines the location of the daughter cells within the tissue leading to polarized growth^[21,22], and, often, differences in cell fate^[23]. Thus, mechanical processes can complement chemical gradients by altering tissue organization. Often chemical signals influence mechanical processes^[24] and vice versa^[25], and so the two morphogenetic processes are interdependent.

In this review, we focus on mitotic spindle positioning, a key mechanical process that shapes and patterns tissues, and ask what are the molecular mechanisms and physical limits that set the precision by which the spindle is positioned and orientated during mitosis (for a general review on mitosis see^[26]).

2. Position and orientation of the mitotic spindle within dividing cells

One of the stunning features of cell division is the accuracy and precision with which the mitotic spindle is centered (Figure 1). At metaphase, when the chromosomes are aligned between the spindle poles, the axis of the bipolar spindle passes through the cell center. The plane of cell division is perpendicular to, and usually bisects the spindle^[27] (see ^[28,29] for exceptions). In symmetric cell division the spindle is centered so that when the mother cell is bisected the daughters have equal size. In asymmetric cell division the spindle is often displaced from the center prior to division so that the daughters have unequal sizes and often different fates^[23,30].

Figure 1. Precision of centering the mitotic spindles during metaphase in various eukaryotic cells and in-vitro systems.

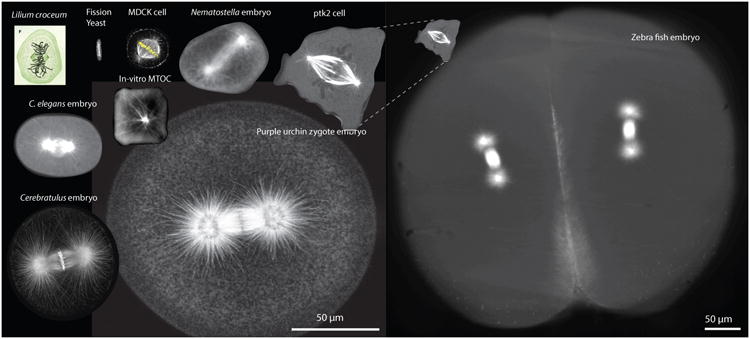
Clockwise from the upper left: Mitotic cell drawn by W. Fleming in 1882 ^[108] (Not at scale). Fission yeast cell (kindly provided by Prof. Iva Tolic). A HeLa cell with fluorescently labeled (α-tubulin antibody) microtubules, DNA and actin (Prof. Linda Wordeman). Single cell from a Nematostella embryo (32-cell stage) fluorescently labeled with EB1-GFP (Dr. Katerina Ragkousi – Gibson Lab). Sea urchin zygote with fluorescently labelled microtubules (Prof. Victoria Foe). Single-cell Cerebratulus marginatus zygote with fluorescently labelled microtubules and DNA (Prof. George von Dassow). C. elegans zygote with fluorescently labelled microtubules (β-tubulin:GFP). Fluorescently labelled microtubules growing from a fluorescently labelled bead inside a squared-shaped chamber (Prof. Marleen Dogterom). Compressed PTK2 cell labeled with GFP-α-tubulin (Joshua Guild – Dumond Lab). Four–cell zebrafish embryo with fluorescently labelled microtubules (Elisa Rieckhoff – Brugues Lab). Notice that the zebrafish embryo has a different scale bar.

Regardless of whether the division is symmetric or asymmetric, the orientation of the spindle is critical for positioning the two daughters within the growing tissue^[21]. For example, in the mouse epidermis, the spindles at embryonic day 12.5 are primarily parallel to the basement membrane, leading to lateral expansion of the single-layer tissue; by embryonic day 15.5 they are primarily perpendicular, leading to stratification of the tissue^[31,32]. Thus, tissue architecture is influenced by the positioning of the spindle. A key question is to understand the molecular mechanisms underlying spindle positioning and their precision.

Spindle positioning has been studied in detail in several model systems ^[33]: bacteria, budding yeast ^[34], fission yeast ^[35], in tissue culture cells ^[36], the early embryo of the nematode worm C. elegans ^[37], the neuroblast of Drosophila ^[23,28], the mammalian skin ^[31] and developing cortex ^[30]. In this review, we concentrate on C. elegans because it exemplifies many of the different types of nuclear, centrosomal and spindle movements during mitosis (Figure 2A). Similar movements are found in other cells and organisms, and the conservation of molecular machineries suggests that related mechanisms are likely operating^[22]. Within this complex choreography (Figure 2B,C), there is a period of few minutes, roughly corresponding to metaphase and termed the maintenance phase, during which the spindle is relatively quiescent (green line in Figure 2C). During this period, while spindle assembly is being completed, the spindle is precisely oriented along the anterior-posterior (AP) axis ^[38]. Because of its long duration, the maintenance phase has proved amenable to mechanical experiments, allowing detailed quantitation of the microtubule-based forces acting on the spindle. These forces, set the precision of the spindle positioning, which is the focus of this review. We will relate principles learnt from this system to other systems.

Figure 2. Movement of the mitotic spindle in the one-cell C. elegans embryo.

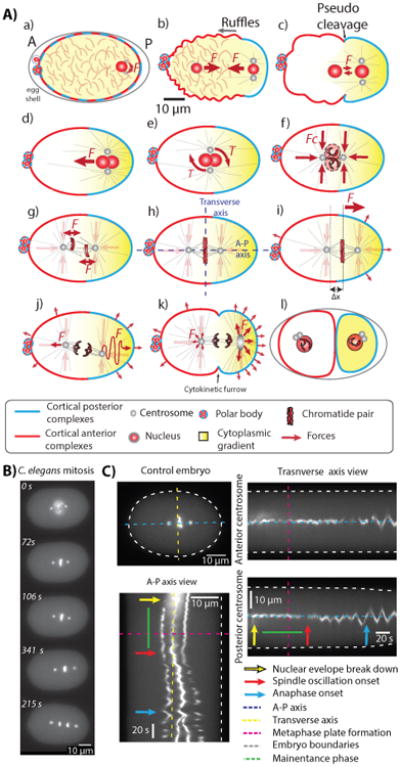
A The various movements in the one-cell embryo. a The oocyte is fertilized by entry of the male nucleus and its associated centrosome, triggering the polarization of the cell membrane (blue and red denotes the par proteins) and activation of actomyosin to produce ruffles (b) and a pseudocleavage (c). d The nuclear-centrosomal complex migrates to the cell center. e The complex rotates at the cell center. f The complex is stably maintained at the cell center. g) The nuclear membrane brakes down and the microtubules of the inner spindle move the chromosomes to the metaphase plate between the two poles (h). i The spindle moves towards the posterior through approximately ∼ 3μm. j The spindle undergoes a series of transverse oscillations (rocking) during anaphase. k The oscillations die out during late anaphase. l Cytokinesis divides the cell in two. See ^[37] B Stills of a movie of the major events during mitosis; the spindle poles are labeled with γ-tubulin-GFP and the chromosomes labeled with histone-4-GFP. From top to bottom: Nuclear envelope break down (time zero), metaphase plate formation together with spindle centering, oscillations onset together with posterior displacement of the spindle, anaphase onset, and late anaphase. See supplementary movie 2. C Kymographs showing the spindle movements during cell division. The A-P view axes shows how the spindle moves towards the posterior of the cell. The transverse axis show how the anterior and posterior poles remain at the cell center during the maintenance phase and fluctuates around the center during spindle oscillations. The major events during cell division are indicated by arrows. The maintenance phase is indicated by the green line.

3. Force-generating mechanisms that mediate spindle positioning

3.1. Key role of microtubules

Microtubules play a key role in spindle positioning. Positioning is sensitive to drugs such as colchicine and nocodazole, which inhibit microtubule polymerization by binding to tubulin ^[39], and taxol, which inhibits microtubule depolymerization by binding to microtubules ^[40]. Mutations or inhibition of the microtubule-based motor protein dynein also interfere with spindle positioning ^[41-43]. Thus, spindle positioning depends both on microtubule dynamics, which is powered by the GTPase activity of tubulin, and on motor proteins, which are powered by ATP hydrolysis. This does not preclude other molecular mechanisms, such as the actin cytoskeleton, also playing a role ^[44].

Three microtubule-based force-generating mechanisms operating on astral microtubules have been proposed: Pushing forces generated by microtubule growth, pulling forces associated with microtubule shrinkage and forces generated by motility along microtubules (cytoplasmic pulling) (Figure 3A).

Figure 3. Models of spindle centering.

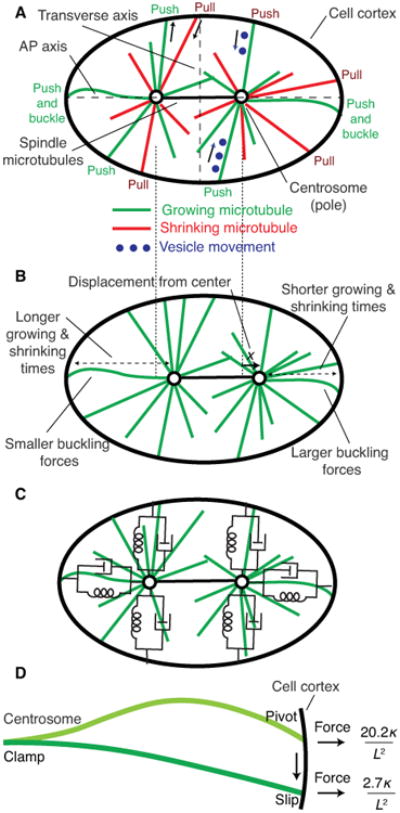
A Three force-generating mechanisms operating on astral microtubules: (i) pushing by microtubules, shown in green, growing against the cell cortex, (ii) pulling by microtubules, shown in red, shortening while maintaining contact with the cortex, and (iii) hydrodynamic force generated by movement of vesicles, shown in blue, moving towards the center of the aster. The pushing and vesicles forces are centering, meaning that they move the aster and the spindle towards the cell center. The pulling forces can be centering or anti-centering depending on the details of cell shape and cortical attachment. B Origins of length-dependent pushing forces. Displacement of the spindle to the right leads to larger leftwards restoring force because (i) the microtubules spend less time growing and shrinking from the right-hand cortex, and (ii) the buckling forces are larger for the shorter microtubules on the right. C Spring and dashboard model of the spindle showing the equivalent mechanical circuit for pushing microtubule arrays. D Microtubule buckling after contact with the cortex (show cortex). Upper microtubule: clamped at the aster center and fixed at the cortex (but free to pivot). Lower microtubule: clamped at the aster center and free to slide along the cortex. If there is friction at the cortex, the microtubule will initially buckle as shown in the upper part, but then transition to the shape shown below after sliding.

3.2. Pushing forces generated by microtubule growth: the astral pushing model

If a microtubule grows out from a centrosome and keeps elongating after its end makes contact with the cell cortex, a compressive force will be generated that pushes until the microtubule shrinks. The energy for this force comes from the GTPase activity of tubulin. Growth occurs by the addition of GTP-tubulin whose concentration in cytoplasm ([T] = 10μM) is much higher than the critical concentration of GTP-tubulin required for growth (K_T ≈ 0.5 μM, based on studies with the non-hydrolyzable GTP analog GMPCPP ^[45]). If the addition of a tubulin dimer increases the length of a microtubule by δ = 0.6 nm (the 8-nm length of a tubulin dimer divided by the 13 dimers per cross-section of the hollow cylinder), then the maximum pushing force is (kT/δ)ln([T]/K_T) ≈ 12 pN, where kT is the Boltzmann constant times absolute temperature ^[38]. This force is consistent with measurements of maximum pushing forces of 5-10 pN using purified tubulin ^[46,47]. Thus, polymerization of microtubules can generate forces that are comparable to the 1-7 pN forces generated by motor proteins such as dynein and kinesin ^[41].

In vitro experiments with purified tubulin show that pushing forces generated by microtubule growth can center an aster of microtubules and maintain its position at the cell center ^[48,49]. In these experiments, the only source of energy is hydrolysis of GTP, suggesting that pushing forces of microtubules growing against the cortex lead to the centering. Centering can be understood by considering that if the centrosome is displaced from the cell center, then the microtubules on the side closer to the cortex will spend a larger fraction of their time pushing, because they spend less time growing to and shrinking from the closer cortex (Figure 3B). This leads to a force imbalance, the centering force, that tends to return the spindle to the center of the cell ^[50]. The centering force is expected to increase in proportion the displacement from the cell center so that this pushing mechanism acts as a spring, with spring constant, the centering stiffness, equal to the force divided by the displacement (Figure 3C). Thus, in vitro experiments augment theoretical ^[50-52] and computational models^[53] that suggest that pushing forces are capable of centering microtubule asters.

In vivo studies have shown that pushing forces can lead to spindle centering in small cells. Laser ablation and cell centrifugation studies show that, in fission yeast, microtubules do indeed push and that pushing centers the nucleus and spindle ^[54-56]. However, it has been argued that in larger metazoan cells, pushing is not an efficient centering mechanism due to microtubule buckling (Figure 3D), which reduces the pushing force ^[57]. A key conclusion of this review is that microtubule pushing is indeed an important centering mechanism even in larger cells, such as the one-cell C. elegans embryos (diameter ∼ 50 μm) and that buckling augments, rather than impedes, centering ^[51].

Recent observations on the one- and two-cell C. elegans embryo provide strong support that a pushing mechanism keeps the spindle centered during metaphase and anaphase.

1. When magnetic tweezers were used to apply forces to the spindles poles, the spindle moved away from the AP axis and returned when the force was removed ^[58,59] (Figure 4A-C). Thus, the spindle has spring-like properties, with a centering stiffness consistent with a pushing mechanism (see Comparisons of the astral pushing model to experimental data).

2. The spindle remained centered during metaphase after RNAi against GPR-1/2, which is required to activate dynein-mediated cortical pulling forces ^[60]. When cortical pulling forces were removed, both the centering force and stiffness increased^[58], suggesting that pulling is anti-centering, as expected (see Pulling forces associated with microtubule shrinkage).

3. Fluctuations in the number of microtubules associated with the pushing mechanism are expected to lead to positional fluctuations ^[50]; the measured amplitude of these fluctuations ^[38] (Figure 4D-F) accords with the pushing model (see Comparisons of the astral pushing model to experimental data). Furthermore, the stability increases, rather than decreases, following GPR-1/2 RNAi, as expected if the cortical pulling forces are anti-centering.

4. The pushing model predicts a drag coefficient, which arises from the slow remodeling of the aster as the constituent microtubules grow and shrink ^[50]. The measured drag coefficient and associated relaxation time ^[58] also accord with the pushing model. The correlation time associated with spindle fluctuations ^[38] also agrees with the pushing model.

5. During metaphase and anaphase phase, growing microtubule ends (marked with EB1-GFP) contact the cell cortex for about one second ^[61,62] and slide up to a micrometer along the surface ^[38,58,63]. This lateral sliding motion indicates growth and is likely associated with bending by compressive forces. If this interpretation is correct, then the microtubules are undergoing a form of buckling, shown in Figure 3B ^[59].

Figure 4. Measurement of spindle forces during metaphase in the one-cell C. elegans embryo using magnetic tweezers.

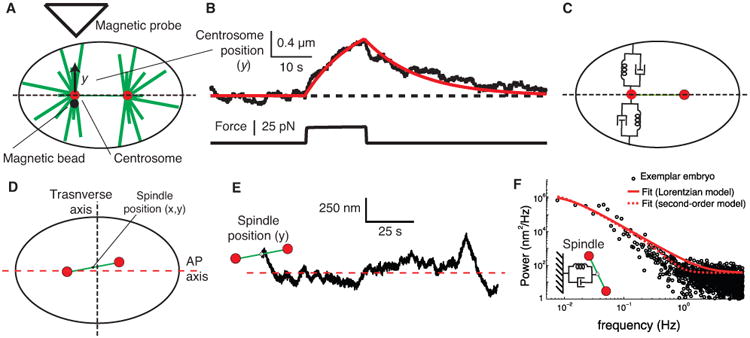
A Magnetic tweezers apparatus induces an upwards force that deflects the centrosome through a distance y. B An individual trace showing the displacement of the centrosome (upper trace) in response to a magnetic force (lower trace). See supplementary movie 2. The embryo has been subjected to RNAi against gpr-1/2 (to reduce the activity of the cortical force generators) and fzy-1 (to prolong metaphase and facilitate recording). The red curve is the prediction of a spring and dashpot model with κ = 20 pN/μm and γ = 260 pM · s/μm. The time constant is τ = γ/κ 13 s. C Spring and dashpot model. See ^[58]. D Definition of spindle coordinate system with respect to the transverse and AP axis. E Transverse position time trace of the spindle center of the embryo during the maintenance phase. F One-sided power spectral density of the y component of the spindle center shown in E (black dots). Least-squares fit to the Lorentzian equation, corresponding to a damped spring with τ = 14.5 ± 3.8 s (solid red line). Least-squares fit to a second-order model (dashed red line). See ^{ref. [38]} for details.

In summary, several lines of evidence suggest that microtubule pushing maintains the C. elegans mitotic spindle at the cell center during metaphase. Cortical pulling forces antagonize centering. A role for cytoplasmic pulling forces (see below) during the maintenance phase, however, cannot be excluded.

3.3. Centering of microtubule asters in interphase cells

In interphase cells, the microtubule cytoskeleton is often nucleated from a single microtubule organizing center (MTOC), which in some cells is centrally located (e.g. ^[64]). MTOC centering may be analogous to mitotic spindle centering, yet it has been attributed to pulling forces generated by cortically anchored dynein rather than to pushing forces. For example, when dynein was inhibited, the MTOC in mouse fibroblasts moved from the center to the cortex, indicating that dynein promotes centering ^[65]. However, it is possible that dynein inhibition alters the pushing forces only on a slow timescale: for example if dynein at the centrosome is needed to anchor the microtubules then inhibiting dynein may permit microtubule to pivot at the centrosome which is expected to abolish centering ^[66]. On the other hand, there is evidence in these cells that pushing forces promote centering: when microtubules were depolymerized on one side of the cell by focal application of nocodazole, the MTOC moved towards the site of microtubule depolymerization ^[65]. In Dictyostelium cells, cortical dynein has anti-centering activity during interphase: when cytoplasmic dynein was over-expressed, the MTOC underwent large erratic movements away from the cell center ^[67]. Thus, aster positioning in mammalian and Dictyostelium interphase cells may have a similar mechanism as mitotic cells, with centering by pushing forces and anti-centering by cortical pulling forces.

3.4. Pulling forces associated with microtubule shrinkage

If the end of a microtubule remains attached to the cell cortex during shrinkage, then a tensile force will bring the centrosome towards the cortex. Assuming that shrinking due dissociation of GDP-tubulin from the end, then the pulling force can be as great as (kT/δ)ln(KD/[D]) ≈ 26 pN, where [D] < 1 μM is the concentration of GDP-tubulin in solution and K_D > 50 μM is the critical concentration of GDP-tubulin required for growth ^[63]. Such high forces have not been measured in vitro, though pulling forces on the order of 1 pN have been observed ^[68] and up to 5 pN have been inferred ^[69]. The force may be augmented if motor proteins such as dynein pull on the microtubule end as it shrinks, or if the motors slide the microtubule along the cell cortex. A key open question is whether the energy that powers pulling derives from the hydrolysis of GTP (microtubule dynamics) or ATP (motors) or both?

There is no doubt, based on the following observations, that pulling forces affect the positioning of mitotic spindles in C. elegans embryos.

1. After cutting the spindle microtubules with a UV laser, the two poles move rapidly towards the cortex on opposite sides of the cell ^[70]. This shows that the spindle is under tension. Following laser-induced disintegration of the poles, centrosomal fragments move towards the cortex, further localizing the pulling forces to the microtubules connecting the poles to the cortex ^[60].

2. These cortical pulling forces also mediate transverse spindle oscillations (rocking of the spindle, Figure 2j), based on laser-cutting experiments showing that the force is larger on the side to which the spindle pole is moving ^[60]. Spindle oscillations due to cortical pulling forces are also observed in mammalian cells ^[71] and fission yeast ^[72].

3. After mild RNAi against the non-muscle myosin NMY-2, membrane invaginations associated with shortening microtubules also indicate tensile forces ^[73].

4. RNAi against GPR-1/2 as well as against the G-proteins GOA and G16 ^[74], the dynein heavy chain ^[42,75], and dynein light chains ^[76] abolish or reduce the posterior displacement and transverse oscillations. Importantly, GPR-1/2 and dynein are located on the cortex and are enriched in the posterior half of the embryo, consistent with an imbalance of cortical pulling forces being responsible for the posterior displacement ^[74]. The oscillation is thought to be due to an unstable tug-of-war between dyneins on opposite sides of the AP axis ^[75].

5. Knockdown of CNSK-1 increases GPR-1/2 expression on the cortex and leads to large spindle movements ^[77], reminiscent of the effect of dynein overexpression on MTOC position in Dictyostelium ^[67]. The theory of dynamical systems ^[74] provides a novel interpretation of these erratic spindle movements. Perhaps the increase in the pulling forces overwhelms the pushing forces and converts the cell center from being a stable fixed point to an unstable one: because the spindle is confined by the cell cortex, its motion is defined by a limit cycle in accordance with the Poincare-Bendixson theorem ^[75].

6. Overexpression of GPR-1/2 induces higher oscillation amplitudes (up to 15 μm amplitude in comparison with ∼3 μm for control embryos), faster spindle velocities and larger spindle displacements towards the posterior, all of which have been associated with pulling forces at the cortex ^[78].

All the evidence in the C. elegans embryo suggests that the pulling forces generated by cortical dynein are anti-centering. The anti-centering caused by cortical pulling can be understood as follows: the fraction of time that microtubules spend pulling will be larger on the closer cortex than on the more distant side, leading to movement towards the closer cortex, which in turn amplifies the force pulling the spindle away from the cell center. In this scenario, pulling forces lead to a negative stiffness ^[50]. The anti-centering activity of dynein is also seen in Dictyostelium (described above) as well as in Drosophila neuroblasts, where it contributes to spindle displacement and asymmetric cell division ^[23,28].

Thus far, we have considered forces generated by cortical dyneins to be anti-centering. However, pulling forces generated by cortical dyneins can theoretically be centering ^{[39,50,52,66,79,80]}, though experimental evidence is lacking. One way that cortical pulling can lead to centering is if the number of cortical motors is exceeded by the number of microtubule ends: in this case, termed limited cortical anchors ^[79], the distant cortex subtends a larger angle on the microtubule array and so will generate a larger force that brings the centrosome back towards the center ^[50]. Thus, cortical pulling can be either centering or anti-centering, depending on the geometry of the cell or the anchoring of the microtubules to the centrosome or the cortex.

3.5. Forces generated by motility along microtubules (cytoplasmic pulling)

Forces can be transmitted through microtubules to the spindle even when the microtubules do not make contact with the cortex. In a classic paper ^[81], microtubules in the sand dollar embryo were depolymerized using colcemid, which is related to colchicine. UV light was used to spatially inactivate colcemid and allow microtubule growth at particular locations, leading to displacement of the aster in the direction of the longer microtubules. Aster movement occurred even if the repolymerized microtubules did not make contact with the cortex, showing that neither cortical pushing nor pulling are necessary. Evidently there is a cytoplasmic mechanism that is capable of displacing microtubule asters.

Forces generated by dyneins acting along cytoplasmic microtubules are thought to center the nuclear-centrosomal complex in C. elegans (Figure 2Ad ^[82]) and the spindles of large embryos such as in the sand dollar ^[81] and perhaps in fish and amphibians ^[83]. This mechanism leads to centering because, when the spindle is displaced away from the cell center, microtubules grow longer on the side towards the center and so the net force will be centering (Figure 3C). While the cytoplasmic pulling mechanism is powered by the dynein ATPase, it still relies on microtubules dynamically adjusting their lengths so that on average they are longer on one side relative to the other.

How can cytoplasmic dyneins exert force on the spindle? One possibility is that dyneins are anchored in the cytoplasm, perhaps on actin filaments. Alternatively, dyneins can move vesicles along microtubules and generate drag forces that will be balanced by a reactive force that moves the spindle towards the moving vesicles ^[84]. Evidence for this latter mechanism comes from RNAi against dynein, as well as against the vesicle proteins Rab7 and RILP, all of which disrupt centering ^[85]. However, the evidence is not definitive as the requirement for vesicle movement may be indirect; for example, vesicles may transport molecules that are required for rigidly anchoring microtubules to the centrosome or that contribute to spindle assembly ^[86,87].

3.6. Principles of centering: length-dependent forces

The key requirement for centering of a microtubule aster is that the centering force acting on the centrosome increases with the inverse distance to the cortex. As a consequence, if the centrosome is displaced to one side, then the force is larger on the side closer to the cortex and moves the centrosome back to the center ^[51]. In this case the centering stiffness is positive. Buckling produces a length-dependent force that decreases with microtubule length (the force depends inversely on the length); buckling therefore centers ^[51]. Microtubule dynamics leads to a length-dependent force because the fraction of the time the microtubule end interacts with the cortex (and therefore the average force) is inversely proportional to the distance (the growing and shrinkage times to and from the further cortex are longer): the centering stiffness associated with microtubule dynamics is positive for cytoplasmic pulling and cortical pushing, meaning that the forces are centering, but is negative for pulling forces ^[50], meaning that the force is anti-centering. The limited cortical anchors model leads to a length-dependent force because the area subtended by a cortical array increases with distance, and the stiffness is positive if the cortical anchors pull. Thus, the spindle forces depend on different molecular and mechanical mechanisms—pushing, pulling, buckling, bending—and on the geometry of the aster and the cell; but whether they are centering or not depends how the net force depends on the distance to the center.

4. Predicted stiffness and stability of the astral pushing model

A crucial question is whether pushing mechanisms can generate the measured force ^[58] and account for the high precision of centering ^[38]. In an earlier theoretical analysis ^[50], the forces and stabilities were calculated for a “one-dimensional spindle” in which microtubules grow in two directions from a microtubule nucleating center to a solid boundary, the cortex. However, to make a quantitative comparison between the models and the experimental data a three-dimensional model is required (see Box 2).

Box 2. Centering stiffness and Stability of astral pushing models.

One Dimension ^[50]

With the help of Figure 5A, the time-averaged force exerted by the growing microtubules on the centrosome depends its the displacement x from the center is:

$$f(x)=[M_{\mathrm{r}}{p}_{\mathrm{r}}(x)-M_1{p}_1(x)]\overline{f}=\frac{M}{2}[p_{\mathrm{r}}(x)-p_1(x)]\overline{f}=\frac{M}{2}\mathrm{\Delta }p(x)\overline{f}$$

where f̄ is the pushing force, M_r (M₁) is the number of microtubules on the right (left), p_r (p₁) is the pushing probability on the right (left), and Δp(x) is the difference in pushing probabilities. We assume that the number of microtubules is the same on both sides, so that the total number of microtubules is M = M_r + M₁. The pushing probability is:

$$p(x)=\frac{{\tau }_{\mathrm{p}}}{{\tau }_{\mathrm{p}}+{\tau }_{\text{np}}+{\tau }_{\mathrm{g}}+{\tau }_{\mathrm{s}}}=\frac{{\tau }_{\mathrm{p}}}{{\tau }_{\mathrm{p}}+{\tau }_{\text{np}}+(R-x)/v+(R-x)/v_{-}}$$

where τ_p is the time pushing, τ_np is the time at the cortex not pushing, τ_s is the time to grow to the cortex and τ_s is the time to shrink from the cortex. We have dropped the subscript as similar expressions hold for both right and left sides (exchange x and −x). R is the cell radius and v₊ (v₋) is the growth (shrinkage) rate. We assume that there are no catastrophes or rescues in the cytoplasm and that microtubules nucleate immediately after shrinking back to the centrosome.

The pushing probability depends on position according to

$$p(x)\approx p(0)+x{p}^{\prime }(0)=p_0+x\frac{p_0(1-p_0)}{R}$$

where p₀ = p(0) and we assume that τ_np ≪ τ_g + τ_s. Thus,

$$\mathrm{\Delta }p(x)\approx 2x\frac{p_0(1-p_0)}{R}$$

The stiffness K is therefore

$$K=f^{\prime }(0)=M{p}_0(1-p_0)\frac{\overline{f}}{2}$$

Because motor pushing is a binomial process, the force variance is

$${\sigma }_f^2=M{p}_0(1-p_0){\overline{f}}^2$$

Therefore, the positional variance is

$${\sigma }_r^2=\frac{{\sigma }_f^2}{K^2}=\frac{R^2}{M{p}_0(1-p_0)}$$

For the case where p₀ ≪ 1, the SD of the positional fluctuation divided by the cell radius is inversely proportional to the square root of the number of pushing microtubules:

$$\frac{{\sigma }_r}{R}\cong \frac{1}{\sqrt{M{p}_0}}$$

Importantly, the positional fluctuations are independent of the pushing force; this is because the thermal fluctuations are very small (see text). In this case, a dimensionality argument indicates that the standard deviation of the fluctuations must scale with radius.

Two dimensions

In 2D, we have to take into consideration that the microtubules at an angle to the x-axis generate only a component of force with respect to the x-axis (Figure 5B). Thus the mean force is

$$f(x)=\frac{M}{2\pi }\overline{f}\underset{-\pi /2}{\overset{+\pi /2}{\int }}\mathrm{\Delta }p(x,\theta )cos\theta d\theta$$

where the cosθ corresponds to the lower forces generated by the off-axis microtubules. We assume that the microtubules are clamped at the centrosome (they cannot rotate) and there is no slippage at the cortex (but see below). In 2D,

$$\mathrm{\Delta }p(x,\theta )=2\frac{p_0(1-p_0)}{R}cos\theta$$

The cosθ arises because the differential distance to the cortex is a maximum along the x-axis (θ = 0) but is zero (for small displacements) orthogonal to the x-axis (θ = π/2). Thus, the stiffness is

$$K=f^{\prime }(0)=\frac{M}{2\pi }\overline{f}\underset{-\pi /2}{\overset{+\pi /2}{\int }}2\frac{p_0(1-p_0)}{R}{cos}^2\theta d\theta =\frac{M{p}_0(1-p_0)\overline{f}}{2R}$$

The 2 in the denominator means that in two dimensions, only half the microtubules contribute effectively to the stiffness because the off-axis microtubules contribute smaller forces.

For the force fluctuations, we square the amplitude of the force component in the x-direction, which is f̄²cos²θ, multiply by the binomial variance and integrate to obtain

$${\sigma }_f^2=\frac{M}{2\pi }{\overline{f}}^2\underset{-\pi /2}{\overset{+\pi /2}{\int }}2p_0(1-p_0){cos}^2\theta d\theta =\frac{1}{2}M{p}_0(1-p_0){\overline{f}}^2$$

Note that the factor of two in the integral comes from the microtubules on each side contributing number fluctuations. Thus, the positional fluctuations are

$${\sigma }_r^2=\frac{{\sigma }_f^2}{K^2}=\frac{R^2}{M{p}_0(1-p_0)}$$

or

$$\begin{array}{cc}\frac{{\sigma }_r}{R}\approx \frac{1}{\sqrt{M{p}_0}}& p_0\ll 1\end{array}$$

Note that in two dimensions, the positional variance still scales inversely with the number of microtubules. This is interesting: all the microtubules are contributing to stability. Yet the off-axis microtubules are contributing only small forces. The reason for this is that the stability is independent of the pushing force, which appears in both the force and the stiffness, and so cancels out. This can be appreciated using a dimensional argument: the stability as measured by the SD of the positional variance has unit length, and scales only with cell radius.

Three dimensions

Now we have to consider the microtubules growing from the displaced centrosome in a conical annulus with angle θ (Figure 5C). The mean force is now

$$f(x)=\frac{M}{2}\overline{f}\underset{0}{\overset{+\pi /2}{\int }}\mathrm{\Delta }p(x,\theta )cos\theta sin\theta d\theta$$

where the sinθ accounts for the smaller area subtended at smaller angles to the x-axis. As before,

$$K=f^{\prime }(0)=\frac{M}{2}\overline{f}\underset{0}{\overset{+\pi /2}{\int }}2\frac{p_0(1-p_0)}{R}{cos}^2\theta sin\theta d\theta =\frac{M{p}_0(1-p_0)\overline{f}}{3R}$$

Thus, the stiffness depends on only one third the total number of microtubules: the effective number of microtubules is reduced both because the off-axis microtubule are contributing less, but also there are fewer on-axis microtubules.

The positional fluctuations again depend inversely on the total number of microtubules

$$\frac{{\sigma }_r}{R}\approx \frac{1}{\sqrt{M{p}_0}}$$

Buckling

In 1D,

$$f(x)=[M_{\mathrm{r}}{p}_{\mathrm{r}}(x){\overline{f}}_{\mathrm{r}}(x)-M_1{p}_1(x){\overline{f}}_1(x)]$$

where

$${\overline{f}}_{\mathrm{r}}(x)=f_{\mathrm{E}}\frac{R^2}{{(R-x)}^2}\approx f_{\mathrm{E}}(1+2\frac{x}{R})$$

and f̄₁(x) is similar except with the sign of x changed. f_E is the Euler force:

$$f_{\mathrm{E}}=\alpha \frac{\mathit{\text{EI}}}{R^2}$$

where α depends on the geometry of buckling: for one end clamped (at the centrosome) and the other end (at the cortex) free to slide, α π²/4 ≈ 2.47. If microtubules are bundled and crosslinked so strongly that they cannot sliding, then the Euler force of each bundle is increased roughly n² (where is n is the number in the bundle); because the number of bundles is only one n^th the number of microtubules, the total force and stiffness will increase n-fold. For one end clamped and the other end fixed but free to pivot α ≈ 20.19 (tanα = α). Thus

$$K=f^{\prime }(0)=\frac{3M{f}_{\mathrm{E}}}{R}{p}_0(1-\frac{1}{3}{p}_0)$$

The stiffness is approximately three times higher. The force fluctuations are the same, but because the stiffness is higher, the positional fluctuations are smaller:

$$\frac{{\sigma }_r}{R}\cong \frac{1}{3\sqrt{M{p}_0}}$$

only one-third the amplitude in the absence of buckling.

Sliding

If the cortex end is free to slide and hits the wall head on, then the clamped-pivot boundary condition will apply. But it is unstable: any fluctuation will lead to slippage and the clamped-sliding condition will prevail. The decrease in force is roughly 8-fold.

The relaxation time is on the order

$$\tau ~\frac{4\pi \eta \kappa }{ln(L/2r)F_{\mathrm{E}}(F-F_{\mathrm{E}})}$$

where η is the viscosity, the microtubule radius and F the polymerization force. Assuming the viscosity of water η = 1 mPa · s and F ≈ 2F_E = 2.6 pN, the time constant is about 6 ms. However, the effective viscosity is likely to be much higher for a microtubule embedded in an aster in the crowded cytoplasm and values up to 100 times higher may not be unreasonable. Thus the relaxation time is expected to be on the order of 0.1 to 1s, similar to the interaction time of the growing microtubule tip with the cell cortex.

The conclusion is that the sliding is expected to decrease the Euler force from 2.3 pN to 0.3 pN over about 1 s. Hence, the highest pushing forces occur shortly after contact with the cortex.

In the case where the microtubules do not buckle and are rigidly anchored at the pole, the stiffness (K) of an array of microtubules growing isotropically the pole and transiently pushing against a solid surface is

$$\begin{array}{cc}K=\frac{M{p}_0(1-p_0)\overline{f}}{nR}& n=1,2,3\text{is thr number of dimensions}\end{array}$$

where M is the total number of microtubules, p₀ is the probability that a microtubule is in the pushing phase (pushing time divided by the total lifetime of the microtubule), f̄ is the force generated by a single microtubule while pushing, and R is the radius of the cell. See Box 2 for details. The stability, defined as the relative standard deviation of the fluctuations from the center, is

$$\frac{\sigma }{R}=\frac{1}{\sqrt{M{p}_0}}$$

^[50] and is independent of the number of dimensions.

The stiffness and stability have interesting scaling properties. The stiffness decreases in higher dimensions because microtubules that are angled with respect to the centering axis contribute only a component of their force to centering. On the other hand, the stability is the same for all dimensions because the positional fluctuations are independent of the pushing force. This is because thermal fluctuations are very small and can be neglected (see below). In this case, a dimensionality argument indicates that the standard deviation of the fluctuations must scale with radius. Thus, while the array is softer in higher dimensions, the stability is not changed. The physiologically relevant case is the three-dimensional one, and the three-fold lower stiffness relative to stability is important for quantitative comparison of the data to the pushing model.

4.1. Buckling increases the centering stiffness and stability

Microtubule buckling, for which evidence in the C. elegans embryo was summarized earlier, has several interesting effects. First, if a microtubule buckles before its maximum polymerization force is reached, then the pushing force is the Euler force

$$f_{\mathrm{E}}=\alpha \frac{\kappa }{R^2}$$

where κ is the flexural rigidity of the microtubule ^[88,89] and α is a constant that depends on the geometry of buckling. If one end is clamped at the centrosome but unable to pivot, and the other end is fixed at the cortex but able to pivot, then α = 20.2; if the cortical end is free to slide along the cortex (consistent with EB1 tracks on the cortex ^[58]), then α = π²/4 ≈ 2.47 ^[87]. We expect that even if the end is free to slide, friction at the cortex or viscous damping on the microtubule will lead to a transient high force (like the clamped-pivot case) which will relax back to the clamp-free case (see Fig. 3D and Box 2).

The second effect of buckling is that the centering stiffness increases roughly three-fold:

$$\begin{array}{cc}K=f^{\prime }(0)\cong \frac{3M{f}_{\mathrm{E}}}{nR}{p}_0& n=1,2,3\text{is the number of dimensions}\end{array}$$

(Box 2). The reason for the increase in stiffness is that as the array moves closer to one cortex, the Euler force increases (because R in the expression for the Euler force decreases); this provides a second length-dependent mechanism (the first is due to microtubule dynamics). The dependence of the Euler force on the square of length brings the stiffness increase to a factor of three.

The third effect is that buckling reduces the positional fluctuations three fold:

$$\frac{{\sigma }_x}{R}=\frac{1}{\sqrt{3M{p}_0}}$$

The reason for the decrease is that while the force fluctuations are unchanged, the higher stiffness leads to smaller positional fluctuations.

4.2. Comparisons of the astral pushing model to experimental data

4.2.1 Stability

During metaphase in the one-cell C. elegans embryo, the positional fluctuations were measured to have a standard deviation of 155 nm (see example in Fig. 4E), corresponding to σ_x/R = 1%, with an upper estimate of 1.3% at the 95% confidence level ^[38]. The total number of pushing microtubules in the entire bipolar spindle was estimated to be Mp₀ = 418, similar to independent estimates from ^[62]. Using this value, the astral pushing model predicts positional fluctuations in the absence of buckling to be 4.9%, inconsistent with the data. However, if there is buckling, then the predicted fluctuation is 1.6%. Thus, the predicted fluctuation is close to the measured fluctuation ^[38].

4.2.2 Stiffness

The stiffness in the one-cell C. elegans embryo was measured using magnetic tweezers to be 16 pN/μm ^[58]. Using this stiffness, the astral pushing model predicts a force per microtubule of KR/Mp₀ = 0.64 pN, small compared to in vitro measurements of polymerization forces (5-10 pN, ^[46,47]). On the other hand, this force per microtubule is consistent with buckling: the Euler force is expected to be between 0.3 and 2.3 pN, assuming a flexural rigidity of 30 pN∙μm^{2 [88]}, a cell radius of 16.25 μm and between 2.47 and 20.2. Buckling of long microtubules is also observed in vitro ^[46,90]. Thus, the high positional stability together with low stiffness and force accord with microtubules pushing and buckling.

The centering spring, though soft, is still rigid enough to quench thermal fluctuations. The centering stiffness is small in the sense that only 10 motors generating a force of 5 pN each, are sufficient to displace the spindle through 3 μm, the distance the C. elegans spindle moves during posterior displacement ^[37] and during transverse oscillations ^[75]. Thus, only a handful of motors are required to fine-tune the position of the spindle. The stiffness of the centering machinery is also remarkably low given that microtubules are among the most rigid cellular polymers. With a Young's modulus E ≈ 2 GPa ^[88], even a single microtubule (cross-sectional area A ≈ 200 nm²) spanning the distance R = 15 μm between the centrosome and the cortex, will have a static compressive stiffness of EA/R ≈ 25,000 pN/μm. This is over 1000 times stiffer than the entire array containing about 10,000 microtubules ^[38]. This suggests that the centering stiffness is determined not by the static properties of microtubules, but rather their dynamical properties, namely conversion between growing and shrinking phases, and/or buckling. By contrast, the stiffness is large in the sense that thermal fluctuations will have a standard deviation of only $\sigma =\sqrt{KT/K}\approx 16\text{nm}$, ten times smaller than the observed fluctuations (155 nm^[75]). Therefore, the stiffness is high enough to quench thermal fluctuations, leaving number fluctuations as the main source of stochasticity. Thus, the value of the stiffness is in a sweet spot that minimizes Brownian motion but still allows fine-tuning of spindle position by the small number of molecular motors that participate in cortical pulling (on the order of 100 distributed around the entire cortex ^[60]).

4.2.3 Damping and time constant

The astral pushing model predicts that the movement of the spindle is slowed by the rearrangement of the astral microtubule through shrinkage and regrowth ^[50]: the spindle cannot move faster than it can control the lengths of its microtubules. The predicted drag coefficient, γ, is close to the measured one, and the predicted time constant (τ = γ/K) is in accord with the measured time constant of about 10 s (Figure 4). The time constant is well matched to the biology of spindle movements: it is long enough to filter out high-frequency fluctuations, but slow enough to allow spindle movements on the 10-second timescale. However, both the force ^[58] and fluctuation ^[75] measurements, hint that the relaxations are more complex than single exponentials (See Fig. 4B & 4F), suggesting that the damped-spring model is a simplification.

4.2.4 Effect of microtubule bundling and branching in the astral pushing model

Thus far, we have considered astral microtubules as independent entities without interactions. In reality, microtubules can associate with one another within cells via cross-linkers and form complex architectures such as bundles (seen fission yeast^[91] and mammalian cells^[92]) or branches (seen in Xenopus egg extracts ^[93,94]). In C. elegans, microtubules in the inner spindle do not form bundles^[95]. However, microtubules in the asters have been reported to form bundles during anaphase ^[96], though this needs to be confirmed by electron microscopy. Bundling could account for the larger centering stiffness in anaphase compared to metaphase ^[58] because the Euler force associated with buckling a bundle of microtubules increases roughly with the square of microtubule in each bundle (Box 2). Finally, branching is expected to increase centering force because it increases the number of microtubule ends, though this has not been explored experimentally or theoretically.

5. Summary and outlook

The most important point made in this review is that pushing forces, generated by microtubule polymerization and using energy derived from the GTPase activity of tubulin, are likely responsible for maintaining the C. elegans mitotic spindle at the cell center during metaphase. Previously, it had been thought that centering during metaphase was due to dynein-dependent cortical pulling forces; however, several mechanical, genetic and theoretical arguments all point to centering by pushing rather than pulling. Indeed, the cortical pulling forces appear to be anti-centering, opposing the pushing forces and tending to move the spindle away from the center. Anti-centering activity by dyneins is observed in other systems including Dictyostelium, Drosophila, and possibly vertebrate tissue culture cells. Thus, cortical pushing and cytoplasmic pulling are likely the principle mechanisms for centering mitotic spindles, while cortical pulling forces are used is move or rotate the spindle away from the cell center.

The interplay between the centering and anti-centering processes ultimately sets the physical limits of the precision of the mitotic spindles. The stability of the centering process is limited by the number of microtubules and the cell size. The more microtubules pushing, the higher the stability; the larger the cell, the lower the stability. Interestingly, because the number of microtubules increases with the cell size (Figure 1), stability will tend to be size invariant.

Spindle centering forces in very large metazoan cells, such as fish and amphibian embryos^[97,98], remain mysterious. Because the astral microtubules do not reach the cortex, none of the three mechanisms discussed—cortical pushing, cortical pulling and cytoplasmic pulling—can apply. One possibility is that these cells have no centering mechanism during mitosis. Is has been suggested that cytoplasmic pulling forces center the centrosome during interphase^[97,98]; the interphase microtubule aster then disassembles and the mitotic spindle is formed at the cell center. If diffusion of the large spindle in the viscous cytoplasm is slow, then the spindle may remain approximately centered without there being an active centering mechanism.

The astral pushing model (as well as the cytoplasmic pulling model) are examples of length dependent processes in which negative feedback leads to positional stabilization. Another example is the antenna model in which motors or cross-linkers that antagonize microtubule growth bind with a rate that increases with polymer length ^[99]. Antenna mechanisms have been proposed to control spindle length ^[99], center the chromosomes within the spindle ^[100,101], regulate the overlap length of polar microtubules ^[102], and to control the length of actin cables in budding yeast ^[103]. The precision of length control is ultimately limited by the number of associated molecules, e.g. microtubules in the case of asters ^[50], or motors in the case of the antenna mechanism ^[104]. Thus, the astral pushing model joins the antenna model, and filament sliding models ^[105] and ciliary growth models ^[106] as a mechanism to regulate the length and position of microtubule-based structures.

An important theoretical finding, is that microtubule buckling, though it decreases pushing forces, actually increases the stability of centering. The low force per microtubule inferred from magnetic tweezers experiments is evidence for buckling. Other evidence for buckling comes from observations that the growing EB1-marked ends of microtubules sliding along the cortex after making contact ^[63,107], suggesting that microtubules continue to grow and bend after they reach the cortex. However, direct evidence for buckling from longitudinal imaging of microtubules is still lacking due to the difficulty of resolving individual microtubules in the aster.

A number of important issues are outstanding. How does the end of a microtubule grow while in contact with the cortex? Is there friction as a microtubule end slides along the cortex ^[52]? How is catastrophe regulated by the cortex? Does dynein regulate catastrophe in addition to generating pulling forces? How does the dynein complex maintain contact with a shrinking microtubule? What are the physical principles that set the precision of the anti-centering process? Does microtubule bundling contribute to the centering process? Clearly more quantitative measurements are needed to resolve the bending and buckling of individual microtubules in asters, and also define more precisely the dynamics of microtubule and spindle movements.

Figure 5. Astral Pushing Models.

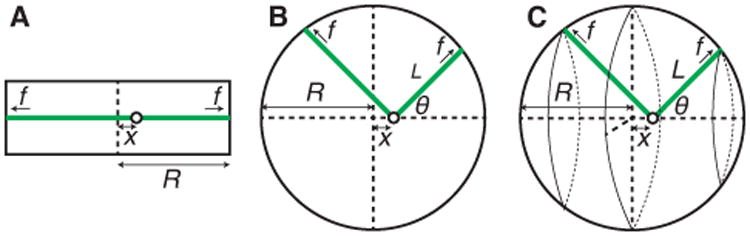
A One-dimensional model. B Two-dimensional model. C Three-dimensional model. The microtubule (green) grows out from the centrosome (open circle) and makes contact with the cortex where it pushes until it converts to the shrinkage phase. See text for definition of parameters.

Box 1.

Accuracy: Conformity of a measure to a true or expected value. For example, how close is the average spindle position to the cell center.

Anterior-posterior (AP) axis: In prolate ellipsoidal cells, such as the one-cell C. elegans embryo, the AP axis corresponds to the long axis.

Astral microtubules: microtubules that nucleate from the centrosomes and grow out towards the cell cortex.

Buckling: When a slender rod is subject to compressive forces acting at their ends, there is a critical force, termed the Euler force, below which the rod remains straight and above which the rod bends into a sinusoidal or hemi-sinusoidal shape (Howard, 2001).

Catastrophe: The conversion of a growing microtubule end to a shrinking one.

Centering force: The force that drives towards and maintains the spindle in the cell center.

Centering stiffness: The centering force divided by the distance between the spindle and the cell center.

Cell cortex: The inner surface of the plasma membrane, usually reinforced by actin, myosin and other actin-binding proteins (Salbreux et al., 2012).

Cortical force generators: A protein complex, including the motor protein cytoplasmic dynein, that binds to the depolymerizing ends of microtubule and generates tensile forces.

Drag coefficient: When multiplied by the velocity equals the force that resists motion.

Euler force: See buckling.

Maintenance phase: In the one-cell C. elegans embryo, the metaphase plate is established between nuclear envelope breakdown and the onset of anaphase. The maintenance phase is a time interval of about 1 to 2 minutes during this period when the centrosomes remained stably centered on the A-P axis, and there is little drift in the transverse direction.

Microtubule dynamics: The polymerization and depolymerization of microtubules, which switch between growing and shrinking phases under the control of tubulin's GTPase cycle(Howard and Hyman, 2003). See catastrophe.

Microtubule organizing center (MTOC): the centrosome of interphase cells from which an aster of microtubules nucleates. In yeast it is the spindle pole body.

Mitotic spindle: A bipolar structure comprising two radial arrays of microtubules emanating from two centrosomes, which form the poles.

Motor protein: An enzyme that uses chemical energy derived from the hydrolysis of ATP to generate directed motion. Dynein and kinesin are two large families of proteins that move along microtubules.

Precision: The repeatability of process; for example, how much spindle position varies from cell to cell. A process can be precise, but not accurate. Accuracy requires precision.

Spindle microtubules: Microtubules that nucleate at the centrosome and grow towards the chromosomes; the K-fibers bind end-on to the kinetochores while the polar/interpolar microtubules are cross-linked to microtubules from the other pole.

Stability: Magnitude of fluctuations around a mean value, measured as the standard deviation. For example, the spindle position fluctuates over time during the maintenance phase.

Thermal fluctuations: Positional variability of particles, such as organelles or the mitotic spindle, driven by impacts from randomly moving solvent molecules.