Significance
A key question in evolutionary biology is: What maintains the abundant genetic variation observed in natural populations? Many organisms experience some seasonality in their habitats, and, if they have multiple generations per year, seasonally fluctuating selection is a potentially powerful mechanism to maintain polymorphism. However, previous research has argued that this occurs rarely. Inspired by recent empirical findings, we reevaluate the potential of seasonally fluctuating selection to simultaneously maintain polymorphism at many loci in the genome. We obtain a more general condition for the maintenance of multilocus polymorphism by seasonally fluctuating selection. This condition may plausibly be satisfied for many species and does not suffer from problems of previous models.
Keywords: temporal heterogeneity, cyclical selection, genetic diversity, marginal overdominance, balancing selection
Abstract
Most natural populations are affected by seasonal changes in temperature, rainfall, or resource availability. Seasonally fluctuating selection could potentially make a large contribution to maintaining genetic polymorphism in populations. However, previous theory suggests that the conditions for multilocus polymorphism are restrictive. Here, we explore a more general class of models with multilocus seasonally fluctuating selection in diploids. In these models, the multilocus genotype is mapped to fitness in two steps. The first mapping is additive across loci and accounts for the relative contributions of heterozygous and homozygous loci—that is, dominance. The second step uses a nonlinear fitness function to account for the strength of selection and epistasis. Using mathematical analysis and individual-based simulations, we show that stable polymorphism at many loci is possible if currently favored alleles are sufficiently dominant. This general mechanism, which we call “segregation lift,” requires seasonal changes in dominance, a phenomenon that may arise naturally in situations with antagonistic pleiotropy and seasonal changes in the relative importance of traits for fitness. Segregation lift works best under diminishing-returns epistasis, is not affected by problems of genetic load, and is robust to differences in parameters across loci and seasons. Under segregation lift, loci can exhibit conspicuous seasonal allele-frequency fluctuations, but often fluctuations may be small and hard to detect. An important direction for future work is to formally test for segregation lift in empirical data and to quantify its contribution to maintaining genetic variation in natural populations.
Ever since biologists were first able to detect population genetic variation at the molecular level, they have been puzzled by its abundance in natural populations (1). Dispute over the underlying reasons gave rise to two scientific schools (2, 3). Proponents of the “(neo)classical” school claim that the bulk of genetic variation is due to neutral or weakly deleterious mutations present at an equilibrium between mutation, genetic drift, and selection. The neoclassical view admits that selection may maintain alleles at intermediate frequency at some loci, but argues that such loci are exceedingly rare on a genomic scale (2). By contrast, the “balance” school posits that a substantial fraction of variation is maintained by some form of balancing selection [with some controversy over the meaning of “substantial” (3)]—for example, heterozygote advantage (overdominance), negative frequency-dependent selection, and spatial or temporal variability in selection pressures (4).
Fifty years later, the debate has not been conclusively settled (5, 6), although the majority view is that (nearly) neutral mutations cause most genetic variation, with overdominance playing a relatively minor part, perhaps acting at only tens of loci per species (7–9). A mechanism considered more common and powerful is spatial environmental heterogeneity. Temporal heterogeneity, by contrast, is believed to be of limited importance (10), despite widespread temporal fluctuations in the strength and direction of selection, both on phenotypes (11) and genotypes (12). In fact, most organisms with multiple generations per year experience a particular type of temporal heterogeneity: seasonality, for example, in temperature, rainfall, resource availability, or in the abundance of predators, competitors, or parasites. Even tropical populations usually experience some seasonality. For example, flowering and fruiting in tropical forests is often synchronized within and between tree species, leading to seasonal changes in food availability for animals (13). Often, there are life-history trade-offs across seasons (14, 15). For example, seasons with abundant resource supply might select for investment in reproduction, whereas stressful seasons may select for investment in survival. Since such life-history traits are usually polygenic, many organisms should experience seasonally fluctuating selection at a large number of loci.
With discrete generations, the fates of genotypes under temporally fluctuating selection depend on their geometric mean fitnesses over time (16). In haploids, two alleles generally cannot coexist because one will have a higher geometric mean fitness and eventually go to fixation (ref. 16, but see refs. 17 and 18). In diploids, polymorphism at a single locus is stable if heterozygotes have the highest geometric mean fitness (“marginal overdominance”), although in any particular generation, one of the homozygotes might be fittest (16, 19, 20).
Extending these results to the multilocus case is nontrivial, and, so far, only two cases are well-understood: (i) multiplicative selection across loci and (ii) temporally fluctuating selection on a fully additive trait. Under multiplicative selection in an infinite population with free recombination, the allele-frequency dynamics at a focal locus are independent of those at other loci. Thus, polymorphism is stable if heterozygotes have the highest geometric mean fitness, as in the single-locus case. However, deviations from multiplicative selection appear to be the rule. In particular, beneficial mutations often exhibit diminishing-returns epistasis (21–23). Additionally, there is the potential problem of genetic load. Genetic load is commonly defined as the difference between the population’s average fitness and the fitness of the fittest possible genotype. Lewontin and Hubby (1) noticed that this value can become unsustainably high if there is strong heterozygote advantage at many loci. This was a conundrum for the neoclassical school, which was worried that with high genetic load, single individuals would have to produce an astronomically large number of offspring. Others have dismissed this concern, arguing, for example, that selection does not generally act on all loci independently or that only relative fitness differences within the population are relevant, not fitness relative to some optimum genotype that might not even exist (24–27). However, debate continues over whether genetic load should be an important consideration (28, 29).
The second previously studied scenario is seasonally fluctuating selection on a trait to which loci contribute additively (30, 31). These models generally assume additivity also within loci, such that the contribution of heterozygotes is exactly intermediate between the contributions of the two homozygotes. Temporally fluctuating selection can then cause intermediate trait values to be best in the long run (32), i.e., select against variance in fitness. Effectively, this is stabilizing selection on the temporal average. As such, it can generally maintain polymorphism at only one locus (33, 34), or two loci if their effect sizes are sufficiently different (35) or if they are closely linked (30). The reason is that with multiple loci and additivity within and between loci, there are multiple genotypes with intermediate phenotypes. For two loci, for example, there is the double heterozygote (“heterozygous intermediate”) and the genotype homozygous at both loci, but for alleles with opposite effects (“homozygous intermediate”). These genotypes may all have the same high fitness. However, matings between heterozygous intermediates produce a range of different genotypes, some of which are less fit than their parents. By contrast, matings between homozygous intermediates only produce new homozygous intermediates. Homozygote intermediates can therefore go to fixation and eliminate all polymorphism.
In summary, multiplicative seasonal selection is a powerful mechanism to maintain multilocus polymorphism, but the assumed independence across loci and the associated load call into doubt its plausibility. On the other hand, selection on additive traits can maintain polymorphism at only a few loci. So far, there has been little need for further exploration because there were no clear empirical examples to challenge the view that temporal heterogeneity rarely maintains variation. This is now changing, however, as advances in sequencing technology allow detailed studies of genetic variation across time and space. For instance, by sampling the same temperate population of Drosophila melanogaster at several time points, Bergland et al. (36) detected seasonal allele-frequency fluctuations at hundreds of sites in the genome. Many of the SNPs are also shared with African populations of D. melanogaster and some even with the sister species Drosophila simulans, indicating that some of them may be ancient balanced polymorphisms. More generally, recent population genomic data appear to suggest that balancing selection contributes more to maintaining genetic variation than previously assumed (37) and that mutation-selection-drift balance alone is not sufficient to reconcile evidence from population genomics and quantitative genetics (38). Thus, we need to reconsider the potential of temporally fluctuating selection to maintain multilocus polymorphism.
As explained above, the conditions for multilocus polymorphism under seasonally fluctuating selection have been examined mostly in two narrow cases. Here, we examine a more general class of seasonal selection models with various forms of dominance and epistasis. Using deterministic mathematical analysis and stochastic simulations, we show that multilocus polymorphism is possible if the currently favored allele at any time is sufficiently dominant, with dominance measured by using a scale on which contributions across loci are additive. This mechanism, which we call “segregation lift,” can maintain polymorphism at a large number of loci across the genome, is robust to many model perturbations, and does not require single individuals to have too many offspring. Depending on the parameter values, allele-frequency fluctuations can be large and readily detectable, or subtle and hard to discern.
Basic Model
We consider a diploid, randomly mating population in a seasonally fluctuating environment. While asymmetry in various model parameters will be explored later, we start with a fully symmetric model having a yearly cycle with generations of winter followed by generations of summer. The genome consists of unlinked loci with two alleles each: one summer-favored and one winter-favored allele. For a given multilocus genotype, let and be the number of loci homozygous for the summer and winter allele, respectively, and the number of heterozygous loci, with .
In the basic model, loci are interchangeable in their effects (see Stochastic Simulations for a more general model), and the fitness of a multilocus genotype can be computed as a function of , and . In the simplest case, fitness depends only on in summer and in winter, i.e., half the number of currently favored allele copies. To allow for dominance effects, we generalize this simple scenario and assume that fitness in summer depends on the summer score
| [1] |
and fitness in winter depends on the winter score
| [2] |
The parameters and quantify the dominance of the currently favored allele in summer and winter, not with respect to fitness, but with respect to the seasonal scores and . Because we are interested in whether temporally fluctuating selection can maintain polymorphism in the absence of other stabilizing mechanisms, we only consider values of and between 0 and 1, and do not allow values >1, which would correspond to standard heterozygote advantage.
The relationship between the seasonal score ( in summer and in winter), and fitness, , is given by a monotonically increasing fitness function . This function specifies the strength of selection and accounts for epistasis. With discrete generations, the allele-frequency dynamics at a focal locus are driven by the relative fitnesses of the three possible genotypes at that locus—for example, the ratio of the fitness of homozygotes and heterozygotes. We say that there is no epistasis if these ratios and thus the strength of selection are independent of the number of other loci and their contributions to . This is the case when fitness is multiplicative across loci:
| [3] |
where is the fitness value at locus . In our model, this is achieved by setting because then Eq. 3 is fulfilled with if locus is homozygous for the currently favored allele, or if it is heterozygous, and if it is homozygous for the currently disfavored allele. With , the multiplicative model is characterized by . We therefore use the second derivative of the logarithm of fitness as a measure of epistasis (see ref. 39 for a similar definition of epistasis). Under positive or synergistic epistasis (), the logarithm of fitness increases faster than linearly with , and thus selection at a focal locus increases in strength with increasing contribution of the other loci to . By contrast, under negative or diminishing-returns epistasis (), selection at a focal locus becomes weaker with increasing contribution of other loci to . We focus on two classes of fitness functions (Fig. 1). The first is of the form
| [4] |
with a positive parameter . Although for in Eq. 4, fitness increases faster than linearly with increasing (Fig. 1A), transformation to the logarithmic scale reveals that epistasis is negative for all (Fig. 1B). Epistasis () becomes more negative with increasing , but and thus the selective advantage of having an additional favored allele still increases with for all . Thus, larger values correspond to overall stronger per-locus selection.
Fig. 1.
Examples for fitness functions generated by Eq. 4 or Eq. 5 with various parameters. In A, fitness is shown on a linear scale, and in B, on a logarithmic scale.
The second class of fitness functions is of the form
| [5] |
with . This function reduces to the multiplicative model with (cyan lines in Fig. 1) and has positive epistasis with (e.g., magenta lines in Fig. 1).
In summary, fitness is computed in two steps. The first maps the multilocus genotype onto a seasonal score to which loci contribute additively, essentially a generalized counter of the number of favored alleles (Eqs. 1 and 2), and the second maps to fitness (Fig. 1). This two-step process disentangles dominance (step 1) from selection strength and epistasis (step 2).
In our model, genotypes with many summer alleles have a high summer score but a low winter score and vice versa, a form of antagonistic pleiotropy. Previous theoretical studies suggest that antagonistic pleiotropy is most likely to maintain polymorphism if for each trait affected by a locus the respective beneficial allele is dominant (40, 41). Such “reversal of dominance” also facilitates the maintenance of polymorphism in single-locus models for temporally fluctuating selection (42). Hypothesizing that reversal of dominance would also help to maintain polymorphism under multilocus temporally fluctuating selection, we assume that and in Eq. 1 and 2 take the same value, , which means that dominance switches between seasons (see Stochastic Simulations for a more general model). For , we have “deleterious reversal of dominance” (41), and the currently favored allele is always recessive, whereas for , we have “beneficial reversal of dominance” (41), and the currently favored allele is always dominant. If , the seasonal score is additive, not just between loci, but also within loci. Importantly, the value of also determines the relative fitness of heterozygous intermediates, multilocus genotypes with the same number of summer and winter alleles and at least some heterozygous loci, compared with homozygous intermediates, which also have the same number of summer and winter alleles, but are fully homozygous (Fig. 2). For , heterozygous intermediates have a lower seasonal score, , and therefore a lower fitness in both seasons than homozygous intermediates. For , heterozygous and homozygous intermediates have the same score and fitness. Finally, for , heterozygous intermediates have a higher score and fitness. Interestingly, because measures dominance not at the scale of fitness but at the scale of the seasonal score, , beneficial reversal of dominance for fitness is neither sufficient nor necessary for (SI Appendix, Fig. S1).
Fig. 2.
Values of the seasonal score, , as a function of the dominance parameter, , for two example four-locus genotypes: a heterozygous intermediate (blue line) and a homozygous intermediate (black solid line).
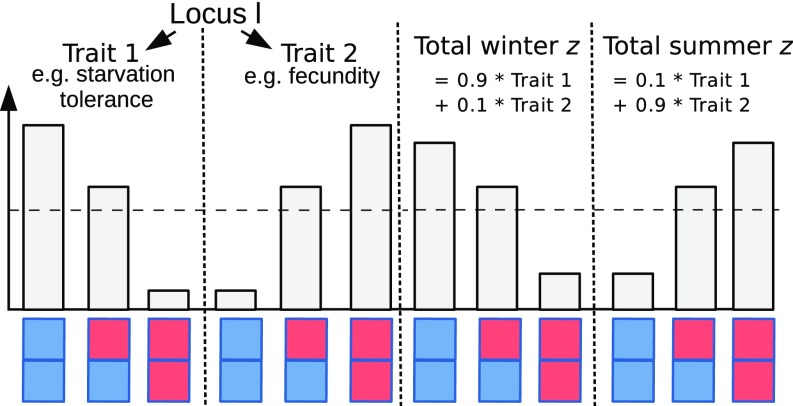
Multiple mechanisms could underlie a seasonal reversal of dominance. For example, metabolic control theory suggests that deleterious mutations affecting multistep metabolic pathways are generally recessive (43). If selection is fluctuating such that each allele is favored during one season and deleterious in the other season, we might thus expect a beneficial reversal of dominance. Alternatively, changes in dominance could be mediated by seasonal changes in gene expression. But even without changes in the genotype–phenotype map, seasonal changes in dominance are possible. In the example scenario in Fig. 3, the additive seasonal score, , is a composite phenotype, a weighted average of two (also additive) traits—for example, starvation tolerance and fecundity—and there is antagonistic pleiotropy. Although the allelic effects on the two traits remain constant throughout the year, because the relative importance of the traits changes between seasons. This scenario requires changes (though not necessarily a reversal; SI Appendix, Fig. S2A) in dominance with respect to the pleiotropic effects of a locus on the two traits. For example, the winter allele (blue) in Fig. 3 produces higher starvation tolerance and is dominant for this trait, whereas it leads to smaller fecundity and is recessive there. One specific way in which such changes in dominance across pleiotropic effects can arise is via branched enzyme pathways with saturation or feedbacks (44).
Fig. 3.
Potential mechanistic underpinning for beneficial reversal of dominance. There is antagonistic pleiotropy for two traits, and the seasonal scores for winter and summer are computed as weighted averages of traits 1 and 2, with the relative importance of the two traits switching between seasons. The dashed line indicates the average of the two homozygote traits. If the heterozygotes are closer to the fitter homozygote with respect to both traits 1 and 2, there is a beneficial reversal of dominance at the level of the seasonal score, . See SI Appendix, Fig. S2 for alternative scenarios.
Deterministic Analysis
In this section, we assume that population size is so large that genetic drift does not play a role. We also assume that mutations are rare enough that the allele-frequency dynamics will equilibrate before a new mutation arises at one of the loci. This simple deterministic framework allows us to develop an intuitive understanding of the conditions for stable polymorphisms for various genotype-to-fitness maps. The intuitions developed here will then be checked and extended with stochastic simulations in the next section.
We will first confirm that the conditions under which seasonally fluctuating selection can maintain polymorphism are restrictive when contributions to the seasonal score are additive within loci ( in Eqs. 1 and 2). Then, for all possible genotypes, and the mean over time is . The long-term success of a genotype depends on its geometric mean fitness, or, equivalently, on the arithmetic mean of the logarithm of fitness, . Jensen’s inequality or simple geometric considerations (Fig. 4) tells us that the arithmetic mean of and for a given genotype will be smaller than or equal to if everywhere (Fig. 4A), equal to if (Fig. 4B), and larger than or equal to if (Fig. 4C).
Fig. 4.
The logarithm of summer fitness (red) and winter fitness (blue) and the average logarithm of fitness (gray) as a function of a genotype’s summer score, . Assuming , the winter score is , leading to the mirror symmetry around . If the fitness function is concave on the logarithmic scale, intermediate types have the highest average log-fitness (A); if the fitness function is log-linear, then all types have the same average log-fitness (B); and if the fitness function is convex on a logarithmic scale, extreme types have the highest average log-fitness and thus the highest geometric mean fitness (C).
The interannual allele-frequency dynamics (e.g., from summer to summer or from winter to winter) with multiplicative fitness () and are thus neutral. No balancing selection emerges. With positive epistasis (), extreme types with either only summer or only winter alleles have the highest geometric mean fitness. Therefore, the population ends up in a state where all loci are fixed for the summer allele or all for the winter allele. With negative epistasis (), the genotypes with the highest geometric mean fitness are those with the same number of summer and winter alleles and thus . There are always some genotypes heterozygous at one or more loci that fulfill this condition (heterozygous intermediates; Fig. 2). For an even number of loci, is also true for genotypes homozygous for the summer allele at half of the loci and homozygous for the winter allele at the other half (homozygous intermediates). When one of the homozygous intermediates fixes in the population, it cannot be invaded by any mutant starting at small frequency (under the assumptions of the deterministic model; see SI Appendix, section S1 for a detailed proof), and all polymorphism is eliminated. For an odd number of loci, homozygous intermediates do not exist, and some polymorphism may be maintained, at least at one locus. This case, which we will examine in more detail below, appears to be the only way in which seasonally fluctuating selection can maintain polymorphism under additivity ().
Next, we explore whether deviations from additivity () can facilitate multilocus polymorphism. Under multiplicative selection, i.e., without epistasis, the conditions for polymorphism at one locus are not affected by the dynamics at other loci. Thus, given the fitness values for individual loci ( for heterozygotes, and for currently favored and disfavored homozygotes, respectively, see text below Eq. 3), we can conclude that polymorphism is possible if
| [6] |
That is, there must be a reversal of dominance with respect to , such that at any time the currently favored allele is dominant.
Now, we explore whether such a beneficial reversal of dominance can also maintain polymorphism in the presence of epistasis. In each case, a necessary condition for polymorphism is that a population fixed for the fittest possible fully homozygous genotype can be invaded by mutants. As we have seen above, with synergistic epistasis (), there are two fully homozygous genotypes with maximum fitness, the one with the summer allele at all loci and the one with the winter allele at all loci. In both cases, the resident type has score in one season and score in the other season, whereas mutants differing in one position have scores and . For mutants to invade, we thus need
| [7] |
Using our example class of fitness functions with positive epistasis, Eq. 5 with , we thus obtain the condition
| [8] |
The critical value of , , at which extreme types become invasible, satisfies
| [9] |
For , takes values 0.707, 0.954, and 0.995, with 1, 10, and 100 loci, respectively. For in general, approaches 1 as the number of loci increases. To see this, note first that the condition in Eq. 9 is always fulfilled for and thus . Thus, as the number of loci, , goes to infinity, becomes small, and we can approximate the second term on the left-hand side of Eq. 9 by a Taylor expansion around 1 to obtain
| [10] |
Multiplying both sides by and letting go to infinity, we can conclude that is approximately 1 if the number of loci is large. Thus, for fitness functions of the type in Eq. 5 with positive epistasis, seasonally fluctuating selection can, in principle, maintain polymorphism at many loci, but the respective favored allele would have to be almost completely dominant, requiring large seasonal changes in dominance.
With diminishing-returns epistasis (), the fittest possible fully homozygous genotype carries the summer allele at half of the loci and the winter allele at the other half of the loci (assuming an even number of loci). Thus, a necessary condition for polymorphism is that this homozygous intermediate type can be invaded by mutants. The resident type has score in both seasons whereas mutants differing in one position have scores and . Thus, the resulting necessary condition for polymorphism is
| [11] |
Again, this condition is always fulfilled for . For fitness functions of the form Eq. 4 with any exponent , the critical dominance coefficient at which homozygous intermediates become invasible satisfies
| [12] |
This quadratic equation has a negative solution, which is not relevant for our model, and a positive solution
| [13] |
From Eq. 13, decreases as increases and approaches 0.5 as goes to infinity. The intuition here is that the second derivative of the logarithm of fitness decreases with increasing . Therefore, for large , epistasis around the intermediate type with is weak, and the conditions for polymorphism approach those without epistasis. In other words, with increasing , selection against temporal variation around the intermediate type becomes weaker, and a smaller change in dominance is sufficient to overcome it.
Our results so far suggest that for a broad class of fitness functions, seasonally fluctuating selection can maintain polymorphism if in both seasons the respective favored allele is sufficiently dominant. We call this mechanism “segregation lift” because it is based on a positive aspect of two alleles segregating at the same locus, as opposed to the negative aspect of segregation load. However, the preceding analysis does not tell us whether polymorphism will be maintained at all loci, or just one or a few of them. Also, it is still unclear how efficient segregation lift is at maintaining multilocus polymorphism in finite populations with genetic drift and recurrent mutations and whether genetic load is a problem. To address these questions, we now turn to stochastic simulations.
Stochastic Simulations
We use Wright–Fisher type individual-based forward simulations (see SI Appendix, section S2 for details). That is, for every individual in a generation independently, two individuals are sampled as parents in proportion to their fitnesses. We focus on diminishing-returns fitness functions of type Eq. 4 both because diminishing-returns epistasis appears to be more common and plausible (e.g., refs. 21–23) and because the above theoretical arguments suggest that it is more conducive to multilocus polymorphism than synergistic epistasis. Specifically, the critical dominance parameter, , for diminishing-returns epistasis in Eq. 13 is generally smaller than the one for synergistic epistasis in Eq. 9. In addition, we run some simulations for the multiplicative model.
Additional parameters in the stochastic simulations are the symmetric mutation probability per allele copy per generation and the population size . We generally keep population size constant, but also run supplementary simulations with seasonal changes in population size. Table 1 gives an overview of the model parameters and the ranges explored. In most simulated scenarios, selection and dominance effects are strong relative to mutation [ and are much larger than the mutation rate ]. Although natural populations are often larger and mutation rates smaller than the values used here, many population genetic processes depend only on the product (e.g., ref. 45). Thus, large populations with small mutation rates may be well approximated by computationally more manageable smaller populations with larger mutation rates.
Table 1.
Overview of model parameters and the ranges explored
| Parameter | Explanation | Range explored |
| Number of generations per season;a year has generations | 1–20 | |
| Population size | 100–10,000 | |
| Number of loci | 1–500 | |
| Mutation probability per allele copy per generation | ||
| Dominance parameter | 0–1 | |
| Exponent of the fitness function Eq. 4 | 0.5–4 |
In addition to the basic model, we design a “capped” model to assess the relevance of genetic load. In this model, each individual can be drawn at most 10 times as a parent of individuals in the next generation, i.e., contribute at most 10 gametes. Once an individual has reached that number, its fitness is set to 0 so that it cannot be drawn again. To better understand the role of offspring-number capping, we also run supplementary simulations with a cap of three, the smallest possible value that still allows for differences in offspring number between individuals in the population.
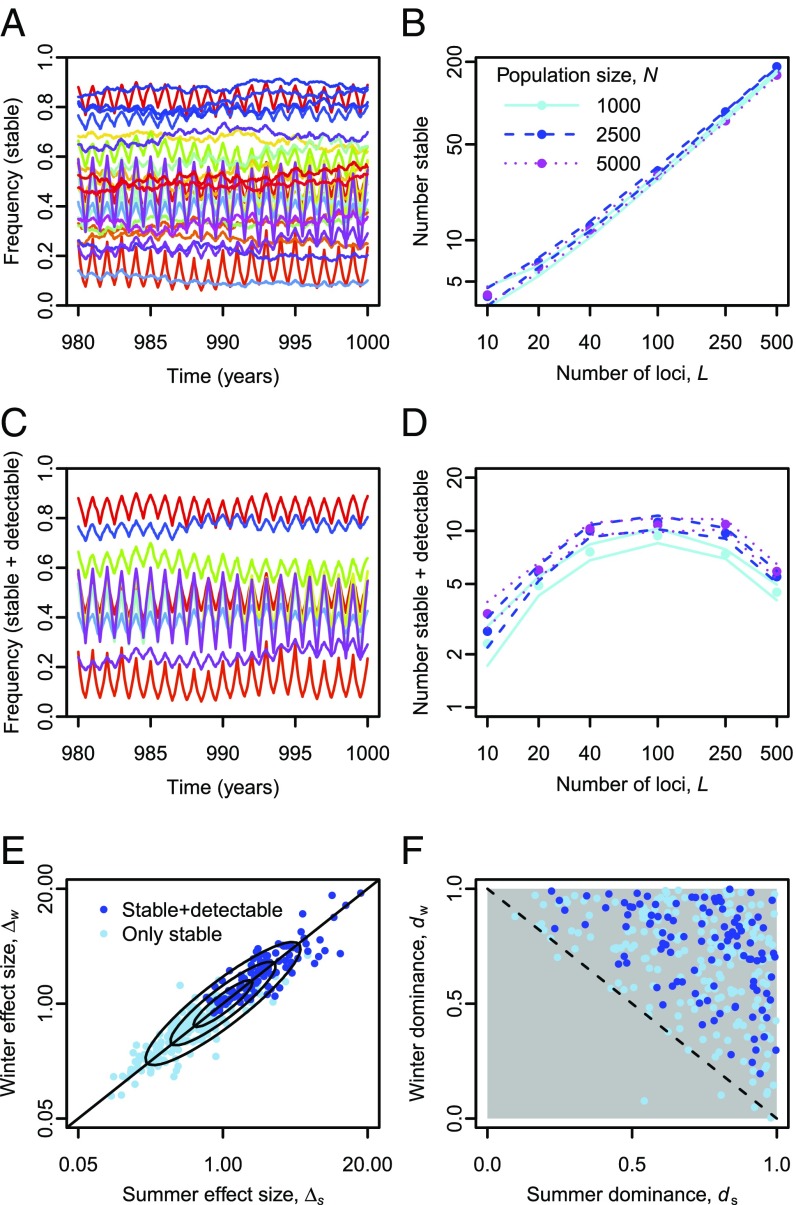
From the simulation output, we estimate an “effective strength of balancing selection” (Materials and Methods and SI Appendix, section S2), which tells us whether and how fast a rare allele increases in frequency over a full yearly cycle. As expected from the above theoretical arguments, additive contributions within loci () are not conducive to multilocus polymorphism (Fig. 5). For even numbers of loci, i.e., situations where both homozygous and heterozygous intermediates exist (Fig. 2), the effective strength of balancing selection estimated from the simulations is negative, indicating that rare alleles tend to become even rarer. For small odd numbers of loci, the effective strength of balancing selection is positive, but only one or two loci at a time fluctuate at intermediate frequency (SI Appendix, Fig. S4). As the number of loci increases, the effective strength of balancing selection eventually becomes negative even for odd numbers, decreases overall in absolute value, and finally approaches zero (effective neutrality) from below (Fig. 5). This behavior is independent of the exponent, , of the fitness function Eq. 4. Also, as expected, effective balancing selection (Materials and Methods) emerges if the dominance parameter, , is larger than a certain critical value, which decreases with the number of loci and is only weakly influenced by mutation rate (Fig. 6).
Fig. 5.
Effective strength of balancing selection ( in Eq. 14 in Materials and Methods) in the additive case () as a function of the number of loci. Solid lines indicate means and dashed lines indicate means two standard errors. Simulations are always run for successive odd and even numbers. .
Fig. 6.
Critical value of the dominance parameter, , such that the effective strength of balancing selection ( in Eq. 14 in Materials and Methods), is positive (stable polymorphism) if , and negative (unstable polymorphism) if . Symbols represent means across replicates, and lines represent averages two standard errors. Since the pattern for odd numbers of loci is more complex (Fig. 5), only even values for the number of loci are included here. .
From now on, we will focus on scenarios with large numbers of loci. For the case of loci, Fig. 7 shows example allele-frequency trajectories for three different dominance parameters, . For small , each locus is almost fixed either for the summer or winter allele. For large , all loci fluctuate at intermediate frequency. The critical dominance parameter, , with 100 loci is close to 0.5, independently of the exponent of the fitness function, (Fig. 8A). For , i.e., if the currently favored allele is recessive, the effective strength of balancing selection is negative and polymorphism is unstable (Fig. 8A). As increases beyond 0.5, i.e., as the currently favored allele becomes more dominant, effective balancing selection becomes stronger (Fig. 8A). Both the stabilizing and destabilizing effects increase with increasing exponent (Fig. 8A).
Fig. 7.
Three examples of allele-frequency trajectories for , and (A), (B), and (C). Only 10 randomly selected loci (shown in different colors) out of 100 loci are shown for 5 years (150 generations) in the middle of the simulation run (years 301–305).
Fig. 8.
Influence of the dominance parameter on effective strength of balancing selection (A; , Eq. 14, Materials and Methods), retardation factor (B), magnitude of fluctuations (C; , Eq. 15, Materials and Methods), and predictability of fluctuations (D). Symbols indicate averages across replicates for the uncapped vs. capped model variant (often overlapping), and solid vs. dashed lines in A, C, and D indicate the respective means two standard errors. Lines in B simply connect maximum-likelihood estimates obtained jointly from all replicates. . See SI Appendix, Fig. S5 for more detailed information on the distribution and frequency dependence of seasonal allele frequency changes. The vertical gray lines are at . Bal. sel., balancing selection; exp., expected.
A tendency for rare alleles to increase in frequency does not guarantee that the average lifetime of a polymorphism is larger than under neutrality (42, 46). This is particularly interesting for fluctuating selection regimes with positive autocorrelation where alleles regularly go through periods of low frequency (42). We therefore compute the so-called retardation factor (46), the average lifetime of a polymorphism in the selection scenario relative to the average lifetime under neutrality (see SI Appendix, section S2 for detailed methodology). The results for 100 loci are consistent with those for the effective strength of balancing selection: For , polymorphism under segregation lift is lost more slowly than under neutrality (Fig. 8B).
To quantify seasonal fluctuations, we compute an effective selection coefficient (Materials and Methods and SI Appendix, section S2). We also compute the predictability of fluctuations as the proportion of seasons over which the allele frequency changes in the expected direction, e.g., where the summer-favored allele increases over a summer season. Both the effective selection coefficient and the predictability of fluctuations have a maximum at intermediate values of and increase with increasing exponent of the fitness function Eq. 4 (Fig. 8 C and D). For even higher values of , fluctuations are not as strong, presumably because heterozygotes are fitter, and therefore more copies of the currently disfavored allele enter the next generation. Also, effective strength of balancing selection, effective selection coefficient, and predictability of fluctuations increase with the number of generations per season (SI Appendix, Fig. S6).
With an offspring-number cap of 10, the results for the capped model generally match the results for the uncapped model in all respects, especially for (Fig. 8). It appears that the capping mechanism only rarely takes effect because of relatively narrow distributions of the seasonal score, , within a generation (SI Appendix, Fig. S7), and consequent relatively low variance in fitness (SI Appendix, Fig. S8). For example, for and , the fittest individual in the population was on average 1.2 times fitter than the least fit individual and 4.9 times fitter for (see SI Appendix, section S4 for a supporting heuristic analysis). When the offspring-number cap is set to three, substantial quantitative differences between uncapped and capped simulations are seen (SI Appendix, Fig. S9). However, 0.5 remains the critical dominance parameter. This result also holds for the multiplicative model (SI Appendix, Fig. S10), but with otherwise larger differences between capped and uncapped model versions, even with an offspring-number cap of 10. Also, the retardation factor for the multiplicative model is often below one, even when the effective strength of balancing selection is positive. The reason appears to be that there is larger variance in fitness under the multiplicative model (SI Appendix, Fig. S11) and that fluctuations are sometimes so large that alleles go to fixation (SI Appendix, Fig. S12). Both of these effects are weakened by offspring number capping, so that the capped multiplicative model behaves more similarly to the diminishing-returns model (SI Appendix, Fig. S10).
Additional simulations for the diminishing-returns model suggest that the finding of stable multilocus polymorphism for still holds under various forms of asymmetry, e.g., when one season has more generations than the other (SI Appendix, Fig. S13); when the exponent of the fitness function, , differs between summer and winter (SI Appendix, Fig. S14); and when there are seasonal changes in population size (SI Appendix, Fig. S15). To explore the effects of asymmetry in the dominance parameters, we fixed the winter dominance parameter, , at 0.4 and varied the summer dominance parameter, . Stable polymorphism then arises for (SI Appendix, Fig. S16), suggesting that stable polymorphism requires an arithmetic mean dominance parameter >0.5. Compared with the diminishing-returns model, the multiplicative model seems less robust to asymmetry (SI Appendix, Fig. S17).
With an increasing number of loci under the diminishing-returns model and with , the strength of balancing selection, the retardation factor, and the magnitude and predictability of fluctuations all decrease (Fig. 9). Population size hardly influences effective strength of balancing selection and effective selection coefficient, measures which are based on average allele-frequency changes (Fig. 9 A and C), but large populations maintain polymorphism for longer (Fig. 9B) and have more predictable allele-frequency fluctuations (Fig. 9D). In small populations, polymorphism can even be lost slightly faster than under neutrality (Fig. 9B).
Fig. 9.
Influence of population size and the number of seasonally selected loci on effective strength of balancing selection (A; in Eq. 14, Materials and Methods), retardation factor (B), magnitude of fluctuations (C; in Eq. 15, Materials and Methods), and predictability of fluctuations (D). Symbols indicate averages across replicates and lines in A, C, and D indicate means two standard errors (in C and D, standard errors are too small to be visible). Lines in B simply connect maximum-likelihood estimates obtained jointly from all replicates. Note that in B, some points are missing because the rate of loss of polymorphism was too small to be quantified. . Bal. sel., balancing selection; exp., expected.
Finally, we consider a generalized model where parameters vary across loci and may be asymmetric between seasons. Independently, for each locus , we draw four parameters: Summer effect size and winter effect size are drawn from a log-normal distribution. For this, we draw a pair of parameters from a bivariate normal distribution with mean 0, SD 1, and correlation coefficient 0.9, and then apply the exponential function to each of them. Summer and winter dominance parameters, and , are drawn independently from a uniform distribution on [0,1]. Seasonal scores are then computed as , where the contribution of locus in summer is 0 for winter–winter homozygotes, for heterozygotes, and for summer–summer homozygotes. Winter contributions are computed analogously. Because all effect sizes are positive, all loci exhibit a trade-off between summer and winter effects. We use here because it led to the most stable polymorphism in the basic model.
The results indicate that polymorphisms with different parameters can be maintained in the same population, with their allele frequencies fluctuating on various trajectories (Fig. 10A). With a sufficiently high total number of loci, hundreds of stable polymorphisms (positive expected frequency change of a rare allele; see SI Appendix, section S2 for details) can be maintained in populations of biologically plausible size (Fig. 10B). The number of loci classified as stable depends only weakly on population size. However, only a small proportion of the polymorphisms classified as stable also exhibit detectable allele-frequency fluctuations, defined as changes in the expected direction by at least 5% in at least half of the seasons (Fig. 10 C and D). The number of detectable polymorphisms is highest at an intermediate total number of loci and increases with population size (Fig. 10D). Detectable polymorphisms tend to have larger summer and winter effect sizes than polymorphisms that are only stable (Fig. 10E). Compared with unstable polymorphisms, stable polymorphisms are more balanced in their summer and winter effect sizes (two-sample -test on , ; Fig. 10E; see also SI Appendix, Fig. S18). Many stable polymorphisms have asymmetric dominance parameters, but for almost all of them, detectable or not, the average dominance parameter across seasons is >0.5 (Fig. 10F).
Fig. 10.
Stability of polymorphism and detectability of allele-frequency fluctuations when parameters vary across loci and seasons. (A) Snapshot of allele-frequency trajectories for stable polymorphisms in one simulation run. (B) Average number of stable polymorphisms as a function of the total number of loci for different population sizes. (C and D) As in A and B, but only for polymorphisms that are also detectable. (E) Winter effect size, , vs. summer effect size, , for stable and detectable and only stable polymorphisms. The plot shows pooled results over ten simulation runs with independently drawn parameters. Oval isoclines indicate the shape of the original sampling distribution, with 75% of the sampling probability mass inside the outermost isocline. (F) Corresponding dominance parameters (see also SI Appendix, Fig. S19). The dominance parameters were originally drawn from a uniform distribution on the unit square. Parameters: and in A, C, E, and F .
Discussion
We study a simple model for seasonally fluctuating selection that maps the multilocus genotype to fitness in two steps. First, we count the number of loci homozygous for the currently favored allele and add the number of heterozygous loci weighted by a dominance parameter. The resulting seasonal score is then mapped to fitness via a monotonically increasing function which accounts for strength of selection and epistasis. The previously studied cases of multiplicative selection and selection on a fully additive phenotype are special cases of our model. We identify a general mechanism, segregation lift, by which seasonally fluctuating selection can maintain polymorphism at tens or hundreds of unlinked loci. Segregation lift requires that the average dominance parameter of the currently favored allele—the summer allele in summer and the winter allele in winter—is sufficiently large. Individuals with many heterozygous loci then have higher scores in both seasons than individuals with the same number of summer and winter alleles, but more homozygous loci. Unlike in previously studied additive models, fully homozygous types thus cannot fix in the population, and multilocus polymorphism is maintained. In some cases, segregation lift may also be interpreted as a type of phenotypic plasticity, where more heterozygous genotypes can better adjust to both summer and winter environments.
The critical value of the dominance parameter required to maintain polymorphism, , depends mostly on the type of epistasis and on the number of loci. Without epistasis, i.e., for multiplicative selection, is 0.5. With synergistic epistasis, it is close to one when there are multiple loci. With diminishing-returns epistasis, the type of epistasis that appears most common, , is substantially larger than 0.5 with few loci, but quickly approaches 0.5 as the number of loci increases.
Robustness and Plausibility of Segregation Lift as a Mechanism to Maintain Variation.
Segregation lift requires that dominance changes over time such that the currently favored allele is on average at least slightly dominant with respect to the seasonal score. As discussed above, there are several potential mechanisms that can plausibly produce such changes in dominance. Moreover, the required changes are small. Unfortunately, there have been only few relevant empirical studies so far. For instance, in the copepod Eurytemora affinis, there appears to be beneficial reversal of dominance for fitness across salinity conditions (47). In experimental Drosophila populations, changes in dominance for gene expression across environments appear to be common (48). More empirical and theoretical work is required to find out how common changes in dominance are, in particular on the relevant scale of the seasonal score. However, even if the required changes in dominance are rare on a per-site basis and the vast majority of polymorphisms are lost under fluctuating selection, there may still be many sites in the genome with appropriate reversal of dominance, and, as we show, those are then the ones that we should see as seasonally fluctuating polymorphisms.
In the focal diminishing-returns scenario, the conditions for stable polymorphism via segregation lift are surprisingly robust to changes in the mutation rate (Fig. 6) and to asymmetries in number of generations, strength of selection, or population size between summer and winter (SI Appendix, Figs. S13–S15), apparently more so than under the multiplicative model (SI Appendix, Fig. S17). When the dominance parameter differs between summer and winter, polymorphism is generally stable at those loci whose average dominance parameter across seasons is >0.5 (Fig. 10F and SI Appendix, Fig. S16). Segregation lift is also robust to variation in effect sizes and dominance parameters across loci (Fig. 10). In reality, the strength of seasonality likely varies in space and time, which could make the maintenance of polymorphism by segregation lift even more robust (SI Appendix, Fig. S2B and ref. 40). Future work needs to explore whether segregation lift is robust also to linkage between selected loci. Since our diminishing-returns fitness function has a particular relationship between epistasis and strength of selection, future work should also consider more general fitness functions allowing for various combinations of epistasis and selection strength.
Whenever there is balancing selection at a large number of loci, genetic load is a potential concern. In the case of segregation lift with diminishing-returns epistasis, however, genetic load does not appear to play an important role. The results for our capped model closely match the results for the original, uncapped model. Apparently, independent segregation at a large number of unlinked loci leads to relatively small variance in seasonal scores within the population and, together with the diminishing-returns fitness function, to relatively small variance in fitness. With a much smaller offspring number cap or with multiplicative selection, differences between the capped and uncapped model are more substantial, but even then, balancing selection emerges for . Thus, unrealistically large offspring numbers are not required for stable multilocus polymorphism via segregation lift.
Magnitude and Detectability of Allele-Frequency Fluctuations.
In addition to stable polymorphism, segregation lift can also produce strong and predictable seasonal fluctuations in allele frequencies. The magnitude of these fluctuations, however, decreases with the number of loci under selection. Thus, the number of detectable polymorphisms may be maximized at an intermediate number of loci (Fig. 10). In SI Appendix, section S3, we use a heuristic mathematical argument to explore the relationship between number of loci and magnitude of fluctuations in a population of infinite size. As the number of loci goes to infinity, the effective strength of selection at each locus is predicted to go to zero, i.e., effective neutrality. This is because more loci lead to higher overall seasonal scores, , which under diminishing-returns epistasis leads to weaker average selection pressures at each locus. Thus, even if segregation lift contributes substantially to maintaining polymorphism at a large number of loci, it is not necessarily easy to detect individual selected loci based on their allele-frequency fluctuations. Future research will need to explore new ways of detecting such subtle seasonal allele-frequency fluctuations at many loci, perhaps based on their collective behavior rather than on patterns at individual sites.
Empirical Evidence, Alternative Hypotheses, and Potential Tests for Segregation Lift.
As mentioned above, a recent pooled-sequencing study by Bergland et al. (36) detected strong seasonal allele-frequency fluctuations at hundreds of sites in a temperate population of D. melanogaster. At many sites, allele frequencies fluctuated by 10% over a single season of 10 generations, and many of the polymorphisms appear to be long-term stable. Based on our results, segregation lift could potentially explain these observations, but caution is warranted for several reasons. First, with hundreds of seasonal SNPs and only few chromosomes, there will necessarily be substantial linkage between some of the sites. Second, the distribution and dynamics of dominance effects at the seasonally selected loci are still unknown. Finally, it is not completely clear whether the observed magnitude of allele-frequency fluctuations can be explained by our segregation lift model, where fluctuations are often more subtle (Fig. 10 C and D, but see Fig. 7C). Based on our current knowledge, we therefore cannot claim that the empirical observations by Bergland et al. (36) are explained by segregation lift. Future work will need to empirically test this model and possible alternatives.
One alternative is that genetic variation is not really stably maintained, but simply induced by recurrent mutation, with selection responsible only for the seasonal fluctuations (31, 49), or by recurrent immigration from other subpopulations where either winter- or summer-favored alleles dominate. However, in the case of the Drosophila observations, this was considered unlikely (36). Alternative mechanisms that could lead to both fluctuations and long-term stability are (i) differential responses to fluctuating resource concentrations and population densities (17, 50–52) and (ii) a so-called “temporal storage effect” where genetic variation can be buffered by a long-lasting life-history stage on which selection does not act, or by some other protected state (51, 53, 54). However, these mechanisms are more commonly studied in ecology as mechanisms for species coexistence, and it is unclear whether they can maintain polymorphism at multiple loci in diploids.
In future empirical tests for segregation lift, a main challenge will be that the pivotal dominance parameter, , is not relative to fitness but relative to the seasonal score, , which mediates between multilocus genotype and fitness, and is itself not directly measurable. Since the shape of the fitness function, , is also generally unknown, it is not possible to infer from fitness measurements of different single-locus genotypes in a common genetic background. In an ideal situation, with fitness measurements for many different multilocus genotypes at different times, we could use statistical methods such as machine learning to jointly estimate parameters of the fitness function, effect sizes, and dominance parameters and thereby assess whether or not there is segregation lift. Such statistical approaches could also take into account the existence of several multiplicative fitness components, each with a set of contributing loci that might exhibit segregation lift and epistatic interactions. In practice, however, measuring fitness is challenging in itself. One productive direction could be to stock a large number of outdoor mesocosms, each with a different multilocus genotype, and track fitness over multiple seasons. However, apart from the logistic challenges, we do not know a priori which loci to focus on. Coming up with a meaningful and feasible way to empirically get at the scale of the seasonal score and estimate the relevant dominance parameters is thus an important research direction arising from this study. An alternative approach is to make predictions for the genetic footprint of selection in linked neutral regions, e.g., look at diversity levels, site-frequency spectra, and patterns of linkage disequilibrium, and use these empirically more accessible patterns to distinguish between multiple possible models.
Conclusions
We identify segregation lift as a general mechanism by which seasonally fluctuating selection can maintain polymorphism at hundreds of unlinked loci in populations of biologically reasonable size. Segregation lift circumvents the problems associated with maintenance of polymorphism under stabilizing selection and does not require highly heterozygous individuals to have unrealistically many offspring. Given the ubiquity of environmental fluctuations, segregation lift could make a substantial contribution to genetic variation in natural populations of many taxa. An important question for future work is how we can use modern molecular biology and sequencing technologies to test for segregation lift and thus make progress on solving the puzzle of genetic variation.
Materials and Methods
For the basic model and the capped model, we assess stability of polymorphism by estimating an effective strength of balancing selection, , from the year-to-year allele-frequency dynamics. For this, we fit a standard balancing selection model (55) of the form
| [14] |
to average changes in allele frequency over one yearly cycle, (see SI Appendix, section S2 for details). Positive values of indicate that rare alleles tend to become more common in the long run, whereas negative values indicate that rare alleles tend to become even more rare. Second, we quantify the magnitude of fluctuations over individual seasons. For this, we fit a standard directional selection model (55)
| [15] |
with an effective selection coefficient , to average allele-frequency changes over one season, (SI Appendix, section S2).
To obtain a measure for statistical uncertainty in our results, we run 10 replicates for every parameter combination and calculate effective strength of balancing selection, , and effective selection coefficient, , independently for each replicate. We do the same for the predictability of fluctuations, i.e., the proportion of seasons in which a locus changes its allele frequency in the expected direction. In all three cases, we report the mean over replicates two standard errors of the mean. To obtain retardation factors, we run 100 replicates until polymorphism is lost at one of the loci or a maximum time of 500 years is reached. From the times of loss for the replicates, we obtain maximum-likelihood estimators for the rate of loss of polymorphism (see SI Appendix, section S2 for details).
C++ simulation code and supporting R scripts are available at https://doi.org/10.6084/m9.figshare.5142262.
Supplementary Material
Acknowledgments
For helpful discussion and/or comments on the manuscript, we thank Michael Desai, Joachim Hermisson, Oren Kolodny, Mike McLaren, Richard Nichols, Pleuni Pennings, Jitka Polechová, and members of D.A.P.’s laboratory, as well as two anonymous reviewers. Simulations were performed on Stanford’s FarmShare Cluster and on the Vienna Scientific Cluster. M.J.W. was supported by fellowships from the Stanford Center for Computational Evolutionary and Human Genomics and from the Austrian Science Fund (M 1839-B29).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: Source code underlying the analyses in this manuscript has been deposited in the figshare repository (available at https://doi.org/10.6084/m9.figshare.5142262).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1702994114/-/DCSupplemental.
References
- 1.Lewontin RC, Hubby JL. A molecular approach to the study of genic heterozygosity in natural populations. II. Amount of variation and degree of heterozygosity in natural populations of Drosophila pseudoobscura. Genetics. 1966;54:595–609. doi: 10.1093/genetics/54.2.595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lewontin RC. The Genetic Basis of Evolutionary Change. Columbia Univ Press; New York: 1974. [Google Scholar]
- 3.Beatty J. Weighing the risks: Stalemate in the classical/balance controversy. J Hist Biol. 1987;20:289–319. [Google Scholar]
- 4.Hedrick PW. Balancing selection. Curr Biol. 2007;17:R230–R231. doi: 10.1016/j.cub.2007.01.012. [DOI] [PubMed] [Google Scholar]
- 5.Barton N, Keightley P. Understanding quantitative genetic variation. Nat Rev Genet. 2002;3:11–21. doi: 10.1038/nrg700. [DOI] [PubMed] [Google Scholar]
- 6.Turelli M, Barton NH. Polygenic variation maintained by balancing selection: Pleiotropy, sex-dependent allelic effects and G x E interactions. Genetics. 2004;166:1053–1079. doi: 10.1534/genetics.166.2.1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Asthana S, Schmidt S, Sunyaev S. A limited role for balancing selection. Trends Genet. 2005;21:30–32. doi: 10.1016/j.tig.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 8.Hedrick PW. What is the evidence for heterozygote advantage selection? Trends Ecol Evol. 2012;27:698–704. doi: 10.1016/j.tree.2012.08.012. [DOI] [PubMed] [Google Scholar]
- 9.Croze M, Živković D, Stephan W, Hutter S. Balancing selection on immunity genes: Review of the current literature and new analysis in Drosophila melanogaster. Zoology. 2016;119:322–329. doi: 10.1016/j.zool.2016.03.004. [DOI] [PubMed] [Google Scholar]
- 10.Hedrick PW, Ginevan ME, Ewing EP. Genetic polymorphism in heterogeneous environments. Annu Rev Ecol Syst. 1976;7:1–32. [Google Scholar]
- 11.Siepielski AM, DiBattista JD, Carlson SM. It’s about time: The temporal dynamics of phenotypic selection in the wild. Ecol Lett. 2009;12:1261–1276. doi: 10.1111/j.1461-0248.2009.01381.x. [DOI] [PubMed] [Google Scholar]
- 12.Thurman TJ, Barrett RD. The genetic consequences of selection in natural populations. Mol Ecol. 2016;25:1429–1448. doi: 10.1111/mec.13559. [DOI] [PubMed] [Google Scholar]
- 13.van Schaik CP, Terborgh JW, Wright SJ. The phenology of tropical forests–Adaptive significance and consequences for primary consumers. Annu Rev Ecol Syst. 1993;24:353–377. [Google Scholar]
- 14.Schmidt PS, Conde DR. Environmental heterogeneity and the maintenance of genetic variation for reproductive diapause in Drosophila melanogaster. Evolution. 2006;60:1602–1611. [PubMed] [Google Scholar]
- 15.Behrman EL, Watson SS, O’Brien KR, Heschel MS, Schmidt PS. Seasonal variation in life history traits in two Drosophila species. J Evol Biol. 2015;28:1691–1704. doi: 10.1111/jeb.12690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Haldane JBS, Jayakar SD. Polymorphism due to selection of varying direction. J Genet. 1963;58:237–242. [Google Scholar]
- 17.Dean AM, Lehman C, Yi X. Fluctuating selection in the Moran. Genetics. 2017;205:1271–1283. doi: 10.1534/genetics.116.192914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Novak R, Barton NH. When does frequency-independent selection maintain genetic variation? Genetics. 2017;207:653–668. doi: 10.1534/genetics.117.300129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dempster ER. Maintenance of genetic heterogeneity. Cold Spring Harb Symp Quant Biol. 1955;20:25–32. doi: 10.1101/sqb.1955.020.01.005. [DOI] [PubMed] [Google Scholar]
- 20.Gillespie JH. Polymorphism in random environments. Theor Popul Biol. 1973;4:193–195. [Google Scholar]
- 21.Chou HH, Chiu HC, Delaney NF, Segrè D, Marx CJ. Diminishing returns epistasis among beneficial mutations decelerates adaptation. Science. 2011;332:1190–1192. doi: 10.1126/science.1203799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Khan AI, Dinh DM, Schneider D, Lenski RE, Cooper TF. Negative epistasis between beneficial mutations in an evolving bacterial population. Science. 2011;332:1193–1196. doi: 10.1126/science.1203801. [DOI] [PubMed] [Google Scholar]
- 23.Kryazhimskiy S, Rice DP, Jerison ER, Desai MM. Global epistasis makes adaptation predictable despite sequence-level stochasticity. Science. 2014;344:1519–1522. doi: 10.1126/science.1250939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Feller W. On fitness and the cost of natural selection. Genet Res. 1967;9:1–15. [Google Scholar]
- 25.Milkman RD. Heterosis as a major cause of heterozygosity in nature. Genetics. 1967;55:493–495. doi: 10.1093/genetics/55.3.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sved JA, Reed TE, Bodmer WF. The number of balanced polymorphisms that can be maintained in a natural population. Genetics. 1967;55:469–481. doi: 10.1093/genetics/55.3.469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Turner JRG, Williamson MH. Population size, natural selection and the genetic load. Nature. 1968;218:700. doi: 10.1038/218700a0. [DOI] [PubMed] [Google Scholar]
- 28.Agrawal AF, Whitlock MC. Mutation load: The fitness of individuals in populations where deleterious alleles are abundant. Annu Rev Ecol Evol Syst. 2012;43:115–135. [Google Scholar]
- 29.Charlesworth B. Why we are not dead one hundred times over. Evolution. 2013;67:3354–3361. doi: 10.1111/evo.12195. [DOI] [PubMed] [Google Scholar]
- 30.Korol AB, Kirzhner VM, Ronin YI, Nevo E. Cyclical environmental changes as a factor maintaining genetic polymorphism. 2. Diploid selection for an additive trait. Evolution. 1996;50:1432–1441. doi: 10.1111/j.1558-5646.1996.tb03917.x. [DOI] [PubMed] [Google Scholar]
- 31.Bürger R, Gimelfarb A. Fluctuating environments and the role of mutation in maintaining quantitative genetic variation. Genet Res. 2002;80:31–46. doi: 10.1017/s0016672302005682. [DOI] [PubMed] [Google Scholar]
- 32.Lande R. Adaptive topography of fluctuating selection in a Mendelian population. J Evol Biol. 2008;21:1096–1105. doi: 10.1111/j.1420-9101.2008.01533.x. [DOI] [PubMed] [Google Scholar]
- 33.Wright S. Evolution in populations in approximate equilibrium. J Genet. 1935;30:257–266. [Google Scholar]
- 34.Bürger R, Gimelfarb A. Genetic variation maintained in multilocus models of additive quantitative traits under stabilizing selection. Genetics. 1999;152:807–820. doi: 10.1093/genetics/152.2.807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nagylaki T. The maintenance of genetic variability in 2-locus models of stabilizing selection. Genetics. 1989;122:235–248. doi: 10.1093/genetics/122.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bergland AO, Behrman EL, O’Brien KR, Schmidt PS, Petrov DA. Genomic evidence of rapid and stable adaptive oscillations over seasonal time scales in Drosophila. PLoS Genet. 2014;10:e1004775. doi: 10.1371/journal.pgen.1004775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gloss AD, Whiteman NK. Balancing selection: Walking a tightrope. Curr Biol. 2016;26:R73–R76. doi: 10.1016/j.cub.2015.11.023. [DOI] [PubMed] [Google Scholar]
- 38.Charlesworth B. Causes of natural variation in fitness: Evidence from studies of Drosophila populations. Proc Natl Acad Sci USA. 2015;112:1662–1669. doi: 10.1073/pnas.1423275112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Desai MM, Weissman D, Feldman MW. Evolution can favor antagonistic epistasis. Genetics. 2007;177:1001–1010. doi: 10.1534/genetics.107.075812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rose MR. Antagonistic pleiotropy, dominance, and genetic variation. Heredity. 1982;48:63–78. [Google Scholar]
- 41.Curtsinger JW, Service PM, Prout T. Antagonistic pleiotropy, reversal of dominance, and genetic polymorphism. Am Nat. 1994;144:210–228. [Google Scholar]
- 42.Hedrick PW. Genetic variation in a heterogeneous environment. II. Temporal heterogeneity and directional selection. Genetics. 1976;84:145–157. doi: 10.1093/genetics/84.1.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kacser H, Burns JA. The molecular basis of dominance. Genetics. 1981;97:639–666. doi: 10.1093/genetics/97.3-4.639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Keightley PD, Kacser H. Dominance, pleiotropy and metabolic structure. Genetics. 1987;117:319–329. doi: 10.1093/genetics/117.2.319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gillespie JH. Population Genetics—A Concise Guide. The John Hopkins Univ Press; Baltimore: 1998. [Google Scholar]
- 46.Robertson A. Selection for heterozygotes in small populations. Genetics. 1962;47:1291–1300. doi: 10.1093/genetics/47.9.1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Posavi M, Gelembiuk GW, Larget B, Lee CE. Testing for beneficial reversal of dominance during salinity shifts in the invasive copepod Eurytemora affinis, and implications for the maintenance of genetic variation. Evolution. 2014;68:3166–3183. doi: 10.1111/evo.12502. [DOI] [PubMed] [Google Scholar]
- 48.Chen J, Nolte V, Schlötterer C. Temperature stress mediates decanalization and dominance of gene expression in Drosophila melanogaster. PLoS Genet. 2015;11:e1004883. doi: 10.1371/journal.pgen.1004883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kondrashov A, Yampolsky L. High genetic variability under the balance between symmetric mutation and fluctuating stabilizing selection. Genet Res. 1996;68:157–164. [Google Scholar]
- 50.Armstrong RA, McGehee R. Coexistence of species competing for shared resources. Theor Popul Biol. 1976;9:317–328. doi: 10.1016/0040-5809(76)90051-4. [DOI] [PubMed] [Google Scholar]
- 51.Chesson P. Mechanisms of maintenance of species diversity. Annu Rev Ecol Syst. 2000;31:343–366. [Google Scholar]
- 52.Yi X, Dean AM. Bounded population sizes, fluctuating selection and the tempo and mode of coexistence. Proc Natl Acad Sci USA. 2013;110:16945–16950. doi: 10.1073/pnas.1309830110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Svardal H, Rueffler C, Hermisson J. A general condition for adaptive genetic polymorphism in temporally and spatially heterogeneous environments. Theor Popul Biol. 2015;99:76–97. doi: 10.1016/j.tpb.2014.11.002. [DOI] [PubMed] [Google Scholar]
- 54.Gulisija D, Kim Y, Plotkin JB. Phenotypic plasticity promotes balanced polymorphism in periodic environments by a genomic storage effect. Genetics. 2016;202:1437–1448. doi: 10.1534/genetics.115.185702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Durrett R. Probability Models for DNA Sequence Evolution. Springer; New York: 2008. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.