Testing the neutral hypothesis of phenotypic evolution

Significance

Despite the universal recognition that adaptation by Darwinian selection can shape phenotypic variations within and between species, it remains unknown whether most phenotypic variations observed have adaptive values, in part because addressing this question requires examining a large, random set of traits while past studies were biased toward traits that are likely adaptive. Here, we study 210 yeast morphological traits chosen purely on the basis of experimental feasibility and expression levels of all yeast genes with reliable measurements. We find that morphological variations, but not expression variations, are largely adaptive, suggesting that different classes of phenotypic traits are subject to adaptive evolution to varying extents.

Abstract

Although evolution by natural selection is widely regarded as the most important principle of biology, it is unknown whether phenotypic variations within and between species are mostly adaptive or neutral due to the lack of relevant studies of large, unbiased samples of phenotypic traits. Here, we examine 210 yeast morphological traits chosen because of experimental feasibility irrespective of their potential adaptive values. Our analysis is based on the premise that, under neutrality, the rate of phenotypic evolution measured in the unit of mutational size declines as the trait becomes more important to fitness, analogous to the neutral paradigm that functional genes evolve more slowly than functionless pseudogenes. However, we find faster evolution of more important morphological traits within and between species, rejecting the neutral hypothesis. By contrast, an analysis of 3,466 gene expression traits fails to refute neutrality. Thus, at least in yeast, morphological evolution appears largely adaptive, but the same may not apply to other classes of phenotypes. Our neutrality test is applicable to other species, especially genetic model organisms, for which estimations of mutational size and trait importance are relatively straightforward.

It is generally accepted that a large fraction of genomic sequence variations within and between species are neutral or nearly so (1). Whether the same is true for phenotypic variations is a central question in biology (2–7). On the one hand, numerous phenotypic adaptations have been documented (2, 8, 9) and even Kimura, the champion of the neutral theory of molecular evolution, believed in widespread adaptive phenotypic evolution (1). However, phenotypic studies are strongly biased toward traits that are likely to be adaptive (9), contrasting genomic studies that are typically unbiased. It is thus imperative to test the neutral hypothesis of phenotypic evolution using traits irrespective of their potential involvement in adaptation.

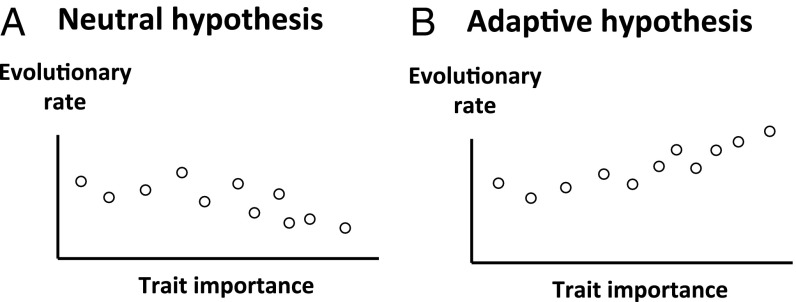
Similar to the neutral hypothesis of molecular evolution (1), the neutral hypothesis of phenotypic evolution allows the presence of purifying selection; neutrality is rejected only when positive selection is invoked. Under the neutral hypothesis, relatively important traits should be subject to stronger purifying selection than relatively unimportant traits; consequently, the former should evolve more slowly than the latter given the same speed of mutational input (Fig. 1A). This is analogous to the neutral paradigm that functional genes evolve more slowly than functionless pseudogenes (10). However, if relatively important traits are found to evolve faster than relatively unimportant traits, the neutral hypothesis is rejected; the only reasonable explanation would be stronger positive selection acting on relatively important traits than on relatively unimportant ones (Fig. 1B). This test of phenotypic neutrality differs from previous tests (3, 4, 11–15), which consider only one trait at a time and effectively require the intensity of positive selection to surpass that of purifying selection to reject neutrality. Because this requirement is sufficient but not necessary for demonstrating positive selection, it is replaced with the criterion of a positive correlation between trait importance and evolutionary rate to improve the power of the test (Discussion and Materials and Methods).

Fig. 1.

Schematic illustrating the test of the neutral hypothesis of phenotypic evolution by comparing evolutionary rates among traits of different levels of importance. (A) Under the neutral hypothesis, relatively important traits evolve more slowly than relatively unimportant traits. (B) Higher evolutionary rates of more important traits reject the neutral hypothesis and support the adaptive hypothesis. Each circle represents a trait.

Results

Adaptive Intraspecific Variations of Yeast Morphological Traits.

We first tested the neutral hypothesis of phenotypic evolution in a set of 210 morphological traits chosen purely on the basis of the feasibility of measurement (16) rather than potential roles in adaptation (Dataset S1, Data S1). These traits were quantified by analyzing fluorescent microscopic images of triple-stained cells (17) from 37 natural strains of Saccharomyces cerevisiae (18). For a given trait, we defined the phenotypic difference between two strains by the absolute difference in their trait value, relative to their average trait value. Phenotypic differences were corrected for potential environmental heterogeneity in the measurement and sampling error to allow among-trait comparison (Materials and Methods and Dataset S1, Data S2). We then estimated, for each trait, the mean evolutionary distance (ED) among all 666 pairs of the 37 strains by averaging their corrected pairwise phenotypic differences.

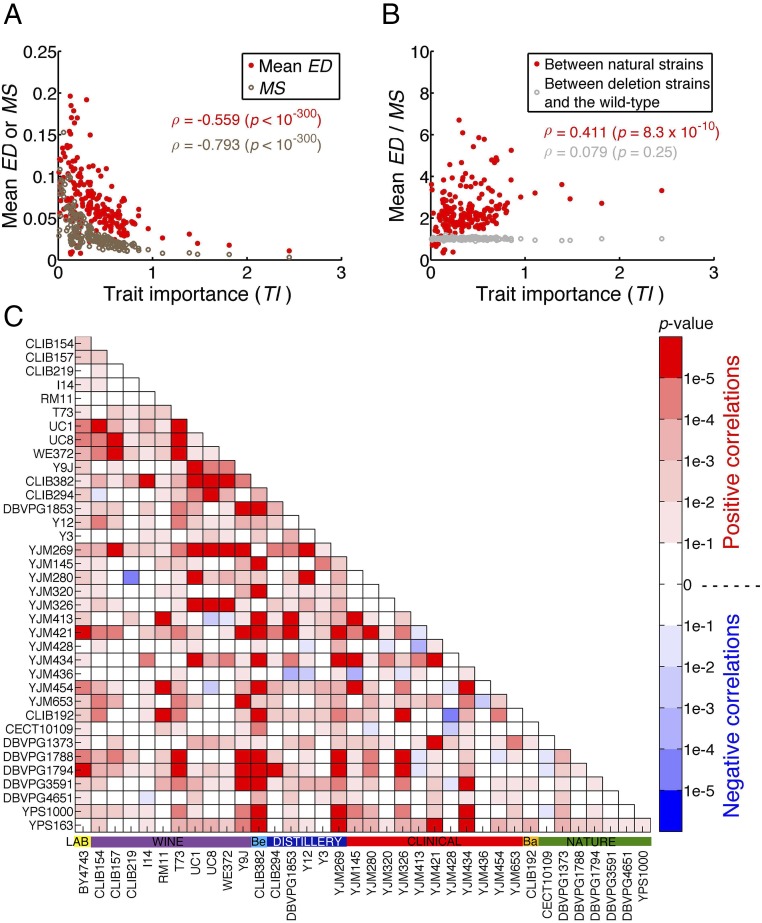
To test the neutral hypothesis, we used measures of trait importance (TI) for the 210 traits (Dataset S1, Data S1), where TI is 100 times the fitness effect caused by 1% change in trait value, estimated using the fitness and phenotype data of thousands of single gene deletion strains of S. cerevisiae (19). We found that mean ED decreases with TI (Fig. 2A), indicating that relatively important traits evolve more slowly than relatively unimportant ones. However, the rate of phenotypic evolution is determined by both the rate of mutational input and the direction and magnitude of natural selection. The rate of mutational input for a trait is the average effect size of a random mutation on the trait (i.e., mutational size or MS) multiplied by the mutation rate per genome per generation. Because the mutation rate is the same for all traits, we need only to consider MS. We estimated MS for a trait by the mean phenotypic effect of 4,718 individual gene deletions (i.e., null mutations) on the trait (19) (Dataset S1, Data S1). Although most spontaneous mutations are expected to have smaller phenotypic effects than null mutations, if null mutations in a gene have larger effects on trait 1 than on trait 2, spontaneous mutations in the gene should on average have larger effects on trait 1 than on trait 2 as well. Therefore, it is reasonable to assume that the average phenotypic effect of spontaneous mutations on a trait is approximately proportional to that of gene deletions on the trait. In other words, MS can be used as a proxy of spontaneous mutational size when different traits are compared. As was previously discovered (19), MS decreases precipitously with TI (Fig. 2A). This observation indicates that relatively important traits are affected by mutations to a smaller degree than are relatively unimportant traits, which has likely resulted from stronger selection for mutational robustness of more important traits (19). Unsurprisingly, traits with larger MS tend to have larger mean ED (Fig. S1A). Therefore, to control the impact of mutational input on the rate of phenotypic evolution, we measured the evolutionary rate of a trait in the unit of its mutational size by dividing mean ED by MS for each trait. We found mean ED/MS to increase significantly with TI (Fig. 2B), suggesting that relatively important traits evolve faster than relatively unimportant traits in the unit of mutational size. To further test the impact of TI on mean ED, we built a multivariate regression model. Because mean ED and MS both exhibit a power-law relationship with TI, we fit the following model: ln(mean ED) = aln(TI) + bln(MS) + c. This model accounts for 44% of variance in mean ED, demonstrating its explanatory power. We found a to be significantly greater than 0 (P = 6.2 × 10⁻³; two-tailed t test), confirming that mean ED increases with TI. Together, the above findings are inconsistent with the neutral hypothesis of phenotypic evolution (Fig. 1A), but support the adaptive hypothesis (Fig. 1B).

Fig. 2.

Prevalent adaptive evolution of morphological traits in the yeast S. cerevisiae. (A) Mean evolution distance (ED) of 666 pairs of natural strains for a trait and the MS of the trait both decrease with TI. Each dot represents a trait. ρ, Spearman’s rank correlation coefficient. (B) Mean ED among 666 natural strain pairs for a trait relative to its MS increases significantly with TI, while the mean ED between 666 gene deletion strains and the wild type relative to MS does not increase significantly with TI. (C) Nominal P values for the Spearman’s correlation between ED/MS and TI for all 666 pairs of natural strains. The horizontal colored bars above the strain names show the ecological environments of the strains. Ba, bakery; Be, beer.

To exclude the possibility that the above result is an artifact of our statistical analysis, we used two negative controls. First, we compared the wild-type BY strain with 666 randomly picked gene deletion strains of the BY background, under the premise that their phenotypic differences should not be adaptive. We computed the average phenotypic difference between these deletion strains and the wild type for each trait as an estimate of mean ED for the trait. As expected, we found a significant, negative correlation between mean ED and TI (Fig. S1B) but no significant correlation between mean ED/MS and TI (Fig. 2B). Second, we examined 89 mutational accumulation (MA) lines, which were produced from the same ancestor in ∼2,000 mitotic generations with an effective population size of ∼10 and, therefore, should not show adaptive signals compared with their common ancestor (20). Only 180 morphological traits are available in the data from MA lines for analysis. While mean ED/MS for the 37 natural strains still increases significantly with TI for these 180 traits (Fig. S1C), mean ED/MS between the MA lines and their ancestor shows no significant correlation with TI (Fig. S1D).

Because the MS and TI used were estimated in haploid yeasts while the 37 natural strains studied are diploid, we also estimated MS and TI using recently published morphological data of 130 diploid gene deletion strains (21). We confirmed that the significant positive correlation between mean ED/MS and TI holds (Fig. S1E). Note that although the MA lines were diploid, their morphological data were collected from haploid derivatives (20).

To examine whether the detected adaptive signal among the 37 natural strains is attributable to a small number of strains or is a general phenomenon of the species, we estimated the rank correlation (ρ) between ED/MS and TI for each of the 666 strain pairs, using the ED value of the strain pair. We found ρ to be positive for the vast majority of the strain pairs (Fig. 2C), suggesting pervasive adaptive morphological evolution in S. cerevisiae, at least for the strains considered here.

Some of the 210 morphological traits are genetically highly correlated (19, 22). To exclude the possibility that the adaptive signal is an artifact of the use of correlated traits, we estimated 210 principal component traits from the original traits (Materials and Methods). Analysis of the principal component traits, which are independent from one another, shows even stronger signals of adaptive evolution (Fig. S2).

If the prevalent positive ρ values among the 37 natural strains (Fig. 2C) truly arise from positive selection, we should expect that (i) the overall rate of morphological evolution is greater for strain pairs with higher ρ values and (ii) this rate disparity is primarily reflected in relatively important traits rather than relatively unimportant ones. We defined the overall rate of morphological evolution between two strains by their morphological dissimilarity across all 210 traits divided by their fractional genomic sequence difference. Consistent with our expectation, the rate of morphological evolution increases with ρ (P = 0.007, one-tailed partial Mantel test with phylogenetic permutation to correct for both the nonindependence among strain pairs and phylogenetic relationships in the data; Materials and Methods). Additionally, when we separated the 210 traits into two equal-sized bins based on TI, the correlation between the rate of morphological evolution and ρ remained significantly positive for the 105 traits with relatively high TI (P < 0.001) but not for the 105 traits with relatively low TI (P = 0.805). These observations support that, the greater the ρ value relative to 0, the stronger the positive selection on the morphological traits, especially those relatively important ones.

What factors determine the ρ value of a strain pair? Because the 210 morphological traits were chosen purely on the basis of experimental feasibility, we do not expect the detected adaptive signals to correlate with any obvious genetic or ecological factor. Indeed, using the partial Mantel test, we found no significant correlation between the ρ value of two strains and the strains’ difference in genome sequence, ecological environment, population membership, or geographic location (Table S1). These findings are consistent with a previous analysis showing that the morphological similarities among the 37 natural strains cannot be explained simply by the strains’ similarities in population history or ecological environment (18). Hence, the selective agents behind the detected morphological adaptations are unclear (Discussion).

Adaptive Interspecific Variations of Yeast Morphological Traits.

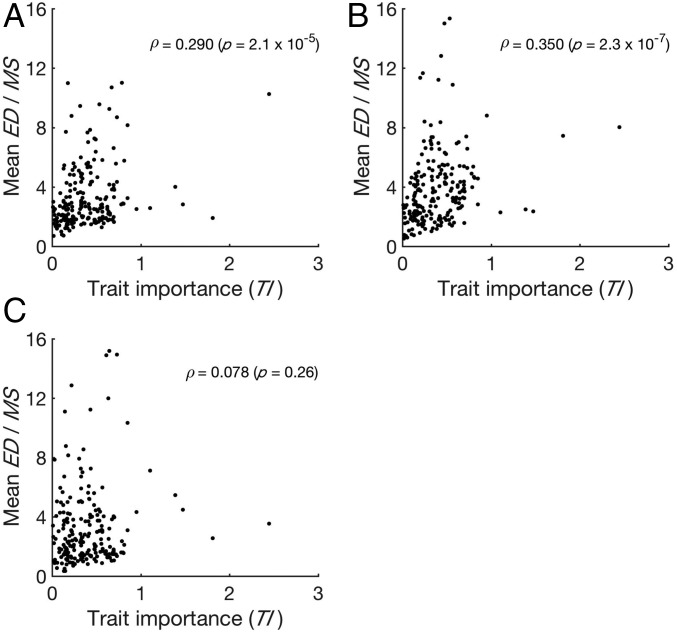
To test the neutral hypothesis of morphological evolution beyond the species level, we collected comparable morphological data from two strains of Saccharomyces paradoxus, the sister species of S. cerevisiae, and one strain of their outgroup species Saccharomyces mikatae (Materials and Methods). We first calculated the mean ED/MS between the 37 S. cerevisiae strains and S. paradoxus strain N17 for each trait (Dataset S1, Data S3). Across the 210 traits, we observed a significant, positive correlation between mean ED/MS and TI (Fig. 3A). A similar pattern was observed between S. cerevisiae and S. paradoxus strain IFO1804 (Fig. 3B). Between S. cerveisiae and the more distantly related species of S. mikatae (Dataset S1, Data S3), however, the positive correlation is no longer significant (Fig. 3C), probably because of the lack of prevalent positive selection or a reduced statistical power as a result of using MS and TI values estimated from S. cerevisiae in tests involving distantly related species.

Fig. 3.

Adaptive morphological evolution between Saccharomyces species. (A) The mean ED/MS between 37 natural S. cerevisiae strains and S. paradoxus strain N17 for a trait increases significantly with TI. (B) The mean ED/MS between 37 natural S. cerevisiae strains and the S. paradoxus strain IFO1804 increases significantly with TI. (C) The mean ED/MS between 37 natural S. cerevisiae strains and S. mikatae increases (but not significantly) with TI. Each dot represents a morphological trait.

Neutral Evolution of Yeast Gene Expression Levels.

To investigate the generality of the above findings of adaptive phenotypic evolution, we turned to another class of traits that can be chosen regardless of their potential roles in adaptation: 3,466 gene expression traits, each being the mRNA expression level of a yeast gene in a rich medium. Using microarray gene expression data, we quantified ED between two S. cerevisiae strains for each trait (Dataset S1, Data S4). We estimated MS from the microarray expression data of 1,486 gene deletion strains, as in the case of morphological traits (19). TI of the expression level of a gene was measured by the fitness reduction caused by the deletion of the gene (19) (Materials and Methods). Similar to the morphological data, gene expression data showed a negative correlation between ED and TI and a negative correlation between MS and TI (Table 1). However, contrary to the morphological traits, expression traits exhibited a significant, negative correlation between ED/MS and TI (Table 1). As a negative control, we estimated the standard deviation (SD_m) in relative expression level among four MA lines (23) and found, as expected, no significant correlation between SD_m/MS and TI (Table 1). While adaptive evolution of the expression levels of some yeast genes has been suggested (24–26), overall we found relatively important genes to evolve more slowly in expression level than relatively unimportant ones upon the control of mutational size, consistent with the neutral hypothesis. Here, we are restricted to intraspecific analysis, because the use of different probes in the microarrays of different species prohibits a reliable comparison of the rate of expression evolution among genes. Use of other types of expression data such as mRNA sequencing data are currently infeasible, because no comparable data are available for estimating MS.

Table 1.

Testing the neutral hypothesis of yeast gene expression evolution

Variables correlated	Spearman’s ρ	P value
ED, TI	−0.147	3.7 × 10−18
MS, TI	−0.142	3.9 × 10−17
ED/MS, TI	−0.087	3.2 × 10−7
SDm/MS, TI	−0.030	0.13

ED, evolutionary distance in gene expression level between S. cerevisiae strains; MS, mutational size measured by gene deletion; SD_m, standard deviation in relative gene expression level among mutation accumulation lines; TI, gene expression trait importance.

Discussion

In summary, our analysis of 210 yeast morphological traits with no a priori bias toward adaptive evolution reveals strong signals of adaptive evolution. If the strains and morphological traits studied are representative, we must conclude that morphological evolution in yeast is frequently adaptive. One caveat is that the 37 S. cerevisiae natural strains analyzed were chosen initially for genome sequencing (27, 28) and subsequently for phenotyping (18) likely because they maximize the genetic and ecological diversities represented. Hence, our conclusion drawn from this diverse set of strains may not apply to random pairs of yeast genotypes, although we found no impact of genomic or ecological dissimilarity on the adaptive signal detected (Table S1).

It is important to note that we measure the TI of each morphological trait by regressing fitness on trait value among thousands of gene deletion strains (Materials and Methods). As a result, our TI estimates are based on correlations and may not reliably reflect the causal relationship between trait value and fitness. In fact, the causality is difficult to establish because it is virtually impossible to experimentally manipulate a phenotypic trait without affecting any other trait. Nevertheless, the finding that even using the noisy TI estimates yields significant evidence for adaptation suggests that the true signal is probably stronger. In other words, our results are likely conservative. This said, the lack of an estimate of causal importance for morphological traits means that some of the adaptive signals detected may be attributable to associated traits. For example, it is possible that a mutation affects both a physiological trait and a morphological trait, but it is the physiological change that increases fitness. In this case, the rapid evolution of the morphological trait is a byproduct of positive selection for the physiological change. Clearly, the evolution of the morphological trait is impacted not only by its causal influence on fitness but also its associated traits’ influences on fitness. This consideration suggests that studying the evolution of a morphological trait should consider the trait’s own importance as well as the importance of its associated traits. By regressing fitness on the focal trait value across gene deletion strains, our estimation of TI indeed includes the influences of the associated traits. In the future, to further understand the biological basis of adaptation, it will undoubtedly be valuable, albeit challenging, to distinguish the fitness impact of the focal trait from those of its associated traits.

It is essential to use a random set of traits to evaluate the prevalence of adaptive phenotypic evolution, but using such traits means that the selective agent would be difficult to discern if adaptation is detected, as in the present case. Nonetheless, there are potential reasons why yeast morphological variations may be adaptive. Yeast morphology is tightly regulated during cell cycle and associated with not only the external cues but also the intracellular physiological state (29, 30). Yeast cell division and population growth is under the control of cell size (31, 32) as well as the polarization of actins (33). Hence, depending on the external and internal environments, the ideal cell morphology may vary. In addition, adaptive signals of morphological evolution may arise from the association of morphological traits with other traits that evolve adaptively, as aforementioned.

It should be emphasized that, although the bar for rejecting neutrality is likely lowered in our test compared with that in most previous tests (3, 4, 11–13), it remains quite high. This is because relatively important traits that could be subject to strong positive selection are also expected to be under strong purifying selection such that an adaptive signal becomes detectable only when the difference in the strength of positive selection among traits surpasses that in the strength of purifying selection. The high bar renders claims of adaptation conservative. However, it also means that failure to reject neutrality, as in the case of yeast gene expression evolution, neither proves neutrality nor refutes adaptation. Nonetheless, based on additional experiments and tests, we recently found unambiguous evidence that the vast majority of gene expression level variations within and between yeast species are nonadaptive (34). Together, these analyses of yeast morphological and gene expression data raise the intriguing possibility that some classes of phenotypic traits evolve generally adaptively while others neutrally. This possibility is worth further investigation in yeast as well as in other species. The methodology developed here is applicable in any organism, especially genetic model organisms, for which mutational size estimation and trait importance estimation are relatively straightforward.

Materials and Methods

A Comparison Between Existing Tests of the Neutral Hypothesis of Phenotypic Evolution and the Newly Proposed Test.

A number of neutrality tests of phenotypic evolution exist in the literature. They all test the neutrality of one trait and can be divided into two categories based on the rationale of the test. The first category compares the observed phenotypic distance in a trait between populations or species with the neutral expectation. Positive (or purifying) selection is inferred when the observed distance is significantly larger (or smaller) than the neutral expectation. The neutral expectation has been derived by considering the stochastic process of phenotypic evolution (3) or genetic models of quantitative traits (4, 13). Various test statistics have been proposed, including, for example, Lande’s N_e (3), Lande’s F (14), Chakraborty and Nei’s B_t/V_t (13), Turelli et al.’s MDE test (12), and Lynch’s Δ (15). These tests usually require the information of effective population size and divergence time. They also require the information on the rate of mutational input such as narrow-sense heritability and mutational variance. If these parameters are unavailable, one may use an alternative approach by comparing Q_ST of a trait with F_ST of neutral loci, which are expected to be the same if the trait evolves neutrally (11). Positive selection is undetectable by any of the above tests unless the intensity of positive selection exceeds that of purifying selection. Because purifying selection is expected to be pervasive even for traits subject to positive selection, all tests in this category have a low power in detecting positive selection.

The second category is the quantitative trait locus (QTL) sign test, which relies on the information from QTL mapping of a trait. Typically, positive selection is inferred when the number of positive-effect QTLs differs significantly from that of negative-effect QTLs (35). Although this category of test is model-free, it cannot distinguish between positive selection and relaxation from purifying selection without other information (25).

Our test of the neutral hypothesis of phenotypic evolution compares the evolutionary rates of many traits that have different levels of importance to fitness. Under the neutral hypothesis allowing purifying selection, relatively important traits evolve more slowly than relatively unimportant traits. If relatively important traits are found to evolve more rapidly than relatively unimportant ones, neutrality is rejected in favor of positive selection. Our test is expected to be more powerful than the above first category of tests, because detecting positive selection no longer requires the intensity of positive selection to exceed that of purifying selection. Rather, the criterion is that the difference in intensity between positive and negative selection is more positive for more important traits. Our test does not suffer from the problem in the above second category of tests, because it is extremely improbable for the relative importance of a large number of traits to be reversed in a second population, compared with that in the original population where trait importance is measured.

One caveat of our test in the present analysis is that the yeast morphological data from natural strains and gene deletion strains, gene expression data, and fitness data of gene deletion strains used for estimating trait importance were all collected under a laboratory-rich medium, which may not equal the natural environments of various yeast strains. Although our test only requires that the same condition be used in phenotyping a trait and in estimating its trait importance, the potential mismatch between the experimental condition and natural environments could make the selective agent more difficult to discern.

Given that both interspecific and intraspecific ED are available in the morphological analysis, adaptation can also be tested by examining whether interspecific ED, relative to intraspecific ED, increases with trait importance. This test, analogous to the McDonald–Kreitman test and derivatives (36–38), should yield a positive result when adaptive signals are stronger between species than within species. It, however, will not give a positive result even in the presence of adaptation if the above condition is unmet. We found that the correlation between TI and the ratio of interspecific ED to intraspecific ED does not significantly differ from 0 when S. cerevisiae and S. paradoxus are compared (ρ = −0.098, P = 0.16 when S. paradoxus N17 is used; ρ = 0.025, P = 0.72 when S. paradoxus IFO1804 is used), suggesting that the adaptive signal between these species is comparable in strength to that within S. cerevisiae (Figs. 2B and 3 A and B). When S. cerevisiae and S. mikatae are compared, ρ = −0.27 (P = 1.1 × 10⁻⁴), suggesting that the adaptive signal between these species is weaker than that within S. cerevisiae, consistent with the result in Fig. 3C.

Yeast Morphological Data.

The morphological traits analyzed here were previously defined (16). Briefly, yeast cultures were grown to 1 × 10⁷ cells per mL in YPD or synthetic complete media. Cells were fixed with 3.7% formaldehyde and stained with fluorescein isothiocyanate-Con A, rhodaminephalloidin, and 4′,6-diamidino-2-phenylindole, which simultaneously mark cell wall, actin cytoskeleton, and nuclear DNA, respectively. After digital images were acquired, cell images were collected and processed by CalMorph (17). In total, 501 morphological traits were measured. Among these morphological traits, we focused on 210 traits, which are defined for individual cells rather than cell populations, have positive trait importance values (19), and were measured in all of the strains analyzed here. The morphological data of S. paradoxus strain N17, S. paradoxus strain IFO1804, and S. mikatae strain IFO1815 were generated with 15, 10, and 5 biological replicates, respectively. On average, ∼60 cells were measured for each trait in each replicate. The morphological data from 37 natural strains of S. cerevisiae were previously collected, with five biological replicates per strain (18). The morphological data of 4,718 haploid and 130 diploid single gene deletion strains of S. cerevisiae were previously published (16, 21).

The morphological data of the haploid derivatives of diploid S. cerevisiae MA lines and their common ancestor were generated previously (20), and the data file “Raw_Data_Additional_Traits.Rfile” was downloaded for analysis. Measurements without the geldanamycin treatment were used. The ancestor and 89 MA lines with two replicates were used. A total of 180 traits that belong to the aforementioned 210 traits had relevant data for our analysis. For two reasons, we did not use MA lines to measure mutational size (MS). First, the MA lines used had an estimated effective population size of ∼10 (39). Thus, large deleterious mutations had been selectively removed. As a result, MS would be underestimated, especially for relatively important traits, biasing our test. Second, each MA line carried only ∼6 point mutations (40). Hence, the amount of mutational size information from the 89 MA lines is an order of magnitude smaller than that from thousands of gene deletion strains. MA lines were used as a negative control of our neutrality test because significant adaptation is not expected for MA lines; in fact, fitness of MA lines generally declined during mutation accumulation (39).

Evolutionary Distance Between Two Strains for a Morphological Trait.

We estimated the mean phenotypic value for a trait in a strain by first calculating the mean trait value among all cells in a replicate population and then averaging this number across all replicate populations. Let x_i and x_j be the mean phenotypic values of a trait in strains i and j, respectively. We estimated the raw evolutionary distance for the trait between strains i and j by ED_ij = |x_i − x_j|/[(x_i + x_j)/2]. Different traits have different levels of environmental variation in phenotyping, different levels of random measurement error, and different levels of among-individual stochastic phenotypic variation. To allow a comparison among traits, we corrected the above estimated raw ED values for these factors (19). Let us assume that strain i has m replicate populations, with population sizes of a₁, a₂, …, a_m, respectively, and strain j has n replicate populations, with population sizes of b₁, b₂, …, b_n, respectively. We generated 100 sets of bootstrap samples for both strain i (i.e., each having m populations with sizes of a₁, a₂, …a_m) and strain j (i.e., each having n populations with sizes of b₁, b₂, …, b_n) using the data from the n populations of strain j. Note that the hierarchical structure of the data is retained in bootstrapping. We then estimated the average ED_ij across these 100 sets of bootstrapped samples and denoted it by pseudo ED_j→i. We similarly estimated pseudo ED_i→j using the data from the m populations of strain i. We then averaged ED_j→i and ED_i→j and subtracted this value from raw ED_ij to obtain the corrected ED_ij. If the corrected ED_ij is negative, we set it at 0. All ED values presented in the main text and figures are corrected ED_ij.

Another potential measure of the evolutionary distance of a trait is the coefficient of variation of the trait among strains (CV). For each trait, we calculated CV among the 37 natural strains (CV₁). Correspondingly, we calculated CV among all 4,718 gene deletion strains (CV₂) as a measure of the mutational size of the trait. Using CV₁/CV₂ as a measure of evolutionary rate, we again observed that the evolutionary rate of a trait is positively correlated with trait importance (ρ = 0.48, P < 10⁻³⁰⁰).

Mutational Size.

The mutational size for a trait was calculated by the average of the previously published net absolute effect sizes (|ES|) of 4,718 haploid single gene deletions on the trait (19). Briefly, we first calculated the raw absolute effect size of deleting gene i on trait j as |x_ij − w_j|/w_j, where x_ij is the mean phenotypic value of trait j in gene deletion strain i, and w_j is the corresponding value in the wild type (averaged across 123 replicate populations). Different traits have different levels of environmental variation in phenotyping, different levels of random measurement error, and different levels of among-individual stochastic phenotypic variation. To control for these variations, we generated 1,000 pseudo phenotypic datasets for each trait in each deletion line. In each pseudo dataset, we randomly chose 1 of the 123 wild-type replicate populations and picked (with replacement) from this population the same number of cells as in the actual gene-deletion data for the trait. We then calculated mean pseudo |ES| across all 1,000 pseudo datasets. The net |ES| is defined as the raw |ES| minus the mean pseudo |ES| if raw |ES| > mean pseudo |ES|; otherwise, the net |ES| is set as zero. Note that our estimation of MS does not assume universal pleiotropy (41), because the net |ES| of a gene deletion on a trait can be zero.

We also estimated MS by the same method but using the recently published morphological data of 130 diploid single gene deletion strains (21) along with the five replicate populations of the corresponding wild type (BY4743) (18). Due to the low number of wild-type replicates, 100 pseudo datasets were generated.

Morphological Trait Importance.

The TI of each of the 210 morphological traits was previously estimated from the negative slope of the linear regression between the corrected phenotypic effect of a gene deletion on the trait and the fitness of the gene deletion strain across 2,779 haploid single gene deletion strains (19). The deletion strains with fitness larger than one were not used. Briefly, for each trait j, we performed a linear regression F_i = a_j − b_j (net |ES_ij|), where net |ES_ij| is the absolute value of the net effect size of deleting gene i on trait j, and F_i is the fitness of the strain lacking gene i relative to the wild type in YPD. In this regression, the estimated slope b_j > 0 is 100 times the reduction in fitness caused by 1% change in the phenotypic value of trait j, while the estimated intercept a_j is the expected fitness when net |ES_ij| = 0. Thus, b_j is a measure of the relative importance of trait j to fitness, or TI.

While only 2,779 gene deletion strains with relative fitness ≤1 were used for calculating TI, all 4,718 gene deletion strains were used for calculating MS. We observed qualitatively the same result when using only 2,779 gene deletion strains to estimate MS. For example, within S. cerevisiae, the rank correlation between mean ED/MS and TI is 0.33 (P < 10⁻⁵).

For diploid gene deletion strains (21), we applied the same method to calculate TI, but in this case only 99 strains with relative fitness ≤1 could be used.

Principal Component Analysis.

To examine if the nonindependence among the 210 morphological traits affects our results, we followed previous studies (19, 22) to perform a principal component analysis to transform the net |ES| matrix M (4,718 genes × 210 traits) described previously (19). Note that net |ES| is the corrected absolute effect size of a gene deletion on a trait. After this function returned a coefficient matrix C (210 × 210), we calculated v′ = v C (1 × 210 principal traits) for each corrected ED vector v (1 × 210 traits) between two strains. The absolute values of v′ provided the corrected ED for each of the 210 orthogonal principal component traits. We also used the transformed net |ES| matrix, M′ = MC (4,718 genes × 210 principal traits), to estimate trait importance for the 210 principal component traits following the method previously used (19).

Mantel Test.

We used Mantel test (42, 43) to evaluate the significance of the correlation between a biological distance (e.g., morphological dissimilarity between two strains) and the correlation (ρ) between ED/MS and TI across 666 pairs of the 37 natural strains of S. cerevisiae. See SI Materials and Methods for details of the Mantel test.

Gene Expression Data and Analysis.

The rich medium microarray gene expression ratio (r) between two S. cerevisiae strains, RM and BY, were previously measured for thousands of genes (44). We defined the intraspecific ED of the expression level for a gene by |x_RM − x_BY|/x_BY, which equals |r − 1|, because r = x_RM/x_BY, where x_RM and x_BY are expression levels of the gene in RM and BY, respectively.

We estimated mutational size for each expression trait by the mean effect size of gene deletion on the expression trait across 1,486 deletion lines, following a previously published method (19) but using a recently published large dataset (45). The TI of a gene expression trait was defined by the fitness decrease caused by deleting the gene (24). Only those genes that have zero or positive TI were considered. After removing genes that miss any kind of data above, we obtained our final dataset with 3,466 expression traits.

As a negative control in the neutrality test for expression traits, we used the square root of variance in the expression level of an evolved line relative to that of the ancestral line (SD_m) among four mutation accumulation lines (23), and correlated between SD_m/MS and TI.