Denoising of MR Spectroscopic Imaging Data Using Statistical Selection of Principal Components

Abstract

Objectives

To evaluate a new denoising method for MR Spectroscopic Imaging (MRSI) data based on Selection of signal-related Principal Components (SSPC)from principal components analysis (PCA).

Materials and Methods

A PCA-based method was implemented for selection of signal-related PCs and denoising achieved by reconstructing the original dataset utilizing only these PCs. Performance was evaluated using simulated MRSI data and two volumetric in vivo MRSI of human brain from normal subject and patient with brain tumor using variable signal to noise ratios (SNR), metabolite peak areas, Cramer-Rao Bounds (CRB) of fitted metabolite peak areas and metabolite linewidth.

Results

In simulated data SSPC determined the correct number of signal-related PCs. For in vivo studies, the SSPC denoising resulted in improved SNR and reduced metabolite quantification uncertainty compared to the original data and two other methods for denoising. The method also performed very well in preserving the spectral linewidth and peak areas. However, this method performs better for regions that have larger numbers of similar spectra.

Conclusion

The proposed SSPC denoising improved the SNR and metabolite quantification uncertainty in MRSI, with minimal compromise of the spectral information, and can result in increased accuracy.

Introduction

MR spectroscopic Imaging (MRSI) enables mapping distributions of several tissue metabolites that are of interest for non-invasive clinical diagnostic purposes, particularly for studies in the brain [1]. The technical challenges in acquiring data from low concentration metabolites require a compromise in the spatial resolution and signal-to-noise ratio (SNR) of the measurement, which can decrease the value for clinical applications. While increased SNR can be achieved by signal averaging, this is frequently impractical for clinical studies due to the increased scan times and susceptibility to movement artifacts.

An alternative approach to improving SNR, and thereby reduce the uncertainty of the MRSI analysis, is to reduce noise in the data as part of the reconstruction procedure. A simple approach is to smooth the data in both the spatial and spectral domains using, for example, a Gaussian function [2], which also results in decreased spatial resolution or increased spectral linewidth respectively [3]. Another popular approach is the thresholding of the data in a transformed domain, such as wavelet and time-frequency, followed by inverse transformation. Ancino-De-Geiff et al. [4] proposed the use of wavelet shrinkage for denoising of MRS data. In this method, the data is transformed to a decorrelated domain by an orthonormal series generated by wavelets and then the denoising is applied through thresholding of wavelet coefficients and inverse transformation [5]. Later, Ojanen et al. [6] proposed the minimal description length method to find the optimal number of wavelet coefficients for the denoising of electrophoresis and mass spectroscopy signals. Laruelo et al. [7] proposed a new wavelet base denoising technique which accounts for signal regularity across the spectral and spatial domains without altering the spectral resolution. Their method includes a proximal algorithm for a fast convex optimization to find the optimal number of wavelet coefficients. They reported improvements in retaining the spectral line shapes compared to the convolution smoothing by a Hanning function [7].Ahmed [8] proposed consecutive projections of the noisy MRS data in different domains, in conjunction with noise filtration for each domain. For these projections, a set of stable, linear, time-frequency transforms was applied with different resolutions [9] and improvements over the wavelet shrinkage method for ³¹P single voxel data were reported [8]. However, for consideration of this method to volumetric MRSI data that can have on the order of 10⁵ spectra, the computational cost of using multiple projections must also be considered.

In a different approach, the denoising can be applied prior to or during MRS signal reconstruction using explicit parametric modelling approaches [10, 11]. Eslami and Jacob [10] proposed a reconstruction scheme for MRSI data that results in a sparser representation of the spectral data that enables the separation and suppression of the noise as well as line shape distortions. Nguyen et al. [11] applied a similar approach with the addition of spectral prior knowledge estimated from k-space data.

It is often assumed that the signal-related (noiseless) data is a lower rank subspace of the original data. Low-rank modeling with recent advances in its algorithm has become a popular method in the medical imaging field [12-14]. Singular Value Decomposition (SVD) and Principal Component Analysis (PCA) provide a representation of complex data in a lower dimensional space that is defined by the significant PCs (principal component directions) [15, 16]. MRSI data can be represented as a product of (i) the PCs, which are orthonormal and ordered by the decreasing amount of commonality in the data they represent; and (ii) their scores or magnitudes, which are the projections of the data onto the corresponding PC. The total number of PCs is usually much larger than the number of independent variations in the dataset. For instance, in vivo MRSI data with 1024 points in the frequency domain will result in 1024 PCs, but if we assume that there are 10 observed metabolite spectral patterns the amplitude, frequency, phase and linewidth variations will result in ∼40 signal related PCs [17, 18] and the remaining PCs will be noise-related. Recalculating the data using only the significant PCs while ignoring the higher noise-related will effectively reduce the noise in the data.

For denoising of MRSI data, Zhu et al. [19] proposed a PCA based denoising technique based on a deformable shape-intensity model. They reported increased SNR up to 2.1 times without distorting spectral lineshapes and linewidths. Nguyen et al. [20] proposed a low rank approximation (LORA) scheme that exploits two low-rank structures. The first structure is derived on the assumption that spatial and temporal variations in MRS data are separable, and the second one is calculated based on the linear predictability assumption in temporal dimension. This study reported a better performance of LORA denoising compared to the wavelet shrinkage and Gaussian smoothing in terms of SNR and spectral quality [20].Kasten et al. [21] proposed a data-driven low rank component analysis for MRSI in which a generative model is estimated from the raw data via regularized variation framework that minimizes the approximation error within the subspace.

One of the challenges of low-rank denoising is the selection of the optimal rank for approximation of the noise-free signal. In the report of Nguyen et al. [20] it was assumed that the rank of the noiseless data is equal to N, if the N^th and (N+1)^th eigenvalues of the original data is greater (or equal) and less (or equal) than the Euclidean norm of the estimated noise, respectively. They also applied the Akaike information criterion [22] where the noiseless data is assumed to be a low-rank Hankel matrix and the noise to be a Gaussian Hankel matrix [20].

Volumetric whole-brain MRSI datasets present an additional challenge for the denoising techniques in that they can contain a wide range of data quality and include regions prone to increased artifacts due to contamination from residual water and unsuppressed subcutaneous lipid signals. Therefore, it is very likely that the spectral decomposition of the data includes PCs that only represent ‘unwanted’ signal artifacts. Thus, it is necessary to examine the information carried by each PC to filter out those that are dominated by either artifact or noise.

In this study a spatial-spectral low-rank method was developed for denoising of volumetric ¹H MRSI data of the brain that was combined with a new approach for selection of the significant signal-related PCs obtained from PCA. In this method, PCs are selected using a statistical test that examined the relative information content describing the metabolite signal. To improve the performance, the denoising step is applied after correction for B0 and phase shifts, which results in a smaller number of signal-related PCs relative to the uncorrected data.

Materials and Methods

Theory

Let s_i(ω) be the noise free spectrum of voxel i, for i = 1, …, N where N is the total number of voxels and ω is the frequency. Assuming s_i(ω) contains M spectral peaks and f_j(ω), j = 1, …, M, represents the normalized spectral shape of the j^th peak, s_i(ω) can be represented as the weighted sum of the shapes:

$${\mathit{s}}_i(\omega )={\sum }_{j=1}^M{\mathit{A}}_j{\mathit{f}}_j(\omega )$$ (1)

where A_j is the amplitude of j^th spectral peak. Let s̄_i(ω) be the acquired MRS spectrum:

$${\overline{\mathit{s}}}_i(\omega )={\mathit{s}}_i(\omega )+\mathit{∊}$$ (2)

where ∊ is complex Gaussian noise with mean 0 and standard deviation σ, i.e. ∊ ∈ N(0,σ²). For volumetric MRSI, let us reform the data to a two dimensional complex matrix S̄(r, ω) with r and ω being the spatial and frequency domains, respectively. Therefore each row will represent a spectrum, S̄_i(ω), and the total number of rows (r) would be N. Let S(r, ω) be the corresponding ‘noiseless’ complex matrix with s_i(ω) in its rows. Therefore, for the volumetric MRSI, Eq. 2 can be represented as:

$$\overline{\mathit{S}}(r,\omega )=\mathit{S}(r,\omega )+\mathit{∊}$$ (3)

PCA is a standard statistical technique for decomposition of S̄ along the axes of the PCs which are ordered by the decreasing amount of commonality in the data they represent:

$$\overline{\mathit{S}}(r,\omega )=\mathit{Z}(r,\omega )\cdot \mathit{P}(\omega ,\omega )$$ (4)

where Z(r, ω) is the matrix of PC scores and P(ω, ω) is the PCs matrix. In the case that the amplitudes of the metabolite peaks A_j (Eq. 1) vary independently from each other, PCA will yield L significant PCs. The rest of the PCs will be noise related. The spectral matrix can be reconstructed only with the first L PCs and thus the data will be ‘denoised’, i.e.:

$$\overline{\mathit{S}}{(r,\omega )}_L\approx \mathit{S}{(r,\omega )}_L$$ (5)

where subscript L indicates the low rank of the matrix based on L significant signal-related PCs. Determining the rank L in in vivo MRSI data, however, is quite challenging as it is not known a priori how many spectral patterns are in the data and, more importantly, there are added noise and additional features from variations in frequency, phase, lineshape, and baseline, which exacerbate the problem.

Method

The proposed method, Statistical Selection of Principal Components (SSPC), determines the signal related PCs in S̄(r, ω). The technique is based on examining each PC and comparing the variance in frequency regions with known metabolites with the variance in the ‘noise’ regions. For this purpose, Levene's test [23] was performed to assess the equality of variances between these two regions. Similar to the F-test, Levene's test is a variance equality test that can handle the non-normality of data. While in Eq. 2 the noise is assumed Gaussian, it should be noted that any apodization, zerofilling or spatial filtering introduces correlation and the noise in MRS after these standard pre-processing procedures cannot be considered normally distributed. Also, the peak amplitudes within the metabolite region generally are not normally distributed. After performing Levene's test, a threshold was applied to the significant difference (p-value) calculated by the test to retain the significant PCs and construct the S̄(r, ω). The selection is applied to all PCs and the result need not be consecutive, i.e. PC_i+1 may be included while PC_i is excluded. In this method, the total number of selected PCs would be equal to the rank L of S̄(r, ω). The choice of the p-value threshold depends on the noise level in the dataset and will be determined by the user. An estimate for the threshold value can be obtained by performing Levene's test for two noise-only regions in last PCs that are noise-related PCs; however, the threshold value can be increased to retain more PCs.

Simulated MRSI Data

Simulated volumetric MRSI datasets were generated for Cartesian k-space sampling using a function in the MIDAS (Metabolite Image Data Analysis System) software package [24]. To examine the performance of the PC selection a MRSI dataset was created for a simple abstract object consisting of three overlapping spherical volumes, each characterized by a different spectral pattern, labeled Line1, Line2 and Line3 (Fig. 1a). Spectroscopy signals were generated with Gaussian lineshapes and constant amplitudes over each region with relative values of 0.8, 0.7 and 1.0. Gaussian noise with mean value 0 and standard deviation of 0.08 was added in the time-domain. The spatial resolution of the simulated datasets was 64×64 voxels in-plane and 4-voxels through-plane. To examine the effect of frequency and phase shifts, a second dataset was generated with randomly shifted phase and frequency between-30° and +30°, and -6 Hz to 6 Hz, respectively.

Fig. 1.

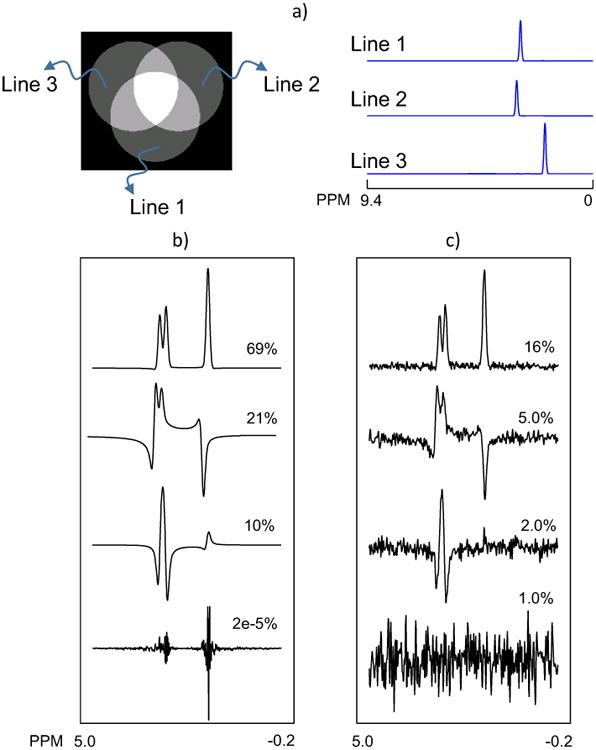
MRS data was simulated by generating an abstract object consisting of three overlapping spherical volumes. Each volume contained a single peak line, shown on the right as Line 1, Line 2 and Line 3. The real part of the first 4 PCs with their corresponding normalized eigenvalues, obtained from PCA analysis of the simulated dataset b) before and c) after adding Gaussian noise.

A third dataset was generated to resemble the volumes and metabolites in an in vivo brain MRSI that included a small lesion with a different spectral pattern. The primary volume had an ellipsoidal shape containing subregions with different spectral patterns that represented a lipid ring, normal brain tissue, ventricles containing only a water signal, and a small region representing a brain lesion (blue region in Fig. 2). In addition, spatial variations of all simulated spectral peaks were created throughout the whole object following a synchronous cubic distribution pattern for all metabolites. The metabolite region included simulated resonances for N-acetylaspartate (NAA_sim), total Creatine (Cr_sim) and total Choline (Cho_sim), whereas in the lesion the NAA peak was set to zero and an overlapped doublet for Lactate (Lac_sim) was included.

Fig. 2.

Phase and frequency shifted MRS data was simulated by generating an abstract object consisting of three overlapping spherical volumes. The real part of the first 8 PCs with their corresponding normalized eigenvalues, obtained from PCA analysis of the simulated dataset b) before and c) after adding Gaussian noise.

In Vivo MRSI Data

Volumetric MRSI data of one normal subject (male, 31 years old) and one brain tumor subject (female, 49 years old) were obtained at 3T (Siemens Trio) with 8-channel detection. Subjects were scanned after obtaining signed informed consent in accordance with the procedure approved by our Institutional Review Board. These data were acquired using a spin-echo acquisition with two-dimensional phase encoding, echo-planar readout in the k_y-time dimensions, frequency-selective water suppression and TR/TE = 1551/17.6. Sequence details have been provided elsewhere [25-27]. The acquisition included a water-reference dataset obtained in an interleaved manner with identical spatial parameters as the metabolite MRSI. MRSI acquisition was preceded by an inversion-recovery preparation, with TI = 198 ms, to suppress signal from subcutaneous lipids [25, 27]. A T1-weighted image (MPRAGE, Magnetization Prepared Rapid Gradient Echo) at 1-mm resolution (TR/TE/TI = 2300/2.4/930 ms) was also acquired for each study.

All data were processed using the MIDAS software package [24]. The processing steps included resampling of the echo-planar imaging (EPI) readout with combination of odd and even echo readouts [28], zero-filling in the spatial domain from 50×50×18 points to 64×64×32 points, zero-filling in the frequency domain from 500 points to 1024 points, Fourier transformation in all three spatial dimensions, and multichannel combination [29]. Spatial smoothing (Gaussian, damping factor of 2.0) was applied as a convolution in the spatial domain after spatial-spectral Fourier transformation, B0 correction, and lipid k-space extrapolation [30]. The resolution of the reconstructed metabolite images corresponded to a voxel volume of 1.55 ml calculated at full width at half maximum.

A high SNR reference dataset was also created from the normal subject dataset by averaging the MRSI data from 64×64 voxels in-plane and 32-voxels through-plane to 10×10 voxels in-plane and 10-voxels through-plane. The averaging was performed after application of processing steps mentioned above. To remove noisy and contaminated averaged spectra based on LW and CSF partial volume criteria, parametric spectral fitting [31] was performed to derive the LW from NAA, Cre, and Cho resonances. A threshold of 2 < LW < 8 was then applied to filter out the unwanted averaged spectra. A noisy version of this dataset was then generated by adding a Gaussian noise with mean value 0, standard deviation of 0.08 based on the maximum amplitudes of NAA in the averaged data. The purpose of this study was to examine the performance of the SSPC denoising method in improving the metabolite quantification for in vivo datasets.

To increase the effectiveness of the SSPC denoising for the in vivo datasets the spectral phase and frequency variations were corrected prior to denoising. This was achieved using two steps. Firstly, following spatial reconstruction a time-domain phase-correction function was applied at each voxel location, with the correction function obtained from the unsuppressed water acquisition. Because some phase variations still remained across the image a second processing step was applied that used spectral fitting of the primary resonances, consisting of NAA, Cre, and Cho singlet resonances only, and then applied the phase and frequency terms determined from this analysis as a correction to the data. Following denoising the parametric spectral fitting [31] was again performed to obtain maps of NAA, Cr and Cho, myo-Inositol, and glutamate plus glutamine (Glx).

For data that had the SSPC denoising applied no spectral smoothing was applied during processing. For comparison to standard processing methods, data were also processed using Gaussian apodization of the time data, prior to spectral Fourier transformation, for a relatively small 2 Hz line-broadening and a value more typically used (for 3 T) with 5 Hz line-broadening.

Data Analysis

SSPC denoising performance was compared with: 1) spectral apodization using Gaussian smoothing, and 2) conventional PCA denoising. For the second method, the rank L was found using the SSPC scheme and the same rank was applied for the PCA reconstruction using the first L consecutive PCs. It should be mentioned that the conventional PCA procedure is equivalent to the first part of the LORA [20] denoising scheme. Since the second part of LORA denoising, which utilizes the Cadzow algorithm [32] for each spectrum, is not coupled to the first part, results of comparisons between the conventional PCA and SSPC denoising would also be valid for the first part of LORA denoising.

For the SSPC method, the noise and signal regions in the PCs are identified in the same manner as in the spectra, with the noise region being the first 150 points (9.4 to 7.90 ppm) and the metabolite region from 4.0 to 1.5 ppm. Qualitative comparisons between individual spectra obtained from different denoising methods are presented for each study. Metabolite peak areas and their Cramer-Rao Bound (CRB), metabolite peak area ratios, linewidth (LW) and SNR were used as the measures for quantitative comparisons. SNR was calculated using the fitted NAA area over the standard deviation (SD) of the noise in the spectral domain, with the noise measurement taken from the last 100 points (0.64 to -0.35 ppm) of the spectrum. For the in vivo studies, the SNR was used since it accounts for changes in linewidth. For the SNR calculation within the tumor region, the fitted Cho area was used instead of the fitted NAA area. In both studies, the SNR measurement was done after application of the spectral fitting. To examine the spatial distributions of the relative performance in more detail, images of metabolite peak area, CRB, LW and SNR were generated for the study of a normal subject. The coefficient of variation (CV) of the root mean square error (RMSE) was also used to calculate errors in the NAA, Cho and Cr fitted areas for the simulated data, as

$$C{V}_{\mathit{\text{RMSE}}}=\frac{\sqrt{\frac{{\sum }_{i=0}^N{({\mathit{M}}_{\mathit{\text{ref}}}-\mathit{M})}^2}{N}}}{\overline{M}}$$ (6)

where M_ref is the known (reference) value at voxel i, M is the fitted area at that voxel, and M̄ is the mean value of the reference areas over N voxels in the ROI.

Results

Simulated MRSI Data

In Fig.1 are shown the central slice from the first simulated dataset and the constituent spectral patterns. PCA was applied to the data before and after adding random noise. The real part of the resultant first 4 PCs with their corresponding normalized eigenvalue percentages are shown in Figs. 1b and 1c, respectively. In the first case, the first 3 PCs contained 100% of the information for reconstruction of the noiseless data. The shape of the 4^th PC with only 2e-5 contribution can be considered as the numerical error of the PCA algorithm used for the spatial-spectral decomposition of data. With added noise (Fig.1c) the first three PCs have only 23% of the total variance; however, the PC shapes remained the same as in the noiseless data. The contribution of the 4^th PC was increased to 1% due to presence of the noise. In both cases, SSPC determined that the first three PCs were signal-related using 0.01 as the p-value threshold for Levene's test. PCs for the second simulated dataset are shown in Figure 2. In this case the number of signal-related PCs was increased to seven due to the variations in the phase and frequency. The SSPC method also detected 7 signal-related PCs using 0.01 as the p-value threshold for Levene's test. This result shows that with additional variability in the data the number of signal-related PCs is increased, however, as long as there is a significant difference between signal variations and noise variations in a given PC the SSPC method can detect and use that PC regardless of shifts in frequency and phase. However, if the frequency and phase shifts are small, such that the difference between the shifted spectrum and corrected spectrum is less than the noise level, they can be ignored. Therefore, it is recommended to perform the SSPC denoising after the phase and frequency corrections.

In Fig.3 are shown example spectra from the simulation studies and the distributions used to generate the simulated MRSI data. For the simulated brain (Fig. 3c and 3d), this consisted of regions containing lipid signals (shown in light yellow), normal metabolites (gray), water (dark gray), and abnormal metabolite signals (blue). SSPC determined that the first four PCs were signal-related using 0.01 as the p-value threshold for Levene's test.

Fig. 3.

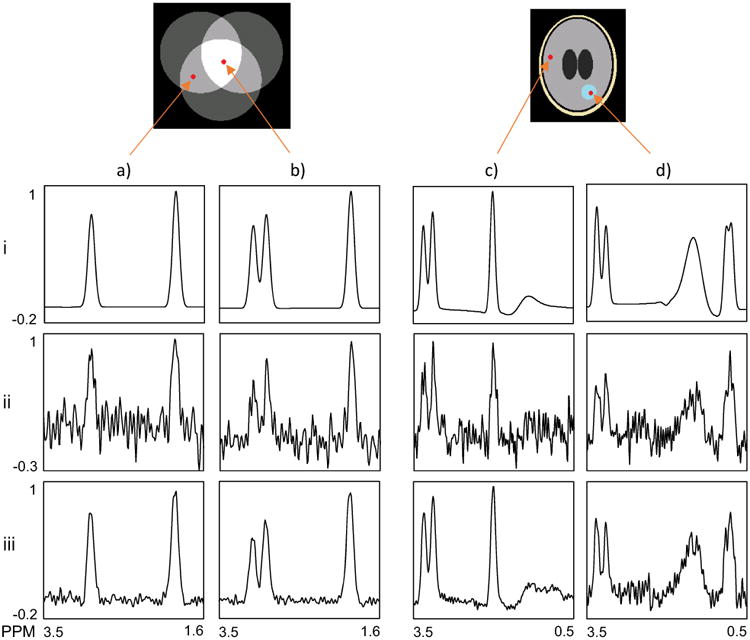
Example spectra from both simulation studies; Spectra in columns a) and b) show results for two voxels selected from the regions indicated in the abstract object, c) and d) show results for two voxels selected from the regions indicated in the ellipsoidal object. The spectra in each row are as follow: (i) noise-free simulated data, (ii) simulated after addition of random noise, and (iii) denoised data using SSPC.

Two noise-free spectra from each of the simulated datasets are shown in the top row in Fig.3. The spectrum in Fig. 3a.i is selected from an area of overlap of two volumes and shows two signals, while that shown in Fig. 3b.i is from the intersection of all three volumes and contains three signals. The examples from the simulated dataset shown in Fig. 3c and 3d are selected to represent “normal” (relatively equal Cr and Cho peaks and high NAA) and a small region of “tumor” (increased Cho, no NAA and large lactate doublet).In the second row are shown the data after adding random noise and in the last row are the results after the SSPC denoising. The results in row (iii) show that the SSPC denoising had a good performance in removing the noise and preserving the peak heights, indicating no loss of information. Note that the reconstructed “tumor” spectrum, Fig. 3.d.iii, is noisier than that from the “normal” region. The tumor spectra are associated with a relatively small volume and therefore they contribute a small fraction of the total variance. As the PCs are ordered by the amount of commonality in the data they explain, the first few PCs are dominated by the signal from the ‘normal’ volumes. The tumor-related variance is in higher order PCs, which in turn contain more noise. These higher order PCs do not contribute in the reconstruction of the normal signals, hence the high SNR and conversely, the lower SNR in the “tumor” spectrum.

For quantitative comparisons, metabolite peak area ratios and SNR obtained from denoising of the simulated MRS data are presented in Table 1. After application of SSPC denoising, the SNR for voxel 1 was increased by 433% and for voxel 2 by 131%. The errors for NAA_sim/Cr_sim and NAA_sim/Cho_sim ratios for voxel 1 were also reduced by 69% and 94%, respectively. For voxel 2, Lac_sim peak was used instead of NAA_sim. The improvements in reducing errors for Lac_sim/Cr_sim and Lac_sim/Cho_sim ratios after the application of denoising were 73% and 12%, respectively. Additional studies (results not shown) examined the denoising of the data using only the first 3 PCs and the first 5 PCs. The former resulted in removing the Lac_sim peaks in the small lesion region, and the latter added more noise to the data with no improvement in peak area ratios.

Table 1.

Simulated metabolite peak area ratios and SNR for the simulated MRS data. (The p-value threshold of the SSPC denoising was 0.01).

	Voxel 1			Voxel 2
	NAAsim/Crsim	NAAsim/Chosim	SNR	Lacsim/Crsim	Lacsim/Chosim	SNR*
Simulated Data	1.228	4.147	-	0.362	0.951	-
Simulated Data Plus Gaussian Noise	1.369	5.337	109.513	0.602	1.404	78.431
SSPC (0.01)	1.185	4.214	584.117	0.425	1.351	181.534

^*For Voxel 2 SNR was calculated using Cho peak area instead of NAA.

In Table 2 are presented the coefficient of variation (CV) of the root mean square error (RMSE) of NAA, Cho and Cr areas for a ROI located outside of the tumor region (25 voxels) and for Cho and Cr within the tumor region (25 voxels). The values are compared with that obtained using Gaussian apodization of 5 Hz, and the original data. These results show that the SSPC denoising reduced errors in ROI 1 by 33%, 68% and 66% for NAA, Cr, and Cho fitted areas, respectively, relative to the analysis of the original data. The improvements in the tumor region (ROI 2) were smaller with the maximum of 5% reduction of error for the Cho area. The CV_RMSE values increased for the case where Gaussian apodization was applied, which we believe is due to the increased linewidth that notably affected fitting of the closely overlapping peaks of Cr and Cho.

Table 2.

CV of RMSEs for NAA, Cr and Cho fitted areas. (ROI 1 is located outside of the tumor region and ROI 2 is within the tumor region)

	ROI 1			ROI 2
	RMSENAA	RMSECr	RMSECho	RMSECr	RMSECho
No Denoising	0.064	0.075	0.086	0.334	0.280
Gaussian Apodization	0.064	0.081	0.089	0.630	0.537
SSPC	0.043	0.024	0.029	0.333	0.266

In Vivo MRSI Data

The aim of the next study was to examine the performance of the SSPC denoising applied to a MRSI dataset of a normal subject. Maps of the peak areas of two metabolites (Cr_Area, Glx_Area), their corresponding CRBs, LW and SNR are shown in each column in Fig. 4. The use of conventional spectral apodization of 2 Hz or 5 Hz line Gaussian smoothing, shown in Fig. 4b and Fig 4c, resulted in increased SNR and reduced CRBs compared to the raw data, but also increased the metabolite LW, especially for 5 Hz line smoothing. To ensure a direct comparison between the conventional PCA and SSPC denoising methods, the same number of PCs, L = 224, were used for Fig. 4d and Fig. 4e, and 65 PCs, L = 65 were used for Fig. 4f and Fig. 4g. For these examples the number of PCs selected, L, was based on the value determined in the SSPC denoising approach with a p-value threshold of 10E-5 or 10E-10, and the first L consecutive PCs were used for the conventional PCA approach. It can be observed that the SSPC denoising (Fig. 4e and Fig. 4g) performed better than the conventional PCA denoising (Fig. 4d and Fig. 4f) in terms of CRB and SNR. The visual improvements in metabolite peak area images were more prominent for the lower concentration metabolite, Glx_Area, compared to the higher concentration metabolite, CR_Area. By comparing Fig. 4e and Fig. 4g, it can be observed that decreasing the p-value threshold from 1E-5 to 1E-10 improved SNR and CRBs without compromising the metabolite information such as LW and metabolite peak area.

Fig. 4.

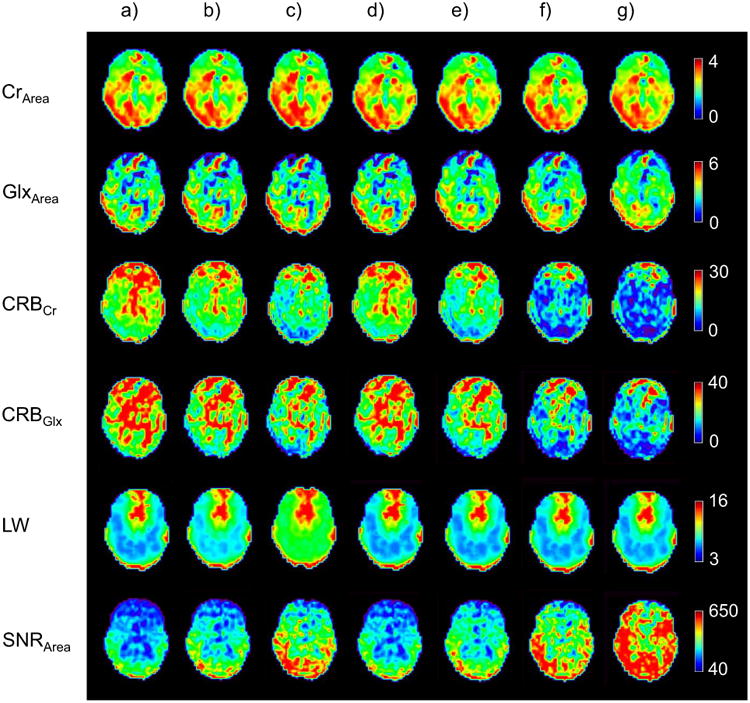
Images of denoising results for a mid-axial slice for a volumetric MRSI study of a normal subject. Results from the spectral fitting are shown in each row for different processing in each column for (a) acquired data with no spectral smoothing, (b) Gaussian apodization (2 Hz), c) Gaussian apodization (5 Hz), d) PCA denoising using the first 224 PCs, e) SSPC denoising with threshold of 1E-5 (the algorithm found 224 PCs for this threshold), and f) PCA denoising using the first 65 PCs, g) SSPC denoising with threshold of 1E-10 (the algorithm found 65 PCs for this threshold)

For the second in vivo study, the high SNR averaged data was used as the reference for the evaluation of the SSPC denoising performance. The SSPC denoising was applied on the noisy data that was generated by adding Gaussian noise to the averaged data, then its results were compared to the original averaged data. The results for analysis of NAA, which has a strong signal with good SNR, and Glx, which exhibits a broad multiplet structure with low SNR, are shown in Fig 5. In Fig 5a are plotted the fitted NAA area results, obtained at multiple voxels before (orange) after (blue) application of the SSPC denoising, against the corresponding reference data result. It can be seen that the fitted NAA areas are clustered toward the center line with R² = 0.91 for the denoised result compared to the noisy data with R² = 0.90. As expected, the improvement is more evident for Glx (Fig. 5b), which showed a 14% increase in R². This result illustrates that the denoising reduces uncertainty of the parametric spectral fitting.

Fig. 5.

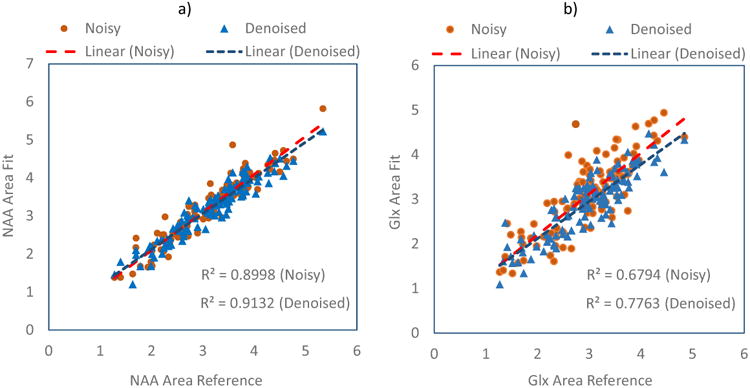
Comparison of the SSPC denoising results against a high SNR reference dataset. (a) Regression plots for NAA area obtained from the noisy and denoised data against the NAA area from the reference; (b) Regression plots for Glx area obtained from the noisy and denoised data against the Glx area from the reference. The results for the noisy data and its linear regression are shown in orange and those for the denoised data are shown in blue.

One of the main challenges of denoising methods is to retain information in small regions of interest, such as small tumors, that have very different signal compositions compared to larger regions of the brain. Therefore, the aim of the third in vivo study was to investigate the performance of the SSPC denoising method inside and outside of a small tumor region. In Fig. 6 is shown a MRI that identifies a tumor on the right side of the image (left side of the brain), with the gross tumor volume of 7.5 ml. Two example spectra, one from a voxel located the normal appearing white matter region on the opposite side of the tumor region (voxel 1), and one from a voxel within the tumor region (voxel 2) are also shown for the original data and following different denoising approaches. A visual evaluation of spectra in Fig. 6a.iii and Fig. 6a.iv indicates that the SSPC denoising performed better than the conventional PCA denoising. The SSPC result with the p-value threshold of 1E-10, Fig 6a.v, appears less noisy compared to other methods. For voxel 2, the denoised spectra are similar in appearance, however, the spectrum shown in Fig. 6b.v obtained from the SSPC denoising with the p-value threshold of 1E-10 appears less noisy and has a smaller Glx peak height compared to the other spectra.

Fig. 6.

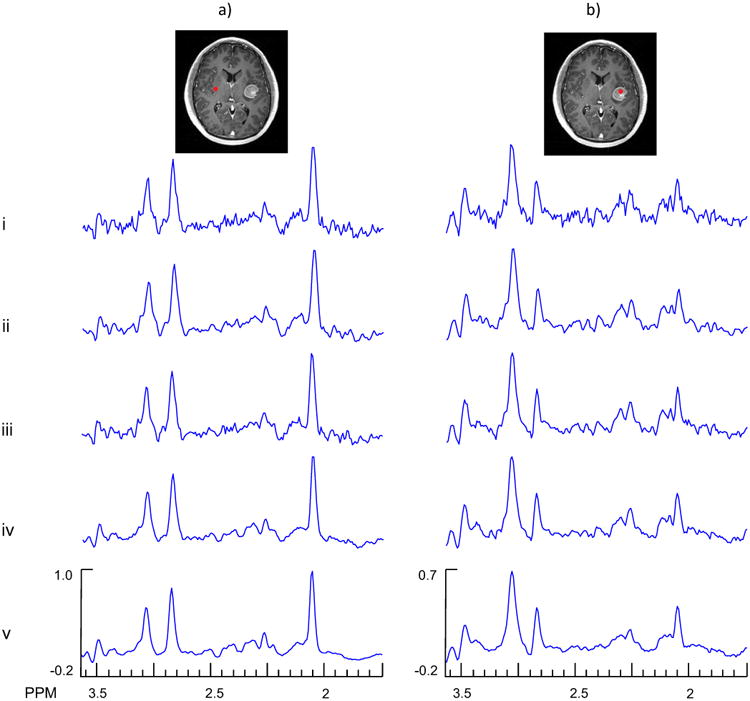
Example spectra from the denoising of an in vivo MRSI study of a subject with brain tumor. In column a) are shown results for a voxel selected from a normal appearing white matter region (voxel 1) and in column b) are shown results for a voxel selected in the tumor region (voxel 2). The rows show results for the original data (i), Gaussian denoising (ii), PCA denoising using the first 119 PCs (iii), SSPC denoising with a threshold of 1E-5 (the algorithm found 119 PCs for this threshold) (iv), and SSPC denoising with a threshold of 1E-10 (the algorithm found 56 PCs for this threshold) (v).

In Table 3 are presented the CRB_Cr, CRB_Glx and the SNR for the two selected voxels. The SSPC denoising with 1E-10 threshold increased the SNR from 92 to 418, or 355%. However, for voxel 2 this improvement was 169% which is more than 2 times smaller than the improvement for voxel 1. The reason for this result is that the denoising algorithm will perform better for larger numbers of voxels that have the same spectral pattern. Similar results were demonstrated using the simulated MRS data that have been presented in Table 1. The SSPC denoising with threshold of 1E-10 resulted in the best CRB values with exception of CRB_Glx for voxel 2, which was due to the reduced Glx peak height (Fig. 6b.v) in this region.

Table 3.

CRB_Cr, CRB_Glx and the SNR for the second in vivo experiment with the brain tumor.

	Voxel 1			Voxel 2
	CRBCr	CRBGlx	SNR	CRBCr	CRBGlx	SNR*
No Denoising	5.439	4.582	91.786	9.499	12.167	31.669
Gaussian Apodization	4.403	3.640	106.486	8.306	11.302	41.833
PCA (119)	4.296	3.592	101.235	8.208	9.689	38.059
SSPC (1E-5)	3.617	3.413	186.706	7.078	10.600	52.614
SSPC (1E-10)	3.170	3.034	418.276	5.850	15.499	86.218

^*For Voxel 2 SNR was calculated using Cho area instead of NAA.

Mean and standard deviation (SD) of the SNR were calculated for two ROIs, one located outside of the tumor region (25 voxels) and one within tumor region (25 voxels). These results are presented in Table 4, which show that the SSPC denoising with a 1E-10 p-value threshold increased SNR by factors of 2.3, 2.3 and 1.1 compared to Gaussian apodization (5 Hz), conventional PCA (with 119 PCs) and SSPC denoising (10E-5 threshold), respectively. For ROI 2 the SNR was calculated from the Cho area, since NAA was absent, and the SSPC denoising with 1E-10 p-value threshold resulted in a SNR increase of 2.3 times compared to the Gaussian apodization case.

Table 4.

Mean and SD of SNR for two ROIs inside and outside of the tumor region. For ROI 2, SNR was calculated using Cho area instead of NAA.

	ROI 1		ROI 2
	Mean	SD	Mean	SD
No Denoising	108.737	20.842	40.857	10.755
Gaussian Apodization	139.167	34.304	56.504	14.931
PCA (119)	138.678	36.816	59.219	16.177
SSPC (1E-5)	273.444	49.911	85.936	18.769
SSPC (1E-10)	314.964	50.154	131.365	22.163

Discussion

This study has presented a PCA based denoising method for MRSI data that incorporates PC selection based on a statistical comparison of spectral regions containing metabolite information and noise. The aim of this statistical examination was to examine the homogeneity of variances between the signal and noise regions derived from each PC. A threshold was then applied to the p-value of Levene's test to select PCs that contained significant metabolite information.

A primary finding of this study is that the SSPC denoising can significantly improve the SNR and metabolite quantification accuracy in simulated spectra, and reduce uncertainty in in vivo data, without significantly compromising metabolite information, provided that a sufficient number of PCs are retained. This method also performed better compared to the conventional PCA based method. Using both simulated and in vivo MRSI data it was shown that the SSPC denoising resulted in higher SNR and lower CRBs values compared to the conventional PCA denoising with the same number of PCs, and that the relative performance varied spatially in a manner that depended on the number of spectra with similar spectral patterns. The SSPC denoising with a p-value threshold of 1E-10 showed the most improvements for the SNR and CRBs values without altering the linewidth, although with some indication of a loss of information for small metabolite resonances (e.g. Fig. 6b.v). A p-value threshold of 1E-5 appears to offer a more conservative approach. The impact of PCA based denoising on the uncertainty of spectral fitting as indicated by CRB values is also greater for lower concentration metabolites (e.g. Glx_Area) than the those with prominent resonances (e.g. Cr_Area), likely reflecting the improved performance of the spectral fitting algorithm used for this study with increasing SNR.

Results of the third in vivo study with a small brain lesion also indicated a good performance of the SSPC denoising in terms of SNR and fitting uncertainty; however, for a voxel located in the lesion the PCA denoising methods resulted in increased CRB_Glx values with a threshold p-value of 1E-10. The reason for this decrease in performance is the small number of voxels with the spectral pattern characteristic of the lesion relative to the rest of the brain. This regional size dependency can be considered as one of the limitations of the PCA (or SVD) based denoising methods.

Limitations of this study include that the effect of residual baseline signals from unsuppressed water or lipid were not considered, and that the effect of altered noise distributions on the spectral fitting algorithm was not specifically examined. If strong baseline signals are consistent and widespread they would be identified as signal-related and maintained in the result. However, commonly these signals are highly variable and although those signal-related PCs will be identified, the corresponding eigenvalues for most voxels will be small and there will be minimal impact on the denoising performance.

Conclusion

In summary, it was shown that the SSPC denoising improved SNR and quantification accuracy using three simulated MRSI datasets, and reduced quantification uncertainty in two in vivo datasets. In addition to providing good performance, this method is simple to implement and computationally efficient with the total computing time less than ∼60 s for spectra from a volumetric in vivo dataset.