Abstract
Biomechanical models of the oropharynx are beneficial to treatment planning of speech impediments by providing valuable insight into the speech function such as motor control. In this paper, we develop a subject-specific model of the oropharynx and investigate its utility in speech production. Our approach adapts a generic tongue-jaw-hyoid model (Stavness et al. 2011) to fit and track dynamic volumetric MRI data of a normal speaker, subsequently coupled to a source-filter based acoustic synthesizer. We demonstrate our model’s ability to track tongue tissue motion, simulate plausible muscle activation patterns, as well as generate acoustic results that have comparable spectral features to the associated recorded audio. Finally, we propose a method to adjust the spatial resolution of our subject-specific tongue model to match the fidelity level of our MRI data and speech synthesizer. Our findings suggest that a higher resolution tongue model – using similar muscle fibre definition – does not show a significant improvement in acoustic performance, for our speech utterance and at this level of fidelity; however we believe that our approach enables further refinements of the muscle fibres suitable for studying longer speech sequences and finer muscle innervation using higher resolution dynamic data.
Keywords: subject-specific modelling, inverse simulation, oropharynx, speech production, skinning
1. Introduction
Speech production is a complex neuromuscular human function that involves coordinated interaction of the oropharyngeal structures. Understanding the underlying neural motor control enhances the ability of speech therapists to diagnose and plan treatments of the various speech disorders, also known as speech impediments. The complexity of the problem increases dramatically considering the vast linguistic diversity in the human population. Experimental approaches to studying speech motor control rely on the analysis of measured data such as acoustic signals, medical images, and electromagnetic midsagittal articulometer (EMMA) and electromyography (EMG) recordings across the population. For example, ultrasound imaging can provide a real-time representation of the tongue surface (Wrench and Scobbie 2011); magnetic resonance imaging (MRI) can capture soft-tissue articulators (tongue, soft palate, epiglottis and lips) (Takano and Honda 2007); and dynamic tagged-MRI can capture movement dynamics by computing the displacement field of tissue points during consecutive repetitions of a speech utterance (Xing et al. 2013).
Such data motivates the use of computational approaches to model speech phenomena (Vasconcelos et al. 2012; Ventura et al. 2009, 2013). On one hand, articulatory speech synthesizers focus on the generated sound as the end product by designing a representation of the vocal folds and tract that is capable of generating the desired acoustics for an observed shape of the oral cavity (Doel et al. 2006; Birkholz et al. 2013). Biomechanical models, on the other hand, aim to simulate dynamics of speech production under biologically and physically valid assumptions about the articulators and motor control (Fang et al. 2009; Stavness et al. 2012). The search for the ideal model that represents both the acoustical and bimechanical characteristrics of the oropharynx continues to this date.
Generic models of the tongue, the main articulator in speech production, have been previously developed (Gerard et al. 2003; Dang and Honda 2004; Buchaillard et al. 2009) and incorporated in the simulation of speech movements (Perrier et al. 2003; Stavness et al. 2012). These models were further enhanced by coupling the jaw and hyoid (Stavness et al. 2011), and the face and skull (Badin et al. 2002; Stavness et al. 2014a). Deformable models of the vocal tract (Fels et al. 2006; Stavness et al. 2014b) were also proposed to enable fluid simulations and speech synthesis (See figure 1). To be clinically relevant, these generic models need to be simulated using some neurological or kinematic measurements such as EMG or EMMA recordings. However, available data is often specific to certain subjects that do not share the exact same geometry with the generic model. A similar issue manifests itself in the validation phase, prohibiting meaningful comparisons of the numeric results of simulation with the subject-specific measurements.
Figure 1.
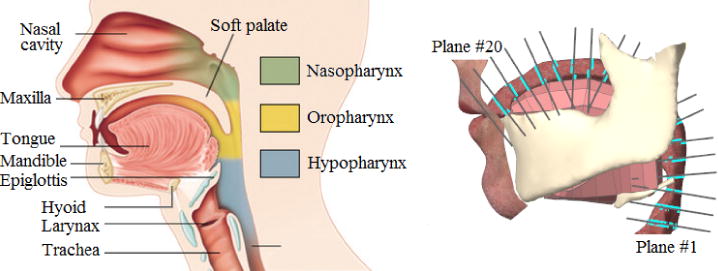
Head and neck anatomy (left) vs. the generic biomechanical model (Stavness et al. 2014a) available in ArtiSynth simulation framework (right).
To alleviate some of the aforementioned issues, one can perform heuristic registration of the subject data to the generic model (Fang et al. 2009; Sanchez et al. 2013) or restrict comparisons to average speech data reported in the literature (Stavness et al. 2012). While these approaches are valuable in providing a proof of concept, they are not suitable in a patient-specific medical setting. Subject-specific biomechanical modelling on the other hand addresses these issues while also enabling the investigation of the inter and intra-subject variability in speech production. In addition, it facilitates further development of a patient-specific platform for computer-assisted diagnosis and treatment planning of speech disorders. Unfortunately, the generation work-flow of the generic models is highly manual, tedious, non-trivial and hence, not suitable for creating subject-specific models at the time-scales required for clinical application.
Current methods for creating subject-specific biomechanical meshes can be organized under two categories: meshing and registration techniques. Meshing techniques tend to generate Finite Element (FE) models only based on a subject’s anatomy. Recently, a mixed-element FE meshing method proposed by Lobos et al. (2012) was shown to generate well-behaved meshes (that approximate anatomical boundaries well) with an adjustable resolution to fit different needs for simulation time and accuracy. However, the final mesh fails to offer the biomechanical information included in the current generic models such as muscle definitions and coupling attachments, and hence introduces prohibitive costs of redesigning these features for each subject’s model. Registration techniques on the other hand try to adapt the current generic models to fit the subject’s domain. Bucki et al. (2010b) proposed a finite element registration method to adapt the geometry of a generic model of the face (Nazari et al. 2010) to morphologies of different speakers segmented from computer tomography (CT) data (Stavness et al. 2014a). Their method includes a post-processing repair step that deals with the low-quality and irregular elements produced during the registration process. However, the repair step only grantees the minimum quality criteria for simulation in the FE simulation package, ANSYS (www.ansys.com, ANSYS, Inc., Canonsburg, PA,) and it was only proposed for hexahedral elements. Moreover, the configuration of the subject-specific FE, such as the design of the elements and the resolution of the mesh, is completely inherited from the generic model and is not under control of the user.
In this work, we propose subject-specific biomechanical modelling and simulation of the oropharynx for the purpose of speech production. Figure 2 shows the proposed work-flow. 3D dynamic MRI is acquired during the speech utterance a-geese (shown in the international phonetic alphabet (IPA) as /ə-gis/). Our approach to generating a subject-specific tongue model combines the advantages of both the registration and meshing approaches to enable adjusting the FE spatial resolution. Furthermore, we use the forward-dynamics tracking method to drive our model based on motion data that we extract from the tagged-MRI of a speech utterance. We finally solve a 1D implementation of the Navier-Stokes equations Doel et al. (2008), to explore the potential of our work-flow for generating acoustics. We then demonstrate that a higher-resolution FE tongue model does not show an appreciable improvement in acoustic performance for our speech utterance at the fidelity level of our MRI data and speech synthesizer.
Figure 2.
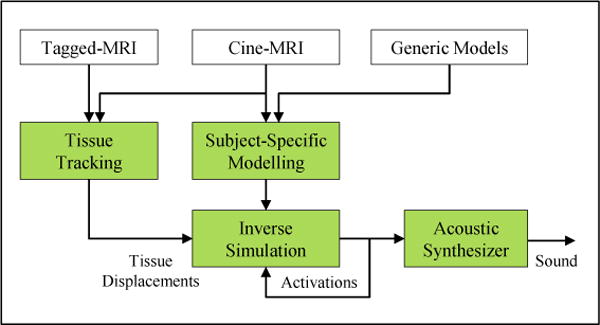
Proposed work-flow for subject-specific modelling and simulation of speech.
2. Multi-modal MRI Data and Tissue Tracking
Our MRI data captures a 22-year-old white American male with mid-Atlantic dialect repeating the utterance ageese to the metronome. Both cine and tagged MRI data were acquired using a Siemens 3.0T Tim-Treo MRI scanner with an 16-channel head and neck coil. The in-plane image resolution was 1.875mm ×1.875mm with the slice thickness of 6 mm. Other sequence parameters were repetition time (TR) 36 ms, echo time (TE) 1.47 ms, flip angle 6, and turbo factor 11. Isotropic super resolution MRI volumes were reconstructed using a Markov random field-based edge-preserving data combination technique, for both tagged and cine MRI and each of the 26 time frames (Woo et al. 2012) (see Figure 3).
Figure 3.
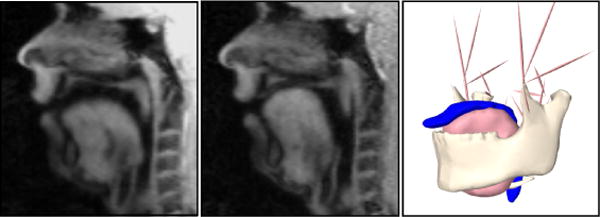
Midsagittal view of the 1st (left) and 17th (middle) time-frame of cine-MRI accompanied with the segmented surfaces of tongue, jaw, hyoid and airway from the 1st time-frame (right).
Points on the tongue tissue were tracked by combining the estimated motion from tagged-MRI and the surface information from cine-MRI. A 3D dense and incompressible deformation field was reconstructed from tagged-MRI based on the harmonic phase algorithm (HARP). The 3D deformation of the surface was computed using diffeomorphic demons (Vercauteren et al. 2009) in cine-MRI. The two were combined to obtain a reliable displacement field both at internal tissue points and the surface of the tongue (Xing et al. 2013).
The tissue trajectories calculated from tagged MRI may still introduce some noise to the simulation, due to registration errors or surface ambiguities. We perform spatial and temporal regularization to reduce the noise. In the spatial domain, we average the displacements vectors of neighbouring tissue points in a spherical region around each control point (FE nodes of the tongue). In the time domain, we pick 6 key frames of the speech utterance and perform a cubic interpolation over time to find the intermediate displacements.
3. Biomechanical Modelling of Oropharynx
We build our subject-specific model based on the information available in the generic model of the oropharynx which is available in the ArtiSynth Simulation framework (www.artisynth.org) and described in Stavness et al. (2011, 2012, 2014a,b). Our model includes the FE biomechanical model of the tongue coupled with the rigid-body bone structures such as mandible, maxilla and hyoid, and attached to a deformable skin for the vocal tract.
3.1 Tongue
The generic FE model of the tongue is courtesy of Buchaillard et al. (2009); it provides 2493 DOFs (946 nodes and 740 elements) and consists of 11 pairs of muscle bundles with bilateral symmetry1. We refer to this generic model as FEgen in the rest of this article.
To create our subject-specific model, we first delineate the surface geometry of the tongue in the first time-frame of the cine-MRI volume – which bears the most resemblance to the neutral position – using the semi-automatic segmentation tool TurtleSeg (Top et al. 2011). We refer to this surface mesh by S. We then proceed by creating two versions of FE tongue model for our subject; our first tongue model (FEreg) is the result of registration of FEgen to S. We use a multi-scale, iterative and elastic registration method called Mesh-Match-and-Repair (Bucki et al. 2010a). The registration starts by matching the two surfaces first, followed by the application of the 3D deformation field to the inner nodes of the generic model via interpolation. A follow-up repair step compensates for possible irregularities of the elements. Note that the elements of FEreg – similar to FEgen – are aligned along the muscle fibres. Therefore the size of the elements depend directly on the density of the muscle fibres in each region of the model. This will result in smaller elements at the anterior inferior region of the tongue – where most fibres originate – and larger elements close to the dorsum of the tongue – where most fibres span into the tongue’s body. Unfortunately, the low resolution elements are located at the region undergoing maximum deformation during speech.
To address our concerns about the resolution of FEreg, we generate our second tongue model (FEhigh) following the pipeline shown in figure 4. First, we use a meshing technique proposed by Lobos et al. (2012) to generate a regular mixed-element FE mesh, referred to as FEmesh. The meshing algorithm starts with an initial grid of hexahedra elements that encloses the surface mesh S. It then gets rid of the elements that present no or small intersection with S, employing a set of mixed-element patterns to fill the generated holes at the surface boundary. Finally, the quality of the mesh is improved using the Smart Laplacian filter (Freitag and Plassmann 2000). FEmesh bares our desired resolution (2841 nodes and 3892 elements) and is well-behaved during simulation. We further augment FEmesh with the definition of muscle bundles available in FEreg: since both FE models are in the same spatial domain, we simply copy the bundle locations from FEreg to FEmesh, replacing their corresponding elements with those of FEmesh who fall into the bundle’s spatial domain. Note that our approach for generating FEhigh provides multiple fundamental advantages over using FEreg. Firstly, we, as the user, have control over the resolution of the mesh. Secondly, the muscle fibre definitions is no longer tied to the configuration of the elements, therefore it is possible to modify the muscle fibres based on different linguistic hypothesis and preferences.
Figure 4.
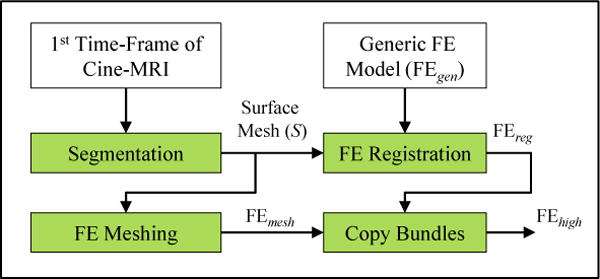
Proposed pipeline for generating high resolution subject-specific FE model of the tongue (FEhigh).
Each muscle bundle in tongue can be further divided into smaller functionally-distinct fibre groups, referred to as functional segments, which are believed to be controlled quasi-independently in a synergistic coordination (Stone et al. 2004). We divide the vertical (GG, VRT) and horizontal (TRNS) muscle fibres into five functional segments (a: posterior to e: interior), as initially proposed by Miyawaki et al. (1975) based on EMG measurements from GG, and later reinforced by Stone et al. (2004) using ultrasound imaging and tagged-MRI information. We also follow Fang et al. (2009) in dividing STY into two functional segments, STYa (the anterior part within the tongue) and STYp (originating from the posterior tongue to the styloid process). Note that FEgen includes only three functional segments for GG and one functional segment for each of TRNS, VRT or STY (Buchaillard et al. 2009).
We use the Blemker muscle model to account for nonlinearity, incompressibility and hyperelasticity of the tongue tissue (Blemker et al. 2005). We use a fifth-order Mooney-Rivlin material as described by Buchaillard et al. (2009). The strain energy, W, is described as:
| (1) |
where I1 is the first invariant of the left Cauchy-Green deformation tensor, C10 and C20 are the Mooney-Rivlin material parameters and the term κ(lnJ)2 reinforces the incompressibility. We used C10 = 1037 Pa and C20 = 486 Pa that was measured by Gerard et al. (2003) from a fresh cadaver tongue and scaled by a factor of 5.4 to match the invivo experiments (Buchaillard et al. 2009). We set the Bulk modulus κ = 100×C10 to provide a Poisson’s ratio close to 0.499. Tongue tissue density was set to 1040 kg.m−3, close to water density. In addition, We used Rayleigh damping coefficients β = 0.03s and α = 40s−1 to achieve critically damped response for the model.
3.2 Jaw and Hyoid
Our subject-specific model of jaw and hyoid has similar biomechanical configuration as the ArtiSynth generic model (Stavness et al. 2011): we couple our tongue FE model with the mandible and hyoid rigid-bodies via multiple attachment points that are included in the form of bilateral constraints in the constitutive equations of the system. We include eleven pairs of bilateral point-to-point Hill-type actuators to activate the mandible and hyoid1 and model the temporomandibular joint by curvilinear constraint surfaces. We set bone density to 2000 kg/m3 as used by Dang and Honda (2004).
To create our subject-specific geometries, we need to segment the bone surfaces from the first time-frame of cine-MRI. However, since bone is partially visible in MRI, the manually segmented surfaces are not complete nor of sufficient quality for detecting sites of muscle insertions. We thus register the generic model of mandible and hyoid bone to their corresponding partial segmented surface using the coherent point drift (CPD) algorithm (Myronenko et al. 2010), which benefits from a probabilistic approach suitable for non-rigid registration of two point clouds. The method is robust in the presence of outliers and missing points.
3.3 Vocal Tract
The vocal tract is modelled as a deformable air-tight mesh – referred to as skin – which is coupled to the articulators (Stavness et al. 2014b). Each point on the skin is attached to one or more master components, which can be either 3-DOF points, such as finite-element nodes, or 6-DOF frames, such as rigid body coordinates. The position of each skin vertex, qv, is calculated as a weighted sum of contributions from each master component:
| (2) |
where is the initial position of the skinned point, is the collective rest state of the masters, wi is the skinning weight associated with the ith master component, and fi is the corresponding blending function. for a point master –such as a FE node – the blending function, fi, is the displacement of the point. For frames – such as rigid bodies – fi is calculated by linear or dual-quaternion linear blending. To provide two-way coupling between the skinned mesh and articulators, the forces acting on the skin points are also propagated back to their dynamic masters.
To create the skin, we initially segment the shape of the vocal tract from the first time-frame of cine-MRI. The skin is attached to and deforms along with the motion of the mandible rigid-body and tongue FE model. We also restrict the motion of the vocal tract to the fixed boundaries of Maxilla and pharyngeal wall.
4. Inverse Simulation
Forward dynamic simulation requires fine tuning of the muscle activations of the model over time. EMG recordings of the tongue were used before (Fang et al. 2009) but they suffer from lack of suitable technology to deal with the moist surface and the highly deformable body of the tongue (Yoshida et al. 1982). Also, the relationship between EMG signal and muscle forces is not straight forward. As an alternative, muscle activations can be predicted from the available kinematics by solving an inverse problem. The results may be further fed to a forward simulation system to provide the necessary feedback to the inverse optimization process. The forward-dynamics tracking method was initially introduced for musculoskeletal systems (Erdemir et al. 2007); Later on, Stavness et al. (2012) expanded the method to the FE models with muscular hydrostatic properties – such as the tongue – that are activated without the mechanical support of a rigid skeletal structure.
In ArtiSynth, the system velocities, u, are computed in response to the active and passive forces:
| (3a) |
| (3b) |
where M is the mass matrix of the system and Λ denotes a nonlinear function of the system positions, q, and the system velocities, u, that relates the muscle activation, a, to the active forces. The inverse solvers uses a a sub-space, v, of the total system velocities as its target: v = Jmu where the target velocity sub-space v is related to the system velocities u via a Jacobian matrix Jm. The inverse solver computes the normalized activations a, by solving a quadratic program subject to the condition 0 ≤ a ≤ 1:
| (4) |
Here ‖a‖ and denote the norm and time-derivative of the vector a; the matrix H summarizes the biomechanical characteristics of the system such as mass, joint constraints and force-activation properties of the muscles; α and β are ℓ2 regularization and damping coefficients. The regularization term deals with muscle redundancy in the system and opts for the solution that minimizes the sum of all activations. The damping term secures system stabilities by prohibiting sudden jumps in the value of activations. The solution converges after iterating between inverse and forward dynamics in a static per time-step process, where the system is simplified to be linear in each integration step. The method is computationally efficient compared to the static methods; however it may lead to sub-optimal muscle activations (Stavness et al. 2012).
5. Acoustic Synthesizer
Articulatory speech synthesizers generate sound based on the biomechanics of speech in the upper airway. Vibration of the vocal folds under the expiatory pressure of the lungs is the source in the system. The vocal tract, consisting of the larynx, pharynx, oral and nasal cavities, constitutes the filter where sound frequencies are shaped. A widely-used physical acoustic model for the vocal tract is a 1D tube, described by an area function A (x, t) where 0 ≤ x ≤ L is the distance from the glottis on the tube axis and t denotes the time.≤ Let ≤ , û and denote the physical quantities of the pressure, air velocity and air density in the tube respectively. As described by Doel et al. (2008), we define the pressure deviation, , and the volume-velocity, u(x, t) = Aû/c, where ρ0 is the average mass density of the air, c is the speed of sound.
We solve for u(x, t) and p(x, t) in the tube using the equation of continuity (5a) in conjunction with the linearised NavierStokes equation (5b):
| (5a) |
| (5b) |
| (5c) |
The right-hand side of (5a) denotes the damping loss of the system. Doel et al. (2008) used d(A) = d0A−3/2 and D(A) = D0−3/2 with the coefficient d0 = 1.6 ms−1 and D0 = 0.002 m3s−1 being empirically set to match the loss function of a hard-wall circular tube in the frequency range of the speech: 250Hz ≤ f ≤ 2000Hz. Equation (5c) indicates the boundary conditions of the system where the volume-velocity u equals to the prescribed volume velocity source ug at the glottis and the pressure deviation p equals to zero at outside the lips. Equation (5) was solved for a dynamic tube using a fast finite volume method, which was shown to be as accurate as a full solution.
We couple the vocal tract to a two-mass glottal model proposed by Ishizaka and Flanigan et al. (1972), which calculates the volume velocity ug in response to lung pressure and tension parameters in the vocal cords. The model was extended to include a lip radiation and a wall vibration model. Solving (5) in the frequency domain will lead to U(w) = T(w)Ug(w) where the Fourier transform is denoted by capitalization, e.g., the Fourier transform of u is U with w the radial frequency. T(w) is the transfer function of the resonating tube which is represented as a digital ladder filter defined based on the cross-sectional areas of 20 segments of the vocal tract. We refer to Doel et al. (2008) for full details on the implementation. The approach is similar to the one proposed by Birkholz (2005) but uses a different numerical integration method.
The frequencies associated with the peaks in ‖T(w)‖ known as formants, are used to define distinct phonemes of speech. In particular, the value of the first(F1)/second(F2) formant is mainly determined by the height/backness-frontness of the tongue body. This means that F1 has a higher frequency for an open vowel (such as /a/) and a lower frequency for a close vowel (such as /i/); and the second formant F2 has a higher frequency for a front vowel (such as /i/) and a lower frequency for a back vowel (such as /u/) (Ladefoged 2001).
In our model, we manipulate the shape of the vocal tract using the muscle activations computed from the inverse simulation. To define A(x, t), we calculate the intersections of our deformable vocal tract with 20 planes evenly distributed along the airway from below the epiglottis (#1) to the lips (#20). We update the center line position and make sure that the planes stay orthogonal to it during the simulation. Note that we refer to the plan located (See figure 1).
6. Results and Discussion
In our experiments, we compare the performance of our model using the two versions of the subject-specific tongue model FEreg and FEhigh that we described in section 3.1. We evaluate our simulation results from three perspectives: morphology, activations and acoustics. We used 21 and 28 target points for FEreg and FEhigh respectively, in the left half of the tongue, while enabling bilateral symmetric muscle excitation. Our proposed distribution of the target points provides adequate tracking information for each individual muscle, and does not overly constrain a single element. Our average tracking error, defined as the distance between the position of the target points in our simulation and in the tagged-MRI, was 1.15mm ± 0.632 using FEreg and 1.04mm ± 0.44 using FEhigh which in both cases is within the accuracy range of the tagged-MRI.
6.1 Muscle Activation
Figure 5 shows the estimated muscle activations of the tongue (FEhigh), jaw and hyoid for the speech utterance /ə-gis/. The motion from /ə/ to /g/ requires the jaw to close and the tongue body to move upward in a large excursion. The jaw muscles move mostly in unison consistent with closing the jaw for /g/, slightly opening it for /i/ and closing it again for /s/. The model identifies several tongue muscles as active for the motion into /g/ and /i/, including GGa,b, VRTa,b, STYa,p, and TRNS(exc-d), all of which help to elevate the tongue body. With STYp decreasing and GGb increasing for /i/ to allow the tongue’s forward motion. The motion into the /s/ provides an interesting muscle activation pattern. Motion from /i/ to /s/ mostly involves lowering and moving the tongue body down and back, unlike motion from a low vowel position into /s/. Thus GGb, which is the most active muscle during /i/, completely deactivates for /s/ allowing the posterior tongue to relax backward into the pharynx. This motion is checked by GGa, and VRTa, which increase activation during /s/ to ensure that there is not too much backing of the tongue root into the pharynx, especially as the subject is lying supine.
Figure 5.
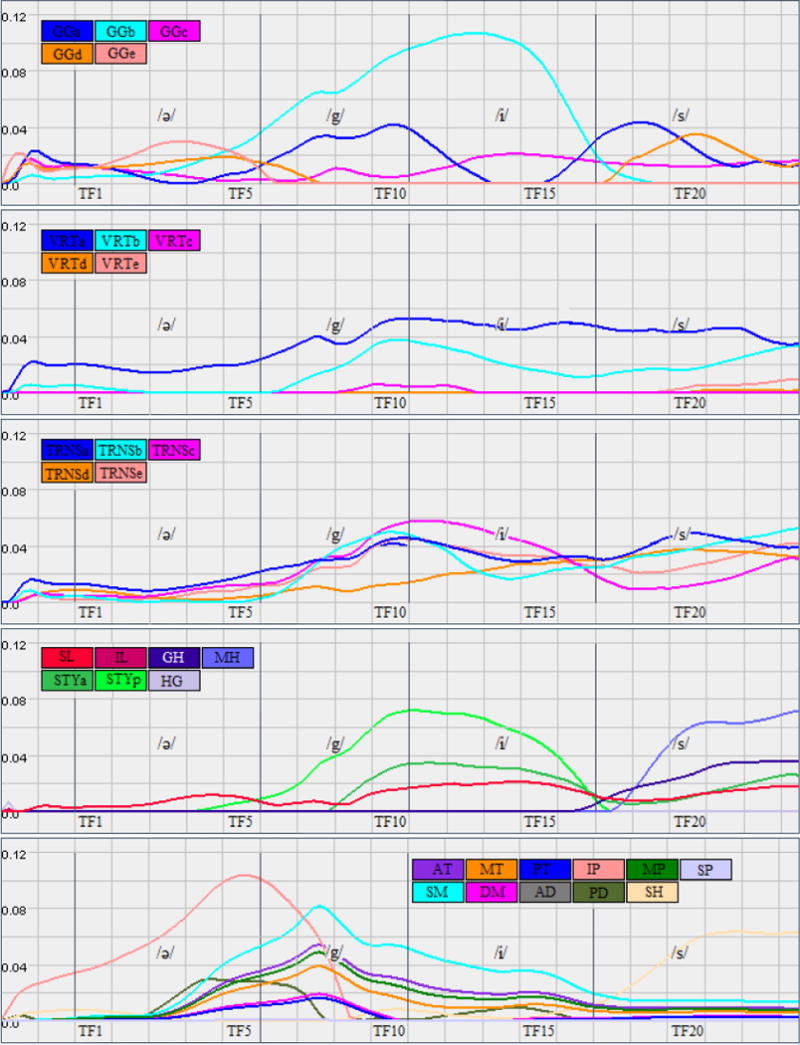
Simulation result: estimated muscle activations of the tongue (FEhigh), jaw and hyoid for the speech utterance /ə-gis/.
Several activations appear to occur in order to counteract the effects of gravity in this supine position. VRTa,b and GGc are active throughout the entire word, which pulls the pharyngeal tongue and root forward, possibly to overcome the effects of gravity in this supine position. Similarly, TRNS is active throughout the word and increases for the /s/. Combined with VRT, TRNS stiffens, and protrudes the tongue, which would further protect the airway from too much tongue backing. Similarly, MH begins activation only for the /s/; it elevates the entire tongue and keeps it from lowering too much.
To form a proper /s/ a continuous groove needs to form along the centre of the tongue, and to narrow anteriorly. GGa creates a groove in the tongue root, to funnel the air anteriorly. The activation of VRTa may facilitate maintenance of a wide groove in this region. GGd pulls down the mid-line tongue dorsum in the palatal region, but it is not accompanied by VRTc or d. The use of GGd only is consistent with the narrowing of the central groove as the air is channelled forward and medially. TRNS also prevents too wide a groove in the tongue by pulling in the lateral margins of the tongue assuring contact with the palate and channelling of the air forward onto the front teeth for /s/. New muscle activations, arising after /s/ begins, continue refining the tongue position by elevating and moving the tongue anteriorly for the upcoming inhalation; these muscles are MH, GH, SL, STYa.
Table 1 provides a summary of main active muscles in the utterance a-geese using FEhigh and FEreg. Note that both FEhigh and FEreg are using the same fibre definition for the functional segments of each muscle. Both simulations result in similar pattern of activations with exception to some muscles such as VRTc-e and TRNSd. Considering the lack of a verified ground truth to compare to, we conclude that the results corroborate each other and hence a lower resolution tongue model is sufficient for the fidelity of our dynamic image data.
Table 1.
Summary of the active muscles calculated by the inverse solver during simulation of the speech utterance /ə-gis/ using FEhigh and FEreg.
| Tongue Muscles | Jaw Muscles | |||
|---|---|---|---|---|
| Phoneme | FEhigh | FEreg | FEhigh | FEreg |
| /ə/ | GGd,e, VRTa | GGc-e | IP, SM, AT, MP, MT | IP |
| /g/ | GGa,b, STYa,p, TRNS, VRTa,b | GGa-c, STYp, TRNS, VRTa,b, SL | SM, AT, MP, MT | SM, AT, MP, IP, SM |
| /i/ | GGb, VRTa, TRNS, STY | GGa-c, VRTb, TRNS, STY | SM | SM, AT, PD, MT, MP |
| /s/ | MH, GH, GGa,d, VRTa,b, TRNS | GGa,d, MH, VRTa,d, TRNS, GH | MT | SH |
6.2 Acoustics
The vocal folds oscillate during vowels and voiced constants (e.g., /m/ or /n/), but are wide open and of no effect in fricatives (e.g., /s/) and stops like /g/. Constrictions or obstructions at certain points in the tract create turbulence that generates high frequency noise responsible for making the fricatives and stops. The synthesis of fricatives depends highly on lung pressure and noise characteristics of the system. Due to the lack of voicing information, we solely focus our acoustic analysis on synthesis of the vowels, specifically /i/in/ə-gis/. The reduced vowel/ə/is only used to help the subject put his tongue in a neutral posture at the start of the speech utterance.
Figure 6 shows the acoustic profile and spectrum of a single repetition of /ə-gis/ as spoken by our subject. As the ground truth, we measure the formant frequencies at the mid-point of the time interval /i/ of the audio signal. We also use the acoustic measurements of the vocal tract mesh that we manually segment from 17th time-frame of the cine-MRI data (corresponding to /i/). Table 2 compares the formant frequencies of our simulations with those of the cine-MRI and audio data. Note that the F2 value calculated from the Cine-MRI data is 9.5% less than the value measured from the audio signal. Possible reasons include ambiguity in MRI segmentation of the vocal tract (close to the teeth, and at posterior pharyngeal side-branches) as well as error caused by the speech synthesizer due to its simplified 1D fluid assumption.
Figure 6.
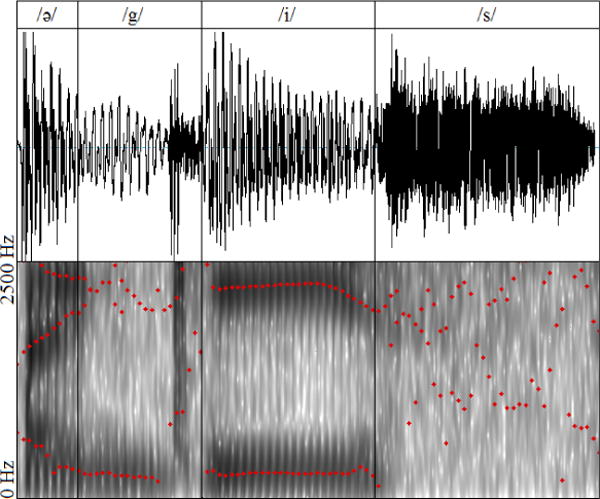
The audio signal and spectra for one repetition of the speech utterance /ə-gis/ as spoken by our subject. The formants are shown in red dots associated with each time instants of audio using Praat phoneme analysis software (Boersma and Weenink 2005).
Table 2.
Simulation result: formant frequencies of the vowel /i/ compared to the audio and cine-MRI data.
| Audio | Cine-MRI | FEreg | FEhigh | |
|---|---|---|---|---|
| F1(Hz) | 268 | 267 | 262 | 256 |
| F2(Hz) | 2272 | 2055 | 1905 | 1995 |
Finally, figure 7 shows the normalized area profile along the vocal tract at /i/ in our simulation compared to the cine-MRI data. Note how both FEreg and FEhigh tongue models are able to capture the expected shape of the vocal tract. The noticeable mismatches happen at the areas that are influenced by lips, soft palate and epiglottis which were not included in our model.
Figure 7.
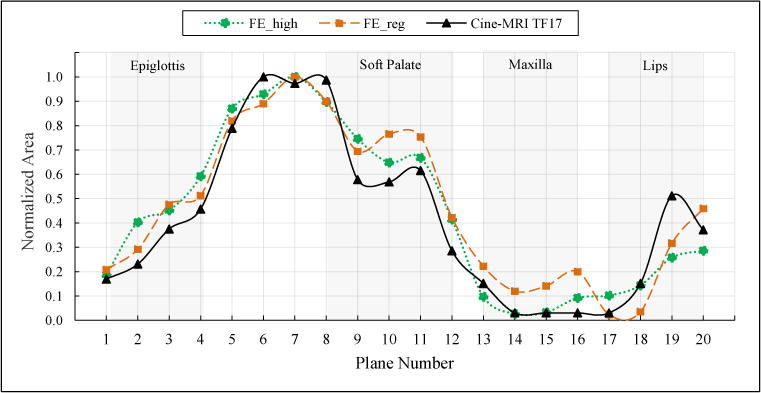
Simulation result: normalized profile of area functions along the vocal tract for the vowel /i/ compared to the cine-MRI at time-frame 17.
These quantitative results suggest that FEreg and FEhigh do not show an appreciable difference in acoustic performance for the simulation of the utterance /ə-gis/ using our source-filter based speech synthesizer (Doel et al. 2008). Thus we conclude that the ArtiSynth generic tongue model proposed by Buchaillard et al. (2009) provides sufficient resolution for subject specific modelling of this utterance at this level of acoustic fidelity and cine-MRI resolution.
7. Conclusion
In this paper, we proposed a framework for subject-specific modelling and simulation of the oropharynx in order to investigate the biomechanics of speech production such as motor control. Our approach for creating the tongue model combines the meshing and registration techniques to benefit from a state-of-the-art generic model (Buchaillard et al. 2009) while providing the opportunity to adjust the resolution and modify the muscle definitions. We further coupled our biomechanical model with a source-filter based speech synthesizer using a skin mesh for the vocal tract. We showed that our model is able to follow the deformation of the tongue tissue in tagged-MRI data, estimating plausible muscle activations, along with acceptable acoustic responses. Our quantitative acoustic results did not show appreciable difference between our low and high resolution FE tongue models; and both models resulted in similar activation patterns.
We believe, however, that our approach for generating FEhigh offers benefits that can be fully investigated in the future. Firstly, we suggest that a higher resolution tongue model provides the opportunity to simulate more complex and longer speech utterances that exhibit more variability in tongue shape. Swallowing is another example where more local tongue motions are observed. Secondly, our proposed approach offers structural independence between the configuration of muscle fibres and finite elements. Hence, it enables the user to modify, add, or delete individual muscle fibres to accommodate more subtlety in neural innervation, as suggested by Slaughter et al. (2005) for IL, SL, and by Mu and Sanders (2000) for GG. A finer fibre structure is also useful in studying different languages where sounds are similar, but not identical. In addition, being able to edit the fibres is beneficial for simulation of speech in disorders such as glossectomy, where the innervation pattern varies based on the missing tissue (Chuanjun et al. 2002). Finally, as resolution of dynamic MRI data improves, we will be able to capture finer shapes of the tongue and, hence, our model should be positioned to present more details. In addition, we suggest that a more advanced speech synthesizer that would solve a set of three dimensional fluid equations, would better account for the acoustics differences between our low and high-resolution FE tongue models.
In the future, we plan to adapt the generic ArtiSynth models of the lips, soft palate and epiglottis into our subject-specific platform and perform more inter and intra-subject experiments using different speech utterances.
Acknowledgments
This work is funded by Natural Sciences and Engineering Research Council of Canada (NSERC), NSERC-Collaborative Health Research Project (CHRP), Network Centre of Excellence on Graphics, Animation and New Media (GRAND) and National Institutes of Health-National Cancer Institute, NIH-R01-CA133015.
Footnotes
Genioglossus anterior (GGA), medium (GGM), posterior (GGP); hyoglossus(HG); styloglossus (STY); inferior longitudinal(IL); verticalis (VRT); transverses (TRNS); geniohyoid (GH); mylohyoid (MH); superior longitudinal(SL).
Mylohyoid: anterior (AM), posterior (PM); temporal: anterior (AT), middle (MT), posterior (PT); masseter: superficial (SM), Deep (DM); pterygoid: medial (MP), superior-lateral (SP), inferior-lateral (IP); digastric: anterior (AD), posterior (PD); stylohyoid (SH).
References
- Badin P, Bailly G, Reveret L, Baciu M, Segebarth C, Savariaux C. Three-dimensional linear articulatory modelling of tongue, lips and face, based on MRI and video images. J Phonetics. 2002;30(3):533–553. [Google Scholar]
- Birkholz P. Ph.D. thesis. Universitat Rostock; 2005. 3D-Artikulatorische Sprachsynthese. [Google Scholar]
- Birkholz P. Modeling Consonant-Vowel Coarticulation for Articulatory Speech Synthesis. PLoS ONE. 2013;8(4):e60603. doi: 10.1371/journal.-pone.0060603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J Biomech. 2005;38(4):657–665. doi: 10.1016/j.jbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Boersma P, Weenink D. Praat: doing phonetics by computer (Version 4.3.01) [Computer program] 2005 Retrieved from http://www.praat.org/
- Buchaillard S, Perrier P, Payan Y. A biomechanical model of cardinal vowel production: Muscle activations and the impact of gravity on tongue positioning. J Acoust Soc Am. 2009;126:2033–2051. doi: 10.1121/1.3204306. [DOI] [PubMed] [Google Scholar]
- Bucki M, Lobos C, Payan Y. A fast and robust patient specific finite element mesh registration technique: application to 60 clinical cases. Med Image Anal. 2010;13(3):303–317. doi: 10.1016/j.media.2010.02.003. [DOI] [PubMed] [Google Scholar]
- Bucki M, Nazari MA, Payan Y. Finite element speaker-specific face model generation for the study of speech production. Comput Meth Biomech Biomed Eng. 2010;13(4):459–467. doi: 10.1080/10255840903505139. [DOI] [PubMed] [Google Scholar]
- Chuanjun C, Zhiyuan Z, Shaopu G, Xinquan J, Zhihong Z. Speech after partial glossectomy: a comparison between reconstruction and nonreconstruction patients. J Oral Maxillofac Surg. 2002;60(4):404–407. doi: 10.1053/joms.2002.31228. [DOI] [PubMed] [Google Scholar]
- Dang J, Honda K. Construction and control of a physiological articulatory model. J Acoust Soc Am. 2004;115:853–870. doi: 10.1121/1.1639325. [DOI] [PubMed] [Google Scholar]
- Doel K van den, Vogt F, English RE, Fels S. Towards Articulatory Speech Synthesis with a Dynamic 3D Finite Element Tongue Model. Proceeding of the 7th Intentional Seminar on Speech Production; Ubatuba, Brazil. 2006. [Google Scholar]
- Doel K van den, Ascher UM. Real-time numerical solution of Webster’s equation on a non-uniform grid. IEEE Trans Audio Speech Lang Processing. 2008;16:1163–1172. [Google Scholar]
- Erdemir A, McLean S, Herzog W, van den Bogert AJ. Model-based estimation of muscle forces exerted during movements. Clin Biomech. 2007;22(2):131–154. doi: 10.1016/j.clinbiomech.2006.09.005. [DOI] [PubMed] [Google Scholar]
- Fang Q, Fujita S, Lu X, Dang J. A model-based investigation of activations of the tongue muscles in vowel production. Acoust Sci Tech. 2009;30(4):277–287. [Google Scholar]
- Fels S, Vogt F, Doel K van den, Lloyd J, Stavness I, Vatikiotis-Bateson E. Developing Physically-Based, Dynamic Vocal Tract Models using ArtiSynth. Proceeding of the 7th Intentional Seminar on Speech Production; Ubatuba, Brazil. 2006. [Google Scholar]
- Freitag L, Plassmann P. Local optimization-based simplicial mesh untangling and improvement. Int J Numer Meth Eng. 2000;49(12):109125. [Google Scholar]
- Grard JM, Wilhelms-Tricarico R, Perrier P, Payan Y. A 3D Dynamical Biomechanical Tongue Model to Study Speech Motor Control. arXiv preprint physics/0606148. [Google Scholar]
- Hong BW, Prados E, Vese L, Soatto S. Shape representation based on integral kernels: application to image matching and segmentation. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; New York (NY), USA. 2006. [Google Scholar]
- Ishizaka K, Flanigan JL. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Syst Tech J. 1972;51:12331268. [Google Scholar]
- Ladefoged P. Vowels and consonants. Phonetica. 2001;58:211–212. [Google Scholar]
- Lobos C. A set of mixed-elements patterns for domain boundary approximation in hexahedral meshes. Stud Health Technol Inform. 2012;184:268–272. [PubMed] [Google Scholar]
- Miyawaki O, Hirose H, Ushijima T, Sawashima M. A preliminary report on the electromyographic study of the activity of lingual muscles. Ann Bull RILP. 1975;9(91):406. [Google Scholar]
- Mu L, Sanders I. Neuromuscular specializations of the pharyngeal dilator muscles: II. Compartmentalization of the canine genioglossus muscle. Anat Rec. 2000;260(3):308–325. doi: 10.1002/1097-0185(20001101)260:3<308::AID-AR70>3.0.CO;2-N. [DOI] [PubMed] [Google Scholar]
- Myronenko A, Song X. Point set registration: Coherent point drift. IEEE Trans Pattern Anal Mach Intell. 2010;32(12):2262–2275. doi: 10.1109/TPAMI.2010.46. [DOI] [PubMed] [Google Scholar]
- Nazari MA, Perrier P, Chabanas M, Payan Y. Simulation of dynamic orofacial movements using a constitutive law varying with muscle activation. Comput Methods Biomech Biomed Eng. 2010;13(4):469–482. doi: 10.1080/10255840903505147. [DOI] [PubMed] [Google Scholar]
- Perrier P, Payan Y, Zandipour M, Perkell J. Influences of tongue biomechanics on speech movements during the production of velar stop consonants: A modeling study. Acoust. 2003;114(3):1582–1599. doi: 10.1121/1.1587737. [DOI] [PubMed] [Google Scholar]
- Sanchez CA, Stavness I, Lioyd J, Fels S. Forward dynamics tracking simulation of coupled multibody and finite element models: Application to the tongue and jaw. Proceedings of the 11th International Symposium on Computer Methods in Biomechanics and Biomedical Engineering.2013. [Google Scholar]
- Slaughter K, Li H, Sokoloff AJ. Neuromuscular Organization of the Superior Longitudinalis Muscle in the Human Tongue. Cells Tissues Organs. 2005;181:51–64. doi: 10.1159/000089968. [DOI] [PubMed] [Google Scholar]
- Stavness I, Lloyd JE, Payan Y, Fels S. Coupled hard-soft tissue simulation with contact and constraints applied to jaw-tongue-hyoid dynamics. Int J Numer Method Biomed Eng. 2011;27(3):367–390. [Google Scholar]
- Stavness I, Lloyd J, Fels S. Automatic Prediction of Tongue Muscle Activations using a Finite Element Model. J Biomech. 45(16):2841–2848. doi: 10.1016/j.jbiomech.2012.08.031. [DOI] [PubMed] [Google Scholar]
- Stavness I, Nazari MA, Flynn C, Perrier P, Payan Y, Lloyd JE, Fels S. Coupled Biomechanical Modeling of the Face, Jaw, Skull, Tongue, and Hyoid Bone. In: Magnenat-Thalmann N, Ratib O, Choi HF, editors. 3D Multiscale Physiological Human. Springer; London: 2014. pp. 253–274. [Google Scholar]
- Stavness I, et al. Unified Skinning of Rigid and Deformable Models for Anatomical Simulations. Proceeding of ACM SIGGRAPH Asia; Shenzhen, China. 2015. [Google Scholar]
- Stone M, Epstein MA, Iskarous K. Functional segments in tongue movement. Clin Linguist Phons. 2004;18(6):507–521. doi: 10.1080/02699200410003583. [DOI] [PubMed] [Google Scholar]
- Takano S, Honda K. An MRI analysis of the extrinsic tongue muscles during vowel production. Speech Comm. 2007;49(1):49–58. [Google Scholar]
- Top A, Hamarneh G, Abugharbieh R. Active learning for interactive 3d image segmentation. Proceedings of the 14th International Conference on Medical Image Computing and Computer Assisted Intervention; Toronto, Canada. 2011. [DOI] [PubMed] [Google Scholar]
- Vasconcelos MJ, Ventura SM, Freitas DR, Tavares JMR. Inter-speaker speech variability assessment using statistical deformable models from 3.0 Tesla magnetic resonance images. P I MECH ENG G-J AER. 2012;226(3):185–196. doi: 10.1177/0954411911431664. [DOI] [PubMed] [Google Scholar]
- Ventura SR, Freitas DR, Tavares JMR. Application of MRI and biomedical engineering in speech production study. Comput Methods Biomech Biomed Engin. 2009;12(6):671–681. doi: 10.1080/10255840902865633. [DOI] [PubMed] [Google Scholar]
- Ventura SR, Freitas DR, Ramos IMA, Tavares JMR. Morphologic differences in the vocal tract resonance cavities of voice professionals: an MRI-based study. J Voice. 2013;27(2):132–140. doi: 10.1016/j.jvoice.2012.11.010. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: Efficient non-parametric image registration. Neuroimage. 2009;45(1):6-1–72. doi: 10.1016/j.neuroimage.2008.10.040. [DOI] [PubMed] [Google Scholar]
- Woo J, Murano E, Stone M, Prince J. Reconstruction of High Resolution Tongue Volumes from MRI. IEEE Trans Biomed Eng. 2012;6(1):1–25. doi: 10.1109/TBME.2012.2218246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wrench AA, Scobbie JM. Very high frame rate ultrasound tongue imaging. Proceedings of the 9th International Seminar on Speech Production; Strasbourg, France. 2011. [Google Scholar]
- Xing F, Woo J, Murano EZ, Lee J, Stone M, Pronce JL. 3d Tongue Motion from Tagged and Cine MR Images. Proceeding of the 16th International Conference on Medical Image Computing and Computer-Assisted Intervention; Nagoya, Japan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida K, Takada K, Adachi S, Sakuda M. Clinical Science EMG Approach to Assessing Tongue Activity Using Miniature Surface Electrodes. J Dent Res. 1982;61(10):1148–1152. doi: 10.1177/00220345820610100701. [DOI] [PubMed] [Google Scholar]


