Brain Extracellular Space: The Final Frontier of Neuroscience

Abstract

Brain extracellular space is the narrow microenvironment that surrounds every cell of the central nervous system. It contains a solution that closely resembles cerebrospinal fluid with the addition of extracellular matrix molecules. The space provides a reservoir for ions essential to the electrical activity of neurons and forms an intercellular chemical communication channel. Attempts to reveal the size and structure of the extracellular space using electron microscopy have had limited success; however, a biophysical approach based on diffusion of selected probe molecules has proved useful. A point-source paradigm, realized in the real-time iontophoresis method using tetramethylammonium, as well as earlier radiotracer methods, have shown that the extracellular space occupies ∼20% of brain tissue and small molecules have an effective diffusion coefficient that is two-fifths that in a free solution. Monte Carlo modeling indicates that geometrical constraints, including dead-space microdomains, contribute to the hindrance to diffusion. Imaging the spread of macromolecules shows them increasingly hindered as a function of size and suggests that the gaps between cells are predominantly ∼40 nm with wider local expansions that may represent dead-spaces. Diffusion measurements also characterize interactions of ions and proteins with the chondroitin and heparan sulfate components of the extracellular matrix; however, the many roles of the matrix are only starting to become apparent. The existence and magnitude of bulk flow and the so-called glymphatic system are topics of current interest and controversy. The extracellular space is an exciting area for research that will be propelled by emerging technologies.

Main Text

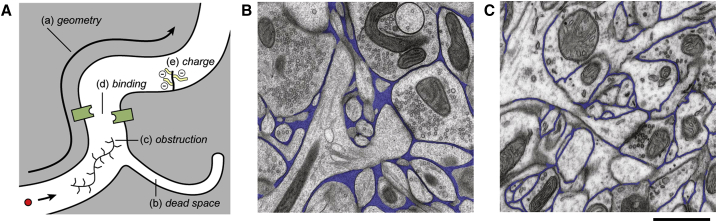
It is fitting that the title paraphrases the opening voiceover from Star Trek V because the extracellular space (ECS) is still largely unknown territory that is ripe for exploration with new technologies. The narrow spaces between the cells of the central nervous system have been a topic of fascination and frustration to a small number of investigators since the 1960s. Having a width estimated in tens of nanometers, the spaces are below the resolution of light microscopy yet they are obliterated by most conventional electron microscopic procedures. Using specialized fixation techniques, electrophysiological methods, and theoretical models, a picture has emerged that shows the narrow intercellular channels to be a complex microenvironment essential to neuronal function, a signaling pathway in its own right, and an important conduit for drug delivery. Fig. 1 A summarizes this picture of the ECS, which will be elaborated below.

Figure 1.

Structure of ECS. (A) Factors affecting the diffusion of molecules. These are: (a) geometry of ECS, which enforces a longer path-length on a diffusing molecule compared to a free medium; (b) dead-space microdomain, where molecules lose time exploring a dead-end (which may be an invagination, as shown, or glial wrapping, or a local expansion of the ECS); (c) obstruction by extracellular matrix molecules such as hyaluronan; (d) binding sites for the diffusing molecule either on cell membranes or extracellular matrix; and (e) fixed negative charges on the extracellular matrix that may affect the diffusion of charged molecules. Graphic image taken from Syková and Nicholson (1). (B) Shown here is the EM of cryofixed neuropil. (C) Shown here is the EM of conventional chemically fixed neuropil. Comparison of (B) and (C) shows reduction in ECS (pseudo-colored in blue) after chemical fixation. (B and C) These images were taken from adult mouse cerebral cortex; the common calibration bar represents 1 μm. Photographs are from Korogod et al. (13). To see this figure in color, go online.

The ECS comprises the fluid-filled spaces external to cell membranes. This would encompass interstitial spaces between cells, the blood vessels, and perivascular spaces as well as the ventricular and subarachnoid spaces of the brain. Commonly though, the ECS is equated with the interstitial space and this is the usage here. The ECS contains an interstitial fluid that closely resembles the cerebrospinal fluid with which it is in communication at the ventricular and subarachnoid spaces. An important constituent of the ECS is the extracellular matrix consisting of proteoglycans, hyaluronan, and sundry small link proteins. The matrix is involved in development but its function in the mature brain is not well understood.

The ECS is a reservoir for ions that are necessary both to maintain cellular resting and action potentials and to allow the release of transmitter molecules at synapses. The resistive properties of the ECS form a volume conductor that is an essential component in the generation of local field potentials. Beyond that, the possibility for ionic or molecular signals propagating through the ECS has long been recognized and called “volume transmission”, also referred to as “extrasynaptic”, “parasynaptic”, “diffuse”, or “paracrine” transmission; see Syková and Nicholson (1) for more detail. Obvious signaling agents in the ECS are K⁺ and Ca²⁺ (Na⁺ and Cl⁻ are present in too high a concentration to allow efficient modulation). Local fluctuations in K⁺ will affect membrane potentials but in a nonspecific manner that may limit their utility as signals. After neuronal activity, the increase in extracellular concentration of K⁺ is controlled both by reuptake into cells and by a passive mechanism of spatial buffering that involves circulating currents through glia cells and the ECS (2). Calcium is a more promising signaling agent because many cellular processes are very sensitive to this ion (3, 4).

Given the limited potential of ionic changes to convey information, it is the transmitter and neuromodulator molecules and their specific receptors that offer the greatest possibilities for signaling via the ECS. Attention has focused on glutamate spillover and the extrasynaptic receptors it might activate (5, 6, 7). Dopamine is another candidate molecule for volume transmission (8). In addition, there is evidence for neuron-glia signaling via the ECS utilizing a variety of substances including glutamate and ATP (9). The range and efficacy of volume transmission for a specific substance will depend on the location and sensitivity of receptors and uptake sites and on its effective diffusion characteristics in the ECS.

Although diffusion is the dominant mechanism for ion and molecular transport over scales below a few 100 μm and timescales of a minute or less, there has been much discussion over the years of whether bulk flow occurs in the ECS when longer distance and timescales are in play (10). This has become a topic of renewed interest with the introduction of the glymphatic hypothesis (11).

Ultrastructure of the ECS

It was long recognized that only electron microscopy (EM) could reveal the ECS but when effective brain fixation by vascular perfusion was introduced in the 1960s, the spaces between cells seemed nonexistent. This created a paradox because indirect techniques using equilibration of radiotracers or impedance measurements suggested a substantial ECS. The problem of how to preserve the ECS at the EM level has persisted (Fig. 1, B and C). Cragg (12) reviewed the topic and advocated use of sucrose in the fixation procedure. More recently, cryofixation techniques (13, 14) showed that the ECS could be preserved in local areas and likely varied in width (Fig. 1 B). An important goal is accurate 3D reconstruction of ECS. One approach (15) took conventionally fixed tissue with reduced ECS volume, reconstructed a 180 μm³ block of tissue from thin sections, then used a computational algorithm to expand the spaces to the accepted volume fraction. This study concluded that the ECS consisted of “tunnels and sheets”. It is hoped that efforts to visualize large brain volumes at the ultrastructural level (e.g., (16)) will also seek to capture the ECS.

The topological structure of the ECS is a highly connected space with every element linked via multiple pathways to every other. Indeed, the ECS has been likened to the “water phase of a foam” (17). Despite having a width measured in only tens of nanometers, the fraction of brain tissue occupied by ECS amounts to ∼20% (see later). An imaging analysis of the blood vessels in the mouse cortex found that the mean distance from the center of a neuronal soma to the nearest microvessel was 15 μm (18), demonstrating the extensive ramification of the vascular system. Nevertheless, the blood volume in the rat was measured with radiotracers at only 2–4.7% of tissue volume, depending on brain region (19), and a study in humans using positron emission tomography gave a cerebral blood volume of 3.8% (20). These volume fractions are small compared to ECS and are not part of the measured ECS volume fraction.

Diffusion with the point-source paradigm quantifies ECS structure

Because EM is time consuming and often fails to provide quantitative data, another method is needed that can measure ECS properties in living tissue and in real time. The biophysics of diffusion provides such an approach. Within the complex microenvironment of the ECS, a suitable diffusing molecule executing a constrained random walk will explore the entire space and, under appropriate conditions, report back on the structure. The realization of this idea involves a population of molecules and a measurement of the concentration distribution at different times. To extract structural information, it is useful to think of the brain and ECS as a porous medium; then two characteristic parameters, volume fraction (α) and tortuosity (λ), may be defined. Starting with a representative elementary volume of tissue, V_Tissue, containing an ECS with volume, V_ECS, α is defined as

$$\alpha =V_{\text{ECS}}/V_{\text{Tissue}}.$$

A small molecule, with a hydrodynamic diameter much less than the gaps between cells, will still experience hindrance because of the increase in path length that it encounters as it traverses the geometry of the ECS, and will have an effective diffusion coefficient, $D^{\ast }$. Comparing this with the diffusion coefficient, D, determined in water or a very dilute gel, leads to a measure of the hindrance called tortuosity:

$$\lambda =\sqrt{D/D^{\ast }}.$$

Then, assuming the validity of the diffusion equation (Fick’s Second Law), a generalized version may be written:

$$\frac{\partial C}{\partial t}=D^{\ast }{\nabla }^{2}C+\frac{Q}{\alpha }-k^{\mathit{\prime }}C-\frac{f\left(C\right)}{\alpha }+\mathbf{v}\cdot \nabla C.$$ (1)

The concentration, C, is the concentration measured in the ECS itself, which is the relevant physiological variable experienced by receptors and transporters (in other contexts, the concentration may be measured with respect to the tissue volume). A source term, Q, accounts for the release of substances within the tissue; other molecules may enter across brain boundaries and be defined by suitable boundary conditions to Eq. 1. A first-order rate constant, k′, accounts for any permanent loss of the probe into cells or blood vessels whereas f(C) encompasses specific kinetics for binding to the matrix, receptors, or transporters. Bulk flow with interstitial pore fluid velocity vector v, if present, is encapsulated in the v⋅∇C term.

This use of diffusion as a probe of the ECS was, to our knowledge, first effectively implemented by Fenstermacher, Patlak and colleagues who perfused the ventricles and subarachnoid space of the brain with radiolabeled probes, such as inulin and sucrose that remained in the ECS. Beginning in the 1960s and continuing through the 1970s, these investigators published many groundbreaking articles (21, 22, 23). Profiles of radioactivity in the tissue were obtained after fixing the tissue at various times after the perfusion. Fitting a 1D solution to Eq. 1 to the profiles led to values for $D^{\ast }$ (hence λ) as well as α that are close to those measured with contemporary methods. The main disadvantages of the radiotracer technique are that there is only one time point per animal, and that spatial resolution is poor.

Many of the shortcomings of the radiotracer method were eliminated when Nicholson and Phillips (24) introduced a method that was later called a “point-source paradigm” based on the use of specific small monovalent ions and ion-selective microelectrodes (ISMs). The ions were released into the brain from an approximation to a point-source consisting of a glass micropipette with a tip diameter of a few micrometers and the resulting ion concentration measured ∼100 μm away with an ISM with a tip diameter similar to that of the source. It was shown that the local inhomogeneity of the tissue on a scale commensurate with cellular structure could be accounted for by volume averaging and this legitimized the use of Eq. 1 (22, 24). Equation 1 is typically solved in a spherically symmetric coordinate system so C is a function of radial distance r from the source. If f(C) and the flow term are neglected and the source is an instantaneous point-source (i.e., δ-function of time and space) at the origin with magnitude Q, then the solution of Eq. 1 is (22)

$$C=\frac{Q}{\alpha }\frac{1}{{\left(4D^{\ast }t\pi \right)}^{3/2}}\text{exp}\left(-\frac{r^2}{4D^{\ast }t}\right)\text{exp}\left(-k^{\mathit{\prime }}t\right).$$ (2)

This is a Gaussian curve multiplied by an exponential loss factor. The shape of the curve yields $D^{\ast }$, and therefore λ may be estimated. The amplitude is a function of $Q/\alpha {\left(D^{\ast }\right)}^{3/2}$, so if Q is known, then α may be found. If the point-source is realized by pressure injection of an amount of substance at t = 0, then Q would be defined by the volume and concentration injected; this is called the real time pressure (RTP) method. In practice, the amount released into the tissue is difficult to measure, so only λ is obtained.

Real-time iontophoresis and modeling reveal and interpret volume fraction and tortuosity

The point-source paradigm reaches its full utility when the source emits molecules using iontophoresis. This technique applies a constant current pulse to the source micropipette, resulting in a constant flux of a suitably charged molecule. So long as the transport number (24) of the micropipette remains constant before and after the experiment, the source amplitude is accurately defined and both α and λ may be found. The convolution of Eq. 2 with this pulse provides the appropriate solution to Eq. 1 (22, 24). This is known as the “real-time iontophoresis” (RTI) method (Fig. 2, A and B), and most commonly the molecule employed is tetramethylammonium (TMA), a monovalent cation with M_r = 74. This molecule is popular because it is possible to make highly selective ISMs for TMA⁺, it does not affect physiological function at low concentrations, and it remains largely extracellular for the duration of measurements. The cation tetraethylammonium and the anions α-naphthalene sulfonate and hexafluoroarsenate also have been used (24). The RTI method may be extended to anisotropic tissue, where λ becomes a tensor (1, 22), and applied in layered, inhomogeneous brain regions such as the hippocampus (25).

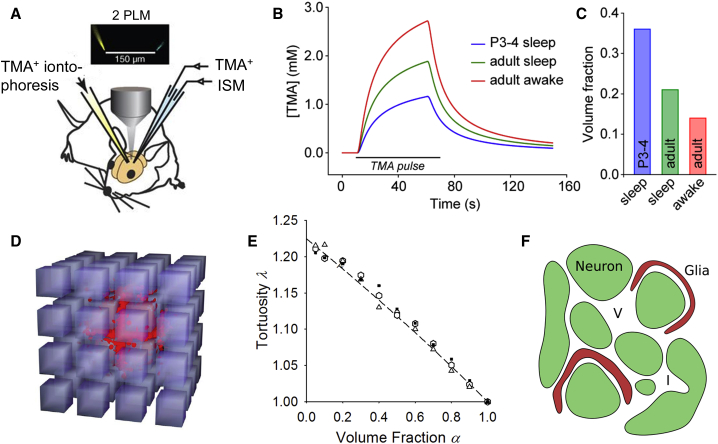
Figure 2.

Real-time iontophoresis and Monte Carlo modeling reveal ECS structure. (A) Given here is the recent implementation of the RTI-TMA method. TMA⁺ was delivered from left-hand source micropipette by iontophoresis in awake or asleep mouse cortex and concentration of TMA⁺ recorded with an ISM 150 μm from the source. The microelectrodes contained fluorescent dyes so the tips could be visualized with two-photon light microscopy (2 PLM). Graphic image taken from Xie et al. (28); reprinted with permission from AAAS. (B) Shown here are the theoretical TMA⁺ concentration curves ([TMA]), for a distance of 100 μm from the source in three examples. (a) Given here is the postnatal (P3–P4) rat anesthetized (i.e., sleep) cortex with α = 0.36 (36%) (26). (b) Given here is the adult anesthetized (i.e., sleep) cortex, with average data for rat or mouse α = 0.21 (21%) (1). (c) Given here is the awake adult mouse cortex α = 0.14 (14%) (28). (C) The amplitudes of the curves are related to α, and the shapes similar because λ ∼ 1.6 in all three cases. (D) Shown here is the Monte Carlo simulation in ensemble of 3D cubic cells packing with small, uniform, separation to form an ECS. A set of molecules (red; size exaggerated) has been released at the center of the ensemble and spread outwards to explore the local microenvironment; image taken from Syková and Nicholson (1). (E) The plot of values of λ versus α extracted from Monte Carlo simulations using three different ensembles is shown. These were: cubes (squares), truncated octahedra (hexagonal symbol), and mixture of three differently shaped convex cells (triangular symbol). In each geometry, α was varied from 0.05 to 0.90, D^∗ was estimated from the molecule distribution, and λ was calculated. All three media had an identical λ-α relation (Eq. 3); plot taken from Tao and Nicholson (32) with permission from Elsevier. (F) Given here are factors that may increase λ from the maximum seen in (E) to the value seen in experiments. These are: dead-space microdomains in the form of local expansion of ECS, i.e., voids (V), invaginations (I) of cellular elements, or glial wrapping (red) around cells; graphic image taken from Nicholson et al. (35) with permission of Springer. To see this figure in color, go online.

The RTI-TMA method has established that in most adult brain tissues α is ∼0.2, so that the ECS occupies no less than 20% of the brain (1). Tortuosity, λ, is typically ∼1.6 (1), meaning that small molecules have an effective diffusion coefficient (D^∗) that is only two-fifths that in an unrestricted medium. Striking departures from these values do exist: in the cortex of newborn rats, α is as large as 40% (Fig. 2, B and C), diminishing to 21% after 21 days, with λ remaining ∼1.6 in this period (26). During severe ischemia or anoxia (27) α diminishes to ∼5%, whereas λ increases to ∼2.1.

A recent and surprising finding using the RTI-TMA method is that α in the awake mouse cortex appears to be 14% compared to 23% in the sleeping or anesthetized animal with no significant difference in λ (28). It was hypothesized that tonic activation of noradrenergic afferents reduced α in the awake state (28). This was supported by a combined EM and RTI-TMA study (29) in rat cortical slices, showing that application of a β-adrenergic agonist reduced α from 22 to 18% through an increase in astrocyte volume. These two studies may explain why α in both slices and anesthetized in vivo animals is ∼20% because both preparations have little active noradrenergic input. The ECS measurements in awake animals would benefit from replication; however, the large body of diffusion data in anesthetized animals and in slices will remain relevant because most experiments are done under these conditions.

Volume fraction admits of a simple interpretation. In contrast, tortuosity is a composite parameter with many potential mechanisms contributing to the hindrance experienced by a molecule. To decompose λ it is necessary to resort to models. Some models have been simplistic (1), but Monte Carlo simulation with the software program MCell (30, 31) (Fig. 2 E) has thrown light on the nature of λ. Such simulations have clarified the role of geometry and shown that an assembly of regularly spaced convex cells (including cubes, truncated octahedra, and more complex ensembles of space-filling objects (32, 33)) would generate a tortuosity given by

$$\lambda =\sqrt{\left(3-\alpha \right)/2},$$ (3)

which is always ≤1.225 (Fig. 2, D and E) and well below the typical experimental value of ∼1.6.

One explanation for the discrepancy between simulation and experiment was provided by RTI experiments in which macromolecules were used to alter ECS geometry (34). This led to the hypothesis that ECS harbors dead-space microdomains where the transport of molecules may be transiently delayed. Modeling with MCell suggests that the dead-spaces could take the form of local enlargement of the ECS, cellular invaginations, or glial wrapping (33, 35) (Fig. 2 F).

Macromolecular probes and imaging reveal new properties of the ECS

The RTI method provides essential insights into the ECS; notable is how α changes under different conditions. The method is limited to small ions for which an ISM may be fabricated, and these ions do not represent all signals trafficked in the ECS. Moreover, drugs may be based on antibodies (36) and drug carriers can be large polymers or viral vectors. To explore the diffusion of macromolecules, Nicholson and Tao (37) introduced the integrative optical imaging (IOI) method. This version of the point-source paradigm releases macromolecules labeled with a fluorophore from a micropipette and images the diffusing cloud of molecules using an epifluorescent microscope. The IOI technique has been implemented with two-photon microscopy (38), but the signal-to-noise ratio was low, probably because the sampling volume was very small.

The macromolecules are ejected by pressure (compare to the RTP method) because iontophoresis is unreliable for complex molecules. By fitting a Gaussian curve (Eq. 2, k′ = 0) to the image intensity distribution at a sequence of times, $D^{\ast }$ and, hence, λ, may be obtained, although α is not available.

Employing the IOI method in the cortex and using a sequence of approximately spherical molecules that included dextran polymers, albumins, and other proteins (Fig. 3 A), it was found that λ increased with hydrodynamic diameter of the molecule (1, 39). An important question, especially for drug delivery, is the maximum size of a molecule that can diffuse through most of the ECS, which is equivalent to asking what the typical width of the ECS is. Employing dextrans and a quantum dot with a hydrodynamic diameter of 35 nm in rat neocortex and using restricted diffusion theory (RDT) to analyze the data, Thorne and Nicholson (40) obtained a value of 38 nm for the width of the ECS, assuming the pores resembled parallel planes or sheets, and 64 nm for a cylindrical or tubelike pore. These data are supported by applying RDT analysis (40) to the data from several studies shown in Fig. 3 A, which gives a width of 40 nm for sheetlike pores (dashed line) and 80 nm for cylindrical pores. Measurements with the IOI method in the molecular layer of the turtle cerebellum suggested that large dextrans (>280 kDa) are flexible and undergo reptation in the ECS (41). Using scaling theory, the study arrived at an ECS width of 31 nm (41). Given that 35-nm quantum dots diffuse, albeit very slowly, in the cortex, and that RDT theory, assuming sheetlike pores, gives a value of ∼40 nm (Fig. 3 A), and that scaling theory gives a value of ∼30 nm, it is plausible that much of the ECS has a width in this range. However, larger, local, voids exist in the ECS (e.g., Fig. 1) and are a likely source of dead-spaces. Smaller gaps that exclude large molecules are also possible. Indeed, application of RDT to diffusion data obtained during ischemia (40) suggests the typical ECS width can fall to <10 nm. The width also could vary dynamically as cells swell and shrink with passage of ions and water. Thus, although a “typical width” of the ECS may be ∼40 nm, it is an open question as to how to interpret this estimate in structural terms.

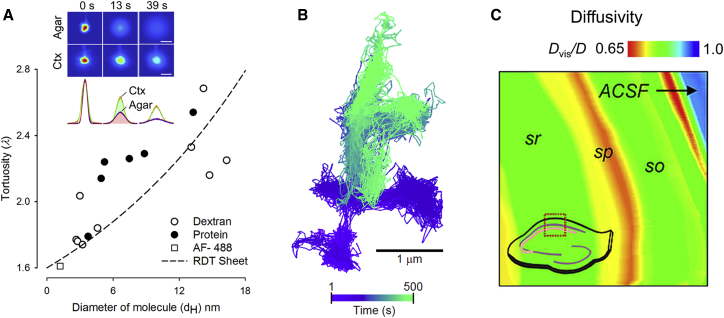
Figure 3.

Imaging methods to study ECS. (A) Given here is a plot of λ measured with IOI in cortex (rat or mouse) versus hydrodynamic diameter (d_H) for macromolecules from several studies (see Table 3 in (1) and (39)). Open circles represent dextrans, solid circles represent proteins, and the open cube is Alexa Fluor 488 dye. The dashed line shows a best fit to these data of RDT for planar or sheetlike pores. (Inset) Pseudo-color diffusion images were obtained with IOI for 3 kDa dextran labeled with Texas Red in agarose (Agar) and in vivo rat cortex (Ctx) at different times after initial injection of molecule from a micropipette. Scale bars indicate 200 μm. The corresponding Gaussian intensity profiles are below. (Inset) Image taken from Thorne and Nicholson (40); copyright 2006 National Academy of Sciences. (B) Shown here is a color-coded trajectory of a single-walled carbon nanotube diffusing in ECS in living cortical slice from a neonatal rat brain (20,000 data points). Image is from Godin et al. (42) and is reprinted by permission from Macmillan Publishers, Ltd: Nature Nanotechnology, copyright 2017. (C) Given here is the diffusivity in interstitial space in slices of rat hippocampus measured with the time-resolved fluorescence anisotropy imaging technique. Values of D_vis/D averaged 0.7, where D_vis is the effective diffusion coefficient attributable to interstitial viscosity, and D is the free diffusion coefficient in ACSF (artificial cerebrospinal fluid), giving an average λ_vis = 1.2 measured across stratum radiatum (sr), stratum pyramidale (sp), and stratum oriens (so). Image was reproduced from Zheng et al. (43). To see this figure in color, go online.

The RTI and IOI data suggest that we will benefit from a finer resolution of local properties of the ECS, and emerging superresolution methods are beginning to provide this. Godin et al. (42) tracked single-walled carbon nanotubes (Fig. 3 B) and measured a range of ECS widths and local viscosities. This is an exciting study, but the technique was applied in neonatal rats where α is much larger than in the adult (26). A different approach to nanoscale imaging was taken by Zheng et al. (43), who used time-resolved fluorescence anisotropy imaging to measure the diffusion of a small dye molecule within the ECS of the rat hippocampus (Fig. 3 C). This revealed that local interstitial viscosity reduced the diffusion coefficient to 70% of that in free solution. This would amount to a viscous tortuosity component of λ = 1.20. A previous study using photobleaching of the larger 70 kDa dextran in mouse spinal cord had inferred a viscous tortuosity component of λ = 1.34 (44). When the viscous component (taken as λ = 1.20) is multiplied with the basic geometrical tortuosity for a 20% volume fraction (λ = 1.18; Eq. 3), it is still insufficient to account for the typical tortuosity (λ = 1.6) measured with TMA or other small molecules. This implies the presence of additional factors, such as dead-spaces.

The diffusion characteristics of the ECS have been explored with other optical methods. The Verkman group introduced a series of techniques and tested them in normal brain, tumors, and edema (reviewed in (45)). The initial studies used fluorescence recovery after photobleaching that was restricted to the surfaces of the cortex and spinal cord. To probe deeper in the tissue, the microfiber epifluorescence photobleaching technique was introduced. Like the IOI method, these photobleaching techniques only measured $D^{\ast }$. To obtain α, a method using two dyes with different quenching characteristics called “pulsed-infusion microfiberoptic photodetection” was devised, but never applied in brain. Finally α was measured using dye partitioning with microfiberoptic detection. In normal tissue, these various methods largely agreed with results already obtained with the RTI and IOI methods. However, the main thrust was technical development, and the new methods have not been applied systematically; the work may stimulate new approaches in future.

The RTI and IOI methods rely on the validity of the classical diffusion equation. This implies that 〈r²〉 ∝ t, where 〈r²〉 is the mean square distance of a molecule from the origin at time, t. The success in fitting the solutions of the diffusion equation to experimental data testifies to the validity of this description. However, Xiao et al. (46) discovered that the IOI results, in the granular layer of the rat cerebellum, deviated from the classical solution and they postulated that the diffusion was anomalous, characterized by 〈r²〉 ∝ ${\mathit{t}}^{{2/d}_w}$ with d_w = 4.8. It was thought that the anomalous diffusion arose from complex dead-spaces formed by the astrocytic glia cell wrapping of the glomerular synaptic junction, and this was supported with Monte Carlo modeling (46).

Extracellular matrix and the control of ECS properties

The ECS harbors an extracellular matrix composed of proteoglycans and hyaluronan. Proteoglycans have a protein backbone from which chains of glycosaminoglycans (GAGs) spread, forming heparan sulfate proteoglycans (HSPGs) or chondroitin sulfate proteoglycans (CSPGs). Proteoglycans are either anchored in or attached to cell membranes. Hyaluronan (HA) is a nonsulfated, often very long, richly hydrated GAG that for the most part is not directly connected to cell membranes. The sulfate groups on CSPGs and HSPGs endow them with numerous negative charges. An important set of CSPGs are the lecticans (comprising aggrecan, versican, neurocan, and brevican). With the small tenascin-R protein and HA, lecticans form important matrix assemblies, including the so-called “perineuronal nets” (47, 48) (Fig. 4 A). The CSPGS play a major role in development, plasticity, and repair of the CNS (48) and the extracellular matrix may be involved in the mobility of postsynaptic receptors and in limiting transmitter spread from the cleft (49).

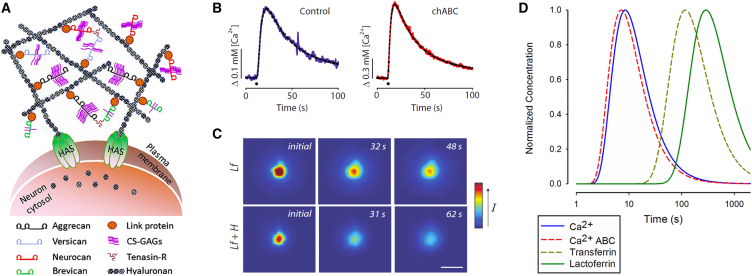
Figure 4.

Interaction of diffusing molecules with the extracellular matrix. (A) Shown here is the structure of the perineuronal net. Hyaluronan, secreted by membrane-bound HA synthase (HAS), binds to members of the lectican family (aggrecan, versican, neurocan, and brevican) and is cross-linked by link proteins and tenascin-R to form supramolecular aggregates on the surface of neurons (chondroitin sulfate-glycosaminoglycans, CS-GAGs). Graphic image is taken from Tsien (62) and derived from Kwok et al. (48) with permission of John Wiley & Sons. (B) Shown here is the diffusion of Ca²⁺ before (Control) (left curve, blue) and after CS glycan had been cleaved with chondroitinase ABC (chABC) (right curve, red) in rat cortical slice. Records were obtained with the RTP method, with time of injection marked by black dot in graphs. Plots are taken from Hrabětová et al. (54) with permission from John Wiley & Sons. (C) Shown here are diffusion measurements with the IOI method in vivo to measure interaction with HSPGs. Lactoferrin (Lf) or Lactoferrin + heparin (Lf + H) solutions were pressure-ejected from a micropipette at a depth of 200 μm in rat neocortex. The larger complex (Lf + H) diffused away more rapidly than the smaller Lf, indicating that the latter was binding to matrix components. Scale bar indicates 200 μm. Graphic panels are taken from Thorne et al. (55), copyright 2008 National Academy of Sciences. (D) Given here are the theoretical diffusion curves at 100 μm from source (Eq. 2, k′ = 0), showing effect of chABC on Ca²⁺ diffusion and comparison of diffusion of transferrin (no binding) and lactoferrin (binds to matrix). Note also the difference in diffusions times for the small Ca²⁺ ion compared to the larger proteins (∼80 kDa). Timescale is logarithmic. To see this figure in color, go online.

Knocking out components of the extracellular matrix leads to changes in ECS properties. Elimination of tenascin-R reduced α from 20 to 15% in the mouse primary somatosensory cortex (50). Eliminating Bral-1, a protein that links HA and several lecticans in the vicinity of nodes of Ranvier, decreased conduction velocity of the myelinated fibers and reduced λ in the white matter of the mouse (51). Elimination of the gene for HA synthase 3 reduced the HA in the mouse hippocampus and diminished α in the stratum pyramidale from 12 to 7%, coincident with the appearance of seizure activity (52).

From a biophysical perspective, the abundance of negative charges on the HSPGs and CSPGs suggests interaction with the cations of the interstitial fluid. Indeed, Morawski et al. (53) used a proton-beam microprobe to obtain evidence that the negative charge density in perineuronal nets might be as high as in cartilage. Charge interaction was confirmed when Hrabětová et al. (54) released Ca²⁺ with the RTP method in combination with application of the enzyme chondroitinase ABC to cleave the chondroitin sulfate groups from the CSPGs. They showed that the effective diffusion coefficient for Ca²⁺ was higher in the enzyme-modified tissue, pointing to rapid reversible equilibrium binding of the divalent ions to chondroitin sulfate (Fig. 4, B and D). Interestingly, the diffusion of the monovalent TMA⁺ was unaffected by the enzyme application, suggesting that the diffusion of K⁺ and Na⁺ would not be affected either.

Evidence for a biophysical interaction with HSPGs was obtained by Thorne et al. (55) using the IOI method (Fig. 4 C). Fluorophore-labeled lactoferrin exhibited more hindered diffusion than the near-identical molecule, transferrin, in the rat cortex (Fig. 4 D). When the lactoferrin was coinjected with heparin, these two molecules formed a larger complex that diffused more rapidly in the brain than lactoferrin alone. This showed that lactoferrin could transiently bind to heparan sulfate groups on the matrix, but the lactoferrin-heparin complex was not able bind to these sites (Fig. 4 C).

Diffusion measurements with Ca²⁺ and lactoferrin conform to Eq. 2, implying the continuing validity of the classical diffusion equation. This means that the interaction with the matrix in both cases takes the form of reversible equilibrium binding that is much faster than the local diffusion process. Under such conditions there will be a decreased effective diffusion coefficient, $D_{\text{m}}^{\ast }$, given by (35, 54, 55)

$$D_{\text{m}}^{\ast }=D^{\ast }/\left(R+1\right).$$ (4)

For lactoferrin, R is related to the dissociation rate constant K_D, such that R = c_B/K_D, where c_B is the concentration of heparan sulfate binding sites on the matrix (55). Using diffusion analysis to probe the extracellular matrix is in its infancy, but holds considerable promise.

Although the matrix may control important aspects of diffusion in the ECS, other mechanisms can alter the characteristics of the space. These include manipulation of osmolarity, edema, ischemia, brain tumors, and other pathological conditions (1).

Bulk flow and the glymphatic hypothesis

As the examples discussed above testify, over short distances, most substances move through the ECS by diffusion. An often-asked question is whether there is also transport by bulk flow. A study from Cserr et al. (23) established that a bolus of radiolabeled substance injected into the rat caudate nucleus cleared from the brain over a period of hours with the same rate constant regardless of molecular weight of the molecules. This was interpreted as elimination by flow rather than diffusion. The evidence for bulk flow was reviewed by Abbott (10), who thought it was likely that flow originated from the movement of salt and water into the ECS, probably across the brain capillary endothelium.

Bulk flow in the ECS has not been directly measured. This hurdle appeared to be partly overcome when the Nedergaard group (11) used two-photon microscopy in the superficial regions of the cortex in an anesthetized mouse combined with fluorescent 3 kDa dextran molecules injected into the cisterna magna. The dextran moved into the perivascular spaces around brain capillaries and then spread through the ECS before apparently leaving the brain via deep perivenous pathways. Based on further experiments where aquaporin-4 water channels had been knocked out, it was conjectured that water flow through perivascular glial endfeet and active transport of salt established a bulk flow that entrained larger molecules to move through 20-nm gaps between the endfeet (11). The brain was thought to lack a lymphatic drainage system (but see (56, 57)), and because glia were an integral part of the hypothesized flow path this new mechanism was termed the “glymphatic pathway”. The potential importance of the glymphatic pathway was highlighted when it appeared that the hypothesized flow increased during sleep (28) and was correlated with an increase in α in the cortex compared to the waking state (Fig. 2, B and C); the investigators suggested this was a mechanism for removing toxic metabolites from the brain (28).

The glymphatic hypothesis has generated controversy (58, 59) and theoretical models (60, 61). One issue is how much of the observed movement of fluorescent molecules (11, 28) may be accounted for simply by diffusion. The Péclet number, Pe, gives a rough estimate of the ratio of flow to diffusive transport (60):

$$Pe=Lu/D^{\ast },$$ (5)

where L is a characteristic length and u is the interstitial flow rate. If the transport path L is taken as 100–250 μm and u as 10 μm min⁻¹, which is probably an overestimate (22), and $D^{\ast }$ as 7 × 10⁻⁷ cm² s⁻¹ for 3 kDa dextran in cortex (1), then Pe < 1, indicating that diffusion may dominate over the typical observation distance. This suggests, as noted by others (60, 61), that diffusion may play a significant role in the observed dispersion of the fluorescent molecules and flow is not essential. In the case of radiotracer bolus injections (23), the timescale was of the order of hours and the implicit path should be long enough for Pe ≫ 1, allowing a low flow rate to dominate, although other factors are likely involved.

There are unresolved questions about the glymphatic hypothesis that suggest interesting avenues for research. These include the complex biophysics postulated at the glial interface between the perivascular space and the ECS. Another question is the extent to which perivascular flow is mediated by vascular pulsation; note that flow in the perivascular system is necessary but not sufficient to confirm the glymphatic mechanism. The clearance of an injected bolus of substance from a brain region (11, 23) lends support to the glymphatic concept; however, the routes by which molecules leave the neuropil have been questioned (59). Finally, the relation between the glymphatic system and the recently characterized meningeal lymphatics (56, 57) is unknown. Crucial experimental confirmation of the glymphatic pathway may have to wait for new techniques (e.g., that can measure flow in the ECS directly); nevertheless, the hypothesis has stimulated a welcome renewal of interest in flow in brain parenchyma and its clinical implications.

The view from the frontier

The ECS has been regarded as a quiet street for many years but is now seen as a bustling and indispensable thoroughfare. From a biophysical perspective, the diffusion characteristics have dominated, both as a tool to probe the elusive structure and as the principle mechanism for the movement of molecular signals and neuromodulators. Three areas that are ripe for further research are the reconstruction of the real 3D geometry at the ultrastructural level, possibly with the aid of single particle tracking, the further characterization of the structure, and functions of the extracellular matrix and a definitive answer to the existence and functional role of bulk flow.

Author Contributions

C.N. wrote the manuscript, and S.H. edited it. S.H. prepared the figures, and C.N. edited them.

Editor: Brian Salzberg.