Resident Calmodulin Primes NMDA Receptors for Ca²⁺-Dependent Inactivation

Abstract

N-methyl-d-aspartate (NMDA) receptors are glutamate- and glycine-gated channels that flux Na⁺ and Ca²⁺ into postsynaptic neurons during synaptic transmission. The resulting intracellular Ca²⁺ transient is essential to physiological and pathological processes related to synaptic development, plasticity, and apoptosis. It also engages calmodulin (CaM) to reduce subsequent NMDA receptor activity in a process known as Ca²⁺-dependent inactivation (CDI). Here, we used whole-cell electrophysiology to measure CDI and computational modeling to dissect the sequence of events that underlies it. With these approaches, we estimate that CaM senses NMDA receptor Ca²⁺ influx at ∼9 nm from the channel pore. Further, when we controlled the frequency of Ca²⁺ influx through individual channels, we found that a kinetic model where apoCaM associates with channels before their activation best predicts the measured CDI. These results provide, to our knowledge, novel functional evidence for CaM preassociation to NMDA receptors in living cells. This particular mechanism for autoinhibitory feedback reveals strategies and challenges for Ca²⁺ regulation in neurons during physiological synaptic activity and disease.

Introduction

Glutamate exerts fast excitatory actions in the mammalian central nervous system by gating cation-selective tetrameric ion channels. Among these, N-methyl-d-aspartate (NMDA) receptors composed of GluN1 and GluN2 subunits have characteristically high conductance, high Ca²⁺-permeability, and slow kinetics, such that their activation produces a significant local rise in intracellular Ca²⁺. Specifically, NMDA receptor-mediated Ca²⁺ transients initiate signaling pathways essential for synaptic development and plasticity and can cause the pathologic apoptosis that underlies excitotoxicity.

Given its critical role in fundamental neurologic processes, NMDA receptor activity is under tight developmental and regional control, and is sensitive to multiple extra- and intracellular cues. Specifically, Ca²⁺ levels affect NMDA receptor currents through several distinct mechanisms. External Ca²⁺ ions bind directly to residues in the outer vestibule of the obligatory GluN1 subunit to reduce channel conductance and gating (1, 2, 3), whereas internal Ca²⁺ ions act indirectly through slow and fast mechanisms. Slow, minute-scale processes initiate Ca²⁺-dependent changes in receptor phosphorylation by kinases (e.g., protein kinase A, protein kinase C, and CaMKII) and/or phosphatases (e.g., calcineurin) to affect channel gating and/or permeation (4, 5, 6, 7), whereas a fast, millisecond-scale process, known as Ca²⁺-dependent inactivation (CDI), which requires calmodulin (CaM) binding to intracellular portions of the GluN1 subunit (8, 9), reduces the NMDA receptor current by increasing its macroscopic desensitization (10, 11).

Numerous other ion channels display CaM-mediated CDI, suggesting that this regulatory mechanism is highly conserved across several protein families and life forms. CaM is ubiquitous to living cells, is highly expressed in neural tissue, and is enriched in dendritic spines (12). CaM control of NMDA receptor activity, primarily by mediating CDI, is a major mechanism for tuning the excitatory postsynaptic current during development and across brain regions (13, 14, 15, 16). However, the process remains insufficiently understood.

NMDA receptors have several CaM binding sites, each with different CaM binding properties. The intracellular sequence immediately adjacent to the M4 transmembrane helix of GluN1, known as C0, is required for CDI (10, 17). In addition to strongly binding calcified CaM, several in vitro studies observed that the C0 peptide can bind CaM in the absence of Ca²⁺ (18, 19, 20). Therefore, CaM may reside on C0, and this proximity to the channel pore positions it optimally for rapid activation by incoming Ca²⁺ (21). However, results remain inconsistent (8, 22) and whether CDI of NMDA receptors occurs by Ca²⁺ binding to freely diffusing or resident apoCaM is unknown. Yet, each mechanism has distinct implications for how intracellular Ca²⁺ transients tune synaptic responses and how disease-associated CaM mutations influence excitatory glutamatergic transmission.

Here we modeled possible mechanisms of CaM-mediated NMDA receptor CDI and tested these with electrophysiological measurements in several rigorously controlled conditions. Results provide the first evidence in living cells that apoCaM preassociates with NMDA receptors and show that this resident apoCaM is sensitive to elevated [Ca²⁺] within nanodomains of the channel pore.

Methods

Molecular biology

Rat GluN1-2a (U08262.1), GluN2A (M91561.1), and GFP cDNAs were cloned in pcDNA3.1 (+) and were transiently transfected at a 1:1:1 ratio into HEK 293 cells (ATTC CRL-1573, passages 26–32) using the Ca²⁺ phosphate precipitation method (23). Transfected cells were maintained in DMEM (10% FBS) supplemented with 10 mM Mg²⁺ and were used for experiments 24 h posttransfection. All CaM constructs were gifts from Drs. Inoue and Ben Johny (24). We introduced all mutations using the QuikChange method (Stratagene, Amsterdam, Netherlands). We verified each construct by sequencing before and after subcloning, and after plasmid amplification (QIAGEN, Valencia, CA).

Western blotting

We transfected HEK293 cells with the indicated constructs; and harvested and lysed them 24 h posttransfection, with 1% SDS lysis buffer, and removed debris and contaminating DNA/RNA by centrifugation 15 min at 13 RPM. Equal amounts of proteins in the supernatant were loaded onto 5% SDS polyacrylamide gel to achieve separation between endogenous CaM (17 kD), GFP (37 kD), YFP-CaM (44 kD), and GluN1-2a (100 kD). Proteins were electrotransferred onto PDF membranes as described in Cummings et al. (25) and probed with rabbit anti-CaM antibody (ab45689, lot: GR123440-4; 1:2500; Abcam, http://www.abcam.com/); mouse anti-GFP (MAB1083, lot: NG1720568; 1:5000; Millipore, Billerica, MA), and rabbit anti-GluN1 pan (MAB1586, lot: 2739489, 1:1000; Millipore). Hybridizations were done overnight at 4° for primary antibodies, and 1 h at room temperature for secondary antibodies (rabbit or mouse anti-HRP, 1:10,000).

Fluorometry

The relative expression of YFP-CaM constructs was quantified as the ratio of fluorescence intensity from a single cell expressing YFP to background autofluorescence from untransfected cells on the same day of recording. All measurements were from cells after electrophysiological recording. Fluorescence was measured with a photomultiplier tube (Hamamatsu Photonics, Hamamatsu City, Japan) and recorded in the software pClamp10.3 (Molecular Devices, Sunnyvale, CA). Data were analyzed in MATLAB 2011a (The MathWorks, Natick, MA).

Electrophysiology

Macroscopic currents were recorded with the whole-cell patch clamp-technique, using borosilicate pipettes (4–5 MΩ) filled with (intracellular) 135 mM CsCl, 35 mM CsOH, 4 mM MgATP, 0.3 mM Na₂GTP, and either BAPTA or EGTA at the specified concentration, buffered to pH 7.4 (CsOH). For Ca²⁺ dialysis experiments, recording pipettes contained (intracellular) 135 mM CsCl, 35 mM CsOH, 4 mM MgATP, 0.3 mM Na₂GTP, 10 mM HEDTA, pH 7.4 with CsOH. Free Ca²⁺ calculations were done with the software MAXC (www.maxchelator.stanford.edu) with CaCl₂. Extracellular solutions contained 150 mM NaCl, 2.5 mM KCl, 10 mM HEPBS, 0.1 mM EDTA, and 0.1 mM glycine; CaCl₂ was added to produce the indicated free Ca²⁺ concentrations according to the software MAXC; they were applied using a pressurized perfusion system with a digitally controlled solenoid valve. Series resistance was monitored to ascertain seal quality. In all experiments, cells were bathed in PBS unless otherwise indicated.

Unitary currents were recorded with the cell-attached patch-clamp technique from membrane patches containing a single receptor (26). Borosilicate pipettes (15–25 MΩ) contained (extracellular) 150 mM NaCl, 2.5 mM KCl, 10 mM HEPBS, 0.1 mM EDTA, 0.1 mM Glycine, 1 mM Glutamate, pH 8 with NaOH, and with CaCl₂ buffered according to the software MAXC. Ca²⁺-only solutions contained 75 mM CaCl₂, 2.5 mM KCl, 10 mM HEPBS, 0.1 mM EDTA, 0.1 mM Glycine, 1 mM Glutamate, pH 8 with Ca(OH)₂. Stationary single-channel data were acquired, processed, and analyzed in the software QuB (www.qub.buffalo.edu). Currents were idealized using the SKM algorithm (27). Single-channel voltage-ramps were recorded and processed in the software pClamp. Analysis of voltage-ramp data was done using custom scripts in MATLAB 2011a (The MathWorks). During voltage ramps, cells were bathed in 142 mM KCl, 5 mM NaCl, 10 mM HEPES, 5 mM EGTA, 1.7 mM MgCl₂, pH = 7.4 with KOH to offset the resting membrane potential of HEK293 cells. Applied voltage was initially stepped from 0 to +100 mV and ramped to −60 mV over 4 s, then stepped back to 0 mV. All sweeps were averaged to yield a time-averaged 〈i〉-amplitude as a function of recording potential (E). To correct for leak current and capacitive transient current during the step pulses, sweeps that contained no channel activity (typically 5–13 sweeps/patch) were averaged to produce a baseline current and this was subtracted from the original 〈i〉-E waveform. The unitary Ca²⁺ current was determined as described in Jahr and Stevens (28) first by fitting 〈i〉-E data with

$$\langle i\rangle =\left(E-E_{\text{rev}}\right)\left({\gamma }_{\text{in}}\cdot \left(\frac{1}{1+e^{p\left(E-E_{\text{rev}}\right)}}\right)+{\gamma }_{\text{out}}\cdot \left(1-\frac{1}{1+e^{p\left(E-E_{\text{rev}}\right)}}\right)\right),$$ (1)

where E_rev is the reversal potential, γ_in and γ_out are the inward and outward conductance, respectively, and p reflects the sharpness of the transition between inward and outward current. The extrapolated γ_in calculated for several external Ca²⁺ served to evaluate the steepness of the conductance/[Ca²⁺] dependency (Eq. 7),

$${\gamma }_{\text{in}}=\frac{0.5\cdot \left[{\text{Ca}}^{2+}\right]\cdot h}{1+0.5\cdot \left[{\text{Ca}}^{2+}\right]\cdot h/{\gamma }_{\min }},$$ (2)

where γ_min is the limiting inward conductance in the presence of high extracellular Ca²⁺ (75 mM), 0.5 is the activity coefficient of Ca²⁺ in physiological solution, and h is a coefficient that sets the steepness with which the limiting conductance is reached. In our cells, we found h = 9.5 pS/mM for GluN1-2a/GluN2A. From these data, the fractional Ca²⁺ current (f_Ca) was calculated directly as

$$f_{\text{Ca}}=\frac{1}{1+{\gamma }_{\max }/0.5\cdot \left[{\text{Ca}}^{2+}\right]\cdot h},$$ (3)

where γ_max is the limiting inward conductance in the absence of extracellular Ca²⁺. Table S1 summarizes these results.

Statistics

Statistical tests were performed with custom scripts in R and MATLAB 2011a. The nonparametric Mann-Whitney U-test was used for comparison because CDI data tended to follow nonnormal distributions as determined from the Lillifore’s and Anderson-Darling tests. Fittings of CDI models to CDI_EQ-P_o data and Jahr models to single-channel voltage-ramp data were performed with custom software with the built-in statistics toolbox fittype command using the least-squares method in MATLAB 2011a.

Results

Define new metric to evaluate specifically CDI of NMDA receptors

Presently the literature documents several metrics to quantify the extent of NMDA receptor CDI but the reported values are difficult to reconcile across experimental conditions, most likely due to uncontrolled confounding factors. Aside from effects on response kinetics, external Ca²⁺ controls NMDA receptor conductance (3); and aside from Ca²⁺, the kinetics and extent of NMDA receptor macroscopic desensitization vary with external glycine concentrations (29, 30), mutations (31), and posttranslational modifications (6, 32, 33). To exclude contributions from these separate Ca²⁺-dependent and Ca²⁺-independent forms of NMDA receptor current modulation, we developed, to our knowledge, a new method to specifically monitor changes in CDI.

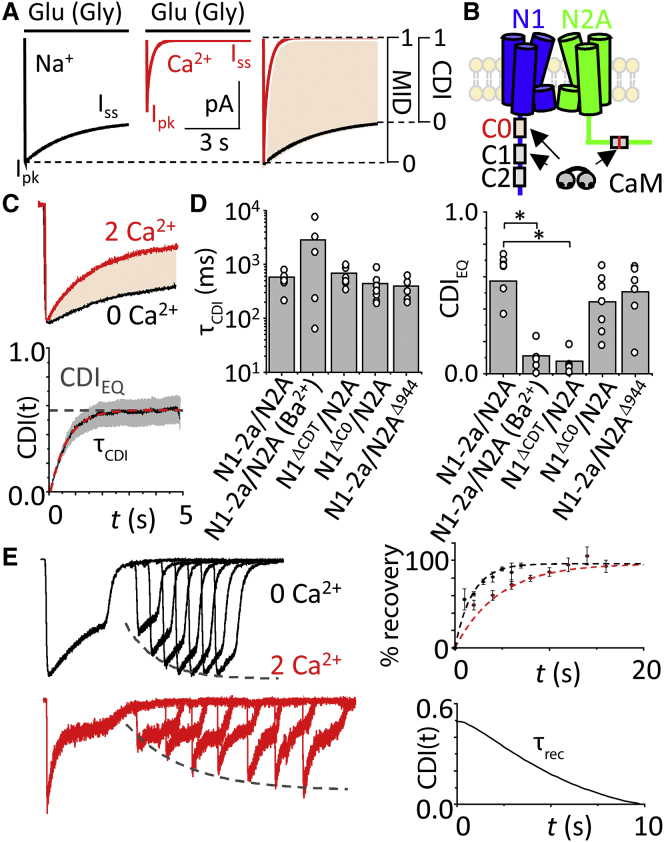
First, we aimed to separate CDI from the intrinsic desensitization of macroscopic NMDA receptor currents (macroscopic intrinsic desensitization, MID). MID can be observed and measured in Ca²⁺-free solutions as the steady-state fractional residual current (1 − I_ss/I_pk), and can theoretically take values from zero (nondesensitizing) to unity (fully desensitizing) (Fig. 1 A). In external Ca²⁺, currents are smaller and desensitize deeper and faster. We define CDI specifically as the increased desensitization of the macroscopic response observed in Ca²⁺, relative to Ca²⁺-free conditions (Eq. 4); it can also take values from zero (noninactivating) to unity (fully inactivating) (Fig. 1 A):

$$CDI\left(t\right)=1-\frac{{\left[I\left(t\right)/I_{\text{pk}}\right]}_{\text{Ca}}}{{\left[I\left(t\right)/I_{\text{pk}}\right]}_{\text{Na}}}.$$ (4)

Similar methodology helped define the CDI of voltage-dependent Ca²⁺ channels (34, 35, 36). To validate the use of this metric for NMDA receptors, we quantified CDI in experimentally recorded currents from wild-type NMDA receptors and from mutants known to lack CDI. Previous reports showed that NMDA receptor CDI requires CaM binding to the GluN1 C-terminal domain C0 segment (10). However, CaM also binds to the alternatively spliced C1 cassette (8) (Fig. 1 B). To eliminate possible confounding effects of Ca²⁺ mediated by the C1 cassette, we used the naturally occurring splice variant GluN1-2a (N1-2a), which lacks C1 (10). We expressed wild-type NMDA receptors (N1-2a/N2A, WT) and wild-type YFP-tagged calmodulin (YFP-CaM_WT) in HEK293 cells and recorded whole cell currents successively without (0 mM) and with (2 mM) Ca²⁺. We elicited currents with pulses of supersaturating glutamate (1 mM, EC₅₀, 1–3 μM) (37) sufficiently long such that both MID and CDI reached steady-state values (5 s), in background glycine (0.1 mM, Gly EC₅₀ <1 μM) (38, 39) (Fig. 1 C), to prevent glycine-dependent desensitization (40). We found that 2 mM Ca²⁺ decreased the steady-state current by 58.8 ± 8.2%. This compares well with values reported with this same metric in neurons (41%) (11) and recombinant (N1-1a/N2A) receptors (46.1%) (41). Next, we used Eq. 4 to calculate CDI as defined here, at all time-points, I(t), in paired recordings (5 sweeps/cell). We found that CDI equilibrated to a midrange value, CDI_EQ = 0.55 ± 0.09 (N = 7), close to previously reported magnitudes, and estimate for the first time, to our knowledge, its relatively fast onset, τ_CDI = 0.56 s (Fig. 1 C), which falls well within our chosen observation time (5 s).

Figure 1.

Measuring pure CDI of NMDA receptors. (A) Shown here are simulated NMDA receptor currents using a declining exponential function. In the absence of external Ca²⁺, (black) currents display (MID, I_pk/I_ss) with values between zero and unity; in 2 mM external Ca²⁺, (red) currents have lower peaks and increased desensitization; superimposed traces normalized to I_pk illustrate the additional desensitization due specifically to Ca²⁺-dependent inactivation (shaded area). (B) Given here is a schematic of GluN1 (N1, blue) with alternatively spliced cassettes C0, C1, and C2, and GluN2A (N2A, green), with W1017 highlighted (red line), illustrating reported CaM-binding sites. (C) (Top) Paired whole-cell currents from HEK293 cells coexpressing N1-2a and N2A subunits with YFP-CaM_WT were recorded in the absence of divalent cations (black) and with Ca²⁺ (red), are shown normalized to peak and superimposed. (Bottom) CDI (black) is quantified with Eq. 4 along the recording coordinate and averaged across cells, with standard error (gray shaded). CDI-time curves were fit with an exponential of form CDI(t) = CDI_EQ + A × e^−t/τCDI. (D) Shown here is the CDI time constant (left) and steady-state levels for the conditions indicated (^∗p < 0.05, Mann-Whitney U-test). (E) (Left) Exemplar whole-cell recordings of N1-2a and N2A subunits with YFP-CaM_WT were recorded using a recovery from MID protocol in the absence (black) and presence (red) of external Ca²⁺. (Dashed curve) Shown here is an exponential function fitted to the data. (Top right) Fraction of recovery from MID defined as the percent of peak current at the test pulse relative to the conditioning pulse. Data represent mean ± SE of N = 5 cells. (Dashed curve) Shown here is a fitted exponential function. (Bottom right) Shown here is recovery from the CDI curve, derived from fitted exponential curves to recovery of MID data above, using Eq. 4. To see this figure in color, go online.

As expected, receptors lacking the GluN1 C-terminal domain (N1^ΔCTD) had no significant CDI (CDI_EQ = 0.08 ± 0.07, N = 6, P = 0.0005 relative to WT) (Fig. 1 D). Therefore, Eq. 4 correctly reports CDI regardless of intrinsic differences in the conductance or gating kinetics of the NMDA receptor preparation used (42). Moreover, we found that adding back the C0 cassette to truncated receptors (N1^ΔC0) rescued CDI to wild-type values (τ_CDI = 0.44 ± 0.10 s, CDI_EQ = 0.44 ± 0.06, N = 7, P = 0.2 relative to WT), further validating the robustness of our CDI measure.

In addition to the two CaM binding-sites in GluN1 subunits, CaM also binds to the GluN2A subunit (43). To learn whether this site (W1017) contributes to CDI, we removed it by truncating the GluN2A subunit at position 944 (N2A^Δ944) and assayed the mutated receptors (N1-2a/N2A^Δ944). This mutant had WT-like CDI (τ_CDI = 0.40 ± 0.07 s, CDI_EQ = 0.40 ± 0.08, N = 6, P = 0.6 relative to WT) consistent with previous reports that the C0 portion of GluN1 subunits is necessary and sufficient for NMDA receptor CDI (Fig. 1 D) (9, 10). Last, we verified the Ca²⁺ dependence of CDI by substituting external Ca²⁺ with Ba²⁺ (9, 41). As expected, our measurements also indicated the absence of CDI in these conditions (CDI_EQ = 0.07; N = 5, P = 0.0002) (Fig. 1 D).

Next, we determined the kinetics of recovery from CDI using a classic two-pulse protocol consisting of a conditioning glutamate pulse (5 s) followed after increasingly longer resting intervals by a test glutamate pulse (2 s) (44), with glycine present continuously. We performed this protocol in Ca²⁺-free and 2 mM Ca²⁺ external solutions (Fig. 1 E, left) and fitted with exponential functions. Values of the corresponding curves were used to determine the recovery time from CDI using Eq. 4, τ_rec = 9.3 s (Fig. 1 E, right). This value is substantially shorter than values reported in previous studies, which did not isolate CDI from MID (45).

Together, these results validate the use of Eq. 4 as a robust, rigorous, and specific metric for NMDA receptor CDI across experimental conditions and preparations. They also establish for the first time, to our knowledge, that CDI equilibrates and recovers faster than previously reported. In subsequent analyses, we use the equilibrium CDI value (CDI_EQ) as a consistent index of CDI magnitude.

Define a cellular system to specifically isolate CDI

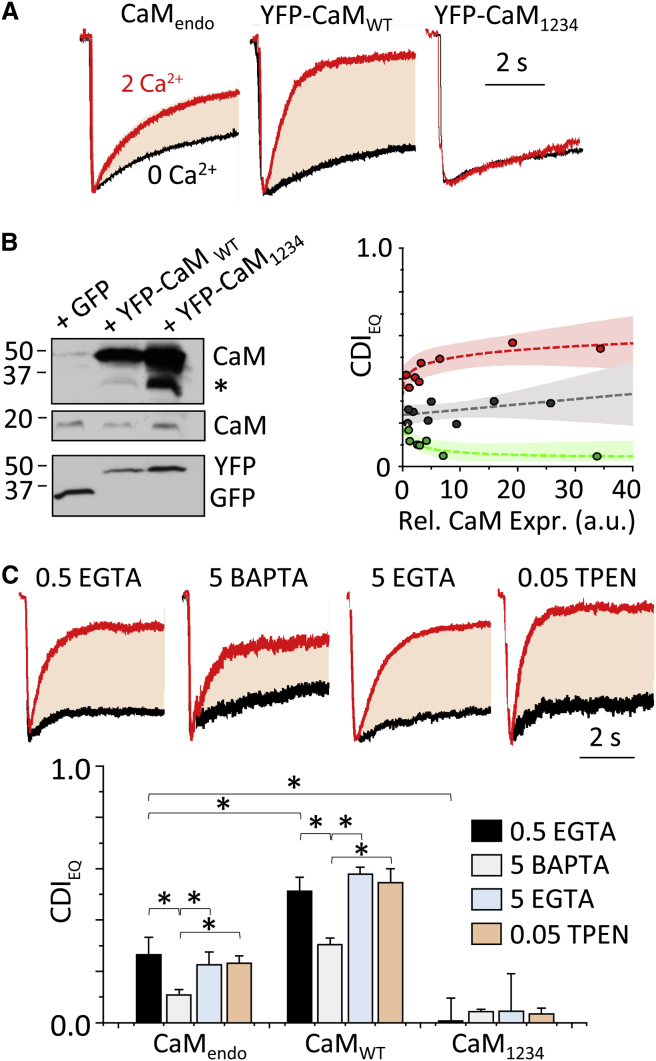
HEK293 cells express low endogenous levels of CaM and CaM-modulated enzymes (46). In the preceding experiments, we overexpressed recombinant CaM to preclude possible variability in the observed CDI due to uncontrolled levels of endogenous CaM. Thus, we asked whether experimental manipulations in CaM expression levels affect NMDA receptor CDI in our system (Fig. 2 A). In cells transfected with only NMDA receptor subunits (N1-2a, N2A, and GFP) the measured CDI (0.26 ± 0.07) was approximately half that observed in cells that overexpressed recombinant CaM_WT (Fig. 1 C). This suggests that the levels of endogenous CaM (CaM_endo) are insufficient to produce full inactivation, and that the extent of NMDA receptor CDI may have been underestimated in previous studies (45). To test this possibility, we overexpressed recombinant CaM₁₂₃₄, a CaM mutant with Asp to Ala substitutions at all four Ca²⁺-binding sites rendering it Ca²⁺ insensitive (47). We reasoned that if the increase in CDI produced by CaM overexpression reflects limitations on CDI imposed by subsaturating levels of endogenous CaM, overexpressing CAM₁₂₃₄ would reduce CDI even further by a dilution effect. Consistent with this scenario, we found that overexpressing CaM₁₂₃₄, abolished CDI (0.01 ± 0.09; P = 0.004 relative to CaM_endo). Taken together, these results indicate that in HEK cells, endogenous levels of CaM produce about one-half of the CDI observed with CaM overexpression and, therefore, manipulating cellular CaM levels can effectively modulate NMDA receptor CDI.

Figure 2.

CaM levels modulate CDI magnitude. (A) Traces illustrate paired whole-cell recordings obtained from HEK293 cells expressing NMDA receptors and CaM as indicated, normalized to peak amplitude and superimposed. (B) (Left) Given here are Western blots of proteins isolated from HEK cells transfected with GFP and YFP-CaM, WT or mutant (indicated at top), and probed with antibodies specific for CaM, GFP, and YFP (indicated at right); (^∗) nonspecific bands from CaM primary antibody are indicated. (Right) CDI dependency on cell-to-cell variation in relative CaM expression (measured as YFP fluorescence) is shown for CaM_WT (red) CaM_endo (GFP, gray), and CaM₁₂₃₄ (green). Shaded regions reflect the upper and lower 95% confidence intervals of the fits (bold lines). (C) (Top) Representative whole-cell currents were recorded under indicated intracellular buffering conditions. (Bottom) Shown here are summary results from measurements as in (A) with the indicated metal chelators included in the recording pipette (mean ± SE; ^∗p < 0.05, Mann-Whitney U-test). To see this figure in color, go online.

This conclusion is supported by Western blots, which show that in HEK293 cells transfected with either wild-type or mutant CaM, we detected substantially more intense staining for the higher molecular weight CaM (YFP-CaM) relative to untagged CaM (endogenous) (Fig. 2 B, top). The blots also showed a lack of low-molecular-weight species in the YFP-stained gel, confirming the integrity of the YFP-CaM protein through the experiment. The measured CDI was independent of cell-to-cell variability in the level of overexpressed CaM, as evaluated by fluorescence intensity, thus controlling for possible nonspecific effects of overexpressed proteins (Fig. 2 B, bottom). Importantly, intracellular EGTA, a slow Ca²⁺ buffer, or TPEN (a nonspecific divalent chelator) did not affect CDI in cells expressing either CaM construct, whereas intracellular BAPTA, a fast Ca²⁺ buffer, substantially reduced CDI in all cases, as previously reported (Fig. 2 C). Intracellular chelators themselves did not exhibit any effect on MID (Fig. 2 C, top).

Our observation that even strong intracellular Ca²⁺ buffering (with BAPTA) preserves a significant fraction of CDI is consistent with previous results and supports the hypothesis that the Ca²⁺ sensor (i.e., the CaM pool responsible for CDI), whether freely diffusing or associated with the channel, resides proximally to the fluxing pore (11). To discern between the preassociation and the Ca²⁺-triggered association models, we set up to estimate the distance between the Ca²⁺-source (channel pore) and the Ca²⁺ sensor (CaM) by first calibrating the magnitude of CDI to intracellular levels of Ca²⁺ and then ascertaining the distance at which fluxed Ca²⁺ reaches the concentration necessary to produce the experimentally observed CDI.

Calibrate the magnitude of CDI to intracellular [Ca²⁺] levels

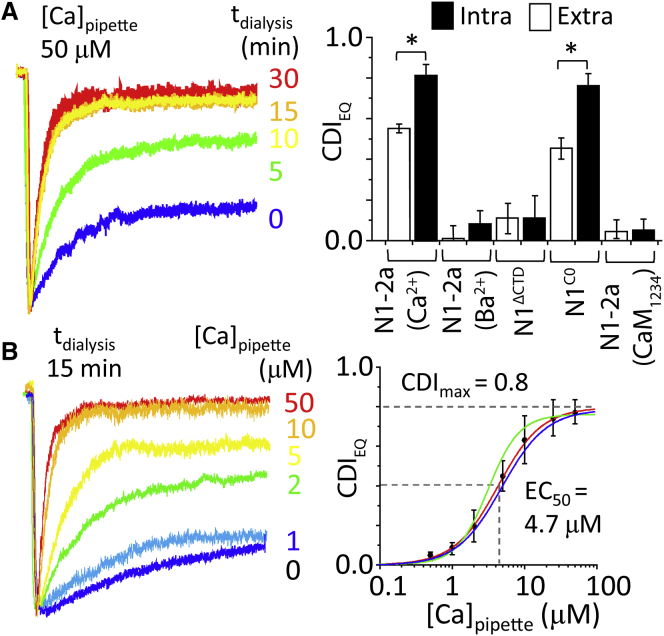
We manipulated intracellular [Ca²⁺] by filling the recording electrode with buffered solutions of controlled free [Ca²⁺] (HEDTA, K_D = 4 μM). In HEK293 cells expressing N1-2a/N2A receptors and CaM_WT, we recorded whole-cell currents in response to glutamate applications (1 mM for 5 s) with background glycine (0.1 mM). Relative to traces recorded in 0 μM intracellular Ca²⁺, which remained stable from sweep to sweep, with 50 μM Ca²⁺, we observed a slow time-dependent decrease in steady-state current levels (Fig. 3 A), as expected for slow dialysis upon break-in. We calculated CDI with Eq. 4 for each sweep by relating its waveform to that recorded at break-in (0 min), ahead of substantial [Ca²⁺] influx. Fitting a monoexponential function to the time-CDI_EQ data, we found that CDI equilibrated within ∼8 min of break-in (data not shown). In subsequent experiments, we used 15 min as a consistent time point to measure CDI for a given intracellular [Ca²⁺]. We verified that the reduction in NMDA receptor current observed upon Ca²⁺ dialysis was Ca²⁺-dependent, CaM-dependent, and C0-dependent as required for CDI (Fig. 3 A). With this approach we varied the intracellular free [Ca²⁺] between 0.5 and 50 μM (Fig. 3 B) and fitted the Hill equation to the Ca²⁺ concentration-dependent increase in CDI to estimate a half-maximal dose EC₅₀ = 4.7 ± 0.3 μM for free [Ca²⁺], a maximal effect CDI_max = 0.80, and a cooperativity factor n = 1.8 (N = 4–7 for each Ca²⁺ dose).

Figure 3.

Determining CDI sensitivity to [Ca²⁺]. (A) (Left) Given here are whole-cell NMDA receptor currents recorded with 50 μM free Ca²⁺ in pipette, at indicated times after break-in. (Right) Shown here is a summary of CDI values at 15 min postbreak-in, with indicated constructs and permeating divalent cation (Ca²⁺ or Ba²⁺; Intra, intracellular; Extra, extracellular). (B) (Left) Currents were recorded from NMDA receptors with indicated free [Ca²⁺] in the pipette recorded at 15 min postbreak-in. (Right) Given here are intracellular Ca²⁺ dose-response data (points) and fitted Hill function for WT receptors (red); pretreated with calcineurin inhibitor (green, EC₅₀ = 3.9 μM; CDI_max = 0.76); or N1^ARPAAR (blue, EC₅₀ = 5.2 μM; CDI_max = 0.78; blue), ^∗P < 0.05, Mann-Whitney U-test. To see this figure in color, go online.

These results show that even in maximally effective intracellular free [Ca²⁺], a considerable residual current persists, and indicates that fully inactivated NMDA receptors continue to gate, with a lower open probability (P_o). This is consistent with previous single-channel recordings of inactivated channels (48, 49). In our hands, the measured CDI sensitivity to internal free [Ca²⁺] was independent of the Ca²⁺-dependent phosphatase calcineurin (6, 50), and was not caused by binding of effluxed Ca²⁺ ions at the external DRPEER motif (1, 2). First, treatment with an inhibitor of calcineurin (6 μM FK-506, 30 min) had no effect on the measured [Ca²⁺] sensitivity of CDI (EC₅₀ = 4.9 ± 1.2 μM; Fig. 3 B, blue). Second, a mutant NMDA receptor that lacks the external Ca²⁺-binding site (N1^ARPAAR) had WT-like sensitivity (EC₅₀ = 2.8 ± 0.6 μM; Fig. 3 B, green). Thus, the dialysis assay measured precisely and specifically the CDI produced by controlled concentrations of free intracellular [Ca²⁺]. Together these experiments demonstrate that CDI magnitude is a robust reporter of the free [Ca²⁺] that engages CaM to initiate CDI. At what distance from the mouth of the NMDA receptor channel can we expect to find this concentration?

Estimate the distance between the Ca²⁺source and CaM

We simulated spatiotemporal Ca²⁺ diffusion profiles from a point source based on Fick’s law in hemispherically symmetrical space as described in the literature (35, 51, 52). This model predicts that channel openings produce steep spatiotemporal [Ca²⁺] gradients near the mouth of the channel, which can be approximated for a given radial distance and a known time-averaged unitary Ca²⁺ flux.

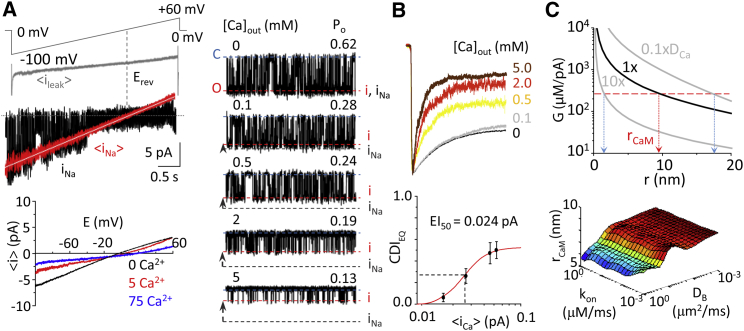
We first determined the unitary fractional Ca²⁺ current (i_Ca) of N1-2a/N2A channels at each external Ca²⁺ tested from conductance changes measured by single-channel voltage ramps (Fig. 4 A; Table S1). Our values were similar to those obtained from native rat hippocampal receptors using this method (28) and with optical measurements (53, 54). We scaled the unitary i_Ca by the equilibrium P_o measured from stationary single-channel records for each extracellular Ca²⁺ concentration (Fig. 4 B; Table S1) to estimate an average unitary Ca²⁺ flux at steady-state (〈i_Ca〉). Because CDI measured from steady-state macroscopic currents reflects the ensemble inactivation produced by the steady-state time-averaged [Ca²⁺], the CDI versus [Ca²⁺] relationship can be transformed to a CDI versus 〈i_Ca〉 function. We varied extracellular Ca²⁺ between 0 and 5 mM (in constant 150 mM Na⁺) and found that half-maximal CDI occurred for EI₅₀ = 0.02 pA Ca²⁺ current. Hereafter, we restricted our analysis to these conditions to avoid reduction in unitary current due to Ca²⁺-block (55). To relate these data into CDI sensitivity to intracellular [Ca²⁺], we determined the [Ca²⁺]/flux ratio, G = [Ca²⁺]/〈i_Ca〉, as EC₅₀/EI₅₀, and for N1-2a/N2A channels, we found this to be G = 235 μM/pA.

Figure 4.

Dependence of CDI on unitary Ca²⁺ influx. (A) (Left, top) Shown here is a schematic of voltage-ramp protocol and average leak current (〈i_leak〉) detected during cell-attached voltage ramps with no channel activity (gray). Given here are single-channel Na⁺-only currents (i_Na) from single sweep (black) and averaged over 70–100 sweeps (red). The averaged current (〈i〉) was recorded at multiple external [Ca²⁺] (0–75 mM). (Bottom) The 〈i〉 was fit with the Jahr and Stevens model (white line) to determine conductance (γ_in), reversal potential (E_rev), and fractional Ca²⁺ current (f_Ca) (28). (Right) Given here are representative stationary unitary currents in cell-attached patches at the indicated external [Ca²⁺]. Unitary current amplitude values (i) C and O indicate closed and open current levels. (B) (Top) Whole-cell currents were recorded with the indicated external [Ca²⁺] (5 mM BAPTA internal). (Bottom) Shown here is CDI measured with increasing external [Ca²⁺] plotted against the equivalent unitary Ca²⁺ current corrected for channel opening, 〈i_Ca〉 (see Table S1). EI₅₀ = 0.024 pA was extracted from the Hill equation fitted to data. (C) (Top) Simulated steady-state Ca²⁺ spatial profile during channel opening is corrected for channel P_o to reflect the time-averaged Ca²⁺ signal driving CDI_EQ in macroscopic recordings plotted for various Ca²⁺ diffusion coefficients. Experimentally derived [Ca²⁺]/flux ratio (EC₅₀/EI₅₀, red horizontal dashed line) predicts r_CaM = 9 nm. When Ca²⁺ diffusion coefficient (D_Ca) is varied across several orders of magnitude, r_CaM likely resides between 2 and 16 nm (vertical pink dashed lines). (C) (Bottom) Systematic error in the model was evaluated as BAPTA kinetic (k_on) and diffusion (D_B) parameters were varied across several orders of magnitude; the estimated distance of r_CaM remains approximately stable for a given value of D_Ca. To see this figure in color, go online.

With this experimental value, we estimated the distance at which CaM resides (r_CaM), using Ca²⁺ diffusion simulations (56, 57) and, using Eq. 5, found this to be 9 nm:

$$G=\frac{E{C}_{50}}{E{I}_{50}}=\frac{\left[{\text{Ca}}^{2+}\right]}{i_{\text{Ca}}}=\frac{1}{4\pi FDr}{e}^{-r/\sqrt{D_{\text{Ca}}/k_{\text{on}}{B}_{\text{T}}}},$$ (5)

Given that Eq. 5 assumes no buffer saturation, which may not hold in close proximity to the pore, we also used an alternative approach. We simulated Ca²⁺ diffusion from a point source using a discretized version of Fick’s laws assuming hemispherical symmetry in the presence of diffusible buffer (see Table S2 and Supporting Material) (35, 51, 52). Results of the Ca²⁺ diffusion simulation show that the temporal Ca²⁺ profile rises within a submillisecond timescale to a steady-state value during channel opening and decays to background Ca²⁺ within a submillisecond timescale of channel closing. Thus, relative to the slow millisecond timescale gating kinetics of the channel, the temporal Ca²⁺ profile in the presence of buffer during channel opening can be approximated well as a stepwise pulse from 0 μM to a steady-state value during channel opening. Therefore, for simplicity we used the steady-state spatial free [Ca²⁺] profile when determining r_CaM. The free Ca²⁺ profile from the simulation is transformed to reflect the single-channel G factor by normalizing the concentration to the measured unitary Ca²⁺ current, i_Ca. Finally, this unitary open channel G factor (G_o) is transformed to reflect channel stochasticity in the steady-state macroscopic response according to the previously derived relation (52):

$$G=G_O\cdot \frac{P_O^{1-n}}{n},$$ (6)

where G is the steady-state macroscopic gain, n is the Hill coefficient determined from intracellular dialysis that we found to be 1.8 (Fig. 3 B), P_o is the single-channel steady-state open probability, and G_o is the free intracellular [Ca²⁺] generated by channel opening normalized by the unitary Ca²⁺ current, i_Ca. Assuming an initial Ca²⁺ diffusion coefficient (D_Ca) of 0.4 μm²/ms (35, 51), we calculated that G corresponded to r_CaM = 9 nm (Fig. 4 C, top), consistent with our first approach. However, D_Ca values are approximate; we varied this parameter, and found that for the range between 10 × D_Ca and 0.1 × D_Ca, r_CaM varied between 3 and 16 nm. Further, systematically varying other buffer diffusion (D_B) and buffer binding kinetics (k_on) parameters also had little effect on the estimate of r_CaM for a given value of D_Ca (Fig. 4 C, bottom). Therefore, in all cases, CaM likely exists well within the Ca²⁺ nanodomain (<50 nm) generated by the channel, and is likely temporally coupled to the receptor’s activity.

Probing CaM/receptor interaction models

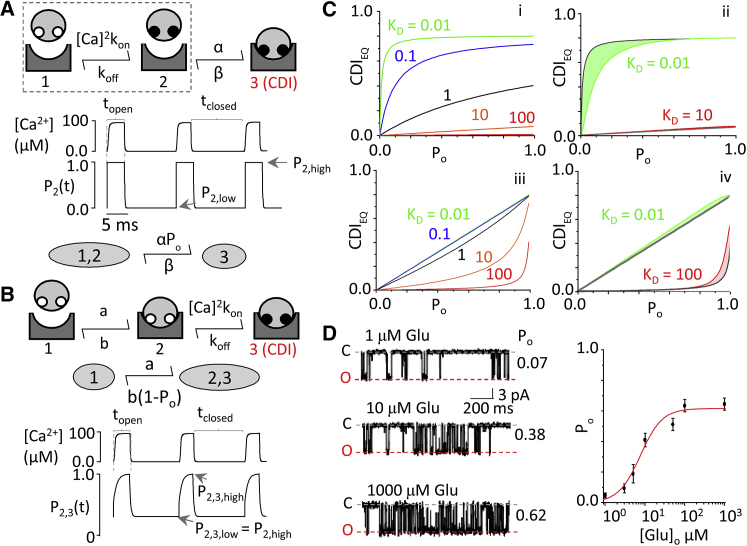
Our observations that CaM₁₂₃₄ can ablate CDI in HEK293 cells and that the receptive CaM resides within nanometers distance from the pore are consistent with a model where apoCaM resides on the C0 segment of the N1. However, given the low level of CaM endogenous to HEK293 cells, it is conceivable that overexpression of CaM₁₂₃₄ excludes CaM_endo from the nanodomain volume, thus reducing its access to the channel. To more rigorously test whether apoCaM preassociates with the channel, we considered the behavior of two conceptual models of CaM/channel interaction and their response to a train of Ca²⁺ spikes produced by channel gating (Fig. 5, A and B). Using reported in vitro values of C0 affinity for apoCaM (19) and holoCaM (8), we found that each model predicted unique time-dependent behaviors. Next, we considered these behaviors as we varied the frequency of the Ca²⁺ trains, by systematically varying the channel P_o (Fig. 5 C, i and iii). To simplify the three-state conceptual models into two-state models, we restricted our analysis to only the fast Ca²⁺-binding lobe of CaM (N-lobe) (Fig. 5, A and B; see Supporting Material). For each model, we derived the equation that predicts the steady-state magnitude of CDI (CDI_EQ) as a function of steady-state Ca²⁺ influx as determined from channel open probability (P_o). For holoCaM association, we have model 1:

$$CD{I}_{\text{EQ}}=CD{I}_{\max }\cdot \frac{\alpha \cdot P_O}{\alpha \cdot P_O+\beta },$$ (7)

where α is the holoCaM binding rate, β is the holoCaM unbinding rate, and CDI_max corrects for the low P_o of inactivated channels. We measured CDI_max directly with our Ca²⁺ dialysis assay, and found it to be 0.8 (Fig. 3). For (apoCaM preassociation), we have model 2:

$$CD{I}_{\text{EQ}}=CD{I}_{\max }\cdot \left(\frac{a}{a+b\cdot \left(1-P_O\right)}-\frac{a\cdot \left(1-P_O\right)}{a+b}\right),$$ (8)

where a is the apoCaM binding rate, and b is the apoCaM unbinding rate. Importantly, even when varying apoCaM and holoCaM affinities for C0, which are known only under in vitro conditions (10, 20), the predicted CDI_EQ-P_o relations remained distinct from each other (Fig. 5 C). Therefore, these relationships impose no assumptions regarding the values of CaM affinity for the channel, and allow us to keep them as free parameters. In addition, we took two important precautions (see Supporting Material). First, we measured CDI in HEK293 cells loaded with 5 mM BAPTA to restrict Ca²⁺ elevations to local Ca²⁺ nanodomains, which synchronize with channel gating and, therefore, with P_o. Second, we coexpressed channels with CaM₃₄, to restrict Ca²⁺ binding to the N-lobe. In our cells, mutants with ablated Ca²⁺-binding at either the N- or C-lobe were fully able to elicit CDI (data not shown). Biochemically, N- and C-lobe mutants are equally capable of displacing actinin from GluN1 C0, which is a likely molecular determinant of CDI (18).

Figure 5.

CDI models reveal unique, testable behaviors. (A) (Top) Model 1 represents NMDA receptor association with holoCaM with subsequent Ca²⁺. apoCaM (open white circles) binds Ca²⁺ (solid circles) before binding to the channel. (Middle) Time-dependent behavior of subsystem (dashed box) is given, representing Ca²⁺ binding to CaM using only fast, N-lobe kinetics in response to a train of Ca²⁺ influx from a gating channel. State 2 (CaM bound with Ca²⁺) of the subsystem is pulsatile between P_2,high and P_2,low occupancy probabilities, in tight synchrony with gating. (Bottom) Shown is simplification of a three-state model given rapid equilibration of its subsystem. (B) (Top) Model 2 represents NMDA receptor association with apoCaM with subsequent Ca binding. (Middle) Given is a simplified model 2 assuming N-lobe kinetics. (Bottom) Shown is behavior of condensed state 2, 3 in response to a train of Ca²⁺ in-flux. The pulsatile system oscillates between P_2,3,high and P_2,3,low. P_2,3,low is set by the fraction of channels preassociated with apoCaM at rest, P_2,high. (C) (i) Given here is evaluation of Eq. 7’s corresponding model 1 across all values of P_o. As CaM affinity for the channel is increased, the system exhibits saturation kinetics. As affinity decreases, the system becomes linear. (ii) Deviations of the simplified model in Eq. 7 from numerical integration to the full three-state model did not affect the overall shape or predicted behavior. (iii) Given here is evaluation of Eq. 8’s corresponding model 2 across all values of P_o. As CaM affinity for the channel is increased, the system exhibits a linear trend. As affinity decreases, the system uniquely develops an upward curvature. (iv) Deviations of the simplified model in Eq. 8 from numerical integration in the full three-state model were minimal and did not affect the overall shape or predicted behavior. (D) (Left) Exampled here is single-channel activity elicited by indicated glutamate concentration. (Right) Given here is a calibration curve for glutamate concentration and P_o determined from cell-attached single-channel recordings. To see this figure in color, go online.

Resident apoCaM mediates CDI

To control the steady-state P_o, we varied the glutamate concentration used to elicit current. Using cell-attached single-channel recordings, we first calibrated the glutamate concentration to the channel equilibrium P_o. The resulting [Glu]-P_o relation allowed the [Glu]-CDI_EQ relation measured from whole-cell recordings to be transformed to a CDI_EQ-P_o relation (Fig. 5 D). Under these conditions, the measured CDI_EQ-P_o relationship is roughly linear, as predicted by model 2 (Fig. 6 A). Fitting Eqs. 7 and 8 to these data estimated the physiological apoCaM K_D = b/a = 0.19 μM (R² = 0.929; sum of squares errors = 0.021). We noted that model 1 could also fit the data when holoCaM k_off ≫ k_on, with a predicted holoCaM K_D = β/α = 0.49 μM (R² = 0.934; sum of squares errors = 0.019). However, this is unlikely to be true given substantial evidence that holoCaM has much higher affinity for C0 than apoCaM (10, 20, 58), weakening the case for model 1.

Figure 6.

CaM preassociates with NMDA receptors. (A) Both model 1 and model 2 describe well the dependency of CDI on P_o (varied by changing glutamate concentrations). (B) (Top) C0 sequence indicates CaM binding region. Residues are color-coded by property relevant to CaM binding: positive charge (blue), negative charge (red), hydrophobic (gray). (Bottom) Whole-cell currents recorded from N1-2a^W858A/N2A receptors have altered CDI at all glutamate concentrations tested. (C) (Top) Given here are unitary currents of high-P_o mutant N1-2a^{A652Y, W858A}/N2A. (Bottom) Given here are whole-cell currents from the mutants indicated. (D) Shown here is a CDI_EQ-P_o profile with pooled data from N1-2a^A652Y/N2A (black circles) and high-P_o double mutant N1-2a^{A652Y, W858A}/N2A (red circle) fit with model 1 (holoCaM association, gray) and model 2 (apoCaM association, blue) (N = 4). To see this figure in color, go online.

We further probed the models by altering CaM affinity for the channel. The main feature distinguishing the models is the upward curvature revealed by model 2 at low affinity values. A previous study pointed to several hydrophobic residues on GluN1 C0 (850–862) as critical for CaM binding (Fig. 6 B, top) (59); specifically, a Trp residue is a critical anchoring site for CaM to many target proteins (60, 61). We introduced a point mutation at W858 on C0 (9, 20), which clearly perturbed CDI (Fig. 6 B, bottom). However, because WT channels have a maximum P_o = 0.62, our ability to resolve the upward curvature was limited. We improved the resolution of the CDI_EQ-P_o relation by incorporating data obtained with the high-P_o mutant (31), GluN1^A652Y (P_o = 0.81) (Fig. 6 C, top). GluN1^A652Y itself did not prevent CDI (Fig. 6 C, bottom left), and the double mutation GluN1^{A652Y, W858} also reduced CDI (Fig. 6 C, bottom right). With these data, we observe clear upward curvature, which is only predicted by model 2 (Figs. 5 C and 6 D). Fitting the model to this pooled dataset, and assuming GluN1^A652Y does not perturb CaM/channel binding, predicted an apoCaM K_D = b/a = 18.17 μM, nearly two orders-of-magnitude larger than predicted for wild-type, and consistent with a critical role for C0 W858 in binding CaM.

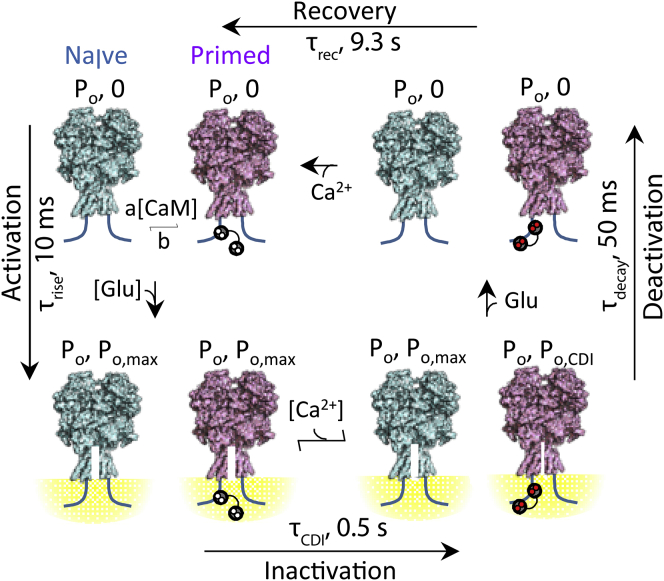
Based on our collective data and consistent with previous results we propose a kinetic mechanism for activity-dependent CDI of NMDA receptors with the following distinguishing features (Fig. 7). At rest, NMDA receptors interconvert between primed (apoCaM bound) and CaM-free forms. Upon agonist binding, both forms activate and initially gate with similar high P_o to initiate Ca²⁺ influx. The fluxed Ca²⁺ reaches ∼140 μM at ∼9 nm distance from the pore, engages apoCaM, and CaCaM-bound channels switch into low P_o (inactivated) to initiate CDI within 0.5 s. Upon glutamate removal, channels deactivate, the Ca²⁺ gradient dissipates, and closed channels recover from inactivation into the resting state, within 9.2 s. This model incorporates numerous means of CDI regulation, including reciprocal affinities of apoCaM and NMDA receptors, apoCaM affinity for Ca²⁺, CaM concentration, and NMDA receptor Ca²⁺-permeability and gating kinetics. Therefore, the model predicts that changes in these parameters, whether physiological or pathological, will influence the rate and extent of NMDA receptor CDI.

Figure 7.

Proposed sequence of molecular events underlying CDI. The model posits that at all times, NMDA receptors exist in a dynamic equilibrium of CaM-free (teal) and CaM-bound (magenta) receptors, which depends on endogenous levels of CaM, and the mutual affinities of the two partners. Upon binding agonist (Glu), receptors transition into highly active (P_o, _max) Ca²⁺-permeable conformations, leading to current influx (τ_rise) and the formation of intracellular Ca²⁺ nanodomains (yellow). Intracellular Ca²⁺ binds CaM, according to the local level of Ca²⁺ in the vicinity of CaM, and only CaM-bound channels transition into inactivated conformations (τ_CDI), which have very low activity (P_o,_CDI), leading to a population of active and inactivated channels. Upon glutamate removal, both active and inactivated receptors lose glutamate and deactivate with unique time constants, and the current decays with complex kinetics (τ_decay). As intracellular [Ca²⁺] dissipates, Ca²⁺ will dissociate from CaM, returning inactivated channels to their resting state (τ_rec). To see this figure in color, go online.

Discussion

We used, to our knowledge, a new rigorously controlled quantification of NMDA receptor CDI, which is independent from the channel’s intrinsic kinetics and conductance. This allowed us to compare CDI across mutants and experimental conditions and to estimate, by two methods, that the pool of CaM responsible for CDI responds to NMDA receptor Ca²⁺-flux within ∼9 nm of the channel pore. In addition, we present evidence that CaM associates with NMDA receptors before receptor activation and measure relatively short inactivation (0.5 s) and recovery (9.2 s) times. To our knowledge, this is the first electrophysiological evidence for apoCaM preassociation with NMDA receptors in living cells. These results and conclusions are consistent with recent experimental data indicating that brief synaptic events initiate NMDA receptor CDI (13). Thus, in addition to a serving as a protective feedback mechanism at extrasynaptic sites, CDI likely serves multiple physiological roles, including modulating Ca²⁺ influx during synaptic transmission.

A standardized metric for Ca²⁺-dependent inactivation

A lack of consistency in the mathematical definition of NMDA receptor CDI across existing studies has likely contributed to the high variability of CDI values reported in the literature and hampered the rigorous investigation of this process. Some studies quantified CDI as the percentage of macroscopic desensitization, which assumes that no desensitization occurs in the absence of Ca²⁺ (9, 22, 41, 62); this approach most likely overestimated CDI. To address this limitation, subsequent studies aimed to eliminate the contribution of glycine-dependent desensitization by focusing on currents elicited with varied agonist concentrations (11). However, agonist concentration also influences channel P_o and thus the influx of Ca²⁺ that triggers CDI (Fig. 6); this approach most likely underestimated CDI. In addition, variability in the preparations used whether due to differences in the NMDA receptor isoforms expressed, or in the levels of endogenous CaM, may have contributed to the broad range of reported CDI values. Here, we adapted a metric initially developed for voltage-gated channels (34, 35, 36), which corrects for intrinsic Ca²⁺-independent desensitization (Eq. 4). With this approach, we show that in some cases endogenous levels of CaM may be insufficient to support full CDI of NMDA receptors (Fig. 2), and that fully inactivated channels gate with substantial open probabilities (Fig. 3).

ApoCaM preassociation is a conserved mechanism of ion channel regulation

CaM is an ancient, highly conserved Ca²⁺ sensor, which through direct interaction with a variety of target proteins, imparts Ca²⁺ sensitivity onto fundamental cellular processes. This general mechanism assumed initially that the interaction between CaM and its target proteins is Ca²⁺-dependent. However, ensuing evidence demonstrated that CaM may interact with targets independently of Ca²⁺ (63). The multiplicity of Ca²⁺ permeable channel families that associate with apoCaM, including Ca_v (64), Na_v (5, 65), TMEM16A/16B (66), RyR (67), SK channels (68), and IP₃R (69), suggests that preassociation with apoCaM is an evolutionarily conserved mode of ion channel regulation. In support of this hypothesis, mutations that upset the apoCaM interaction with Ca²⁺ or with the channel correlate with pernicious diseases (70, 71, 72, 73). Our functional evidence for apoCaM preassociation with NMDA receptors adds NMDA receptors to the list of channels that use this regulatory mechanism. Our in situ estimated K_D for the NMDA receptor/apoCaM interaction (0.19 μM) is lower than that observed in vitro (19, 20). This may reflect key differences in the undisturbed cellular milieu, which may affect CaM affinity for its targets, such as posttranslational modifications (74). Further, additional factors may control apoCaM association with its targets; for example, within dendritic spines, high levels of neurogranin increase Ca²⁺ dissociation from CaCaM, and thus increase the fraction of apoCaM within this microenvironment (12, 75). Such a local enrichment of the mobile pool of apoCaM may increase its association with NMDA receptors to affect the range of CDI values.

Divergent mechanisms for local/global Ca²⁺ signaling

From a physiological standpoint, CDI of Ca²⁺-permeable channels may represent an autoinhibitory mechanism likely safeguarding against excess Ca²⁺ influx and its cytotoxic effects. However, aside from being sensitive to this local Ca²⁺ influx, CDI may reflect the response to other, proximal or more distant, Ca²⁺ sources (global Ca²⁺). Sensitivity to local and/or global Ca²⁺ is ascertained experimentally by examining the effects of intracellular application of fast (BAPTA) and slow (EGTA) Ca²⁺ buffers (57). This approach established that Ca_v channels can respond differentially to local and global Ca²⁺ transients (76) due to distinct affinities of the two CaM lobes for Ca²⁺, combined with distinct affinities of CaM-binding sites in Ca_v channels for apoCaM and CaCaM (35).

Our data together with previous studies strongly suggest that in NMDA receptors, the apoCaM and CaCaM sites overlap (10), thus predicting low or nonexistent lobe-specific spatial selectivity to the Ca²⁺ source. Therefore, both local and global Ca²⁺ may initiate NMDA receptor CDI. This hypothesis is consistent with evidence suggesting that CDI of NMDA receptors may occur in response to Ca²⁺ sources other than the target receptors (11, 77). However, if, as proposed in our model, during NMDA receptor activation all primed channels inactivate, additional Ca²⁺ elevations from other sources (global Ca²⁺) would play only a minor role during periods when NMDA receptors are active. This mode of primary sensitivity to local Ca²⁺ may dominate, especially in dendritic spines where spine geometry and endogenous buffering restrict Ca²⁺ diffusion away from the source.

Insights into the molecular mechanism of CDI

Given that CDI has been predominantly studied using macroscopic currents, which manifest on a slow timescale (>1 s), it was previously deemed unlikely that CDI of NMDA receptors would play a role in modulating fast excitatory synaptic transmission (11). However, in this study we revealed that the rates of inactivation (0.5 s) and recovery (9.3 s) are faster than reported earlier (Fig. 1, C and E). Even based on these new faster values, complete inactivation is unlikely to occur during a single synaptic event (<100 ms; Fig. 7). However, the fraction of primed channels and their gating properties at the time of stimulation will influence the extent to which inactivation develops and set the stage for a broad dynamic CDI range. This activity-dependent autoinhibitory feedback allows the cell to tune individual channels within a designated range of activity. Consistent with this, applying purified CaM on the intracellular leaflet of outside-out membrane patches accelerates the deactivation kinetics of macroscopic currents in response to a brief glutamate pulse, in agreement with the hypothesis that CDI can manifest rapidly (48), including during a single synaptic event (13, 78). Given that CDI of NMDA receptors will also depend on numerous other intracellular factors such as α-actinin and CaMKII (9, 18, 58), derivation of kinetic models for CDI in physiological conditions remains an area of future research.

Physiological roles of NMDA receptor CDI

At central synapses, upon binding glutamate, NMDA receptors transition into highly active (P_{o, max}) Ca²⁺-permeable conformations (Fig. 7) (79) and their activity sets the decay kinetics of the synaptic response. This decay is critical in setting the pre/postsynaptic spike interval necessary for determining the magnitude and direction of plasticity. To recapitulate the experimental observations, computational models of spike-timing-dependent plasticity required the inclusion of a direct CaM/NMDA receptor inhibitory interaction (15). Specifically, when the postsynaptic spike preceded the presynaptic spike, the inhibitory CaM/NMDA receptor interaction was necessary to decrease the NMDA receptor mediated Ca²⁺ influx, to predict long-term depression. Although brief synaptic events can initiate NMDA receptor CDI, complete inactivation requires longer periods of activity. Such prolonged activations may occur during periods of high frequency stimulation that engage not only synaptic receptors, but also nonsynaptic receptors through glutamate spillover (80). In this context, factors that affect CDI may serve to control the amplitude and time course of the synaptic current as well as influx at nonsynaptic locations.

In summary, based on the results reported here we put forth a dynamic model of interactions among Ca²⁺, CaM, and NMDA receptors that describes quantitatively the phenomenon presently referred in the literature as “Ca²⁺-dependent inactivation”. This model explains how multiple factors/mechanisms can control NMDA receptor CDI by changing the fraction of active/inactivated receptors. However, several specific questions remain regarding NMDA receptor regulation by CDI, including the molecular mechanism of CDI sensitivity to global Ca²⁺, the kinetic mechanism of CDI, and delineation of the cellular factors regulating CDI. Precise characterization of these events promises to reveal new tools to modulate NMDA receptor activity and may have translational value in addressing Ca²⁺-related disorders and calmodulinopathies.

Author Contributions

G.J.I. and G.K.P. conceived the work, designed experiments, and drafted and revised the paper. G.J.I. performed data acquisition and analysis.

Editor: Vasanthi Jayaraman.