External Evaluation of Two Fluconazole Infant Population Pharmacokinetic Models

ABSTRACT

Fluconazole is an antifungal agent used for the treatment of invasive candidiasis, a leading cause of morbidity and mortality in premature infants. Population pharmacokinetic (PK) models of fluconazole in infants have been previously published by Wade et al. (Antimicrob Agents Chemother 52:4043–4049, 2008, https://doi.org/10.1128/AAC.00569-08) and Momper et al. (Antimicrob Agents Chemother 60:5539–5545, 2016, https://doi.org/10.1128/AAC.00963-16). Here we report the results of the first external evaluation of the predictive performance of both models. We used patient-level data from both studies to externally evaluate both PK models. The predictive performance of each model was evaluated using the model prediction error (PE), mean prediction error (MPE), mean absolute prediction error (MAPE), prediction-corrected visual predictive check (pcVPC), and normalized prediction distribution errors (NPDE). The values of the parameters of each model were reestimated using both the external and merged data sets. When evaluated with the external data set, the model proposed by Wade et al. showed lower median PE, MPE, and MAPE (0.429 μg/ml, 41.9%, and 57.6%, respectively) than the model proposed by Momper et al. (2.45 μg/ml, 188%, and 195%, respectively). The values of the majority of reestimated parameters were within 20% of their respective original parameter values for all model evaluations. Our analysis determined that though both models are robust, the model proposed by Wade et al. had greater accuracy and precision than the model proposed by Momper et al., likely because it was derived from a patient population with a wider age range. This study highlights the importance of the external evaluation of infant population PK models.

INTRODUCTION

Invasive candidiasis is a common cause of morbidity and mortality in extremely premature infants (1). In a prospective multicenter study of extremely low birth weight (birth weight, <1,000 g) infants, over 30% of premature infants with candidiasis died prior to discharge, despite antifungal treatment. Moreover, 73% of the surviving infants experienced either neurodevelopmental impairment postinfection or died at long-term follow-up (2). Given the lack of clinical outcome data to guide dosing in this vulnerable patient population, the use of externally evaluated pharmacokinetic (PK) models is of paramount importance to optimize the dosing of antifungal agents.

Fluconazole is a triazole antifungal agent that is highly active against both Candida albicans and C. parapsilosis, the two most common species of Candida isolated in infants (1). Fluconazole has been shown to be effective for the treatment of invasive candidiasis and may be preferred over alternatives, such as amphotericin B, given its superior side effect profile (3). Available as an injection, tablet, and oral (p.o.) suspension, fluconazole is well absorbed, with its oral bioavailability (F) estimated to be >90% (4, 5). Following oral administration, fluconazole reaches its maximum concentration (C_max) in approximately 1 to 2 h (4). After absorption, fluconazole demonstrates excellent penetration into common areas of colonization/infection, including the central nervous system and lungs (4). The level of plasma protein binding of fluconazole is low at 11 to 12%, and it has a relatively long half-life, estimated to be 30 h in adult patients and 5 to 89 h in pediatric patients (6, 7). Fluconazole undergoes extensive renal elimination, as approximately 80% of the parent drug is excreted unchanged in urine (4). Due to its activity against these organisms, as well as its favorable PK properties, fluconazole is considered an optimal agent for prophylaxis against Candida infection and is one of the most common drugs used in the neonatal intensive care unit (8).

The population PK of fluconazole in infants have been previously described in two separate studies. The first study combined data for premature and term infants from two open-label PK studies performed through the Pediatric Pharmacology Research Unit (PPRU) (9). This study is henceforth referred to as the “PPRU study.” The second study characterized the disposition of fluconazole using data collected through a multicenter, randomized, placebo-controlled trial evaluating the efficacy and safety of fluconazole prophylaxis in infants weighing <750 g at birth (5). This study is henceforth referred to as the “prophylaxis study.” Both the PPRU and prophylaxis studies used a one-compartment PK model to describe the fluconazole concentration data, and both identified patient age and the serum creatinine concentration (SCR) to be important covariates explaining the interindividual variability (IIV) in the clearance (CL) of fluconazole (5, 9).

While the use of population PK modeling is the principal method for uncovering sources of PK variability among individuals in a target population, evaluation of these models is crucial to ensure that they are both accurate and reproducible. External evaluation, considered to be the most stringent form of evaluating a model, allows investigators to identify whether model procedures and/or study-related factors produced bias in a population PK model (10). Unfortunately, external evaluations of population PK models are infrequently performed. Investigators reported in 2007 that only 7% of all population PK models published underwent external evaluation (11). This is particularly concerning in population PK models for children, which are often developed using relatively small sample sizes and sparse data. Given the clinical importance of optimizing fluconazole dosing in infants, we sought to perform an external evaluation to characterize the robustness of both the PPRU and prophylaxis study population PK models. Therefore, the objective of this study was to perform an external evaluation of two infant fluconazole population PK models against one another.

RESULTS

Patient-level data from the PPRU and prophylaxis studies were used for the analyses. In addition, a combined data set was created by merging these two data sets together (henceforth referred to as the “merged data set”). Next, the predictive performance of the PPRU study model was evaluated using both the prophylaxis study data and the merged data set, and vice versa. For each of these evaluations, measures of bias and precision, prediction-corrected visual predictive check (pcVPC) plots, and normalized prediction distribution errors (NPDE) were generated and bootstrap analyses were performed to help evaluate each model's performance.

PPRU study model external evaluation.

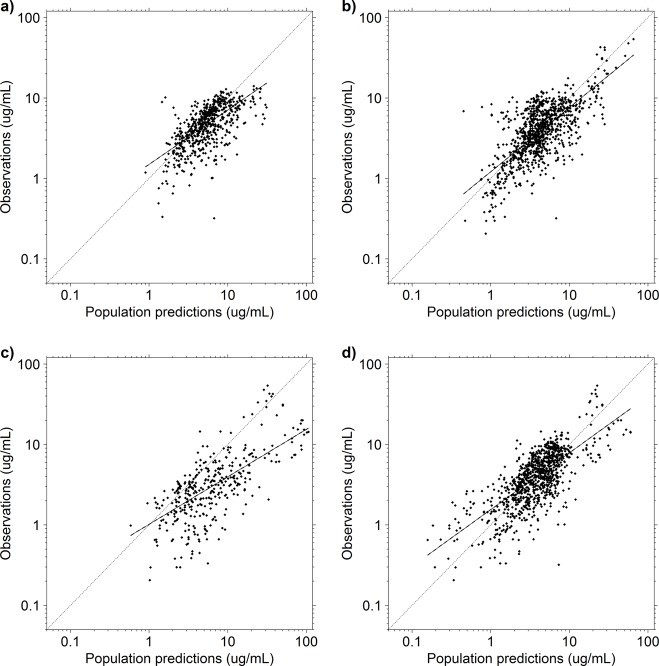
A summary of the demographic and clinical characteristics of the patients from the PPRU study, from the prophylaxis study, and for the merged data set is presented in Table 1. The population predicted concentration (PRED)-versus-observation plots obtained using the prophylaxis study data and merged data set and the PPRU study model are shown in Fig. 1 (top row). A visual inspection of the diagnostic plots suggests that there is bias in the PRED-versus-observations plots, such that there appears to be a consistent overprediction of PRED. The conditional weighted residuals (CWRES)-versus-PRED and CWRES-versus-time after the last dose plots for the PPRU study model demonstrated no consistent residual trend and had means near 0 (see Fig. S1 in the supplemental material).

TABLE 1.

Population demographics and clinical characteristics for patients from the PPRU and prophylaxis studies and for the merged data set

Covariatea	PPRU studyb (n = 55)	Prophylaxis studyc (n = 141)	Merged data set (n = 196)
Median (range) gestational age (wk)	26.0 (23.0–40.0)	24.7 (22.6–28.7)	25.0 (22.6–40.0)
Median (range) PNA (days)	17 (2–90)	23 (3–47)	21 (2–93)
Median (range) PMA (wk)	29.1 (24.0–49.6)	28.3 (23.7–35.1)	28.6 (23.7–49.6)
Median (range) actual wt (kg)	1.02 (0.450–7.14)	0.710 (0.350–2.68)	0.730 (0.350–7.14)
Median (range) serum creatinine concn (mg/dl)	0.5 (0.1–5.5)	0.7 (0.1–3.6)	0.7 (0.1–5.5)
No. (%) subjects
Male	31 (56)	57 (40)	88 (44)
African American race	20 (36)	75 (53)	95 (49)
Non-Hispanic ethnicity	50 (91)	124 (88)	174 (89)

^aDemographics and clinical characteristics recorded at the time of the first study dose were used to calculate descriptive statistics.

^bPatients in the Pediatric Pharmacology Research Unit (PPRU) study received fluconazole at 3 to 12 mg/kg i.v., given every 1 to 3 days.

^cPatients in the prophylaxis study received fluconazole at 6 mg/kg twice weekly (Tuesdays and Fridays) i.v. or p.o.

FIG 1.

Population predicted concentrations versus observations for the prophylaxis study data set and the PPRU study model (a), the merged data set and the PPRU study model (b), the PPRU study data set and the prophylaxis study model (c), and the merged data set and the prophylaxis study model (d). The parameter values for each respective model were fixed, and the model was used to generate population predicted concentrations for each data set. The values on all axes are log transformed. Dashed and solid black lines, the line of identity and the least-squares regression curve, respectively.

The quantitative measures of bias and precision of the PPRU study model are summarized in Table 2. For the PPRU model, all median PE values were in proximity to 0, and the 2.5th to 97.5th percentile ranges varied. When evaluated with its original data set, the PPRU model's prediction error (PE), mean prediction error (MPE), and mean absolute prediction error (MAPE) values were all less than those obtained with the external and merged data set with the PPRU study model. Estimates of MPE were the greatest when the PPRU study model was evaluated using the prophylaxis study data, and these estimates improved when this model was evaluated with the merged data set. Estimates of MAPE were comparable between the prophylaxis study and merged data sets.

TABLE 2.

Comparison of quantitative measures of bias and precision for the PPRU study and prophylaxis study models

Model and data set	PEc (μg/ml)	MPEd (%)	MAPEe (%)
PPRU study modela
PPRU study	0.132 (−4.76, 8.39)	15.3 (−51.1, 153)	35.7
Prophylaxis study	0.429 (−3.31, 11.2)	41.9 (−43.3, 302)	57.6
Merged	0.338 (−6.10, 9.86)	33.7 (−64.4, 296)	59.2
Prophylaxis study modelb
Prophylaxis study	0.339 (−3.61, 3.10)	12.2 (−47.4, 141)	31.8
PPRU study	2.45 (−4.05, 65.4)	188 (−40.3, 848)	195
Merged	−0.245 (−5.15, 9.66)	20.1 (−66.4, 250)	53.9

^aPatients in the PPRU study received fluconazole at 3 to 12 mg/kg i.v., given every 1 to 3 days.

^bPatients in the prophylaxis study received fluconazole at 6 mg/kg twice weekly (Tuesdays and Fridays) i.v. or p.o.

^cPE, prediction error, which is presented as the median (2.5th percentile, 97.5th percentile).

^dMPE, mean prediction error, which is presented as the mean (2.5th percentile, 97.5th percentile).

^eMAPE, mean absolute prediction error.

The pcVPC plots, obtained by fixing the PPRU study model parameter estimates, demonstrated that the model captured the central tendency of both the external and merged data sets (Fig. 2a and b). The percentages of observations falling outside the 90% prediction interval for the external and merged data set model were 14.6% (88 points) and 4.99% (48 points), respectively. These percentages show a marked difference from the ideal percentage of 10% of observations falling outside the prediction interval. Lastly, visual inspection of the PPRU study model's pcVPC demonstrated that when it was evaluated with the external data set, the PPRU study model poorly predicted the observed concentrations at early time points after the last dose in its first bin (0 to 11.5 h).

FIG 2.

Prediction-corrected visual predictive check (pcVPC) plots of the prophylaxis study data and the PPRU study model with fixed parameter values (a), the merged data set and the PPRU study model with fixed parameter values (b), the PPRU study data set and the prophylaxis study model with fixed parameter values (c), and the merged data set and the prophylaxis study model with fixed parameter values (d). All pcVPC plots are based on time after the last dose, and the data on the y axis are log transformed. Dashed lines, the 5%-50%-95% interval for the observed data; gray shaded regions, the 90% prediction interval for the predicted concentrations.

The relationship between postmenstrual age (PMA) and SCR versus population typical values of weight-normalized CL for the PPRU study model with the merged data set is depicted in Fig. S2a and b in the supplemental material. There was a positive relationship between PMA and population typical values of CL, and there was a strong negative relationship between SCR and population typical values of CL.

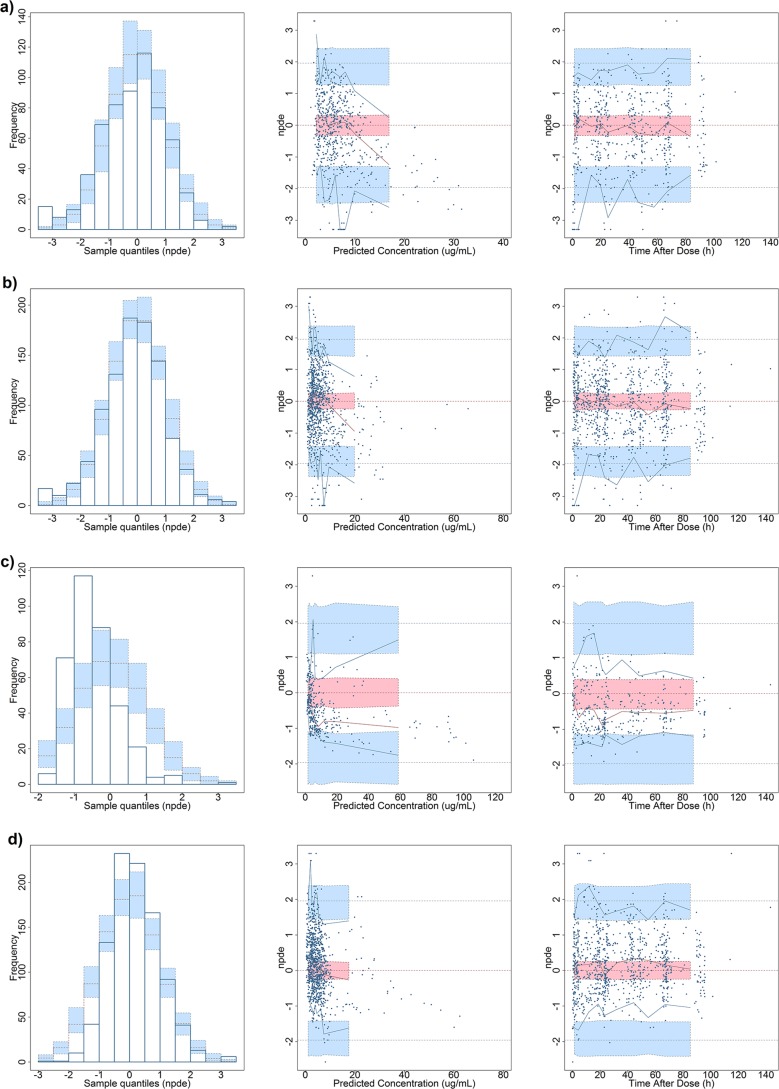
No major bias in the NPDE versus either the time after dosing or PRED was detected for the PPRU study model, though there was a notable bias present at concentrations of >20 μg/ml with the external data set (Fig. 3). The NPDE distribution histogram appears normal and centered on 0 for both scenarios. However, the results of the t test and Fisher's variance test indicated that the NPDE distribution of the model with the external and merged data sets had a mean and a variance that were significantly different from 0 and 1, respectively. Since NPDE yields information on the accuracy of the predictive performance of a model by calculating the mean and variance values of the predicted errors, this is likely due to overprediction by the model at higher concentrations. This result is in agreement with other metrics used in this analysis.

FIG 3.

Normalized prediction distribution error (NPDE) plots of the prophylaxis study data set and the PPRU study model (mean, −0.180 [P < 0.05]; variance, 1.33 [P < 0.05]) (a), the merged data set and the PPRU study model (mean, −0.121 [P < 0.05]; variance, 1.20 [P < 0.05]) (b), the PPRU study data set and the prophylaxis study model (mean, −0.446 [P < 0.05]; variance, 0.459 [P < 0.05]) (c), and the merged data set and the prophylaxis study model (mean, 0.192 [P < 0.05]; variance, 0.677 [P < 0.05]) (d). (Left) Histogram showing the NPDE frequency distribution. The blue prediction intervals are obtained by simulation from the theoretical normal (0, 1) distribution. (Middle) Scatterplot of time after the last dose versus NPDE. (Right) Scatterplot of population predicted concentrations versus NPDE. In the middle and right scatterplots, the pink areas are the prediction interval for the median, while the blue areas show the prediction areas for the boundaries of the 95% prediction intervals. Reference lines of y = ±2 are provided for the last two plots in the middle and on the right. Inscribed below are the mean and variance from each run.

The PPRU study population PK model parameter values were reestimated using the external and merged data sets (Table 3). The majority of the model's fixed effect parameter values were within 20% of their respective original parameter values. None of the values of the newly reestimated parameters were outside the 95% confidence interval of the values from the bootstrap analysis. The external and merged data set fitting resulted in an effect of SCR markedly less pronounced than that in the original fit. Of the few reestimated parameters with values falling outside this range, one notable divergence was the parameter estimation for the effect of SCR on CL in the PPRU study model. This may have been due to the difference in the model implementation (the PPRU study model only considers SCR values over 1.0 mg/dl) and the overall distribution of the SCR values (Fig. S3) between the two models. The relationship between birth gestational age (BGA) and SCR and individual empirical Bayesian estimates (EBEs) of weight-normalized CL predicted using the PPRU study model is depicted in Fig. S4a to d.

TABLE 3.

PPRU study model parameter comparison using the original data set, the external data set (prophylaxis study data), and the merged data set

Parameter	Parameter value (% RSE) from PPRU study modela			Results of bootstrap analysis (n = 1,000)b with prophylaxis study data (external data set) fitted using PPRU study model			Results of bootstrap analysis (n = 1,000)c with merged data set fitted using PPRU study model
	PPRU study data fitting (internal data set)	Prophylaxis study data fitting (external data set)	Merged data set fitting	2.5%	50%	97.5%	2.5%	50%	97.5%
Fixed effects
V (liters/kg)	1.02 (4)	0.950 (5)	1.03 (3)	0.647	0.880	0.977	0.964	1.02	1.09
CL (liters/h/kg0.75)	0.015 (6)	0.010 (5)	0.015 (3)	0.007	0.009	0.010	0.014	0.015	0.016
Exponent for SCR as a covariate on CL	−4.90 (21)	−0.708 (15)	−0.925 (22)	−0.997	−0.719	−0.523	−1.33	−0.911	−0.658
Exponent for PNA as a covariate on CL	0.237 (25)	0.829 (7)	0.337 (11)	0.732	0.827	0.965	0.257	0.336	0.406
Exponent for BGA as a covariate on CL	1.74 (18)	4.56 (14)	1.91 (14)	3.27	4.56	5.98	1.30	1.91	2.42
Ka (1/h)	—d	1.08 (24)	0.960 (fixede)	0.645	1.09	1.75	—	—	—
F1	—	1.00 (fixed)	1.00 (fixed)	—	—	—	—	—	—
IIV
ω2 (V)	0.057 (31)	0.221 (14)	0.029 (34)	0.051	0.207	0.492	0.008	0.027	0.049
ω2 (CL)	0.108 (20)	0.140 (61)	0.089 (17)	0.029	0.140	0.309	0.059	0.087	0.121
Covariance (CL − V)	0.014 (150)	0.136 (36)	0.008 (159)	0.030	0.132	0.365	−0.017	0.007	0.032
Residual errorf
σ2 (Prop, non-SCAV)	0.027 (30)	0.074 (30)	0.049 (15)	0.024	0.071	0.111	0.028	0.045	0.064
σ2 (Add, non-SCAV) (mg/ml)	0.040 (99)	0.505 (66)	0.030 (84)	0.004	0.513	1.34	0.000	0.028	0.237
σ2 (Prop, SCAV)	0.081 (35)	0.053 (31)	0.066 (15)	0.021	0.054	0.095	0.043	0.065	0.089
σ2 (Add, SCAV) (mg/ml)	0.023 (143)	0.687 (50)	0.059 (38)	0.000	0.685	1.46	0.001	0.054	0.214

^aCL (in liters per hour) = 0.015 · (WT/1)^0.75 · (BGA/26)^1.739 · (PNA/2)^0.237 · SCR^−4.896 (when SCR is >1.0 mg/dl) and V (in liters) = 1.024 · (WT/1), where CL is clearance, WT is actual body weight, BGA is birth gestational age, PNA is postnatal age, SCR is the serum creatinine concentration, V is the volume of the central compartment, K_a is the absorption rate constant, F₁ is the oral bioavailability, IIV is the interindividual variability, ω² is the variance of the IIV term, σ² is the variance of the residual error term, RSE is the residual standard error, and PPRU is the Pediatric Pharmacology Research Unit.

^bA total of 947 (94.7%) runs successfully minimized the covariance step and 999 (99.9%) runs completed the covariance step.

^cA total of 948 (94.8%) runs successfully minimized the covariance step and 1,000 (100%) runs completed the covariance step.

^d—, estimated parameter value not applicable.

^eFixed, the parameter was fixed to the original estimate from the prophylaxis study model in order for the covariance step to run.

^fResidual error model in which the result is equal to 1 if the samples were scavenged; otherwise, the value for the scavenged sample is equal to 0. Y₁ = F · [1 + ERR(1)] + ERR(2) for protocol-driven PK specimen, Y₂ = F × THETA_scav × [1 + ERR(3)] + ERR(4) for scavenged PK specimens, and Y = (Y₂ × SCAV) + [Y₁ × (1 + SCAV)], where SCAV is a dichotomous variable equal to 1 if the PK sample is scavenged from discarded blood, Y₁ is an expression for the predicted concentration value (nonscavenged sample), F is IPRED, ERR(1) is the proportional residual error (nonscavenged sample), ERR(2) is the additive residual error (nonscavenged sample), Y₂ is an expression for the predicted concentration value (scavenged sample), THETA_scav is the theta estimate for the SCAV variable, ERR(3) is the proportional residual error (scavenged sample), ERR(4) is the additive residual error (scavenged sample), Y is a composite expression for model-predicted concentrations, Prop is the proportional error term, and Add is the additive error term.

Prophylaxis study model external evaluation.

The PRED-versus-observation plots obtained using the PPRU study and merged data sets and the prophylaxis study model are shown in Fig. 1c and d. A visual inspection of the diagnostic plots indicated that there was a more pronounced bias (consistent overprediction) in the PRED-versus-observation plots than in the PPRU study model external evaluation. Notably, these overpredictions appeared to be the most pronounced with the PPRU data set predicted using the prophylaxis study model. The CWRES-versus-PRED and CWRES-versus-time after the last dose plots for the prophylaxis study model demonstrated no consistent residual trend and had means near 0 (Fig. S5).

For the prophylaxis study model, all median PE values were in proximity to 0, and the 2.5th to 97.5th percentile ranges varied (Table 2). The 97.5th percentile PE of the prophylaxis study model with the external data set was notably high (65.4 μg/ml). The external evaluation also had the highest MPE (188% of the observed concentration). The MAPE value from the original prophylaxis model was less than that obtained with the external and merged data sets with the prophylaxis study model. The MAPE value from the prophylaxis study model with the external data set had a notably high MAPE of 195% of the observed concentration, which was almost four times the MAPE value of the same model with the merged data set.

The pcVPCs demonstrate that the prophylaxis study model captured the central tendency of both the external and the merged data sets (Fig. 2c and d). For the prophylaxis study model, the percentages of observations falling outside the 90% prediction interval for the external and the merged data sets were 7.84% (28 points) and 7.28% (70 points), respectively.

The relationship between postmenstrual age (PMA) and SCR versus population typical values of the weight-normalized CL for the prophylaxis study model with the merged data set is depicted in Fig. S2c and d. Like the PPRU study model, there was a positive relationship between PMA and population typical values of CL, and there was a strong negative relationship between SCR and population typical values of CL.

Figure 3 illustrates the NPDE analysis results for the prophylaxis study model. No major bias in either the NPDE versus time after dose or population predictions was detected for all prophylaxis study model external evaluation scenarios, though the PRED-versus-NPDE plot demonstrated that the model tended to overpredict at higher concentrations (>30 μg/ml). The NPDE distribution histogram appeared to be normal and centered on 0 for the prophylaxis study model with the merged data set. However, the NPDE distribution histogram was noticeably skewed to the right for the prophylaxis study model with the external data set. The results of the t test and Fisher's test indicated that the NPDE distribution of the model with the external and merged data sets had a mean and a variance that were significantly different from 0 and 1, respectively, likely due to the model overpredicting at higher concentrations. This result is in congruence with the other metrics used in this analysis. The majority of the prophylaxis study model's fixed effect parameter values were within 20% of their respective original parameter values, with a notable exception of the effect of the parameter SCR on CL (Table 4). Similar to the results seen in the PPRU study external evaluation, the exponent of the parameter SCR on CL fell outside this range. The external and merged data set fitting resulted in an effect of SCR less pronounced than that in the original fit. Again, this may have been due to the difference in the model implementation and the overall distribution of the SCR values between the two models. None of the values of the newly reestimated parameters were outside the 95% confidence interval from the bootstrap analysis. The relationship between BGA and SCR and the EBEs of the weight-normalized CL predicted using the prophylaxis study model is depicted on Fig. S4e to h.

TABLE 4.

Prophylaxis study model parameter comparison using the original data set, the external data set (PPRU study data), and the merged data set

Parameter	Parameter value (% RSE) from prophylaxis study modela			Results of bootstrap analysis (n = 1,000)b with PPRU study data (external data set) fitted using prophylaxis study model			Results of bootstrap analysis (n = 1,000)c with merged data set fitted using prophylaxis study model
	Prophylaxis study data fitting (internal data set)	PPRU study data fitting (external data set)	Merged data set fitting	2.50%	50%	97.50%	2.50%	50%	97.50%
Fixed effects
V (liters/kg)	1.00 (4)	1.00 (5)	1.01 (3)	0.913	1.0	1.10	0.952	1.01	1.06
CL (liter/h/kg0.75)	0.013 (3)	0.012 (10)	0.012 (3)	0.009	0.011	0.013	0.011	0.012	0.013
Exponent for SCR as a covariate on CL	−0.410 (12)	−0.160 (34)	−0.262 (15)	−0.291	−0.168	−0.075	−0.348	−0.262	−0.189
Exponent for PMA as a covariate on CL	2.05 (17)	1.64 (20)	1.88 (12)	0.757	1.66	2.22	1.39	1.89	2.29
Ka (1/h)	0.961 (26)	—d	1.00 (fixede)	—	—	—	—	—	—
F1	0.995 (7)	—	1.00 (fixed)	—	—	—	—	—	—
IIV
ω2 (V)	0.017 (61)	0.064 (33)	0.032 (32)	0.019	0.062	0.115	0.010	0.030	0.052
ω2 (CL)	0.051 (29)	0.140 (26)	0.082 (18)	0.072	0.133	0.242	0.054	0.081	0.113
Covariance (CL − V)	−0.021 (58)	0.010 (282)	0.002 (589)	−0.052	0.007	0.056	−0.024	0.002	0.025
Residual errorf
σ2 (Prop)	0.214 (12)	0.207 (24)	0.224 (9)	0.061	0.201	0.275	0.178	0.223	0.263
σ2 (Add) (mg/ml)	0.505 (36)	0.266 (64)	0.356 (34)	0.002	0.064	0.267	0.012	0.121	0.328

^aCL (in liters per hour) = 0.0127 · (WT/1)^0.75 · (SCR/0.8)^−0.41 · (PMA/28)^2.05, V (in liters) = 1.00 × (WT/1), K_a (in 1/hour) = 0.96, F₁ = 100%, where CL is clearance, WT is actual body weight (in kilograms), SCR is the serum creatinine concentration (in milligrams per deciliter), PMA is postmenstrual age (PMA; in weeks), V is the volume of the central compartment; K_a is the absorption rate constant, F₁ is the oral bioavailability, IIV is the interindividual variability, ω² is the variance of the IIV term, σ² is the variance of the residual error term, RSE is the residual standard error, and PPRU is the Pediatric Pharmacology Research Unit.

^bA total of 995 (99.5%) runs successfully minimized the covariance step and 1,000 (100%) runs completed the covariance step.

^cA total of 1,000 (100%) runs successfully minimized the covariance step and 1,000 (100%) runs completed the covariance step.

^d—, estimated parameter value not applicable.

^eFixed, the parameter was fixed to the original estimate from prophylaxis model in order for the covariance step to run.

^fResidual error model: W = SQRT(THETA_error²) and Y = IPRED + ERR(1) × W × IPRED + ERR(2), where W is the proportional residual error term, SQRT is square root, THETA_error is the theta estimate of the proportional residual error, Y is a composite expression for model-predicted concentrations, IPRED is the individual predicted concentration, ERR(1) is fixed at 1.00, ERR(2) is the additive residual error, Prop is the proportional error term, and Add is the additive error term.

DISCUSSION

Two external evaluations of previously published population PK models of fluconazole in infants were performed. The models' predictive performance with the external and merged data sets was characterized through the use of standard measures of model fitness and goodness-of-fit plots. To date and to our knowledge, this is the first published external evaluation of fluconazole infant population PK models. Although external evaluation of population PK models is critical to ensure that proposed models are robust, these analyses are rarely performed in pediatric settings. There are several reasons why these analyses are infrequently performed. Notably, the lack of available PK data to serve as a data set for external evaluation and the ethical concerns regarding the repeat of PK studies in infants and children serve as significant barriers to external evaluation analyses for these patients. Our study was made possible due to two important factors. First, the use of fluconazole as prophylaxis against Candida infections in infants is not universally accepted as the standard of care. Therefore, a prospective PK and efficacy study to inform dosing in this population was merited. Second, our study was able to leverage pooled clinical data from multiple study sites with numerous scavenged samples, which significantly enhanced the amount of data available and allowed an external evaluation to be performed. This underscores the importance of collecting scavenged samples in pediatric clinical trials (assuming that appropriate stability tests are performed) to increase the amount of PK data available for infants without burdening patients with additional blood draws.

When fitted with an external data set, the PPRU study model had a notably lower bias and a greater precision than the prophylaxis study model. This was clearly demonstrated by a comparison of the NPDE distribution histograms for both models with the external data set, the notable overprediction seen in the prophylaxis study model's PRED-versus-observation plot, and the quantitative measures of bias and precision. In contrast, when fitted with data from the merged data set, both models had comparable biases and precisions, a finding which indicates that both models adequately described the data from the merged data set. However, it is important to note that the prophylaxis study contributed to the merged data set almost twice as many PK samples as the PPRU study.

This external evaluation also confirms that age and SCR are important covariates that explain the interindividual variability (IIV) in fluconazole CL. This is supported by clinical evidence; fluconazole CL is primarily based on renal function (12), and infant renal function is primarily determined by age. In fact, at birth infants have 35% to 40% of a typical adult's glomerular filtration rate (GFR), and the infant GFR does not reach 50% of the typical adult GFR until 47.7 weeks PMA (13). Therefore, the median PMA for infants in both external data sets (PPRU study, 29.1 weeks [range, 24.0 to 49.6 weeks]; prophylaxis study, 28.3 weeks [range, 23.7 to 35.1 weeks]) suggests that the CL of fluconazole in these subjects is constantly changing due to underlying changes in renal physiology.

The discrepancy between the models' performances may be attributed to notable differences in the demographic and clinical characteristics of the infants enrolled in each study, specifically, the BGA at birth, birth weight, and postnatal age. Importantly, the prophylaxis study contained infants younger than those in the PPRU study. Though both study populations had a similar median BGA, the PPRU study enrolled both term and premature infants (10 infants [18%] in the PPRU study had a BGA of >37 weeks), whereas the prophylaxis study enrolled premature infants (BGA, 23 to 29 weeks) only. The PPRU study collected PK samples from infants with a wider range of postnatal ages (PNA; 2 to 90 days) than the prophylaxis study, whereas the oldest infant in the prophylaxis study had a PNA of 47 days. Consequently, the PPRU study patient population had a wider weight range at the time of PK sampling than the prophylaxis study (8 infants [15%] in the PPRU study had a body weight of >2.68 kg, the maximum weight in the prophylaxis study). Since the prophylaxis study model was developed with data from infants with a narrower age range and a narrower weight range, its concentration predictions for term infants or infants with body weights of >2.68 kg in the external data set would be considered an extrapolation.

In addition to the differences in the characteristics of the patients in the PPRU and prophylaxis studies, there were some differences between the modeling methodologies used. The most notable difference was the implementation of SCR as a covariate on CL. The PPRU study model incorporated SCR as a covariate on CL only for values of >1.0 mg/dl. This contrasts with the prophylaxis study model, which included SCR as a covariate on CL for all values. In addition, 15% of the infants in the PPRU study but 36% of the infants in the prophylaxis study had SCR values of >1.0 mg/dl. This difference in the implementation of SCR as a covariate on CL and the difference in the underlying sample size could have affected the final parameter estimate of the exponent for SCR as a covariate on CL for both model evaluations. In addition, this may have contributed to the prophylaxis study model's relatively high MAPE value when the model was externally validated.

The external evaluation analysis described herein has several notable limitations. First, the external data set, though similar to the original data set, contained data for patients of different age ranges and with different indications. The PPRU study enrolled both premature and term infants with indications for both prophylaxis and treatment, whereas the prophylaxis study enrolled only premature infants with indications for prophylaxis. It is conceivable that differences in developmental physiology and disease status between the patients in the two studies may have contributed to some of the differences in the predictive performance of the two models observed. Second, there were important differences in the study design between the two studies. The PPRU study collected PK samples following intravenous (i.v.) administration, whereas the prophylaxis study collected PK samples following both i.v. and oral administration. This required an assumption about the absorption parameters to be made when the PPRU study model was externally validated using the prophylaxis study data. Lastly, both studies leveraged the use of scavenged samples, which meant that the timing and the number of samples varied significantly across patients. Despite these limitations, this analysis demonstrates the value of externally evaluating population PK models in pediatric populations, particularly when these models will be used to inform dosing.

Given the dearth of clinical data to guide dosing in infants, it is of paramount importance to optimize the dosing of fluconazole in this setting through the use of externally evaluated PK models. We performed an external evaluation analysis to characterize the robustness of both the PPRU and prophylaxis study population PK models by evaluating model fitness and performance with validated data sets. Our analysis determined that though both models are robust, the PPRU study model has less bias and greater precision than the prophylaxis study model, likely because it was derived from data for a population with a wider age range. These validated models could potentially lead to better-informed dosing guidance for fluconazole in infants to attain optimal plasma concentrations by, for example, featuring the patient's serum creatinine level and age as determinants in dosing guidance. Overall, the fact that two similar population PK models performed differently when they were externally validated in this study highlights the need to externally validate other infant population PK models in future investigations.

MATERIALS AND METHODS

Patient data.

Patient-level data from two separate studies were used for the analyses described herein. The study designs of these two studies have been previously described in detail, and, again, these are referred to as the “PPRU study” (9) and the “prophylaxis study” (5).

Briefly, the PPRU study (ClinicalTrials.gov registration no. NCT00514358) combined data from two separate clinical studies. In both of these studies, dosing was performed per routine clinical practice, and no exclusion criteria were used. The first study included in the PPRU study was a multicenter (n = 8), open-label, PK study that enrolled premature and term infants and stratified enrollment on the basis of BGA (23 to 25 weeks, 26 to 29 weeks, 30 to 33 weeks, and ≥34 weeks) and PNA (<14 days and 14 to 119 days). The second study included in the PPRU study was an open-label PK study of antimicrobial drugs performed at a single institution (Duke University Hospital). Dosing according to routine clinical practice ranged from 3 to 12 mg/kg of body weight/dose i.v., and the majority of doses were given every 1 to 3 days (9). For reference, Fig. S3 in the supplemental material depicts a comparison of the density distribution of SCR and BGA for each data set.

The prophylaxis study (ClinicalTrials.gov registration no. NCT00734539) leveraged PK data collected in an efficacy and safety study of fluconazole prophylaxis in extremely low birth weight premature infants. This study was a multicenter, randomized, placebo-controlled trial that included infants with a birth weight of ≤750 g. Infants randomized to the treatment arm of the trial received fluconazole at 6 mg/kg twice weekly (Tuesdays and Fridays) either i.v. or orally starting within 5 days of birth and continuing for 42 days (5).

PK samples.

The PPRU study used a total of 357 plasma samples which were collected from 55 infants. The study data set contained 140 scavenged plasma samples (39% of total samples) that were collected during the course of treatment. There were no samples with concentrations below the limit of quantification (BQL), and all samples were included in the analysis. In the PPRU study, infants were randomly assigned to one of two PK sampling schedules (schedule A, preinfusion, end of infusion, and 1, 6 to 8, 24, and 48 h postinfusion; schedule B, preinfusion, end of infusion, and 3, 10 to 12, 24, and 48 h postinfusion). In the prophylaxis study, a total of 619 plasma samples were collected from 141 premature infants. The prophylaxis study data set contained 368 scavenged samples (59% of total samples). Fifteen samples with concentrations BQL were excluded, leaving a total of 604 plasma samples for final analysis. Infants in the prophylaxis study were also randomized to one of eight sampling schemes with a maximum of three timed blood samples per infant. Each infant had two PK samples drawn after a single dose, and these samples were collected at about dose 3, 5, 7, or 9. In addition, one sample was collected after the final dose, and up to 10 scavenged samples collected through routine care were included per infant (5). The demographic characteristics and laboratory values for infants in each data set and the merged data set are presented in Table 1. The concentration-versus-time after dose plot of each data set is shown in Fig. S6. The numbers of infants and PK samples included in the external evaluation analyses described herein are the same as those used for the original population PK model development (5, 9).

For both studies, plasma samples were analyzed for fluconazole concentrations using a validated liquid chromatography method with tandem mass spectrometric detection (LC-MS/MS). The lower limit of quantitation (LLOQ) for fluconazole in both studies was 0.01 μg/ml (5, 9). The accuracy and intraday precision of the assay used in the PPRU study did not exceed ±4.0% (of the theoretical value) and ±10.8%, respectively (14). The accuracy and intraday precision of the assays used in the prophylaxis study did not exceed ±13.1% (of the theoretical value) and ±8.5%, respectively (OpAns, LLC, Durham, NC). It was demonstrated that the assays used for each study are indeed comparable. Both studies determined that the scavenged samples were stable, the concentrations in scavenged samples were indistinguishable from those in scheduled samples, and the inclusion of scavenged samples did not introduce bias to the parameter estimates (5, 9).

Original models.

The PPRU study data were well described by a one-compartment linear PK model. Separate additive and proportional residual error terms were used for scavenged and nonscavenged samples. CL was scaled by actual body weight (WT) using a fixed exponent allometric relationship (WT^0.75), and the volume of distribution (V) was scaled linearly by actual body weight (WT^1.0). Significant covariates included in the model included BGA, PNA, and SCR. The typical population PK parameter estimates in the model were as follows: CL (in liters per hour) = 0.015 · (WT/1)^0.75 · (BGA/26)^1.739 · (PNA/2)^0.237 · SCR^−4.896 (the SCR term was included only when SCR was >1.0 mg/dl) and V (in liters) = 1.024 · (WT/1), where WT is in kilograms, BGA and PNA are in weeks, and SCR is in milligrams per deciliter (9).

The population PK model developed in the prophylaxis study was a one-compartment linear PK model with first-order oral absorption. The authors used additive and proportional residual error terms without differentiating between scavenged and nonscavenged samples. Because data obtained after both p.o. and i.v. drug administration were included in the analysis, the absorption rate constant (K_a) and F parameters, in addition to CL and V, were estimated. CL was scaled by WT using a fixed exponent allometric relationship (WT^0.75), and V was linearly scaled (WT^1.0). PMA and SCR were identified as significant covariates in the model. The typical population PK parameter estimates in the final model were as follows: CL (in liters per hour) = 0.0127 · (WT/1)^0.75 · (SCR/0.8)^−0.41 · (PMA/28)^2.05, V (in liters) = 1.00 · (WT/1), K_a (in 1/hour) = 0.96, and F₁ = 100%, where WT is in kilograms, SCR is in milligrams per deciliter, and PMA is in weeks (5).

For both final models, parameter estimation was performed using the first-order conditional estimation (FOCE) method with the eta-epsilon interaction in the software NONMEM (Icon Development Solutions, Ellicott City, MD, USA). The PPRU and prophylaxis study models were implemented using the ADVAN1 TRANS2 and ADVAN2 TRANS2 subroutines in NONMEM, respectively.

Model evaluations.

We used three data sets in our analysis: patient-level data from the PPRU study, patient-level data from the prophylaxis study, and a combined data set created by merging the first two data sets together. We used these three data sets to perform a total of four evaluation procedures. The first evaluation consisted of validation of the final PK model from the PPRU study using the raw data obtained in the prophylaxis study. Similarly, in the second evaluation that we performed, the raw data obtained in the PPRU study were used to validate the final PK model in the prophylaxis study. Finally, we performed two additional evaluations by using the merged data set that we created to validate both the PPRU and prophylaxis study population PK models separately.

Analyses were performed using NONMEM, version 7.3 (Icon Development Solutions, Ellicott City, MD, USA). Because the PPRU study model was developed using data collected after i.v. dosing, when its predictive performance was evaluated using the prophylaxis study and merged data sets (which included records from both infants receiving i.v. dosing and infants receiving p.o. dosing), the ADVAN2 TRANS2 subroutine was used, and the K_a and F₁ parameters were incorporated into the model. All data manipulation was performed using R (version 3.3.1) and RStudio (version 0.99). Data visualization was performed using the R packages lattice, latticeExtra, and gridExtra (15–17).

The predictive performance of each model was evaluated by fixing the parameter estimates to those reported in the original publications and generating the following goodness-of-fit plots: PRED versus observations, CWRES versus time after the last dose, and CWRES versus PRED. For the external evaluation of the PPRU study model, since all doses were given i.v., we assumed that the F and K_a parameters from the prophylaxis study could be used to model absorption with the external data set.

The bias of each model was evaluated by comparing the observations to PRED and computing the jth prediction error (PE_j) and MPE (equations 1 and 2). The precision was assessed by calculating the MAPE (equation 3) (18, 19).

$${\text{PE}}_j=({\text{PRED}}_j-{\text{observation}}_j)$$ (1)

$$\text{MPE}=\frac{1}{N}\sum _{}\left(\frac{{\text{PRED}}_j-{\text{observation}}_j}{{\text{observation}}_j}\right)\times 100$$ (2)

$$\text{MAPE}=\frac{1}{N}\sum _{}\left(\left|\frac{{\text{PRED}}_j-{\text{observation}}_j}{{\text{observation}}_j}\right|\right)\times 100$$ (3)

where N is the number of observations, PRED_j is the jth predicted concentration, and observation_j is the jth observation.

We also used the Perl-speaks-NONMEM tool kit (PsN tool kit; version 3.6.2; Uppsala Pharmacometics, Uppsala, Sweden) and the R package xpose4 to generate a pcVPC based on 1,000 simulations for each scenario, assessed on the basis of the parameter estimates fixed to the original model values (20, 21). In addition, for each of the four scenarios evaluated, we performed NPDE analyses using the add-on R package npde on the basis of parameter estimates fixed to the original model values (22). For these analyses, a total of 1,000 simulations were performed for each scenario, and then observations were compared to the simulated reference distribution (22, 23). The population typical values of CL for both models with the merged data set were plotted against patient PMA and SCR. A histogram of the NPDE distribution and plots of NPDE versus PRED and time were used to evaluate each model. The validity of NPDE assumes that the values follow a normal distribution with a mean of 0 and a variance of 1. Therefore, for each NPDE analysis, we performed a t test to assess whether the mean of the distribution was different from 0 and Fisher's test to evaluate whether the variance of the distribution was different from 1. A P value of <0.05 was used to assess statistical significance.

Lastly, the values of the parameters of each respective model were reestimated using the external and merged data sets. A bootstrap analysis (n = 1,000) was performed for each model using the PsN tool kit. The reestimated parameter values for each model were compared against the bootstrap 95% confidence interval to assess the precision of the model parameter values.