Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Oct 3;89(22):12306–12313. doi: 10.1021/acs.analchem.7b03279

Absolute Quantification of Amyloid Propagons by Digital Microfluidics

Manuela Pfammatter †, Maria Andreasen ‡,§, Georg Meisl ‡, Christopher G Taylor ‡, Jozef Adamcik ⊥, Sreenath Bolisetty ⊥, Antoni Sánchez-Ferrer ⊥, David Klenerman ‡, Christopher M Dobson ‡, Raffaele Mezzenga ⊥, Tuomas P J Knowles ‡,∥, Adriano Aguzzi †, Simone Hornemann †,*
PMCID: PMC5700450  PMID: 28972786

Abstract

graphic file with name ac-2017-032797_0006.jpg

The self-replicating properties of proteins into amyloid fibrils is a common phenomenon and underlies a variety of neurodegenerative diseases. Because propagation-active fibrils are chemically indistinguishable from innocuous aggregates and monomeric precursors, their detection requires measurements of their replicative capacity. Here we present a digital amyloid quantitative assay (d-AQuA) with insulin as model protein for the absolute quantification of single replicative units, propagons. D-AQuA is a microfluidics-based technology that performs miniaturized simultaneous propagon-induced amplification chain reactions within hundreds to thousands of picoliter-sized droplets. At limiting dilutions, the d-AQuA reactions follow a stochastic regime indicative of the detection of single propagons. D-AQuA thus enables absolute quantification of single propagons present in a given sample at very low concentrations. The number of propagons quantified by d-AQuA was similar to that of fibrillar insulin aggregates detected by atomic-force microscopy and to an equivalent microplate-based assay, providing independent evidence for the identity of insulin propagons with a subset of morphologically defined protein aggregates. The sensitivity, precision, and accuracy of d-AQuA enable it to be suitable for multiple biotechnological and medical applications.

Digital microfluidic assays have revolutionized quantitative biology, as they facilitate the precise and accurate quantification of absolute numbers of biomolecules.1,2 The use of digital microfluidics offers the possibility of performing a very large number of individual experiments in small droplet compartments in a short time, yielding the data volumes needed for digital analysis. Microfluidics therefore enables assays with higher throughput, greater reliability, and sensitivity than conventional methods.1,3−5 The miniaturization to picoliter (pL)-sized droplets further allows for an effective reduction in the consumption of rare biological samples, costs, potential contamination, and surface effects due to the absence of air–water interfaces.1−3 This concept has already transformed several applications in DNA technology, including the further development of the digital polymerase chain reaction (dPCR)6,7 to droplet digital PCR (ddPCR),8−11 DNA microarrays,12,13 and next-generation sequencing,14 as it enables large numbers of parallel experiments for absolute quantification of specific targets even at low concentrations. Digital microfluidics has also been applied to cell-based assays,15−17 protein biomarker detection,18 isothermal amplification chemistry,19 studies on amyloid growth,20 and high-throughput applications.1 In this paper, we describe the extension of digital microfluidics to amyloid amplification assays.

Amyloid amplification assays have recently been developed to address the urgent need for reliable and sensitive in vitro detection of amyloid aggregates—which cause a range of neurodegenerative disorders, including transmissible spongiform encephalopathies, Alzheimer’s, Parkinson’s, and many other diseases21−23—for basic research and for diagnostic applications.24−27 These diseases are associated with the ability of proteins to self-assemble into amyloid fibrils in a nucleation-dependent polymerization reaction.28,29 This process typically follows a sigmoidal kinetic progression involving primary nucleation, aggregate growth and fibril elongation, along with secondary processes, such as fragmentation and surface-induced nucleation events that serve to amplify the number of aggregates.30,31 The process of amyloid formation therefore involves the generation of “propagons”,32 defined as all those aggregated species, including fibrils, that are able to seed or propagate the conversion of monomeric proteins into a higher number of active propagons in a template-catalyzed way.

Amyloid amplification assays are built on the self-propagation principle, promoting the amplification of minute amounts of active pathological species to readily detectable levels in the presence of their monomeric counterparts. Assays that use either cyclic sonication for efficient amplification, as in the protein misfolding cyclic amplification (PMCA) assay,24 or agitation in a microplate, as in the real-time quaking-induced conversion (RT-QuIC) assay,25 have been developed for sensitive detection of prions and prionoids33 in biological samples.26,27,34 These assays, however, have certain limitations with respect to automation and high-throughput applications and are, because of their analogue nature, able to measure only average concentrations. Digital microfluidics can potentially overcome these limitations, because of its ability to perform high numbers of pL-sized volume reactions, allowing the precise quantification of absolute numbers of single low-abundance entities present in a system.

Here, we describe the development of a digital amyloid quantitative assay, d-AQuA, using droplet-based microfluidics. We demonstrate that d-AQuA represents a powerful method for the ultrasensitive detection of single insulin propagons contained in a sample and their absolute quantification. D-AQuA also showed a significantly better performance with respect to sensitivity, precision, and speed than an equivalent assay in a microplate. We therefore anticipate that d-AQuA holds great potential for advancing a wide range of biotechnological and medical research applications and opens up new avenues for ultrasensitive and precise high-throughput digital diagnostics.

Experimental Section

Materials

Human insulin was purchased from Sigma-Aldrich (SAFC Biosciences) and used without further purification. All chemicals were purchased from Sigma-Aldrich unless otherwise specified.

Standard Fibril Sample Preparation

Fibrils were assembled in vitro by incubating 1 mM monomeric human insulin in a 10 mM HCl water solution at pH 2.0 (HCl, pH 2.0) at 65 °C and agitation at 600 rpm for 72 h. Residual monomeric species were removed by intense washing with HCl (pH 2.0) using Amicon centrifugal filters (MWCO 100 kDa; Merck Millipore).35 Fibrils were lyophilized and stored at −20 °C until usage. The sample was diluted to a concentration of 400 μM (monomer equivalents) to yield the standard fibril sample.

Standard Fibril Sample Characterization

The standard fibril sample was characterized using atomic force microscopy (AFM), dynamic light scattering (DLS), Fourier transform infrared spectroscopy (FTIR), far-UV circular dichroism (CD), and a self-propagation activity assay. The details are described in SI Materials and Methods.

Microdroplet Device Fabrication

Microfluidic flow-focusing devices (Figure S1) were fabricated using standard soft-lithography techniques.36 Briefly, the device design was patterned on a silicon wafer using SU-8 negative photoresist (MicroChem) to produce a negative mold. Microfluidic channels were cast into poly(dimethylsiloxane) (PDMS; Dow Corning Sylgard 184 Silicone Elastomer) on the silicon mold, and the PDMS stamp was cured at 65 °C for 150 min before peeling off the mold. Channel inlets and outlets were punched into the PDMS stamp before oxygen plasma bonding it to a glass slide to seal the channels. To make channel walls hydrophobic, the device was flushed with the water repellent agent Aquapel (PPG Industries) for 30 min before washing with isopropanol and then blow-drying with a nitrogen stream.

D-AQuA Assay

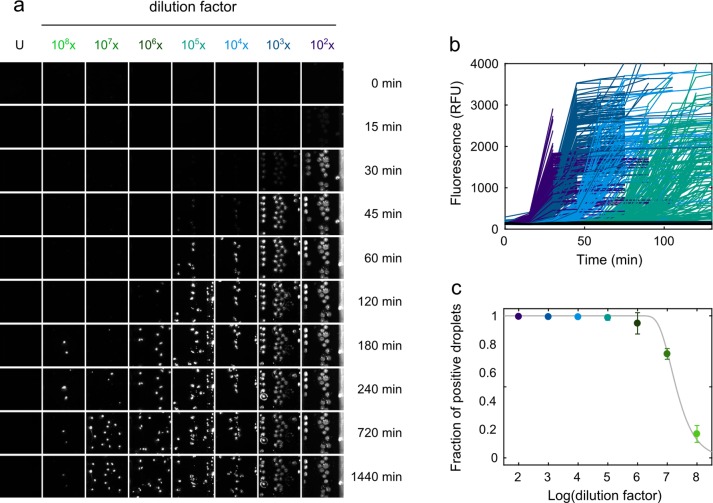
Lyophilized insulin was dissolved in HCl (pH 2.0) at a concentration of 6 mg mL–1 and filtered (50 kDa Amicon centrifugal filters; Millipore UFC505096) to remove higher-molecular-weight species. The protein was dissolved to a final assay concentration of 400 μM in HCl (pH 2.0) containing 0.1 M GdmCl and 40 μM Thioflavin (ThT). Serial 10-fold dilutions of the standard fibril sample were prepared in HCl (pH 2.0) and added to the reaction mixture immediately before encapsulating the mixture into microdroplets. Negative controls were incubated with the same volume of HCl (pH 2.0) instead of fibrils. Amplification reactions were encapsulated into water-in-oil-emulsions using a microfluidic device with flow focusing geometry. The sample containing monomeric substrate, fibrils, and ThT was injected into the middle inlet on the chip at a flow rate of 200 μL h–1. The carrier oil phase made of fluorinated FC-40 (Sigma) with 4% (w/v) triblock copolymer (ABA) surfactant (where A is a perfluorinated poly(propylene oxide) block and B a poly(ethylene oxide) block, synthesized as previously described37) was injected into the outer inlet at a flow rate of 300 μL h–1 to generate droplets with a radius of ∼25 μm (volume ∼65 pL). Fluid flow rates were controlled with a Cetoni neMESYS syringe pump (Cetoni GmbH). Between 500 and 1400 replicate droplets were collected per dilution at the outlet into Rectangular Borosilicate capillaries (CM Scientific), and the capillaries were sealed with wax plugs to prevent sample evaporation. Before imaging the capillaries containing samples at different fibril dilutions, capillaries were aligned on a glass slide for amplification and imaging. The aligned capillaries were placed on the automated motorized stage of a custom-built epifluorescence laser microscope (Figure S1) and covered with a hot plate heated to 65 °C to induce amplification. To track aggregate formation within the droplets, fluorescent images were acquired every 15 min for approximately 24 h using laser excitation at 445 nm (diode laser (MLD445, Cobolt)). Individual droplets were identified manually, and the average intensity of the droplet area was extracted for all frames. The brightness of the images of the 102 capillary in Figure 3a was adjusted to account for minor differences in brightness arising from imaging on different frames of the automated-stage laser (for original figure, see Figure S4). Fluorescent traces in Figure 3b were considered complete, once the plateau region was obtained.

Figure 3.

Figure 3

Open in a new tab

D-AQuA for single propagon quantification. (a) Representative fluorescence image sections of the capillaries containing microdroplets with 10-fold serial dilutions from 102 to 108 of the standard fibril sample (in monomer equivalents). Droplets containing newly formed aggregates appeared as ThT fluorescence positive, whereas droplets without preformed fibrils were fluorescence negative. U: unseeded control. (b) Representative time courses of insulin fibril formation within microdroplets for different fibril dilutions (colored; unseeded controls in black) monitored by ThT fluorescence. 200 representative reactions are shown per dilution. (c) Fraction of fluorescence-positive droplets as a function of the logarithm of the dilution factor. Every data point represents the mean ± SD from two independent experiments of d-AQuA. A Poisson distribution (gray line) was fitted to the data to quantify the number of propagons in the standard fibril sample.

Microplate Amyloid Amplification Assay

Lyophilized insulin was dissolved in HCOOH (pH 3.0) at a concentration of 6 mg mL–1 and filtered using 50 kDa Amicon Ultra centrifugal filters (Millipore, prod. no. UFC505096). The protein was dissolved to a final concentration of 2 μM in 0.75 M D-mannitol, 1 M GdmCl, 10 μM ThT, HCOOH (pH 3.0) in a reaction volume of 28.5 μL per well. To each reaction, either 1.5 μL of serial 10-fold dilutions from 104 to 1015 of the standard fibril sample (dissolved in HCOOH, pH 3.0) or HCOOH (pH 3.0, negative control) was added. Each dilution and the control were performed in 16 technical replica on black 384-well polystyrene microplates (Corning, prod. no. 3540) covered with sealing tape (Sarstedt, prod. no. 95.1999). Microplates were incubated at a constant temperature of 30 °C with cyclic agitation (1 min at 300 rpm followed by 2 min quiescent) on a SpectraMax Paradigm microplate reader (Molecular Devices). To monitor the aggregation kinetics, ThT fluorescence was measured at 482 nm following excitation at 440 nm every 3 min from the bottom of the microplate. The error of the assay was calculated from three independent replicate measurements of the microplate assay (for data analysis see section Digital Data Analysis). The replicate measurements are shown in Figure 5 and Figure S3.

Figure 5.

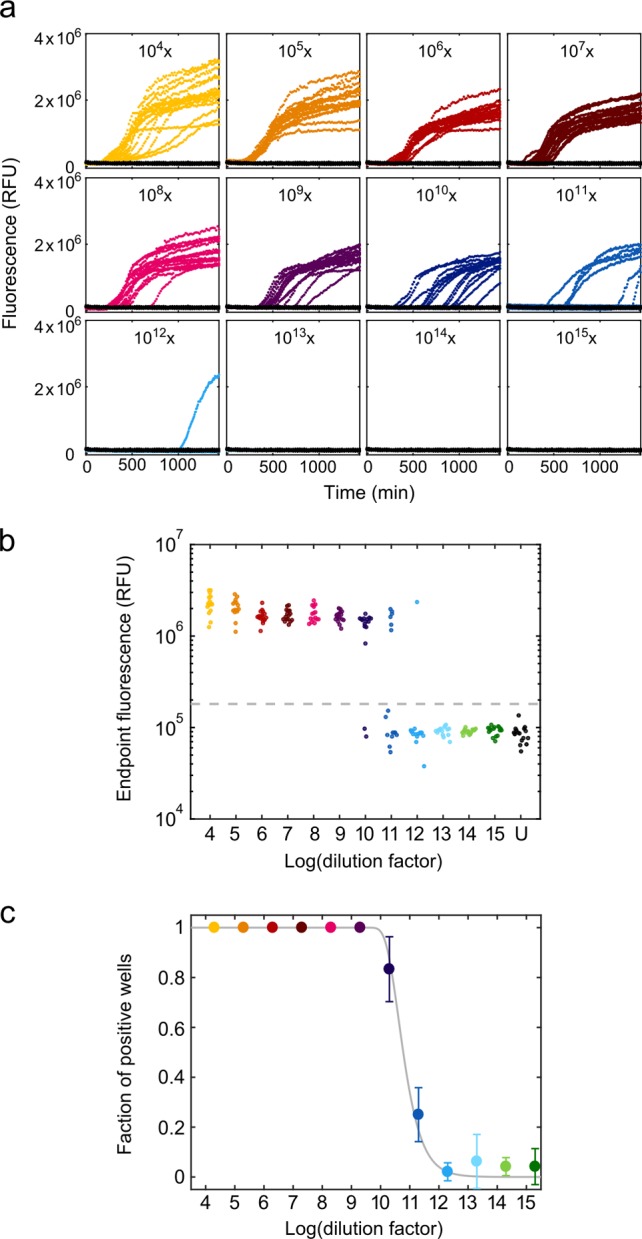
Figure 5

Open in a new tab

Assay for 384-well microplate. (a) Real-time ThT fluorescence time courses of insulin fibril formation with 10-fold serial dilutions from 104 to 1015 of the standard fibril sample on a microplate (colored; unseeded controls in black). Each dilution and the control was performed in 16 technical replica. (b) Fluorescence end point signals at different fibril dilution factors (colored; unseeded controls in black, U). The gray dashed line shows the threshold (x̅0 + 5σ0) used for the positive/negative scoring of the signals. (c) Fraction of positive wells as a function of the logarithm of the dilution factor. Data represent the mean ± SD from three independent experiments.

Digital Data Analysis

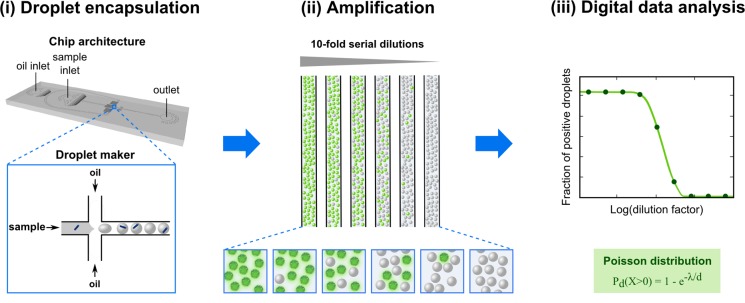
To digitize the assay readout for absolute propagon quantification, fluorescence end point values of the amplification reactions were transformed into positive and negative signals by thresholding. For the microplate assay, the threshold was set five standard deviations above the mean of the unseeded negative control reactions (x̅0 + 5σ0), and any signal above the threshold was regarded as a positive signal. For d-AQuA, droplets which showed positive ThT fluorescence at the end point were scored positive. The fraction of positive droplets at every dilution was then calculated from the number of positive droplets and the total number of droplets counted in the corresponding brightfield images. The absolute number of propagons in both assays was calculated using the Possion distribution model. The probability of finding k propagons in a reaction compartment, if the average number of propagons per reaction compartment is λ, is described by the Poisson distribution

graphic file with name ac-2017-032797_m001.jpg 1

The probability of having one or more propagons per reaction compartment (the probability of a positive signal) is given by

graphic file with name ac-2017-032797_m002.jpg 2

where P(X = 0) is the probability of not having any propagons in the reaction compartment (the probability of a negative signal). For the different dilution factors d, the probability of having one or more propagons per compartment can be described as

graphic file with name ac-2017-032797_m003.jpg 3

where λ is the average number of propagons in the original sample and d is the dilution factor. The fraction of positive signals can be related to the dilution factors using eq 3, and therefore, the absolute number of propagons in the original sample λ can be calculated. All data analysis was carried out using Matlab (The MathWorks, U.S.A.).

Fibril Quantification by AFM

The number of fibrils per unit volume of the standard fibril sample was estimated from AFM length distribution and mass conservation. The distribution of fibrils Ni(L) as a function of the contour length measured by AFM is shown in Figure 4b. This distribution is essentially the same distribution of fibrils per unit volume, differing by a mere normalization constant α, so that the distribution of fibrils per unit volume is simply αNi(L). The constant α can be obtained from the total mass per unit volume, which is obtained from the initial molar concentration of monomer cm, i.e. cmMW. Therefore, by mass conservation this results in

graphic file with name ac-2017-032797_m004.jpg 4

where ρ is the density of the monomer and the fibril, that are assumed here to be identical. This then gives α = cmMW/(∑Ni(L)·Liπr2ρ), since all the terms on the right-hand are known.

Figure 4.

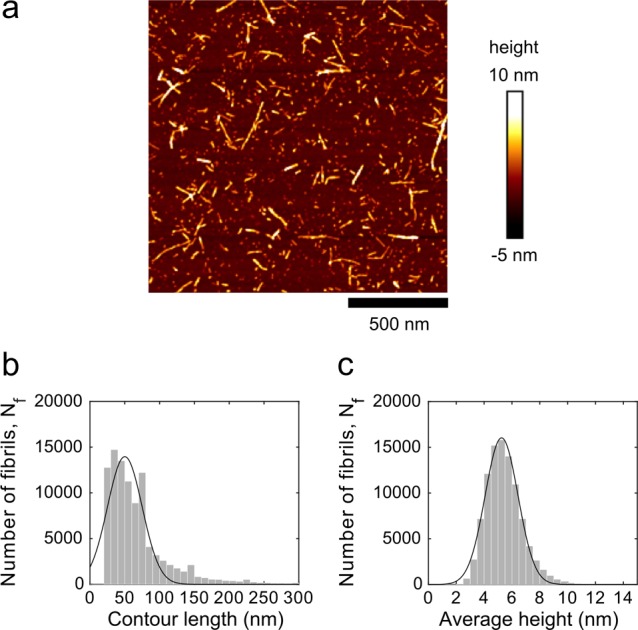
Figure 4

Open in a new tab

Quantitative AFM measurements. (a) AFM height image of preformed insulin fibrils. (b) Histogram of the fibril contour length distribution of preformed insulin fibrils. (c) Histogram of the average height distribution of the preformed insulin fibrils. A Gaussian distribution (solid line) was fitted to the data to obtain the means ± SD of the contour lengths and the fibril heights.

The total number of fibrils per unit volume, 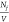Inline graphic, is then

graphic file with name ac-2017-032797_m006.jpg 5

where both ∑Ni(L)·Li and ∑Ni(L) are known from the distribution of fibrils as a function of the contour length in Figure 4b.

Results and Discussion

Workflow of d-AQuA

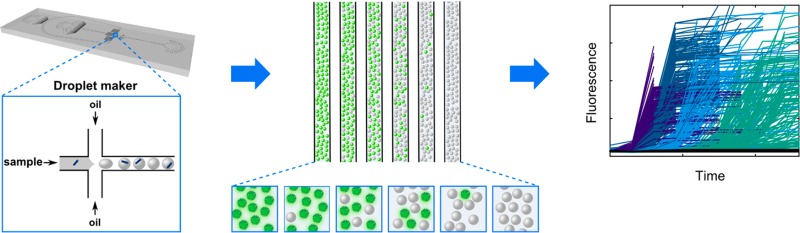
The setup of d-AQuA is schematically depicted in Figure 1. We used a microfluidic chip with flow focusing geometry to generate uniform droplet compartments for highly parallel amplification of single propagons in thousands of pL-droplets. This high number of parallel measurements enables a digital interpretation of the data for precise and accurate quantification of the absolute number of propagons contained in a sample. Individual droplets encapsulating the soluble substrate protein, Thioflavin T (ThT), a fluorescent dye that allows specific detection of amyloid aggregates, along with a series of 10-fold dilutions of a propagon-containing sample, are formed from water-in-oil emulsions at kilohertz frequency. Droplets of each fibril dilution are stored inside glass capillaries, and amplification is carried out in the individual droplets to the end-point. Droplets containing amplified aggregates induced by propagons are detected by their positive ThT fluorescence signals, and the number of fluorescence positive and negative droplets is counted. As d-AQuA enters a stochastic regime at limiting dilutions, the Poisson distribution model becomes valid and is applied for determining the absolute number of propagons in the original sample.

Figure 1.

Figure 1

Open in a new tab

D-AQuA workflow. (i) Samples containing 10-fold serial dilutions of the standard fibril sample (blue dashes) are mixed with soluble substrate protein and ThT. The mixtures are partitioned into several thousand pL-droplets using a microfluidic flow-focusing device (inset). (ii) Microdroplets are collected into glass capillaries for end-point amplification and detection by ThT fluorescence (green). (iii) ThT-positive droplets are counted, and the absolute number of propagons in the standard fibril sample is quantified by Poisson statistics.

Standard Fibril Sample Generation

For the development of d-AQuA, we used the hormone insulin as a model system, because it readily forms amyloid fibrils analogous to those of disease relevant amyloidogenic proteins,38 and is therefore widely used as experimental model protein to study amyloid formation.39−41 We first generated a standard fibril sample, a well-characterized sample of preformed insulin fibrils with reproducible propagation properties. Insulin fibrils were reconstituted in vitro by incubating human insulin at a concentration of 1 mM in HCl (pH 2.0) at 65 °C and agitation at 600 rpm for 72 h. Residual monomeric species were removed by intense washing with 1 mM HCl (pH 2.0) using Amicon centrifugal filters (MWCO 100 kDa).35 The remaining fibrils were lyophilized and stored at −20 °C. The fibrils were diluted to a concentration of 400 μM (monomer equivalents) to yield the standard fibril sample. We analyzed this sample for the typical morphological and biophysical characteristics of amyloid fibrils and its self-propagation activity in a seeded propagation assay (Figure 2). Dynamic light scattering (DLS) measurements showed that the fibrils have a mean hydrodynamic radius of 85 nm (Figure 2a). Furthermore, both Fourier transform infrared (FTIR) and circular dichroism (CD) spectra indicated a high β-sheet content, which is characteristic of amyloid fibrils40,42 (Figure 2b,c). To assess the propagation activity of the sample, the kinetics of fibril formation by monomeric insulin in the presence of preformed fibrils from the standard sample were monitored by optical density at OD370 nm (Figure 2d). Increasing concentrations of preformed fibrils (1, 2, and 5% of total protein concentration) were found to shorten the lag phase of the aggregation reaction gradually, as expected for a nucleated self-assembly process. These results indicate that the standard fibril sample exhibits the typical biophysical characteristics of amyloid fibrils.

Figure 2.

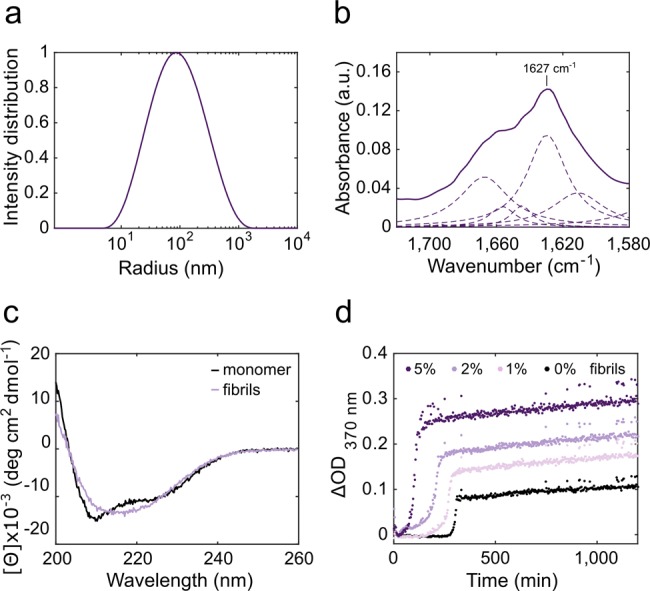
Figure 2

Open in a new tab

The standard fibril sample was characterized by DLS (a), FTIR spectroscopy (b, shown are the whole spectrum as a solid line and its deconvoluted peaks as dashed lines), far-UV CD spectroscopy (c) and a self-propagation activity assay (d).

Development of d-AQuA

Next, we established the experimental conditions for d-AQuA (Figure 1; experimental setup in Figure S1). Initially, 400 μM insulin in HCl (pH 2.0), 0.1 M guanidinium chloride (GdmCl), and 40 μM ThT were encapsulated inside microdroplets together with serial 10-fold dilutions ranging from 102 to 108 of the standard fibril sample (in monomer equivalents). We found that the use of a high concentration of the substrate and the addition of low amounts of GdmCl which accelerates aggregation by inducing partial unfolding of the monomeric species,43 were important for efficient amplification. Droplets without (i.e., unseeded controls) and with different dilutions of preformed fibrils were collected in separate capillaries, mounted on a microscope slide and heated to 65 °C to accelerate the growth and proliferation of the propagons. Fluorescence images were taken every 15 min to follow the amplification process in the individual droplets over 24 h (Figure 3a,b). For the absolute quantification of the number of propagons, we analyzed between 500 and 1400 droplets per dilution and digitized the readout by grouping the fluorescence end point signals into positive and negative outcomes by thresholding (see Experimental Section for details). A Poisson distribution was fitted to the number of fluorescence positive (i.e., propagon containing) droplets for each dilution factor at the assay end point with the best fits yielding an average number of 2.1·1011 propagons per μL (accurate to within a factor of 1.1, n = 2) in the standard fibril sample (Figure 3c and Experimental Section). Moreover, under these conditions, we obtained a very low average false positive rate of only ∼0.4% spontaneously aggregating reactions in a total of about 700 droplets of the unseeded control (Figure S2). Because of the high level of conformity of the data to the Poisson distribution model, we conclude that the assay is capable of amplifying single propagons in picoliter droplets and allows the precise quantification of absolute numbers of propagons at low femtomolar concentrations.

Validation of the Number of Propagons by AFM

To monitor the number of propagons determined by d-AQuA with an alternative method, we used AFM to estimate the dimensions and the physical number of fibrillar aggregates present in the standard fibril sample (Figure 4a). The average contour length of the fibrils was (50 ± 35) nm (Figure 4b) and the height was (5.3 ± 1.7) nm (Figure 4c). We used these dimensions and mass conservation to calculate the physical number of fibrils per unit volume of the standard fibril sample (see Experimental Section for details). The calculations yielded an average number of 1.1·1012 μL–1 fibrils. This number is closely similar (less than an order of magnitude, i.e. within a factor of ∼5) to the number of propagons determined by d-AQuA (2.1·1011 propagons μL–1). A possible explanation for the small difference between these numbers might be that not all fibrillar aggregates detected by AFM also act as active propagons in d-AQuA. We therefore conclude that the active propagons detected by d-AQuA are essentially identical to a fraction of morphologically defined fibrillar aggregates.

Comparison to a Digital Amyloid Amplification Assay in a Microplate

Microplate-based amyloid amplification assays in 96-well plate formats with an analogue read-out are the current standard assays for detecting amyloid aggregates in biological samples.26,27,34 To enable a direct comparison between the sensitivity of this method with d-AQuA, we developed an amyloid amplification assay for insulin in a microplate with a digital read-out (Figure 5). As the precision of digital read-outs increases with the number of replicate reactions, we established the assay in a 384-well format. We also adapted the experimental conditions to account for the higher volumes and larger surface areas used in the microplate assay. A range of experimental parameters including substrate protein concentration, temperature, shaking cycles, pH-value, buffer conditions, and additives were systematically screened and optimized for best assay performance. Especially crucial was the addition of d-mannitol, which has been reported to suppress spontaneous nucleation of insulin by stabilization of the monomer, while enhancing the growth rate of existing fibrils.44 HCOOH at pH 3.0 was chosen as the solvent, because of its reported ability to reduce spontaneous aggregation of monomeric insulin.45 Finally, we identified a concentration of 2 μM soluble substrate protein in 0.75 M D-mannitol, 1 M GdmCl, 10 μM ThT, HCOOH (pH 3.0) with cyclic agitation (1 min at 300 rpm, 2 min quiescent) at 30 °C as optimal assay conditions. These conditions resulted in an efficient reduction of spontaneous aggregation to a false positive rate of 1–2% in 384 replicas over the course of the experiment (24 h; Figure S2), while yielding highly reproducible aggregation kinetics of the propagon-catalyzed reactions (Figure 5a).

For digital quantification of the propagon number in our standard fibril sample, we again performed serial 10-fold dilutions of the standard fibril sample (104- to 1015-fold dilutions in monomer equivalents) using 16 replicas per dilution. The aggregation time course was monitored by real-time ThT fluorescence over 24 h (Figure 5a). At low dilutions (104- to 109-fold), we observed lag times of approximately 8 h, which gradually increased with higher dilutions of preformed fibrils. End-point fluorescence signals of reactions with low dilution factors (≤109-fold) of preformed fibrils were all positive, whereas at higher dilutions, only fractions of the replicate reactions appeared positive (14, 6, and 1 out of 16 replicas for 1010-, 1011- and 1012-fold dilutions, respectively). All reactions at dilution factors ≥1013-fold, as well as the control (without preformed fibrils) were scored negative (Figure 5b). The fraction of positive signals was correlated to the dilution factors, and a Poisson distribution was fitted to the data (Figure 5c and Experimental Section). The best fit yielded an average number of 1.4·109 propagons μL–1 (accurate to within a factor of 1.2, n = 3) in the standard fibril sample (Figure 5c and Figure S3). These data show that the microplate assay (1.4·109 propagons μL–1) is also capable of detecting individual propagons, but when compared to d-AQuA (2.1·1011 propagons μL–1) 2 orders of magnitude less propagons were detected.

The detection of a lower number of active propagons in the microplate assay might be attributed to a loss of fibrils to various solid surfaces during the extensive pipetting steps or to their adherence to the microplate surface. Alternatively, the absence of solid contact surfaces in the microdroplets or the small droplet sizes, associated with higher effective concentrations,1 might result in a higher number of effective propagons. High losses of propagons, however, might significantly impair the sensitivity and reproducibility of the assay and thus lead to an inaccurate quantification of the number of propagons. Compared to the microplate assay, d-AQuA also exhibited a greatly reduced average false positive rate of unspecific amplification reactions in the unseeded control (∼0.4% compared to 1–2%) and decreased assay time (∼8 h compared to 24 h).

D-AQuA also offers several important advantages over the most commonly used amyloid amplification assays, PMCA24 and RT-QuIC.25,46 First, the ability of d-AQuA to perform large numbers of replicate measurements (up to 1400 in d-AQuA compared to typically 3 to 8 in PMCA24 and RT-QuIC25,34) yielded highly precise data sets. D-AQuA therefore enabled the detection of single propagons at the ultimate limit of detection and absolute propagon quantification, whereas the concentration in PMCA and RT-QuIC, is typically quantified either in gram or mol or given as amyloid seeding activity (SD50) or in tissue dilutions24,25,46 and thus does not define the number of propagons. When compared to PMCA,24 d-AQuA also provided a simpler and faster read-out by using ThT fluorescence instead of detection by immunoblotting. In experiments described in this study, d-AQuA also showed a significantly decreased assay time (∼8 h compared to typically 1–3 days in PMCA24,46 and RT-QuIC46), reduced labor-intensive and time-consuming pipetting steps and associated errors. Moreover, the use of pL-droplets instead of μL-volumes significantly reduced the consumption of reagents and, in particular, of the analyte, which is crucial, when precious clinical samples with a low concentration of propagons need to be analyzed. Hence, d-AQuA offers a substantial improvement over the microplate assays for determining exact numbers of propagons, a result that is of major importance in the context of ultrasensitive detection and precise quantification of the number of low-abundance propagons in a given sample.

Conclusions

In conclusion, we present a proof-of-concept method, d-AQuA, for using digital microfluidics in combination with amyloid amplification assays. We used insulin as model system and showed that d-AQuA allowed us to run simultaneously up to 1400 parallel amplification reactions per fibril dilution in pL droplets for extremely accurate and precise digital data analysis. Our results showed that d-AQuA enables the measurement of the activity of single propagons and the digital quantification of the absolute number of propagons present in a sample. D-AQuA thus reached the ultimate sensitivity limit of detection with the capability to detect a single propagon.

Compared to a complementary microplate assay, which also reached the ultimate level of sensitivity, d-AQuA was shown to be the more rapid and precise method and to have a higher recovery rate of low-abundance propagons. This opens up the possibility for multiple applications. For example, d-AQuA provides the potential, by correlating its data with mathematical models, to address specific scientific questions for a more fundamental understanding of the molecular mechanisms of amyloid formation. In addition, d-AQuA might be of practical use for the detection of even the smallest traces of insulin aggregates that cannot be detected with existing analytical methods in biopharmaceutical preparations of insulin products used for therapy in diabetes patients47−49 and may lead to an immune response in patients after subcutaneous injection.49 Our technology also holds the potential to be used for rapid, ultrasensitive and highly parallel preclinical and clinical diagnosis through the detection of early pathological propagons in protein misfolding and aggregation (PMA) diseases for personalized medicine. In particular, a small-volume, single-use disposable chip with the ability to diagnose accurately PMA diseases from body fluids holds great promise for novel automated diagnostic approaches. Finally, the technological innovations of d-AQuA are well suited to the establishment of powerful high-throughput screening platforms for the identification of novel aggregation inhibitors, both in the context of stabilizing reagents for biopharmaceutical products or as drugs to cure PMA diseases. We therefore envisage that d-AQuA has great potential for advancing biomedical research and sensitive point-of-care diagnostics for PMA diseases.

Acknowledgments

We thank Rita Moos and Lisa Caflisch for technical help, Tom Mason for surfactant synthesis, and Elisabeth J. Rushing for editing the manuscript. This work was funded and supported by Sanofi-Aventis Deutschland GmbH within a research collaboration of the University of Zurich and Sanofi-Aventis Deutschland GmbH. M.P. is the recipient of a Forschungskredit of the University of Zurich (grant no. FK-16-026) and an EMBO Short-Term Fellowship. M.A. is the recipient of an individual postdoctoral grant from the Danish Council for Independent Research, Natural Sciences (FNU-11-113326). G.M. is supported by the European Research Council and Sidney Sussex College, Cambridge. C.G.T. is supported by the Frances and Augustus Newman Foundation. D.K. is supported by the European Research Council and Royal Society. C.M.D. is supported by the Wellcome Trust and the Cambridge Centre for Misfolding Diseases. T.P.J.K. is supported by the Biotechnology and Biological Sciences Research Council, the Frances and Augustus Newman Foundation, Cancer Research UK, and the European Research Council and the Cambridge Centre for Misfolding Diseases. A.A. is the recipient of an Advanced Grant of the European Research Council, a European Union Framework 7 Grant (NEURINOX), and is supported by the Swiss National Foundation, the Clinical Research Priority Programs “Small RNAs” and “Human Hemato-Lymphatic Diseases”, SystemsX.ch, and the Gelu Foundation. S.H. is the recipient of grants from SystemsX.ch (SynucleiX) and the commission innovations of the University Hospital of Zurich.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.analchem.7b03279.

  • Materials and methods, experimental setup of d-AQuA (Figure S1), comparison of false positive rates between d-AQuA and the microplate assay (Figure S2), Poisson analysis of three individual microplate assays (Figure S3), and raw images of Figure 3a (Figure S4) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ac7b03279_si_001.pdf (512.3KB, pdf)

References

  1. Guo M. T.; Rotem A.; Heyman J. A.; Weitz D. A. Lab Chip 2012, 12, 2146–2155. 10.1039/c2lc21147e. [DOI] [PubMed] [Google Scholar]
  2. Theberge A. B.; Courtois F.; Schaerli Y.; Fischlechner M.; Abell C.; Hollfelder F.; Huck W. T. S. Angew. Chem., Int. Ed. 2010, 49, 5846–5868. 10.1002/anie.200906653. [DOI] [PubMed] [Google Scholar]
  3. Mitchell P. Nat. Biotechnol. 2001, 19, 717–721. 10.1038/90754. [DOI] [PubMed] [Google Scholar]
  4. Dressler O. J.; Solvas X. C. i.; deMello A. J. Annu. Rev. Anal. Chem. 2017, 10, 1–24. 10.1146/annurev-anchem-061516-045219. [DOI] [PubMed] [Google Scholar]
  5. Hong J. W.; Quake S. R. Nat. Biotechnol. 2003, 21, 1179–1183. 10.1038/nbt871. [DOI] [PubMed] [Google Scholar]
  6. Sykes P. J.; Neoh S. H.; Brisco M. J.; Hughes E.; Condon J.; Morley A. A. BioTechniques 1992, 13, 444–449. [PubMed] [Google Scholar]
  7. Vogelstein B.; Kinzler K. W. Proc. Natl. Acad. Sci. U. S. A. 1999, 96, 9236–9241. 10.1073/pnas.96.16.9236. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Beer N. R.; Hindson B. J.; Wheeler E. K.; Hall S. B.; Rose K. A.; Kennedy I. M.; Colston B. W. Anal. Chem. 2007, 79, 8471–8475. 10.1021/ac701809w. [DOI] [PubMed] [Google Scholar]
  9. Beer N. R.; Wheeler E. K.; Lee-Houghton L.; Watkins N.; Nasarabadi S.; Hebert N.; Leung P.; Arnold D. W.; Bailey C. G.; Colston B. W. Anal. Chem. 2008, 80, 1854–1858. 10.1021/ac800048k. [DOI] [PubMed] [Google Scholar]
  10. Hindson B. J.; Ness K. D.; Masquelier D. A.; Belgrader P.; Heredia N. J.; Makarewicz A. J.; Bright I. J.; Lucero M. Y.; Hiddessen A. L.; Legler T. C.; Kitano T. K.; Hodel M. R.; Petersen J. F.; Wyatt P. W.; Steenblock E. R.; Shah P. H.; Bousse L. J.; Troup C. B.; Mellen J. C.; Wittmann D. K.; Erndt N. G.; Cauley T. H.; Koehler R. T.; So A. P.; Dube S.; Rose K. A.; Montesclaros L.; Wang S.; Stumbo D. P.; Hodges S. P.; Romine S.; Milanovich F. P.; White H. E.; Regan J. F.; Karlin-Neumann G. A.; Hindson C. M.; Saxonov S.; Colston B. W. Anal. Chem. 2011, 83, 8604–8610. 10.1021/ac202028g. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Pinheiro L. B.; Coleman V. A.; Hindson C. M.; Herrmann J.; Hindson B. J.; Bhat S.; Emslie K. R. Anal. Chem. 2012, 84, 1003–1011. 10.1021/ac202578x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Situma C.; Hashimoto M.; Soper S. A. Biomol. Eng. 2006, 23, 213–231. 10.1016/j.bioeng.2006.03.002. [DOI] [PubMed] [Google Scholar]
  13. Wang Y.; Vaidya B.; Farquar H. D.; Stryjewski W.; Hammer R. P.; McCarley R. L.; Soper S. A.; Cheng Y.-W.; Barany F. Anal. Chem. 2003, 75, 1130–1140. 10.1021/ac020683w. [DOI] [PubMed] [Google Scholar]
  14. Lan F.; Haliburton J. R.; Yuan A.; Abate A. R. Nat. Commun. 2016, 7, 11784. 10.1038/ncomms11784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Macosko E. Z.; Basu A.; Satija R.; Nemesh J.; Shekhar K.; Goldman M.; Tirosh I.; Bialas A. R.; Kamitaki N.; Martersteck E. M.; Trombetta J. J.; Weitz D. A.; Sanes J. R.; Shalek A. K.; Regev A.; McCarroll S. A. Cell 2015, 161, 1202–1214. 10.1016/j.cell.2015.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Klein A. M.; Mazutis L.; Akartuna I.; Tallapragada N.; Veres A.; Li V.; Peshkin L.; Weitz D. A.; Kirschner M. W. Cell 2015, 161, 1187–1201. 10.1016/j.cell.2015.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Mazutis L.; Gilbert J.; Ung W. L.; Weitz D. A.; Griffiths A. D.; Heyman J. A. Nat. Protoc. 2013, 8, 870–891. 10.1038/nprot.2013.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Mok J.; Mindrinos M. N.; Davis R. W.; Javanmard M. Proc. Natl. Acad. Sci. U. S. A. 2014, 111, 2110–2115. 10.1073/pnas.1323998111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mazutis L.; Araghi A. F.; Miller O. J.; Baret J.-C.; Frenz L.; Janoshazi A.; Taly V.; Miller B. J.; Hutchison J. B.; Link D.; Griffiths A. D.; Ryckelynck M. Anal. Chem. 2009, 81, 4813–4821. 10.1021/ac900403z. [DOI] [PubMed] [Google Scholar]
  20. Knowles T. P. J.; White D. A.; Abate A. R.; Agresti J. J.; Cohen S. I. A.; Sperling R. A.; De Genst E. J.; Dobson C. M.; Weitz D. A. Proc. Natl. Acad. Sci. U. S. A. 2011, 108, 14746–14751. 10.1073/pnas.1105555108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Prusiner S. Science 1982, 216, 136–144. 10.1126/science.6801762. [DOI] [PubMed] [Google Scholar]
  22. Aguzzi A.; Falsig J. Nat. Neurosci. 2012, 15, 936–939. 10.1038/nn.3120. [DOI] [PubMed] [Google Scholar]
  23. Knowles T. P.; Vendruscolo M.; Dobson C. M. Nat. Rev. Mol. Cell Biol. 2014, 15, 384–396. 10.1038/nrm3810. [DOI] [PubMed] [Google Scholar]
  24. Saborio G. P.; Permanne B.; Soto C. Nature 2001, 411, 810–813. 10.1038/35081095. [DOI] [PubMed] [Google Scholar]
  25. Wilham J. M.; Orrú C. D.; Bessen R. A.; Atarashi R.; Sano K.; Race B.; Meade-White K. D.; Taubner L. M.; Timmes A.; Caughey B. PLoS Pathog. 2010, 6, e1001217. 10.1371/journal.ppat.1001217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Salvadores N.; Shahnawaz M.; Scarpini E.; Tagliavini F.; Soto C. Cell Rep. 2014, 7, 261–268. 10.1016/j.celrep.2014.02.031. [DOI] [PubMed] [Google Scholar]
  27. Shahnawaz M.; Tokuda T.; Waragai M.; Mendez N.; Ishii R.; Trenkwalder C.; Mollenhauer B.; Soto C. JAMA Neurol. 2017, 74, 163–172. 10.1001/jamaneurol.2016.4547. [DOI] [PubMed] [Google Scholar]
  28. Cohen S. I. A.; Linse S.; Luheshi L. M.; Hellstrand E.; White D. A.; Rajah L.; Otzen D. E.; Vendruscolo M.; Dobson C. M.; Knowles T. P. J. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 9758–9763. 10.1073/pnas.1218402110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Jarrett J. T.; Lansbury P. T. Cell 1993, 73, 1055–1058. 10.1016/0092-8674(93)90635-4. [DOI] [PubMed] [Google Scholar]
  30. Ferrone F. A.; Hofrichter J.; Eaton W. A. J. Mol. Biol. 1985, 183, 611–631. 10.1016/0022-2836(85)90175-5. [DOI] [PubMed] [Google Scholar]
  31. Knowles T. P. J.; Waudby C. A.; Devlin G. L.; Cohen S. I. A.; Aguzzi A.; Vendruscolo M.; Terentjev E. M.; Welland M. E.; Dobson C. M. Science 2009, 326, 1533–1537. 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
  32. Cox B.; Ness F.; Tuite M. Genetics 2003, 165, 23–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Aguzzi A. Nature 2009, 459, 924–925. 10.1038/459924a. [DOI] [PubMed] [Google Scholar]
  34. McGuire L. I.; Poleggi A.; Poggiolini I.; Suardi S.; Grznarova K.; Shi S.; de Vil B.; Sarros S.; Satoh K.; Cheng K.; Cramm M.; Fairfoul G.; Schmitz M.; Zerr I.; Cras P.; Equestre M.; Tagliavini F.; Atarashi R.; Knox D.; Collins S.; Haïk S.; Parchi P.; Pocchiari M.; Green A. Ann. Neurol. 2016, 80, 160–165. 10.1002/ana.24679. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nilsson M. R.; Dobson C. M. Protein Sci. 2003, 12, 2637–2641. 10.1110/ps.0360403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. McDonald J. C.; Duffy D. C.; Anderson J. R.; Chiu D. T.; Wu H.; Schueller O. J. A.; Whitesides G. M. Electrophoresis 2000, 21, 27–40. . [DOI] [PubMed] [Google Scholar]
  37. Holtze C.; Rowat A. C.; Agresti J. J.; Hutchison J. B.; Angile F. E.; Schmitz C. H. J.; Koster S.; Duan H.; Humphry K. J.; Scanga R. A.; Johnson J. S.; Pisignano D.; Weitz D. A. Lab Chip 2008, 8, 1632–1639. 10.1039/b806706f. [DOI] [PubMed] [Google Scholar]
  38. Jiménez J. L.; Nettleton E. J.; Bouchard M.; Robinson C. V.; Dobson C. M.; Saibil H. R. Proc. Natl. Acad. Sci. U. S. A. 2002, 99, 9196–9201. 10.1073/pnas.142459399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nettleton E. J.; Tito P.; Sunde M.; Bouchard M.; Dobson C. M.; Robinson C. V. Biophys. J. 2000, 79, 1053–1065. 10.1016/S0006-3495(00)76359-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Bouchard M.; Zurdo J.; Nettleton E. J.; Dobson C. M.; Robinson C. V. Protein Sci. 2000, 9, 1960–1967. 10.1110/ps.9.10.1960. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Ivanova M. I.; Sievers S. A.; Sawaya M. R.; Wall J. S.; Eisenberg D. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 18990–18995. 10.1073/pnas.0910080106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Nelson R.; Sawaya M. R.; Balbirnie M.; Madsen A.; Riekel C.; Grothe R.; Eisenberg D. Nature 2005, 435, 773–778. 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Ahmad A.; Millett I. S.; Doniach S.; Uversky V. N.; Fink A. L. Biochemistry 2003, 42, 11404–11416. 10.1021/bi034868o. [DOI] [PubMed] [Google Scholar]
  44. Saha S.; Sharma A.; Deep S. RSC Adv. 2016, 6, 28640–28652. 10.1039/C5RA27206H. [DOI] [Google Scholar]
  45. Brange J.; Andersen L.; Laursen E. D.; Meyn G.; Rasmussen E. J. Pharm. Sci. 1997, 86, 517–525. 10.1021/js960297s. [DOI] [PubMed] [Google Scholar]
  46. Orru C. D.; Wilham J. M.; Vascellari S.; Hughson A. G.; Caughey B. Prion 2012, 6, 147–152. 10.4161/pri.19430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Chi E. Y.; Krishnan S.; Randolph T. W.; Carpenter J. F. Pharm. Res. 2003, 20, 1325–1336. 10.1023/A:1025771421906. [DOI] [PubMed] [Google Scholar]
  48. Nielsen L.; Khurana R.; Coats A.; Frokjaer S.; Brange J.; Vyas S.; Uversky V. N.; Fink A. L. Biochemistry 2001, 40, 6036–6046. 10.1021/bi002555c. [DOI] [PubMed] [Google Scholar]
  49. D’Souza A.; Theis J. D.; Vrana J. A.; Dogan A. Amyloid 2014, 21, 71–75. 10.3109/13506129.2013.876984. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ac7b03279_si_001.pdf (512.3KB, pdf)

Articles from Analytical Chemistry are provided here courtesy of American Chemical Society

RESOURCES