Multiple imputation to evaluate the impact of an assay change in national surveys

Abstract

National health surveys, such as the National Health and Nutrition Examination Survey, are used to monitor trends of nutritional biomarkers. These surveys try to maintain the same biomarker assay over time, but there are a variety of reasons why the assay may change. In these cases, it is important to evaluate the potential impact of a change so that any observed fluctuations in concentrations over time are not confounded by changes in the assay. To this end, a subset of stored specimens previously analyzed with the old assay is retested using the new assay. These paired data are used to estimate an adjustment equation, which is then used to ‘adjust’ all the old assay results and convert them into ‘equivalent’ units of the new assay. In this paper, we present a new way of approaching this problem using modern statistical methods designed for missing data. Using simulations, we compare the proposed multiple imputation approach with the adjustment equation approach currently in use. We also compare these approaches using real National Health and Nutrition Examination Survey data for 25-hydroxyvitamin D.

1. Introduction

Missing data is a common problem in medical studies and surveys and can arise for a myriad of reasons. A primary problem caused by missing data is the severe bias that can occur when respondents differ from non-respondents. However, not all missing data is unplanned. Graham et al. [1] have proposed a type of planned missingness in the setting of questionnaire design to obtain more high-quality information, without dramatically increasing the costs or the number of questions asked of each respondent. This is achieved by dividing the questions up in a specific way, ensuring a core set of questions are answered by all respondents, and using modern missing data methods to impute answers to questions that were not asked of specific sets of respondents. In our setting, when an assay has changed in a large national survey, it is cost prohibitive and often not possible because of lack of specimen availability, to go back and re-test all previously tested specimens using the new assay. This paper proposes measuring the new assay on a designated sub-sample of the originally sampled National Health and Nutrition Examination Survey (NHANES) specimens, followed by using multiple imputation to address any bias induced by changing the biomarker assay. Multiple imputation was proposed previously as a solution to bridge changes in measurement systems in large public datasets [2–5]. However, it has never been used in NHANES as a form of planned missingness to account for a change in biomarker assays.

The NHANES are a series of cross-sectional national surveys of health and nutritional status conducted on a periodic basis by the National Center for Health Statistics (NCHS) of the US Centers for Disease Control and Prevention (CDC) [6]. NHANES is the only US national survey that collects biological specimens and as such is uniquely suited to assess trends on a wide variety of health and nutritional biomarkers measured using clinical laboratory assays [7]. Ideally, for any given nutritional biomarker, the same assay is used over time so that any changes in the concentration can be evaluated and interpreted as actual changes in the nutritional status of the US population. However, because of discontinuation or advances in laboratory methods, changes in an assay are unavoidable.

In a laboratory, it is routine to perform a method comparison study to evaluate the potential impact of a change in the assay. In the context of a national survey, if two assays are not interchangeable, the method comparison study is used to derive adjustment equations for the old assay into equivalent units of the new assay. These types of equations are published in the NHANES documentation with a recommendation that users interested in trends derive predicted values of the new assay given the old assay using the adjustment equation [8–10]. The nomenclature varies, but the adjustment equation derived from this type of method comparison study may be referred to as a crossover, bridging, or a calibration study [8–16]. In NHANES, the results of bridging studies are reported in the documentation for serum and whole blood folate, plasma homocysteine, serum ferritin, glucose, and serum 25-hydroxyvitamin D and used for analyzing trends in NHANES [8–13,17–22].

The adjustment equation derived from the bridging study is often used in NHANES to replace all the values from old assay with equivalent unit data of the new assay, and then the statistical analysis proceeds as if these were real data from the new assay. This ad hoc approach to deal with an assay change fails to account for important sources of variability, which in turn leads to underestimated standard errors, confidence intervals that are too narrow and incorrect p-values. Further, even though the new assay is used on a subset of the NHANES specimens to perform the bridging study, these actual measured values are not used but rather replaced themselves with predicted values. This historical approach is common practice in NHANES and was proposed as a core approach to standardize of vitamin D [15,16] and folate [23] measurements in national surveys. This paper will refer to the ad hoc approach of using the data from a bridging study to develop an equation as the adjustment equation approach.

Reframing this problem as a missing data problem, allows the use of all the statistical theory and methodology under the rubric of missing data to solve some of the shortcomings associated with the historical approach. The multiple-imputation approach has several advantages over the adjustment-equation approach. First, it provides a natural way to accommodate the uncertainty associated with replacing missing data with predictions (also called imputations). Second, this approach will not discard the actual measurements made by the new assay. Lastly, this approach places the focus on developing a proper imputation model rather than finding the single best adjustment equation from a subset of the specimens. Therefore, model fit issues such as transformations, heteroskadisticity, errors in variables, and linearity falls under the broader scope of developing a formal imputation model. Section 2 provides a background on the assays that measure serum 25-hydroxyvitamin D in NHANES and a brief review of missing data terminology and methods. Section 3 describes the proposed multiple imputation method, and for comparison, the single imputation methods considered. Section 4 illustrates the application of these imputation methods to serum 25-hydroxyvitamin D (25OHD) from NHANES 2001–2006. Section 5 outlines the details of the simulation to demonstrate how the adjustment equation approach falls short of a more principled approach. Section 6 presents some concluding remarks and a brief discussion.

2. Background

2.1. Vitamin D

Serum 25OHD is a biomarker in NHANES currently used to assess vitamin D status in the US population. A radioimmunoassay (RIA) was used to measure 25OHD in NHANES from 1988 to 1994 and 2001–2006. During these periods, the assay suffered from some bias, fluctuations, and imprecision. The CDC lab regularly uses bench and blind quality control (QC) pools that are run concurrently with patient samples to monitor the consistency of an assay's performance. Using QC pools run during 1988–2006, it was discovered that during some periods the QC pools measured higher (or lower) than in other periods. A round table was convened to address these problems [16]. The round table recommended changing the assay to an accuracy-based Liquid chromatography–tandem mass spectrometry (LC–MS/MS) method starting in 2007. In preparation for the change to the LC–MS/MS approach, a bridging study was undertaken to develop equations to adjust 25OHD measurements made with RIA to LC–MS/MS equivalent units. The details of these adjustment equations and the subsequent complete trend analysis are already published [19,20]. The adjusted data were released by NCHS on the NHANES website in October 2015 to facilitate assessing the vitamin D trends in the US population going forward [8]. In this paper, we will consider the data from the 25OHD bridging studies performed for NHANES 2001–2006 (n = 943). Unweighted descriptive statistics comparing RIA and LC–MS/MS for each of the survey cycles is shown in Table I, and the Bland–Altman plots are shown in Figure 1. The mean bias is statistically significant for cycles 2001–2002 (p-value < 0.0001) and 2005–2006 (p-value < 0.0001), and more importantly, the 95% limits of agreement are too wide to consider LC–MS/MS interchangeable with RIA. Because trends of the mean serum 25-OHD concentrations, reference intervals (2.5th–97.5th percentiles), and/or prevalence of vitamin D deficiency is used to assess the vitamin D status in the US population, a statistically valid approach is needed to estimate a variety of parameters under a change of assay.

Table I. Unweighted descriptive statistics of serum concentrations of 25-hydroxyvitamin D by radioimmunoassay and LC–MS/MS using a bridging data set: National Health and Nutrition Examination Survey 2001–2006 [20].

Survey period	n	Variable	Mean	SD
2001–2002	371	RIA	57.4	30.8
		LC–MS/MS	61.1	30.7
		Difference	−3.7	9.2
2003–2004	289	RIA	60.4	28.7
		LC–MS/MS	61.1	29.7
		Difference	−0.7	9.3
2005–2006	283	RIA	53.9	27.8
		LC–MS/MS	60.6	29.0
		Difference	−6.8	10.6
2001–2006	943	RIA	57.3	29.4
		LC–MS/MS	61.0	29.9
		Difference	−3.7	9.9

LC-MS/MS, Liquid chromatography–tandem mass spectrometry; RIA, radioimmunoassay.

Figure 1.

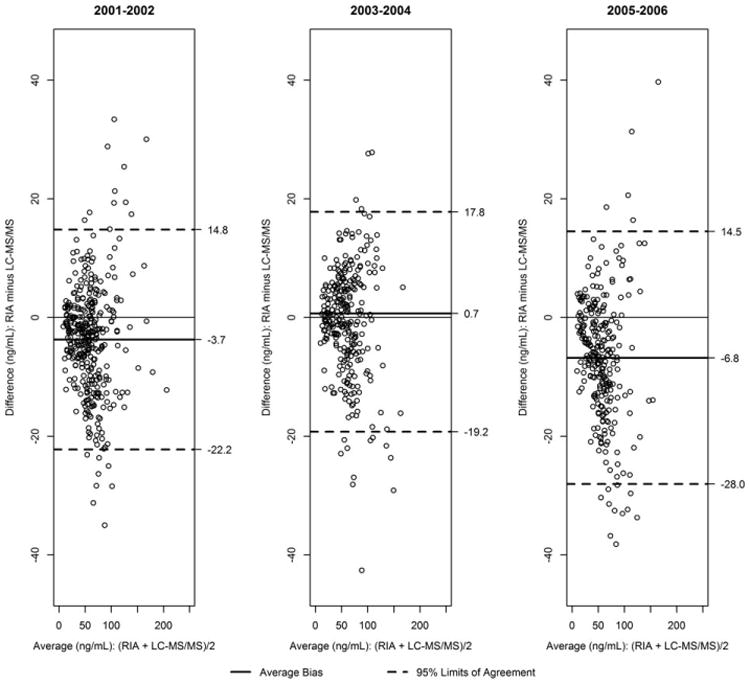
Bland–Altman plots comparing the serum concentrations of 25-hydroxyvitamin D by radioimmunoassay and liquid chromatography–tandem mass spectrometry (LC–MS/MS) using a bridging data set for National Health and Nutrition Examination Survey 2001–2006. RIA, radioimmunoassay.

2.2. Review of missing data methods

Missing data methods are commonly used to fill in the missing data with plausible value(s). This practice is often referred to as imputation. The goal for any viable imputation approach is not to predict the missing values per se but to be able to draw accurate inferences about population parameters [24]. There are many excellent reviews [24–31] and textbooks [32,33] of statistical methods to address missing data problems. Every review always starts with a discussion about the mechanism of missingness and whether the missing data is ignorable or non-ignorable. There are two ignorable missing data mechanisms: missing completely at random (MCAR) and missing at random (MAR). Rubin [32] formalized the notions of MCAR and MAR by specifying the missing data mechanism as part of the full posterior distribution in a Bayesian framework and showed that when the missing data are either MCAR or MAR, the missing data mechanism can be ignored and likelihood based approaches provide valid unbiased estimates. For this reason modern missing data methods are generally valid under MCAR or MAR.

A common approach to dealing with missing data is referred to as complete-case analysis. In other words, cases that are missing in the proposed analysis are simply dropped. This kind of approach will only provide valid estimates under MCAR, with some loss in power due to the reduction of the sample size. Imputation methods can be classified as either a single imputation or a multiple imputation method. A single imputation method replaces each missing datum with a single plausible value and typically proceeds as if the completed data are real. Some single-value imputation methods are ad hoc, such as mean imputation or last observation carried forward and known to provide biased inferences. Other single imputation methods are able to provide unbiased estimates of some population parameters under MAR but generally underestimate the standard error by ignoring the uncertainty added by imputing the missing data [33]. The adjustment equation approach used by NHANES, while not described in any textbook, can be considered an ad hoc single imputation approach that applies conditional mean imputation to impute all the values, including those actually observed. The problem with most single imputation approaches, including the adjustment equation, is that they underestimate the standard error by failing to account for two important sources of variation (i) sampling variability (ii) imputation uncertainty. Improvements on this front can be made by using a stochastic version of conditional mean imputation which adds a randomly drawn residual from the estimated error distribution of the missing data given the observed data to each predicted value. Additionally, some replication based variance estimation methods such as jackknife and bootstrapping have been proposed to address sources of uncertainty when single imputation is used [34,35].

Multiple imputation is a general term for methods that replaces a single missing value with M plausible values (M > =2). These imputed values are used to fill in the missing values and create M separate complete datasets. The M complete datasets are each analyzed separately using valid statistical procedures and the resulting estimates and standard errors are then combined to form a single inference using Rubin's formulas to approximate the posterior mean and variance of the selected parameter [32]. The variation across the M imputations reflects the uncertainty associated with replacing missing values with imputed values. The M imputations can be simulated from the posterior predictive distribution of the missing data given the observed data. This approach was used to obtain imputations under the multivariate normal distribution and applied to NHANES III data to deal with non-response, using data augmentation, a class of Markov chain Monte Carlo methods [36]. Another multiple imputation algorithm, which may have less of a theoretical basis, is to use separate chained equations, also known as sequential regression [37] or fully conditional specification [38]. In contrast to specifying the full parametric of joint distribution, it specifies each separate conditional probability distribution through a series of related (chained) regression models. Simulations suggest that this approach works well [38] and was used to deal with missing dual-energy X-ray absorptiometry data in NHANES [39].

3. Description of imputation methods for assay changes

The old assay values (X) will be completely observed by design, the new assay value (Y) will be partially observed on the basis of whether or not specimens are selected to be part of the bridging study. This type of missing data pattern is known as monotone missingness and can simplify the multiple imputation algorithm. In fact, if the joint distribution of (X, Y) is bivariate normal, a fully Bayesian approach for this problem with non-informative priors or a fully conditional specification will be asymptotically equivalent. Let X = X_obs = (X₁, X₂, …., X_N) denote the values from the fully observed old assay on N specimens. K specimens are selected at random from N (K < N) and tested using the new assay, Y. We denote elements Y that are observed and missing as Y_obs and Y_miss, respectively.

3.1. Single imputation models

The estimated least squares linear regression model using the complete cases (X_obs, Y_obs) forms the basis of both single imputation models considered in this paper: the adjustment equation approach and stochastic conditional regression. Let Ŷ = β̂₀ + β̂₁X be the predicted value of Y given X using the least squares estimates from the observed data. Of course, the regression form selected might include more flexible forms such as splines and/or include higher order terms, but for the purposes of this exposition we will use ordinary least squares. The adjustment equation approach uses the estimated regression equation to replace all the values of Y = (Y_miss, Y_obs), thereby discarding the actual measurements of Y_obs. In contrast, stochastic conditional mean imputation fills in the N-K unknown/missing values, Y_miss, using the estimated regression equation after adding a randomly drawn residual (r_i) from a Normal distribution with mean zero and variance equal to the estimated residual squared error of the regression line, $r_i~N(0,{\widehat{\sigma }}_{y|x}^2)$; such that, the predicted value for the ith case is calculated as Ŷ = β̂₀ + β̂₁X̂_i + r_i.

These two single imputation approaches are compared graphically in Figure 2 using a subset of data from the bridging study to develop equations to adjust 25OHD measurements. The open circles are the observed data (X_obs, Y_obs), where the x-values are the original RIA measurements made in 2007 and the y-values are the corresponding paired LC–MS/MS measurements. The estimated least squares regression line is drawn in each graph. The solid circles along the x-axis are the selected observed values of the old assay (RIA), that need to be imputed for the new assay (LC–MS/MS). The plus signs are the imputed values made on the basis of the selected method. Notice how the adjustment equation approach replaces all the values with imputations including the original Y_obs (Figure 2a). In stark contrast, stochastic conditional mean imputation only imputes the missing values, that is, the solid circles (Figure 2b) and includes the sampling variability around the estimated line. This graph illustrates why these single imputation approaches underestimate the variability in the new assay as they fail to capture the variability associated with the actual imputations. However, the adjustment equation approach has more drawbacks. First, as noted, the adjustment equation approach further underestimates the variance of the new assay because all the newly imputed data lie exactly along the estimated regression function. Second, discarding valid measurements made on the new assay in favor of values predicted by the regression model makes little sense and leads to a further underestimation of the variance. Third, the correlation between the two assays is severely biased to 1. Lastly, these single imputation approaches ignore the imputation uncertainty of the selected regression model. These shortcomings are resolved with a multiple imputation approach which replaces each missing value with M independent values and incorporates both the uncertainty because of the sampling variability around the line as well as the uncertainty of the parameters of the selected regression model.

Figure 2.

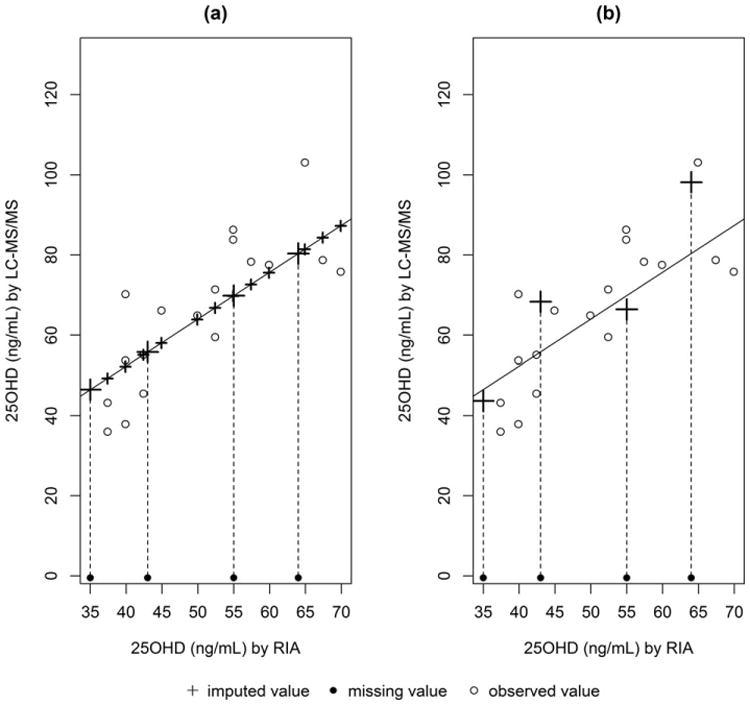
Single regression imputation approaches (a) adjustment equation adjustment equation (b) stochastic conditional regression. LC–MS/MS, Liquid chromatography–tandem mass spectrometry; RIA, radioimmunoassay.

3.2. Multiple imputation model

We propose a Bayesian linear regression model as the basis of the imputation model for our problem where the new assay is only partially observed. It is a common practice in laboratories to use a standard linear regression to describe the relationship between two assays such as Y=β₀+β₁X+ε, where $\epsilon ~N(0,{\sigma }_{y|x}^2)$. There may be times when additional covariates may be considered, or higher order terms, weighting, and/or transformations are needed to meet the standard assumptions of a linear regression model. These extensions can easily be incorporated into the approach described here.

Assume that (X_i, Y_i) comes from a bivariate normal distribution with mean μ = (μ_x, μ_y) and covariance matrix, $\sum =\left[\begin{array}{cc}{\sigma }_x^2& \rho {\sigma }_x{\sigma }_y\\ \rho {\sigma }_x{\sigma }_y& {\sigma }_y^2\end{array}\right]$ where ${\sigma }_x^2$ and ${\sigma }_y^2$ is the variance of x and y, respectively and ρ is the correlation been X and Y. Then the conditional distribution of Y_i given X_i is Normal with mean μ_y|x = β₀+β₁x, where β₀ = μ_y − β₁μ_x and ${\beta }_1=\rho \frac{{\sigma }_y}{{\sigma }_x}$, and variance ${\sigma }_{y|x}^2={\sigma }_y^2(1-{\rho }^2)$.

Under a Bayesian formulation of the aforementioned simple linear regression model, we assume all the parameters, μ_x, ${\sigma }_x^2$, β₀, β₁, ${\sigma }_{y|x}^2$, are random, and specify non-informative prior distributions. Start with the available cases to get initial values ${\widehat{\beta }}_0^{(0)}$, ${\widehat{\beta }}_1^{(0)}$, ${\widehat{\sigma }}_{y|x}^{2(0)}$ via least squares, followed by an iterative algorithm, known as data augmentation, which cycles between an imputation step (I-step) and posterior step (P-step). At the jth I-step, we simulate the missing values from the conditional predictive distribution $Y_{\mathit{\text{miss}},i}^{(j)}|x_i$, Y_obs, ${\beta }_0^{(j-1)}$, ${\beta }_1^{(j-1)}$, ${\sigma }_{y|x}^{2(j-1)}$. The P-step involves drawing from the conditional posterior distributions of ${\widehat{\sigma }}_{y|x}^{2(j)}$, ${\widehat{\beta }}_1^{(j)}$, ${\widehat{\beta }}_0^{(j)}|Y_{\mathit{\text{miss}}}^{(j)}$, Y_obs to obtain updated estimates ${\widehat{\beta }}_0^{(j)}$, ${\widehat{\beta }}_1^{(j)}$, ${\widehat{\sigma }}_{y|x}^{2(j)}$. Under the Normal Bayesian linear model, the conditional posterior distributions of ${\widehat{\sigma }}_{y|x}^{2(j)}$, ${\widehat{\beta }}_1^{(j)}$, ${\widehat{\beta }}_0^{(j)}|Y_{\mathit{\text{miss}}}^{(j)}$, Y_obs have well-known probability distributions. Using ${\widehat{\beta }}_0^{(j)}$, ${\widehat{\beta }}_1^{(j)}$, ${\widehat{\sigma }}_{y|x}^{2(j)}$, we obtain the ith subject's missing value by drawing from the conditional predictive distribution Y_miss,i|x_i, Y_obs, β₀, β₁, ${\sigma }_{y|x}^2$ (see Appendix for details). In order to get M imputations for the ith subject with the new assay, these steps are repeated for j = 1…M.

Rubin [32] provided the theoretical foundation for multiple imputation using a Bayesian formulation. Using these M imputations, M separate ‘filled in’ datasets are created and each of these datasets is analyzed separately using a statistical analysis as if there was no missing data. The last stage combines these M separate results using Rubin's formulas into a single inference. Using the conventional notation, let Q be the parameter of interest, such as a mean, prevalence, or percentile, so that Q̂_i is the point estimate and V_i the estimated variance of Q̂_i from the ith ‘filled in’ data set for i = 1…M. Rubin [32] shows that the complete data posterior mean of Q can be found by averaging the individual estimates, $\overline{Q}=\frac{1}{M}{\sum }_{i=1}^M{\widehat{Q}}_i$. Using the Q̃_i's, we can compute the between imputation variance $B=\frac{1}{(M-1)}{\sum }_{i=1}^M{({\widehat{Q}}_i-\overline{Q})}^2$ and the average of the estimated variances $\overline{V}=\frac{1}{M}{\sum }_{i=1}^M{V}_i$ as the within imputation variance to obtain an estimate of the standard error for Q̄ as $\sqrt{(1+M^{-1})B+\overline{V}}$. The relative increase in the variance due to the imputation can be calculated as $r=\frac{(1+M^{-1})B}{\overline{V}}$. The value of r can be used to construct $\lambda =\frac{r+\frac{2}{3+(M-1){(1+r^{-1})}^2}}{r+1}$, the fraction of missing data. Additionally, r is used to compute the approximate degrees of freedom. Let df be the appropriate degrees of freedom associated with the variance of the complete data for a given estimator. When the degrees of freedom is small, the following formula is recommended to calculate the degrees of freedom [40]

$${(\frac{1}{(M-1){(1+r^{-1})}^2}+\frac{1}{\left(\frac{\mathit{\text{df}}+1}{\mathit{\text{df}}+3}\right)[1-(\frac{r\overline{V}}{(\overline{V}+(1+M^{-1})B)}\left)\right]\mathit{\text{df}}})}^{-1}.$$

4. Application serum total 25-hydroxyvitamin D (25OHD) in National Health and Nutrition Examination Survey

In this section, we compare the adjustment equation approach and stochastic conditional regression with multiple imputation. The adjusted 25OHD data released on the NHANES website in October of 2015 are based on the previously published adjustment equations [8,19,20]. These equations are reproduced, along with the respective estimated mean square error (MSE) and elements of the variance–covariance matrix of the coefficients in Table II for each 2-year cycle from 2001 to 2006. (sas Institute, Carey, NC, US) v 9.3 [41] was used to perform both stochastic conditional regression (rannor statement) and the multiple imputations. To be conservative, a large number of multiple imputations are used (M = 40). Multiple imputations are performed separately for each cycle, similar to the adjustment equations developed by NCHS [19,20]. Two distinct multiple imputation models are considered. MI model 1 uses the measurements made from the completely observed RIA and partially observed LCMS/MS. MI Model 2 adds covariates to MI model 1. The covariates are age, race (four dummy variables), gender, and the 2-year survey mobile examination center (MEC) weight. SAS-callable SUDAAN 11.0.0 [42] is used to estimate the weighted mean 25OHD concentration and the weighted prevalence of deficiency for each of the imputation methods described using the MEC weights. Taylor series linearization for variance estimation is used to account for the stratified cluster design.

Table II.

Estimated linear regression models from a bridging study to predict serum concentrations of LC–MS/MS-equivalent 25-hydroxyvitamin D from original radioimmunoassay 25-hydroxyvitamin D for National Health and Nutrition Examination Survey, 2001–2006 [19,20].

Survey Period	n	Equation	Mean Square Error	Variance of intercept	Variance of slope	Covariance of intercept and slope
2001–2001	371	LC–MS/MSequivalent = 6.43435 + 0.95212 * RIAoriginal	83.38	1.00689	0.00024	−0.01362
2003–2004	289	LC–MS/MSequivalent = 1.72786 + 0.98284 * RIAoriginal	85.88	1.61349	0.00036	−0.02179
2005–2006	283	LC–MS/MSequivalent = 8.36753 + 0.97012 * RIAoriginal	112.38	1.89393	0.00052	−0.02779

LC-MS/MS, Liquid chromatography–tandem mass spectrometry; RIA, radioimmunoassay.

The results in Tables III and IV are limited to persons 12 years of age and older, stratified by survey cycle (2001–2002, 2003–2004, and 2005–2006) and grouped by demographic variables or vitamin D supplement use. The estimated weighted means are fairly stable regardless of the imputation method. The magnitude of the increase in the standard error under multiple imputation models relative to the adjustment equation approach varies depending on the subgroup and year, and for MI Model 1 ranges from around 1%–44% (median ∼ 12%), further confirming inferences based on the adjustment equation are too liberal. Table IV presents the prevalence of LC–MS/MS-equivalent serum 25OHD concentrations below the 30 nmol/L cutoff. There is a noticeable difference between the imputation methods when it comes to estimating characteristics around the tails. The estimates of the prevalence are similar for both multiple imputation models and stochastic conditional regression but differ from those based on the adjustment equation. Additionally, there can be a severe underestimation of the standard error with the adjustment equation approach, which leads to confidence intervals that are too narrow for the stated coverage. The multiple imputation (MI model 1) standard errors are 5%–190% (median ∼ 40%) larger than the adjustment equation approach. The magnitude depends on the subgroup, year, and the magnitude of the prevalence itself; such as when the prevalence is low. Lastly, except for a few subgroups, the addition of the selected covariates to MI Model 1 appears to have little to no effect on the mean 25OHD concentration and prevalence <30 nmol/L estimates as compared with MI model 1 alone. The exceptions are in the 2005–2006 survey cycle: 12–19 year olds, Non-Hispanic Black and Non-Hispanic Whites.

Table III.

Weighted mean LC–MS/MS-equivalent serum 25-hydroxyvitamin D concentrations for person 12 y of age and older, stratified by survey, and grouped by demographic variables or vitamin D supplement use, NHANES 2001–2006: A comparison of imputation methods.

Group	2001–2002		2003–2004		2005–2006
	Mean	SE	Mean	SE	Mean	SE
All
MI Model 1	62.27	0.98	62.64	1.70	60.85	1.38
MI Model 2	62.63	1.14	63.30	1.74	61.70	1.37
Stochastic CR	62.17	0.90	62.74	1.55	61.14	1.11
AE	62.25	0.88	62.72	1.62	61.00	1.12
Age, y
12–19
MI Model 1	62.97	1.13	63.77	2.20	61.92	1.84
MI Model 2	63.19	1.27	64.24	2.22	64.27	1.68
Stochastic CR	62.99	1.10	64.34	2.18	62.34	1.72
AE	63.00	1.04	63.91	2.10	61.92	1.62
20–39
MI Model 1	62.80	1.13	62.85	1.97	62.35	1.72
MI Model 2	62.90	1.39	63.28	1.99	62.91	1.68
Stochastic CR	62.50	1.06	62.94	1.81	62.68	1.41
AE	62.76	1.02	62.93	1.84	62.53	1.44
40–59
MI Model 1	62.35	1.28	62.12	2.01	59.90	1.47
MI Model 2	62.91	1.49	62.98	2.16	60.27	1.68
Stochastic CR	62.44	1.22	62.22	1.88	60.09	1.25
AE	62.38	1.14	62.18	1.98	60.12	1.15
≥60
MI Model 1	60.55	1.31	62.40	1.40	59.35	1.40
MI Model 2	61.12	1.56	63.21	1.64	60.34	1.65
Stochastic CR	60.41	1.17	62.25	1.19	59.68	1.06
AE	60.44	1.16	62.49	1.17	59.45	1.14
Sex
Males
MI Model 1	63.24	1.05	62.93	1.78	60.93	1.36
MI Model 2	64.24	1.23	62.97	1.95	62.20	1.43
Stochastic CR	63.43	0.96	62.90	1.64	61.33	1.17
AE	63.22	0.90	63.07	1.71	61.06	1.01
Females
MI Model 1	61.36	1.13	62.36	1.69	60.77	1.52
MI Model 2	61.13	1.38	63.61	1.72	61.23	1.67
Stochastic CR	60.99	1.06	62.60	1.53	60.96	1.25
AE	61.34	1.04	62.39	1.58	60.95	1.30
Race-ethnicity
Mexican American
MI Model 1	55.07	1.54	54.10	1.78	50.97	2.11
MI Model 2	55.64	2.12	54.10	2.06	51.08	1.37
Stochastic CR	55.40	1.53	54.15	1.73	51.21	1.86
AE	55.06	1.44	54.23	1.62	51.17	1.87
Non-Hispanic Black
MI Model 1	39.28	0.79	40.87	1.74	41.40	1.34
MI Model 2	37.57	1.01	40.88	1.65	39.17	1.66
Stochastic CR	38.97	0.59	41.01	1.57	41.28	1.22
AE	39.34	0.55	40.91	1.48	41.67	1.03
Non-Hispanic White
MI Model 1	67.36	1.11	68.33	1.69	66.13	1.28
MI Model 2	68.57	1.24	69.51	1.78	68.13	1.32
Stochastic CR	67.35	1.02	68.46	1.57	66.50	0.99
AE	67.33	0.99	68.40	1.63	66.23	0.99
Vitamin D supplement use
Yes
MI Model 1	68.15	1.13	68.64	1.60	66.60	1.43
MI Model 2	68.44	1.28	69.42	1.69	67.15	1.47
Stochastic CR	67.92	0.97	68.42	1.38	67.02	1.06
AE	68.03	0.96	68.62	1.46	66.74	1.12
No
MI Model 1	58.95	1.03	59.08	1.82	57.21	1.51
MI Model 2	59.57	1.18	59.77	1.84	58.33	1.51
Stochastic CR	58.94	0.98	59.33	1.71	57.42	1.26
AE	58.98	0.93	59.21	1.75	57.38	1.28

Abbreviations: SE, standard error; MI model 1, multiple imputation with assay data only; MI model 2, multiple imputation with assay data, age, race, sex, and MEC survey weight; Stochastic CR, stochastic conditional regression; AE, adjustment equation.

LC–MS/MS, Liquid chromatography–tandem mass spectrometry; NHANES, National Health and Nutrition Examination Survey.

Table IV.

Weighted prevalence of LC–MS/MS-equivalent serum 25-hydroxyvitamin D concentrations below or above 30 nmol/L for person 12 y of age and older, stratified by survey, and grouped by demographic variables or vitamin D supplement use, NHANES 2001–2006: a comparison of imputation methods.

Group	2001–2002		2003–2004		2005–2006
	Mean	SE	Mean	SE	Mean	SE
Overall
MI Model 1	7.89	0.86	9.29	1.43	8.82	1.19
MI Model 2	8.04	1.02	9.03	1.43	8.62	1.26
Stochastic CR	7.78	0.71	9.23	1.29	8.65	0.89
AE	5.37	0.67	7.48	1.18	5.16	0.71
Age, y
12–19
MI Model 1	6.59	1.17	8.09	1.58	8.56	1.58
MI Model 2	7.13	1.28	8.02	1.61	7.90	1.56
Stochastic CR	6.26	1.16	8.23	1.30	8.67	1.48
AE	4.11	0.85	6.46	1.30	5.26	1.12
20–39
MI Model 1	8.28	1.10	10.18	1.78	8.71	1.40
MI Model 2	8.63	1.27	10.05	1.82	8.84	1.52
Stochastic CR	8.39	0.86	10.60	1.59	8.40	1.05
AE	5.99	0.73	8.23	1.40	5.10	0.79
40–59
MI Model 1	8.07	1.10	9.21	1.69	9.11	1.56
MI Model 2	8.00	1.29	8.94	1.65	9.17	1.66
Stochastic CR	7.65	1.06	8.49	1.61	9.21	1.14
AE	5.74	0.93	7.07	1.45	5.52	0.90
≥60
MI Model 1	7.78	1.33	8.72	1.31	8.64	1.47
MI Model 2	7.67	1.41	8.16	1.36	7.83	1.47
Stochastic CR	7.94	0.75	8.87	0.73	8.07	0.98
AE	4.41	0.61	7.59	1.08	4.60	0.73
Sex
Males
MI Model 1	5.98	0.80	7.18	1.40	7.74	1.21
MI Model 2	5.81	0.84	7.52	1.52	7.41	1.30
Stochastic CR	6.05	0.62	7.31	1.28	7.86	1.02
AE	3.76	0.39	5.14	1.10	4.06	0.61
Females
MI Model 1	9.70	1.12	11.29	1.58	9.83	1.41
MI Model 2	10.11	1.41	10.45	1.55	9.77	1.58
Stochastic CR	9.40	0.93	11.05	1.33	9.38	0.96
AE	6.89	1.07	9.69	1.35	6.20	0.94
Race-ethnicity
Mexican American
MI Model 1	9.31	1.32	12.55	2.28	13.62	2.61
MI Model 2	8.28	1.99	12.22	2.66	13.13	2.94
Stochastic CR	6.85	0.62	14.10	2.41	13.72	2.66
AE	5.26	0.76	9.32	1.56	7.69	2.04
Non-Hispanic Black
MI Model 1	32.63	2.20	31.38	3.76	28.93	2.87
MI Model 2	35.54	2.78	31.47	3.42	33.15	3.86
Stochastic CR	32.63	1.38	30.22	3.04	29.40	2.79
AE	28.46	1.90	29.57	3.41	21.79	2.19
Non-Hispanic White
MI Model 1	3.96	0.60	4.93	0.84	4.59	0.84
MI Model 2	3.19	0.65	4.28	0.85	3.22	0.73
Stochastic CR	4.07	0.44	4.74	0.74	4.35	0.50
AE	2.17	0.29	3.50	0.56	2.11	0.29
Supplement use
Yes
MI Model 1	3.06	0.63	4.22	0.94	3.77	0.87
MI Model 2	3.25	0.66	4.11	0.95	3.89	0.99
Stochastic CR	2.48	0.37	3.68	0.67	3.57	0.69
AE	1.69	0.33	2.35	0.67	1.16	0.33
No
MI Model 1	10.61	1.20	12.25	1.78	11.97	1.54
MI Model 2	10.62	1.37	11.82	1.77	11.53	1.56
Stochastic CR	10.73	1.03	12.50	1.64	11.84	1.09
AE	7.38	0.97	10.48	1.46	7.66	0.96

Abbreviations: SE, standard error; MI model 1, multiple imputation with assay data only; MI model 2, multiple imputation with assay data, age, race, sex, and MEC survey weight; Stochastic CR, stochastic conditional regression; AE, adjustment equation.

LC–MS/MS, Liquid chromatography–tandem mass spectrometry; NHANES, National Health and Nutrition Examination Survey.

5. Simulation study

5.1. Details of simulation study

The primary challenge to our problem is that the bridging study is based on a rather small subset of the original data, usually between 5 and 10% of the original sample. We perform simulations to evaluate the conditions under which multiple imputation can provide reasonable statistical inference for a variety of parameters in our setting. Factors that affect the magnitude of the missing data uncertainty include the percent of missing data, the predictive ability of observed (or utilized) information to make accurate imputations, and the number of imputations M. The relative efficiency of selecting M imputations over an infinite number of imputations can be estimated as ${(1+\frac{\lambda }{M})}^{-1}$, where λ is the fraction of missing data [32]. Using this formula, it can be shown if λ ≤ 0.50, that M = 10 has a relative efficiency ≥0.95. For higher rates of missing information (λ > 0.50), this formula suggests selecting a larger value of M. We selected M = 25 to be conservative because our focus is on cases with a high percent of missing data, although the fraction of missing information (λ) may be much smaller than the actual percent of missing data when the two assays are highly correlated. M is also related to the degrees of freedom, a larger choice of M helps minimize the complexities that can arise from limited degrees of freedom. To assess these issues, we performed simulations under the following three scenarios:

1. X and Y have a bivariate normal distribution with mean μ = (μ_x = 50, μ_y = 60), covariance matrix $\sum =\left[\begin{array}{cc}190& 190\\ 190& 225\end{array}\right]$ and correlation is 0.9189;

2. X and Y have a bivariate normal distribution with mean μ = (μ_x = 50, μ_y = 60), covariance $\sum =\left[\begin{array}{cc}190& 103\\ 103& 225\end{array}\right]$ and correlation is 0.4982;

3. √X and √Y have a bivariate normal distribution with mean μ = (μ_x = 7.1, μ_y = 7.6), covariance matrix $\sum =\left[\begin{array}{cc}3.24& 3.3\\ 3.3& 4\end{array}\right]$ and correlation is 0.9167. The detransformed values of X and Y are obtained by squaring the simulated data. It can be shown that the expected value of Y and X are ${\mu }_y^2+{\sigma }_y^2={(7.6)}^2+4=61.76$ and ${\mu }_x^2+{\sigma }_x^2={(7.1)}^2+3.24=53.65$; respectively [43].

The population means and correlation used in scenarios 1 and 3 are motivated from the bridging study for serum 25OHD using a subset of data from NHANES 2001–2006. Prevalence of vitamin D deficiency is often a parameter of interest. To investigate the behavior of this estimator, simulated values <30 were considered deficient [44]. Scenario 3 is probably most consistent with serum 25OHD values because these measurements are often approximately normal after a square root transformation [19].

Two different missing data mechanisms are considered for the Y variable. The first is based on a Bernoulli distribution. The probability a datum is missing, π, ranged from 0.5 to 0.95. Thus, the sample size of the simulated bridging study ranged from 5% to 50% of the original sample size. The other missing data mechanism is based on a systematic random sample. The sample is selected by sorting the X values and sampling across the full range of the X with an appropriate sampling interval such that 50%–95% of the values are missing. To ensure that the full range of the X measurement is included, this latter sampling approach is consistent with how calibration curves are developed for assays in clinical laboratories and the sampling strategy for previous bridging studies in NHANES. The simulation and analysis was implemented in R [45] using the package MICE [46]. The multiple imputation in MICE was performed with Bayesian linear regression under non-informative Jeffrey prior, bivariate normality, and monotone missingness. We perform 1000 simulations of each scenario where each complete dataset has 2000 observations and M = 25 multiple imputations. We selected a large sample size N, as about 5000 subjects of all ages are sampled in NHANES each year [7].

5.2. Results of the simulation study

We compared the results of the imputation methods described in Section 3 for a variety of estimands commonly used to assess nutritional status using biomarkers in NHANES [22]. The estimators for the following parameters are assessed: population mean, population reference range (population percentiles 2.5th and 97.5th), and population prevalence of deficiency (<30). The 95% confidence intervals for the percentiles are calculated using the Woodruff method [47]. For each imputation method, Tables V–VII (and Tables S1 and S2) present the average across the 1000 simulations of each selected estimate, the width of the 95% confidence interval and coverage of the confidence interval for various levels of missing data. Each table presents averages based on the full original data before missing data mechanism is applied to Y, complete case analysis, adjustment equation (AE), stochastic conditional regression (stochastic CR), and multiple imputation (MI). In the case of simulation scenario 3 where the detransformed data is not normal, the results are based on two different imputation models. The first model addresses the non-normality of the data by taking a square root transform of the detransformed data to develop the imputation model and then back-transforming (squaring) the imputations. The second model simply proceeds with the detransformed data.

Table V.

Estimates of the mean obtained under various models averaged over 1000 simulations N = 2000, M = 25.

π = proportion missing	Scenario 1 under Bernoulli MCAR			Scenario 2 under Bernoulli MCAR			Scenario 1 under Systematic MCAR			Scenario 3 with square root transform			Scenario 3 with no transform
	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)
Expected	60.00	NA	95.0	60.00	NA	95.0	60.00	NA	95.0	61.76	NA	95.0	61.76	NA	95.0
π = 0.95
Full data	59.98	1.32	95.7	59.99	1.31	95.6	60.01	1.31	95.7	61.75	2.71	94.4	61.75	2.71	94.4
complete case	59.98	5.94	95.0	60.06	5.94	95.1	60.00	5.96	100.0	61.86	12.31	94.5	61.86	12.31	94.5
MI	60.01	2.79	95.7	60.01	5.56	96.1	60.01	2.77	94.5	61.85	5.83	95.1	61.81	5.84	94.4
Stochastic CR	60.01	1.31	67.3	60.02	1.31	37.2	60.00	1.31	67.7	61.83	2.71	66.3	61.80	2.71	67.5
AE	60.01	1.21	63.3	60.02	0.65	19.6	60.00	1.21	64.1	61.18	2.48	57.5	61.81	2.48	62.6
π = 0.90
Full data	60.02	1.31	94.8	60.00	1.32	93.5	60.00	1.31	94.9	61.74	2.71	95.1	61.74	2.71	95.1
complete case	60.05	4.18	95.2	59.99	4.19	95.7	60.00	4.19	99.9	61.73	8.62	94.3	61.73	8.62	94.3
MI	60.04	2.09	94.3	59.98	3.89	95.9	60.00	2.11	95.6	61.75	4.41	94.4	61.74	4.40	93.9
Stochastic CR	60.04	1.31	77.9	59.97	1.32	50.9	60.00	1.31	78.7	61.74	2.71	74.4	61.73	2.71	73.3
AE	60.04	1.21	75.4	59.97	0.66	27.2	60.01	1.21	76.4	61.10	2.48	65.0	61.74	2.48	71.0
π = 0.85
Full data	60.01	1.32	95.7	60.02	1.31	94.8	60.01	1.32	95.5	61.76	2.71	95.5	61.76	2.71	95.5
complete case	59.97	3.41	94.2	60.06	3.40	95.4	60.03	3.23	100.0	61.69	7.02	94.2	61.69	7.02	94.2
MI	59.99	1.85	93.5	60.06	3.16	94.3	60.03	1.79	94.6	61.76	3.85	95.4	61.75	3.85	95.6
Stochastic CR	59.99	1.31	83.3	60.04	1.32	57.5	60.03	1.31	81.7	61.75	2.71	83.5	61.75	2.71	83.7
AE	59.99	1.21	81.0	60.05	0.65	33.6	60.03	1.21	81.3	61.11	2.48	70.9	61.75	2.47	82.3
π = 0.50
Full data	59.99	1.31	94.9	60.01	1.32	94.3	59.99	1.32	95.7	61.77	2.71	94.0	61.77	2.71	94.0
complete case	60.00	1.86	95.1	60.02	1.86	94.7	59.99	1.86	99.0	61.73	3.84	94.7	61.73	3.84	94.7
MI	60.00	1.42	95.3	60.02	1.77	94.9	59.99	1.42	95.4	61.76	2.94	94.7	61.77	2.94	94.4
Stochastic CR	60.00	1.31	94.0	60.01	1.32	80.9	59.99	1.32	93.2	61.77	2.71	91.5	61.77	2.71	92.2
AE	60.00	1.21	90.8	60.02	0.66	56.3	59.99	1.21	91.1	61.13	2.48	77.4	61.76	2.48	90.0

Abbreviations: CI, Confidence Interval; NA, not applicable; MI, multiple imputation; Stochastic CR, stochastic conditional regression; AE, adjustment equation. MCAR, missing completely at random.

Table VII.

Estimates of the 2.5th percentile obtained under various models averaged over 1000 simulations N = 2000, M = 25.

π = proportion missing	Scenario 1 under Bernoulli MCAR			Scenario 2 under Bernoulli MCAR			Scenario 1 under Systematic MCAR			Scenario 3 with square root transform			Scenario 3 with no transform
	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)
Expected	30.60	NA	95.0	30.60	NA	95.0	30.60	NA	95.0	13.54	NA	95.0	13.54	NA	95.0
π = 0.95
Full data	30.63	3.60	95.5	30.65	3.62	94.4	30.70	3.63	95.2	13.65	3.51	94.9	13.65	3.51	94.9
complete case	31.93	12.61	84.5	32.09	12.53	84.1	31.54	13.75	94.8	15.18	11.25	84.7	15.18	11.25	84.7
MI	30.53	6.84	98.3	30.37	11.16	97.3	30.51	6.80	96.7	13.52	6.75	97.1	9.75	11.33	79.7
Stochastic CR	30.68	3.61	76.6	30.76	3.63	55.5	30.72	3.62	75.8	13.70	3.49	74.8	10.06	4.89	23.6
AE	33.09	3.32	37.0	45.50	1.78	0.0	33.11	3.32	37.6	16.21	3.52	36.0	17.34	3.36	21.5
π = 0.90
Full data	30.69	3.64	95.4	30.68	3.60	95.3	30.68	3.61	95.9	13.62	3.52	94.4	13.62	3.52	94.4
complete case	31.31	15.26	93.7	31.26	15.34	93.3	31.31	16.37	99.3	14.46	12.52	93.1	14.46	12.52	93.1
MI	30.60	5.60	98.1	30.35	8.20	97.0	30.53	5.61	98.2	13.54	5.55	98.1	10.02	8.70	68.5
Stochastic CR	30.75	3.61	84.9	30.58	3.60	61.9	30.66	3.62	82.7	13.68	3.49	82.8	10.23	4.83	21.9
AE	33.11	3.31	31.6	45.31	1.81	0.0	33.04	3.31	35.5	16.18	3.48	32.7	17.32	3.32	14.7
π = 0.85
Full data	30.66	3.61	94.2	30.70	3.63	94.5	30.69	3.58	94.6	13.67	3.51	95.4	13.67	3.51	95.4
complete case	31.06	11.43	93.8	31.10	11.45	95.2	31.05	10.50	98.5	14.04	9.99	95.6	14.04	9.99	95.6
MI	30.53	5.17	98.8	30.54	7.05	97.9	30.60	5.04	98.6	13.53	5.10	99.0	10.31	7.59	66.0
Stochastic CR	30.68	3.61	87.5	30.73	3.65	71.1	30.73	3.58	87.1	13.68	3.56	88.5	10.57	4.72	24.6
AE	33.04	3.36	35.2	45.44	1.80	0.0	33.11	3.31	34.1	16.18	3.51	32.2	17.39	3.34	10.3
π = 0.50
Full data	30.64	3.61	94.6	30.67	3.61	94.7	30.65	3.62	94.2	13.63	3.54	95.1	13.63	3.54	95.1
complete case	30.73	5.23	93.5	30.78	5.19	95.5	30.70	5.26	96.2	13.63	5.04	94.1	13.63	5.04	94.1
MI	30.55	4.28	98.4	30.55	4.81	99.2	30.51	4.29	98.0	13.48	4.24	98.8	11.70	5.22	80.7
Stochastic CR	30.69	3.62	92.3	30.70	3.63	90.3	30.64	3.63	93.5	13.60	3.53	92.2	11.87	4.23	51.8
AE	33.06	3.33	32.1	45.39	1.80	0.0	33.01	3.33	33.0	16.10	3.48	29.3	17.30	3.31	5.1

Abbreviations: CI, Confidence Interval; NA, not applicable; MI, multiple imputation; Stochastic CR, stochastic conditional regression; AE, adjustment equation. MCAR, missing completely at random.

The purpose of presenting the results from the full data set before applying a missing data mechanism and the complete case results is to set expectations to compare the imputation results. With a sample size of 2000, we expect the average coverage of the 95% confidence intervals for the estimators of the full data set to be close to 95% and the estimates to be unbiased. We have similar expectations for the complete case approach under MCAR, although as the percent of missing data increases, we see an increase in the average width of the confidence interval in order to maintain the 95% coverage. In addition, under the complete case approach as the percent missing data increases (i.e., observed sample size gets smaller), the asymptotic assumptions associated with the confidence intervals for some estimators breaks down, for example, prevalence not having exact 95% coverage. It is also worth noting that the complete case approach overestimates the sampling error (the traditional formula for the variance) when the sampling frame is ordered under systematic random sampling and the order is highly correlated with the outcome of interest [48]. While there is no unbiased way to estimate the variance from a systematic sample of an ordered list, it is clear that the sampling variability of the sample mean is smaller than under simple random sampling, and this is reflected by having higher than expected coverage (>95%) of the confidence intervals, especially when the order of the sampling frame is highly correlated with the new assay. Figure 3 compares the sampling distribution of the sample mean from data simulated from scenario 1 when there is no missing data or when only the complete cases are used (90% of the data is missing). As expected, the sampling error associated with having no missing data (and therefore a larger sample size) is the smallest, and the sampling error associated with the complete cases selected under the systematic random sampling is much smaller than under the simple random sampling.

Figure 3.

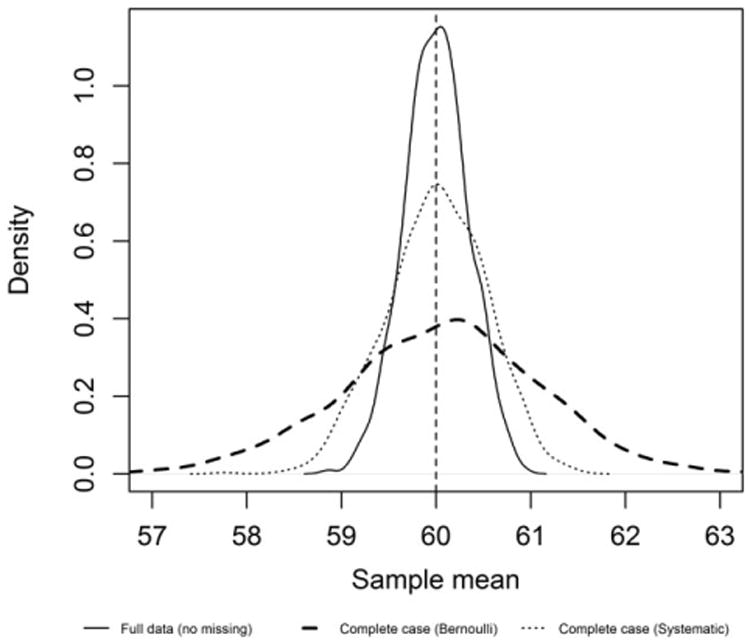
Sampling distribution of the sample mean based on 1000 simulations under scenario 1 with 90% missing data. The vertical line represents the true value of the parameter (population mean).

Regardless of the percent of data missing, all the imputation methods provide an unbiased estimate of the population mean (Table V). On the other hand, the coverage of the adjustment equation's 95% confidence intervals is well below the expected 95% because the variability of the sample mean (i.e., the standard error) is severely underestimated. In fact, the adjustment equations' average width of the 95% confidence interval is routinely smaller than the full-data scenario. This undesirable feature demonstrates why the adjustment equation is not a viable imputation approach when any statistical inference is a primary goal of the analysis. The severity of the undercoverage for both the adjustment equation and stochastic conditional regression methods is related to the percent of data that is missing, as well as the underlying true correlation between X and Y. These findings are consistent with the literature [33].

Estimates at the tails such as the prevalence of less than 30 (Table VI), the 2.5th (Table VII), and 97.5th (Table S1) percentiles are always biased using the adjustment equation. Even the 25th and 75th percentiles are biased (results not shown). However, it appears that this bias may be remedied with the stochastic conditional regression approach even when the correlation is weaker. The coverage of the 95% confidence intervals continues to be poor for both these single imputation approaches because they underestimate the uncertainty associated with the imputations. The adjustment equation method always has the worst bias and coverage of the 95% confidence intervals. In some cases, the coverage of the 95% confidence interval for the adjustment equation is as low as 63% when estimating the mean (Table V) and 30% when estimating the prevalence (Table VI).

Table VI.

Estimates of the prevalence of less than 30 obtained under various models averaged over 1000 simulations N = 2000, M = 25.

π = proportion missing	Scenario 1 under Bernoulli MCAR			Scenario 2 under Bernoulli MCAR			Scenario 1 under Systematic MCAR			Scenario 3 with square root transform			Scenario 3 with no transform
	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)	Estimate	Width 95% CI	CI Coverage (%)
Expected	2.23	NA	95.0	2.23	NA	95.0	2.23	NA	95.0	14.43	NA	95.0	14.43	NA	95.0
π = 0.95
Full data	2.29	1.31	95.7	2.28	1.30	94.2	2.26	1.30	93.6	14.40	3.08	95.3	14.40	3.08	95.3
complete case	2.26	5.70	99.8	2.13	5.57	99.9	2.36	5.81	100.0	14.28	13.62	93.5	14.28	13.62	93.5
MI	2.33	2.48	97.3	2.50	4.22	96.3	2.34	2.46	96.2	14.43	6.36	95.9	14.55	7.59	98.2
Stochastic CR	2.30	1.30	75.4	2.32	1.29	54.0	2.28	1.30	73.7	14.37	3.07	67.9	14.52	3.08	67.9
AE	1.50	1.05	29.7	0.02	0.19	0.0	1.49	1.05	29.1	12.32	2.87	32.9	11.57	2.79	21.6
π = 0.90
Full data	2.27	1.30	93.6	2.27	1.30	93.9	2.27	1.30	93.4	14.41	3.08	95.0	14.41	3.08	95.0
complete case	2.28	4.02	91.7	2.27	4.03	92.5	2.23	4.03	98.1	14.35	9.69	93.9	14.35	9.69	93.9
MI	2.28	2.01	97.4	2.43	3.05	96.9	2.30	2.01	97.7	14.43	5.01	97.1	14.55	5.76	98.5
Stochastic CR	2.26	1.30	81.6	2.36	1.31	62.2	2.29	1.30	83.1	14.42	3.08	79.0	14.55	3.09	78.4
AE	1.47	1.04	22.5	0.01	0.18	0.0	1.49	1.05	24.9	12.33	2.88	29.5	11.58	2.80	15.2
π = 0.85
Full data	2.28	1.30	93.9	2.27	1.30	93.5	2.26	1.30	92.2	14.43	3.08	95.1	14.43	3.08	95.1
complete case	2.29	3.33	91.9	2.27	3.31	90.7	2.23	3.14	97.5	14.49	7.95	95.6	14.49	7.95	95.6
MI	2.29	1.85	98.4	2.33	2.55	97.4	2.27	1.80	98.4	14.42	4.47	97.2	14.51	5.00	99.0
Stochastic CR	2.28	1.30	86.1	2.28	1.30	70.7	2.25	1.29	85.0	14.43	3.08	85.1	14.49	3.08	83.8
AE	1.49	1.05	24.9	0.01	0.18	0.0	1.47	1.04	23.4	12.32	2.88	27.2	11.54	2.80	11.5
π = 0.50
Full data	2.28	1.31	93.6	2.28	1.30	94.1	2.29	1.31	94.5	14.41	3.08	95.0	14.41	3.08	95.0
complete case	2.28	1.84	93.2	2.25	1.83	94.3	2.30	1.85	96.8	14.42	4.35	95.9	14.42	4.35	95.9
MI	2.28	1.50	97.8	2.28	1.70	98.8	2.30	1.51	97.2	14.41	3.50	97.9	14.45	3.65	99.0
Stochastic CR	2.27	1.30	90.6	2.27	1.30	89.6	2.30	1.31	93.5	14.40	3.08	93.1	14.45	3.08	93.6
AE	1.48	1.05	20.4	0.00	0.18	0.0	1.49	1.06	21.1	12.34	2.88	23.2	11.58	2.80	6.3

Abbreviations: CI, Confidence Interval; NA, not applicable; MI, multiple imputation; Stochastic CR, stochastic conditional regression; AE, adjustment equation. MCAR, missing completely at random.

In contrast, multiple imputation produces unbiased estimates for all the estimands investigated and maintains approximately 95% coverage at all levels of missing data even when the correlation between X and Y is low (0.5). Figure 4 compares the sampling distribution of the 2.5th percentile under simulation scenario 1 (90% data missing). The adjustment equation's sampling distribution is shifted to the right of the other sampling distributions; demonstrating the severe bias in estimating features in the tails of the distribution.

Figure 4.

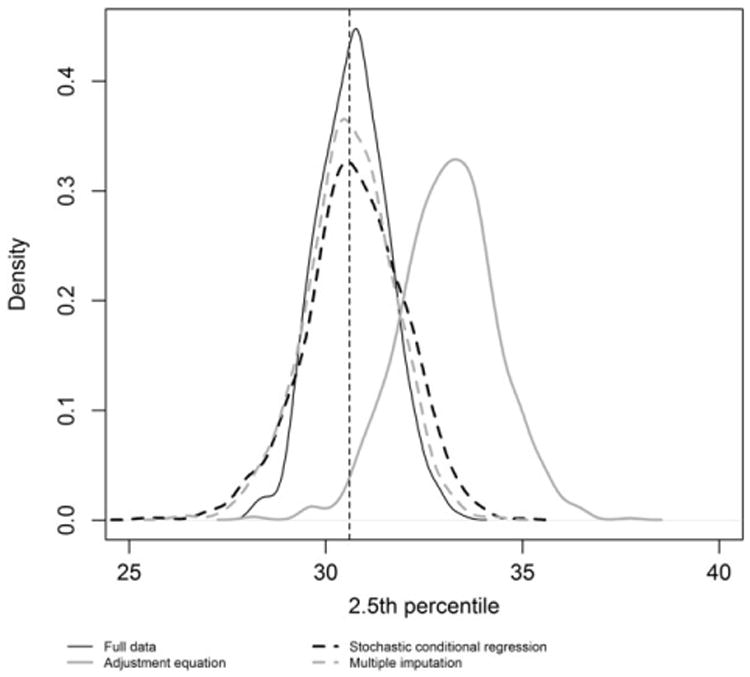
Sampling distribution of the 2.5th percentile based on 1000 simulations under scenario 1 with 90% missing data. The vertical line represents the true value of the parameter (population 2.5th percentile).

Scenario 3 allows us to investigate the impact of ignoring the non-normality or pre-transforming the data to fit the imputation model. Under the conditions considered here (square root), the choice has limited impact when estimating the mean. However, it is clear that estimates at the tails are impacted, and it is preferable to use an imputation model that is faithful to the distribution of the original data. Figure 5 compares the sampling distribution of the 2.5th percentile (90% data missing) based on the adjustment equation, stochastic conditional regression and multiple imputation when the imputation model transforms the data or ignores the lack of normality. As with earlier simulations, the adjustment equation is severely biased when estimating features around the tails of the distribution, regardless of the model. On the other hand, both the multiple imputation and stochastic conditional regression models indicate that it is important to be loyal to the distribution of the data in order to obtain unbiased estimates, especially for features around the tails. As with previous simulations, only the multiple imputation approach maintains at least 95% coverage for the confidence intervals; but even for multiple imputation, it can be important to select an imputation model that is consistent with the distribution of the original data.

Figure 5.

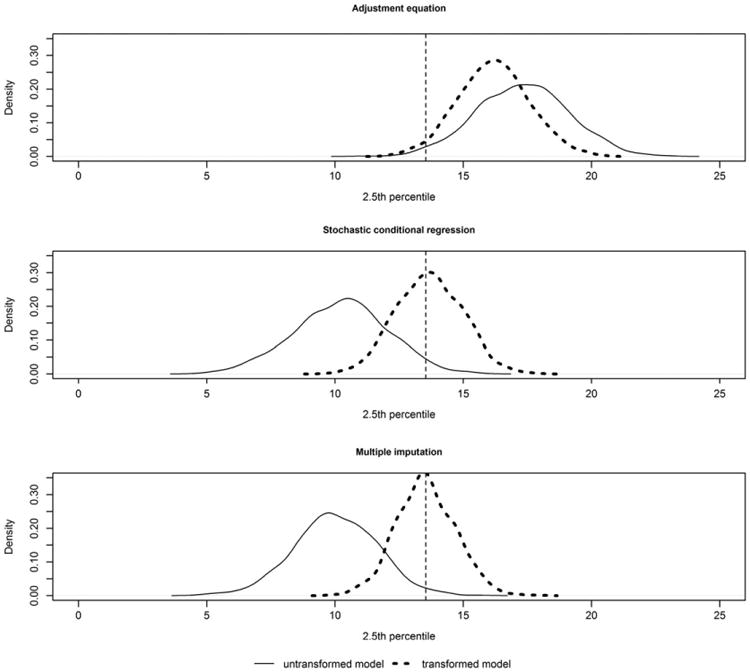
Sampling distribution of the 2.5th percentile based on 1000 simulations under scenario 3 with 90% missing data comparing models that either does or does not transform the data before fitting the imputation model. The vertical line represents the true value of the parameter (population 2.5th percentile).

In order to demonstrate how multiple imputation maintains the correlation between X and Y, the Pearson correlation was estimated using data from each method. While in the context of this setting, the correlation of X and Y may not be a parameter of direct interest, there are many other variables in a national survey whose correlation with the new assay may be of interest. If the correlation between X and Y is biased, then the correlation between any variable in the national survey and the newly imputed variable will be biased. Table S2 presents the average estimated correlation between X and Y for each method across 1000 simulations for each scenario. As expected, the correlation between the values imputed by the adjustment equation and X is exactly 1 with no sampling variability. Clearly, this is a result of using a linear transformation to impute the new assay from the old. The stochastic conditional regression approach appears to improve the bias of the correlation between X and Y but still underestimates the variability of the sample correlation leading to poor coverage of the 95% confidence intervals. Multiple imputation, in contrast, continues to achieve unbiased estimates, standard errors that properly reflect the uncertainty because of the imputation, and approximate 95% coverage.

6. Discussion

This paper describes an application of multiple imputation for nutritional biomarkers in large national surveys when there is an assay change over time and demonstrates that multiple imputation can be used effectively to estimate various population parameters. This is important because estimands such as reference intervals (2.5th–97.5th percentile) are as important as central tendency, when describing nutritional biomarkers [22]. A key, untestable assumption for multiple imputation, is an ignorable missing data mechanism (i.e., MCAR or MAR). In our setting, the missingness is planned in advance and so the missing data mechanism is known. There is a tremendous amount of research and discussion about the performance of multiple imputation under far more complicated settings than the problem addressed in this paper [2–5,36,39,49–52]. For example, multiple imputation was used to bridge changes in the industry and occupation classification system used by the Bureau of Census [2–4] and to impute single-race categories from multiple-race reporting in the National Health Interview Survey [5]. Our proposal has several similarities to these papers: application to a large public-use dataset with access to many completely observed covariates; the need to impute a single variable to assess trends; a large percent of the data is missing; and the missing data mechanism is known. The previous work [2–5] imputed codes for categorical variables using logistic regression primarily with categorical covariates, where spare data can be problematic. In contrast, the imputed variable (new assay) in our setting is continuous and based on a highly correlated continuous covariate (old assay, r > 0.9). This makes our setting nicely suited for multiple imputation under a multivariate normal distribution using regression methods for monotone missing data. Generally, in our setting, there is no reason to expect changes over time in the relationship between the two assays or with the other variables, as there might be with occupation and race codes. However, if there are assay drifts over time, as for the 25OHD RIA assay, the quality control measures at the CDC laboratory can detect them in advance and use this information as part of the study design, as was done for the 25OHD bridging study [16].

The simulations are intended to illustrate the improved properties of multiple imputation over the adjustment equation approach for selected estimands. However, the simulations may not be generalizable to complex surveys, as they are based on a simple random sample from infinite population. Previous research has shown that multiple imputation can yield biased estimates of variance when characteristics of the survey design are related to the variable(s) under study [53–55]. This is equally true of single imputation methods, so multiple imputation methods still offer more advantages than disadvantages in this regard. Simulations by Reiter et al. [55] suggest that ignoring the design variables in an imputation model may provide reasonable inferences if the outcome and the design variables have little correlation. These authors also estimated the bias of three estimates from NHANES by comparing the results from imputation models that either included or excluded the design variables. The results suggested that including design variables that are weakly associated with the outcomes led to more conservative inferences, unlike the current adjustment equation approach, which leads to liberal inferences. When analyzing the NHANES data in this paper, neither multiple imputation model considered included all the design variables. Therefore, there may be biases and/or inefficiencies that cannot be generalizable to other settings, and certainly not to other biomarkers. We showed empirically that including some of the design variables such as age, sex, race, and the survey weights had little practical effect on the resulting estimates, compared with a multiple imputation model with only using assay data, although on aggregate it did appear that the standard error was larger, suggesting that some of the covariates may be irrelevant. More research needs to be performed to determine the necessity and impact of including the design variables and other covariates into the proposed multiple imputation solution for this problem. An additional point, this paper primarily considered a single variable, the old assay, in developing the imputation models. This is because the method currently in use, the adjustment equation approach, generally only considers this variable (old assay). The primary purpose of this paper is demonstrate how multiple imputation can be performed with the same amount of observed information as the adjustment equation approach and provide much more valid inferences.

Using multiple imputation instead of the adjustment equation approach method with a properly designed bridging study does not require much more effort. Developing an imputation model under multiple imputation is equally challenging as under a single imputation method and subject to similar assumptions. Multiple imputation naturally incorporates missing data uncertainty leading to valid statistical inferences, unlike the adjustment equation method. In addition, the full Bayesian nature of the proposed solution can take advantage of the wealth of data and experience in the laboratory with the new and old assay, which can be used to inform the prior distributions of the Bayesian linear regression model. If necessary, one can build in measurement error for X, using historical information and a prior distribution. The selected functional form need not always be linear, as used in this paper. Rather one could include more flexible forms such as higher order terms or splines or utilize transformations. For example, a log transformation is useful with many nutritional biomarkers, as they are often skewed right. Alternatively, more robust alternatives could be considered for the imputation model such as quantile regression [56]. The primary technical challenge with a multiple imputation approach is ensuring convergence [57,58].

Implementing the proposed solution does have its logistical challenges. All the data in NHANES are publically released on the internet allowing data analysts all over the world access to the data to obtain nationally representative estimates of the civilian US population. When there is an assay change, the online NHANES documentation is updated to provide the adjustment equation(s) developed from the bridging study [6–10], but no new data is released (re-release of vitamin D data was an exception). Currently, the documentation does not report the mean square error or the variance–covariance matrix of the coefficients of the adjustment equation. One recommendation is that the NHANES documentation publishes both the MSE and the variance–covariance matrix along with the estimated adjustment equation. This information could be used to either perform multiple imputation (see Appendix) [37] or at a minimum add a residual to the adjustment equation to ensure at least that estimates at the tails are less biased. However, those solutions are still undesirable because measurements made with the new assay are not used, because they are not publically available. We recommend that in addition to providing the MSE and variance–covariance matrix of the adjustment equation(s) in the documentation, the data is re-released to include the new assay values, where measured, along with the originally measured values. In this way, the data analyst can either use these data to develop their own multiple imputation model or use the published information in the documentation. The drawback is different multiple imputation models will produce slightly different national estimate(s). This is because the M multiple imputed values are simulated from the posterior conditional distribution of the missing data given the observed data; depending on the random number generator and the seed, every analyst will have an ever so slightly different estimate, even if the same imputation model and same statistical method is used. One way around this is to release M publically available data sets, where the agency develops the imputation model, as was done with the Dual X-ray data in NHANES [39,59]. There is an advantage to have the agency develop the multiple imputation model because they have access to far more information than the average data user including the original survey design variables and other confidential data. With this approach to the data release, data analysts will obtain the same estimates when using the M datasets for the same complete data statistical analysis. While this approach requires some added storage and some additional computational requirements to implement the multiple imputation solution, it is a minor inconvenience given software to do this is readily available in SAS, R, SPSS, Stata, S-Plus, and SUDAAN [23].

6.1. Disclaimer

The findings and conclusions in this report are those of the author(s) and do not necessarily represent the official position of the Centers for Disease Control and Prevention/the Agency for Toxic Substances and Disease Registry.

Appendix

Under a Bayesian formulation of simple linear regression model, we assume all the parameters, μ_x, ${\sigma }_x^2$, β₀, β₁, ${\sigma }_{y|x}^2$, are random, and specify prior distributions. X is completely observed, therefore it is reasonable to assume that the parameters (μ_x, ${\sigma }_x^2$) are independent from (β₀, β₁, ${\sigma }_{y|x}^2$) [32]. The bivariate normal likelihood can written as the product of the marginal normal density of X and the conditional normal density of Y given X:

$$f(x_i,y_i|\mu ,\sum )=f(x_i|{\mu }_{\mathrm{x}}{\sigma }_x^2)f(y_i|x_i,{\beta }_0,{\beta }_1,{\sigma }_{y|x}^2)$$

If there is no prior information, we can specify a non-informative Jeffrey's prior such that

$$\begin{array}{l}\begin{array}{ccc}P({\beta }_0,{\beta }_1)\propto 1& -\infty <{\beta }_0<\infty ,& -\infty <{\beta }_1<\infty \end{array}\hfill \\ \mathit{\text{so}}\hfill \\ \begin{array}{cc}P({\beta }_0,{\beta }_1,{\sigma }_{y|x}^2)\propto \frac{1}{{\sigma }_{y|x}^2}& {\sigma }_{y|x}^2>0\end{array}\hfill \end{array}$$

With this assumption in place, the joint posterior distribution of (β₀, β₁, ${\sigma }_{y|x}^2$) can be derived using the second term of the bivariate normal likelihood:

$$P({\beta }_0,{\beta }_1,{\sigma }_{y|x}^2|Y,X)\propto \prod _{i=1}^{K}f(y_i|x_i,{\beta }_0,{\beta }_1,{\sigma }_{y|x}^2)P({\beta }_0,{\beta }_1,{\sigma }_{y|x}^2)$$

It can be shown from standard Bayesian theory with a Jeffrey's prior that the posterior distribution of ${\sigma }_{y|x}^2$ is ${\sigma }_{y|x}^2|Y,X~\mathit{\text{Inv}}-{\chi }^2(K-2,{\widehat{\sigma }}_{y|x}^2)$, where ${\widehat{\sigma }}_{y|x}^2=\frac{1}{K-2}{\sum }_{i=1}^K{(y_i-({\widehat{\beta }}_0+{\widehat{\beta }}_1{x}_i\left)\right)}^2$. The conditional posterior distribution of β₀, ${\beta }_1|{\sigma }_{y|x}^2$, X, Y is bivariate normal distribution centered around the least squares estimate for β₀, β₁, such that

$${\beta }_0,{\beta }_1|{\sigma }_{y|x}^2,Y,X~\mathit{\text{BVN}}\left(\right[{\widehat{\beta }}_1=\frac{\begin{array}{l}{\widehat{\beta }}_0=\overline{y}-{\widehat{\beta }}_1\overline{x}\hfill \\ \sum _{i=1}^K(x_i-\overline{x})({\overline{y}}_i-\overline{y})\hfill \end{array}}{\sum _{i=1}^k{(x_i-\overline{x})}^2}],[\begin{array}{cc}\frac{\sum _{i=1}^k{x}_i^2}{n\sum _{i=1}^k{(x_i-\overline{x})}^2}& \frac{-\sum _{i=1}^k{x}_i}{n\sum _{i=1}^k{(x_i-\overline{x})}^2}\\ \frac{-\sum _{i=1}^k{x}_i}{n\sum _{i=1}^k{(x_i-\overline{x})}^2}& \frac{1}{\sum _{i=1}^k{(x_i-\overline{x})}^2}\end{array}\left]{\sigma }_{y|x}^2\right).$$

These results suggest a way to create the multiple imputations simulated from the posterior predictive distribution of the parameters that accounts for the sampling variability in the linear regression, as well as uncertainty about the unknown model parameters β₀, β₁, ${\sigma }_{y|x}^2$.

Start with the available cases to get initial values ${\widehat{\beta }}_0^{\left(0\right)}$, ${\widehat{\beta }}_1^{\left(0\right)}$, ${\widehat{\sigma }}_{y|x}^{2\left(0\right)}$, via least squares, followed by an iterative algorithm, known as data augmentation, that cycles between an imputation step (I-step) and posterior step (P-step). At the jth I-step we simulate the missing values from the conditional predictive distribution $Y_{\mathit{\text{miss}},i}^{\left(j\right)}|x_i$, Y_obs, ${\beta }_0^{(j-1)}$, ${\beta }_1^{(j-1)}$, ${\sigma }_{y|x}^{2(j-1)}$. The P-step involves drawing from the conditional posterior distributions of ${\widehat{\sigma }}_{y|x}^{2\left(j\right)}$, ${\widehat{\beta }}_1^{\left(j\right)}$, ${\widehat{\beta }}_0^{\left(j\right)}|Y_{\mathit{\text{miss}}}^{\left(j\right)}$, Y_obs, which under the Normal Bayesian linear model will have well- known probability distributions, to obtain updated estimates ${\widehat{\beta }}_0^{\left(j\right)}$, ${\widehat{\beta }}_1^{\left(j\right)}$, ${\widehat{\sigma }}_{y|x}^{2\left(j\right)}$.

Specifically, we obtain a draw from ${\sigma }_{y|x}^2|Y_{\text{miss}}^{\left(j\right)}$, Y_obs, by drawing from g, a chi-square random variable on K-2 degrees of freedom, and compute ${\widehat{\sigma }}_{y|x}^{2\left(j\right)}=\frac{{\widehat{\sigma }}_{y|x}^{2\left(j\right)}(K-2)}{g^{\left(j\right)}}$. Next, to draw from ${\beta }_0^{\left(j\right)}$, ${\beta }_1^{\left(j\right)}|{\widehat{\sigma }}_{y|x}^{2\left(j\right)}$, $Y_{\text{miss}}^{\left(j\right)}$, Y_obs, X we take two independent draws ${\mathrm{z}}_0^{\left(\mathrm{j}\right)}$ and ${\mathrm{z}}_1^{\left(\mathrm{j}\right)}$ from the standard normal distribution and compute

$$\left(\begin{array}{c}{\beta }_0^{\left(j\right)}\\ {\beta }_1^{\left(j\right)}\end{array}\right)=\left(\begin{array}{c}{\widehat{\beta }}_0^{(j-1)}\\ {\widehat{\beta }}_1^{(j-1)}\end{array}\right)+{\widehat{\sigma }}_{y|x}^{2\left(j\right)}\left[\begin{array}{cc}\sqrt{\frac{\sum _{i=1}^k{x}_i^2}{n\sum _{i=1}^k{(x_i-\overline{x})}^2}}& 0\\ \frac{-\sum _{i=1}^k{x}_i}{\sqrt{\sum _{i=1}^k{x}_i^2}\sqrt{n\sum _{i=1}^k{(x_i-\overline{x})}^2}}& \frac{1}{\sqrt{\sum _{i=1}^k{x}_i^2}}\end{array}\right]\left(\begin{array}{c}{z}_0^{\left(j\right)}\\ z_1^{\left(j\right)}\end{array}\right)$$

Drawing from ${\beta }_0^{\left(j\right)}$, ${\beta }_1^{\left(j\right)}|{\widehat{\sigma }}_{y|x}^{2\left(j\right)}$, $Y_{\mathit{\text{miss}}}^{\left(j\right)}$, Y_obs, X can also be achieved by sampling from the conditional posterior distribution ${\beta }_1^{\left(j\right)}|{\widehat{\sigma }}_{y|x}^{2\left(j\right)}$, $Y_{\mathit{\text{miss}}}^{\left(j\right)}$, Y_obs, $X~N({\widehat{\beta }}_1^{(j-1)},\frac{{\widehat{\sigma }}_{y|x}^{2\left(j\right)}}{K{\sum }_{i=1}^K{(x_i-\overline{x})}^2})$ and then from the conditional posterior distribution of ${\beta }_0^{\left(j\right)}$, $|{\widehat{\beta }}_1^{\left(j\right)}$, ${\widehat{\sigma }}_{y|x}^{2\left(j\right)}$, $Y_{\mathit{\text{miss}}}^{\left(j\right)}$, Y_obs, $X~~N(\overline{y}-{\widehat{\beta }}_i^{\left(j\right)}\overline{x},\frac{{\widehat{\sigma }}_{y|x}^{2\left(j\right)}}{K}).\mathrm{s}$

Now, the ith subject's missing value can be drawn from the conditional predictive distribution Y_miss,i|x_i, Y_obs, β₀, β₁, ${\sigma }_{y|x}^2~N({\beta }_0+{\beta }_1{x}_i,{\sigma }_{y|x}^2)$ by computing $Y_{\mathit{\text{miss}},i}^{(j+1)}={\widehat{\beta }}_0^{\left(j\right)}+{\widehat{\beta }}_1^{\left(j\right)}{x}_i+r_i^{\left(j\right)}{\widehat{\sigma }}_{y|x}^{\left(j\right)}$, where r_i is drawn independently form standard normal distribution. In order to get M imputations for the ith subject with the new assay, these steps are repeated for j=1…M.