Dynamic Mechanical Interactions between Neighboring Airspaces Determine Cyclic Opening and Closure in Injured Lung

Abstract

Rationale

Positive pressure ventilation exposes the lung to mechanical stresses that can exacerbate injury. The exact mechanism of this pathological process remains elusive.

Objectives

Describe Recruitment/Derecruitment (R/D) at acinar length scales over short time frames and test the hypothesis that mechanical interdependence between neighboring lung units determines the spatial and temporal distributions of R/D, using a computational model.

Methods

Experiments were performed in anaesthetized rabbits ventilated in Pressure Controlled mode (PCV). The lung was consecutively imaged at ~1.5 min intervals, at each Positive End-Expiratory Pressure (PEEP) of 12, 9, 6, 3 and 0 cmH₂O before and after injury. The extent and spatial distribution of R/D was analyzed by subtracting subsequent images. In a realistic lung structure we implemented a mechanistic model in which each unit has individual pressures and speeds of opening and closing. Derecruited and Recruited lung fractions (F_derecruited, F_recruited) were computed based on the comparison of the aerated volumes at successive time points.

Results

Alternative R/D occurred in neighboring alveoli over short time scales in all tested PEEP levels and despite stable PCV. The computational model reproduced this behavior only when parenchymal interdependence between neighboring acini was accounted for. Simulations closely mimicked the experimental magnitude of F_derecruited and F_recruited when mechanical interdependence was included, while its exclusion gave F_recruited values of zero at PEEP ≥ 3 cmH₂O.

Conclusions

These findings give further insight into the microscopic behavior of the injured lung and provide a means of testing protective-ventilation strategies to prevent R/D and subsequent lung damage.

INTRODUCTION

Patients with Acute Respiratory Distress Syndrome (ARDS) invariably require mechanical ventilation in order to manage the work of breathing and improve gas exchange. Despite the indisputable effectiveness of this therapy, positive pressure ventilation imposes mechanical stresses on the parenchyma that can worsen lung injury, a condition known as Ventilator-Induced Lung Injury (VILI) [1–3].

The exact mechanisms leading to VILI at the acinar level remain elusive, although it is generally accepted that mechanical strain due to exaggerated deformation at the cellular level can lead both to structural deterioration and inflammation of the parenchyma through mechanotransduction responses [4, 5]. In particular, high pressure and large volume excursions have been demonstrated to induce mechanical injury in the lung [1]. This mechanism, termed volutrauma, is suggested by the decrease in mortality in ARDS patients observed when tidal volume (VT) and plateau pressures are limited [6, 7]. Nevertheless, low VT can still lead to injury [2, 8] by potentiating inflammation through three mechanisms that are unrelated to volutrauma, namely: 1) cyclic R/D of peripheral airspaces, referred to “atelectrauma” [9]; 2) displacement of air-liquid interfaces along small airways, which injures epithelial cells [10, 11]; 3) mechanical interdependence, which causes the pulling forces between adjacent aerated and collapsed alveoli to produce local pressures that substantially surpass transpulmonary pressure [12–14].

The R/D events giving rise to VILI are dynamic, occurring more or less rapidly depending on the severity of lung injury [14, 15], whether recruitment maneuvers have been applied, and what mechanical ventilation settings, such as PEEP and driving pressure, are employed [16]. Previously, Ma & Bates [17] proposed a computational model of R/D dynamics based on a symmetrically bifurcating airway tree in which each branch has a critical closing and opening pressure as well as opening and closing speeds. This model has successfully reproduced the observed time-dependent changes in lung elastance observed following deep inspiration maneuvers in experimental models of VILI in mice [18], suggesting that it captures essential aspects of R/D dynamics.

However, this model makes no predictions about how VILI is distributed throughout the lung, while the lung damage that occurs in VILI is known to be spatially heterogeneous. Furthermore, the presence of mechanical interdependence between adjacent regions of the lung parenchyma suggests that VILI, and the R/D events that cause it, are likely to be spatially correlated [13, 18]. In addition, the dynamic nature of R/D suggests that the extent and distribution of VILI is highly dependent on pressure and volume history [17], and that the R/D that occurs over short time scales (order of minutes [19]) has a strong influence on lung aeration and mechanics over longer periods of time (order of hours). The pathogenesis of VILI is thus likely to be critically determined by the short-term temporal dynamics of R/D and their spatial distribution at the acinar level, yet we currently have little understanding of either phenomenon.

Accordingly, the present study was undertaken to quantify the extent and distribution of R/D at the acinar scale in a lavage-induced rabbit model of VILI using in vivo synchrotron radiation phase-contrast imaging. Using a computational model based on that of Ma & Bates adapted to include a morphologically realistic 3D airway tree, we investigated the hypothesis that mechanical interaction between neighboring terminal lung units could potentially contribute to our experimental observations.

METHODS

A detailed description of the experimental procedures is provided in the online supplement (Text S1). The care of animals and the experimental procedures were in accordance with the Directive 2010/63/EU of the European Parliament and were approved by the Evaluation Committee for Animal Welfare of the European Synchrotron Radiation Facility. Briefly, the experiments were performed on four male New Zealand rabbits. The animals were anaesthetized, paralyzed, and mechanically ventilated in PCV mode, with a pressure above PEEP set in order to obtain a VT of 6 mL/kg; F_IO₂ of 0.6; I:E ratio of 1:2; a baseline PEEP of 3 cmH₂O; and a respiratory rate set to obtain a PaCO₂ of approximately 40 mmHg. Plateau pressure was limited to 35 cmH₂O. Animals were immobilized in the upright position for imaging. We used synchrotron phase-contrast CT imaging [20, 21] with an acquisition time of 21.7 s for a 2.5 mm thick volume at a voxel size of 47.5 μm³.

Study Protocol

The imaging protocol started with a recruitment maneuver (20 cmH₂O, 10 s). The lung was imaged 9 times at end-expiration at approximately 1.5 min intervals at each subsequent PEEP level of 12, 9, 6, 3 and 0 cmH₂O. Thereafter the rabbits underwent 5 sequential whole lung normal saline lavages (100 mL/kg), followed by 120 min of injurious ventilation with a peak inspiratory pressure of 35 cmH₂O, zero PEEP, respiratory rate of 20/min, and F_IO₂ of 100%. Following injurious ventilation, the same imaging protocol was repeated.

Simulation of R/D in a realistic airway tree structure

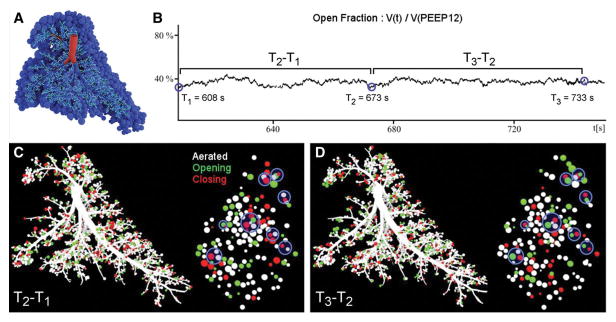
In a morphologically realistic right rabbit lung airway tree (Figure 4A), we implemented a computational model in which each airway and acinar unit has an opening and closing pressure as well as an opening and closing speed according to Bates [15]. The model was modified to account for the PCV mode of ventilation and to include mechanical interdependence between neighboring acini; at each time point the opening and closing pressures of a given unit depended on the state of each surrounding unit in inverse proportion to the square of their separation distance and in direct proportion to their relative volumes.

Figure 4. Computational simulation of airway and acinar behavior under positive pressure ventilation in injured lung, in a 3-dimensional morphologically realistic right rabbit lung at PEEP 6 cmH₂O.

A: right lung structural model comprising 7175 airways feeding 3843 acinar units B: short-term changes of the lung open fraction over time; 3 arbitrary time points approximately 1 min apart are selected for comparison with the experimental data. C,D: recruitment/derecruitment distribution computed in between the 3 selected time points. White: stable aerated; Black: stable collapsed; Green: opening (recruitment); Red: closing (derecruitment); Blue Circles: alternating recruitment/derecruitment behavior. Distributions are shown for the same time points as in B. Left: Full lung; Right: 2 mm slice similar to the experimental images.

RESULTS

Lung injury was severe with a significant decrease in the paO₂/FIO₂ ratio (528±52 to 115±47 mmHg) and in respiratory compliance (2.78±0.14 to 0.22±0.09 mL/cmH₂O, Table S2).

Figure 1A and B show volumetric renderings of the aerated fraction obtained by segmentation of two images acquired 84 s apart in a representative injured lung at PEEP 6 cmH₂O. Corresponding raw CT slices are shown in the online supplement (Figure S3). Figure 1C shows a volumetric map of the changes in regional lung aeration from one time point to the next, computed using registration of the sequential images. Four regions of interest within the parenchyma are enlarged in Figure 1D–K. Figure 1D, H, F, and J show the differences in aeration between time T₁ and T₂, while Figure 1E, I, G, and K show those between T₂ and T₃. First, these images show that the post-injury regional distribution of lung aeration was spatially heterogeneous. Second, we identified both aerated (white) and non-aerated (black) lung regions that were stable over the imaged time intervals, as well as other regions that were highly unstable over the same time course. A remarkable finding was that adjacent and communicating airspaces subtended by the same terminal airway did not all behave in the same way, but rather exhibited alternating patterns of recruitment and derecruitment. Indeed, in Figure 1D a terminal airway (*) and part of an acinus (†) are recruited, while other regions within the acinus are either closing (§) or remain closed. Thirty respiratory cycles later (Figure 1E) the terminal airway has closed (*), and some regions of the subtended acinus are opening (†) while closely adjacent areas to these are closing (§). Figure 1H and I show an example of the closure of a small airway (*), which remained closed in the following time interval, while subtended acinar regions were closing (§) and opening (†). Similar findings were obtained in the other animals and are included in the online supplement (Figure S4). On rare occasions (Figure 1F and G) the images suggest the presence of liquid bridges moving within the airway lumen (*). However, in the majority of cases complete small airway closure occurred along a certain airway length Figure 1J and K.

Figure 1. Alveolar recruitment/derecruitment occurring alternately in neighboring lung units over short time scales ~1 min, in injured lung at PEEP 6 cmH₂O.

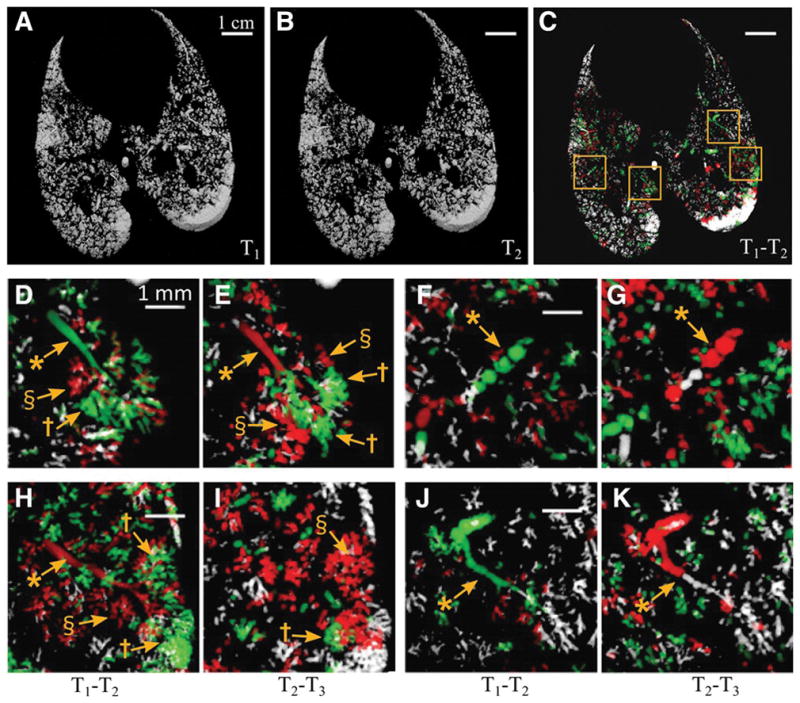
A,B,C :3D renderings of aerated lung regions obtained by segmentation of Synchrotron phase-contrast CT images at 0 s (A) and 84 s (B) in a 2.5 mm thick slice, in injured lung at PEEP 6 cmH₂O; C: Recruitment/Derecruitment map quantified using image registration between T₁ (A) and T₂ (B). White: aerated, no change; Black: non aerated, no change; Green: Opening; Red: Closing. Yellow squares delineate regions of interest magnified in panels D–K with D,F,H,J computed from 2 successive images acquired at 0 and 84 s (T_{2 –} T₁) and E,G,I,K from the subsequent time interval between 84 and 159 s (T₃-T₂). *: bronchioles; †: recruiting airspaces; §: derecruiting airspaces. Raw images are shown in the online supplement (Figure S3).

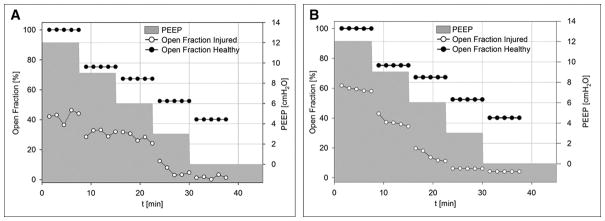
Interestingly, R/D occurred in the face of perfectly stable mechanical ventilation settings and in spite of the fact that the animals were ventilated in PCV mode. In all animals, unequal magnitude of recruitment and derecruitment led to fluctuations in the aerated lung fraction at each PEEP level, as illustrated in Figure 2. Initially, the average aeration in the imaged lung differed between animals, likely due to disparity in the severity of lung injury. Although the average aeration of the injured lung improved with PEEP, the short-term fluctuations in aeration fraction were observed at all PEEP levels including the highest level of 12 cmH₂O.

Figure 2. Short-term history of aerated lung fraction vs. time and PEEP level.

experimental data at baseline and after lung injury. Aerated fraction expressed as percentage of baseline lung volume at PEEP 12 cmH₂O. Black: Healthy Lung, White: Injured Lung, Grey: PEEP history. A–D: Experimental data in rabbits 1 to 4, respectively.

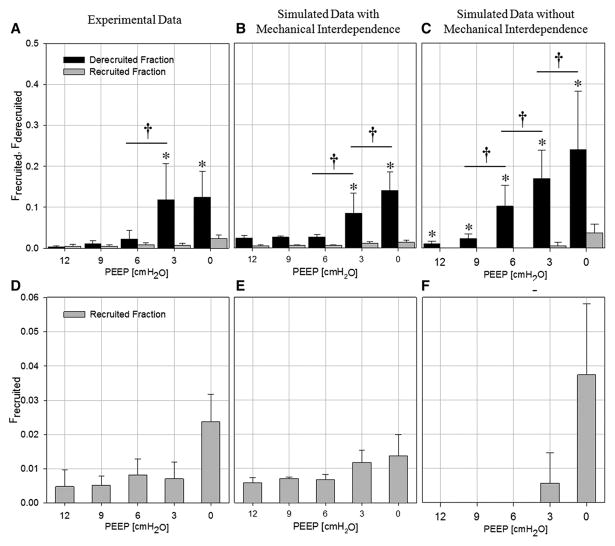
Figure 3A and D shows the fractions of derecruited and recruited lung volume (F_recruited, F_derecruited ; see: supplemental Methods) calculated between two consecutive scans. The magnitude of R and D was not different for PEEP levels ≥ 6 cmH₂O. However, F_derecruited significantly increased below this PEEP level, while the increase in F_recruited was not statistically significant.

Figure 3. Fractions of recruited (F_recruited) and derecruited (F_derecruited) lung.

Data are mean±SD for all animals and time intervals, or time intervals only for simulations. A,D: experimental data; B,E: simulated data including mechanical interdependence between peripheral lung units; C,F: simulated data not including mechanical interdependence. D,E,F: Enlarged scale for F_recruited. †: p<0.001 vs. PEEP level; *: p<0.001 vs. F_derecruited.

The cardinal features of the experimental findings were reproduced in silico, by the model proposed by Ma [17] modified to include mechanical interdependence between acinar parenchyma. In the simulation of a normal lung (Figure 5A and B, black symbols), the model produced no fluctuations of the aerated fraction at the end of expiration. In the simulation of an injured lung (Figure 5A, white symbols), the model mimicked the experimental fluctuations in aerated fraction over short time intervals despite PCV (compare with experimental data in Figure 2). An illustration of such fluctuations under PEEP 6 cmH₂O is presented in Figure 4B. These instabilities were due to successive R/D as illustrated in Figure 5C and D where it can be appreciated that the distribution of R/D was spatially correlated, i.e., adjacent units alternately recruited and derecruited over the same short time interval. Moreover, the model yielded to F_recruited and F_derecruited values that were similar in magnitude and in dependence upon PEEP, to the experimental values (Figure 3B and E).

Figure 5. Short-term history of aerated lung fraction vs. time and PEEP level: in simulated data.

Aerated fraction expressed as % of baseline lung volume at PEEP 12 cmH₂O. Black: Healthy Lung, White: Injured Lung, Grey: PEEP time course. A: Simulated data including mechanical interdependence between airway units; B: Simulated data without mechanical interdependence between airway units.

When the mechanical interdependence was not included in the computational model, both the temporal volume fluctuations and the spatial R/D correlation disappeared (Figure 5B). In this case, the fractional aeration merely showed a decrease as a result of progressive derecruitment with time. Short-term dynamics and spatial distributions of R/D in the computational model are exemplified in the online supplement (Video S5). Under this condition, the F_derecruited values rose more rapidly with decreasing PEEP than in the case where peripheral lung units were mechanically interdependent (Figure 3C and F). Conversely, F_recruited was zero above PEEP 3, and increased only below this PEEP level.

DISCUSSION

In this study, the comparison of serial volumetric phase-contrast synchrotron images of the injured lung revealed dynamic regional R/D of terminal airways and acini over short time intervals on the order of 1.5 min. We found that adjacent and communicating airspaces subtended by the same terminal airway did not all behave in the same way, but rather exhibited alternating patterns of recruitment and derecruitment implying that they are influencing each other’s behavior. These patterns of R/D occurred in spite of mechanical ventilation being under pressure control with constant settings. The short-term fluctuations in aeration fraction as a result of unbalanced R/D were observed at all PEEP levels, even at the highest PEEP of 12 cmH₂O. To our knowledge, this is the first experimental observation of such phenomena at this spatial resolution in the lung in situ.

Previous theoretical studies of VILI have suggested that the expansion of aerated alveoli in the vicinity of collapsed alveoli produces stress concentrations in the lung tissue close to the interface between these regions [12–14]. Exaggerated mechanical stress is thought to potentially trigger or amplify inflammation, which could worsen lung injury [4, 9]. The experimental demonstration that R/D phenomena occurred at small length scales and within the same time intervals in adjacent regions of the lung is therefore highly significant. Closer examination of our images (Figure 1D–K) suggests that the total closure of small peripheral airways occurred over a limited length along the airway and resulted in gas trapping in the subtended acinar region.

It has been suggested that small airways can close due to fluid-elastic instabilities that lead to the formation of liquid bridges and subsequent collapse of the airway wall [22]. This mechanism, termed “compliant collapse”, is more likely to occur when the surface tension of the airway lining liquid is increased, as was the case due to the lung injury induced in the present study, and in small peripheral airways with more compliant walls [22, 23]. An alternative mechanism that has been proposed is liquid occlusion due to the formation of menisci [24]. This mechanism is promoted by the excess of airway lining liquid which was also likely the case in the present study. Indeed, on a few occasions we observed liquid menisci within the airways, manifest as dense bridges across the airway lumen (Figure 1C and G). While the latter mechanism cannot be excluded, our experimental data suggest that “compliant collapse” probably was the predominant cause of airway closure.

We also observed the curious phenomenon of collapsed lung regions becoming recruited at end expiratory pressure, in a few breathing cycles and in PCV mode, which is not predicted by the original computational model of Ma & Bates [17]. In that model, R/D phenomena are time-dependent as a result of airway opening and closure speeds that reflect the dynamics of formation and disruption of liquid bridges. In the model, since PC implies that the intraluminal pressure varies between the PEEP level and a set maximal pressure during inspiration, a non-aerated unit at the end of expiration will be closed in expiration through all forthcoming breathing cycles. This does not, however, take into account the possible effects of mechanical interdependence [12, 25]. We therefore modified the model by considering a morphologically realistic airway tree where the linear distance between any given pair of lung units was known. By modeling the effects of mechanical interdependence between neighboring acini we simulated how closure of a unit affects the critical opening and closing pressures of nearby units, thereby mimicking the change in stress distribution within the parenchymal network [13]. Furthermore, the comparison of F_derecruited and F_recruited between the experimental data and model simulation showed a close agreement only when mechanical interdependence between peripheral lung units was simulated (Figure 3B). The simulated outputs show that when mechanical interdependence is included, alternating R/D of neighboring units can indeed occur despite stable PCV settings, whereas this phenomenon was far more limited in the alternative case, resulting merely in a pendelluft effect within trapped lung regions below PEEP 6 cmH₂O (Video S5). Also, the more rapid derecruitment in the absence of mechanical interaction can be attributed to the stabilizing effect of the mutual structural support provided by the interconnected acinar structures. These findings suggest that the dynamic nature of opening and closing and the mechanical interdependence between adjacent peripheral lung units are sufficient conditions for R/D to occur in alternating patterns during PCV.

Another important finding in this study is that although R/D phenomena were reduced by increasing PEEP they were still present even at the highest PEEP of 12 cmH₂O. We assume that the severity of injury did not significantly evolve during the course of post-injury data acquisition (~2 h), based on pilot studies. An interpretation of this finding is that the critical opening and closing pressures are scattered over a wide range of values [26]. This means that a significant proportion of the airspaces have opening and closing pressures that remain within the driving pressure range, making them vulnerable to cyclic R/D.

These findings may have translational implications in terms of detecting R/D in a clinical setting. Indeed, we noticed that R/D caused sudden small-amplitude spikes in the flow curve monitored at the airway opening. Previously, Hantos [27] used transients in the airway flow signal from isolated dog lung lobes to detect reopening of collapsed lung regions via avalanches, analogous to those observed in our imaging data. Similarly, Victorino [28] showed sudden lung volume increases when collapsed lung was reopened during a sustained insufflation. We speculate that these flow signals could be used to monitor R/D phenomena continuously in patients with ARDS and hence personalize mechanical ventilation settings aiming at minimizing R/D.

CONCLUSIONS

In summary, synchrotron phase-contrast imaging allowed us to visualize dynamic regional R/D of terminal airways and acini over short time intervals. We observed alternating patterns of R/D occurring within the same time frame in adjacent airspaces subtended by the same terminal airway. Using a computational model we were able to simulate such alternating R/D phenomena during PCV, also mimicking how these phenomena varied with PEEP. Our model suggests that R/D over short time scales occurs as a result of complex interactions between the time-dependence of opening and closing pressures and the mechanical interdependence between neighboring lung units.

Supplementary Material

Figure S3

Figure S3: Raw synchrotron phase-contrast CT image slices at 3 successive time points (T₁,T₂,T₃) at 0 (A), 84 (B) and 159 s (C), in an injured lung at PEEP 6 cmH₂O. Yellow squares delineate regions of interest magnified in Figure. 1–C

Figure S4

Figure S4: Sample data showing alveolar recruitment/derecruitment occurring over short time scales ~2 min, in healthy and injured lung in all animals. White: stable aerated regions; Black: stable collapsed; Green: opening (recruitment); Red: closing (derecruitment). Left: normal lung, Right: Injury. Row 1 to 4: Rabbit 1 to 4; Colum 1: Healthy at PEEP 12; Colum 2 to 6: Injured at PEEP 12,9,6,3 and 0 cmH₂O.

Supplemental Text S1 _Method and Discussion_. Text S1.

Detailed description of the materials and methods

Supplemental Video File. Video S5: 9 MB Ludovic Broche 1 min 0s.

Computational simulation of airway and acinar behaviour in healthy lung (0 to 20 s) and in injured lung (20 to 60 s) under positive pressure ventilation (PEEP of 12 cmH₂O: from 20 to 40 s and PEEP of 6 cmH₂O from 40 s to 60 s).

Table S2

Table S2: Gas exchange and respiratory mechanics measured at PEEP 3 cmH₂O before and after injury. paO₂/FIO₂ : arterial partial pressure to fractional inspired oxygen ratio.