Partial breaking of the Coulombic ordering of ionic liquids confined in carbon nanopores

Abstract

Ionic liquids are composed of equal quantities of positive and negative ions. In the bulk, electrical neutrality occurs in these liquids due to Coulombic ordering, in which ion shells of alternating charge form around a central ion. Their structure under confinement is far less well understood. This hinders the widespread application of ionic liquids in technological applications. Here we use scattering experiments to resolve the structure of the widely used ionic liquid (EMI-TFSI) when it is confined inside nanoporous carbons. We show that Coulombic ordering reduces when the pores can only accommodate a single layer of ions. Instead, equally-charged ion pairs are formed due to the induction of an electric potential of opposite sign in the carbon pore walls. This non-Coulombic ordering is further enhanced in the presence of an applied external electric potential. This finding opens the door for the design of better materials for electrochemical applications.

Ions are ubiquitous in liquids surrounding us in nature and man-made systems. When they are dissolved in aqueous or organic solutions, they are coordinated by a shell of solvent molecules. This solvation shell plays a key role in many physical processes, such as the diffusion¹ or the adsorption of ions at interfaces². However, confinement in nanoscale pores prevents this bulk structure from being formed, leading to partial desolvation of ions, i.e., decreasing number of solvent molecules in the solvation shell^3–13. In the case of ionic liquids (ILs), the situation is even more complex^14,15. These liquid salts are made of ions only, making it impossible to view them using a simple solvation concept. Instead, each ion is surrounded by successive shells of opposite charge, a situation that is commonly described as Coulombic ordering¹⁶. The intermolecular force between nearest-neighbors is very strong, and replacing a cation in the coordination shell immediately around an anion by another anion is a costly process from the energetic standpoint.

Spurred by the wide range of electrochemical applications of ILs¹⁷, many experimental^18–23 and theoretical^24–27 studies have aimed at understanding their structure at electrified interfaces. Kondrat and Kornyshev predicted using a mean-field theory that ILs confined in nanopores of electrically conductive materials could form a unique superionic state²⁸. In this state, the Coulombic ordering of the liquid is broken: Ions of the same charge neighbor each other due to a screening of their electrostatic interactions by the image charges induced in the pore walls. A variety of experimental methods have been used to study the local structure and transport of ILs in carbon nanopores, including neutron and X-ray scattering^6,7,9,13,18, NMR^8,10,21 and in situ electrochemical techniques^11,19,20. However, reaching the precision necessary to probe the inter-ionic structure at the local scale is difficult, and, so far, these studies could neither confirm nor invalidate the possible existence of the superionic state. However, very recently, Prehal et al. used in-situ small angle X-ray scattering to show that the dehydration of inorganic ions could more easily occur in carbon nanopores by the application of an external electric field¹³. Bringing the same level of experimental elucidation to the inter-ionic structure of highly concentrated electrolytes in carbon nanopores would fundamentally shift the capacity to develop technologies in which confined ions play an important role such as, for example, supercapacitors^{25,26, 29–31}, water desalination³² and energy generation from salinity difference³³.

In this study, X-ray scattering data were measured for two ILs. They were then analyzed using hybrid reverse Monte Carlo (HRMC)^6,7,34 simulation to recover the structure of ILs confined in well-characterized carbide-derived carbon (CDC) nanopores³⁵ of different average sizes. This allows us to investigate the various scenarios shown schematically in Fig. 1.a, i.e. the persistence (or screening) of Coulombic ordering under both monolayer and bilayer confinement conditions. We show that for 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (EMI-TFSI), a widely used IL ^19,21,30, the coordination shell of anions deviates significantly from the Coulombic ordering seen in the bulk phase, with the deviation being increased under an applied electric field. These results therefore provide direct evidence of the formation of a superionic state^28,36 in ILs.

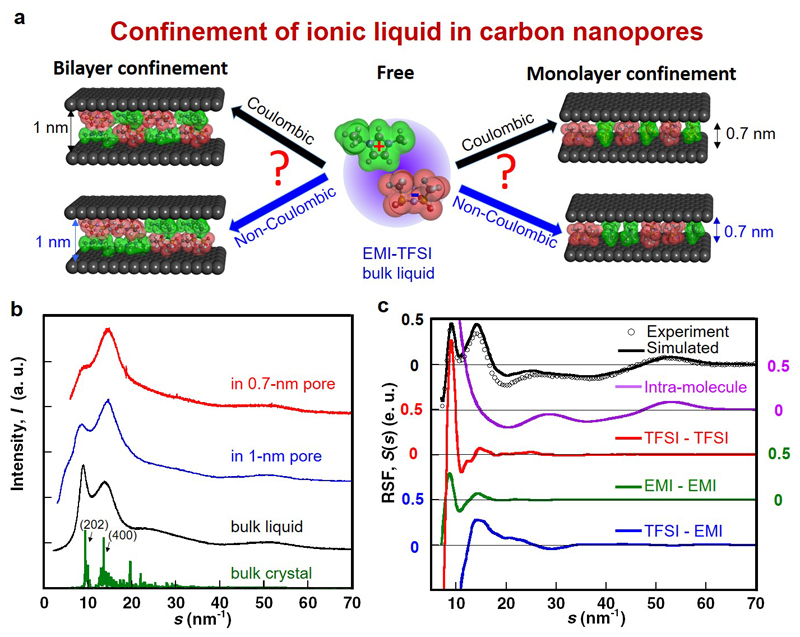
Figure 1. Structural anomalies of EMI-TFSI confined in unpolarized carbon pores.

a, Conceptual images of the structure of EMI-TFSI confined inside carbon nanopores with or without Coulombic ordering. b, X-ray scattering profiles of EMI-TFSI bulk liquid (black), EMI-TFSI in 1-nm pores (blue) and EMI-TFSI in 0.7-nm pores (red). X-ray diffraction pattern of bulk EMI-TFSI crystal from ref. 37 is shown as a green solid line. c, Total X-ray reduced scattering function (RSF) of bulk EMI-TFSI liquid as obtained from hybrid reverse Monte Carlo (HRMC) simulation (black), and contributions from the intra-ion (purple) and inter-ion structures for TFSI-TFSI (red), EMI-EMI (green) and TFSI-EMI (blue) pairs.

Anomalous co-ion pairs formation in carbon nanopores

The X-ray scattering profiles of liquid and confined EMI-TFSI in Fig. 1b show two features below s = 20 nm^-1, which are reminiscent of the reflections from (202) and (400) planes of the bulk crystal (green). They arise from the periodicities of cation-cation, anion-anion and cation-anion arrangements (Supplementary Fig. S1a-d)³⁷. For the bulk liquid (black), the peak at 9.0 nm^-1 corresponding to medium-range order is sharper and more intense than the one at 14.1 nm^-1, which reflects short-range order (first neighbors). In contrast, confinement of EMI-TFSI in CDC pores yields an inversion of these peak intensities. This inversion is particularly visible for EMI-TFSI in the 0.7-nm pores (red), where the feature at 9.0 nm^-1 only appears as a shoulder of the dominant peak. Furthermore, the position of the latter is shifted to higher values as confinement increases.

The reduced structure function (RSF) of bulk EMI-TFSI obtained from the X-ray scattering profiles³⁸ is shown in Fig. 1c. Here the main difficulty is to extract the signal due to intermolecular correlations from the total RSF of the liquid. To this end, we use HRMC, which fits explicit atomic positions and interaction potentials with the experimental data. This allows us to deconvolute the total RSFs (black) into intra-ion (purple) and three different inter-ion (red, green and blue) contributions. The experimental RSF (open circle) is well matched by the HRMC simulation, irrespective of a slight difference in the s-range of 15 to 25 nm^-1 explained by the use of a rigid molecular model (Supplementary information SI). In a similar way as done for the bulk liquid, RSFs of the EMI-TFSI adsorbed inside the carbon pores were deconvoluted into individual contributions of intra-ions, inter-ions and carbon wall-ion to gain an insight about the structural organization of the IL inside the nanopores (Supplementary Fig. S1e-g). Good agreement is also obtained with experimental data, despite the use of a simplified slit shape of carbon pores (see Supplementary Fig. S1f,g) - the dispersity of the pore sizes should be taken into account for a complete description. The marked difference in the inter-ion contribution of the RSFs between the bulk and confined EMI-TFSI suggests strong confinement effects.

The electron radial distribution functions (ERDFs) for the bulk liquid and two confined systems obtained by Fourier transformation of the experimental and simulated RSFs are shown in Fig. 2a-c. The ERDF of bulk EMI-TFSI liquid is in agreement with previously reported data³⁹. The main differences between the total ERDFs for the three systems are: (i) the peak intensity at 0.5 nm observed for confined EMI-TFSI is greater than the one of the bulk EMI-TFSI liquid, and (ii) the confined EMI-TFSI does not show a clear peak at 1.5 nm, which reflects the absence of long-range order. In order to interpret these differences, we now analyze the individual contributions of the ions. In particular, we focus on the anion-anion ERDF (blue lines in Fig. 2a-c) because the larger number of electrons present in TFSI results in a stronger contribution to the X-ray scattering⁴⁰. The data for anion-cation and cation-cation ERDFs are given in Supplementary Fig. S2a and b. In the 1-nm pore (Fig. 2b), the anion-anion ERDF shows small deviations with respect to the bulk, that is a broadening of the peak at 1.5 nm.

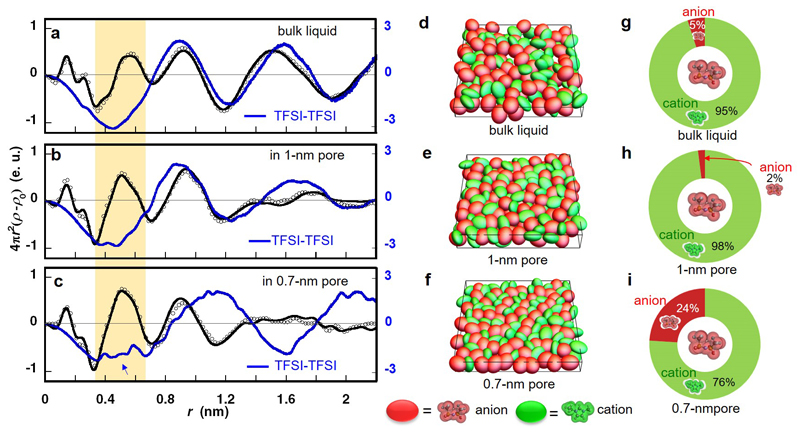
Figure 2. Pore size-dependent anion-anion structure in unpolarized carbon nanopores.

(a, b, c) Experimental (open circles) and HRMC-simulated (black lines) electron radial distribution functions (ERDFs) from X-ray scattering of EMI-TFSI in bulk liquid (a), the 1-nm pore (b) and the 0.7-nm pore (c). The blue line shows the simulated ERDF for the TFSI-TFSI correlations. Snapshots of EMI-TFSI in bulk liquid (d), 1-nm pore (e), and 0.7-nm pore (f); EMI and TFSI ions are shown by green and red ellipsoids, respectively. Population in the first coordination shell around a TFSI ion in bulk liquid (g) and 1-nm pore (h) and 0.7-nm pore (i).

More dramatic differences are observed in the 0.7-nm pores (Fig. 2c) compared to the larger pore and to the bulk liquid. Firstly, the positive peaks at 0.9 and 1.6 nm of the bulk IL are shifted to longer distances, by 0.25 and 0.4 nm, respectively. This indicates a two-dimensionally orientated alignment of anions along the slit-pore walls, which will be characterized later. However, the most striking difference is the large decrease of the intensity of the negative peak at 0.45 nm; this evidences the intrusion of anions into the cationic coordination shell surrounding a central anion. Snapshots from the HRMC simulation are shown in Fig. 2d-f in order to visualize the structure adopted by the ions (green: EMI; red: TFSI). The inter-ionic structure of the bulk liquid is disordered (Fig. 2d), whereas a more evident orientation ordering of confined EMI-TFSI is observed in the 0.7 nm slit-pore (Fig. 2f); co-ion chains of cations and anions are formed and arrange alternatively in a 0.7-nm pore. Note that here co-ions designate ions of the same sign as the central ion since the pore walls are not polarized. Fig. 2g-i report the corresponding proportions of each ion type in the nearest coordination shell around an anion. Coulombic ordering is preserved under confinement of IL in the 1-nm pore, since this coordination shell is almost completely occupied by the counter-ions. However, in the case of the 0.7-nm pore, surprisingly, 24% of the ions in the coordination shell are of the same charge (Fig. 2i), i.e. nearly a five-fold increase compared to the bulk liquid. In contrast, the anion population in the next nearest coordination shell surrounding a central anion appeared to be less affected by confinement in the 0.7-nm pore: the anion populations in this shell were 54 %, 64 % and 61 % for the 0.7-nm pore, 1-nm pore and bulk liquid, respectively.

Similar results were obtained for another IL, 1-ethyl-3-methyl-imidazolium tetrafluoroborate (EMI-BF₄) (Supplementary Fig. S3 and SI). For the latter, 11% of anions are present in the cationic coordination shell surrounding a central anion in 0.7-nm pore, to be compared with 5% in the bulk (Supplementary Fig S3h and g). This increase is not marked compared to that of EMI-TFSI, because the ion size of BF₄ ion is too small to induce an intensive screening effect, and the low electron density contrast between EMI and BF₄ ions results in a lower structural resolution. This intrusion of anions into the cationic coordination shell indicates that the Coulombic ordering, which is the main structural feature of ionic liquids, is partially broken under strong confinement. For cations in EMI-TFSI, the proportion of other co-ions in the first coordination shell in 0.7-nm pores is 19%, being slightly larger than in the case of bulk IL (16%) (Supplementary S2c-e and SI). Therefore, the confinement effect on their local structure is not as evident as the one observed for anions. This can be attributed to the formation of nonpolar domains of aggregated alkyl chains, which is typical of imidazolium-based ILs⁴¹. Even if this effect is relatively small for EMI cations due to the short length of the two chains, it introduces a small proportion of pairing between them even in the bulk.

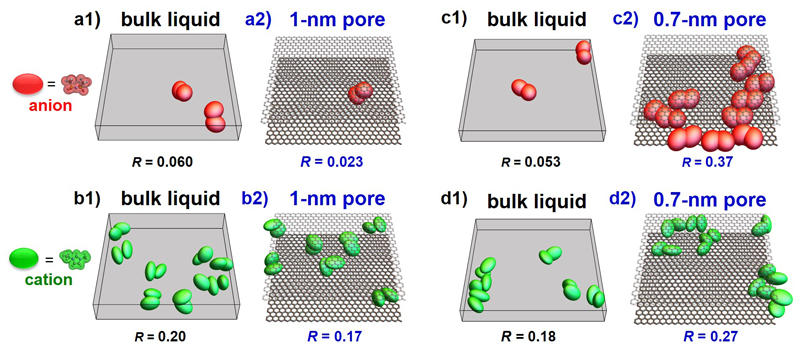
A detailed analysis of the HRMC-derived snapshots helps to understand further the structure of EMI-TFSI in carbon nanopores. As intrusion of anions into coordination shell of co-ions suggests the creation of anion-anion pair arrangements, the anion-anion and cation-cation pair numbers were evaluated (Fig. 3). The ion-pair distance is defined by the first maximum of differential electron density of the ERDF (i.e. 0.55 nm). Inside 1-nm pores, the fraction of paired co-ions is smaller than in the bulk for both anions and cations while the confinement inside 0.7-nm pores enhances the formation of both pairs: The fractions increase from 0.053 to 0.37 for anions and from 0.18 to 0.27 for cations.

Figure 3. Enhanced co-ion pair formation in carbon nanopores of decreasing pore size.

(a1, b1, c1, d1), Snapshots of co-ion pairs of anions (a1, c1) and cations (b1, d1) for EMI-TFSI bulk liquid (opposite charge ion pairs are not shown since they are the regular pattern of such ionic liquids). The co-ion pairs are extracted from bulk EMI-TFSI snapshots in 1-nm (a1, b1) and 0.7-nm slit spaces (c1, d1). (a2, b2, c2, d2), Snapshots of anion pairs (a2, c2) and cation pairs (b2, d2) for EMI-TFSI in 1-nm (a2, b2) and 0.7-nm pores (c2, d2). R is the ratio of paired anion (or cation) number to total anion (or cation) number. EMI and TFSI ions are shown as green and red ellipsoids, respectively. For narrower pores, repulsion of ions with the same charge is suppressed by electronic screening of Coulomb interactions by the conducting walls, which leads to an enhancement in the number of co-ion pairs. Note that here co-ions designate ions of the same sign as the central ion and that the pore walls have no net charges since they are not polarized.

Monolayer and bilayer confinements

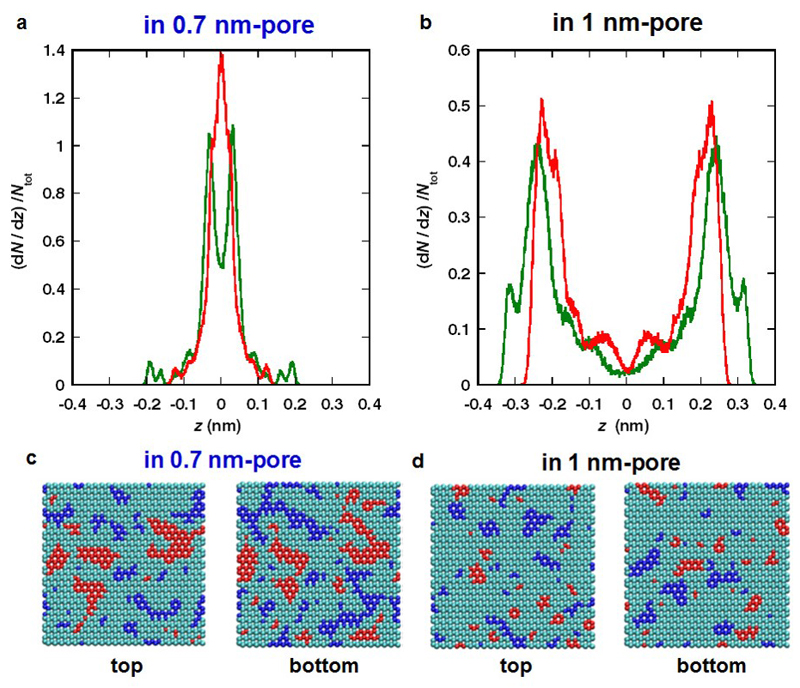
We now try to understand better the variation of the structure of the IL with respect to the pore size. Fig. 4 shows distribution profiles of EMI (green line) and TFSI (red line) ions across the pore width (i.e., z-axis) for 0.7-nm and 1-nm pores (Fig. 4a and b) obtained from averages over the HRMC snapshots, indicating the formation of monolayer and bilayer, respectively. These results agree with the pore size dependent adlayer structure of EMI-TFSI in carbon slit-pores predicted by MD simulation²⁷. The monolayer confinement in the 0.7-nm pore is therefore likely to play an important role on the breaking of the Coulombic ordering.

Figure 4. The distributions of IL molecules and induced charges on carbon pore walls in monolayer and bilayer confinement.

Density profiles of EMI (green) and TFSI (red) ions in 0.7-nm (a) and 1-nm pores (b). Molecular centers of EMI and TFSI are their electron distribution centers. z represents the coordinate perpendicular to carbon walls (z = 0 at pore center). Induced charge distributions on top and bottom pore walls of 0.7-nm (c) and 1-nm pores (d) by the adsorption of EMI-TFSI ionic liquid. Carbon atoms in blue and those in red have high negative (q < -0.01e) and positive (q > 0.01e) charges, respectively; cyan ones have intermediate charges between blue and red atoms.

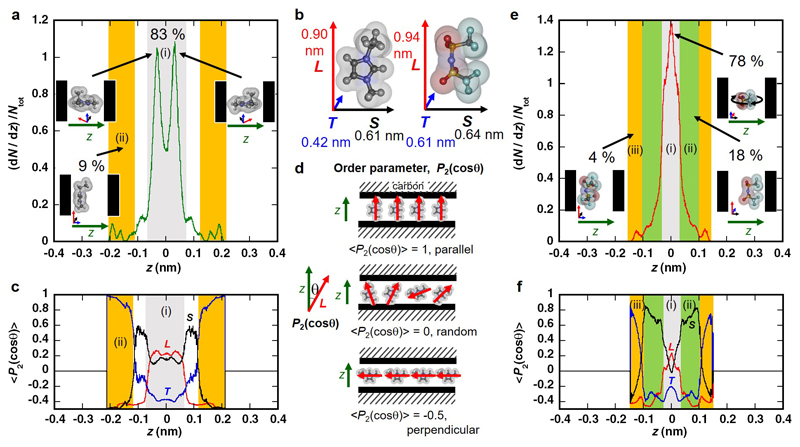
The formation of a monolayer may also lead to preferable orientations of the ions. We analyzed the orientational structure of ions in HRMC simulation snapshots, by using the averaged second Legendre polynomial <P₂(cos θ)> = <1/2(3cos² θ - 1)> as an orientational order parameter⁴², where θ is the angle between the various vectors characterizing the geometry of the EMI or TFSI ions (Fig. 5b). A detailed analytical explanation and the definition of molecular planes are provided in the caption of Fig. 5. This analysis shows that the molecular planes of the cation and anion at the center of the pore are mainly perpendicular to the pore walls with pseudo-stacking arrangement along the 0.7-nm pore direction (in Fig. 5a, c, e, f). The detailed explanation is provided in SI for the molecular orientations of EMI-TFSI in 1-nm pore (Supplemental Fig. S4).

Figure 5. Pore size-sensitive oriented structures of EMI cations and TFSI anions in carbon nanopores of 0.7 nm.

b, Definition of molecular vectors L, S and T. For EMI cation, L passes through both N atoms in the imidazolium ring and S is normal to L in the imidazolium ring. For TFSI anion, L passes through both S atoms in S-N-S bonding and S is normal to the S-N-S plane. d, Examples of molecular orientation for the L vector of cations to z-axis as <P₂(cosθ)> = -0.5 (perpendicular), 0 (random) and 1 (parallel). (a, e) Density profiles of EMI (a) and TFSI (e) ions across the slit width. a, 83% of EMI cations located in the grey region (i) with double peaks due to the cation's T vector being well-aligned to the pore walls in two configurations, as shown in the inset. Cations adjacent to the pore walls contribute only 9% of the total density in the orange region (ii). Their long and small molecular axes (vector L and S) are oriented parallel to pore walls. The residual cations between the grey and orange regions have a vector L parallel to pore walls. e, 78% of TFSI anions locate in the grey region (i). In that region, anions have a vector T parallel to pore walls, whereas vectors L and S have no preferred orientation, as shown in the inset. Anions adjacent to the pore walls (4% of the total density) in the orange region (iii) have vectors L and S oriented parallel to the pore walls. The residual anions in the light green region (ii) have vectors L and T parallel to pore walls. (c, f) Order parameter <P₂(cosθ)> changes of L, S and T vectors against z-axis. The colored regions are the same as in (a) or (e).

Screening of electrostatic repulsion by image charges

Our results suggest the existence of a molecular-scale mechanism that reduces the Coulombic repulsion energy between co-ions that become closer to each other. The repulsive energy for two co-ions (i.e., ions of the same charge) at 0.5 nm distance, estimated from a simple Coulombic interaction using point charges and a dielectric constant of 12.0⁴³, is 12 kJ mol^-1. However, Kondrat and Kornyshev have predicted a fast exponential decay of Coulombic interactions due to the screening by the metallic walls²⁸, proposing the presence of a superionic state of ions^28,36, in which nanopores are entirely occupied with only counter-ions. Although van der Waals interaction between ions could also be modified by the metallic surfaces⁴⁴, the dispersion interaction between pore wall and molecules then becomes comparable to the Coulombic interaction in the narrow pores, eventually breaking the alternate array structure of cations and anions. Thus, the creation of image charges and their interaction with the adsorbed ions has a great impact on the ion arrangement in carbon nanopores.

To confirm the importance of this screening effect, we computed the induced charge distribution on both carbon walls using an algorithm that allows us to fix the potential on the carbon atoms. The resulting charge distributions are shown in Fig. 4c and d. Carbon atoms with high positive (q > 0.01e) or negative charges (q < -0.01e) are shown in red and blue, respectively; carbon atoms with intermediate charge between -0.01e and 0.01e are shown in cyan. The blue and red domains for the 0.7-nm pore (Fig 4c) are more extensive compared to those for the 1-nm pore, where the highly-charged domains are also more dispersed (Fig 4c). The domains of iso-charge on both walls are more correlated in the case of the 0.7-nm pore, reflecting the fact that they arise from a monolayer as opposed to a bilayer in the case of the larger pore. The carbon atoms of the 0.7-nm pore carry a higher average absolute charge (0.0111e C nm^-2) than the ones of the 1-nm pore (0.0088e C nm^-2). This shows that image charges on the carbon atoms increase when the pore size decreases, in agreement with previous simulations²⁵. The computation also provides the total energy of the systems. By differentiating this energy with and without the induced charges on the carbon, stabilization energies of 7 and 22 kJ mol^-1 are obtained for the 1-nm and 0.7-nm pores, respectively. Although these values likely overestimate the screening, since carbon is a non-ideal electrically conductive material⁴⁵, we can deduce that the formation of image charges is a strong driving force allowing the packing of co-ions in the vicinity of each other inside narrow nanopores.

Effect of electric potentials on association of co-ions

The X-ray scattering profiles of EMI-TFSI in 0.7-nm pores under electric potentials (obtained from external polarization source) using an in-situ X-ray scattering electrochemical cell (Supplementary Fig. S9a-c) are shown in Fig. 6a. The in-situ cell exhibits a typical capacitive signature (i.e. C_cell = 25 F g^-1, that is C_electrode = 100 F g^-1), giving a rectangular CV curve as reported by Lin et al.³⁰ evidencing a double layer charge storage mechanism.

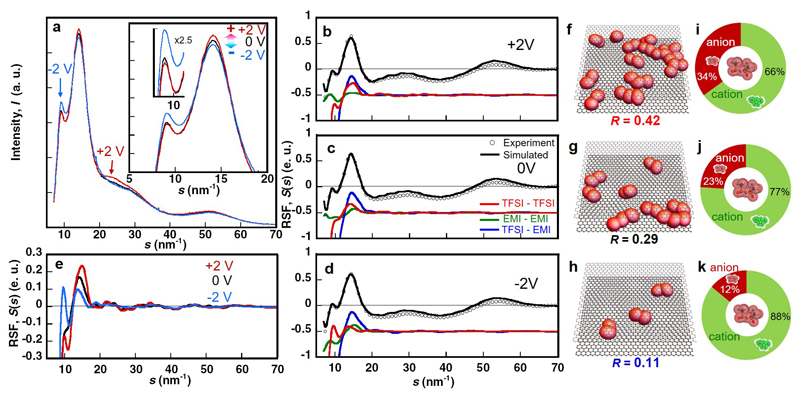
Figure 6. The effect of electrode potential on the structural ordering of ionic liquid inside ultra-narrow pores.

(a) Change in In-situ X-ray scattering profile of EMI-TFSI in the monolayer confinement of carbon nanopores of 0.7 nm under constant potentials of 0 V (black) and ± 2 V (+: red and -: blue). Here, we express application of the electric potentials of 2 V for positive and negative electrodes as +2 V and -2 V, respectively. (b, c, d) Experimental X-ray Reduced Structure Functions (RSFs) of EMI-TFSI in the 0.7-nm pores under +2 V (b), 0 V (c) and -2 V (d) with open circles. The HRMC-simulated RSFs are plotted with black solid lines. The simulated RSFs for the TFSI-TFSI correlation (red), EMI-EMI correlation (green) and TFSI-EMI correlation (blue) are given as solid lines. (e) Single plots of RSFs of TFSI-TFSI correlation in the 0.7-nm pores under +2 V (red), 0 V (black) and -2 V (blue). (f, g, h) Snapshots of co-ion pairs of anions of EMI-TFSI in the 0.7 nm-pore under +2 V (f), 0 V (g) and -2 V (h). R is the ratio of paired anion number to total anion number. TFSI anions are shown as red ellipsoids. (i, j, k) Population in the first coordination shell around a TFSI anion in the 0.7-nm pore under +2 V (i), 0 V (j) and -2 V (k).

Under polarization at +2V, we observe an increase of the intensity in the 20-30 nm^-1 region, which arises from intramolecular scattering of TFSI. This indicates an enrichment of anions inside the nanopores. The peaks at 14 and 9 nm^-1, which are respectively due to first and second neighbor intermolecular scattering (i.e., short-range and medium-range ordering), display opposite trends. The intensity at 14 nm^-1 increases, suggesting a stronger ordering at short-range. This supports the enrichment of anions in the nearest coordination shell around an anion. It is accompanied by a decrease of the intensity at 9 nm^-1, which implies that this enrichment occurs with a diminution of the medium-range order. Opposite trends are observed in the negatively polarized electrode.

These changes in the X-ray scattering indicate an intermolecular reorganization within the ILs under polarization. To analyze them further, the obtained RSFs were deconvoluted, as given in Fig. 6b-d. The most striking change is observed for TFSI-TFSI correlation under +2 V, 0 V and -2 V (Fig.6e). The formation of pairs of anions (Fig. 6f-h) is largely facilitated in positively charged pores, resulting in an explicit increase of the proportion of anions in cationic coordination shells around a central anion (Fig. 6i-k) that increases from 23% at 0 V up to 34% at +2 V. On the other hand, the number of paired anions decreases in negatively charged pores (12% at -2 V). Similar trends were observed for the EMI-EMI structures by application of electric fields (Supplementary Fig. S9f-k). The preliminary measurement of the in-situ X-ray scattering of EMI-TFSI in the 1-nm pores under the electric potentials showed less marked changes of the peaks than those in the 0.7 nm-pores, supporting the uniqueness of monolayer confinements of ILs. The in-situ results support the superionic state formation theory irrespective of the degree of pore filling with counter ions.

Conclusion

In conclusion, the structure of EMI-TFSI and EMI-BF₄ IL electrolytes confined in carbon nanopores has been determined from HRMC simulation-aided X-ray scattering technique. This approach shows that these ILs adopt monolayer or bilayer arrangement depending on the average pore size, which corresponds well to the two situations shown in Fig. 1a. Bilayer confinement does not compromise the Coulombic ordering as ordered adlayers can form on each carbon wall. Monolayer confinement, on the other hand, breaks Coulombic ordering and leads to the formation of anion and cation pairs. The non-Coulombic structure formation is made possible by the repulsive electrostatic interactions between co-ions being offset by image charges induced in the carbon walls. This compensation effect induces a highly dense ionic structure of co-ions, which can explain the increase of the capacitance measured in small nanopores, when the ion dimensions are close to the average pore size, as reported in previous studies³⁰. Furthermore, the in-situ X-ray scattering measurements achieved under polarization confirmed the marked enhancement of the densification of co-ions in the oppositely charged pores. This study therefore validates experimentally the existence of a superionic state theoretically predicted by Kondrat and Kornyshev²⁸. The present approach provides guidelines for designing porous carbons for supercapacitors, i.e. with high electrical conductivity and pore structure inducing larger image charges at the surface. The conclusions of this study should be applicable to other conducting materials forming slit-pores, e.g., between 2D layers of transition metal dichalcogenides, carbides, nitrides and oxides⁴⁶. The convincing evidence of partial breaking of Coulombic ordering of ions confined in subnanometer carbon pores may also provide key information for a wide range of new technologies, such as capacitive deionization³² and energy production from a salinity difference³³ since breaking of symmetry principles plays an essential role in nature.

Methods

We used two types of TiC-CDCs with average pore sizes of 0.7 and 1 nm, which were evaluated by nitrogen adsorption isotherms at 77 K (Supplementary Fig. S5 and SI) using a volumetric equipment (Autosorb-iQ, Quantachrome Instruments). EMI-TFSI (99 wt%, Iolitec) and EMI-BF₄ (> 97.0 %, Tokyo Chemical Industry Co., Ltd.) were used without further purification. The EMI-TFSI was introduced in the CDC pores in an acetonitrile (99.5 wt%, Kishida Chem. Co., Ltd.) solution of ca. 9 wt% EMI-TFSI. The removal of acetonitrile was then conducted by heating the samples at 343 K overnight and at 393 K in vacuo (<0.1 Pa) over two days in order to measure only the X-ray scattering of EMI-TFSI inside pores. The EMI-BF₄ adsorbed in CDC (average pore width: 0.7 nm) was also obtained with similar treatments. Further N₂ adsorption experiments on CDCs at 77 K after the filling procedure with EMI-TFSI (Supplementary Fig. S6b and d), indicates that the pores are occupied by IL molecules. The weight loss measured by Thermal Gravimetric Mass Spectrometry (TGMS, Rigaku Co.) under He atmosphere at 800 K (Supplementary Fig. S7) provides the amount of EMI-TFSI inside the nanopores; the actual fractional filling of the nanopores with EMI-TFSI is 0.88 and 0.97 for the 0.7-nm pores and 1-nm pores, respectively. The removal of EMI-TFSI on the external surfaces of CDC sample was confirmed by the intensity decrease of X-ray scattering in the small angle region (Supplementary Fig. S6a and c).

The EMI-TFSI adsorbed CDC samples and CDC powders were placed in a glass capillary of 0.7 mm in diameter (0.01 mm wall thickness) and then the capillary was sealed after heat-treatment at 393 K under vacuum for 1 h to avoid adsorption of water vapor by humidity. X-ray scattering profiles of IL-adsorbed CDC samples, CDC samples and EMI-TFSI bulk liquid were measured in the synchrotron radiation facility of SPring-8 with an imaging plate (IP); the wavelength (λ = 0.09989 and 0.07997 nm) monochromated with Si (111) plane was determined with CeO₂ powder (the crystal system is cubic and the lattice parameter is 0.54111 nm). The X-ray scattering profile of a glass capillary without samples was also measured for a background correction.

We also measured the in-situ X-ray scattering of EMI-TFSI in the charged state of CDC electrodes. The 0.7-nm CDC electrodes (CDC: carbon black: PTFE = 8:1:1 in weight percent³⁰) were inserted into two capillaries with Pt wires (the diameter is 0.1 mm) and then the capillaries were filled with EMI-TFSI and connected within 0.2 mm distances with glass microfiber filter as a separator (Fig. S9a-c). Cyclic voltammetry of the in-situ X-ray scattering cell was conducted using IVIUMSTAT (Ivium Technologies B. V.) with 0.5 mV/s scanning rate (Fig. S9e) to assess the quality of the microcell. The in-situ X-ray scattering measurements were conducted in the synchrotron radiation facility of Aichi SR with 4 sets of 2D detectors of PILATUS; the wavelength (λ = 0.079966 nm) monochromated with Si (111) plane. The CDC electrode of the left-hand side of the in-situ X-ray scattering cell (Supplemental Fig. S9a-c) was selectively irradiated with X-ray for 10 minutes after charging and discharging at constant voltage of -2, 0 and +2 V for 1.5h with a potentiostat of HA200 (Hokuto Denko Co.). The chronoamperometry plots under these experimental conditions (Fig S9d) show a stable leakage current after 1.5 h polarization, which enables the measurement of in-situ-X-ray scattering at the steady-state.

The obtained X-ray scattering profile includes the self-scattering of adsorbed EMI-TFSI molecules and of the CDC carbon frames, as well as the cross terms between them. The corresponding partial RSFs were extracted with the appropriate correction procedures³⁸ given in SI. We have then determined the real-space structure of the samples by performing hybrid reverse Monte Carlo (HRMC) simulations^5,6,34. In this method, we determine an energetically-favourable configuration of ionic molecules within a model slit-shaped pore of infinite extent that shows a structure compatible with the RSF extracted from X-ray scattering.

This is achieved by minimizing the following function

$$F=W_S{F}_S+W_E{F}_E,$$ (1)

The first term in this equation measures the difference between the structure factors of the model (S_sim) and experiment (S_exp)

$$F_S={\displaystyle {\Sigma }_{i=1}^n{\left(S_{\text{sim}}\left(s_i\right)-S_{\exp }\left(s_i\right)\right)}^2,}$$ (2)

where both are defined in terms of n discrete points along the absolute scattering vector, s. The second term in Equation (1) is the total energy of the system, which is given by the expression

$$F_E=E_{ii}+E_{ip},$$ (3)

where E_ii is the sum of the interaction energies between the ions within the pore, which are modelled using Coulomb’s Law with Ewald summation method⁴⁷ and Lennard-Jones model with Lorentz-Berthelot mixing rules⁴⁷ and E_ip is the sum of the interaction energies between the ions and the pore walls as determined by the 10-4-3 Steele model⁴⁸. We used a slit-shaped model of carbon pores, because high resolution transmission microscopic images show the presence of such pores⁴⁹. Although the slit-pore is an approximate model for such carbons in the long range, as shown by Palmer et al.³⁵, it remains correct for studying the arrangements of the ions at the ranges which interest us here, which is below 2-3 nm. However slight deviations from this approximation are likely to appear, as discussed below.

The terms in Equation (1) are scaled by suitable weights. In the case of the energy-related term, the weight is the inverse of the thermal energy, W_E = β = 1/k_BT, where k_B is the Boltzmann Constant, and T the temperature (298.15 K). The weight for the structure factor-related term is selected to ensure that the entire term is comparable in scale to the energy-related term. For the bulk and 1-nm pore simulations, Ws = 1.33x10⁵. For 0.7-nm pore simulation Ws = 1.33x10⁶. The HRMC simulation starts from an initial charge-neutral configuration. The density is fixed, and periodic boundary conditions are used in all Cartesian directions for the bulk IL or along the x and y axis only for the model slit-pores. The dimension of the box was (6 nm x 6nm x w nm), where w is 6 nm for the bulk and the effective pore size for the carbon nanopores. The numbers of ion pairs inside the box were fixed to 508 in the bulk liquid, and to 80 and 58 for slit-pores of 1 nm and 0.7 nm, respectively, which corresponds to a fractional filling of 0.95. For HRMC simulation in charged pores, we assumed these charges on carbon pore walls are induced by the imbalance of anion and cation numbers to keep the electroneutrality. So the number of charges (i.e. number difference of anions and cations) are calculated from the results of chronoamperometry at 2 V after keeping 0 V for 3 h for the in-situ X-ray scattering cell. The evaluated charges for +2 V and -2 V simulation on carbon pore walls were +20e and -20e, respectively. 25 sites of +0.4e and -0.4e are located at even intervals on both side of carbon pore walls in -2 V and +2 V simulation boxes, respectively. To keep total molecular number density, 10 molecules of cations and anions increase and decrease, respectively, from 0 V simulation condition to +2 V simulation. The -2 V simulation was done oppositely. The positions of charges on carbon pore walls were fixed in the simulation.

The ions were placed randomly in the initial structure. Their arrangement then evolved towards a plausible structure by repeatedly applying ‘moves’ to ions selected at random. Two different types of moves are applied with equal probability. The first is a random displacement, which can be expressed as

$$\delta x_{\alpha }=\delta x_{\alpha ,max}\left({\xi }_{\alpha }-0.5\right),$$ (4)

where δx_α,max is the maximum possible displacement allowed in the α-coordinate direction, and 𝜉_α are corresponding random numbers independently selected in a uniform way from the range [0,1].

The second move is a random rotation of the ion around its centre of mass, which can be expressed as

$$\delta {\theta }_{\alpha }=\delta {\theta }_{\alpha ,max}\left({\xi }_{\alpha }-0.5\right),$$ (5)

where δθ_α,max is the maximum possible rotation allowed around the α-coordinate direction.

Each attempt of move is accepted, provided a random number selected uniformly in the [0,1] range is less than the probability

$$P=\text{min}\left(1,\text{exp}\left[-\Delta F\right]\right),$$ (6)

where ΔF measures the variation of F due to the move. This equation ensures that the move is always accepted if ΔF ≤ 0. The values of the maximum linear and rotational displacement are adapted throughout the simulation so as to yield a move acceptance ratio (the ratio of accepted moves to total attempted moves) of 40%.

The simulation results which we discussed in this paper were obtained as follow; at first, 1x10⁷ steps of simple MC simulations were conducted and then, HRMC simulations were conducted for 2x10⁷ steps with equilibrated structure by MC simulations as the starting configurations. The value of the function expressed in Equation (1) converges after 1x10⁷ steps of HRMC simulations so the configurational information is averaged over the final 1x10⁷ steps of these simulations in order to compute all the structural properties.

The molecular structure, LJ parameters and Coulombic parameters of ions³⁹ are listed in Supplementary Fig. S8. In our simulations, a rigid model was employed for molecular structure for nonplanar staggered EMI and C1 conformer of TFSI³⁹. The Coulombic interaction between EMI-TFSI ions and their image charges in the pore wall was not taken into account in this HRMC simulation procedure. It is worth noting that the image charges of the carbon surfaces are not explicitly included in the HRMC interaction potential. However, it is present in the experiments, so that the formation of ion pairs of the same sign is clearly enforced by the structure factor-related term during the procedure. The slight disagreement between the experimental and simulated RSFs in Supplementary Fig. S1f and g mostly arises from the assumption of a simplified slit shape for the pores. The dispersity of the pore sizes should also be taken into account for a complete description.

Although we did not include the image charge-associated interaction in the HRMC simulation, we evaluated their effect by calculating them explicitly for the equilibrated structures extracted from the HRMC simulation. This was made by assigning fixed partial (point) charges to the IL atoms (the charges of the Canongia Lopes & Padua force field were used⁵⁰), and Gaussian charge distributions for the carbon atoms. The values of the latter were then determined by imposing a constant electric potential condition²⁵ within the carbon structure.

Supplementary Material

Supplementary information is available in the online version of the paper.