Abstract
Researchers have reported on the importance of the rib cage in maintaining mechanical stability in the thoracic spine and on the validity of a compressive follower preload. However, dynamic mechanical testing using both the rib cage and follower load has never been studied. An in vitro biomechanical study of human cadaveric thoracic specimens with rib cage intact in lateral bending, flexion/extension, and axial rotation under varying compressive follower preloads was performed. The objective was to characterize the motion and stiffness of the thoracic spine with intact rib cage and follower preload. The hypotheses tested for all modes of bending were (i) range of motion, elastic zone, and neutral zone will be reduced with a follower load, and (ii) neutral and elastic zone stiffness will be increased with a follower load. Eight human cadaveric thoracic spine specimen (T1-T12) with intact rib cage were subjected to 5 Nm pure moments in lateral bending, flexion/extension, and axial rotation under follower loads of 0 to 400 N. Range of motion, elastic and neutral zones, and elastic and neutral zone stiffness values were calculated for functional spinal units and segments within the entire thoracic section. Combined segmental range of motion decreased by an average of 34% with follower load for every mode. Application of a follower load with intact rib cage impacts the motion and stiffness of the human cadaveric thoracic spine. Researchers should consider including both aspects to better represent the physiologic implications of human motion and improve clinically relevant biomechanical thoracic spine testing.
Keywords: Thoracic Spine, Rib Cage, Follower Load, Biomechanics
1. Introduction
The kyphotic nature of the thoracic spine and the presence of the rib cage create a mechanical phenomenon in the thoracic spinal section that is unlike the lumbar and cervical sections, and is not fully understood. Biomechanical testing of the thoracic spine provides necessary information for comprehension of instability in the spine and for creation of new treatment methods and improved device design. Previous research has reported the importance of the rib cage in providing stiffness to the thoracic spine (Watkins et al., 2005; Brasiliense et al., 2011; Mannen et al., 2015). These findings provide unanimous agreement that rib cage removal when performing mechanical testing of the thoracic spine is not indicative of the physiological stability present in the thoracic skeleton, and as such, the rib cage should remain intact during mechanical testing. However, these studies did not use a compressive follower preload with the rib cage attached.
Because the spine operates under compressive conditions in vivo, researchers have reported on the use of a follower load to simulate this condition during mechanical testing in other sections of the spine. As defined by Patwardhan, a follower load applies the compressive preload approximately tangential to the curve of the spine, passing through the centers of rotation of the spinal segments (Patwardhan et al., 1999). Conversely, direct compressive loading does not follow the curvature of the spine and can cause buckling in multilevel spine segments. A compressive follower preload allows each individual vertebra to be loaded in nearly pure compression. Patwardhan et al. initially found a high increase in load-carrying capacity of the lumbar spine under compressive follower loads relative to direct loading, and proved this finding for the cervical and thoracolumbar spine in subsequent studies (Patwardhan et al, 2000; Stanley et al., 2004). Shirazi-Adl et al. has also successfully applied the follower load method using finite element models in the thoracolumbar spine (Shirazi-Adl et al., 2000). This increase in load-carrying capacity corresponds to the ability of these spinal segments to support in vivo muscle forces and the weight of the upper body with engagement of ligaments and other essential tissues. The muscle forces present in the thoracic spine are mainly created by the erector spinae muscle group, which provides a major part of the stability to the thoracic spine (Kurtz et al., 2005).
The purpose of this study was to implement a compressive follower load on the thoracic spine with an intact rib cage, and examine the effects of the follower load on the in vitro range of motion and stiffness of the thoracic spine with rib cage intact. Motions of both individual functional spinal units (FSUs) and spinal segments within the entire thoracic spine were examined. FSUs consist of two adjacent vertebrae, all interconnecting soft tissues, and the associated articulations of the ribs. The spinal segments were defined as upper (T1-T4), middle (T4-T8), and lower (T8-T12). The following hypotheses were tested through the course of this experiment: for individual FSUs and segments in all modes of bending, (i) range of motion (ROM), elastic zone (EZ), and neutral zone (NZ) will be significantly reduced with an increase in applied follower load, and (ii) neutral and elastic zone stiffness (NZS and EZS) will be significantly larger with an increase in applied follower load.
2. Methods
2.1 Experimental Design
Eight fresh-frozen adult human thoracic cadaveric spines (T1-T12) were used in this study, four male and four female. Average age was 66.9 ± 4.4 years. The specimens were dissected to include the rib cage, spinal column, and stabilizing ligamentous structures. Muscular and fatty tissues were removed. Specimens were thawed prior to testing and experiments were performed at room temperature. Hydration of the specimens was maintained with saline solution.
T1 and T12 were potted parallel to their vertebral endplates with screws inserted into the vertebral bodies and auto body filler (Bondo, 3M, St. Paul, MN). Bolts were rigidly fixed to the inferior potting and mounted on a FS20 Biomechanical Spine Test System (Applied Test Systems, Butler, PA) that allows 6 degrees of freedom with a pure continuous moment applied to the unconstrained, superior end (T1) (Mannen et al., 2015). The pure moment was applied at a 1 degree/second rate to a displacement control of +/- 5 Nm in three modes of bending: lateral bending, flexion/extension, and axial rotation. Five cycles were run for each test, with the third cycle used for data analysis, in accordance with previous literature (Wilke et al., 1998). The motion of T1, T2, T4, T5, T8, T9, and T11 vertebrae were tracked using orthopaedic research pins (Optotrak, Northern Digital Inc., Waterloo, Ontario, Canada) rigidly fixed into the left pedicles. The FSU and segment levels chosen were reasonably spaced throughout the thoracic spine, producing representative motions of the top, middle, and bottom of the spine. Motion data from all seven pins and load data from the test machine were recorded.
2.2 Follower Load Implementation
Follower load instrumentation was based on the methods reported by Patwardhan et al. (Patwardhan et al., 1999). Modifications were made to account for the space-limiting presence of the rib cage. Instead of the use of U-shaped mounts around each individual vertebra, fully-threaded steel rods were inserted into the approximate center of rotation of the vertebral bodies of T3 through T11. The center of rotation was determined by use of lateral radiographs with the specimen in a neutral kyphotic position. Female ball joint rod ends were screwed onto both ends of all threaded rods, as shown in Figure 1. A steel wire cable was guided through the ball joint rod ends bilaterally, with the ball joint rod ends allowing the cable to remain tangential to the curvature of the spine as deformation took place under loading. The top of the cable was threaded through the superior end of the potting, distributing the weight of the follower load from T1 to T11. The two bottom ends of the cable passed through pulleys to maintain the curve of the spine. Weights were hung from the knotted ends of the cable, with half the weight on each side, creating total load levels of 0 N, 200 N, and 400 N. Figure 2 shows the experimental setup with the specimen mounted on the machine. Reaction forces and moments were measured at the base of the specimen using a six degree-of-freedom load cell, in order to ensure that the force acting on the spine was occurring in the proper direction. Anderson et al. reports application of follower loads on the same specimens as used in the present study, but in static loading only. Anderson et al. presented no significant difference seen in sagittal tilt with the addition of each of the load levels, providing further validation of the path of the follower load (Anderson et al., 2016).
Figure 1.

Inferior view of the interior of the rib cage, displaying the ball joint rod ends and rods threaded through the approximate centers of each vertebrae, T3-T11. The wire cable, not pictured, was then threaded superior to inferior through all of the ball joint rod ends seen.
Figure 2.
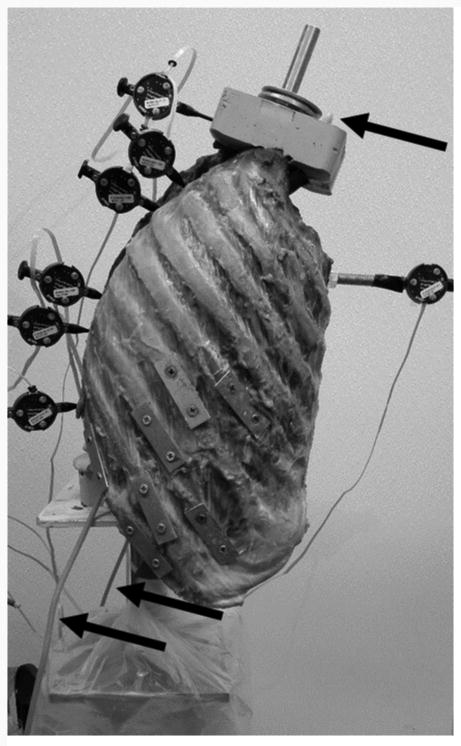
Sagittal view of the entire specimen, with the inferior potting mounted on the test machine. The motion tracking pins are shown at the various vertebral levels. The arrows refer to the steel wire cable, which is threaded from the superior end, through the ball joint rod ends on the interior of the rib cage, and out the inferior end of the specimen.
2.3 Data Analysis and Statistics
Data analysis and statistics were performed in Matlab (Mathworks, Natick, MA). Rotations were calculated using Euler decomposition techniques. The order of rotation used in the decomposition was, for (1) lateral bending: lateral, axial, sagittal; (2) axial rotation: axial, lateral, sagittal; (3) flexion/extension: sagittal, axial, lateral. For all three modes of bending, ROM, EZ, NZ, EZS, and NZS were computed (Wilke et al., 1998). NZ was defined as the difference in angulation at zero load between the two phases of motion, and EZ was defined as the angular displacement from the end of the NZ to the point of maximal loading (Wilke et al., 1998). These parameters are depicted in Figure 3. Comparisons were drawn between the baseline case (0 N) and each level of follower load applied (200 N and 400 N), as well as between the two levels of load applied. With specimen data being normally distributed, a one-way repeated measures analysis of variance (ANOVA) was completed with a significance level of α = .05. No correction factor was used in the statistical analysis because the need for adjustment remains controversial, and some researchers have found that the use of corrections can increase the chance of Type II error when small sample sizes are used, as in this study (Perneger, 1998; Nakagawa, 2004).
Figure 3.
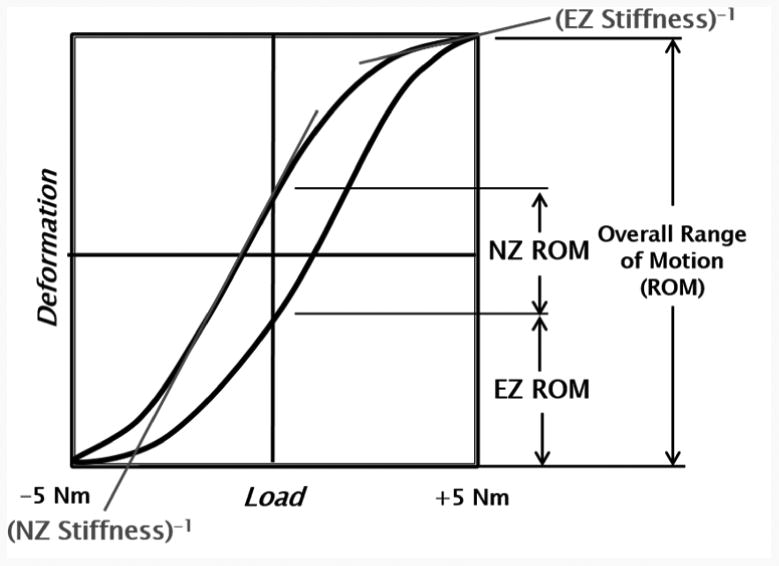
Deformation versus load of a typical testing cycle. The parameters of overall range of motion, elastic zone ROM, neutral zone ROM, EZ stiffness, and NZ stiffness are depicted. NZ is defined as the difference in angulation at zero load between the two phases of motion, while EZ is defined as the angular displacement from the end of the neutral zone to the point of maximal loading.
3. Results
The combined segmental absolute value of ROM for all modes of bending is shown in Figure 4. This figure demonstrates the trend in ROM as the follower load increases. Not all specific segment or FSU changes, however, were found to be statistically significant. Segment and FSU data for lateral bending ROM are shown in detail in Figures 5 and 6 because of the large number of significant differences seen (p < .05). Compared to the 0 N load, segmental lateral bending ROM decreased by an average of 62.4% for a 200 N follower load, and by an average of 75.9% for a 400 N follower load. Compared to the 0 N load, FSU lateral bending ROM decreased by an average of 61.7% for a 200 N follower load, and by an average of 72.3% for a 400 N follower load. Significant decreases in EZ measurements were seen at every FSU level for lateral bending, except for T1/T2 (p < .05). Compared to the 0 N load, the EZ in lateral bending for all FSU levels decreased by an average of 64.5% for a 200 N follower load, and by an average of 75.6% for a 400 N follower load. Table 1 and Table 2 display all ROM, EZ, and NZ values for all modes of bending of FSUs and segments, respectively. Significance was seen for every FSU and segment of lateral bending ROM in at least one follower load comparison.
Figure 4.
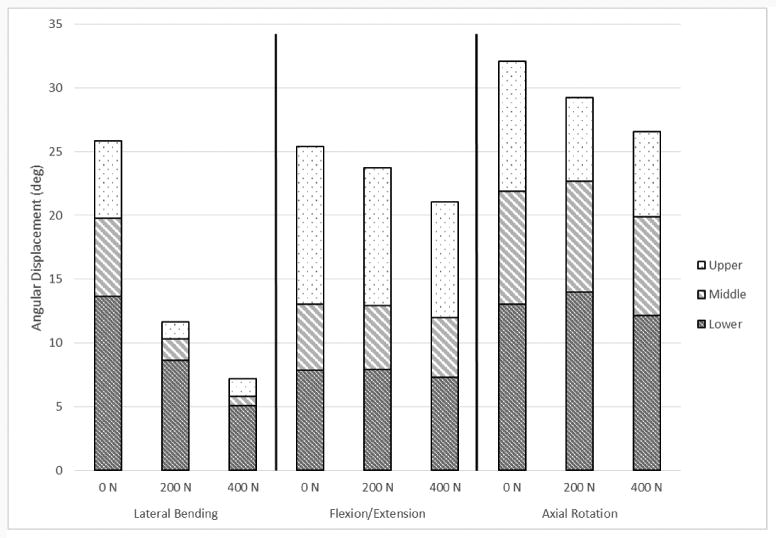
Mean combined segmental angular displacement range of motion values, displaying the difference between each load level and mode of bending.
Figure 5.
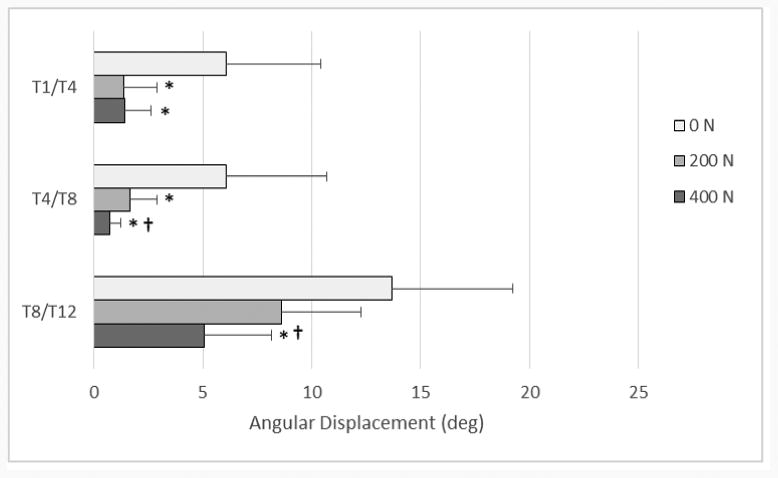
Mean (+ SD) segmental angular displacement range of motion values for lateral bending, comparing the baseline case of 0 N to the two other load levels, 200 and 400 N. * denotes statistically significant values between 0-200 N and 0-400 N (p < .05) † denotes statistically significant values between 200-400 N (p<.05)
Figure 6.
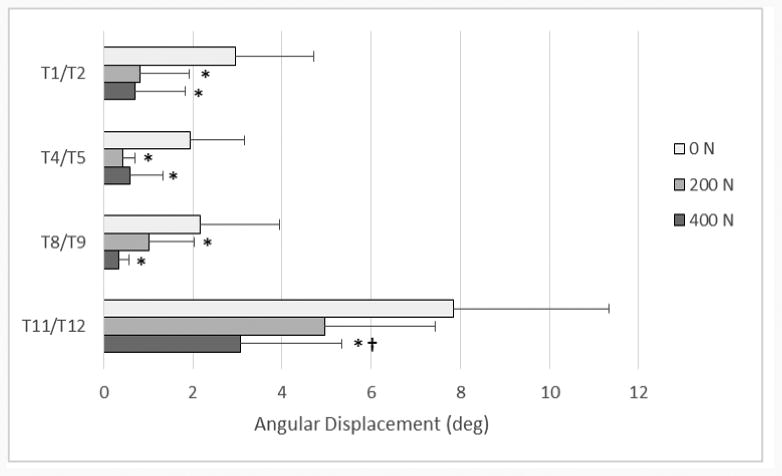
Mean (+ SD) individual FSU angular displacement range of motion values for lateral bending, comparing the baseline case of 0 N to the two other load levels, 200 and 400 N. * denotes statistically significant values between 0-200 N and 0-400 N (p < .05) † denotes statistically significant values between 200-400 N (p<.05)
Table 1.
Mean (SD) Angular Displacement Values for Individual FSU Range of Motion, Elastic Zone, and Neutral Zone.
| FSU Level | Load Level | Lateral Bending | Flexion/Extension | Axial Rotation | Flexion | Extension | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
| ROM (°) |
EZ (°) |
NZ (°) |
ROM (°) |
EZ (°) |
NZ (°) |
ROM (°) |
EZ (°) |
NZ (°) |
ROM (°) |
ROM (°) |
||
| T1/T2 | 0 N | 2.96 (1.76) |
0.62 (0.41) |
1.50 (0.97) |
7.23 (5.73) |
2.70 (1.96) |
2.01 (1.63) |
4.76 (3.00) |
1.57 (0.9 2) |
1.02 (0.69) |
4.58 (3.73) |
2.79 (1.99) |
| 200 N | 0.81 (1.11)* |
0.29 (0.42) |
0.29 (0.22)* |
6.19 (4.37) |
2.37 (1.62) |
1.36 (0.86) |
4.37 (1.40) |
1.49 (0.4 2) |
0.83 (0.73)* |
4.19 (3.09) |
1.91 (1.04) |
|
| 400 N | 0.80 (1.19)* |
0.27 (0.39) |
0.33 (0.33)* |
4.59 (3.03)† |
1.72 (1.22) |
0.93 (0.48)† |
3.51 (1.67) |
1.38 (0.6 4) |
0.76 (0.55) |
2.91 (2.14) |
1.46 (0.74)*† |
|
| T4/T5 | 0 N | 1.95 (1.21) |
0.49 (0.29) |
0.95 (0.85) |
1.53 (1.06) |
0.61 (0.44) |
0.23 (0.15) |
1.78 (1.37) |
0.75 (0.53) |
0.35 (0.27) |
1.10 (0.89) |
0.42 (0.21) |
| 200 N | 0.42 (0.28)* |
0.15 (0.10)* |
0.32 (0.31)* |
1.53 (1.57) |
0.65 (0.57) |
0.36 (0.40) |
1.64 (0.87) |
0.72 (0.4 0) |
0.33 (0.30) |
1.04 (1.21) |
0.49 (0.40) |
|
| 400 N | 0.60 (0.73)* |
0.14 (0.14)* |
- | 1.49 (1.26) |
0.53 (0.41) |
0.44 (0.54) |
1.46 (0.70) |
0.63 (0.3 0) |
0.15 (0.08)* |
0.82 (0.69) |
0.63 (0.55) |
|
| T8/T9 | 0 N | 2.47 (1.68) |
0.71 (0.32) |
0.76 (0.93) |
1.57 (1.00) |
0.60 (0.33) |
0.35 (0.37) |
4.05 (2.32) |
1.73 (0.9 6) |
0.58 (0.48) |
1.12 (0.76) |
0.44 (0.25) |
| 200 N | 1.02 (1.02)* |
0.20 (0.21)* |
0.78 (0.68) |
1.46 (1.30) |
0.47 (0.36) |
0.50 (0.57) |
3.03 (1.65) |
1.81 (1.0 1) |
0.80 (0.80) |
0.95 (0.91) |
0.48 (0.38) |
|
| 400 N | 0.34 (0.24)* |
0.09 (0.09)* |
- | 1.34 (1.27)† |
0.40 (0.31)*† |
0.52 (0.64) |
3.72 (2.27)* |
1.54 (0.7 8) |
0.64 (0.73) |
0.83 (0.85)† |
0.49 (0.41) |
|
| T11/T 12 | 0 N | 7.85 (3.48) |
3.12 (1.28) |
1.62 (1.29) |
3.90 (2.54) |
1.28 (0.80) |
1.28 (1.02) |
3.18 (1.71) |
1.37 (0.7 7) |
0.48 (0.24) |
2.62 (1.75) |
1.23 (0.81) |
| 200 N | 4.96 (2.47) |
1.14 (0.70)* |
2.68 (1.12) |
3.98 (2.39) |
1.15 (0.71) |
1.62 (0.98) |
3.61 (1.59) |
1.46 (0.56) |
0. 68 (0.68) |
2.31 (1.66) |
1.60 (1.06)* |
|
| 400 N | 3.08 (2.26)*† |
0.40 (0.28)*† |
2.34 (1.76) |
3.58 (2.31) |
0.90 (0.50) |
1.70 (1.28) |
3.09 (1.32) |
1.31 (0.54) |
0.47 (0.45) |
1.93 (1.47)† |
1.58 (0.87) |
|
denotes missing values due to less than five specimen contributing to the average value
denotes statistically significant values between 0-200 N and 0-400 N (p < .05)
denotes statistically significant values between 200-400 N (p<.05)
Table 2. Mean (SD) Angular Displacement Values for Segmental Range of Motion, Elastic Zone, and Neutral Zone.
| Segme nt | Load Level | Lateral Bending | Flexion/Extension | Axial Rotation | Flexion | Extension | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
| ROM (°) |
EZ (°) |
NZ (°) |
ROM (°) |
EZ (°) |
NZ (°) |
ROM (°) |
EZ (°) |
NZ (°) |
ROM (°) |
ROM (°) |
||
| Upper (T1/T4) |
0 N | 6.06 (4.34) |
1.24 (0.87) |
3.58 (2.84) |
12.3 (8.09) |
4.76 (3.03) |
2.85 (1.99) |
10.2 (5.29) |
3.75 (1.88) |
2.66 (1.74) |
8.23 (5.60) |
4.08 (2.54) |
| 200 N | 1.36 (1.55)* |
0.54 (0.55) |
0.32 (0.35)* |
10.8 (6.60) |
4.13 (2.32) |
2.38 (1.39) |
6.58 (2.05) |
2.89 (0.77) |
1.00 (0.77)* |
7.39 (4.60) |
3.19 (1.55) |
|
| 400 N | 1.43 (1.21)* |
0.57 (0.49) |
0.34 (0.23)* |
9.07 (5.35)*† |
3.40 (1.75)*† |
2.01 (1.49) |
6.69 (3.42) |
2.76 (1.60) |
0.94 (0.69)* |
6.13 (3.52)† |
2.67 (1.32)*† |
|
| Middle (T4/T8) |
0 N | 6.10 (4.57) |
1.62 (1.15) |
2.90 (2.49) |
5.17 (3.27) |
2.09 (1.42) |
0.96 (0.60) |
8.85 (6.41) |
3.59 (2.96) |
1.68 (1.10) |
3.70 (2.50) |
1.44 (0.81) |
| 200 N | 1.67 (1.21)* |
0.20 (0.19)* |
1.48 (1.00)* |
5.02 (3.62) |
1.93 (1.38) |
1.09 (0.99) |
8.66 (6.16) |
3.76 (2.51) |
1.16 (1.20) |
3.39 (2.73) |
1.56 (0.95) |
|
| 400 N | 0.71 (0.53)*† |
0.22 (0.13)* |
0.59 (0.21)*† |
4.64 (3.50)† |
1.70 (1.20)*† |
1.13 (1.18) |
7.72 (5.05) |
3.48 (1.98) |
0.95 (1.03) |
2.90 (2.28)*† |
1.63 (1.17) |
|
| Lower (T8/T12) |
0 N | 13.7 (5.55) |
5.31 (1.54) |
3.35 (2.71) |
7.88 (4.36) |
2.80 (1.51) |
2.20 (1.58) |
13.1 (3.80) |
5.58 (1.76) |
1.89 (1.36) |
5.63 (3.28) |
2.17 (1.14) |
| 200 N | 8.62 (3.65) |
1.71 (0.90)* |
5.21 (2.06) |
7.93 (4.64) |
2.45 (1.42)* |
2.89 (1.8 6) |
14.0 (4.43) |
5.89 (1.80) |
2.23 (1.48) |
5.07 (3.47) |
2.73 (1.50)* |
|
| 400 N | 5.07 (3.07)*† |
0.65 (0.42)*† |
3.84 (2.27)† |
7.33 (4.49) |
2.05 (1.07)*† |
3.09 (2.3 4) |
12.2 (3.7 9) |
5.45 (1.4 8) |
1.73 (1.38) |
4.40 (3.12)† |
2.79 (1.32) |
|
denotes missing values due to less than five specimen contributing to the average value
denotes statistically significant values between 0-200 N and 0-400 N (p < .05)
denotes statistically significant values between 200-400 N (p<.05)
All stiffness values for all conditions of FSUs and segments are displayed in Table 3 and Table 4, respectively. Significant increases in NZS values were seen in the lower FSU and segment for lateral bending for all follower load comparisons. Significant differences were seen in NZS for axial rotation at the T4/T5, T8/T9, and T11/T12 levels, along with the lower segment.
Table 3. Mean (SD) Stiffness Values for Individual FSU Elastic Zone Stiffness and Neutral Zone Stiffness.
| FSU Level | Load Level | Lateral Bending | Flexion/Extension | Axial Rotation | Flexion | Extension | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
||
| T1/T2 | 0 N | 6.30 (3.54) |
3.05 (3.42) |
8.96 (10.3) |
1.20 (1.25) |
4.75 (1.71) |
1.59 (1.22) |
3.63 (2.81) |
1.23 (1.04) |
3.06 (1.63) |
1.18 (1.49) |
| 200 N | - | - | 4.76 (7.33) |
2.37 (2.77) |
5.31 (1.12) |
2.76 (2.63) |
1.18 (0.45) |
2.41 (1.80) |
3.21 (1.59) |
2.33 (4.14) |
|
| 400 N | - | - | 6.33 (9.64) |
2.26 (1.43) |
5.26 (1.92) |
3.43 (2.95) |
2.22 (2.19) |
3.14 (2.21)† |
3.29 (1.90) |
1.38 (0.75) |
|
| T4/T5 | 0 N | 8.71 (4.36) |
3.90 (1.73) |
19.6 (8.47) |
6.72 (3.92) |
7.84 (3.48) |
3.53 (2.44) |
7.92 (4.01) |
7.70 (3.83) |
- | 4.68 (3.27) |
| 200 N | - | - | 9.04 (3.57)* |
5.31 (3.32) |
11.3 (3.38)* |
4.74 (2.67) |
4.51 (1.99) |
7.01 (4.30) |
13.6 (5.39) |
3.62 (2.41) |
|
| 400 N | - | - | 11.1 (5.91)* |
4.13 (2.55) |
6.79 (2.05) |
5.77 (2.96) *† |
- | 5.39 (3.65) |
- | 2.86 (1.52) |
|
| T8/T9 | 0 N | 8.00 (3.57) |
2.92 (2.11) |
30.7 (35.8) |
7.22 (2.88) |
7.56 (3.59) |
1.72 (1.01) |
8.64 (3.43) |
10.6 (4.10) |
- | 3.82 (2.87) |
| 200 N | 5.26 (1.56) |
10.1 (2.4 0) |
43.8 (76.7) |
7.39 (3.67) |
5.63 (1.72) |
1.82 (1.04) |
6.95 (4.59) |
10.4 (4.22) |
14.7 (4.88) |
4.35 (3.21) |
|
| 400 N | - | - | 22.4 (14.4) |
8.21 (4.77) |
5.81 (2.56) |
2.37 (1.19)* |
8.83 (4.72) |
11.0 (5.90) |
- | 5.38 (3.87) |
|
| T11/T1 2 | 0 N | 3.81 (1.84) |
0.73 (0.47) |
9.88 (6.55) |
3.97 (3.58) |
4.87 (2.35) |
2.18 (1.03) |
7.31 (5.94) |
6.10 (5.66) |
8.07 (4.03) |
1.83 (1.70) |
| 200 N | 3.75 (1.79) |
1.99 (1.19)* |
8.23 (4.23) |
2.99 (2.02) |
5.71 (3.73) |
2.24 (0.98) |
7.43 (4.57) |
4.43 (3.02) |
6.84 (5.03) |
1.55 (1.20) |
|
| 400 N | 4.65 (4.78) |
5.19 (2.76)*† |
5.44 (3.31) |
3.06 (1.82) |
3.61 (0.93) |
3.06 (1.68)† |
5.41 (3.93) |
4.22 (2.66) |
5.47 (3.71) |
1.91 (1.60) |
|
denotes missing values due to less than five specimen contributing to the average value
denotes statistically significant values between 0-200 N and 0-400 N (p < .05)
denotes statistically significant values between 200-400 N (p<.05)
Table 4. Mean (SD) Stiffness Values for Segmental Elastic Zone Stiffness and Neutral Zone Stiffness.
| Segment | Load Level | Lateral Bending | Flexion/Extension | Axial Rotation | Flexion | Extension | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
EZS (Nm/°) |
NZS (Nm/°) |
||
| Upper (T1/T4) |
0 N | 4.11 (3.11) |
2.09 (2.36) |
2.71 (1.66) |
0.83 (0.83) |
3.13 (1.79) |
0.59 (0.36) |
2.55 (1.92) |
1.02 (1.05) |
2.88 (2.56) |
0.64 (0.69) |
| 200 N | 6.90 (3.75) |
5.50 (4.41) |
2.32 (2.48) |
0.81 (0.62) |
2.57 (1.05) |
1.30 (0.72) |
2.07 (3.43) |
1.15 (0.89) |
2.57 (1.66) |
0.48 (0.36) |
|
| 400 N | 6.85 (2.09) |
5.66 (3.84) |
2.29 (1.75) |
1.05 (0.62)† |
3.28 (3.60) |
2.94 (4.42) |
1.62 (1.59) |
1.43 (0.84)† |
2.96 (2.11) |
0.66 (0.43)† |
|
| Middle (T4/T8) |
0 N | 4.98 (4.12) |
1.19 (0.74) |
9.91 (8.98) |
2.41 (1.58) |
2.43 (0.89) |
0.92 (0.59) |
4.17 (3.55) |
3.41 (2.34) |
6.83 (4.67) |
1.41 (0.86) |
| 200 N | 5.48 (3.43) |
8.13 (6.05) |
6.08 (5.12) |
2.80 (2.82) |
3.08 (2.18) |
2.19 (2.95) |
3.50 (3.41) |
3.91 (4.22) |
6.44 (4.14) |
1.69 (1.45) |
|
| 400 N | 8.30 (5.50) |
- | 4.74 (4.10)* |
3.27 (3.91) |
4.51 (6.13) |
2.04 (2.49) |
4.69 (5.63) |
2.55 (1.27) |
4.79 (3.40) |
2.73 (4.09) |
|
| Lower (T8/T12) |
0 N | 1.91 (0.62) |
0.35 (0.16) |
18.5 (40.5) |
1.97 (1.73) |
1.61 (0.50) |
0.47 (0.33) |
3.19 (3.63) |
3.12 (2.84) |
6.88 (5.78) |
0.82 (0.68) |
| 200 N | 1.70 (0.58) |
1.20 (0.60)* |
9.88 (17.0) |
1.58 (1.26) |
1.66 (0.52) |
0.49 (0.31) |
3.26 (3.61) |
2.43 (2.03) |
4.31 (3.43) |
0.72 (0.55) |
|
| 400 N | 2.87 (4.72) |
3.10 (1.25*† |
2.97 (2.23) |
1.79 (1.72) |
2.31 (2.89) |
0.59 (0.29)* |
2.22 (1.73) |
2.78 (3.15) |
3.72 (3.35)* |
0.80 (0.60) |
|
denotes missing values due to less than five specimen contributing to the average value
denotes statistically significant values between 0-200 N and 0-400 N (p < .05)
denotes statistically significant values between 200-400 N (p<.05)
Statistical significance was found for NZ at the T1/T2 level for lateral bending ROM, for both load comparisons. Very little significance was found in EZS for any mode of bending, and the significance seen appeared randomly. Significance was seen at every segment for flexion ROM for at least one follower load comparison.
4. Discussion
As hypothesized, lateral bending ROM significantly decreased for segments and FSUs with an increase in follower load. However, significant results for ROM were not consistent in segments and FSUs for axial rotation and flexion/extension. Also as hypothesized, various FSUs in axial rotation had a significant increase in NZS with an increase in follower load, while stiffness values in other modes of bending produced inconsistent results.
4.1 Range of Motion and Neutral Zone
The results of this study show that there was an effect on range of motion and stiffness in some modes of bending with a follower load, which is consistent with previous research that a follower preload is seen to have an effect on the loading capabilities of the spine. Although no rib cage was used, the 2004 thoracolumbar study by Stanley et al. relates closely with the overarching goals of this research, permitting the next logical progression to be application of a follower load in the thoracic section of the spine (Stanley et al., 2004).
Direct comparisons between this study and past research were not possible, as no other studies have examined the same parameters at these anatomical levels with an intact rib cage and a follower preload. However, some trend comparisons can still be drawn between this study and others. In the study by Stanley et al., there was a decrease in ROM with a follower load for T2-T11 in flexion-extension, which is similar to the trend seen in the present study. Figure 4 clearly demonstrates this trend of decreasing overall combined range of motion with an increase in follower load, although not all ROM values were statistically significant. The absence of a significant difference could be because of the limited flexibility inherent in the thoracic section of the spine due to the presence of the rib cage, mechanics of the facets, and the overlapping spinous processes (Kurtz et al., 2005). Oda et al. has reported on ROM and NZ values for the canine thoracic spine with intact rib cage from T5-T8, relating most closely with the middle segment (T4-T8) tested in the current study with no follower load (Oda et al., 1996). The same trend of average NZ values is seen in both studies, with lateral bending having the largest NZ and flexion/extension having the smallest NZ.
The significant differences found in the NZ measurements, particularly in lateral bending, are interesting, as NZ relates to the laxity of the specimen. Other research in this area has been inconclusive when looking for a significant decrease in NZ, however, it was seen at quite a few levels in multiple modes of bending in the current study (Mannen et al., 2015). Panjabi indicated that an increase in NZ relates to an increase in pain, forcing the spine to overcompensate with increased activation of muscles and other internal stiffening methods (Panjabi, 2003). Because of this pain relationship and the mechanical impact it has on the body, the significant impact of follower load on NZ is important to note.
4.2 Neutral Zone Stiffness and Elastic Zone Stiffness
Because stability holds importance in the clinical community, biomechanical test methods that effect stability should be considered. Pope has described instability in the spine as a loss of stiffness (Pope et al., 1985). While stability was not measured in this study, the relationship between stability and the stiffness parameters can be used to draw some conclusions about the importance of calculating stiffness. Based on the definition from Pope et al., the various significant increases in NZS for some FSUs in lateral bending and axial rotation with a follower load could be indicative of an increase in mechanical stability. This implies that application of a follower load is important when assessing stability in spine testing.
More significant increases in stiffness are most likely not present due to the large influence that the rib cage itself has on thoracic stiffness (White et al., 1990). Various researchers have reported on the significant decrease in overall stiffness that is seen with and without a rib cage (Watkins et al., 2005; Mannen et al., 2015). Future work should be performed to further address this relationship of stiffness with and without the rib cage in tandem with the follower load used in the current study.
Some individual EZS and NZS values were much larger than others found within the same category, causing a high standard deviation. The variance in data seen at a particular level is the result of some specimens having much different magnitudes of stiffness compared to the mean. Having variations between specimens is not unusual in this type of testing.
4.3 Limitations
While there is not currently a standard procedure for applying a follower load in the thoracic section with the rib cage intact, this study successfully demonstrated that the technique can be applied in this context. With the presence of the rib cage, some of the instrumentation utilized in the protocols of the previous studies, such as the U-shaped mounts enveloping every vertebra, was not feasible because of lack of physical space in which to access the vertebral bodies. The methods employed in this study involved reasonable alterations of the previously used method by Patwardhan et al (Patwardhan et al., 1999). Use of a six degree of freedom load cell and the ball joint rod ends in the test setup, as well as performing analysis on any possible differences in sagittal tilt, provide sufficient validation that the follower load was applied appropriately.
In previous literature, follower load levels have varied based on the spinal section being studied. A 250 N load limit has been applied to the cervical spine, an 800 N limit applied to the thoracolumbar spine, and a 1200 N limit applied to the lumbar spine (Patwardhan et al., 1999; Patwardhan et al., 2000, Stanley et al., 2004). One FE model study applied loads as high as 2700 N in the lumbar spine when simulating the Patwardhan follower load method (Shirazi-Adl et al., 2006). Using the more conservative limits from the Patwardhan cadaveric studies, a follower load of 400 N was chosen for the thoracic spine in this study, applied in increments of 200 N. The loading was completed in increments to simulate the range of minimal to moderate muscle effort (Patwardhan et al., 2000). All specimens sustained a 400 N compressive follower preload without noticeable tissue damage. The discrepancy between the 400 N load level in this study compared to the 800 N load level in Stanley's thoracolumbar study without the rib cage should be researched further. This could be completed by repeating the current study's methodology with the rib cage removed, in order to better mimic the Stanley study.
The majority of research exploring the follower load technique focuses on measuring parameters in flexion/extension only. However, Renner et al. has performed initial validation research on all three modes of bending for the lumbar spine (Renner et al., 2007). The finite element model generated and proved by this research group for the lumbar spine allows the opportunity for translation of all three modes of bending in the thoracic spine, as well. Because of this initial validation and for the sake of comparisons with other studies, all three modes of bending are presented in this study, with the understanding that more work needs to further explore the efficacy of this loading technique with lateral bending and axial rotation.
As in common with experimental testing, issues such as out-of-bound sensors and low motion values occurred in this study. Exclusion criteria were generated for range of motion and stiffness values, and applied to the resultant data. Due to these exclusions, various levels at some loads had less than five specimen contributing to the average value. Data gathered from these levels was not presented because of this small sample size, and are notated by a dash in the data tables.
It is important to understand the biomechanical behavior of individual levels and segments of the thoracic spine because of the large incidence rates of vertebral fractures occurring in the middle and lower thoracic sections, frequently occurring with little or no trauma (Cooper et al., 1992). Findings in previous in vitro research have centered on the analysis of individual FSUs (Wilke et al., 1998). This trend is due to the clinical relevance of FSUs in patient diagnosis and invasive treatment, as back pain and diseases are typically attributed to disc and facet issues at a specific vertebral level. Conversely, typical in vivo human motion research focuses on segmental analysis because of the desire for examining motion patterns in separate sections of the overall spine (Menegoni et al., 2008). Segmental analysis is a clinically relevant ideology and is as beneficial and translatable to patient treatment as the commonly used FSU analysis. Because of the desire to normalize the two fields of cadaveric and human motion spine testing, future work should be done to compare values found in cadaveric spine studies to those found in human motion spine studies. Finding a relationship between these two testing methods could give significant insight into the field of spine testing.
It is noted that the distribution of force from the follower load is not identical to physiologic loading of the thoracic spine. In order to better mimic physiologic loading, different sections of the thoracic spine should ideally carry varying weights and the load levels based on a percentage of the body weight of the individual specimen. This study, however, presented a repeatable and reasonable loading method for the complicated thorax construct.
Application of a follower load with an intact rib cage does impact the motion and stiffness of the human cadaveric thoracic spine. Future work in this area should aim to include both a follower load and the intact rib cage in order to better represent the physiologic implications of human motion and improve clinically relevant biomechanical testing.
Acknowledgments
This study was supported by the National Institute on Aging (K99AG042458) and by a Mentored Career Development Award from the American Society for Bone and Mineral Research (DEA). The authors state that they have no conflict of interest to disclose. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors thank Nikki Galvis for her help in dissections and testing.
Footnotes
Conflict of Interest Statement: The authors stated that they have no conflict of interest to disclose.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson D, Mannen E, Sis H, Wong B, Cadel E, Friis E, Bouxsein M. Effects of follower load and rib cage on intervertebral disc pressure and sagittal plane curvature in static tests of cadaveric thoracic spines. Journal of Biomechanics. 2016 doi: 10.1016/j.jbiomech.2016.02.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brasiliense L, Lazaro B, Reyes P, Dogan S, Theodore N, Crawford N. Biomechanical contribution of the rib cage to thoracic stability. Spine. 2011;36:E1686–93. doi: 10.1097/BRS.0b013e318219ce84. [DOI] [PubMed] [Google Scholar]
- Cooper C, Atkinson E, MichaelO'Fallon W, Melton J. Incidence of clinically diagnosed vertebral fractures: a population-based study in Rochester, Minnesota, 1985-1989. Journal of Bone and Mineral Research 7. 1992 doi: 10.1002/jbmr.5650070214. [DOI] [PubMed] [Google Scholar]
- Kurtz S, Edidin A. Spine Technology Handbook. Elsevier; 2005. [Google Scholar]
- Mannen E, Anderson J, Arnold P, Friis E. Mechanical analysis of the human cadaveric thoracic spine with intact rib cage. Journal of Biomechanics. 2015;48:2060–2066. doi: 10.1016/j.jbiomech.2015.03.021. [DOI] [PubMed] [Google Scholar]
- Mannen E, Anderson J, Arnold P, Friis E. Mechanical contribution of the rib cage in the human thoracic cadaveric thoracic spine. Spine. 2015;40:1–7. doi: 10.1097/BRS.0000000000000879. [DOI] [PubMed] [Google Scholar]
- Mannen E, Ranu S, Villanueva A, Friis E. Validation of a novel spine test machine. Journal of Medical Devices. 2015;9 [Google Scholar]
- Menegoni F, Vismara L, Capodaglio P, Crivellini M, Galli M. Kinematics of trunk movements: protocol design and application in obese females. Journal of Applied Biomaterials and Biomechanics. 2008;6:178–185. [PubMed] [Google Scholar]
- Nakagawa S. A farewell to Bonferroni: the problems of low statistical power and publication bias. Behavioral Ecology. 2004;15:1044–1045. [Google Scholar]
- Oda I, Abumi K, Lu D, Shono Y, Kaneda K. Biomechanical role of the posterior elements, costovertebral joints, and rib cage in the stability of the thoracic spine. Spine. 1996;21:1423–1429. doi: 10.1097/00007632-199606150-00005. [DOI] [PubMed] [Google Scholar]
- Panjabi M. Clinical spinal instability and low back pain. Journal of Electromyography and Kinesiology. 2003;13:371–379. doi: 10.1016/s1050-6411(03)00044-0. [DOI] [PubMed] [Google Scholar]
- Patwardhan A, Havey R, Ghanayem A, Diener H, Meade K, Dunlap B, Hodges S. Load-carrying capacity of the human cervical spine in compression is increased under a follower load. Spine. 2000;25:1548–54. doi: 10.1097/00007632-200006150-00015. [DOI] [PubMed] [Google Scholar]
- Patwardhan A, Havey R, Meade K, Lee B, Dunlap B. A follower load increases the load-carrying capacity of the lumbar spine in compression. Spine. 1999;24:1003–9. doi: 10.1097/00007632-199905150-00014. [DOI] [PubMed] [Google Scholar]
- Perneger T. What's wrong with Bonferroni adjustments? British Medical Journal. 1998;316:1236–1238. doi: 10.1136/bmj.316.7139.1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pope M, Panjabi M. Biomechanical definitions of spinal instability. Spine. 1985;10:255–256. doi: 10.1097/00007632-198504000-00013. [DOI] [PubMed] [Google Scholar]
- Renner S, Natarajan R, Patwardhan A, Havey R, Voronov L, Guo B, Andersson G, An H. Novel model to analyze the effect of a large compressive follower pre-load on range of motion in a lumbar spine. Journal of Biomechanics. 2007;40:1326–1332. doi: 10.1016/j.jbiomech.2006.05.019. [DOI] [PubMed] [Google Scholar]
- Shirazi-Adl A. Analysis of large compression loads on lumbar spine in flexion and in torsion using a novel wrapping element. Journal of Biomechanics. 2006;39:276–275. doi: 10.1016/j.jbiomech.2004.11.022. [DOI] [PubMed] [Google Scholar]
- Shirazi-Adl A, Parnianpour M. Load-bearing and stress analysis of the human spine under a novel wrapping compression loading. Clinical Biomechanics. 2000;15:718–725. doi: 10.1016/s0268-0033(00)00045-0. [DOI] [PubMed] [Google Scholar]
- Stanley S, Ghanayem A, Voronov L, Havey R, Paxinos O, Carandang G, Zindrick M, Patwardhan A. Flexion-extension response of the thoracolumbar spine under compressive follower preload. Spine. 2004;29:E510–14. doi: 10.1097/01.brs.0000145417.94357.39. [DOI] [PubMed] [Google Scholar]
- Watkins RT, Watkins R, III, William L, Ahlbrand S, Garcia R, Karamanian A, Sharp L, Vo C, Hedman T. Stability provided by the sternum and rib cage in the thoracic spine. Spine. 2005;30:1283–6. doi: 10.1097/01.brs.0000164257.69354.bb. [DOI] [PubMed] [Google Scholar]
- White A, Panjabi M. Clinical Biomechanics of the Spine. Lippincott; 1990. [Google Scholar]
- Wilke H, Wenger K, Claes L. Testing criteria for spinal implants: recommendations for the standardization of in vitro stability testing of spinal implants. European Spine Journal. 1998;7:148–154. doi: 10.1007/s005860050045. [DOI] [PMC free article] [PubMed] [Google Scholar]


