Model‐Based Interspecies Scaling of Glucose Homeostasis

Abstract

Being able to scale preclinical pharmacodynamic response to clinical would be beneficial in drug development. In this work, the integrated glucose insulin (IGI) model, developed on clinical intravenous glucose tolerance test (IVGTT) data, describing dynamic glucose and insulin concentrations during glucose tolerance tests, was scaled to describe data from similar tests performed in healthy rats, mice, dogs, pigs, and humans. Several approaches to scaling the dynamic glucose and insulin were investigated. The theoretical allometric exponents of 0.75 and 1, for clearances and volumes, respectively, could describe the data well with some species‐specific adaptations: dogs and pigs showed slower first phase insulin secretion than expected from the scaling, pigs also showed more rapid insulin dependent glucose elimination, and rodents showed differences in glucose effectiveness. The resulting scaled IGI model was shown to accurately predict external preclinical IVGTT data and may be useful in facilitating translations of preclinical research into the clinic.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Interspecies scaling of pharmacokinetics has been shown to work well in many cases. Interspecies scaling of pharmacodynamics, such as glucose homeostasis, is not as thoroughly investigated.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ Glucose homeostasis during IVGTT can be scaled from human data to precinical species through a mathematical model.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ Allometric scaling of glucose homeostasis can predict preclinical glucose and insulin profiles well. Insulin sensitivity in healthy pigs is equal to human insulin sensitivity. Dogs and pigs show slower insulin secretion than expected based on size and rodents display different glucose effectiveness.

HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS

☑ The model enables translation of exposure response relationships from several preclinical species to the clinic.

One of the challenges in drug development is to translate preclinical results to the clinic and make useful predictions of the expected magnitude of the effect of an intervention. One reason for this is that preclinical studies often are underpowered, having too small sample size, and thereby not being able to reliably detect differences between groups with high enough probability.1 Mathematical models for the time‐course of response have been shown to allow several fold smaller sample size while maintaining the same power compared to conventional statistical analysis.2 In addition, mathematical models are useful tools in understanding complex relationships, such as glucose homeostasis.

The integrated glucose insulin (IGI) model is a mathematical model that describes dynamic glucose and insulin concentrations simultaneously in humans during glucose tolerance tests, with both i.v. and orally administered glucose.3, 4 The IGI model has been used in drug development to quantify drug effects and to optimize the design of clinical trials by making the trials richer in information.5, 6 The model consists of a glucose submodel with distribution and with elimination by two routes, an insulin‐dependent route and an insulin‐independent route. In the model, glucose concentrations above baseline inhibit endogenous glucose production and stimulate second‐phase insulin secretion. Insulin is described as having a basal secretion and first‐order elimination. After i.v. administration of glucose, rapid first‐phase secretion of insulin is triggered. A graphical representation of the model can be seen in Figure 1.4 The IGI model was developed on data from healthy volunteers and patients with type 2 diabetes (T2D).

Figure 1.

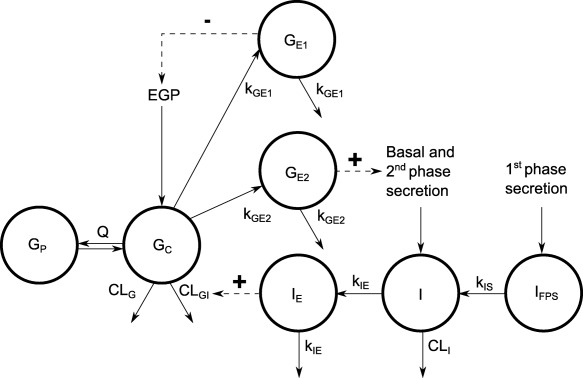
Schematic presentation of the IGI model. The model includes total glucose, insulin, regulation of glucose production, second‐phase insulin secretion, and glucose elimination. Full arrows indicate flows and broken arrows indicate control mechanisms. G_C and G_P, central and peripheral compartments of glucose; G_E1 and G_E2, effect compartments for control of glucose production and insulin secretion; I, insulin disposition compartment; I_FPS, delay compartment the first‐phase insulin secretion; I_E, effect compartment for control of glucose elimination; Q, CL_G, and CL_GI, clearance parameters of the glucose model; EGP, endogenous glucose production; CL_I and k_IS, parameters of the insulin model; k_GE1, k_GE2, and k_IE, rate constants of the effect compartments.4

The model behavior during a glucose tolerance test in preclinical species is currently unexplored. Hence, the objective of this work was to investigate if the model can be scaled to describe intravenous glucose tolerance test (IVGTT) data from several of the most commonly used preclinical species and to facilitate the usage of the model in bridging from the preclinical to the clinical phase of drug development.

METHODS

Allometric scaling

Many methods of scaling preclinical results between species exist. In the field of pharmacokinetics, allometric scaling has been widely used to scale pharmacokinetic parameters between different species. It is based on the observation that many physiological factors, such as basal metabolic rate and blood flow, are related to the body weight of the animal.7 The relationship is described by the allometric equation (Eq. 1):

$$Y=a\ast {WT}^b$$ (1)

where WT is the body weight, a is the intercept, and b is the slope of the regression line on the log‐log scale. The allometric equation is applied to scale a pharmacokinetic parameter determined in humans to another animal through (Eq. 2):

$$P_A=P_H\ast {\left(\frac{{WT}_A}{{WT}_H}\right)}^b$$ (2)

where P_A is the parameter value in the animal of interest, P_H is the parameter value in humans, WT_A is the weight of the animal, WT_H is the weight of humans (70 kg in this analysis), and b is the allometric exponent. It has been shown that the allometric exponent for clearance (CL) and volume (V) often takes the values 0.75 and 1, respectively. Rate constants (k) are calculated by (Eq. 3):

$$k=\frac{CL}{V}$$ (3)

Thus, the allometric exponent for rate constants is −0.25 (logarithmic rules apply and renders an exponent = 0.75–1) if the values of 0.75 and 1 for clearance (CL) and volume (V) are used.

During model development, the glucose and insulin baselines as well as the residual error were estimated for all species. All other parameters in the IGI model were fixed to the previously published values.4

In a first step of this analysis, allometric scaling based on total body weight was investigated. The most suitable value for the allometric exponent of clearances, volumes, and rate constants was investigated, based on objective function value, parameter uncertainty, and model complexity. All clearances, volumes, and rate constants were initially modeled together with one allometric exponent for each parameter type: clearance, volume, and rate constants. However, in the IGI model, there are a few parameters that are not defined as clearances, volumes, or rate constants. For example, the control mechanisms describing glucose inhibition of endogenous glucose production and glucose stimulation of insulin secretion are parametrized as power functions:

$$PROD={PROD}_0\ast {\left(\frac{G_E}{G_{SS}}\right)}^{\gamma }$$ (4)

where PROD is the glucose or insulin production, PROD ₀ is the production at baseline, G_E is the glucose concentration in blood with a time delay, G_SS is the glucose concentration at baseline, and γ controls the dependence on the delayed glucose concentration. To the best of our knowledge, there are no prior empirical studies that suggest how to scale exponents between species, hence, allometric scaling of these exponents were investigated as well. Another parameter that is not clearance, volume, or rate constant, is the first‐phase insulin secretion, which is described as an amount of insulin that enters the blood after administration of i.v. glucose. The allometric exponent for this parameter was investigated iteratively, estimating it together with clearance, volume, or rate constants, as well as estimating separately during this work. In the original publication of the IGI model, only a small range of doses were administered and, thus, a glucose dose‐independent first‐phase insulin secretion was estimated, which is also how the parameter was used in this work.

In a second step, scaling parameters with physiological factors (summarized in Table 2)8, 9, 10 relevant to a particular parameter was investigated. Insulin‐independent glucose clearance is, in part, mediated by the brain and was scaled with the brain weight of the different species. Muscle and fat express most of the insulin‐dependent glucose transporters in the body; hence, the insulin‐dependent glucose clearance was scaled with the muscle and fat weight of the animals. Insulin can be eliminated by the liver and kidneys, and, thus, insulin clearance was scaled with liver and kidney weight.11 Insulin volume was scaled with the plasma volume of the different animals. The first‐phase secretion of insulin was scaled with pancreas weight as well as the fraction of beta cells in the islets of Langerhans. The physiological scaling was performed by multiplying the body weight with the species‐specific weight‐related fractions of the organ/tissue weights, listed in Table 2,8, 9, 10 estimating the allometric exponent.

Table 2.

Summary of physiological relationships investigated in the different species

Parameter	Physiology	Dog	Human	Mouse	Pig	Rat
CLG	Brain weight (%)	0.80a	2.00a	1.70a	0.4b	0.60a
CLGI	Muscle weight (%)	45.70a	40.00a	38.40a	40b	40.40a
	Adipose weight (%)	15.00a	21.40a	7.00a	30b	7.00a
CLI	Liver weight (%)	3.30a	2.60a	5.50a	2.94b	3.40a
	Kidney weight (%)	0.50a	0.40a	1.70a	0.4b	0.70a
VI	Plasma volume (%)	5.15a	4.29a	5.00a	6b	3.12a
IFPS	Pancreas weight (%)	0.23a	0.14a	0.60a	0.14b	0.32a
	Beta cells (% of islet)	50c	54c	87c	54c	87c

CL_G, glucose clearance; CL_GI, insulin‐dependent glucose clearance; CL_I, insulin clearance; IFPS, insulin first phase secretion.

^aBrown et al., 1997⁸; ^bUpton et al., 2008⁹; ^cSteiner et al., 2010¹⁰.

In the third and last step, species‐specific adaptations, which could not be described by allometric scaling or physiological factors, were investigated.

Analysis data

The data included in the analysis was gathered from previously published studies,12, 13, 14, 15, 16, 17 in which IVGTTs were performed; the studies are summarized in Table 1, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and included data from dogs (n = 11), humans (n = 24), mice (n = 10), pigs (n = 11), and rats (n = 16). In the study performed in dogs and one of the human studies, a bolus dose of insulin was administered 20 minutes after the glucose dose; so‐called insulin‐modified IVGTT. The inclusion criteria for included studies were: healthy untreated glucose homeostasis, normal body weight, normal diet, IVGTT performed in a conscious state, repeated glucose and insulin concentrations sampled, and body weight recorded. Body weights range from 20 g to 70.3 kg from the lightest mouse to the heaviest human.

Table 1.

Summary of the study designs

Species	Subspecies	No.a	Mean BW kg (RSD%)	Glucose dose (g/kg)	Insulin dose (U/kg)	Reference
Analysis data, individual level
Dog	Mongrel	11	28.7 (9)	0.3	0.03 @ 20 min	15
Human	–	14	66.5 (10)	0.25–0.33	–	16
Human	–	10	70.0 (0)	0.33	0.03 @ 20 min	17
Mouse	C57BL6	10	0.03 (8)	1.0	–	12
Pig	Large white	11	21.6 (35)	0.5	–	14
Rat	Wistar	16	0.29 (7)	0.2, 0.5, 1.0	–	13
External validation data, summary level
Dog	Beagle	6	10b	0.5	–	22
Human	–	8	70b	0.3	–	21
Monkey	Cynomolgus	7	3.6	0.5	–	19
Pig	Ossabaw	7	29.4	0.5	–	20
Rat	Sprague Dawley	7	0.25b	1	–	19

BW, body weight; RSD, relative standard deviation.

^aNumber of individuals.

^bImputed weight.

External validation

To determine if the allometrically scaled model can describe data from other studies as well as for a species that the model has not been developed on, the mean and SDs of glucose and insulin concentrations from published IVGTT studies performed in dogs, humans, pigs, monkeys, and rats were digitalized.18, 19, 20, 21, 22 Mice were not included because no study that fulfilled the inclusion criteria and presented glucose and insulin profiles was found for this species, except the study used for data analysis.12 Dogs, pigs, and monkeys received an i.v. glucose dose of 0.5 g/kg, humans 0.3 g/kg, and rats 1 g/kg. The reported average body weight of pigs and monkeys were 29.4 kg and 3.6 kg, respectively. The body weight was not reported for dogs (Beagles), rats (Sprague Dawley), and humans. However, they were known to be lean, hence, 10 kg, 0.25 kg, and 70 kg were used in the simulations. Profiles for 1,000 subjects of each species were simulated using the reported glucose and insulin baseline with 10% and 25% interindividual variability, respectively. The mean glucose and insulin concentrations of the simulated individual subjects was calculated and overlaid on the digitalized reported summary measurements to assess model prediction accuracy.

Parameter estimation and model selection

Nonlinear mixed effects models were applied using NONMEM version 7.3 with the first‐order conditional estimation method and the differential equation solver ADVAN13.23 For dataset formatting and creation of goodness‐of‐fit plots, R version 3.1.0 was used.24 Simulations (including prediction corrected visual predictive checks (VPCs)25) were performed in NONMEM using PsN version 4.6.0. Model selection was primarily guided by simulation‐based diagnostics, such as VPCs to assess the models' predictive performance. Model selection was also guided by physiological plausibility, goodness‐of‐fit plots, parameter uncertainty, and changes in objective function value (OFV). A difference of at least 6.63 in OFV was considered statistically significant for hierarchical models with one parameter difference. This corresponds to a significance level of <0.01 when comparing nested models with one degree of freedom. Parameter uncertainty for the final model was obtained using sampling importance resampling.26

RESULTS

First, it was determined that scaling of the first‐phase insulin secretion using an exponent of 0.75, corresponding to allometric exponents of clearance, gave a better fit to the data compared to using an exponent of 1 (corresponding to volume). Figure 2 shows how the allometrically scaled IGI model describes the data using the empirical values of the allometric exponent: 0.75 for clearances, 1 for volumes, −0.25 for rate constants, the human value for the power functions of the control mechanisms (i.e., unscaled), and 0.75 for first‐phase insulin secretion. This initial approach show that rat insulin data are well described but rat glucose data is slightly underpredicted. Mouse glucose concentrations are underpredicted, whereas insulin concentrations are well described. The second‐phase insulin secretion for dogs is underpredicted as well as the peak concentration of the insulin dose, whereas glucose concentrations are overpredicted at glucose nadir. Pigs show severe overprediction of the first‐phase insulin secretion, whereas glucose concentrations seem to be well described. However, with a better description of pig insulin, glucose would be overpredicted.

Figure 2.

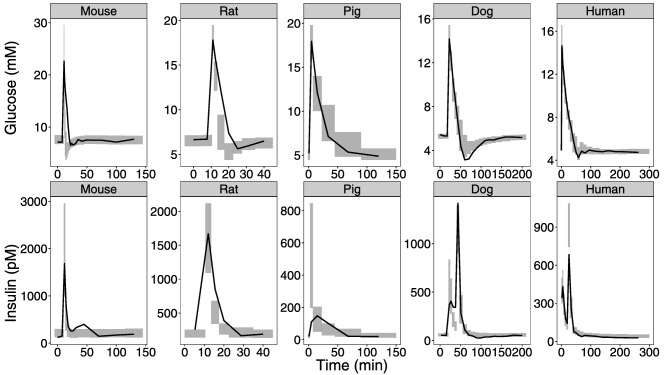
Internal model evaluation of basic allometric model. Visual predictive checks are shown comparing observations with simulated glucose and insulin data for the different species when the exponent for clearance and volume are set to the empirical values of 0.75 and 1. The solid line is the median based on the observed data. The shaded area is the 95% confidence interval around the median based on the simulated data.

Estimation of the allometric exponent gave a value of 0.89 for clearances, 0.92 for glucose volumes, 1.05 for insulin volumes, and −0.26 for rate constants. The estimation of an allometric exponent for the power functions of glucose effect on glucose production and insulin secretion (GPRG, IPRG) did not improve the fit and were only determined with high uncertainty. Thus, the values were kept fixed to the human values. There was no additional benefit of estimating a separate allometric exponent for first‐phase secretion; hence, it was estimated together with the exponent for clearances. None of the investigated scaling relationships with species‐specific organ weights improved the fit across all species and was, thus, not more predictive than using body weight alone.

When the allometric relationships had been determined, dogs showed slower first‐phase secretion than the model predicted and the corresponding parameter (k_IS) was estimated to be 0.093 min⁻¹ for dogs; 19% of the allometrically scaled value. Similarly, the pigs showed a later insulin peak than the model predicted and k_IS was estimated to be 0.085 min⁻¹ for pigs; 16% of the allometrically scaled value. When the rate constant of first‐phase secretion was estimated, there was no additional benefit of estimating the magnitude of the first‐phase secretion for dogs and pigs. This result can be interpreted as pigs and dogs having a slower release, however, it was the same weight‐adjusted amount of first‐phase insulin as the other included species. The model also predicted slower glucose elimination in pigs than indicated by data, and, therefore, insulin‐dependent glucose clearance (CL_GI) was estimated. The estimated value for pigs is almost three times higher than the allometrically scaled value, on par with the human value without scaling for body weight. It has been proposed that glucose effectiveness (insulin‐independent glucose disposal) is the major determinant of i.v. glucose tolerance in rodents.27, 28 To investigate this, a proportionality factor was estimated on CL_GI as well as the insulin‐independent glucose clearance (CL_G) for rodents. The estimated values for the factors on CL_GI and CL_G were 0.28 and 1.66, respectively. Upon estimating the proportionality factors for rodents, estimation of the allometric exponents became less important, and using the theoretical exponents with estimated proportionality factors gave an increase in OFV of 34.7 with two fewer estimated parameters. Although this is statistically significant, the simpler model that incorporates current knowledge of rodent glucose metabolism was considered preferable over the model with estimated exponents. Table 3 ⁴ displays the parameter values for the final allometrically scaled IGI model. Figure 3 shows an overall good description of the data for all the species using the final model compared to the naïve initial approach in Figure 2. With the final model, the return to glucose baseline for rat and mouse is better described as well as the first‐phase insulin secretion for dogs and the time‐course of insulin in pigs.

Table 3.

Final parameter estimates

Parameter	Unit	Typical value	RSE, %	IIV, %	RSE, %
Glucose baseline
Dog	mM	5.3	1	3.3	44
Human	mM	4.9	2	8.2	21
Mouse	mM	7.4	3	9.4	32
Pig	mM	5.1	4	12.2	49
Rat	mM	6.3	4	14.6	44
Insulin baseline
Dog	pM	50.4	10	31.8	40
Human	pM	39.2	14	66.5	17
Mouse	pM	188.2	11	28.8	50
Pig	pM	15.1	13	30.1	96
Rat	pM	184.7	13	47	39
Insulin
CLI	L/min	1.22	–	29	–
VI	L	6.09	–	41	–
IFPS	mU	704	–	67	–
kIS	min−1	0.384	–	–	–
kIE	min−1	0.0213	–	58	–
IPRG	–	1.42	–	35	–
Glucose
VG	L	9.33	–	30	–
VP	L	8.56	–	30	–
CLGI	(L/min)/(mU/L)	0.00829	–	53	–
CLG	L/min	0.0894	–	59	–
Q	L/min	0.442	–	85	–
kGE1	min−1	0.0573	–	–	–
kGE2	min−1	0.0289	–	85	–
GPRG	–	−2.79	–	–	–
Species specific
kis, Dog	min−1	0.0931	23	–	–
kIS, Pig	min−1	0.0845	16	–	–
CLG factorrodent	–	1.66	16
CLGI factorrodent	–	0.28	18
CLGI, Pig	L/min/(mU/L)	0.0078	12	53	–
Correlations
CorrVG‐Q	–	−0.75	–	–	–
CorrVG‐VI	–	0.71	–	–	–
CorrQ‐VI	–	−0.35	–	–	–
Residual error insulin
Dog	%	34	19	–	–
Human	%	26	9	–	–
Mouse	%	52	11	–	–
Pig	%	60	12	–	–
Rat	%	28.4	9	–	–
Residual error glucose
Dog	%	5	14	–	–
Human	%	4	6	–	–
Mouse	%	11	6	–	–
Pig	%	7	15	–	–
Rat	%	8	11	–	–
Early residual error a
Dog	–	1.24	72	–	–
Human	–	3.6	10	–	–
Mouse	–	1.35	12	–	–
Rat	–	0.4	14	–	–

Parameters: b_CL, allometric exponent for clearances; b_{V, glu}, allometric exponent for glucose volumes; b_{V, ins}, allometric exponent for insulin volume; b_K, allometric exponent for rate constants; CL_GI, insulin‐dependent glucose clearance; CL_G, insulin‐independent glucose; CL_I, insulin clearance; GPRG, shape of glucose inhibition on glucose production; IFPS, insulin first‐phase secretion; IIV, interindividual variability in percent; IPRG, shape of glucose stimulation of insulin secretion; k_GE1, rate constant for the glucose effect compartment of glucose inhibition on glucose production; k_GE2, rate constant for the glucose effect compartment of glucose stimulation of insulin secretion; k_IE, rate constant for insulin effect on glucose clearance; k_IS, rate constant for first phase secretion; Q, inter‐compartmental clearance; RSE, relative standard error; V_G, central volume of glucose distribution; V_I, insulin volume; V_P, peripheral volume of glucose distribution.

Estimated parameters are in bold, other parameters are fixed to the human values obtained by Silber et al.4

^aMultiplying factor for a time‐varying difference in the residual error between early (0–2 minutes) and late (>2 minutes) time‐points as described by Silber et al.4

Figure 3.

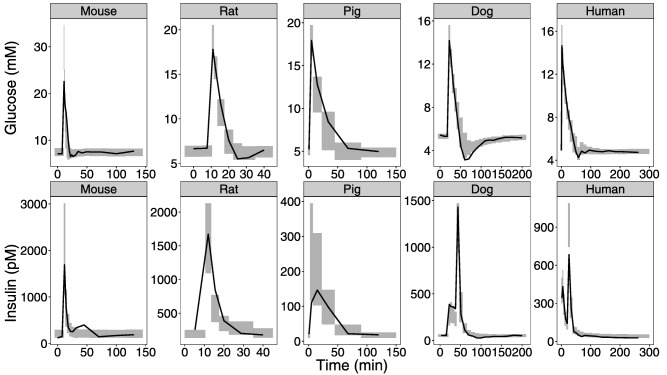
Internal model evaluation final model. Visual predictive checks are shown comparing observations with simulated glucose and insulin data for the different species for the final model. The solid line is the median based on the observed data. The shaded area is the 95% confidence interval around the median based on the simulated data.

In addition, dose‐dependent first‐phase secretion was investigated on the rat data because these animals received glucose doses of 0.2, 0.5, and 1.0 g/kg. However, applying a fully flexible model with 1 parameter for each glucose dose only reduced OFV of −1.3, which was not significant. Thus, a dose‐dependent first‐phase secretion model would not perform better and further investigations were stopped. A VPC of the final model (not including dose‐response of first‐phase secretion of insulin) on the rat data stratified the on glucose dose can be seen in Supplementary Figure S1. The inability to describe a dose‐dependent first‐phase secretion is most likely related to lack of data to support such estimation; a statement supported by the high uncertainty of the predictions can be seen in Supplementary Figure S1.

As a final step, simulation of published IVGTT studies in dogs, humans, monkeys, pig, and rats (Figure 4) show that the proposed model as well as the naïve initial approach using basic allometric scaling of the IGI model can predict glucose and insulin concentrations in other studies of the investigated species as well as in one other species than the model was developed on.

Figure 4.

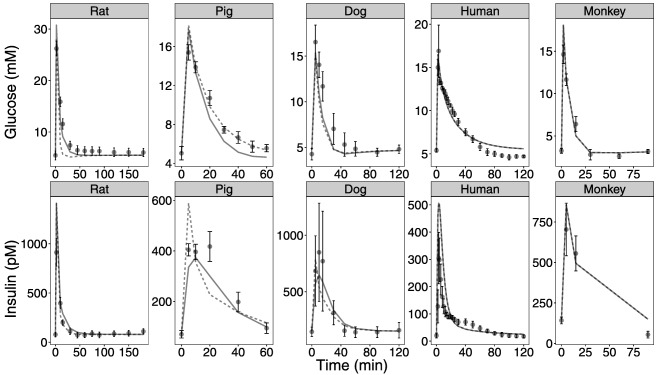
External model evaluation of basic allometric and final model. Simulations of published intravenous glucose tolerance test studies in rats, pigs, dogs, humans, and monkeys. The black dots and error bars are the observed means and SDs. Lines are the mean of 1,000 simulated animals. The dashed and solid lines are simulated mean of the model without species adaptations and the final developed model, including species adaptations, respectively.

DISCUSSION

The herein developed scaling approach of an integrated glucose insulin model was able to accurately describe the glucose and insulin concentrations after IVGTT in humans and of several preclinical species, including dogs, mice, monkeys, pigs, and rats.

Allometric scaling of pharmacodynamic (PD) response has previously been investigated by Zuideveld et al.29 for 5‐HTtA1 receptor‐mediated response. Scaling was performed from rat to human and the authors conclude that “allometrically scaled mechanism based PK‐PD models are promising as a means of predicting the pharmacodynamic responses in man.” In this paper, yet another example is presented of successful scaling of PD using a mechanism‐based model in another therapeutic area and the scaling was performed for several animal species.

In general, glucose scales better than insulin‐based on goodness‐of‐fit plots (see Supplementary Figures S2–S5). As insulin is a protein and a large molecule, the kinetics are more complex and the amino acid sequences are not identical in the different species.30 Additionally, we have assumed in the modeling that exogenously administered insulin (for dogs and one human study15, 17) can be kinetically described as endogenous insulin, which is not necessarily true. Exogenous administration of insulin may give rise to different ratios of peripheral to hepatic insulin that may lead to different overall uptake of glucose. In the current work, total insulin was measured not discriminating between exogenous and endogenous insulin. Consequently, the effect of total insulin was investigated assuming the same effect of exogenous and endogenous insulin. However, the impact of this assumption may be minor as no difference on glucose disposal between exogenous and endogenous insulin was seen in previous work with the IGI model.32

Allometric exponents of parameters related to parameters other than clearance, volume and rate constants were investigated. The first‐phase secretion of insulin was shown to scale better with an allometric exponent closer to 0.75 than 1, which supports the observation that metabolic processes typically scale well with an allometric exponent of 0.75.7 The exponents of the control mechanisms (IPRG and GPRG) were shown not to improve with allometric scaling, indicating that the dependence of glucose concentration in relation to the baseline for control mechanisms is independent of species and weight. Whether this is related to an inability to estimate such parameter based on the data or indeed a way to scale control mechanisms remains to be further investigated.

First‐phase secretion was estimated to be slower for pigs and dogs. Insulin secretion might be expected to be different for species depending on their natural diet being high or low in carbohydrates. To avoid variability related to this, only omnivores with similar diet to humans were selected in this study. Despite this, differences were present. The first‐phase insulin secretion is only present in IVGTT study designs, and the unusually high glucose concentrations resulting from the challenge may highlight species differences, although only omnivores were investigated. The importance of accurately predicting first‐phase insulin secretion may also be questioned. In oral glucose tolerance tests (OGTTs) or meal tolerances tests, much more commonly used in drug development, first‐phase secretion of insulin is not present.

Pigs showed a three times higher insulin‐dependent glucose clearance than the allometrically scaled value. Pigs are widely used in preclinical research due to their phenotypic similarities with humans.31 This analysis indicates that the size of healthy pigs should not be considered when performing extrapolations of insulin sensitivity to humans, but rather as a one‐to‐one comparison. Using pigs for experiments with s.c. injections of insulin have not been investigated in this work and the absorption profile of insulin from the subcutaneous tissue may well be better predicted by pigs than rodents, given the difference between the species in subcutaneous fat. For this setting, pig skin is more similar to human skin than any other species. Other aspects of human glucose homeostasis, such as glucose absorption from the intestine and the incretin effect, might be better predicted through pigs than rodents. This, however, was not investigated with the IVGTT designs in the current work.

Several different analytical assays have been used when analyzing glucose and insulin concentrations in the included experiments. The assays have different precision and accuracy, which will affect our modeling results. To handle this in the model, the residual variability and the baseline glucose and insulin concentrations were estimated. Species‐specific residual variability will handle any difference in precision between studies, whereas species‐specific baselines will handle any systematic bias in glucose and insulin concentrations because it sets the system on the appropriate concentration scale from the start. Thus, we do not believe this difference in assays will affect our conclusions. However, insulin data are highly variable, about five times more variable than glucose in this analysis. The high variability of insulin and the small number of dogs and pigs in this analysis may influence the finding that the first‐phase secretion is slower in these species.

The wide distribution in body weights from mice to humans gives good support for accurate estimation of the allometric exponents, which is reflected in the low uncertainty of a few percentages in the parameter estimates of the allometric exponents. The estimated compared to the theoretical exponents mainly influence mice and rats because they are furthest away from humans in body weight, however, adjusting for higher glucose effectiveness in rodents gave a similar fit as estimating the exponents.

The IGI model was developed on IVGTT data with only one dose of glucose (0.3 g/kg), hence, no dose‐response relationship could be included. Supplementary Figure S1 shows how the model describes the dose‐response in rats without dose‐dependent first‐phase secretion. Overall, the observed median falls within the simulated confidence interval. However, the confidence intervals are wide due to the few numbers of rats in each dose group 2, 10, and 4 rats in the 0.2, 0.5, and 1 g/kg dose groups, respectively. The prolonged insulin secretion that is seen for the highest dose group may be an experimental artifact because of the few numbers of rats, because the mice that also were given 1 g/kg of glucose have a much steeper declining insulin profile.

Allometric scaling of the IGI model using both the theoretical values without species adaptations as well as the final model with species adaptations were shown to describe the external validation data well. In the original publication of the IGI model, the data were well described.4 However, in our external validation, the misspecification in the different species, including humans on whom the IGI model was developed, are of equal magnitude; indicating that inter‐study variability is a large determinant of variability in IVGTT experiments. One aspect of this is that different subspecies were used in the external validation data compared with the analysis data, Sprague Dawley vs. Wistar rats, Beagles vs. Mongrel dogs, and Ossabaw vs. Large white pigs. The insulin profiles in the external validation data show prolonged insulin secretion for dogs and pigs, supporting the finding that insulin secretion deviates from allometry in these species. Monkeys are phenotypically closest to humans, of the species included in the current study, and should be the species that scales most accurately.

An underlying assumption in this analysis is that the structural model is the same and that size can describe most of the differences seen in IVGTT between the different species. It has been proposed that insulin‐independent glucose disposal is the major determinant of glucose tolerance in rodents.27, 28 This was corroborated in our analysis where CL_G and CL_GI for rodents were estimated to be 166% and 28% of the allometrically scaled values, respectively; changing the ratio between the 2 pathways by a factor of 6. However, even with these estimates, insulin‐dependent elimination will still be a substantial part of the total glucose disposal during an IVGTT. Insulin‐independent glucose disposal or glucose effectiveness includes apart from the insulin‐independent glucose elimination also glucose inhibition of endogenous glucose production. The IGI model was developed on a rich dataset containing radiolabeled glucose. This facilitated the simultaneous estimation of elimination and inhibited production of glucose. In the current dataset, radiolabeled glucose was not available, hence, the inhibition of endogenous glucose production was assumed to be the same as humans to facilitate estimation of the rodent factors on clearance.

When investigating animal models of diabetes, it is of most importance that glucose scales well, because insulin secretion and regulation often is diminished to mimic diabetes. In this work, only healthy animals were included, however, it would be possible to extend this work to diabetic animals because the IGI model has a set of parameters for patients with T2D. One issue with applying the model to diabetic animals is the heterogeneity in the data related to differences in disease induction methods and varying degree of insulin‐resistance between animal models. This might be resolved by estimating the CL_GI as a strain/animal model‐specific parameter. This parameter is the parameter that corresponds best to insulin sensitivity. Another factor to consider is that patients with T2D most often are obese, which might have implications on allometric scaling by body weight. Other size descriptors, such as lean body weight, might be more appropriate.33 [Correction made here after initial online publication.] Another extension of this work is to include preclinical data from OGTTs to investigate if the model scales well also for oral glucose provocations. Investigation whether the oral absorption of glucose and the incretin effect can be scaled between species would be of interest. In this work, we have shown that the basic principles of allometric scaling can be applied to a complex homeostatic system to facilitate translational scaling between species. A useful application would be to determine the effect of drugs during an OGTT in animals with T2D and scale those results to humans. How drug effects can be applied in the IGI model has been described previously.5, 31, 32 An approach to translate from animal to humans would be to first characterize an half‐maximal effective concentration (EC₅₀) in vitro‐in vivo correlation for a set of substances of a new drug class in the animals tested and apply the in vitro‐in vivo correlation on human in vitro EC₅₀ to render human in vivo EC₅₀ to be used in the predictions. This approach will, however, assume that the maximum effect of the drug is the same in the species. Additionally, species‐specific protein binding may be needed in the translation.

In conclusion, the allometrically scaled IGI model developed in this project can accurately predict preclinical IVGTT data in many different species. The allometrically scaled IGI model may be used in drug development to facilitate better translations of preclinical research into the clinic.

Conflict of Interest

The authors declared no conflict of interest.

Author Contributions

O.A. and M.K.J. wrote the manuscript. O.A., M.K.J., and M.K. designed the research. O.A., M.K.J., and M.K. performed the research. O.A. analyzed the data.

Supporting information

Supplementary Figure S1 Glucose observations plotted against population and individual predictions, stratified on species. Red line is a smooth, black line is the line of identity.

Supplementary Figure S2 Insulin observations plotted against population and individual predictions, stratified on species. Red line is a smooth, black line is the line of identity.

Supplementary Figure S3 Conditional weighted residuals for glucose plotted against time, stratified on species. Red line is a smooth.

Supplementary Figure S4 Conditional weighted residuals for insulin plotted against time, stratified on species. Red line is a smooth.

Supplementary Figure S5 Visual predictive check for rats illustrating the predictive performance of the developed model across glucose doses. Gray line is the median of the data, and the blue line is the median of 1,000 simulated rats.

Run265b.mod

Modelfile – contains the code of the model file. No title.